Investigations on Dynamical Stability in 3D Quadrupole Ion Traps
Abstract
1. Introduction
Investigations on Classical and Quantum Dynamics Using Ion Traps
2. Analytical Model
2.1. Dynamical Stability for Two Coupled Oscillators in a Radiofrequency Trap
2.2. Solutions of Coupled System of Equations
3. Dynamic Stability for Two Oscillators Levitated in a RF Trap
3.1. System Hamiltonian Hessian Matrix Approach
3.2. Solutions of the Equations of Motion for the Two Oscillator System
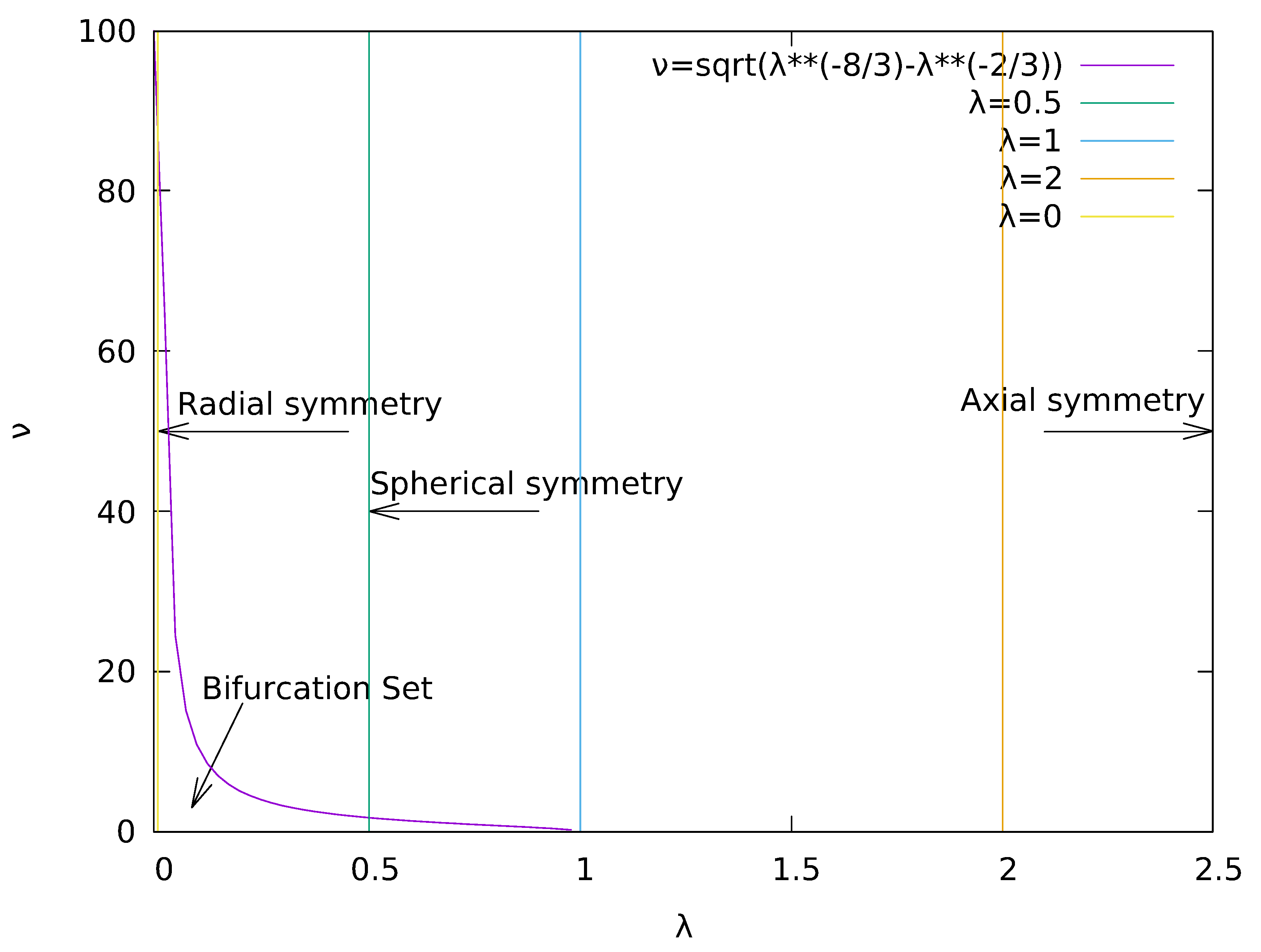
3.3. Critical Points. Discussion.
4. Quantum Stability and Ordered Structures for Many-Body Systems of Trapped Ions
5. Hamiltonians for Systems of N Ions
6. Highlights
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 3D | 3 Dimensional |
| CM | Centre of Mass |
| LIT | Linear Ion Trap |
| QED | Quantum Electrodynamics |
| QIP | Quantum Information Processing |
| QIT | Quadrupole Ion Trap |
| RF | Radiofrequency |
| SCCS | Strongly Coupled Coulomb Systems |
| SET | Surface Electrode Trap |
Appendix A. Interaction Potential, Electric Potential of The Trap
Appendix B. Dynamical Stability
Appendix C. Quantum Stability
References
- Major, F.G.; Gheorghe, V.N.; Werth, G. Charged Particle Traps: Physics and Techniques of Charged Particle Field Confinement. In Springer Series on Atomic, Optical and Plasma Physics; Springer: Berlin/Heidelberg, Germany, 2005; Volume 37. [Google Scholar] [CrossRef]
- Quint, W.; Vogel, M. (Eds.) Fundamental Physics in Particle Traps; Springer Tracts in Modern Physics; Springer: Berlin/Heidelberg, Germany, 2014; Volume 256. [Google Scholar] [CrossRef]
- Wineland, D.J.; Leibfried, D. Quantum information processing and metrology with trapped ions. Laser Phys. Lett. 2011, 8, 175–188. [Google Scholar] [CrossRef]
- Sinclair, A. An Introduction to Trapped Ions, Scalability and Quantum Metrology. In Quantum Information and Coherence; Andersson, E., Öhberg, P., Eds.; Scottish Graduate Series; Springer: Berlin/Heidelberg, Germany, 2011; Volume 67, pp. 211–246. [Google Scholar] [CrossRef]
- Wineland, D.J. Nobel Lecture: Superposition, entanglement, and raising Schrödinger’s cat. Rev. Mod. Phys. 2013, 85, 1103–1114. [Google Scholar] [CrossRef]
- Bruzewicz, C.D.; Chiaverini, J.; McConnell, R.; Sage, J.M. Trapped-ion quantum computing: Progress and challenges. Appl. Phys. Rev. 2019, 6, 021314. [Google Scholar] [CrossRef]
- Micke, P.; Stark, J.; King, S.A.; Leopold, T.; Pfeifer, T.; Schmöger, L.; Schwarz, M.; Spieß, L.J.; Schmidt, P.O.; Crespo López-Urrutia, J.R. Closed-cycle, low-vibration 4 K cryostat for ion traps and other applications. Rev. Sci. Instrum. 2019, 90, 065104. [Google Scholar] [CrossRef]
- Burt, E.A.; Prestage, J.D.; Tjoelker, R.L.; Enzer, D.G.; Kuang, D.; Murphy, D.W.; Robison, D.E.; Seubert, J.M.; Wang, R.T.; Ely, T.A. The Deep Space Atomic Clock: The first demonstration of a trapped ion atomic clock in space. Nat. Portf. 2020. [Google Scholar] [CrossRef]
- Safronova, M.S.; Budker, D.; DeMille, D.; Kimball, D.F.J.; Derevianko, A.; Clark, C.W. Search for new physics with atoms and molecules. Rev. Mod. Phys. 2018, 90, 025008. [Google Scholar] [CrossRef]
- Warring, U.; Hakelberg, F.; Kiefer, P.; Wittemer, M.; Schaetz, T. Trapped Ion Architecture for Multi-Dimensional Quantum Simulations. Adv. Quantum Technol. 2020, 3, 1900137. [Google Scholar] [CrossRef]
- Stoican, O.; Mihalcea, B.M.; Gheorghe, V. Miniaturized trapping setup with variable frequency. Rom. Rep. Phys. 2001, 53, 275–280. Available online: http://www.rrp.infim.ro/archive/RRP-3-8-2001-transa-3-attachments_2011_05_06/art28.pdf (accessed on 24 March 2021).
- Conangla, G.P.; Nwaigwe, D.; Wehr, J.; Rica, R.A. Overdamped dynamics of a Brownian particle levitated in a Paul trap. Phys. Rev. A 2020, 101, 053823. [Google Scholar] [CrossRef]
- Dodonov, V.V.; Man’ko, V.I.; Rosa, L. Quantum singular oscillator as a model of a two-ion trap: An amplification of transition probabilities due to small-time variations of the binding potential. Phys. Rev. A 1998, 57, 2851–2858. [Google Scholar] [CrossRef]
- Mihalcea, B.M. A quantum parametric oscillator in a radiofrequency trap. Phys. Scr. 2009, T135, 014006. [Google Scholar] [CrossRef]
- Mihalcea, B.M. Nonlinear harmonic boson oscillator. Phys. Scr. 2010, T140, 014056. [Google Scholar] [CrossRef]
- Blümel, R.; Kappler, C.; Quint, W.; Walther, H. Chaos and order of laser-cooled ions in a Paul trap. Phys. Rev. A 1989, 40, 808–823. [Google Scholar] [CrossRef] [PubMed]
- Moore, M.; Blümel, R. Quantum manifestations of order and chaos in the Paul trap. Phys. Rev. A 1993, 48, 3082–3091. [Google Scholar] [CrossRef] [PubMed]
- Farrelly, D.; Howard, J.E. Double-well dynamics of two ions in the Paul and Penning traps. Phys. Rev. A 1994, 49, 1494–1497. [Google Scholar] [CrossRef] [PubMed]
- Blümel, R.; Bonneville, E.; Carmichael, A. Chaos and bifurcations in ion traps of cylindrical and spherical design. Phys. Rev. E 1998, 57, 1511–1518. [Google Scholar] [CrossRef]
- Walz, J.; Siemers, I.; Schubert, M.; Neuhauser, W.; Blatt, R.; Teloy, E. Ion storage in the rf octupole trap. Phys. Rev. A 1994, 50, 4122–4132. [Google Scholar] [CrossRef]
- Mihalcea, B.M.; Niculae, C.M.; Gheorghe, V.N. On the Multipolar Electromagnetic Traps. Rom. J. Phys. 1999, 44, 543–550. [Google Scholar]
- Gheorghe, V.N.; Werth, G. Quasienergy states of trapped ions. Eur. Phys. J. D 2000, 10, 197–203. [Google Scholar] [CrossRef]
- Mihalcea, B.; Filinov, V.; Syrovatka, R.; Vasilyak, L. The Physics and Applications of Strongly Coupled Plasmas Levitated in Electrodynamic Traps. arXiv 2019, arXiv:1910.14320. [Google Scholar]
- Menicucci, N.C.; Milburn, G.J. Single trapped ion as a time-dependent harmonic oscillator. Phys. Rev. A 2007, 76, 052105. [Google Scholar] [CrossRef]
- Mihalcea, B.M.; Vişan, G.G. Nonlinear ion trap stability analysis. Phys. Scr. 2010, T140, 014057. [Google Scholar] [CrossRef]
- Akerman, N.; Kotler, S.; Glickman, Y.; Dallal, Y.; Keselman, A.; Ozeri, R. Single-ion nonlinear mechanical oscillator. Phys. Rev. A 2010, 82, 061402(R). [Google Scholar] [CrossRef]
- Ishizaki, R.; Sata, H.; Shoji, T. Chaos-Induced Diffusion in a Nonlinear Dissipative Mathieu Equation for a Charged Fine Particle in an AC Trap. J. Phys. Soc. Jpn. 2011, 80, 044001. [Google Scholar] [CrossRef]
- Shaikh, F.A.; Ozakin, A. Stability analysis of ion motion in asymmetric planar ion traps. J. Appl. Phys. 2012, 112, 074904. [Google Scholar] [CrossRef]
- Landa, H.; Drewsen, M.; Reznik, B.; Retzker, A. Modes of oscillation in radiofrequency Paul traps. New J. Phys. 2012, 14, 093023. [Google Scholar] [CrossRef]
- Roberdel, V.; Leibfried, D.; Ullmo, D.; Landa, H. Phase space study of surface electrode Paul traps: Integrable, chaotic, and mixed motion. Phys. Rev. A 2018, 97, 053419. [Google Scholar] [CrossRef]
- Rozhdestvenskii, Y.V.; Rudyi, S.S. Nonlinear Ion Dynamics in a Radiofrequency Multipole Trap. Tech. Phys. Lett. 2017, 43, 748–752. [Google Scholar] [CrossRef]
- Maitra, A.; Leibfried, D.; Ullmo, D.; Landa, H. Far-from-equilibrium noise-heating and laser-cooling dynamics in radio-frequency Paul traps. Phys. Rev. A 2019, 99, 043421. [Google Scholar] [CrossRef]
- Fountas, P.N.; Poggio, M.; Willitsch, S. Classical and quantum dynamics of a trapped ion coupled to a charged nanowire. New J. Phys. 2019, 21, 013030. [Google Scholar] [CrossRef]
- Zelaya, K.; Rosas-Ortiz, O. Quantum nonstationary oscillators: Invariants, dynamical algebras and coherent states via point transformations. Phys. Scr. 2020, 95, 064004. [Google Scholar] [CrossRef]
- Gheorghe, V.N.; Vedel, F. Quantum dynamics of trapped ions. Phys. Rev. A 1992, 45, 4828–4831. [Google Scholar] [CrossRef] [PubMed]
- Mihalcea, B.M. Semiclassical dynamics for an ion confined within a nonlinear electromagnetic trap. Phys. Scr. 2011, T143, 014018. [Google Scholar] [CrossRef]
- Mihalcea, B.M. Squeezed coherent states of motion for ions confined in quadrupole and octupole ion traps. Ann. Phys. 2018, 388, 100–113. [Google Scholar] [CrossRef]
- Landa, H.; Drewsen, M.; Reznik, B.; Retzker, A. Classical and quantum modes of coupled Mathieu equations. J. Phys. A Math. Theor. 2012, 45, 455305. [Google Scholar] [CrossRef]
- Gutiérrez, M.J.; Berrocal, J.; Domínguez, F.; Arrazola, I.; Block, M.; Solano, E.; Rodríguez, D. Dynamics of an unbalanced two-ion crystal in a Penning trap for application in optical mass spectrometry. Phys. Rev. A 2019, 100, 063415. [Google Scholar] [CrossRef]
- Gutzwiller, M.C. Chaos in Classical and Quantum Mechanics. In Interdisciplinary Applied Mathematics; John, F., Kadanoff, L., Marsden, J.E., Sirovich, L., Wiggins, S., Eds.; Springer: New York, NY, USA, 1990; Volume 1. [Google Scholar] [CrossRef]
- Dumas, S.H. The KAM Story: A Friendly Introduction to the Content, History, and Significance of Classical Kolmogorov-Arnold-Moser Theory; World Scientific: Singapore, 2014. [Google Scholar] [CrossRef]
- Lynch, S. Dynamical Systems with Applications using MATLAB, 2nd ed.; Birkhäuser-Springer: Cham, Switzerland, 2014. [Google Scholar] [CrossRef]
- Foot, C.J.; Trypogeorgos, D.; Bentine, E.; Gardner, A.; Keller, M. Two-frequency operation of a Paul trap to optimise confinement of two species of ions. Int. J. Mass. Spectr. 2018, 430, 117–125. [Google Scholar] [CrossRef]
- Blümel, R. Loading a Paul Trap: Densities, Capacities, and Scaling in the Saturation Regime. Atoms 2021, 9, 11. [Google Scholar] [CrossRef]
- Chang, K.C. Infinite Dimensional Morse Theory and Multiple Solution Problems. In Progress in Nonlinear Differential Equations and Their Applications; Birkhäuser: Boston, MA, USA, 1993; Volume 6. [Google Scholar] [CrossRef]
- Keller, J.; Burgermeister, T.; Kalincev, D.; Didier, A.; Kulosa, A.P.; Nordmann, T.; Kiethe, J.; Mehlstäubler, T.E. Controlling systematic frequency uncertainties at the 10−19 level in linear Coulomb crystals. Phys. Rev. A 2019, 99, 013405. [Google Scholar] [CrossRef]
- Mihalcea, B.M. Study of Quasiclassical Dynamics of Trapped Ions using the Coherent State Formalism and Associated Algebraic Groups. Rom. J. Phys. 2017, 62, 113. Available online: http://www.nipne.ro/rjp/2017_62_5-6/RomJPhys.62.113.pdf (accessed on 25 March 2021).
- Mandal, P.; Das, S.; De Munshi, D.; Dutta, T.; Mukherjee, M. Space charge and collective oscillation of ion cloud in a linear Paul trap. Int. J. Mass Spectrom. 2014, 364, 16–20. [Google Scholar] [CrossRef][Green Version]
- Li, G.Z.; Guan, S.; Marshall, A.G. Comparison of Equilibrium Ion Density Distribution and Trapping Force in Penning, Paul, and Combined Ion Traps. J. Am. Soc. Mass Spectrom. 1998, 9, 473–481. [Google Scholar] [CrossRef]
- Singer, K.; Poschinger, U.; Murphy, M.; Ivanov, P.; Ziesel, F.; Calarco, T.; Schmidt-Kaler, F. Colloquium: Trapped ions as quantum bits: Essential numerical tools. Rev. Mod. Phys. 2010, 82, 2609–2632. [Google Scholar] [CrossRef]
- Lynch, S. Dynamical Systems with Applications using Python; Birkhäuser: Basel, Switzerland, 2018. [Google Scholar] [CrossRef]
- Saxena, V. Analytical Approximate Solution of a Coupled Two Frequency Hill’s Equation. arXiv 2020, arXiv:2008.05525. [Google Scholar]
- Yoshimura, B.; Stork, M.; Dadic, D.; Campbell, W.C.; Freericks, J.K. Creation of two-dimensional Coulomb crystals of ions in oblate Paul traps for quantum simulations. EPJ Quantum Technol. 2015, 2, 2. [Google Scholar] [CrossRef]
- Kozlov, M.G.; Safronova, M.S.; Crespo López-Urrutia, J.R.; Schmidt, P.O. Highly charged ions: Optical clocks and applications in fundamental physics. Rev. Mod. Phys. 2018, 90, 045005. [Google Scholar] [CrossRef]
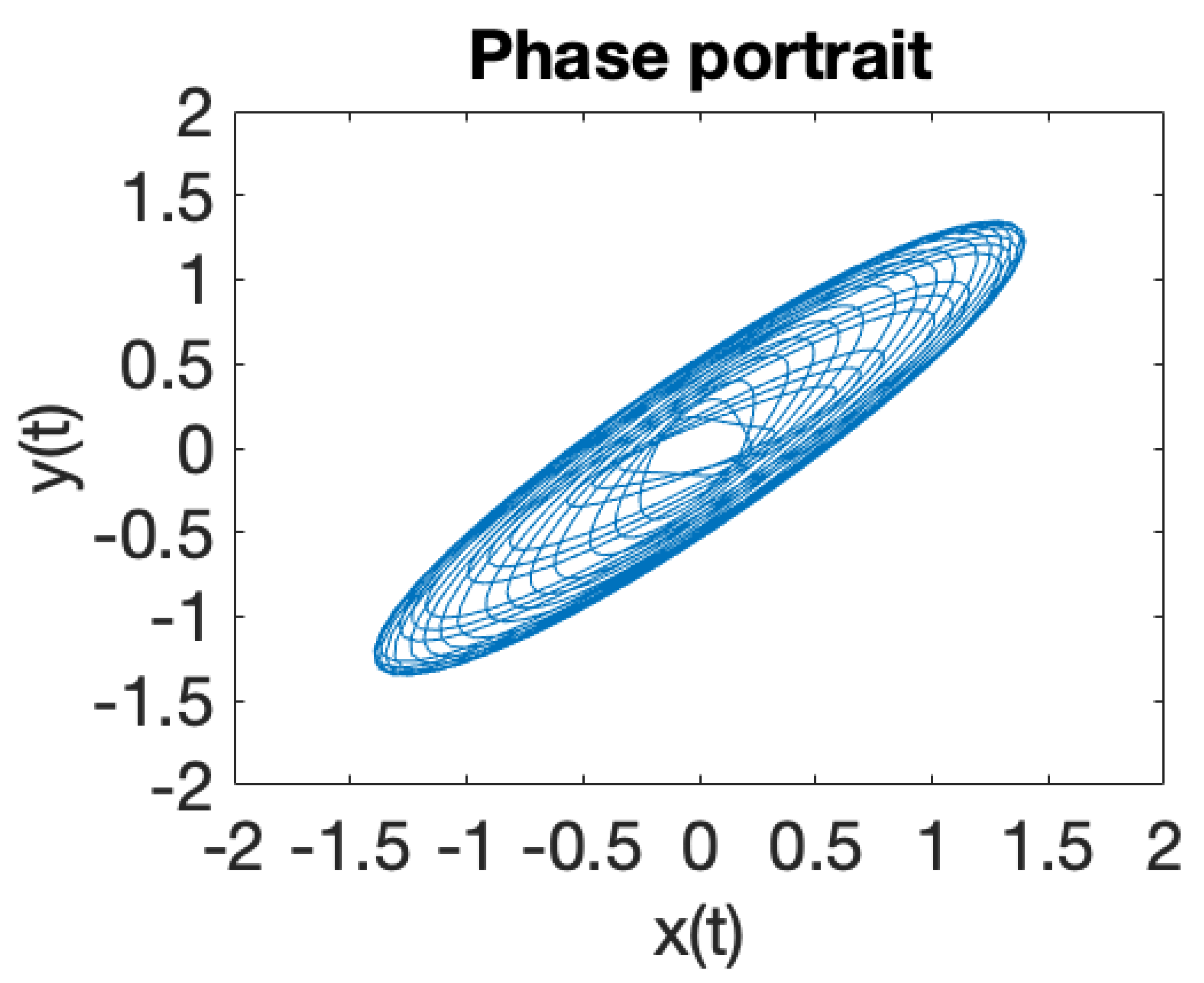
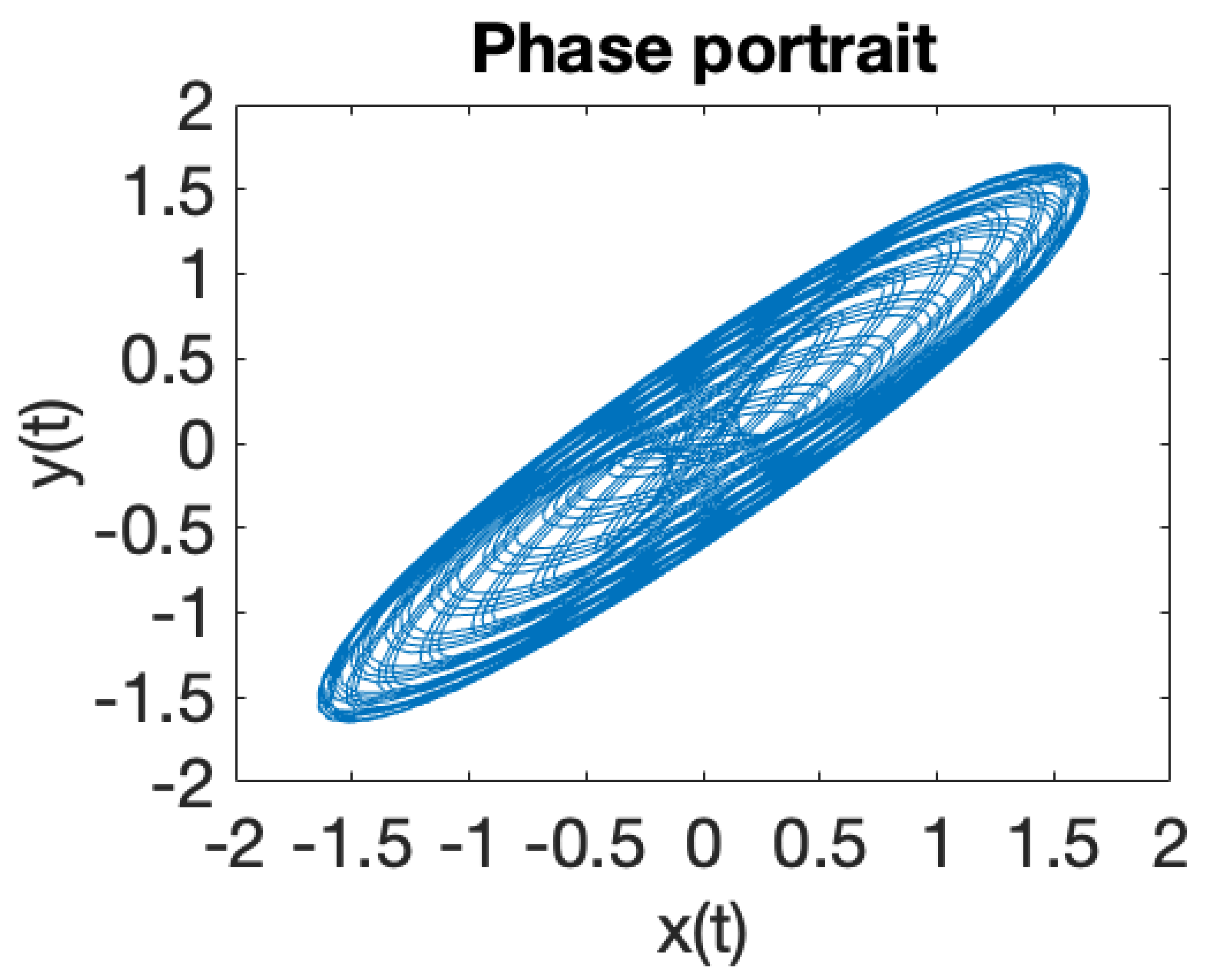
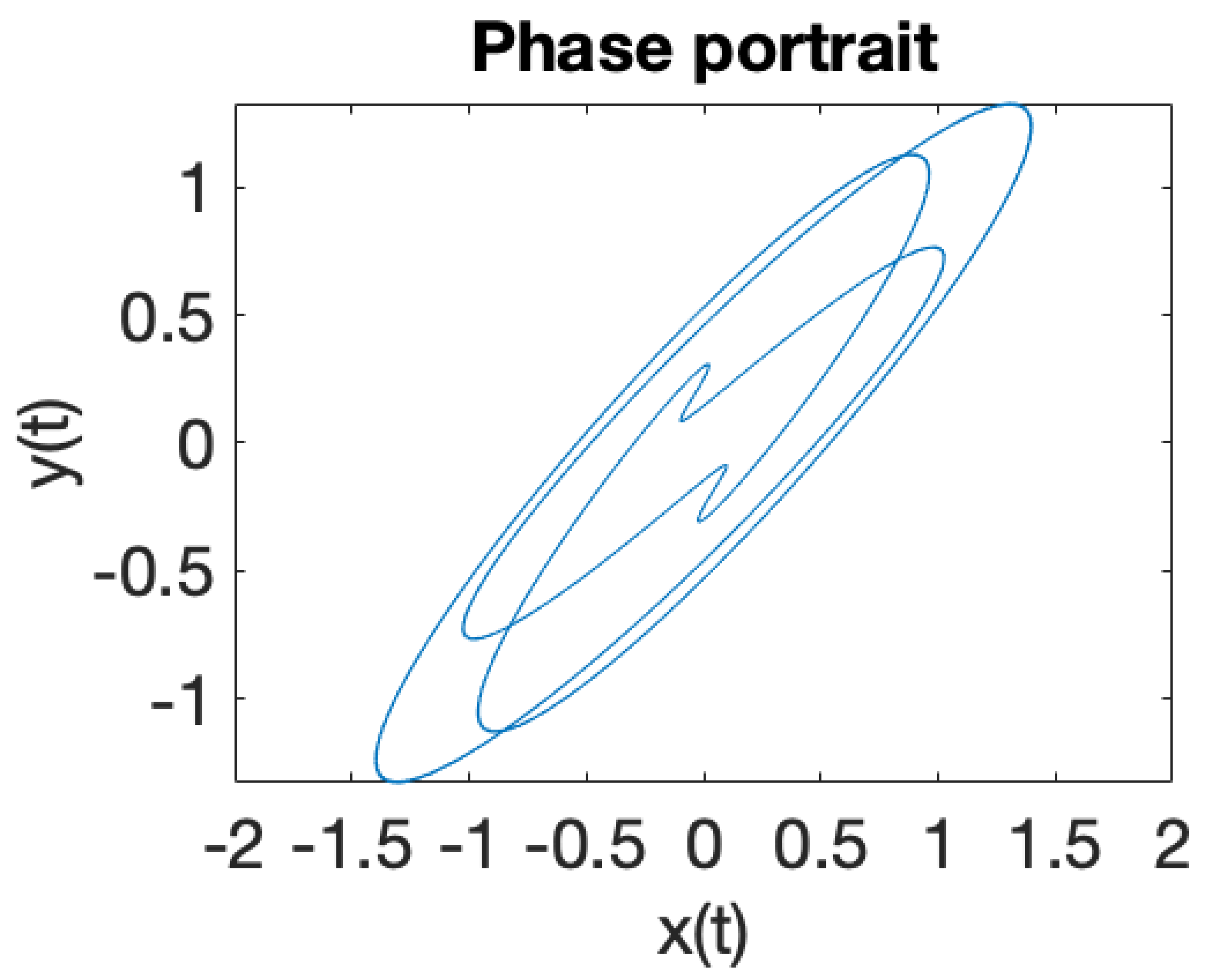
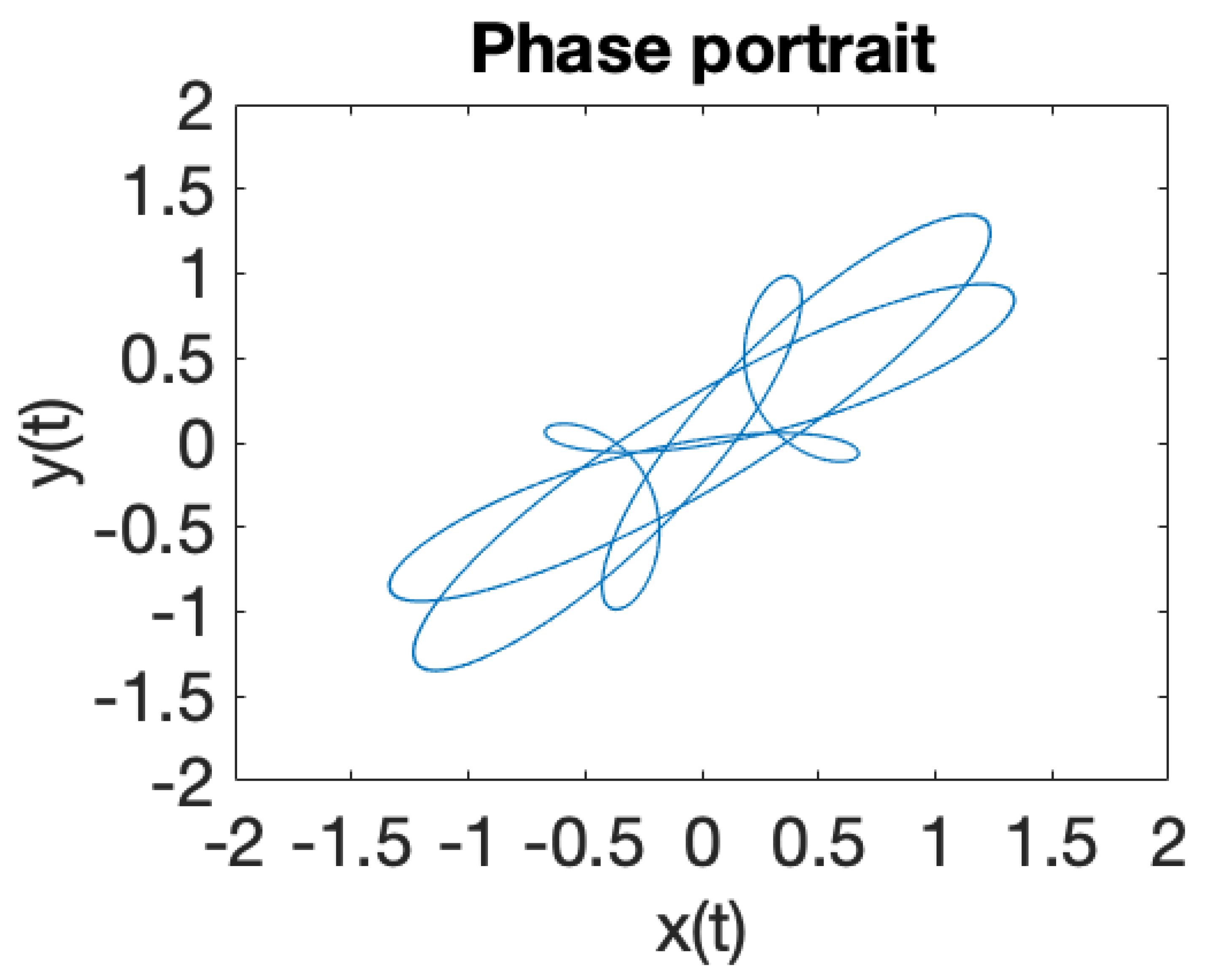
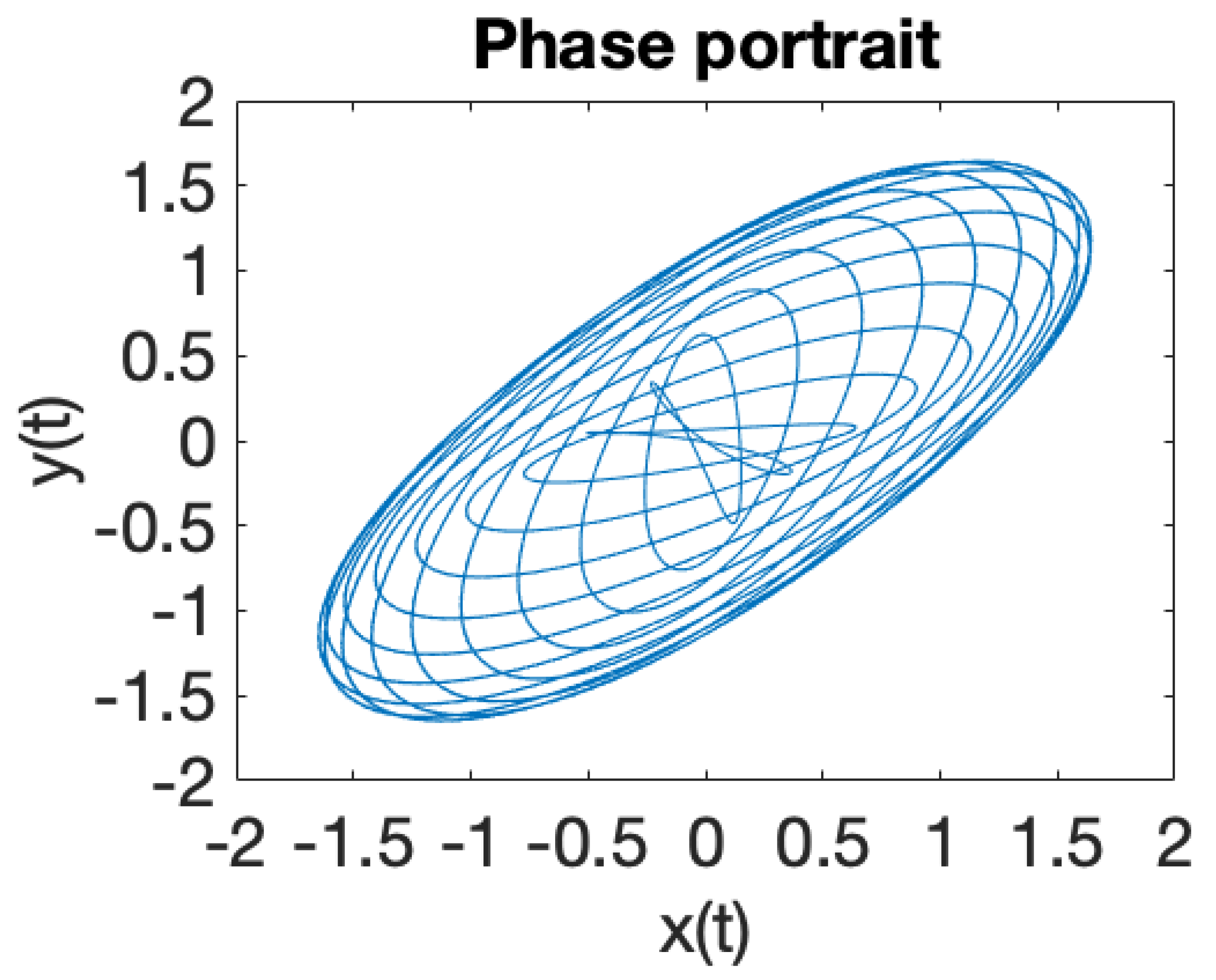
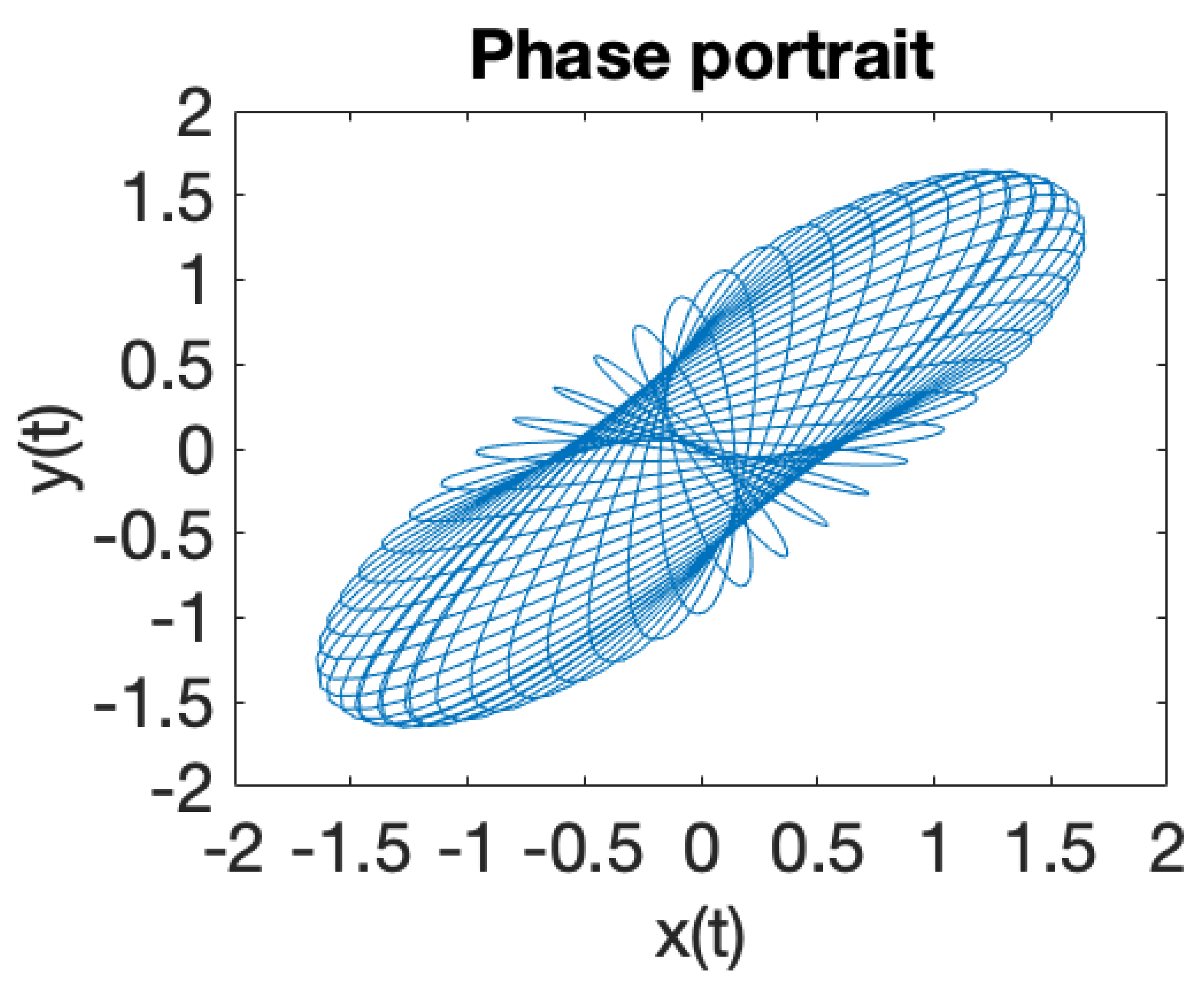
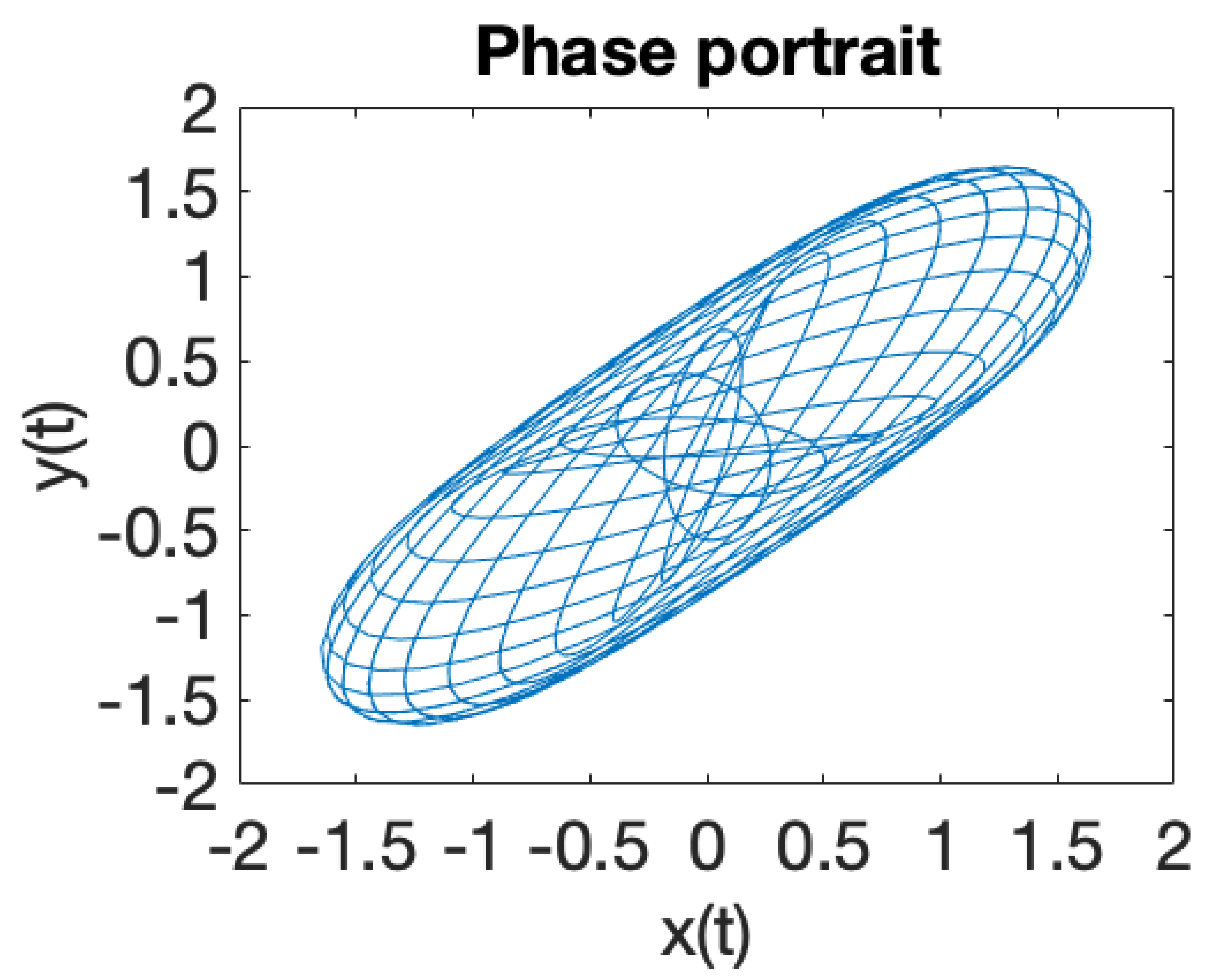
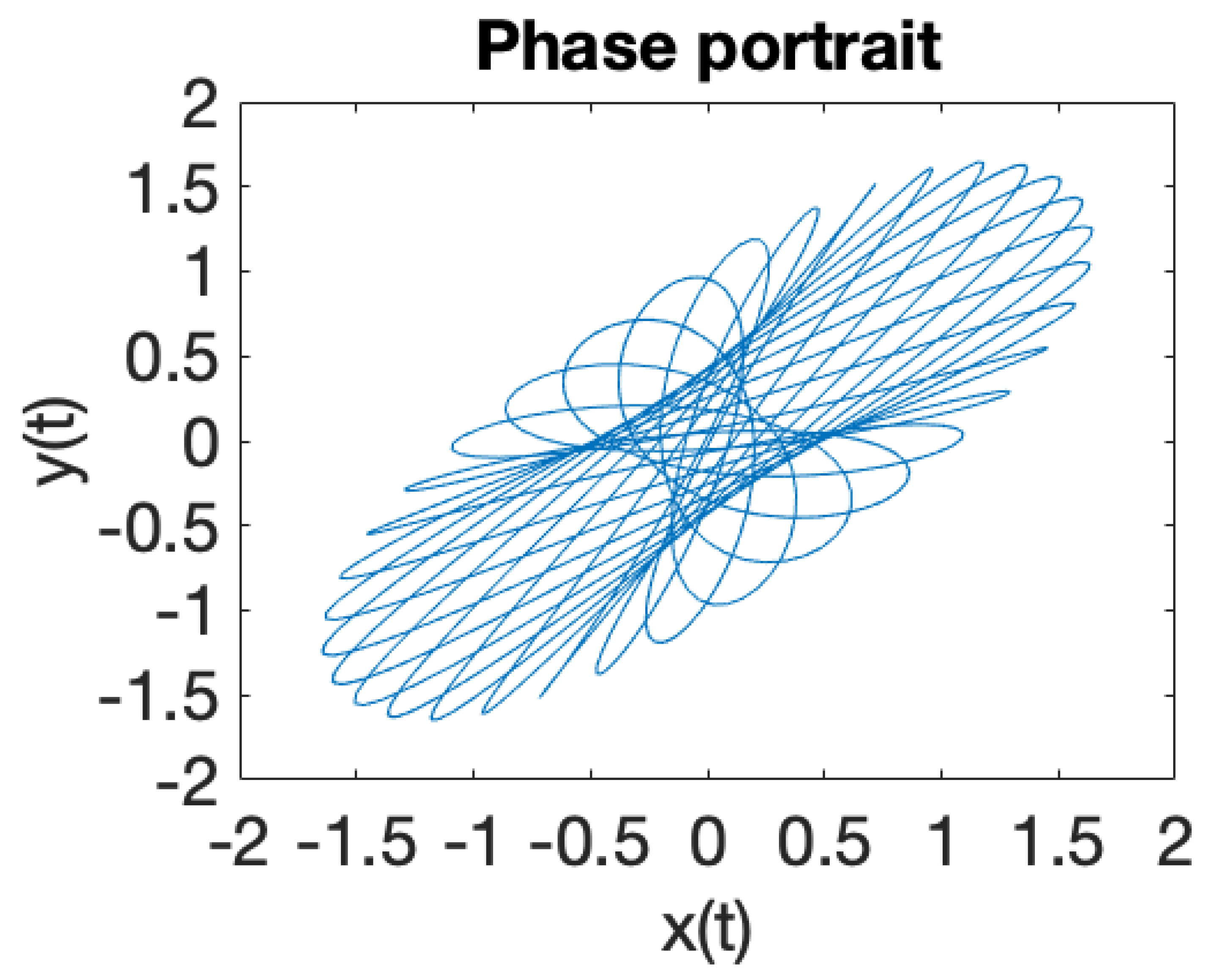
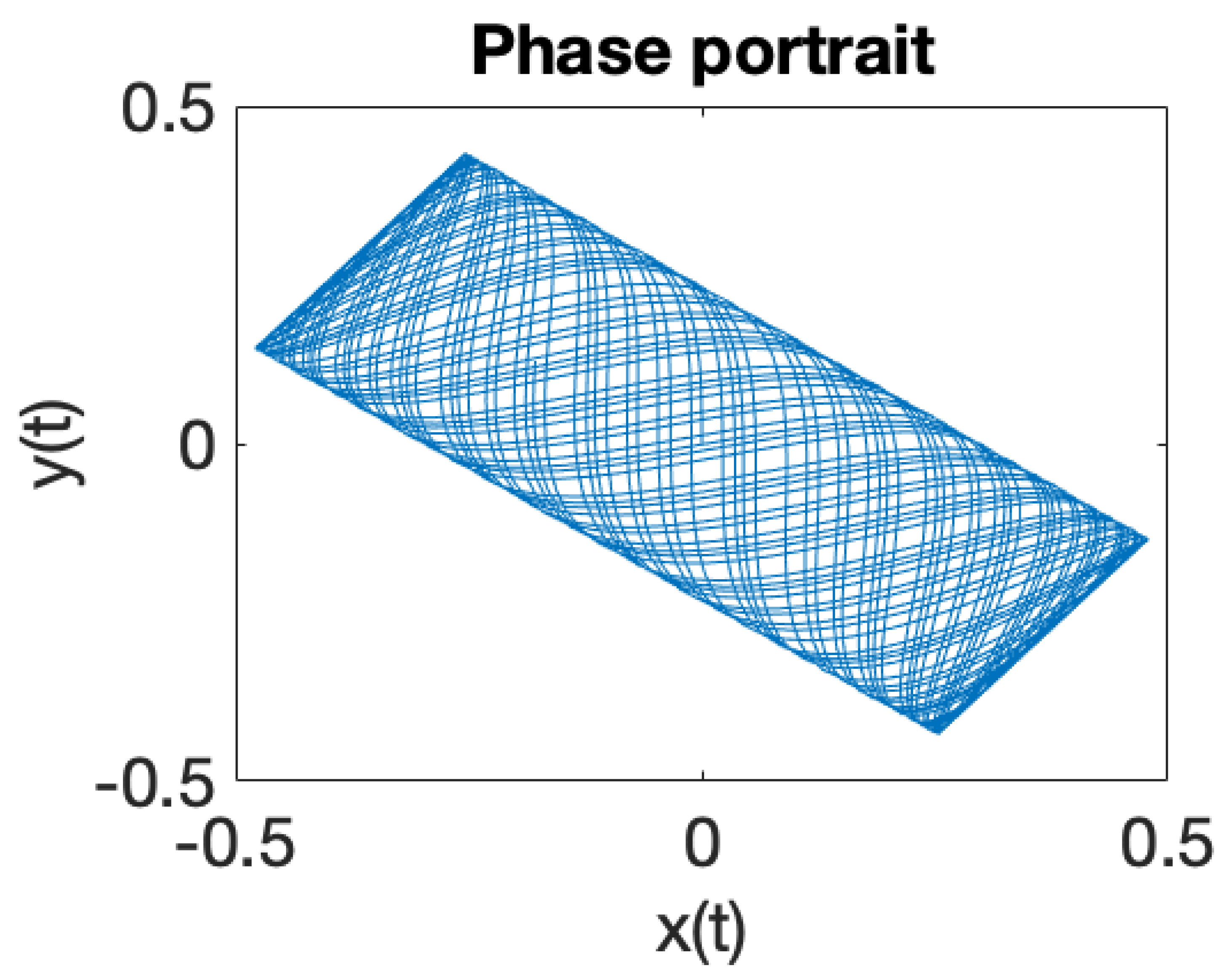
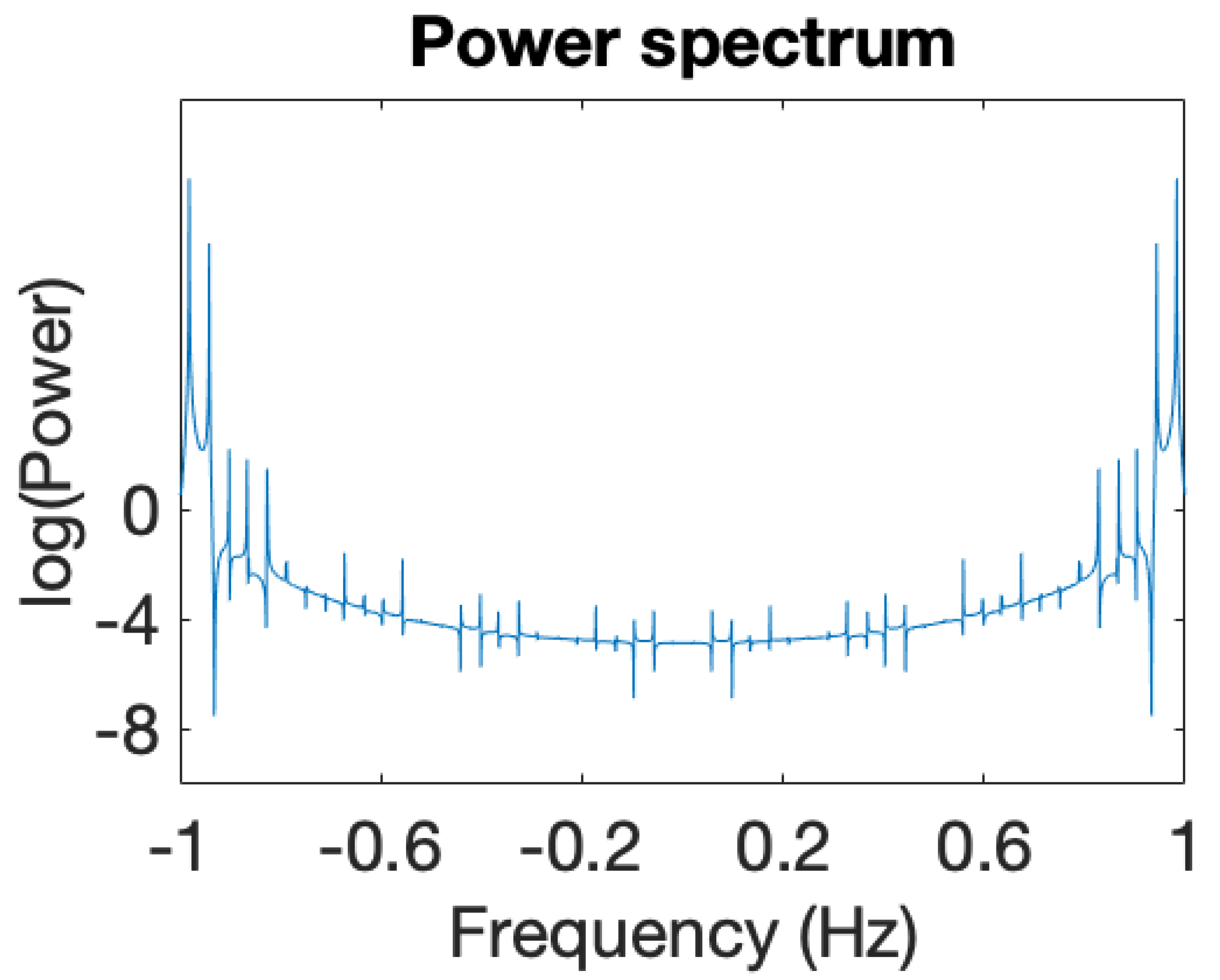
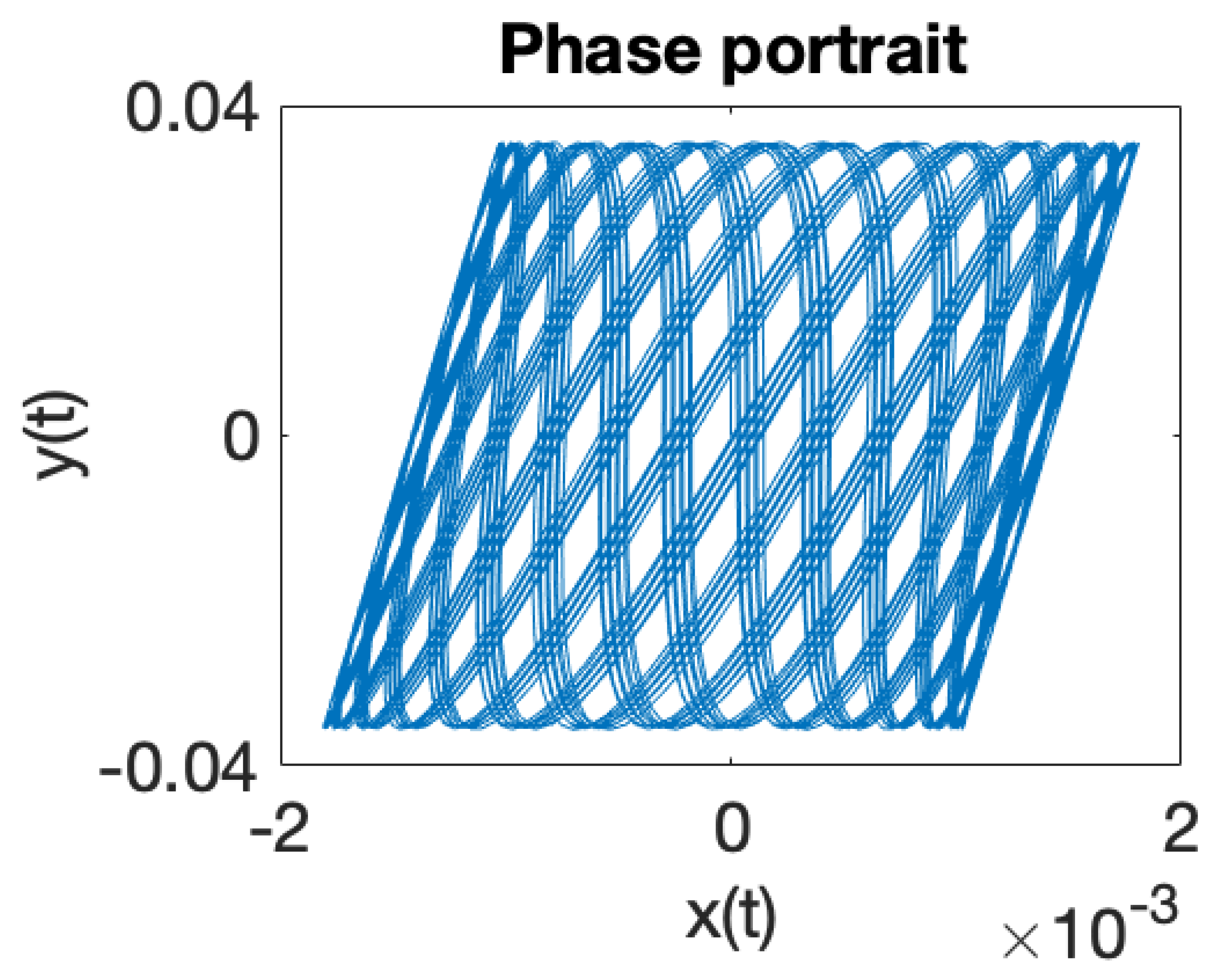
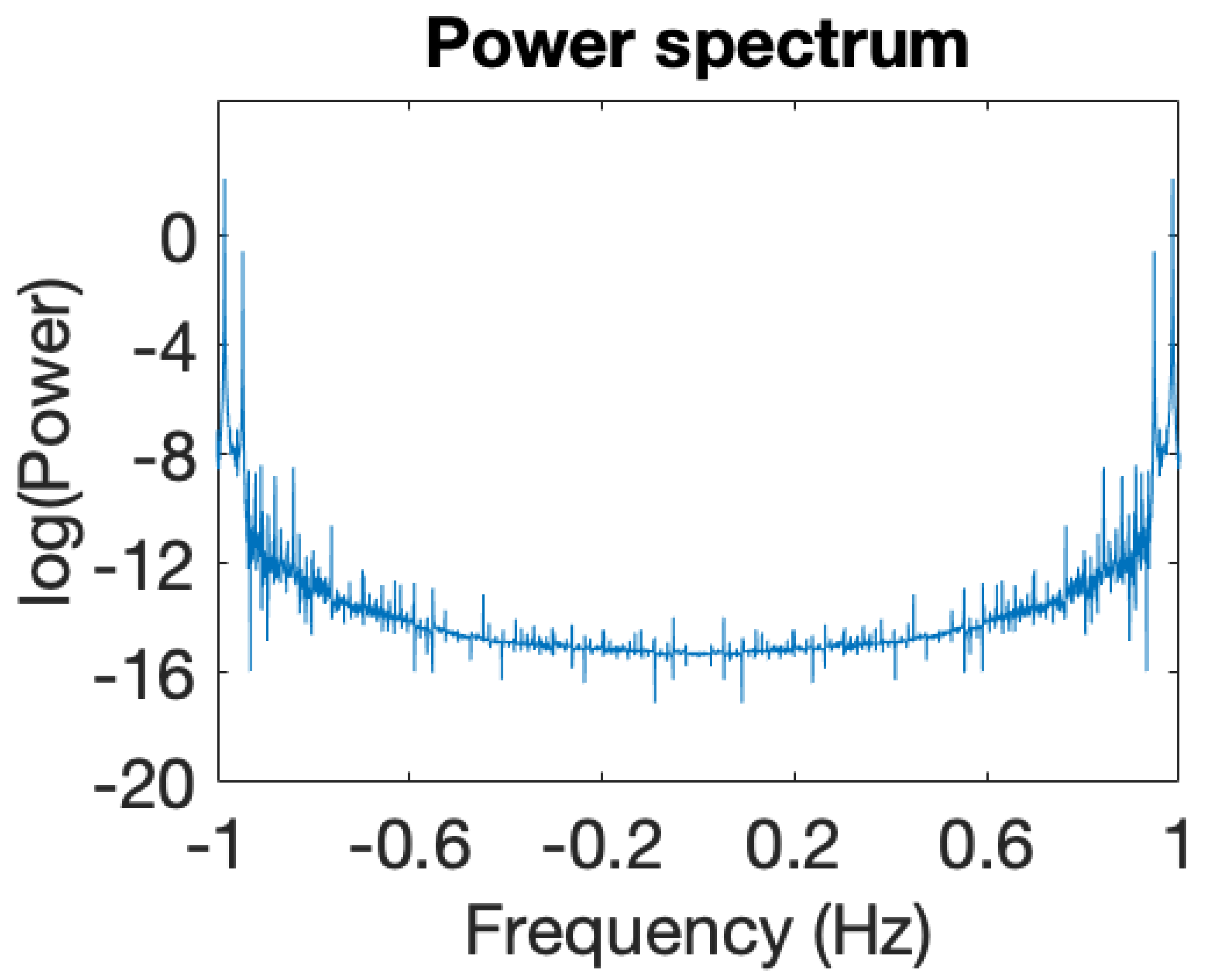
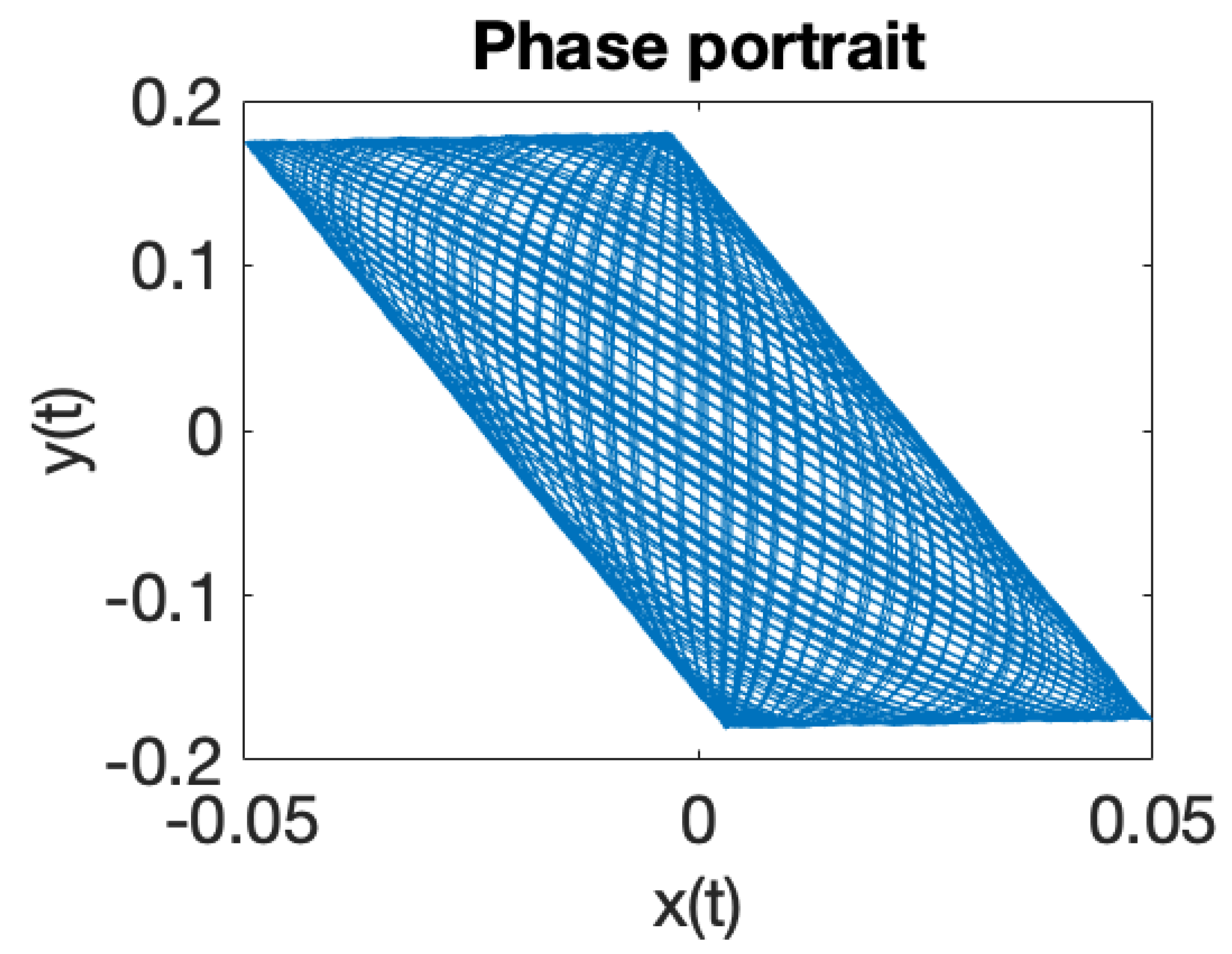
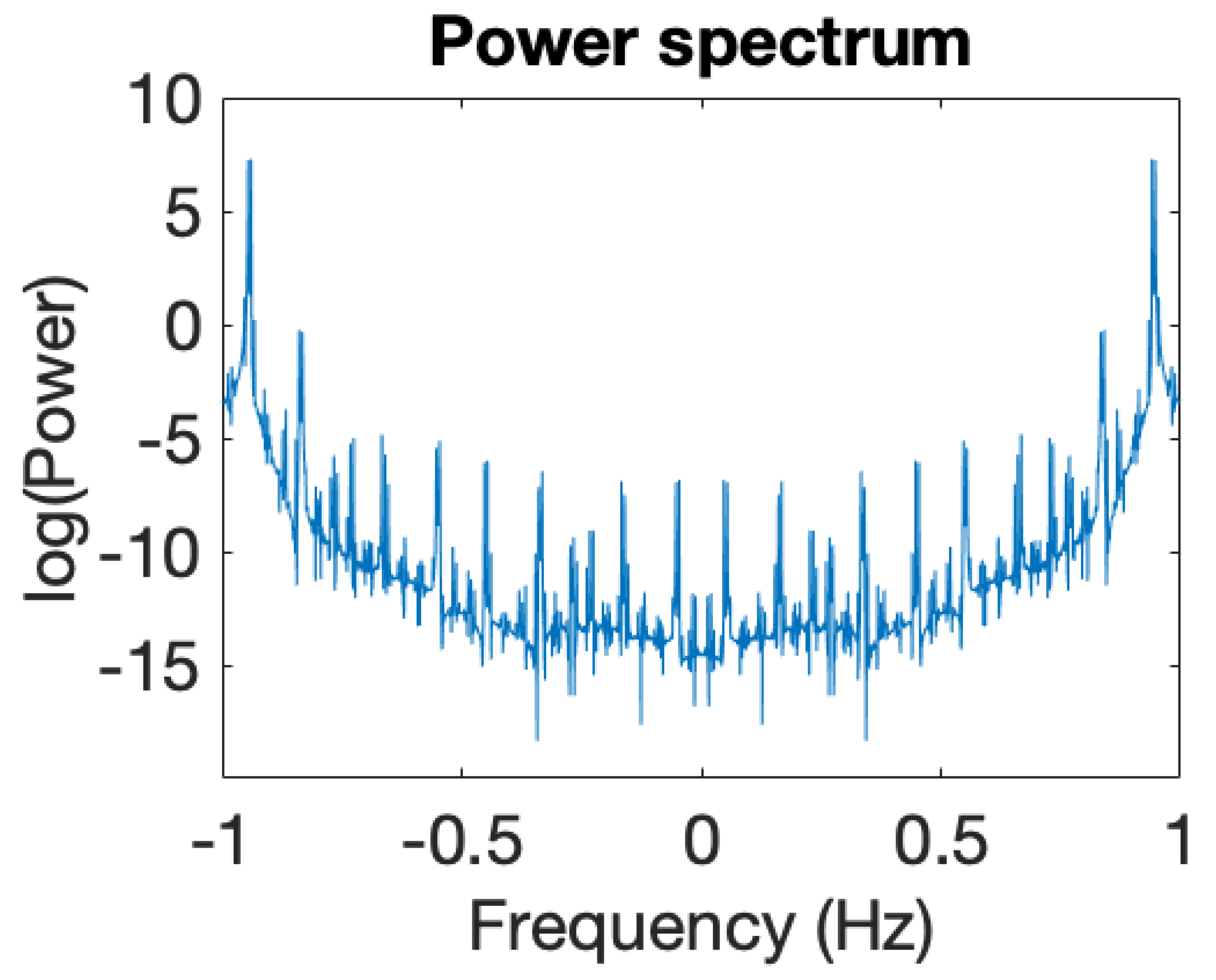
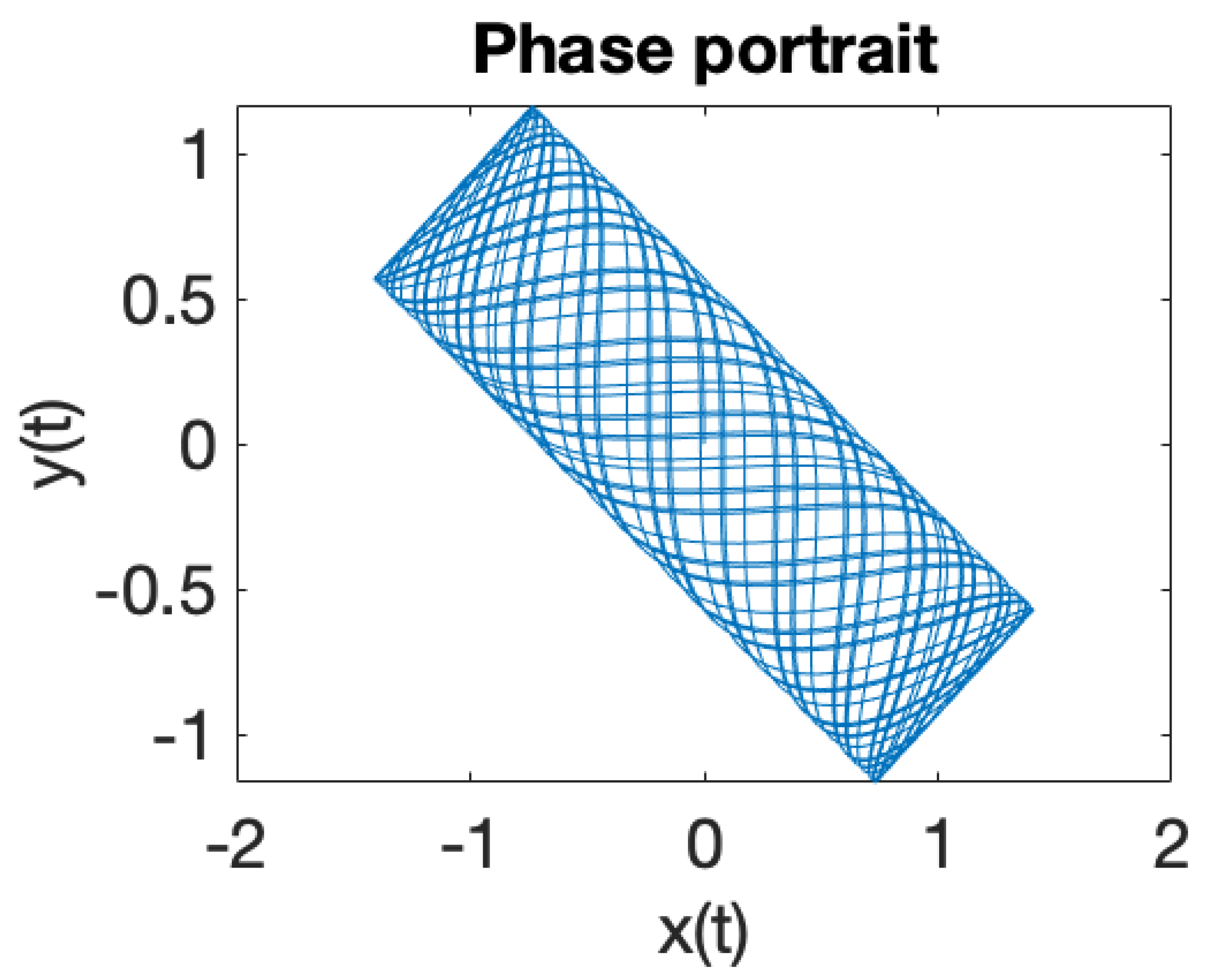
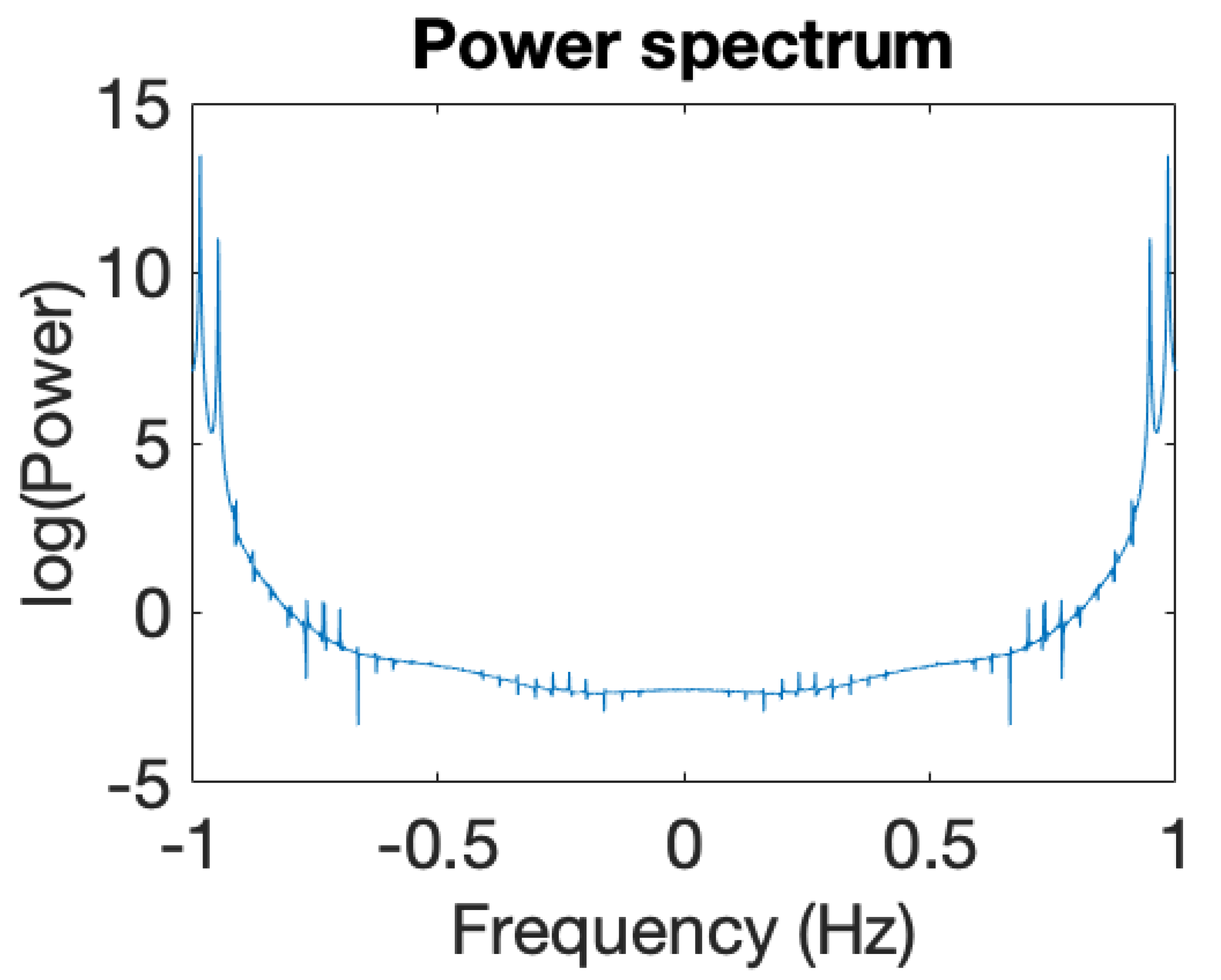
| Critical Point | |||
|---|---|---|---|
| Minimum | |||
| 0 | Degeneracy | ||
| Saddle point |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mihalcea, B.M.; Lynch, S. Investigations on Dynamical Stability in 3D Quadrupole Ion Traps. Appl. Sci. 2021, 11, 2938. https://doi.org/10.3390/app11072938
Mihalcea BM, Lynch S. Investigations on Dynamical Stability in 3D Quadrupole Ion Traps. Applied Sciences. 2021; 11(7):2938. https://doi.org/10.3390/app11072938
Chicago/Turabian StyleMihalcea, Bogdan M., and Stephen Lynch. 2021. "Investigations on Dynamical Stability in 3D Quadrupole Ion Traps" Applied Sciences 11, no. 7: 2938. https://doi.org/10.3390/app11072938
APA StyleMihalcea, B. M., & Lynch, S. (2021). Investigations on Dynamical Stability in 3D Quadrupole Ion Traps. Applied Sciences, 11(7), 2938. https://doi.org/10.3390/app11072938







