A Symmetric Three-Layer Plate with Two Coaxial Cracks under Pure Bending
Abstract
Featured Application
Abstract
1. Introduction
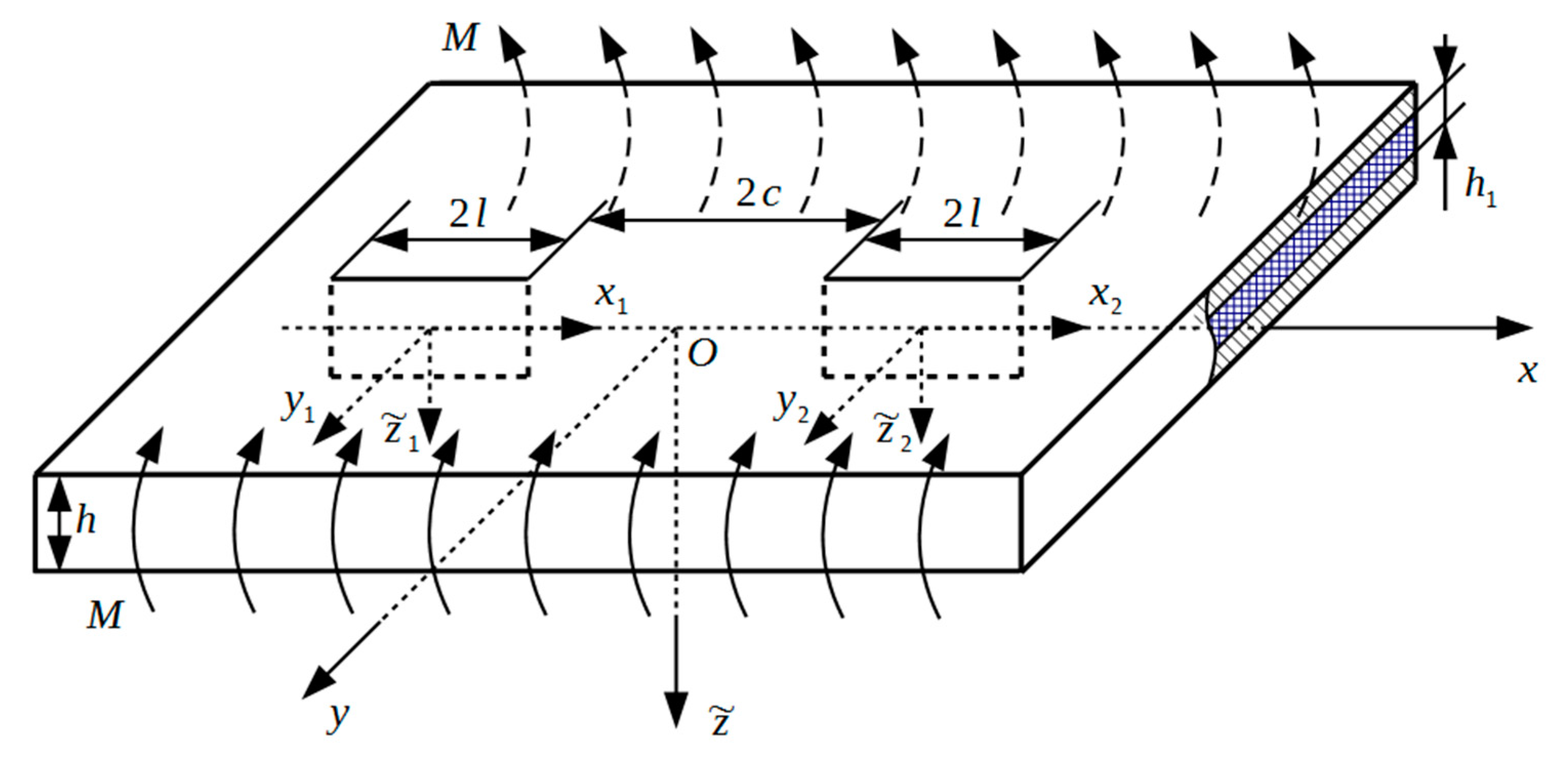
2. Materials and Methods
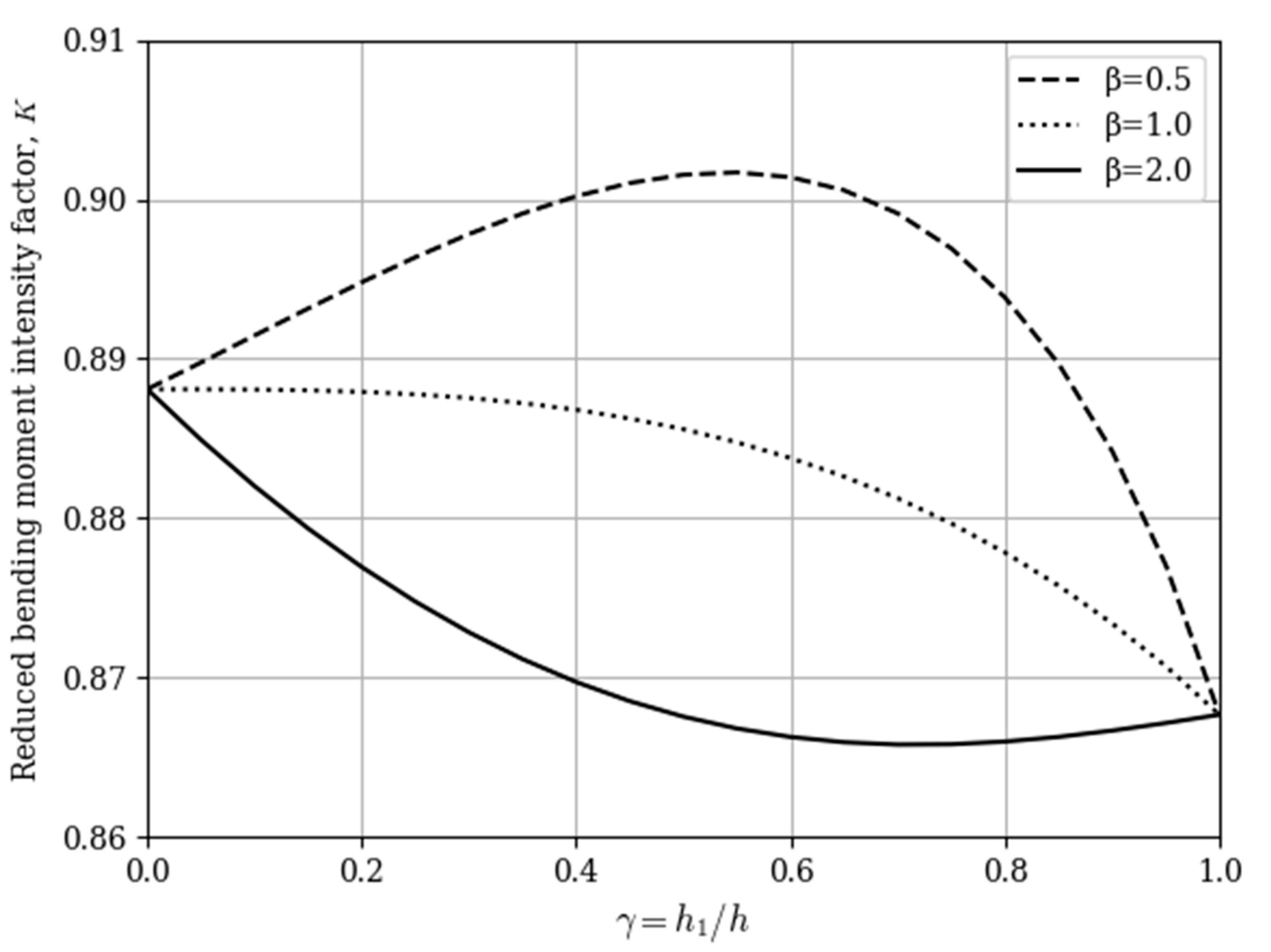
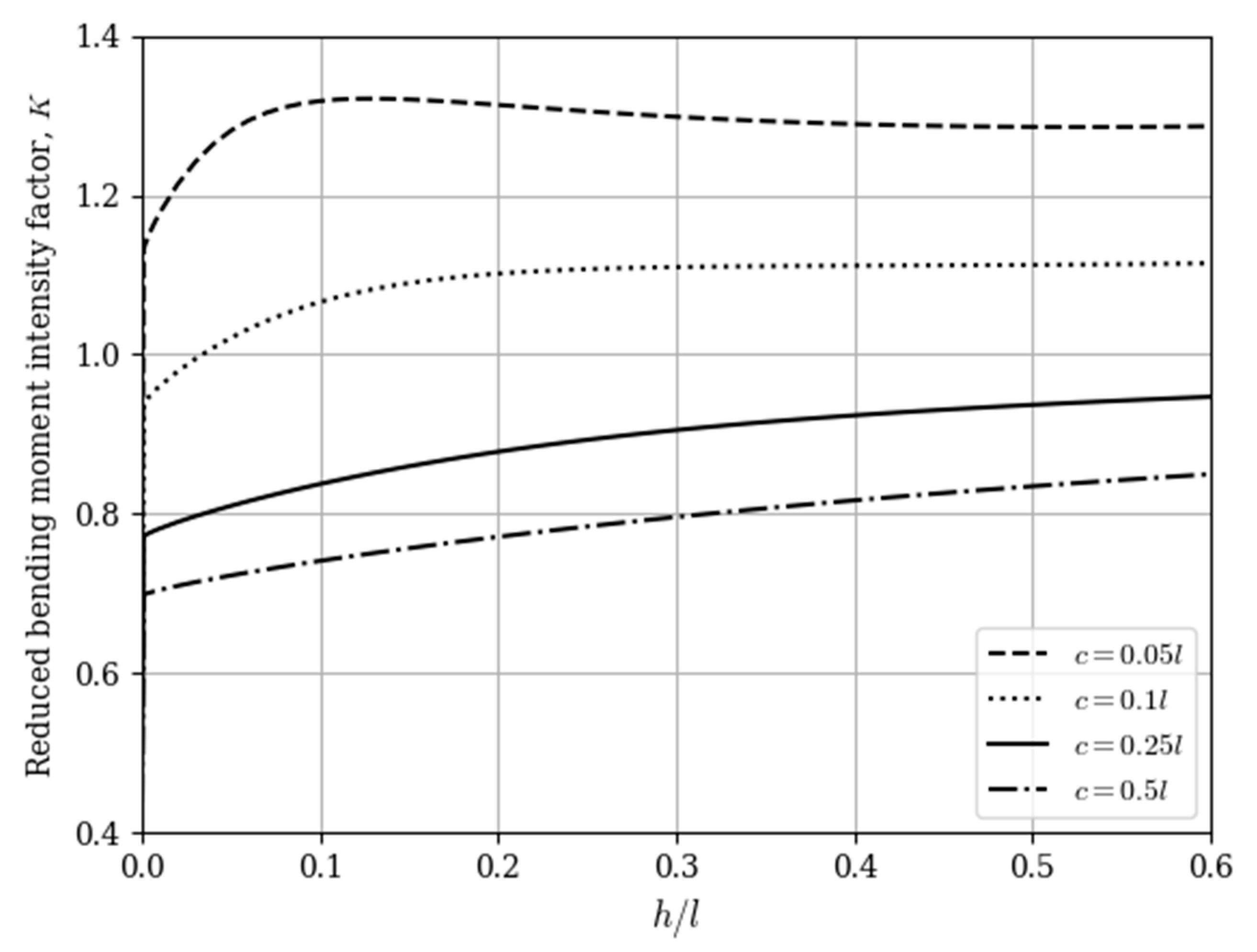
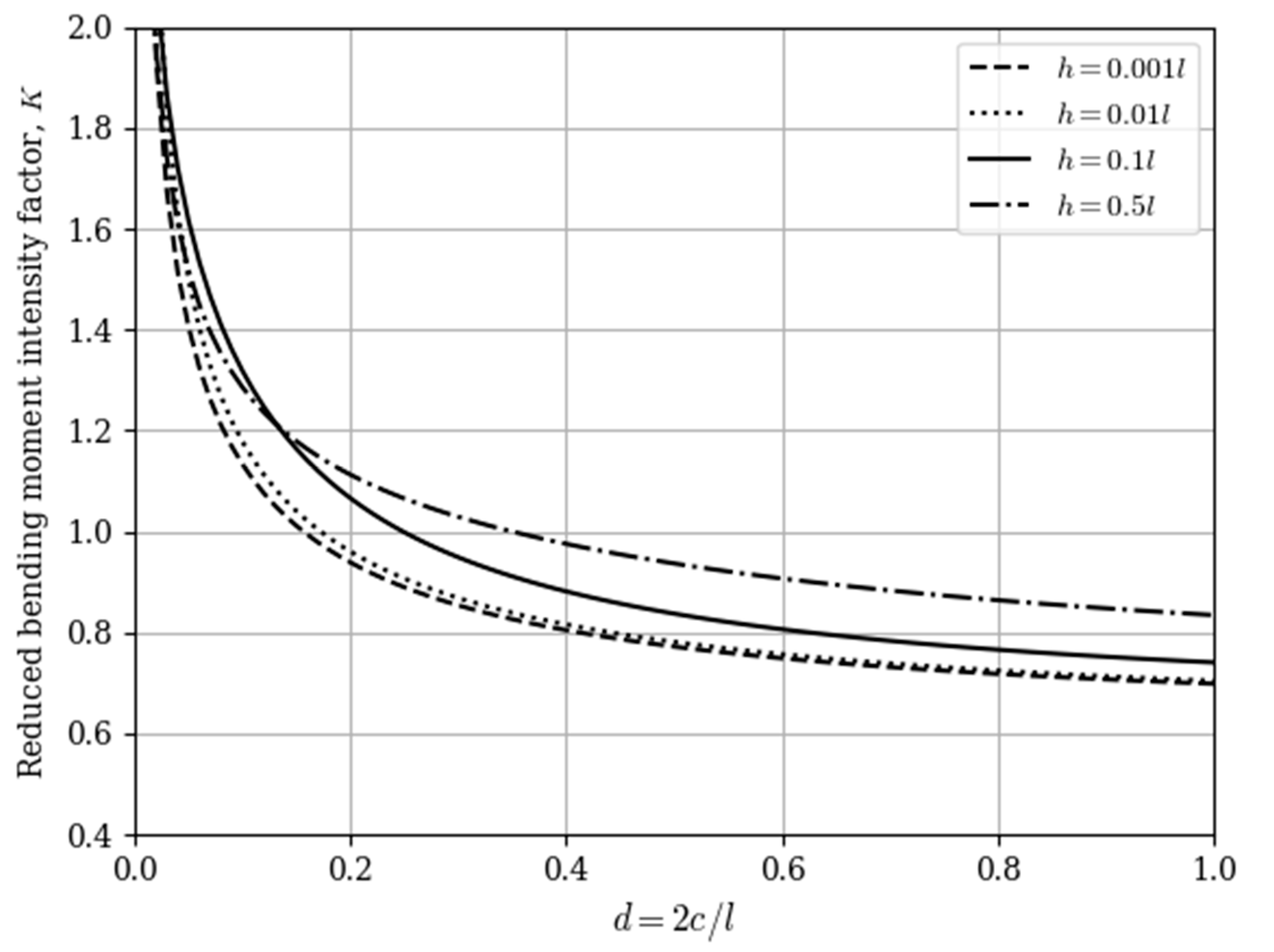
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Murakami, Y. (Ed.) Stress Intensity Factors Handbook; Oxford etc. Pergamon Press: Oxford, UK, 1987; Volume 2, 1456p. [Google Scholar]
- Zehnder, A.T.; Viz, M.J. Fracture mechanics of thin plates and shells under combined membrane, bending, and twisting loads. Appl. Mech. Rev. 2005, 58, 37–48. [Google Scholar] [CrossRef]
- Corbani, S.; Miranda, A.C.; Martha, L.F.; Castro, J.T.; Carter, B.J. Investigations in a cracked plate under bending. Mecánica Comput. 2010, 29, 5163–5171. [Google Scholar]
- Bäcker, D.; Kuna, M.; Häusler, C. Eigenfunctions of crack problems in the Mindlin plate theory. ZAMM—J. Appl. Math. Mech. 2015, 95, 763–777. [Google Scholar] [CrossRef]
- Opanasovych, V.K.; Seliverstov, R.H. Bending of a plate with two identical collinear rectilinear cracks according to the theory of Reissner. Mater. Sci. 2001, 37, 59–64. [Google Scholar] [CrossRef]
- Yatsyk, I. Reissner′s plate bending containing periodic system of collinear through-the-thickness cracks taking into account contact region width of their faces (in Ukrainian). Visnyk Lviv Univ. Ser. Mech.-Math. 2010, 73, 155–164. [Google Scholar]
- Sulym, H.; Opanasowych, W.; Jacyk, I. Zginanie płyty Reissnera ze szczelinami przy uwzglednieniu szerokosci strefy kontaktu brzegów szczelin. Acta Mech. Autom. 2011, 5, 85–93. [Google Scholar]
- Maksymovych, O.; Illiushyn, O. Stress calculation and optimization in composite plates with holes based on the modified integral equation method. Eng. Anal. Bound. Elem. 2017, 83, 180–187. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, X.; Yu, D.; Wang, X. Analysis of semi-elliptical surface cracks in the interface of bimaterial plates under tension and bending. Theor. Appl. Fract. Mech. 2018, 93, 155–169. [Google Scholar] [CrossRef]
- Hsieh, M.C.; Hwu, C. Anisotropic elastic plates with holes cracks inclusions subjected to out-of-plane bending moments. Int. J. Solids Struct. 2002, 39, 4905–4925. [Google Scholar] [CrossRef]
- Yankovsky, A.P. Refined model of thermo-elastic-plastic bending of layered plates of regular structure. II. Modeling problems. J. Math. Sci. 2021, 253, 122–135. [Google Scholar] [CrossRef]
- Khosravani, M.R.; Zolfagharian, A.; Jennings, M.; Reinicke, T. Structural performance of 3D-printed composites under various loads and environmental conditions. Polim. Test. 2020, 91. [Google Scholar] [CrossRef]
- Shao-Tzu, C.; Li, H. Boundary-based finite element method for two-dimensional anisotropic elastic solids with multiple holes and cracks. Eng. Anal. Bound. Elem. 2017, 79, 13–22. [Google Scholar] [CrossRef]
- Khezri, M.; Rasmussen, K.J.R. An energy-based approach to buckling modal decomposition of thin-walled members with arbitrary cross sections, Part 1: Derivation. Thin-Walled Struct. 2019, 138, 496–517. [Google Scholar] [CrossRef]
- Berezhnytsky, L.T.; Delyavskyy, M.V.; Rudnytsky, I.I. Bending of a layered plate with a crack at the arbitrary distribution of displacements over the thickness (in Russian). Strength Mater. 1984, 10, 68–72. [Google Scholar]
- Berezhnytsky, L.T.; Delyavskyy, M.V.; Mazurak, L.P. Account of the asymmetry of tangential stresses for the bending of layered plates with cracks (in Russian). Int. Appl. Mech. 1985, 21, 81–86. [Google Scholar]
- Opanasovych, V.K.; Seliverstov, R.H. A bending of a layered plate with two parallel unshifted cracks (in Ukrainian). Mech. Eng. 2002, 6, 17–19. [Google Scholar]
- Panasyuk, V.V.; Savruk, M.P.; Datsyshyn, A.P. Stress Propagation Near the Cracks in Plates and Shells (in Russian); Naukova Dumka: Kiev, Ukraine, 1976. [Google Scholar]
| Mark | Mark Meaning |
|---|---|
| plate thickness | |
| Young′s modulus of outer layers in the plane of isotropy | |
| Young′s modulus of inner layer in the plane of isotropy | |
| Poisson′s ratio of outer layers in the plane of isotropy | |
| Poisson′s ratio of inner layer in the plane of isotropy | |
| shear modulus of outer layers in the transverse direction | |
| shear modulus of inner layer in the transverse direction | |
| crack length | |
| coordinates of the center of j-th crack | |
| distance between inner tips of cracks | |
| bending loads at infinity | |
| bending moments | |
| twisting moments | |
| shear forces | |
| components of displacement vector in the k-th layer | |
| components of stress tensor in the k-th layer | |
| unknown functions | |
| complex variable | |
| complex potentials | |
| Macdonald function of i-th order | |
| bending moment intensity factor | |
| reduced moment intensity factor |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Delyavskyy, M.; Opanasovych, V.; Seliverstov, R.; Bilash, O. A Symmetric Three-Layer Plate with Two Coaxial Cracks under Pure Bending. Appl. Sci. 2021, 11, 2859. https://doi.org/10.3390/app11062859
Delyavskyy M, Opanasovych V, Seliverstov R, Bilash O. A Symmetric Three-Layer Plate with Two Coaxial Cracks under Pure Bending. Applied Sciences. 2021; 11(6):2859. https://doi.org/10.3390/app11062859
Chicago/Turabian StyleDelyavskyy, Mykhaylo, Viktor Opanasovych, Roman Seliverstov, and Oksana Bilash. 2021. "A Symmetric Three-Layer Plate with Two Coaxial Cracks under Pure Bending" Applied Sciences 11, no. 6: 2859. https://doi.org/10.3390/app11062859
APA StyleDelyavskyy, M., Opanasovych, V., Seliverstov, R., & Bilash, O. (2021). A Symmetric Three-Layer Plate with Two Coaxial Cracks under Pure Bending. Applied Sciences, 11(6), 2859. https://doi.org/10.3390/app11062859






