Numerical Investigation on Crack Propagation for a Central Cracked Brazilian Disk Concerning Friction
Abstract
:1. Introduction
2. Integral and Crack Propagation Criteria
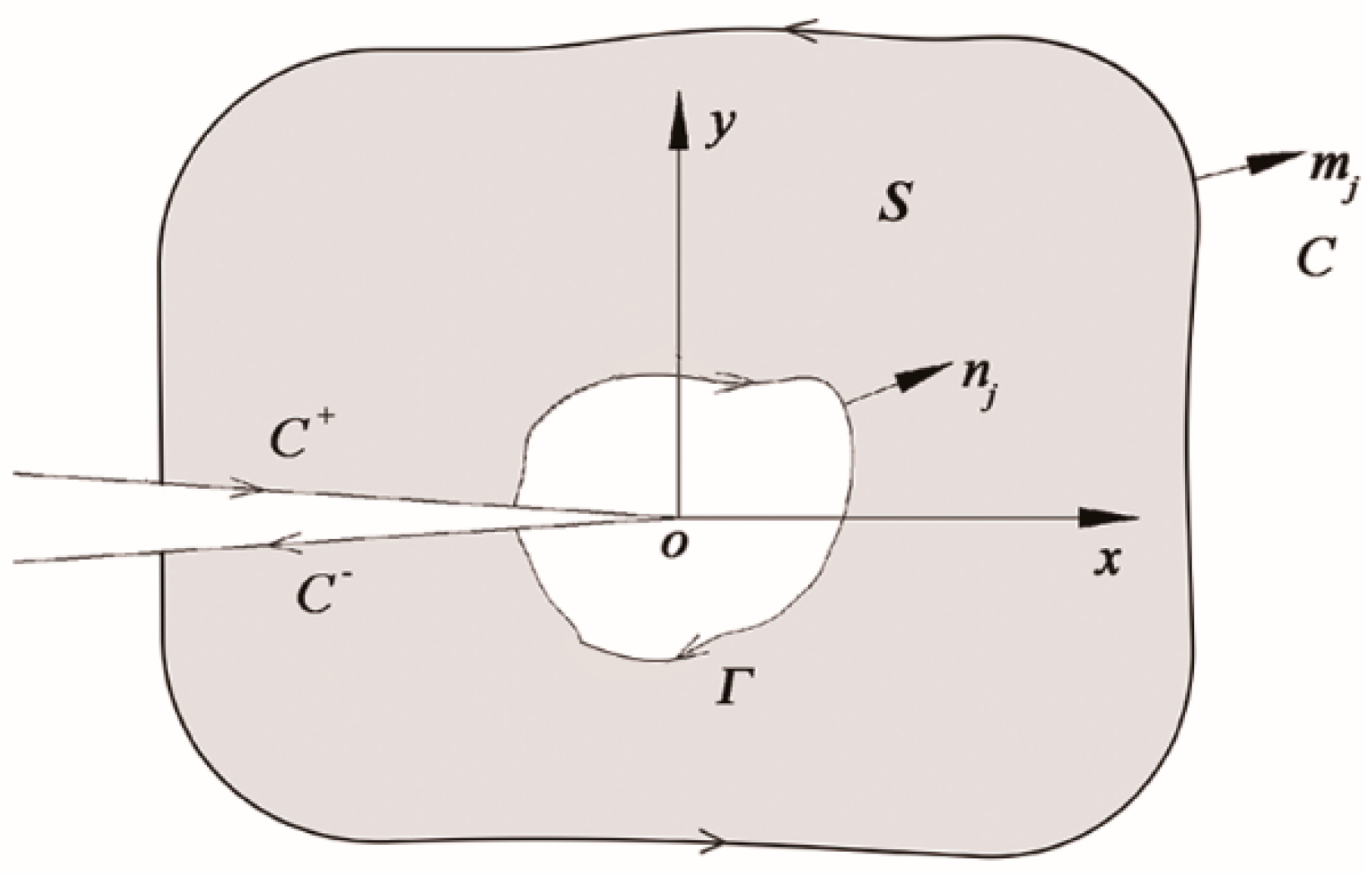
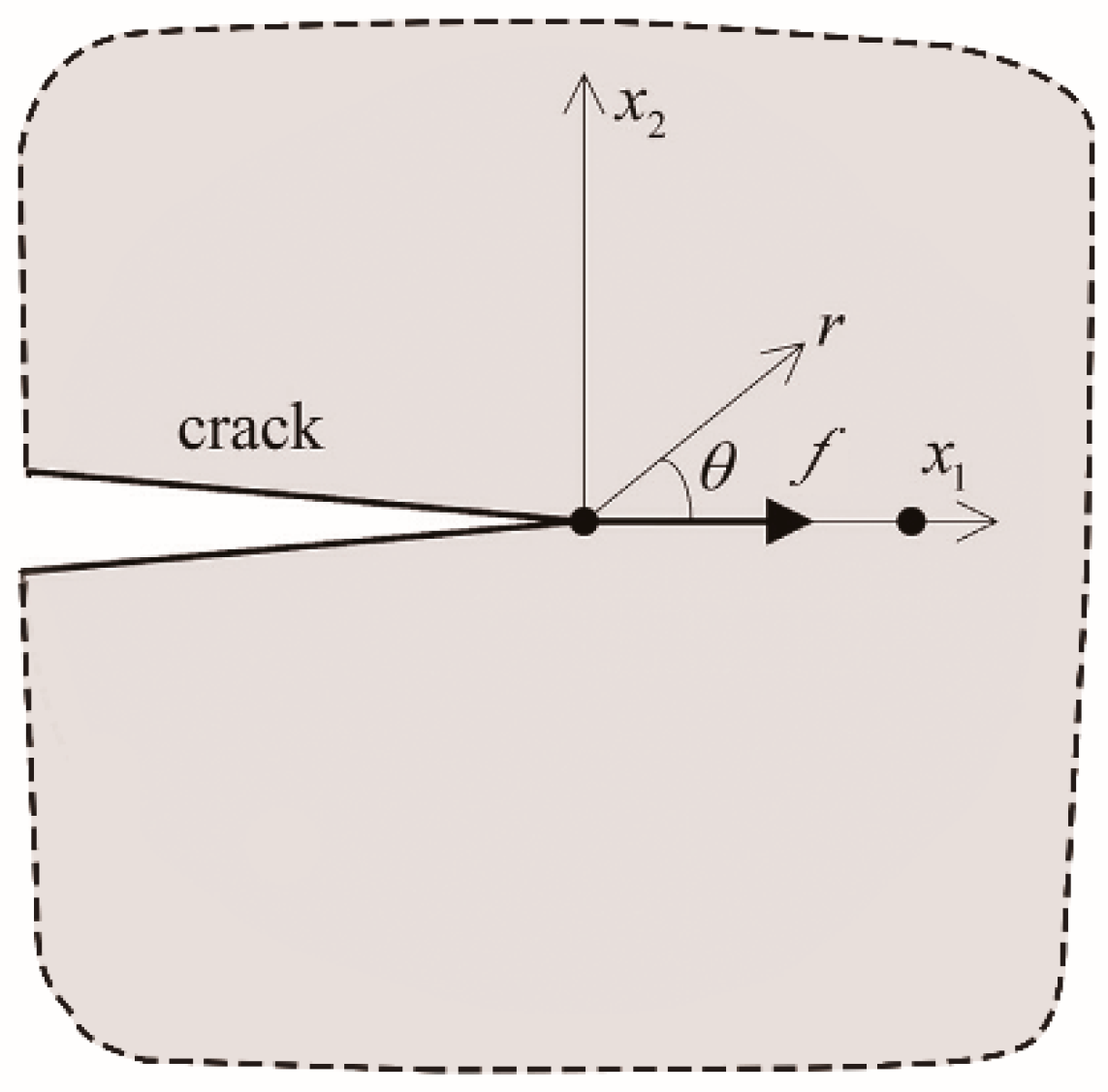
2.1. Two-Dimensional Interaction Integral with MFEM
2.2. Criteria for Crack Propagation
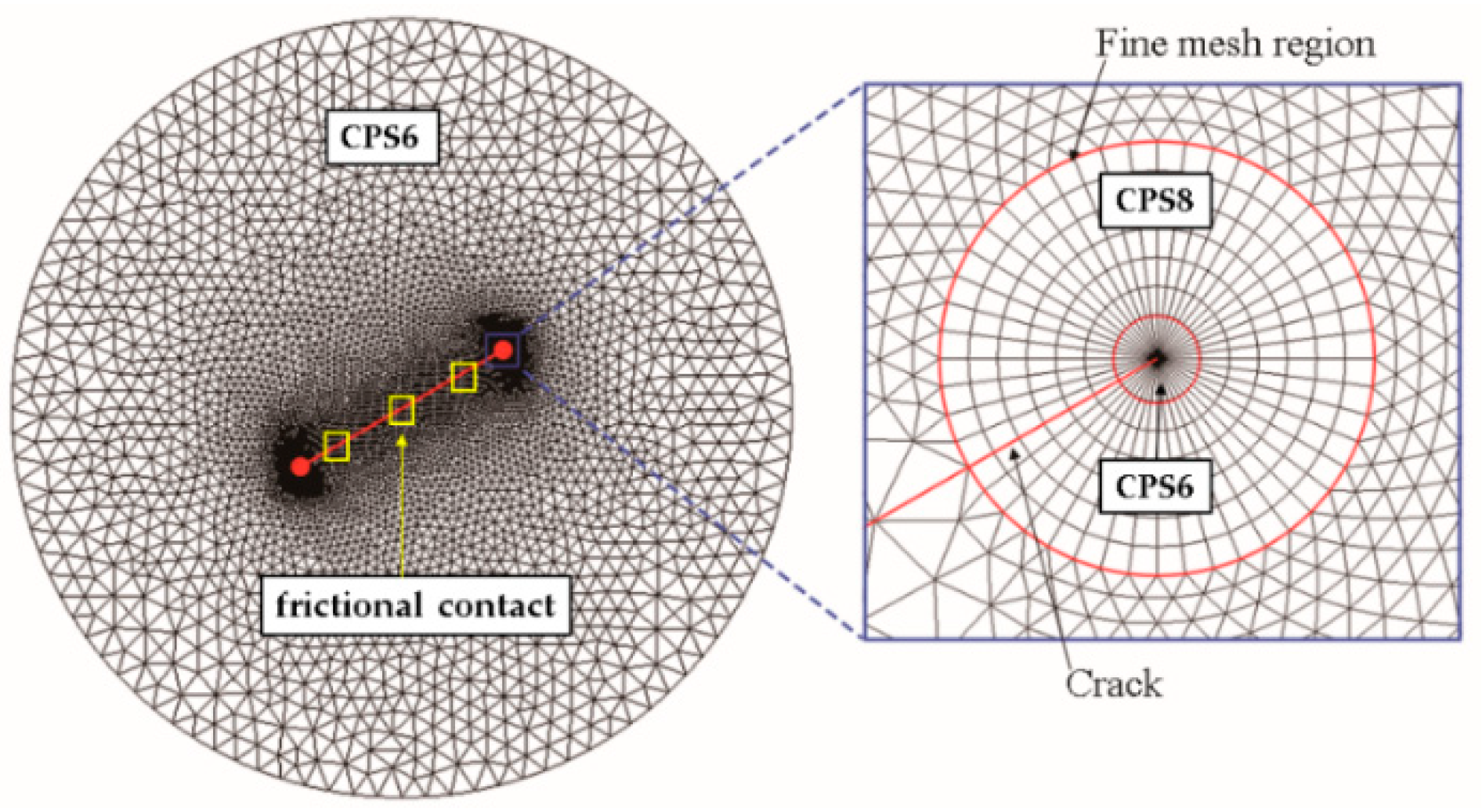
3. The WFM Concerning Frictional Contact
4. Results and Discussion
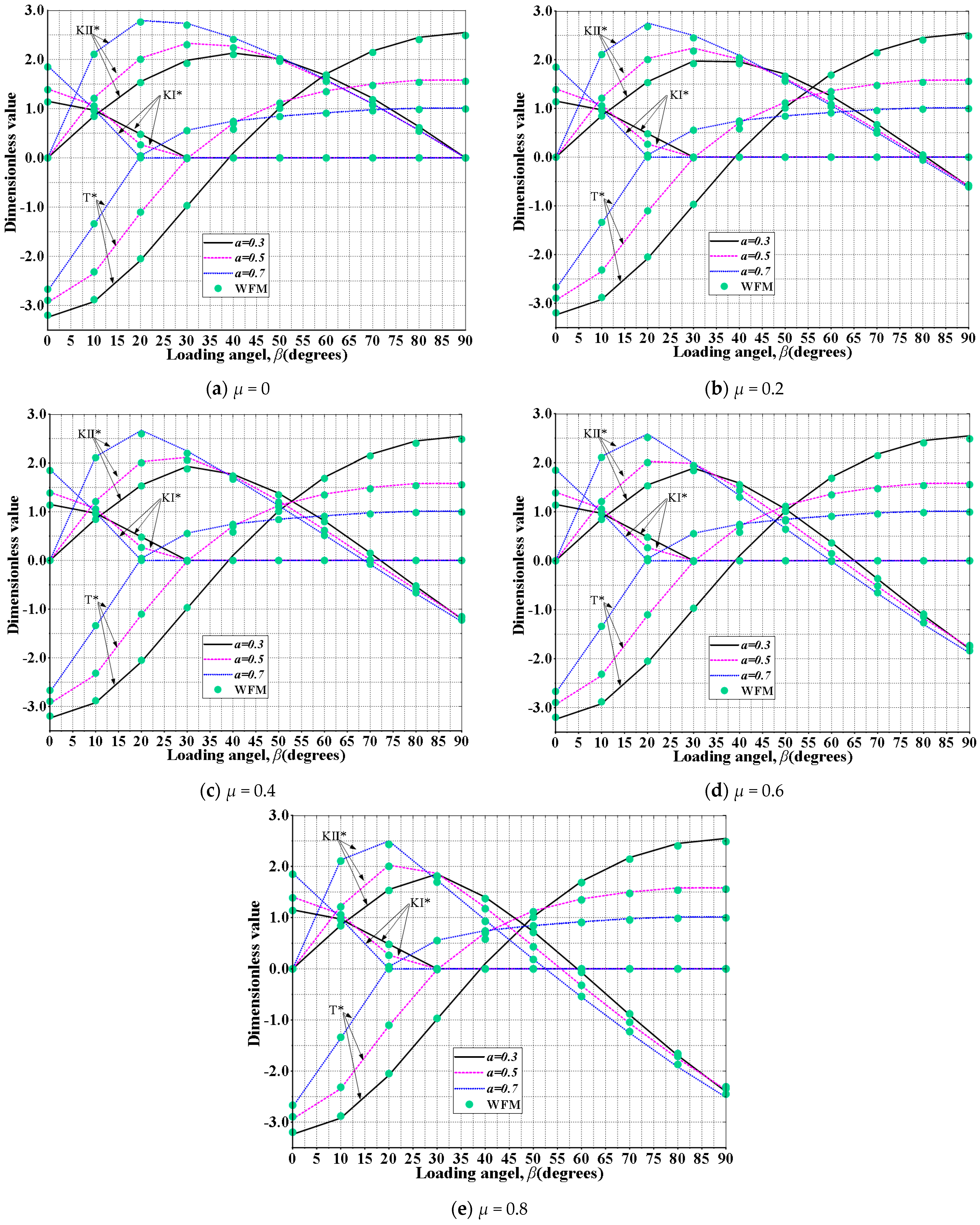
4.1. SIFs and T-Stress Concerning Frictional Contact
4.2. Crack Initiation and Propagation Concerning Frictional Contact
4.2.1. Crack Initiation
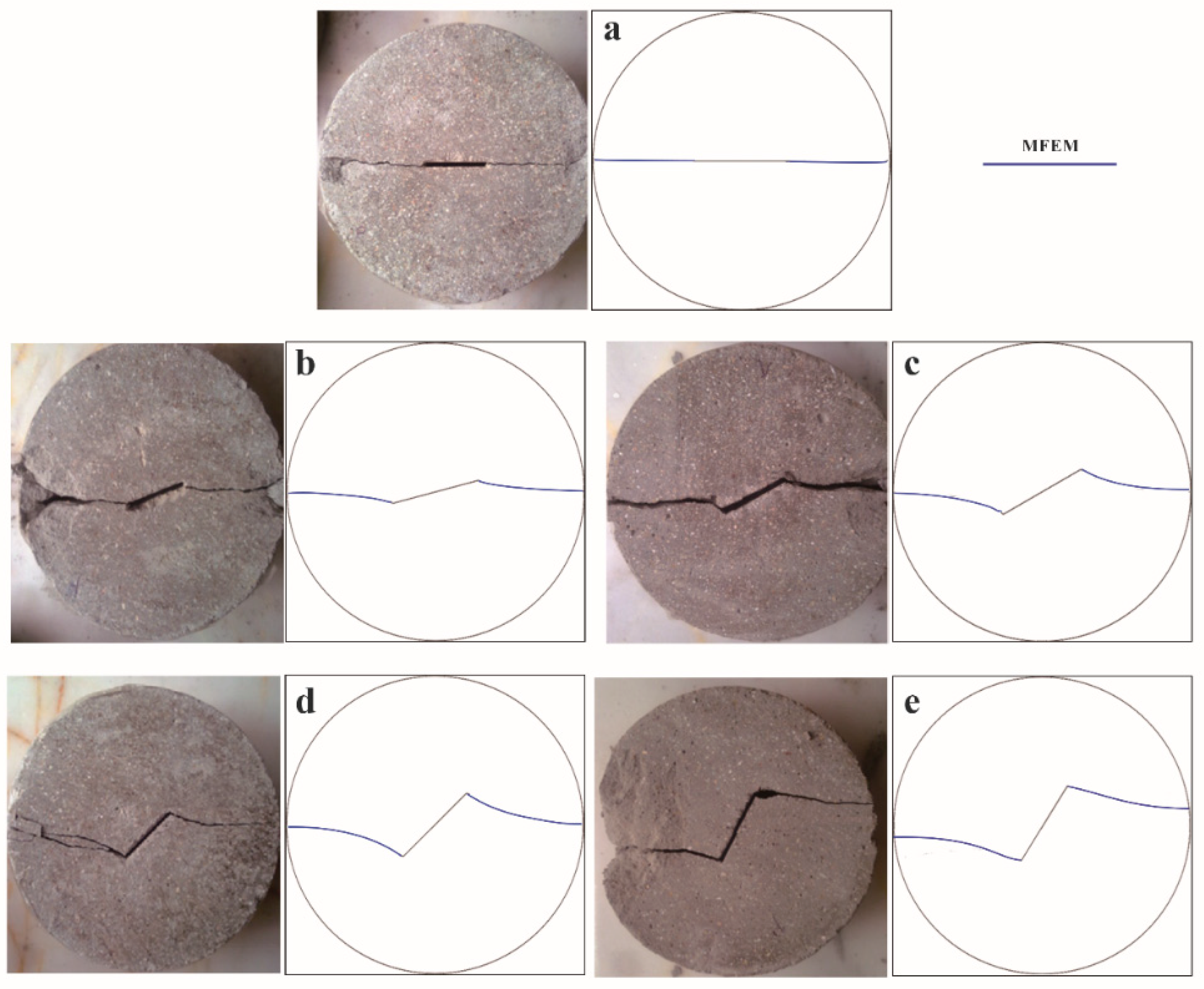
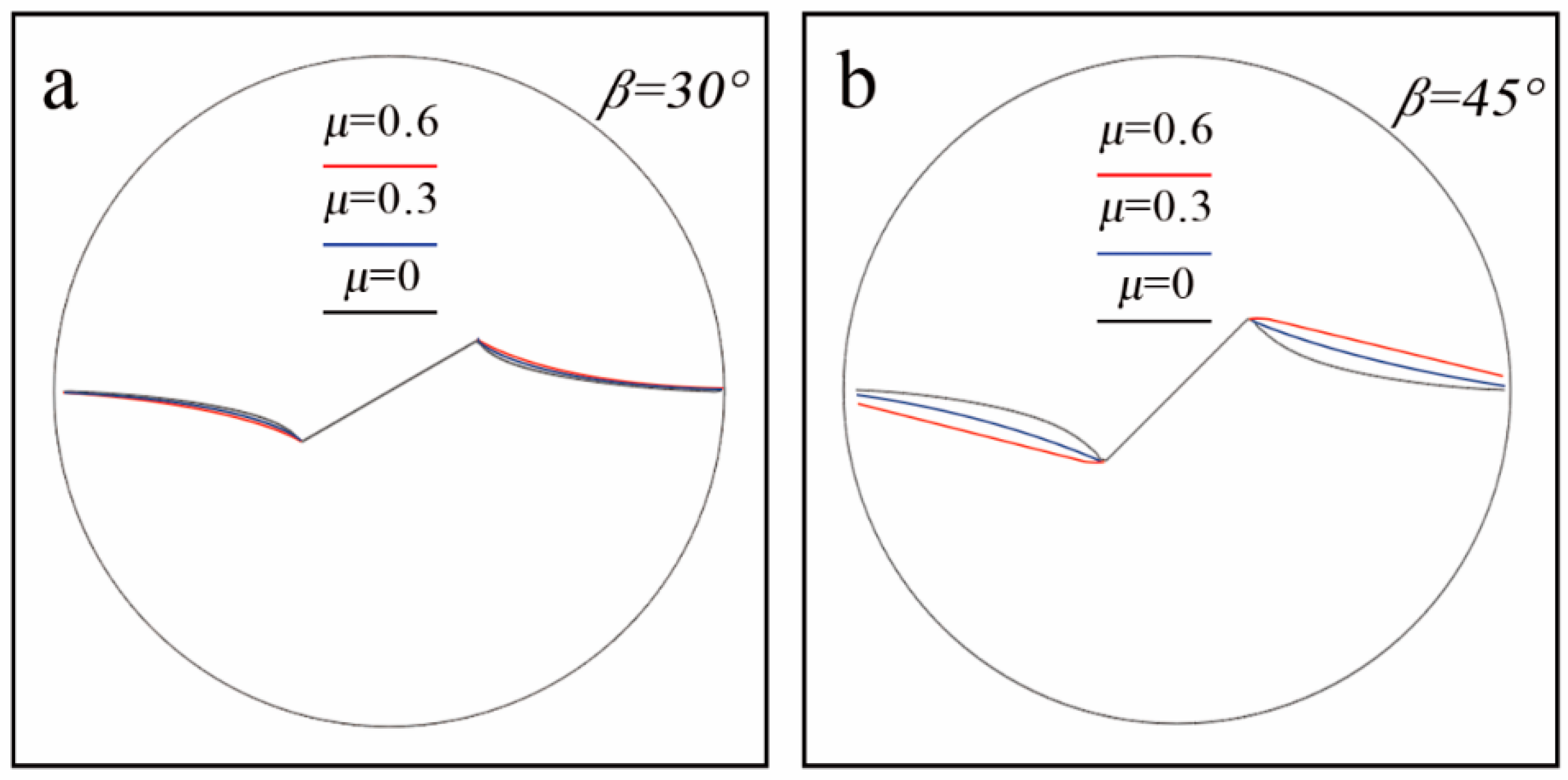
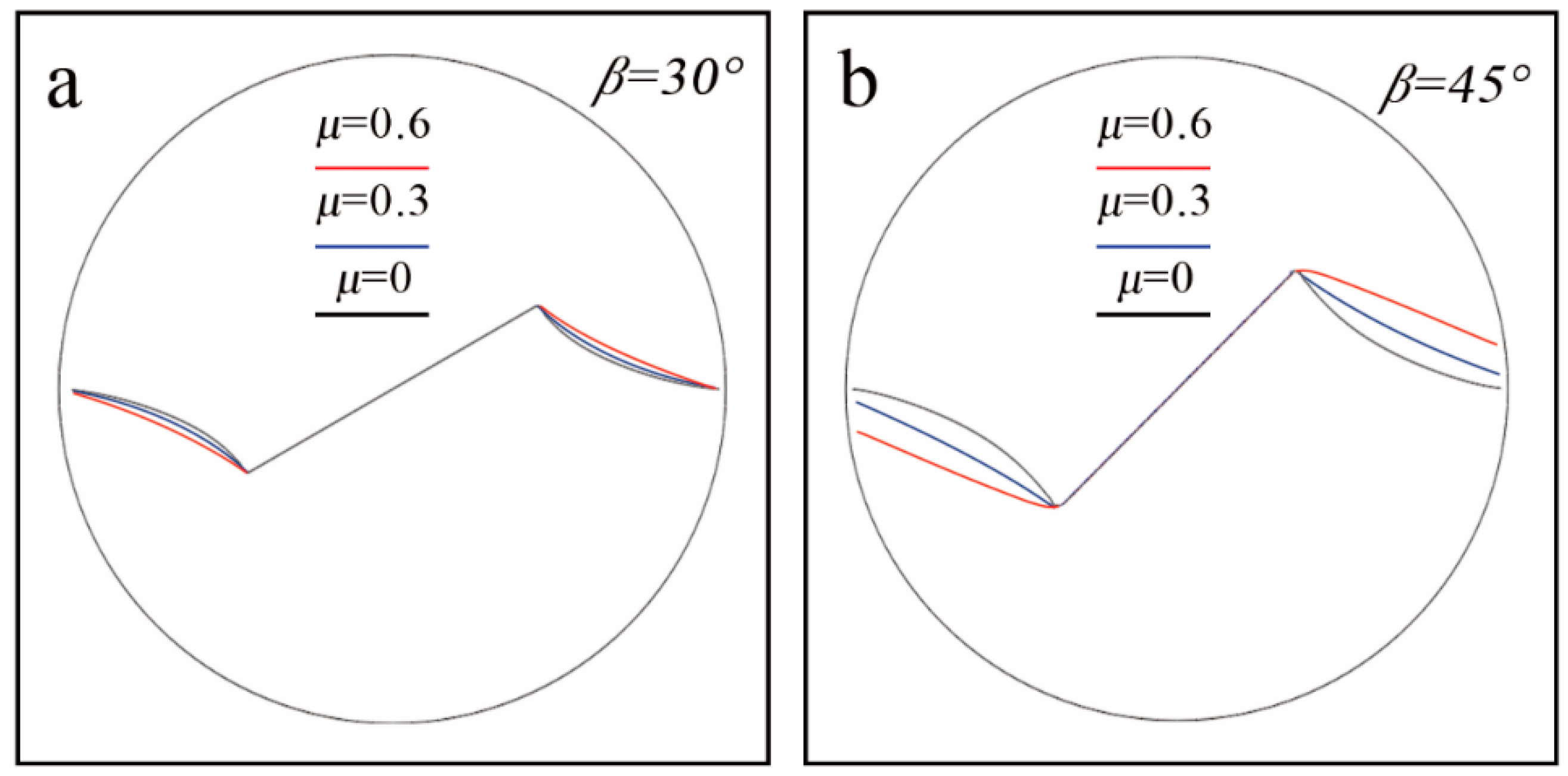
4.2.2. Crack Propagation Trajectory
5. Conclusions
- (1)
- The friction has a significant effect on the mode II SIF after the crack is closed, but has no influence on the stress intensity factor of mode I and T-stress. When the crack is closed, the mode II SIF decreases obviously as increasing the friction.
- (2)
- There are significant effects on the crack propagation angle and crack propagation trajectory due to the change of the friction after the crack is closed with the appropriate relative crack length and loading angle.
- (3)
- When T-stress is positive, the influence of friction becomes obvious and the crack propagation angle increases with a lager friction coefficient.
- (4)
- After the crack is closed, as increasing the friction, the amount of the deviation increases and the curvature of the path decreases. Furthermore, the crack type is easier to change with the increase of friction.
- (5)
- The effects of friction on the mode II SIF and the propagation path are more obvious with the larger the relative crack length and loading angle.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| W | interacting strain energy density |
| , , | stresses, displacements and strains of the actual fields |
| , , | stresses, displacements and strains of the auxiliary fields |
| , C, C+, C- | different integral contours |
| E*, E | elastic modulus |
| v | Poisson’s ratio |
| , | stress intensity factors of the auxiliary fields |
| , | stress intensity factors of the actual fields |
| T-stress | |
| P | radial force |
| B | thickness of the CCBD |
| R | radius of the CCBD |
| a | half the length of the crack |
| , , | dimensionless forms of stress intensity factors and T-stress |
| f | a line load |
| polar co-ordinates | |
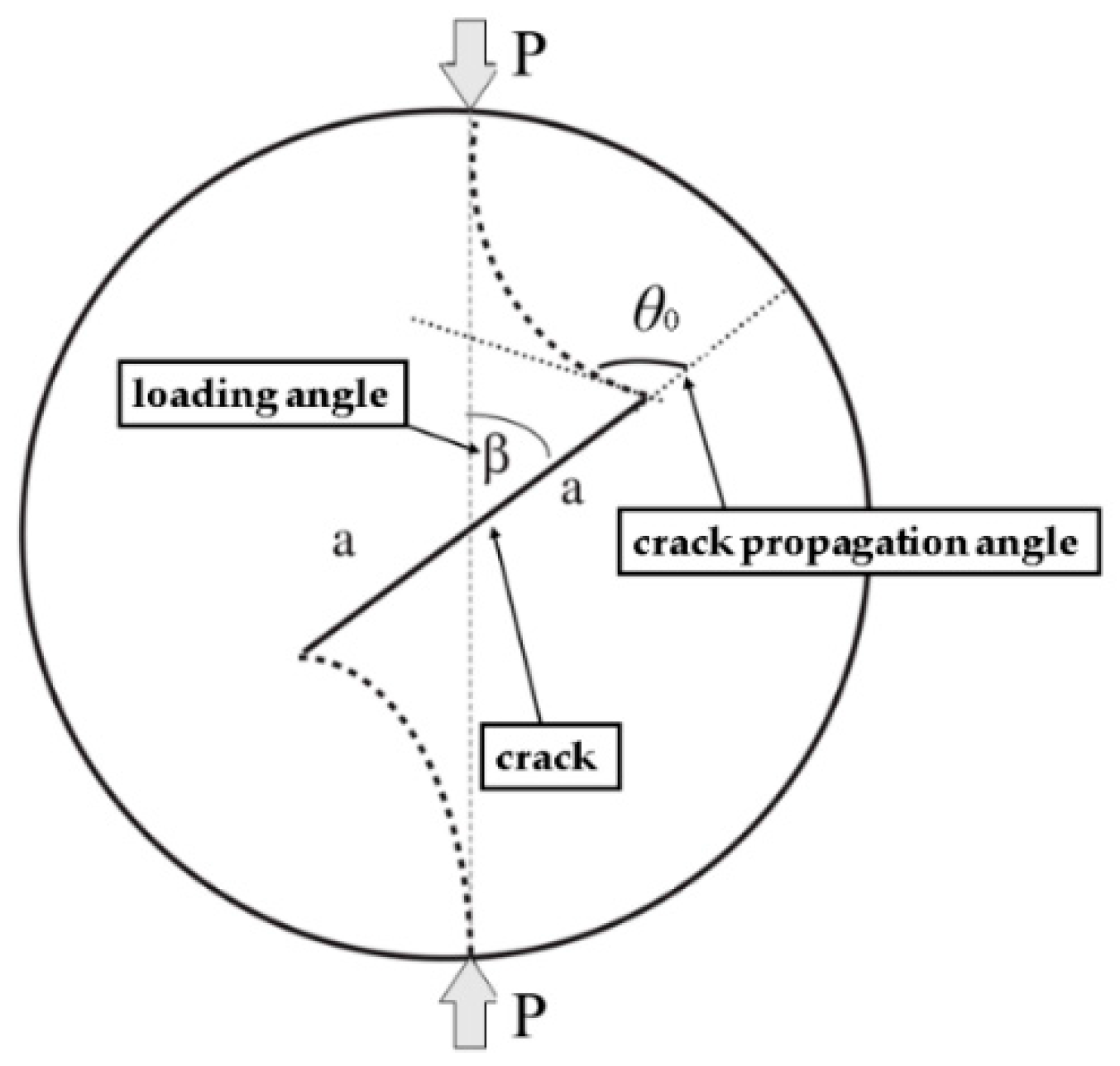
| β | loading angle |
| θ0 | crack propagation angle |
References
- Dong, S.; Wang, Y.; Xia, Y. Stress intensity factors for central cracked circular disk subjected to compression. Eng. Fract. Mech. 2004, 71, 1135–1148. [Google Scholar] [CrossRef]
- Markides, C.F.; Pazis, D.N.; Kourkoulis, S.K. Stress intensity factors for the Brazilian disc with a short central crack: Opening versus closing cracks. Appl. Math. Model. 2011, 35, 5636–5651. [Google Scholar] [CrossRef]
- Wu, B.; Yao, W.; Xia, K. An Experimental Study of Dynamic Tensile Failure of Rocks Subjected to Hydrostatic Confinement. Rock Mech. Rock Eng. 2016, 49. [Google Scholar] [CrossRef]
- Erarslan, N.; Williams, D.J. Mixed-Mode Fracturing of Rocks Under Static and Cyclic Loading. Rock Mech. Rock Eng. 2013. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Horii, H. Compression-induced nonplanar crack extension with application to splitting, exfoliation, and rockburst. J. Geophys. Res. Solid Earth 1982, 87. [Google Scholar] [CrossRef]
- Cotterell, B. Brittle fracture in compression. Int. J. Fract. Mech. 1972, 8, 195–208. [Google Scholar] [CrossRef]
- Hoek, E.; Bieniawski, Z.T. Brittle fracture propagation in rock under compression. Int. J. Fract. 1965, 1, 137–155. [Google Scholar] [CrossRef]
- Wong, L.N.Y.; Einstein, H.H. Systematic evaluation of cracking behavior in specimens containing single flaws under uniaxial compression. Int. J. Rock Mech. Min. Sci. 2009, 46, 239–249. [Google Scholar] [CrossRef]
- Park, C.H.; Bobet, A. Crack initiation, propagation and coalescence from frictional flaws in uniaxial compression. Eng. Fract. Mech. 2010, 77, 2727–2748. [Google Scholar] [CrossRef]
- Basu, A.; Mishra, D.A.; Roychowdhury, K. Rock failure modes under uniaxial compression, Brazilian, and point load tests. Bull. Eng. Geol. Environ. 2013, 72, 457–475. [Google Scholar] [CrossRef]
- Hua, W.; Xu, J.; Dong, S.; Song, J.; Wang, Q. Effect of confining pressure on stress intensity factors for cracked Brazilian disk. Int. J. Appl. Mech. 2015, 7, 1550051. [Google Scholar] [CrossRef]
- Li, N.; Dong, S.; Hua, W. Analysis of the effect of crack face contact on stress intensity factors for a centrally cracked Brazilian disk. Rock Soil Mech. 2017, 38, 2395–2401. [Google Scholar] [CrossRef]
- Tang, S.B. Stress intensity factors for a Brazilian disc with a central crack subjected to compression. Int. J. Rock Mech. Min. Sci. 2017, 93, 38–45. [Google Scholar] [CrossRef]
- Hua, W.; Li, Y.; Dong, S.; Li, N.; Wang, Q. T-stress for a centrally cracked Brazilian disk under confining pressure. Eng. Fract. Mech. 2015, 149, 37–44. [Google Scholar] [CrossRef]
- Hua, W.; Li, J.; Huang, J.; Dong, S. Theoretical Error Analysis of the T-Stress for a Central Cracked Brazilian Disk Specimen. Int. J. Appl. Mech. 2020. [Google Scholar] [CrossRef]
- Tang, S.B. The effect of T-stress on the fracture of brittle rock under compression. Int. J. Rock Mech. Min. Sci. 2015, 79, 86–98. [Google Scholar] [CrossRef]
- Spagnoli, A.; Carpinteri, A.; Terzano, M. Mode II crack shielding in a compressed rough crack with friction. Theor. Appl. Fract. Mech. 2020, 107. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, L.; Berto, F.; Zhou, L. Comprehensive study on the crack tip parameters of two types of disc specimens under combined confining pressure and diametric concentrated forces. Theor. Appl. Fract. Mech. 2019, 103, 102317. [Google Scholar] [CrossRef]
- Huang, J.; Li, J.; Pan, X.; Xie, T.; Hua, W.; Dong, S. Numerical Investigation on Mixed Mode (I-II) Fracture Propagation of CCBD Specimens Under Confining Pressure. Int. J. Appl. Mech. 2020, 12, 2050111. [Google Scholar] [CrossRef]
- Hou, C.; Wang, Z.; Liang, W.; Yu, H.; Wang, Z. Investigation of the effects of confining pressure on SIFs and T-stress for CCBD specimens using the XFEM and the interaction integral method. Eng. Fract. Mech. 2017, 178, 279–300. [Google Scholar] [CrossRef]
- Lim, I.L.; Johnston, I.W.; Choi, S.K. A finite element code for fracture propagation analysis within elasto-plastic continuum. Eng. Fract. Mech. 1996, 53, 193–211. [Google Scholar] [CrossRef]
- Haeri, H.; Shahriar, K.; Marji, M.F.; Moarefvand, P. Experimental and numerical study of crack propagation and coalescence in pre-cracked rock-like disks. Int. J. Rock Mech. Min. Sci. 2014, 67, 20–28. [Google Scholar] [CrossRef]
- Zhou, X.P.; Bi, J.; Qian, Q.H. Numerical Simulation of Crack Growth and Coalescence in Rock-Like Materials Containing Multiple Pre-existing Flaws. Rock Mech. Rock Eng. 2015, 48, 1097–1114. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, X.; Xu, X. Numerical simulation of propagation and coalescence of flaws in rock materials under compressive loads using the extended non-ordinary state-based peridynamics. Eng. Fract. Mech. 2016, 163, 248–273. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, X. Phase field model for simulating the fracture behaviors of some disc-type specimens. Eng. Fract. Mech. 2020, 226, 106870. [Google Scholar] [CrossRef]
- Ty, B.; Black, T. Elastic Crack Growth in Finite Elements with Minimal Remeshing. Int. J. Numer. Method Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Dolbow, J.; Moës, N.; Belytschko, T. An extended finite element method for modeling crack growth with frictional contact. Comput. Methods Appl. Mech. Eng. 2001, 190, 6825–6846. [Google Scholar] [CrossRef] [Green Version]
- Taniguchi, T. Crack propagation analysis in civil engineering structures. Comput. Struct. 1991, 41, 1295–1303. [Google Scholar] [CrossRef]
- Wang, Z.; Ma, L.; Yu, H.; Wu, L. Dynamic stress intensity factors for homogeneous and non-homogeneous materials using the interaction integral method. Eng. Fract. Mech. 2014, 128, 8–21. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, L.; Huang, K.; Bai, X.; Zhang, Z. A numerical method for the thermal-shock crack problems of nonhomogeneous materials with inclusions based on an interaction energy integral method. Eng. Fract. Mech. 2017, 190. [Google Scholar] [CrossRef]
- Kim, J.-H.; Paulino, G.H. T-stress, mixed-mode stress intensity factors, and crack initiation angles in functionally graded materials: A unified approach using the interaction integral method. Comput. Methods Appl. Mech. Eng. 2003, 192, 1463–1494. [Google Scholar] [CrossRef]
- Yu, H.; Wu, L.; Guo, L.; Li, H.; Du, S. T-stress evaluations for nonhomogeneous materials using an interaction integral method. Int. J. Numer. Method Eng. 2012, 90, 1393–1413. [Google Scholar] [CrossRef]
- Williams, M.L. On the Stress Distribution at the Base of a Stationary Crack. J. Appl. Mech. 1957, 24, 109–114. [Google Scholar] [CrossRef]
- Yu, H.; Wang, J.; Shimada, T.; Wu, H.; Wu, L.; Kuna, M.; Kitamura, T. An I-integral method for crack-tip intensity factor variation due to domain switching in ferroelectric single-crystals. J. Mech. Phys. Solids 2016. [Google Scholar] [CrossRef]
- Erdogan, F.; Sih, G. On the Crack Extension in Plates Under Plane Loading and Transverse Shear. J. Basic Eng. 1963, 85. [Google Scholar] [CrossRef]
- Lin, Q.; Wang, S.; Pan, P.Z.; Ji, W.W.; Lu, Y. Fracture initiation under pure shear revisited: Remarks on the mode II fracture in quasi-brittle materials. Theor. Appl. Fract. Mech. 2020. [Google Scholar] [CrossRef]
- Sih, G.C. Strain-energy-density factor applied to mixed mode crack problems. Int. J. Fract. 1974, 10, 305–321. [Google Scholar] [CrossRef]
- Hussain, M.A.; Pu, S.L.; Underwood, J. Strain Energy Release Rate for a Crack Under Combined Mode I and Mode II. Irwin, G.R., Ed.; ASTM International: West Conshohocken, PA, USA, 1974; Volume 28, pp. 2–28. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Aliha, M.R.M.; Hassani, M.M. Mixed mode brittle fracture in PMMA—An experimental study using SCB specimens. Mater. Sci. Eng. A 2006, 417, 348–356. [Google Scholar] [CrossRef]
- Akbardoost, J.; Ayatollahi, M.R. Experimental analysis of mixed mode crack propagation in brittle rocks: The effect of non-singular terms. Eng. Fract. Mech. 2014, 129, 77–89. [Google Scholar] [CrossRef]
- Hua, W.; Dong, S.; Xu, J. Experimental study on the fracture toughness of rust stone under mixed mode loading condition. Mater. Res. Innov. 2015, 19, 531–536. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Aliha, M.R.M. Mixed mode fracture analysis of polycrystalline graphite–A modified MTS criterion. Carbon 2008, 46, 1302–1308. [Google Scholar] [CrossRef]
- Fett, T. T -stresses in rectangular plates and circular disks. Eng. Fract. Mech. 1998, 60, 631–652. [Google Scholar] [CrossRef]
- Fett, T. Stress intensity factors and T-stress for internally cracked circular disk under various boundary conditions. Eng. Fract. Mech. 2001, 68, 1119–1136. [Google Scholar] [CrossRef]
- Atkinson, C.; Smelser, R.E.; Sanchez, J. Combined mode fracture via the cracked Brazilian disk test. Int. J. Fract. 1982, 18, 279–291. [Google Scholar] [CrossRef]
- Jaeger, J.C.; Cook, N.G.W.; ZImmerman, R.W. Fundamentals of Rock Mechanics, 4th ed.; Wiley-Blackwell: Oxford, UK, 2007. [Google Scholar]
- Shephard, M.S.; Yehia, N.A.B.; Burd, G.S.; Weidner, T.J. Automatic crack propagation tracking. Comput. Struct. 1985, 20, 211–223. [Google Scholar] [CrossRef]
- Mardon, D.; Kronenberg, A.K.; Handin, J.; Friedman, M.; Russell, J.E. Mechanisms of fracture propagation in experimentally extended Sioux quartzite. Tectonophysics 1990, 182, 259–278. [Google Scholar] [CrossRef]
- Basista, M.; Gross, D. A Note on Crack Interactions Under Compression. Int. J. Fract. 2000, 102, 67–72. [Google Scholar] [CrossRef]
- Dorogoy, A.; Banks-Sills, L. Effect of crack face contact and friction on Brazilian disk specimens—A finite difference solution. Eng. Fract. Mech. 2005, 72, 2758–2773. [Google Scholar] [CrossRef]
- Xie, Y.J.; Duo, Y.L.; Yuan, H. Potential fracture paths for cracked rocks under compressive-shear loading. Int. J. Rock Mech. Min. Sci. 2020, 128, 104216. [Google Scholar] [CrossRef]


| Categories | Values | |
|---|---|---|
| Geometry characters | R (mm) | 50 |
| B (mm) | 30 | |
| Material properties | Compressive strength σc (MPa) | 28 |
| Tensile strength σt (MPa) | 3.81 | |
| Poisson’s ratio v | 0.21 | |
| Young’s modulus E (GPa) | 15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, J.; Pan, X.; Li, J.; Dong, S.; Hua, W. Numerical Investigation on Crack Propagation for a Central Cracked Brazilian Disk Concerning Friction. Appl. Sci. 2021, 11, 2839. https://doi.org/10.3390/app11062839
Huang J, Pan X, Li J, Dong S, Hua W. Numerical Investigation on Crack Propagation for a Central Cracked Brazilian Disk Concerning Friction. Applied Sciences. 2021; 11(6):2839. https://doi.org/10.3390/app11062839
Chicago/Turabian StyleHuang, Jiuzhou, Xin Pan, Jianxiong Li, Shiming Dong, and Wen Hua. 2021. "Numerical Investigation on Crack Propagation for a Central Cracked Brazilian Disk Concerning Friction" Applied Sciences 11, no. 6: 2839. https://doi.org/10.3390/app11062839
APA StyleHuang, J., Pan, X., Li, J., Dong, S., & Hua, W. (2021). Numerical Investigation on Crack Propagation for a Central Cracked Brazilian Disk Concerning Friction. Applied Sciences, 11(6), 2839. https://doi.org/10.3390/app11062839






