Design, Modeling, and Simulation of a Wing Sail Land Yacht

Featured Application

This work describes the design, modeling, and simulation of a free-rotating wing sail solution for an autonomous environmental land yacht probe. The adopted method involves the application of land sailing principles for the design, the usage of Fusion 360 tool for 3D modeling, and the integration of Gazebo with the Robotic Operating System (ROS) framework for the simulation of the land yacht.

Abstract

Autonomous land yachts can play a major role in the context of environmental monitoring, namely, in open, flat, windy regions, such as iced planes or sandy shorelines. This work addresses the design, modeling, and simulation of a land yacht probe equipped with a rigid free-rotating wing sail and tail flap. The wing was designed with a symmetrical airfoil and dimensions to provide the necessary thrust to displace the vehicle. Specifically, it proposes a novel design and simulation method for free rotating wing sail autonomous land yachts. The simulation relies on the Gazebo simulator together with the Robotic Operating System (ROS) middleware. It uses a modified Gazebo aerodynamics plugin to generate the lift and drag forces and the yawing moment, two newly created plugins, one to act as a wind sensor and the other to set the wing flap angular position, and the 3D model of the land yacht created with Fusion 360. The wing sail aligns automatically to the wind direction and can be set to any given angle of attack, stabilizing after a few seconds. Finally, the obtained polar diagram characterizes the expected sailing performance of the land yacht. The described method can be adopted to evaluate different wing sail configurations, as well as control techniques, for autonomous land yachts.

1. Introduction

In the last decades a broad range of research has been conducted in autonomous systems, ranging from land to marine or aerial robots, since these vehicles are useful in a very broad spectrum of tasks, due to their ability to remove humans from dangerous environments, relieve them of tedious tasks, or simply go to locations otherwise inaccessible or inhospitable [1]. Diverse applications have been envisaged for these platforms, from exploration of remote places [2] to warfare [3].

In order to have truly autonomous systems, they must present not only control autonomy but also energy autonomy. A possibility for granting energy autonomy to land and marine vehicles is to make use of wind to propel the vehicle [4] and, eventually, to power its on-board systems [5,6,7]. To propel these vehicles, traditional fabric sails (the most common approach), rigid wing sails, and mechanical devices, such as Flettner rotors or vertical and horizontal axis turbines, or even more uncommon options, such as different sail concepts or towing kites [8], can be adopted.

Sailing has been practiced all around the world for thousands of years and virtually all boats, apart from those in recent sailing history, used conventional fabric sails [4]. Although flexible fabric sails have a number of useful properties, especially when controlled by a human sailor, they also present a number of limitations and / or drawbacks which can be overcome by alternative sail types, in particular rigid wing sails [8]. Among the advantages of using rigid wing sails for autonomous systems are the fact that its control is easier to automate and their increased reliability [8]. Given these advantages, the use of rigid wing sails has been proposed, for example, for powering commercial ships [9].

The vast majority of robotic sailing research is focused on wind propelled water platforms—sailboats; however, there is a lesser common type of sailing vehicles—land yachts. As autonomous robotic platforms, land yachts can play an important role in the context of environmental monitoring, namely, in the case of open flat windy regions, such as iced planes or sandy shorelines. As a result, autonomous land yachts can be used to monitor river, lake or ocean shoreline environments, or even for planetary exploration [10]. Like a sailboat, a land yacht does not require motors for propulsion, as it uses the wind, resulting in a considerable increase in power autonomy [11,12,13].

Although the majority of the autonomous sailing research addresses sailboats, there are also works on land yachts. The latter include the contributions of:

• Landis et al. [10,14] propose the National Aeronautics and Space Administration (NASA) Zephyr land sailing rover. It is intended to be used in Venus, a harsh, windy planet. The conceptual design uses a NACA0015 airfoil with a wingspan of 5.44 m, a lateral area of 12 m², and weight of 49 kg. The chassis has a triangular shape with three wheels and weighs 35 kg.
• Xie et al. [11] present the Autonomous Controlled Four-Wheeled Land Yacht concept. This land vehicle is propelled by a single wing sail with a symmetrical profile, 1 m wingspan, a lateral area of 0.25 m², a mass of 2.15 kg, and a rotation range of 0°–360°. The chassis is composed by an aluminium hull and two front and two rear wheels with a total mass of 19 kg.
• Chen et al. [15] propose the Multiple Wing Sail Land Yacht. It adopts a triple wing sail design to reduce the wind velocity required to start the vehicle motion. The remaining features are equal to those of the previous example.
• Zhu et al. [13] adopt a free-rotating NACA0015 wing sail with a wingspan of 2.5 m and a lateral area of 1.25 m² design to rig a land yacht. The steel chassis has one front wheel and two rear wheels. Although not fully autonomous, the angle of attack of the free-rotating wing sail is set by controlling the tail flap, which induces torque on the wing sail.
• Mirzaei et al. [16] describe a land yacht developed with a NACA0012 airfoil. The airfoil has a wingspan of 1 m and a lateral area of 0.5 m². The chassis has a triangular shape with a front wheel and two rear wheels and has a mass of 8 kg.
• Dong et al. [17] describe a land yacht with a wing sail and a chassis. The NACA0015 airfoil has a wingspan of 0.8 m, a lateral area of 0.24 m², and a rotation range of 0°–270°. The chassis has four steel wheels and plastic frame.
• Reina et al. [18] detail a land yacht model which has a NACA0012 airfoil with a wingspan of 3 m and a lateral area of 2 m². The triangular chassis has three wheels and weighs 100 kg.

The main characteristics of the above reviewed land yachts are compared in

Table 1. Reviewed autonomous land yachts.

Source	Wing Sail						Chassis
	Airfoil	Free Rot.	Angle Range	Wingspan	Lat. Area	Mass	Material	Wheels	Mass
			(°)	(m)	(m2)	(kg)			(kg)
Xie et al. [11]	NACA0018	No	0–360	1	$0.25$	$2.15$	Aluminum	4	19
Chen et al. [15]	3 × NACA0018	No	0–360	3 × 1	3 × 0.25	3 × 2.15	Aluminum	4	19
Zhu et al. [13]	NACA0015	Yes	0–360	$2.5$	$1.25$	-	Steel	4	-
Mirzaei et al. [16]	NACA0012	No	-	1	$0.5$	-	-	3	8
Dong et al. [17]	NACA0015	No	0–270	$0.8$	$0.24$	-	Steel & Plastic	4	-
Reina et al. [18]	NACA0012	No	-	3	$0.66$	-	-	3	100
Geoffrey et al. [10]	NACA0015	No	-	$5.44$	12	49	-	3	35

. All these prototypes share the type of sail—symmetrical wing sails—and perception sensors—Global Navigation Satellite Systems (GNSS) receivers, inertial and wind direction, and velocity units. Apart from the proposals of Reference [13,17,18], the remaining platforms adopt a four-wheeled chassis with a higher rear wheel baseline. This design option provides, according to Reference [11,15,16], greater stability and maneuverability.

Land yachts are not only governed by the principles of sailing [4], but sail design is an essential part of their development [19]. The research and development performed on rigid-wing sails has a much bigger scope than just land yachts. This type of sails is, as previously stated, commonly used in marine vessels, such as sailboats. Like the autonomous land yachts, several autonomous rigid-wing sailboats have been developed by the scientific community. Some examples of these vessels are: (i) the Atlantis autonomous catamaran [20] which uses a NACA0015 airfoil as the wing sail with a wingspan of 5.37 m and a lateral area of 7.8 m². Furthermore, the wing sail is free rotating, meaning it is not controlled directly and aligns with the wind direction (as it is a symmetrical airfoil). Instead, the wing sail is controlled by a wing flap that induces torque on the wing sail, making it shift slightly to an angle of attack; (ii) the Autonomous Robot for Ocean Observation sailboat [21] which uses a rigid-wing sail with a wingspan of 1.30 m and a lateral area of 0.23 m²; (iii) the ASPire [22], which uses a free-rotating wing sail with a NACA${63}_2$-618 profile. The wing sail wingspan is of $2.8$ $\mathrm{m}$, and the lateral area is of $2.1$ $\mathrm{m}$².

Considering the modeling and/or simulation of platforms propelled by wing sails, there is scant research on land yachts:

• Chen et al. [23] derive a mathematical model for a four-wheel land yacht powered by a wing sail. They model the structure, steering gear, servomotors and force of wing sail and, then, simulate the motion of land yacht according to the mathematical model. The mathematical model analyzes both the linear and steering motions. The simulation and actual experimental results confirm the feasibility and reliability of the proposed land-yacht modeling.
• Dong et al. [17] present the design, simulation and development of a wind-driven land yacht propelled by a wing sail. The authors conduct a theoretical analysis and use ANSYS Fluent simulation software to determine the lift and drag coefficients corresponding to each combination of attack and heading angles, and the best attack angle corresponding to each different heading angle. The simulation and experimental upwind results were concordant.

The modeling and/or simulation of sailboat platforms equipped with wing sails is more abundant. The following list holds a set of representative works:

• Rynne and von Ellenrieder [24] design, simulate and develop a wind (rigid wing sail) and solar-powered autonomous surface vehicle (ASV). Before building the ASV, the control simulation was performed with a velocity prediction program (VPP). Initial field trials showed that the experimental and simulated boat speeds and wind speed/directions were consistent.
• Enqvist et al. [25] design and simulate a simple, reliable and highly autonomous sailboat. They choose a symmetrical, free-rotating wing sail with an additional tail for actuating the wing and controlling its angle of attack. The design was further investigated with a computation flow dynamics simulation software.
• Augenstein et al. [26] design and simulate small ( 1 $\mathrm{m}$) semi-autonomous robotic sailboat platform variants equipped with a symmetric airfoil sail, a thin, bulbed keel, and a tail-vane rudder, replacing the traditional water rudder. They adopt MATLAB to perform 2D and 3D dynamic simulations of the tail-vane rudder design.
• Setiawan et al. [27] design and simulate an autonomous sailboat dynamic model with four degrees of freedom. The simulations were carried out with MATLAB/Simulink to determine the effect of flap and rudder deflection angles on boat dynamics.

This survey on the simulation of platforms propelled by wing sails shows that none utilizes the Robotic Operating System (ROS) middleware and the Gazebo simulator. The work presented in this article offers a novel simulated environment for autonomous land yachts using the ROS middleware and the Gazebo simulator. Furthermore, two Gazebo plugins are developed to (i) act as a wind sensor and (ii) to set the flap angular position.

This article is a condensed version of the thesis presented in Reference [28] and contributes to robotic sailing through the design, modeling, and simulation of an autonomous rigid wing sail land yacht, which can be used to survey and monitor the shoreline (more specifically sandy areas), with the help of the Gazebo (Gazebo simulator website: http://gazebosim.org, accessed on 19 March 2021) simulator and the Robot Operating System (ROS) (ROS website: https://www.ros.org, accessed on 19 March 2021) middleware. Moreover, the proposed method can be followed to perform a priori evaluation of alternative wing configurations and control algorithms, i.e., without the need to build the actual land yachts. The proposed method constitutes a novel approach to the design and simulation of free rotating wing sail autonomous land yachts. This kind of sail, which is is controlled trough the tail flap, minimizes the energy consumed by the sail control system. Once actuated, the flap generates a linear force that induces torque on the wing sail. This shifts slightly the wing sail from the wind direction, defining the sail’s angle of attack.

2. Materials and Methods

This work applies the principles of land sailing physics to the design, modeling, and simulation of a shore monitoring land yacht. The next subsections cover these different stages, detailing the relevant steps required to reproduce the results.

A rigid-wing sail land yacht uses an airfoil as a sail instead of a conventional fabric sail [12]. The wing sail generates aerodynamic forces, such as lift and drag, and is more efficient, robust and easier to control than conventional fabric sails as, generally, these fabric sails require more than one actuator to be controlled and a wing sail only requires one [12]. Even though wind propelled vehicles, when compared with their fuel or electricity based counterparts, display greater power autonomy, it can be further increased with the adoption of a free rotating wing sail equipped with a wing flap.

By default, a free rotating wing sail automatically aligns to the wind direction, defining an angle between the cord of the wing and the oncoming wind flow, called angle of attack. This angle of attack can be controlled by changing the direction of the wing flap. Specifically, when the angle between the wing flap and the apparent wind changes, it generates a linear force that induces torque on the wing sail, defining a new angle of attack.

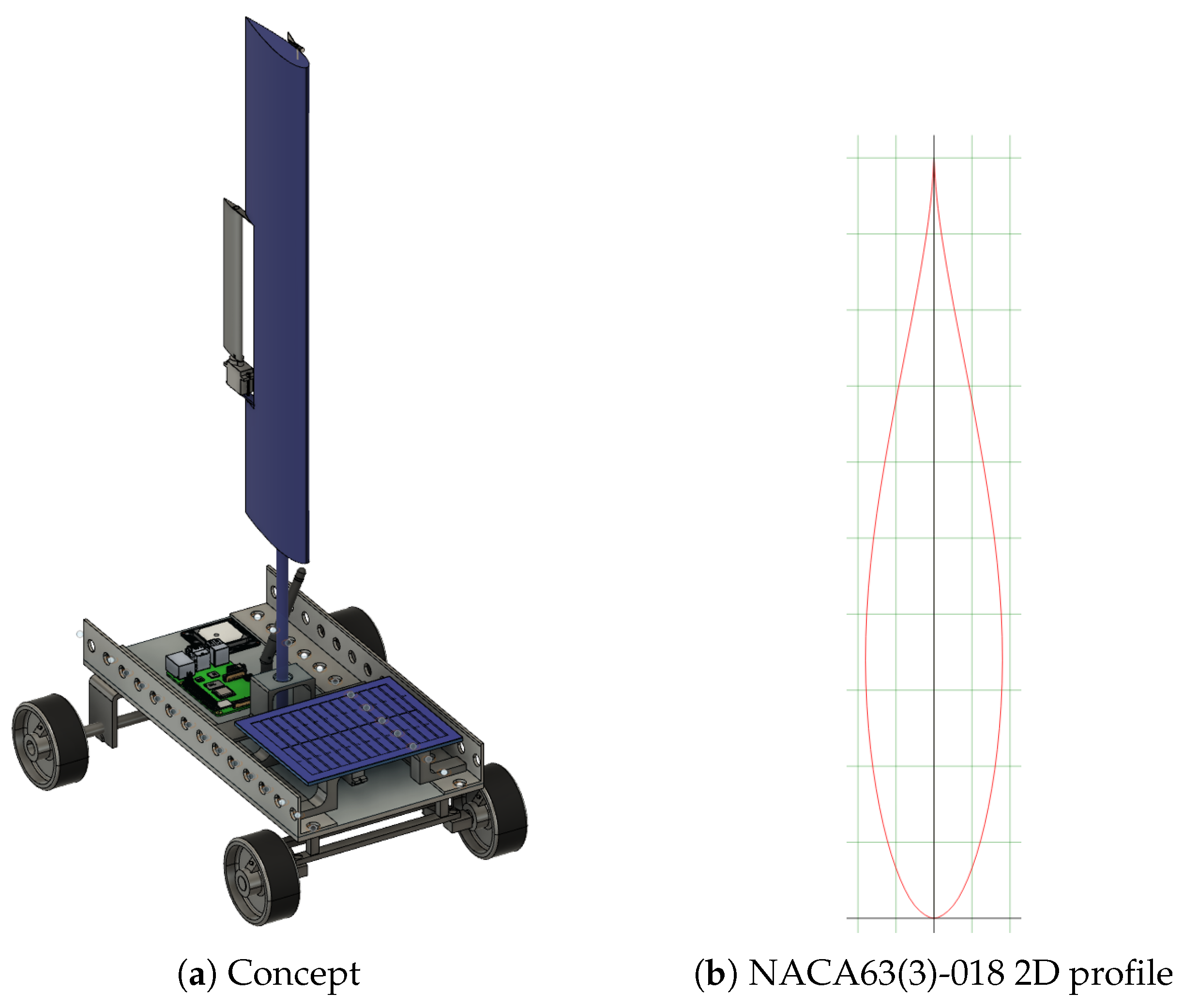
2.1. Platform Design

The proposed land yacht has a four-wheeled chassis, similar to the prototypes presented in Reference [11,15,17]. The chassis, made of stainless steel grade 316 L with a density of 7990 $\mathrm{k}\mathrm{g}$/${\mathrm{m}}^3$, has a parallelepipedic shape with a width of 360 mm, a length of 700 mm and a thickness of 5 mm, totaling 10 $\mathrm{kg}$. Together, the wing, flap and mast weigh 6 $\mathrm{kg}$. The wing and flap airfoils share the same symmetrical National Advisory Committee for Aeronautics (NACA) profile. The expected maximum payload of the land yacht is 4 $\mathrm{kg}$.

The land yacht determines its current state with the help of a set of sensors: (i) a GNSS receiver for the position, an inertial sensor for the attitude, an absolute rotary encoder for the wing sail direction; (ii) a wind sensor for the apparent wind direction; and (iii) from the previous sensor information, the angle of attack of the wing sail. Given a mission, the land yacht calculates the desired heading angle (yacht) and angle of attack (wing sail) to go to the next way point and actuates two servo motors to control the wing flap and the steering mechanism accordingly. The concept of the designed land yacht is shown in Figure 1a.

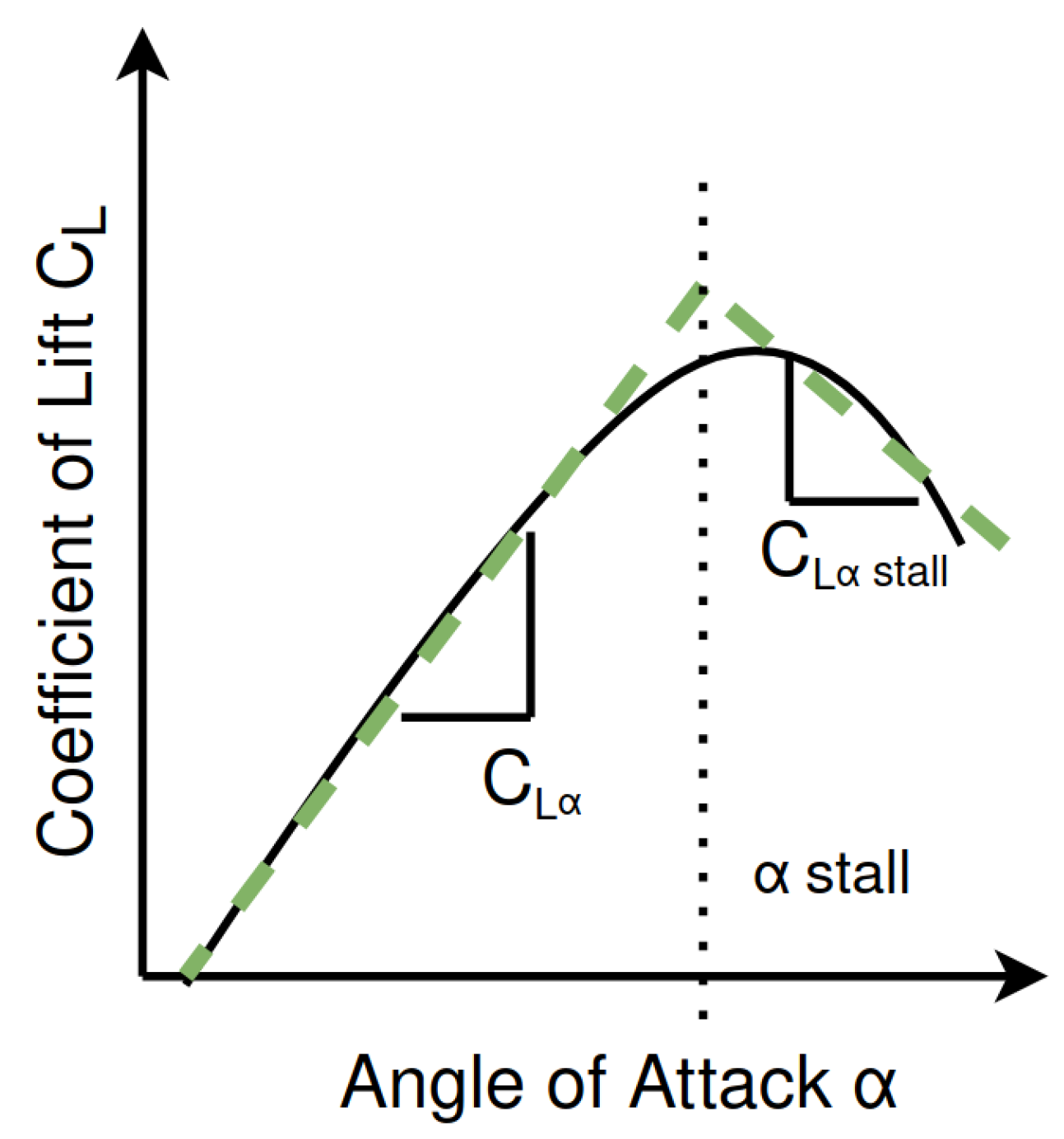
2.2. Wing Sail Design

The method adopted to define the physical characteristics of the wing sail was suggested by Reference [29]. The angle of attack $\alpha$ of a wing sail corresponds to the angle between the wing chord and the apparent wind direction. Non-null $\alpha$ values generate perpendicular and parallel forces relative to the apparent wind, known as lift (L) and drag (D), and their magnitude depends on the corresponding lift ($C_L$) and drag ($C_D$) coefficients [30].

The selected wing profile was a NACA63(3)-018 symmetrical airfoil as it provides a high lift to drag ratio (73) for an $\alpha =6.75{}^{°}$, as well as keeps a low drag coefficient (0.02) at $\alpha =10{}^{°}$, with a Reynolds number of 500,000 [31,32]. The 2D profile of the NACA63(3)-018 airfoil is presented in Figure 1b.

The lift and drag forces produced in a sail depend on its shape and dimensions. In this case, the area of the wing sail surface needs to generate sufficient lifting force to move the land yacht. The lift force is presented in Equation (1), where $\rho$ is the air density, V is the apparent wind velocity, A is the airfoil lateral area (chord × wingspan), and $C_L$ is the airfoil lift coefficient.

$$L=\frac{1}{2}\rho V^{2}A{C}_L.$$

(1)

The drag force is given by Equation (2), where $\rho$ is the air density, V is the apparent wind velocity, A is the airfoil lateral area (chord × wingspan), and $C_D$ is the airfoil drag coefficient.

$$D=\frac{1}{2}\rho V^{2}A{C}_D.$$

(2)

Figure 2 displays the lift L and drag D components of the generated aerodynamic force R, the angle between the vehicle’s heading and the apparent wind $\theta$, the wing sail angle of attack $\alpha$, and the driving or thrust T force and lateral or heel H force applied to the vehicle.

The force required to put the land yacht in motion is given by Newton’s second law presented in Equation (3), where m and a are the land yacht mass and acceleration, respectively. In this case, the mass of the vehicle, comprising the chassis, wing set and maximum payload, is assumed to be $20.0$ $\mathrm{kg}$.

$$F=ma.$$

(3)

Replacing the force with the lift expression presented in Equation (1) and adding the friction force, results in Equation (4), where $\mu$ is the friction coefficient, and g is the gravitation acceleration.

$$\frac{1}{2}\rho V^{2}A{C}_L=ma+\mu mg.$$

(4)

Given that the lift force is perpendicular to the apparent wind direction and the drag force is parallel to the apparent wind direction, the thrust force required to move the land yacht forward T, which is parallel to the vehicle’s x axis, is related to the lift and drag through $\theta$, the angle of the apparent wind. This thrust force can, then, be expressed by Equation (5).

$$T=Lsin\theta -Dcos\theta .$$

(5)

From the combination of Equations (4) and (5) results in Equation (6), which represents the equilibrium of forces involved in the forward motion of the land yacht.

$$\frac{1}{2}\rho V^{2}A{C}_L(Lsin\theta -Dcos\theta )=ma+\mu mg.$$

(6)

Identically, the lateral or heel force applied to the vehicle’s y axis is expressed by Equation (7), where $\theta$ represents the apparent wind angle.

$$H=Lcos\theta +Dsin\theta .$$

(7)

Assuming that: (i) the land yacht has a mass of $20.0$ $\mathrm{kg}$, an initial acceleration of $0.15$ $\mathrm{m}$/s² (to start moving), and a rolling friction coefficient of 0.002 (bicycle tires on dry concrete (http://physicalcycling.com/tire-traction, accessed on 19 March 2021)); (ii) the apparent wind has a velocity of 5 $\mathrm{m}$/$\mathrm{s}$, an angle $\theta \le {45}^{°}$ and the air density is $1.225$ $\mathrm{kg}$/${\mathrm{m}}^3$; and (ii) the NACA63(3)-018 symmetrical airfoil profile has a lift coefficient of 0.75 with $\alpha$ = 10 ${}^{°}$ [31], the wing area given by Equation (6) is approximately $0.4$ m². Based on this set of assumptions, the NACA63(3)-01 wing sail has a chord of 400 mm and a wingspan of 1000 mm, whereas the NACA63(3)-01 flap presents a chord of 130 mm and a wingspan of 330 mm.

To determine if the stability of the vehicle, it is necessary to consider the existing rolling and anti-rolling moments. According to Reference [12], the rolling moment $M_r$ generated by the lateral wind on the wing sail is given by Equation (8), where $L_e$ is the wing sail wingspan, $\Delta h$ is the wing sail mounting distance, $P_r$ is the true atmospheric pressure, $P_s$ is the mass-specific gas constant, and $T_r$ is the air temperature.

$$M_r=\frac{88.296P_r{V}^{2}A(C_{L}cos\left(\theta \right)+C_{D}sin\left(\theta \right))[L_e^2-{100}^2+2\Delta h(L_e-100)]}{(273.15+T_r)P_s{L}_e}.$$

(8)

The anti-rolling moment moment $M_a$, generated by the vehicle as a whole, is given by Equation (9) [12], where $B_1$ and $B_2$ are the front and rear wheel base lines, respectively.

$$M_a=mg(B_1+B_2)/4.$$

(9)

The critical vehicle tipping wind velocity occurs with lateral apparent wind, i.e., $\theta =90{}^{°}$ and $\alpha =90{}^{°}$. From Equation (8), $\theta =90{}^{°}$, $C_L=0$ (value of $C_L$ for $\alpha =90{}^{°}$[31]) and $C_D=2$ (value of $C_D$ for $\alpha =90{}^{°}$ [31]), results in Equation (10).

$$V\le \sqrt{\frac{(273.15+T_r)(B_1+B_2)mg{L}_e{P}_s}{724.33A(L_e^2+2\Delta h{L}_e-{100}^2-200\Delta h)P_r}}.$$

(10)

Finally, assuming that $T_r$ = 20 °C, $B_1$ = $0.5$ $\mathrm{m}$, $B_2$ = $0.38$ $\mathrm{m}$,m = 20 $\mathrm{k}$$\mathrm{g}$, g = $9.81$ $\mathrm{m}$/$\mathrm{s}$², $L_e$ = 1 $\mathrm{m}$, $P_s$ = $8.31432\times {10}^3$ N m kmol${}^{-1}$ K${}^{-1}$, $\Delta h$ = $0.1$ $\mathrm{m}$, and $P_r$ = 101,325 Pa, the maximum wind velocity that the vehicle can withstand is 12 $\mathrm{m}$/$\mathrm{s}$.

2.3. Platform Simulation

The simulation was performed with the Gazebo simulator and the ROS middleware. The Gazebo simulator, which is a three-dimensional open-source dynamics simulator for robotic platforms, was chosen as it allows the definition of new models in Simulation Description Format (SDF), provides a plugin that simulates aerodynamic forces and is ROS compatible. SDF models comprise collections of: (i) links, corresponding to body parts and including collision (geometry), visual (visualization), and inertia (dynamics) elements; (ii) joints between links, specifying the parent and child relationship, the axis of rotation, and limits of the joint; (iii) sensors that collect world data for plugins; and (iv) plugins which control the behavior of the model [33].

2.3.1. 3D Model

The vehicle and wing sail model were created using the Fusion 360 Computer-Aided Design software from AutoDesk. The resulting 3D mesh files were imported to Gazebo through the SDF model file, which describes the links and joints of the different parts of the land yacht and loads model related plugins, such as the aerodynamics or the sensor plugins. Listing 1 defines a link and imports the corresponding 3D mesh file into Gazebo. The link element contains the link name, the link pose relative to the base link (in this case, the base link is the chassis), the inertial properties (such as mass and the inertial matrix), the link collision properties (in this case, the collision zone is the same as the model format), and the link visual format.

Listing 2 specifies a joint between two links, including the joint type (since it is connecting a wheel, then the joint type is revolute), the joint name, the pose relatively to the child link, the child and parent links (in this case, it is the wheel and the chassis, respectively), the rotation axis (in this case, the joint rotates in the y axis), and the joint friction and damping.

Listing 1. Simulation Description Format (SDF) link example.

Listing 1. Simulation Description Format (SDF) link example.

Listing 2. SDF joint example.

Listing 2. SDF joint example.

Finally, the SDF world file loads the land yacht model file, as well as the environmental characteristics, such as the ambient light and ground plane, and the world related plugins. The land yacht model presented in Figure 3 is composed of a chassis, four wheels, a steering mechanism composed of 4 links, a wing sail, and a flap (11 links and 12 joints).

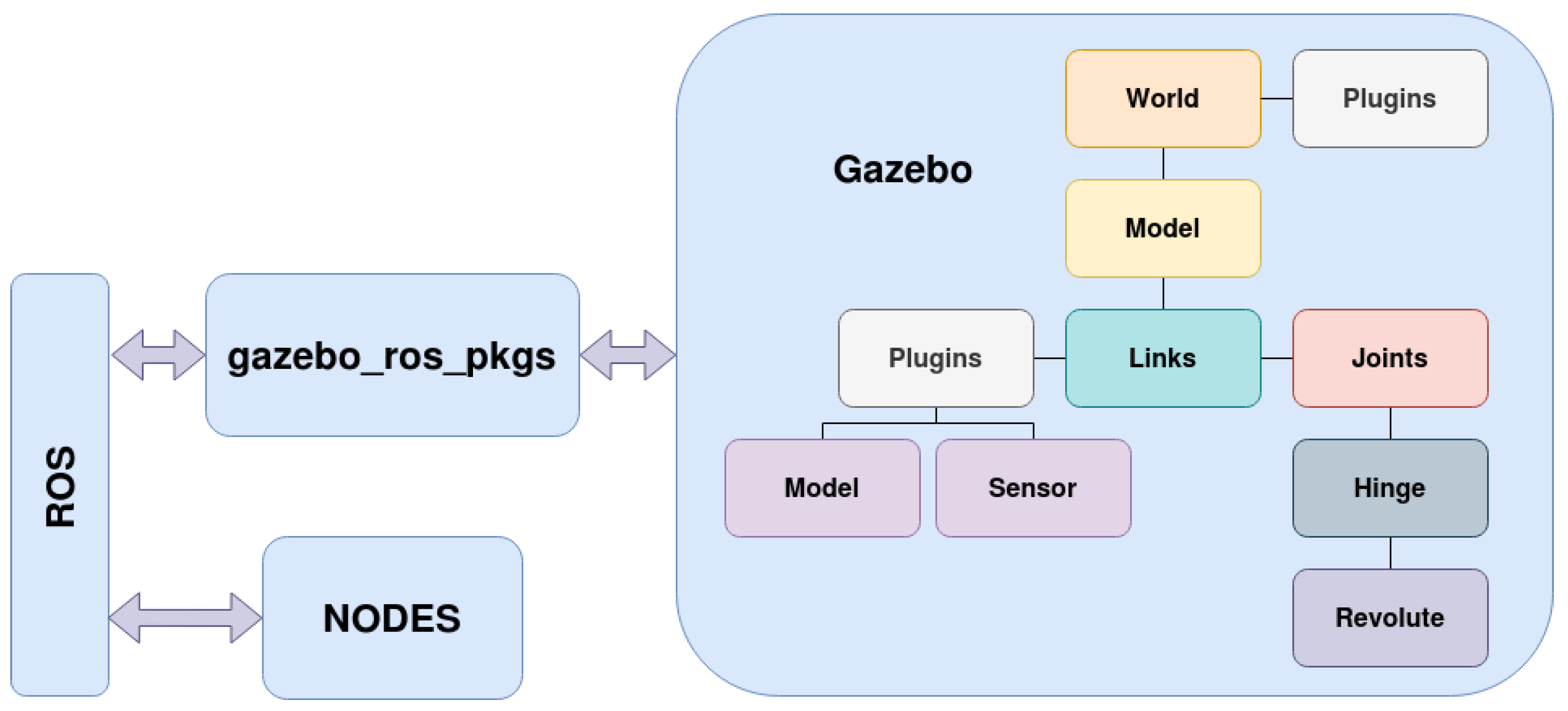
2.3.2. ROS Integration

To launch Gazebo using ROS, the package gazebo_ros_pkgs (gazebo_ros_pkgs website: http://wiki.ros.org/gazebo_ros_pkgs, accessed on 19 March 2021) was reused. This package enables the interface between ROS and Gazebo, allowing also the creation of ROS nodes inside Gazebo plugins. A ROS package, named land_yacht, was created specifically for the development of the simulation. This package uses a launch file to load an empty world from gazebo_ros_pkgs together with the model of the land yacht, and a node responsible for the control of the wing flap and the steering. This empty world serves merely as an interface between gazebo_ros_pkgs and land_yacht. For this to be possible, the world file, which loads the vehicle model, must be stored in a subfolder of the ROS package named worlds. A block diagram of this setup is presented in Figure 4.

2.3.3. Gazebo Plugins

The simulation of the land yacht uses three plugins: a modified liftdragplugin (Gazebo aerodynamics plugin: http://gazebosim.org/tutorials?tut=aerodynamics&cat=physics, accessed on 19 March 2021) and two new plugins named land_yacht_plugin and land_yacht_appar_wind. The land_yacht_plugin enables the control from ROS of the wing sail flap and of the land yacht steering; and the land_yacht_appar_wind plugin simulates an apparent wind sensor (velocity and direction of the wind relative to the land yacht).

The liftdragplugin simulates the aerodynamic forces and the pitching moment on an airfoil (the torque generated by the wind on the airfoil), since it was developed for airplanes. Given that an airfoil on a land yacht is positioned vertically, the plugin will calculate the yawing moment. In short, the liftdragplugin, apart from generating lift and drag forces, also aligns the wing sail to the direction of the wind. However, this plugin was created to simulate these forces on aeroplanes or fixed wing drones in windless conditions. In other words, this plugin assumes the world’s wind velocity corresponds to the world’s linear velocity of the vehicle, which, in this case, is only partially correct. The plugin was modified to add the world’s wind velocity to the world’s linear velocity of the vehicle. For example, if the vehicle is moving westward with a linear velocity of 1 $\mathrm{m}$/$\mathrm{s}$ and there is a westerly wind of 2 $\mathrm{m}$/$\mathrm{s}$, then the two linear velocities are added, generating a total apparent wind velocity of 3 $\mathrm{m}$/$\mathrm{s}$. Without this change, the apparent wind velocity would remain 1 $\mathrm{m}$/$\mathrm{s}$. Finally, the plugin was also adapted to subscribe a ROS topic that broadcasts the world’s wind velocity in the x and y axis. Figure 5 displays a diagram that details the processing pipeline of the modified plugin. Before calculating the lift and drag forces, the plugin subtracts the vehicle linear velocity and the true wind velocity in the world frame and, subsequently, uses the vehicle orientation to establish the apparent wind, which corresponds to the relative wind to the vehicle. With the apparent wind and the wing sail angular position, the plugin calculates the wing sail angle of attack (AoA) and, using the linearized airfoil parameters, determines the lift and drag coefficients. With these coefficients, the plugin calculates the lift and drag forces to get the resulting force. This resulting force is applied to the wing sail pressure point; in this case, it is situated in the middle of the wing, and is also used to calculate its yawing moment. This yawing moment is translated into torque and, finally, applied to the wing sail.

The land_yacht_plugin is composed of a ROS node that subscribes two topics—the flap angle and steering angle—and publishes the vehicle ground truth for control and debugging. When the plugin receives new messages from the subscribed topics, it sets the corresponding joint angle to the broadcasted value.

The land_yacht_appar_wind plugin converts the true wind (velocity and direction in the world reference frame) into the vehicle’s apparent wind (velocity and direction in the vehicle reference frame). It subscribes the true wind topic, transforms the true into the apparent the wind, using the vehicle’s heading and velocity in the world reference frame, and, finally, publishes the result in a new topic.

Plugins can be loaded in the model or the world SDF file. Listing 3 illustrates the loading of the liftdragplugin. The NACA63(3)-018 airfoil characteristics correspond to the stall and the slopes of the lines obtained from linearizing the characteristic lift and drag coefficient curves [31], shown in the example presented in Figure 6. Each curve is approximated by two lines which intersect at the stall of the curve, and these line slopes are used to describe the airfoil.

Listing 3. SDF plugin example.

Listing 3. SDF plugin example.

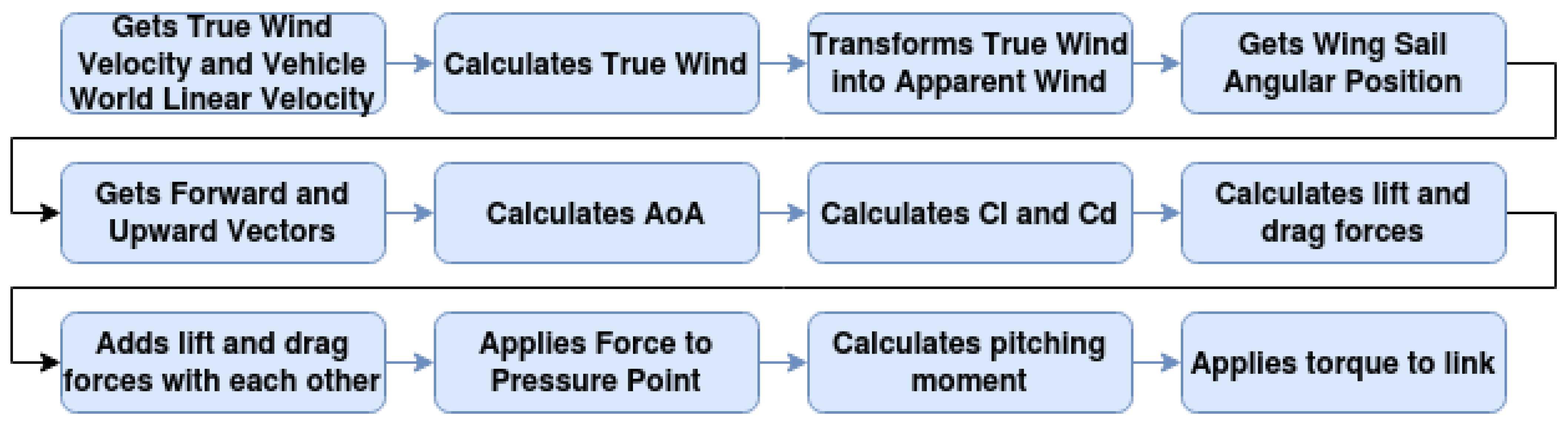
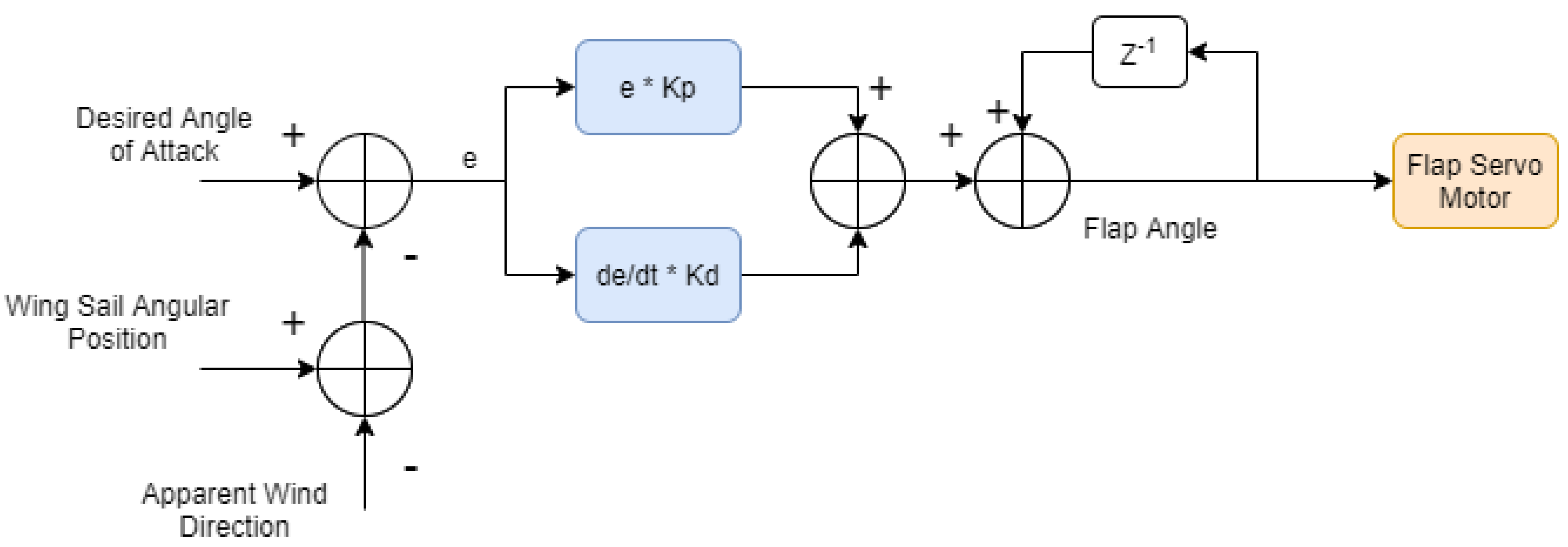
2.3.4. Wing Sail Control

The control of the angle of attack of the wing sail is indirect, i.e., it is set through the flap. The flap has a Proportional-Differential (PD) controller, which uses as inputs the apparent wind direction (published in the apparent wind topic) and the wing sail angular position (published in the sail rotation topic), and outputs the desired flap angle. A block diagram of the wing flap control is presented in Figure 7, where e is the error, and $de$ the differential error, between the desired and the current angle of attack, and $K_p$ and $K_d$ are the proportional and differential gains, respectively.

3. Results & Discussion

3.1. Experimental Setup

Figure 8 presents the set of nodes and topics involved in this experimental setup. The Gazebo environment (gazebo node) subscribes the wind, steering, and flap topics and publishes the ground truth, as well as the sail rotation and apparent wind topics. The control node (land_yacht_control) subscribes the ground truth, the sail rotation, and the apparent wind from Gazebo and publishes the flap control topics. The true_wind_generator node generates and publishes the real time true wind conditions (in the world reference frame). The teleop_key_pub manual control node reuses the teleop_twist_keyboard (teleop_key_pub website: http://wiki.ros.org/teleop_twist_keyboard, accessed on 19 March 2021) package and was added to the setup for debugging purposes.

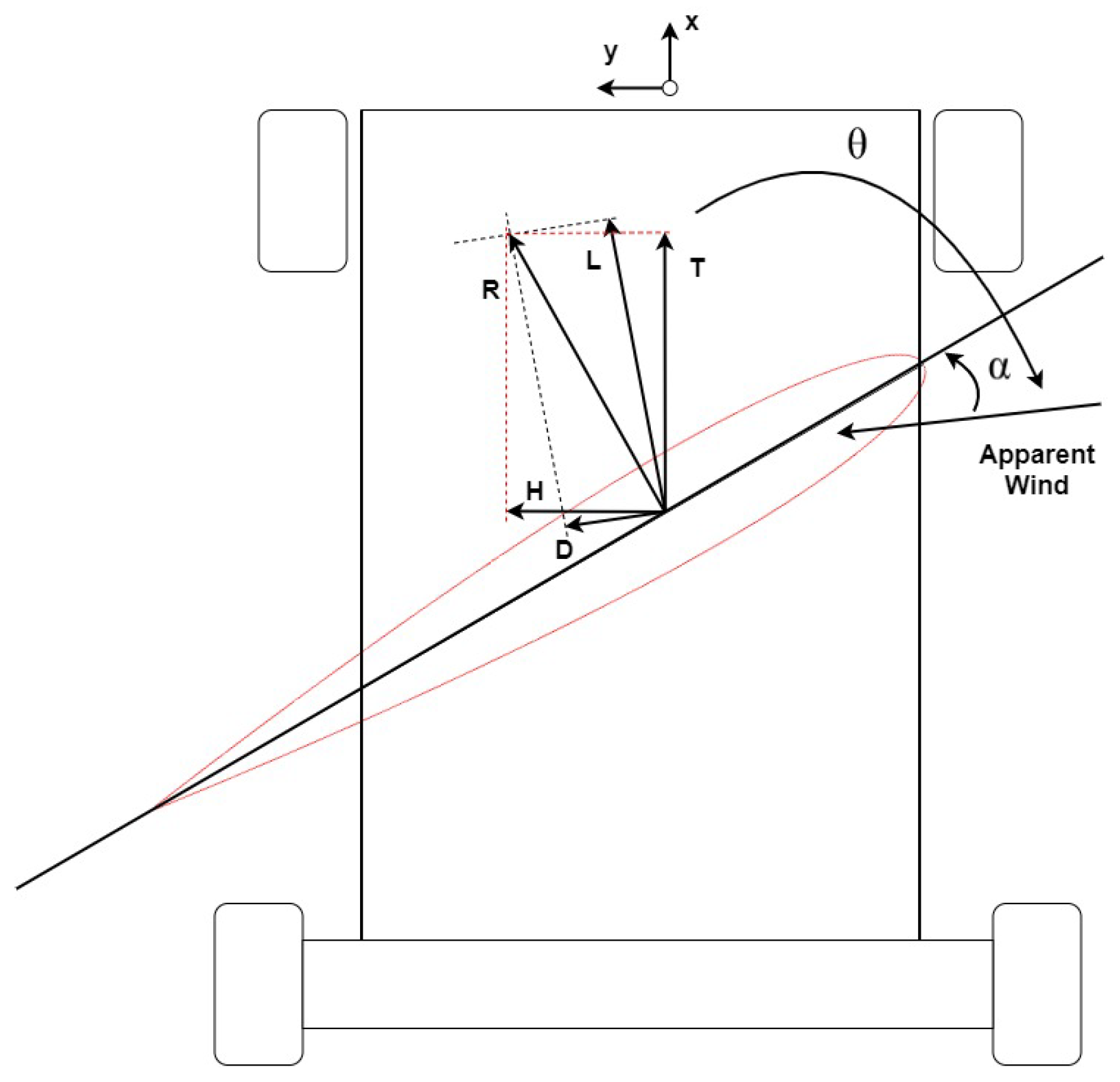
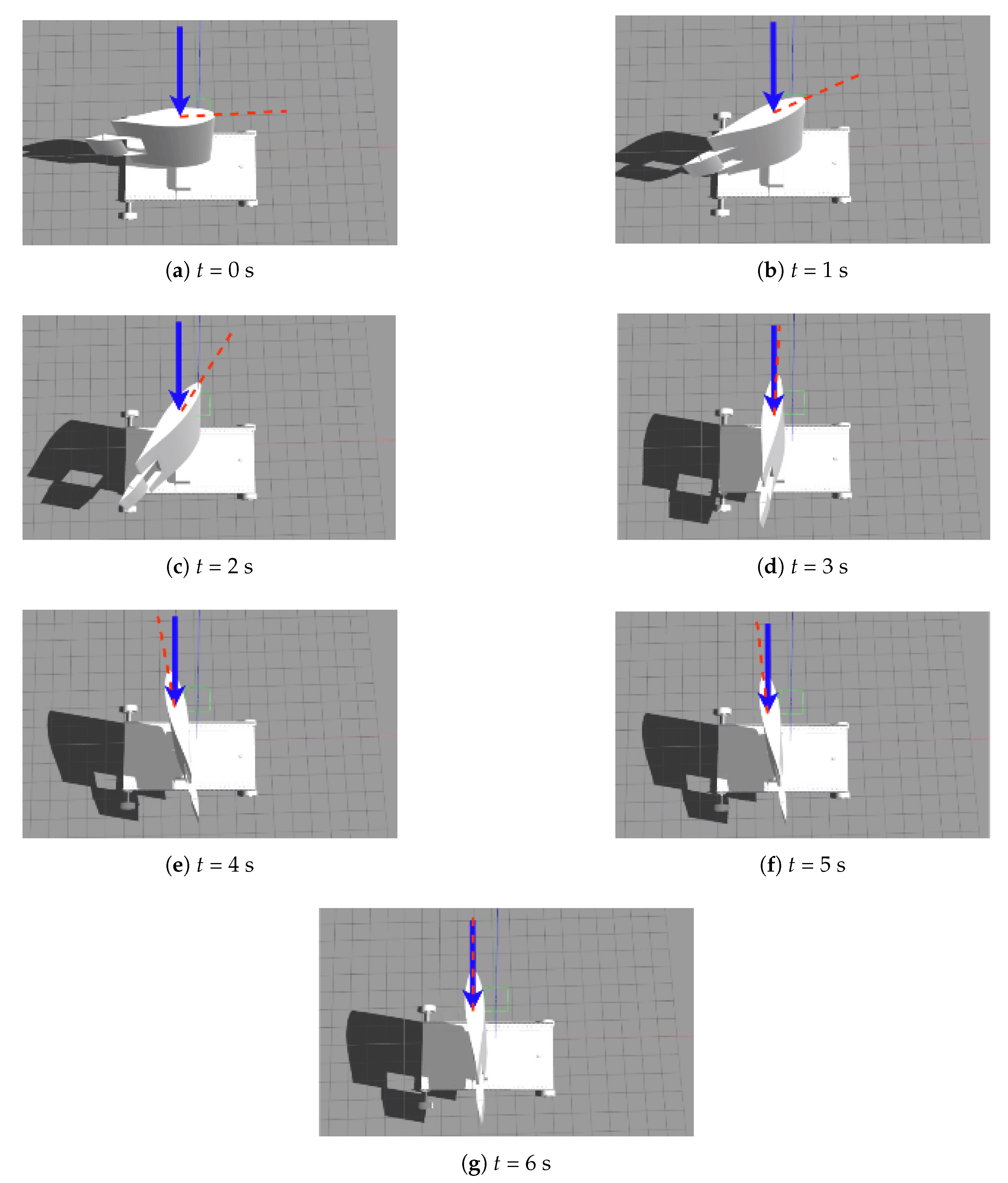
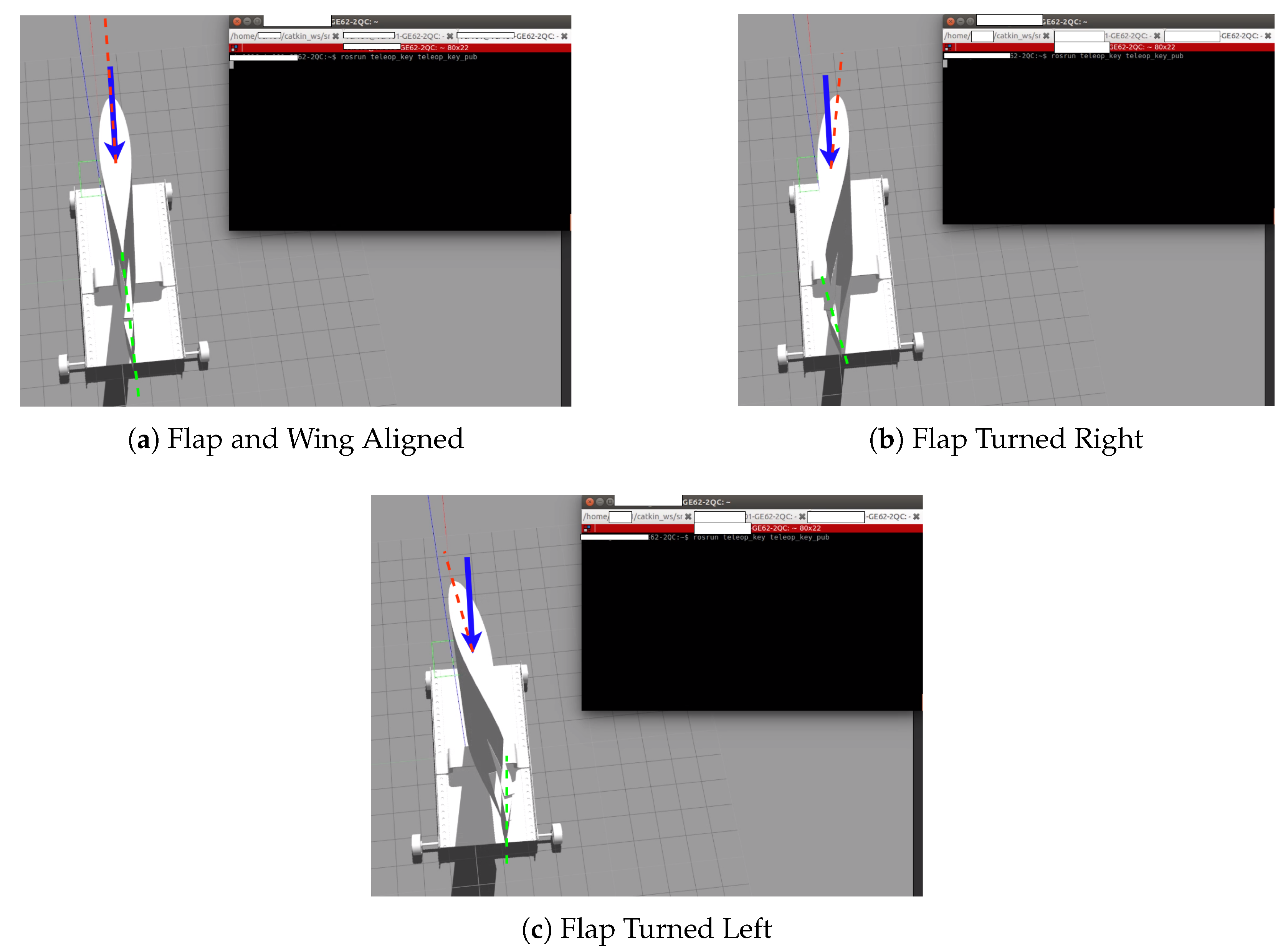
3.2. Wing Sail Alignment to the Wind

This test validates the wing sail alignment to the wind without any control on the flap (the flap remains aligned with the wing sail at all times). The behavior of the wing sail was tested with an initial apparent wind direction of 90° (${\alpha }_i=90{}^{°}$) and apparent wind velocities of 8 , 9 , and 10 . The final desired angle of attack is 0° (${\alpha }_f=0{}^{°}$). The wing sail response is presented in Figure 9, where the blue arrow is the wind direction, and the dashed red line is the wing sail direction.

Figure 10 displays the time response of the wing sail angle of attack. These results show that, when the wing and tail are aligned, the wing sail aligns automatically to the wind due to the yawing moment of the aerodynamics plugin. Although the wing sail takes identical time to stabilize with different wind velocities, the higher the wind velocity, the higher the overshoot.

3.3. Wing Sail Response to the Flap Angle

These tests verify if the wing sail turns correctly given a change in the flap angle. Initially, the wing sail was aligned to the apparent wind direction (${\alpha }_i=0{}^{°}$) and the flap angle was set to 0°. The test consisted of turning the flap manually, using the keyboard, to the left and to the right, as is presented in Figure 11.

The wing sail responded correctly to the flap angle change. It turned to the right when the flap angle was set to the left, and to the left when the flap angle was set to the right.

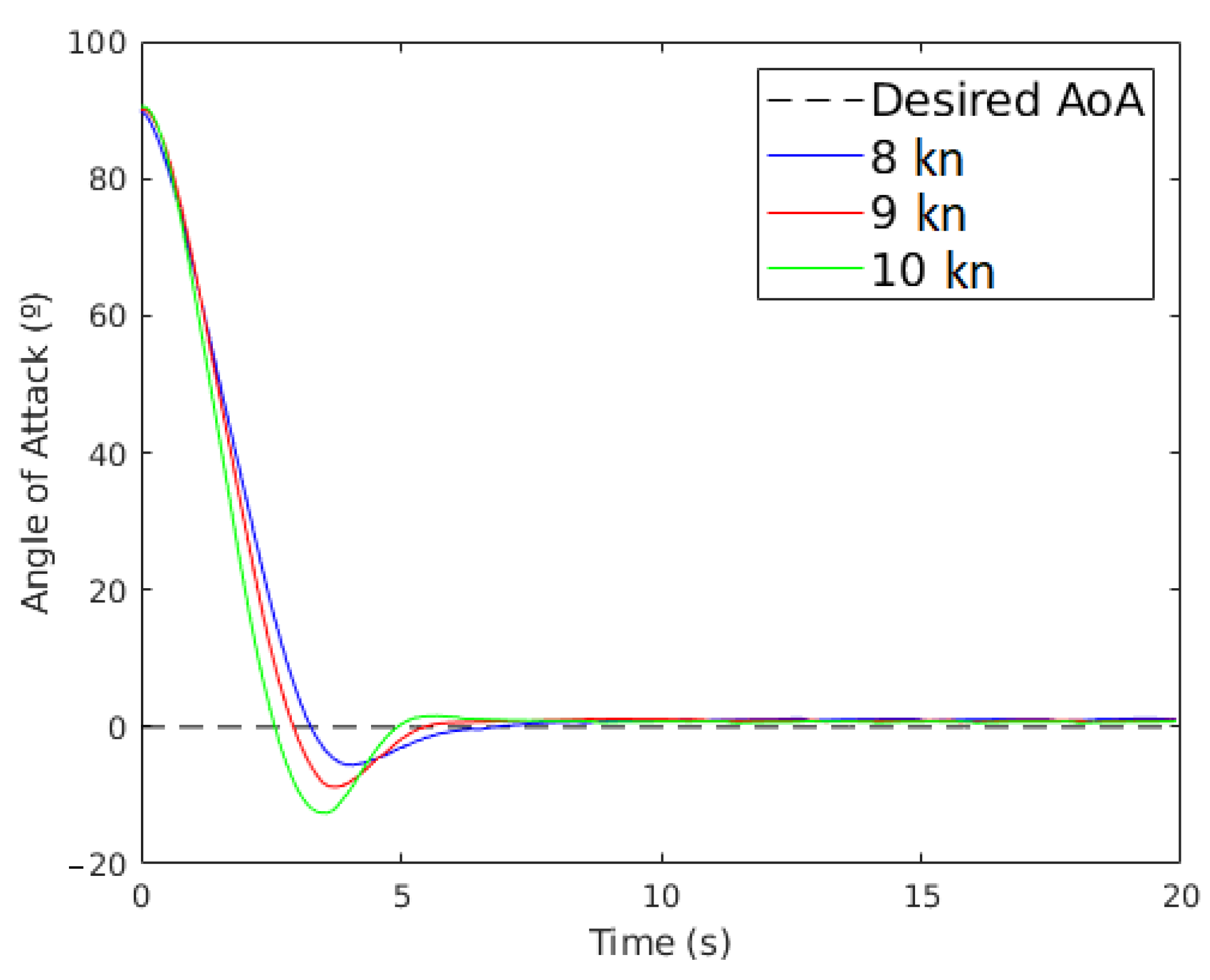
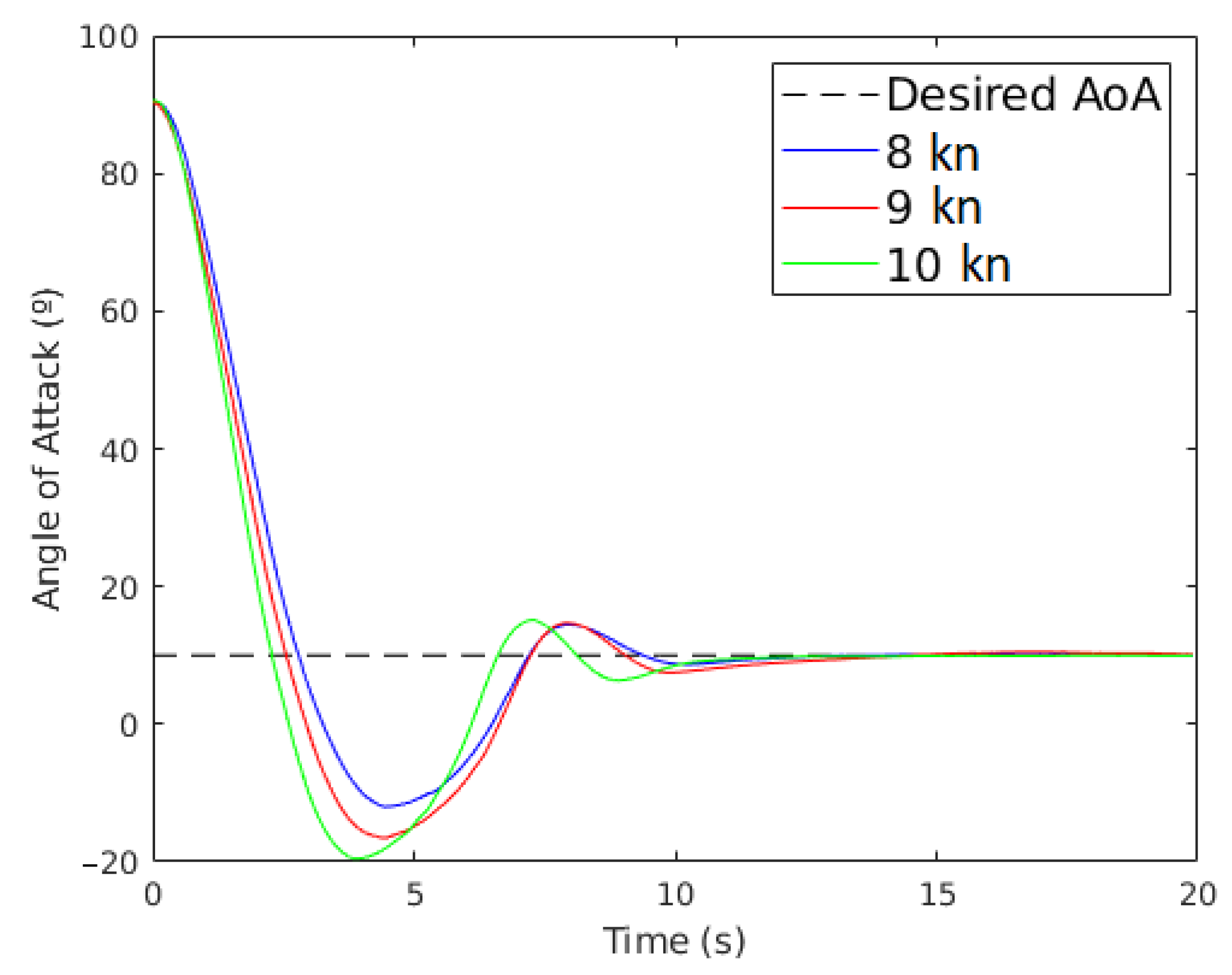
3.4. Setting the Wing Sail to an Angle of Attack

These tests check if the wing sail direction is controllable through the flap angle. Specifically, it verifies if the wing sail stabilizes at a defined angle of attack. The apparent wind direction was set to 90° (${\alpha }_i=90{}^{°}$), the apparent wind velocity to 8 kn, 9 kn, and 10 kn, and the final desired angle of attack (${\alpha }_f$) to 10°. Figure 12 plots the obtained time responses. The wing sail direction overshoots the desired angle of attack but stabilizes after a few seconds. These results validate the wing sail control as it successfully stabilized the wing sail to the defined angle of attack.

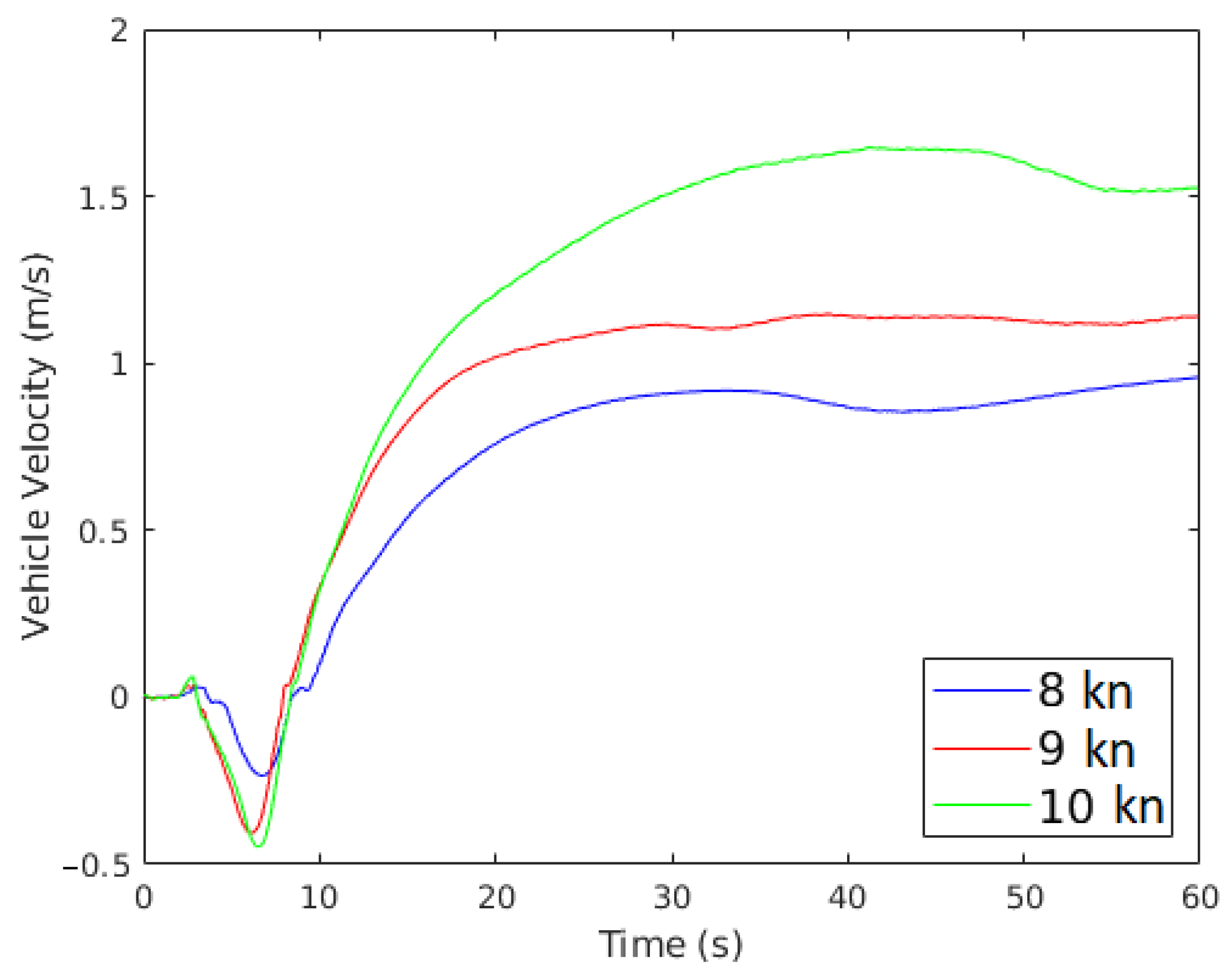
3.5. Vehicle Motion

The final experiment tests if the wing sail provides enough lift to displace the vehicle. The initial apparent wind direction was set to 90° (${\alpha }_i=90{}^{°}$), the apparent wind velocity to 8 kn, 9 kn, and 10 kn, and the final desired angle of attack (${\alpha }_f$) to 10°. Figure 13 shows the vehicle velocity over time.

Initially, the vehicle displays negative velocities because the wing sail overshoots the desired angle of attack for a short period of time. With negative angle of attack values, negative lift coefficients are obtained, and, consequently, negative accelerations, making the vehicle move slightly backwards. After this period, the vehicle starts moving forward with positive acceleration. The velocity increases until the acceleration of the vehicle becomes null or the terminal maximum velocity is achieved. The velocity can be reduced by changing the angle of attack of the wing sail until, ultimately, it becomes zero, eventually stopping the vehicle. This experiment shows that the wing sail was able to provide enough lift to move the vehicle.

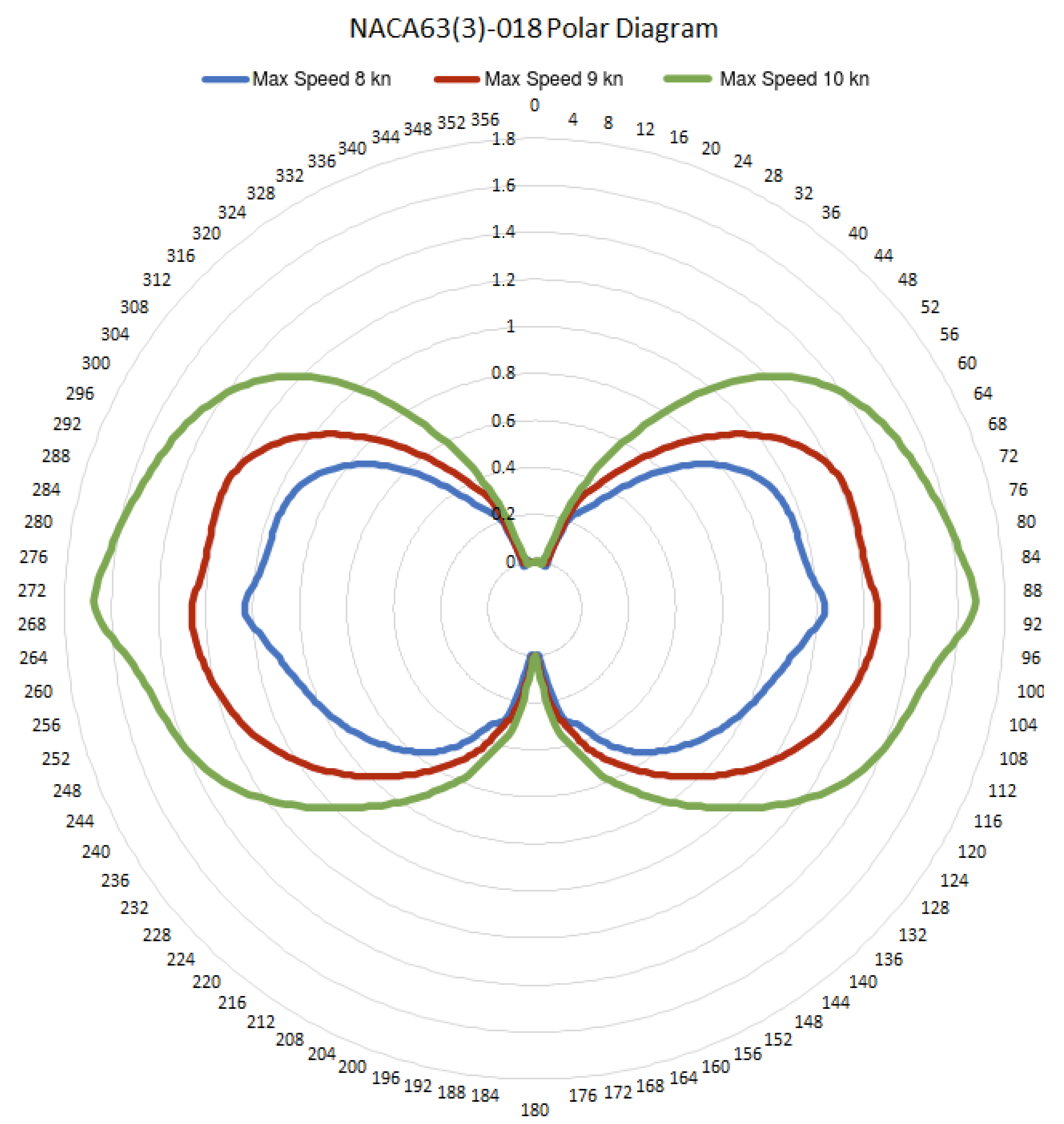
3.6. Polar Diagram

The polar diagram characterizes the optimal performance of a wind propelled platform as a function of the wind velocity and apparent wind angle. In this test, the autonomous flap control was responsible for the optimization of the lift force applied to the wing sail. Three different wind velocities were simulated (8 kn, 9 kn, and 10 kn) together with apparent wind direction increments of 5° from 0° to $\pm 180$${}^{°}$.

The velocity started increasing at approximately $\pm 45$${}^{°}$ until peaked at $\pm 90$${}^{°}$. After peaking, the maximum velocity started decreasing until it reached null values near $\pm 180$${}^{°}$, as shown in the polar diagram presented in Figure 14. The no go zone is visible between $-45$${}^{°}$ and $+45$${}^{°}$, and between $-135$ ${}^{°}$ and $+135$${}^{°}$.

4. Conclusions

The design, modeling, and simulation of an autonomous wing sail land yacht was successful as the wing sail responded correctly to the wind direction and to changes in the flap angle. Furthermore, the sailing behavior of the designed land yacht is characterized by its polar diagram. Some of the values used in the modeling and simulation were arbitrated since there was no possibility of obtaining them through experimentation. This simulated environment can be further enhanced to provide several different scenarios, such as sandy coastal regions, and can be utilized by a different modeled land yacht with a different type of airfoil, provided the airfoil characteristics. Although the control was not the main focus of this work, it can also be refined to solve the identified frailties. Future work will focus on experimenting with different types of airfoils and control techniques.