The results will be discussed at the aerodynamic and aeroacoustics sub-sections. The aerodynamic force measurements were conducted in the aerodynamic wind tunnel under a wide range of angles of attack –15° ≤ α ≤ 15° at free-stream U = 24 ms−1, corresponding to Reynolds number of Re = 2.4 × 105. The Tu in this case is quite low at 0.3%. The aeroacoustics measurements were conducted in a separate aeroacoustics wind tunnel at α = 0° across 2.0 × 105 ≤ Re ≤ 5.0 × 105, which correspond to 20 ≤ U ≤ 50 ms−1, respectively. For the aeroacoustics experiments, the elevated Tu is about 4.5%. No boundary layer tripping devices are implemented for both experiments.
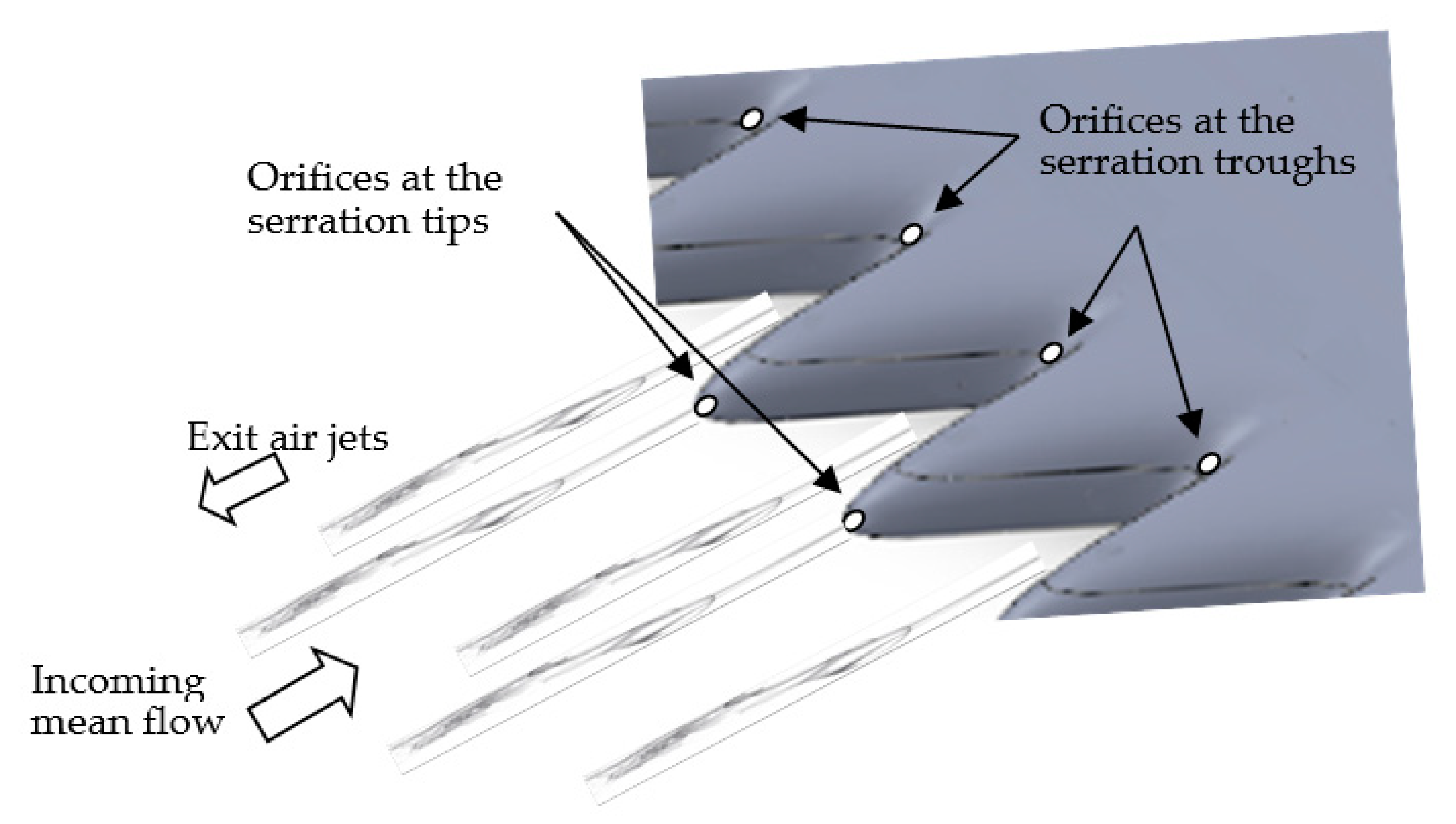
In the following sections, the naming of each serrated leading edge is made in accordance to the values of their serration wavelength
λ, and serration amplitude
A. For example, the serrated leading edge that has a serration wavelength of 5 mm and serration amplitude of 15 mm will be named as
λ5
A15 (see
Table 1). The same strategy is adopted for the leading edge blowing case. For example, a spanwise orifice distance of 5 mm and a blow rate of
Q ’ = 3.2 L/minute for each orifice will be named as
λ’5
Q ’3.2.
3.1. Aerodynamic Forces
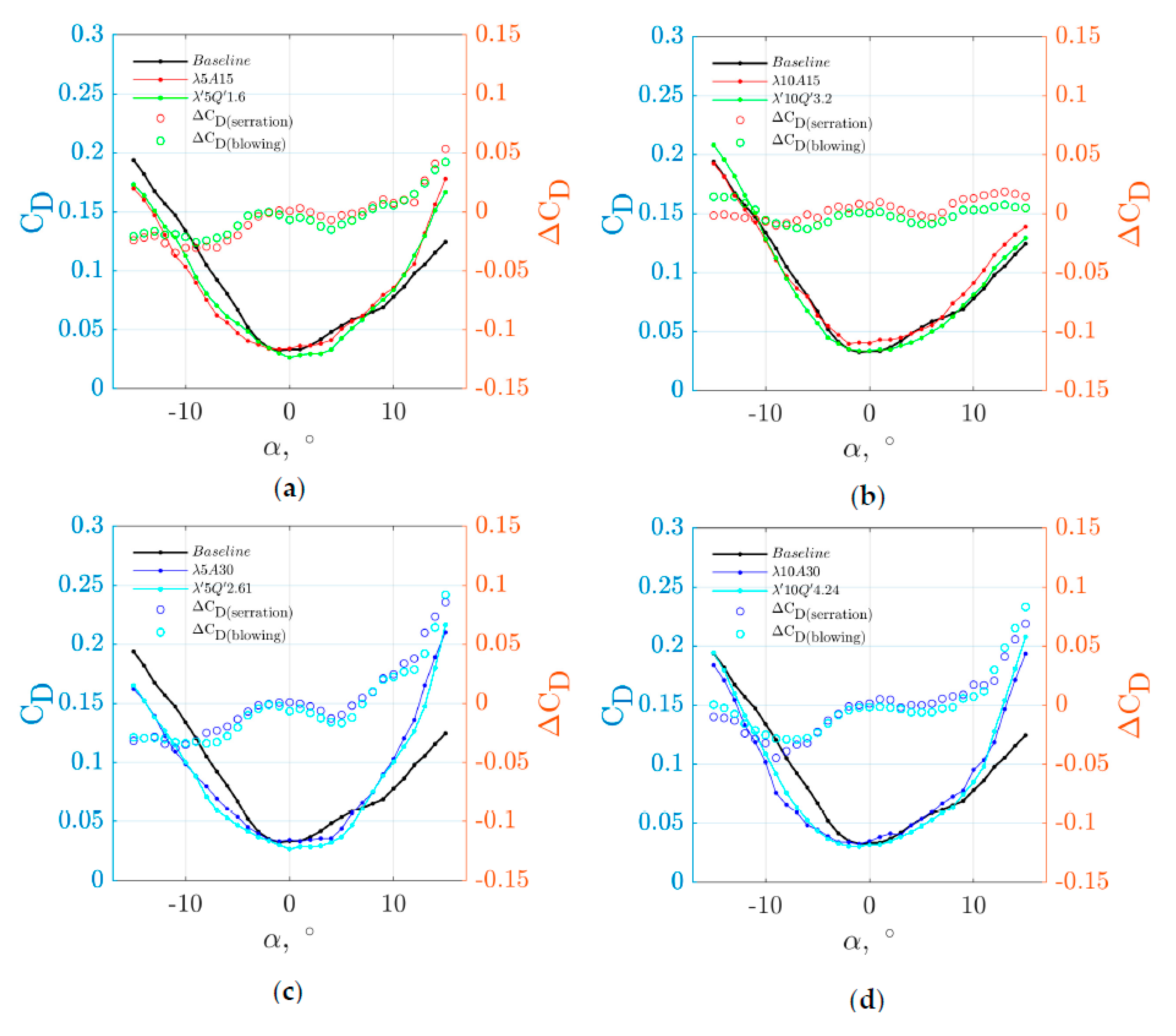
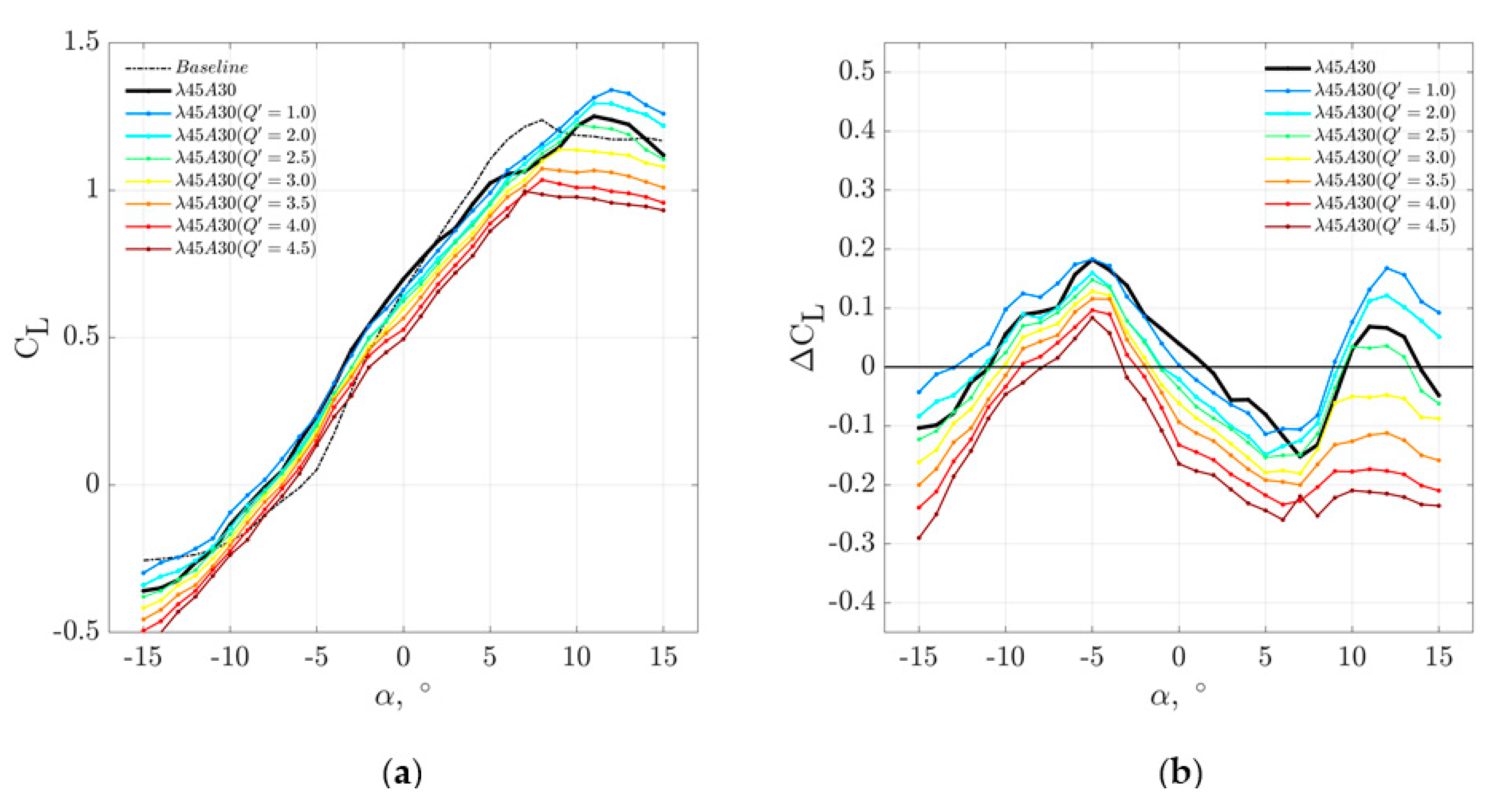
Figure 5 compares the aerodynamic lift coefficient C
L generated by the aerofoil as a function of angle of attack
α. Three cases are examined. First is the baseline leading edge. Second is when the aerofoil is subjected to leading edge serration, and third is the leading edge blowing. In all cases the planform areas (
C ×
S) are the same, which enable an unambiguous definition of the C
L. Four types of serrated leading edges are used in this study:
λ5
A15,
λ10
A15,
λ5
A30 and
λ10
A30. The figure also includes the ΔC
L, which is defined as follow:
where a positive value of ΔC
L denotes a higher lift coefficient generated by either the serrated leading edge or blowing leading edge, at a particular
α, compared to the baseline aerofoil. The opposite is true. The difference in the drag coefficient ΔC
D (to be shown in
Figure 6) is also defined in a similar fashion, i.e., a positive ΔC
D means that a larger drag coefficient is produced by the treated aerofoil, and vice versa.
It can be seen that for the baseline case the corresponding CL curve follows largely the classical thin aerofoil theory where a lift curve slope dCL/dα≈2π is evident at –6° ≤ α ≤ 8°. At α > 8°, the aerofoil starts to stall and the lift coefficient begins to drop. On the other hand, at α < –6° the CL does not vary much at increasingly negative angle of attack.
Generally, it is observed that a smaller serration wavelength (i.e., λ = 5 mm), regardless of the serration amplitude A, can preserve the lift curve slope of 2π at –6° ≤ α ≤ 8°. For a larger serration wavelength, such as the λ = 10 mm case, a smaller value of lift curve slope (dCL/dα≈0.08) is produced by the serrated aerofoil. With regard to the effect of the serration amplitude, it can be concluded that a smaller serration amplitude (i.e., A = 15 mm) is more effective than the larger serration amplitude (A = 30 mm). The effectiveness is measured in two phenomena. First, the stall angle is usually larger. Second, the values of the CL as a function of α are larger. This trend remains true at the post-stall regime as clearly demonstrated in the ΔCL distributions. Based on the above observation, the most superior serrated aerofoil in terms of the lift generation are the λ5A15 and λ10A15.
The analysis now focuses on the aerofoil with leading edge blowing. As mentioned earlier, the spanwise distributions of the leading edge orifices are defined by
λ’ = 5 mm and 10 mm. These two spacing correlate with the serrated aerofoil with
λ = 5 mm and 10 mm, respectively. For the
λ’ = 5 mm leading edge configuration, the blowing rates would vary between 1.6 ≤
Q ‘ ≤ 3.06 L/min. For the
λ’ = 10 mm, the blowing rates vary between 3.2 ≤
Q ‘ ≤ 6.12 L/min. It is worth mentioning that the lower limits of
Q ‘ for both the
λ’ = 5 mm and 10 mm leading edge configurations (
λ’5
Q ‘1.6 versus
λ’10
Q ‘3.2) stem from the same bulk mass blowing rate
Q into the aerofoil. The same applies to the upper limits (
λ’5
Q ‘3.06 versus
λ’10
Q ‘6.12). After analysing from a large experimental dataset, it can be concluded that a lower blow rate
Q ‘ tends to increase the C
L and stall angle. The effect of the blow rate to the C
L can also be affected by the
λ’. For example, in
Figure 5 the
λ’5
Q ‘1.6 is found to produce the best resemblance to the
λ’10
Q ‘3.2 in terms of their C
L curves. This can be confirmed by another example where the
λ’5
Q ‘3.06 matches the best C
L curve with the
λ’10
Q’6.12 (not shown here for brevity). However, it should be noted that the
dC
L/
dα produced by the different combinations of
λ’ and
Q ‘ can still be very different.
Within the
Q ‘ range described above, it is possible to match some of the C
L curves produced by the leading edge blowing against those produced by the serrated aerofoil. The comparison can also be found in
Figure 5. First, a trend is discernible whereby an increase of the serration amplitude from
A = 15 mm to 30 mm can re-produce somewhat very similar C
L variations with the
α by an increase of the blowing rate from
Q ‘ = 1.6 L/min to 2.61 L/min (when
λ’ = 5 mm), or 3.2 L/min to 4.24 L/min (when
λ’ = 10 mm). In other words, a doubling of the serration amplitude corresponds to a Δ
Q ‘≈1 L/min.
Interestingly, a second trend concerning the correlation between the serration wavelength λ and the leading edge blow rate Q ‘ also emerges. In order to match the same CL curves, a doubling of the serration wavelength from λ = 5 mm to 10 mm will also correspond to a doubling of the Q ‘.
Both trends suggest that the manipulation of the CL distributions and the mitigation of boundary layer stall at high angles of attack by the leading edge serration and leading edge blowing are governed by similar flow mechanisms. More importantly, the λ’ and Q ‘ can indeed mimic the λ and A, respectively, to produce the same aerodynamic performances. This is a significant finding.
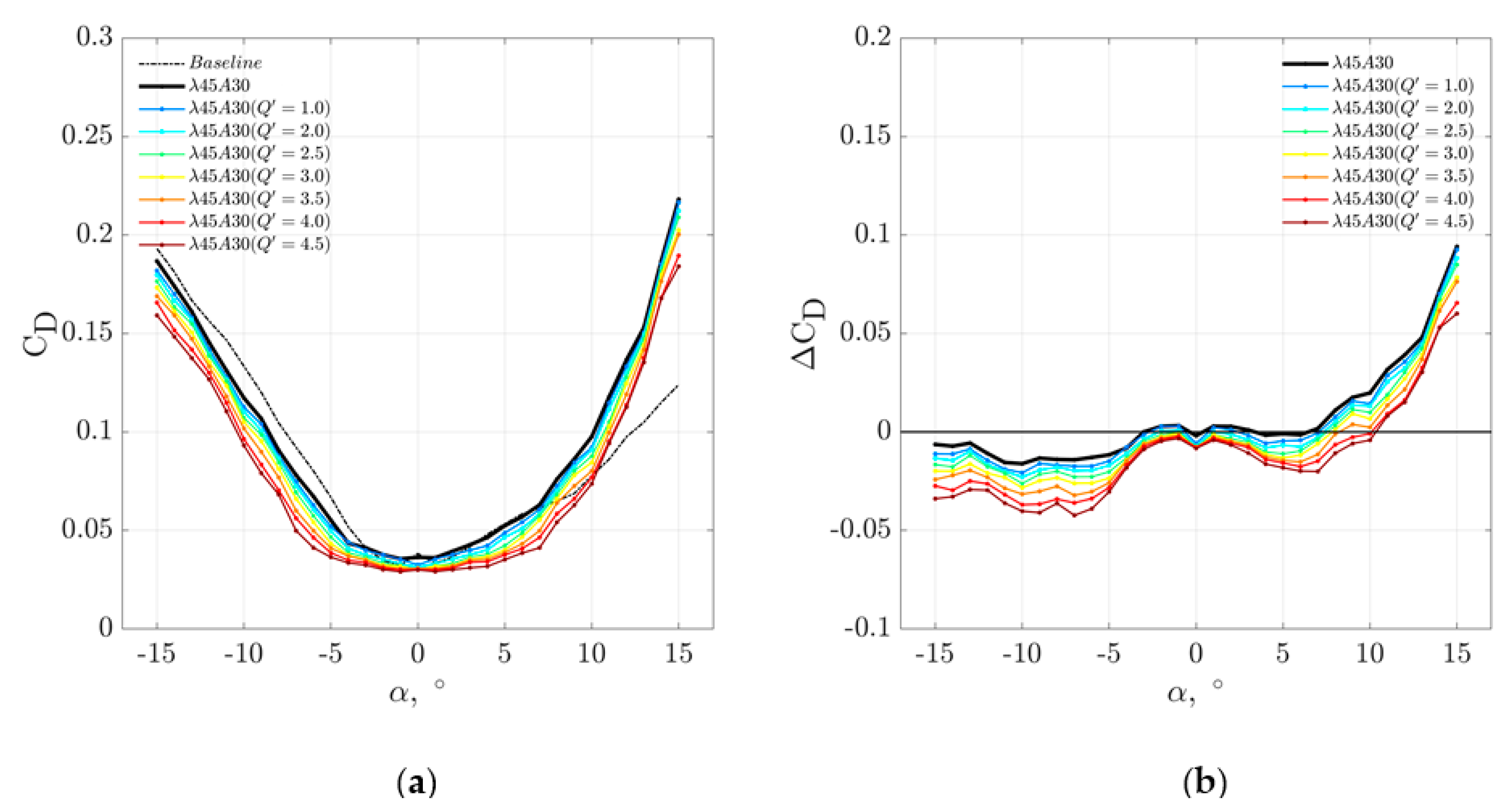
Further corroboration can be made in
Figure 6 for the variations of the drag coefficients C
D, as well as the ΔC
D, against the
α. Similar to their C
L counterparts, each paring between the serrated leading edge and blowing leading edge for the C
D across –15° ≤
α ≤ 15° is also very well matched. All curves have roughly the same point of interception with C
D≈0.03 at
α = 0°. Majority of the (
λ,
A) and (
λ’,
Q ‘) pairing, when compared with the baseline leading edge, would exhibit a reduction of C
D across –15° ≤
α ≤ 0°, but an increase of C
D across 0° <
α ≤ 15°. The increase of the C
D at the post-stall regime is noticeable for both the blowing leading edge and serrated leading edge. The exception is the pairing between the
λ10
A15 and
λ’10
Q ‘3.20 where the C
D curves follow closely the baseline one throughout the range of angle of attack investigated here, including the otherwise post-stall regime. This particular control configuration represents an optimal and reliable choice in terms of the minimal drag production.
3.2. Acoustic Results
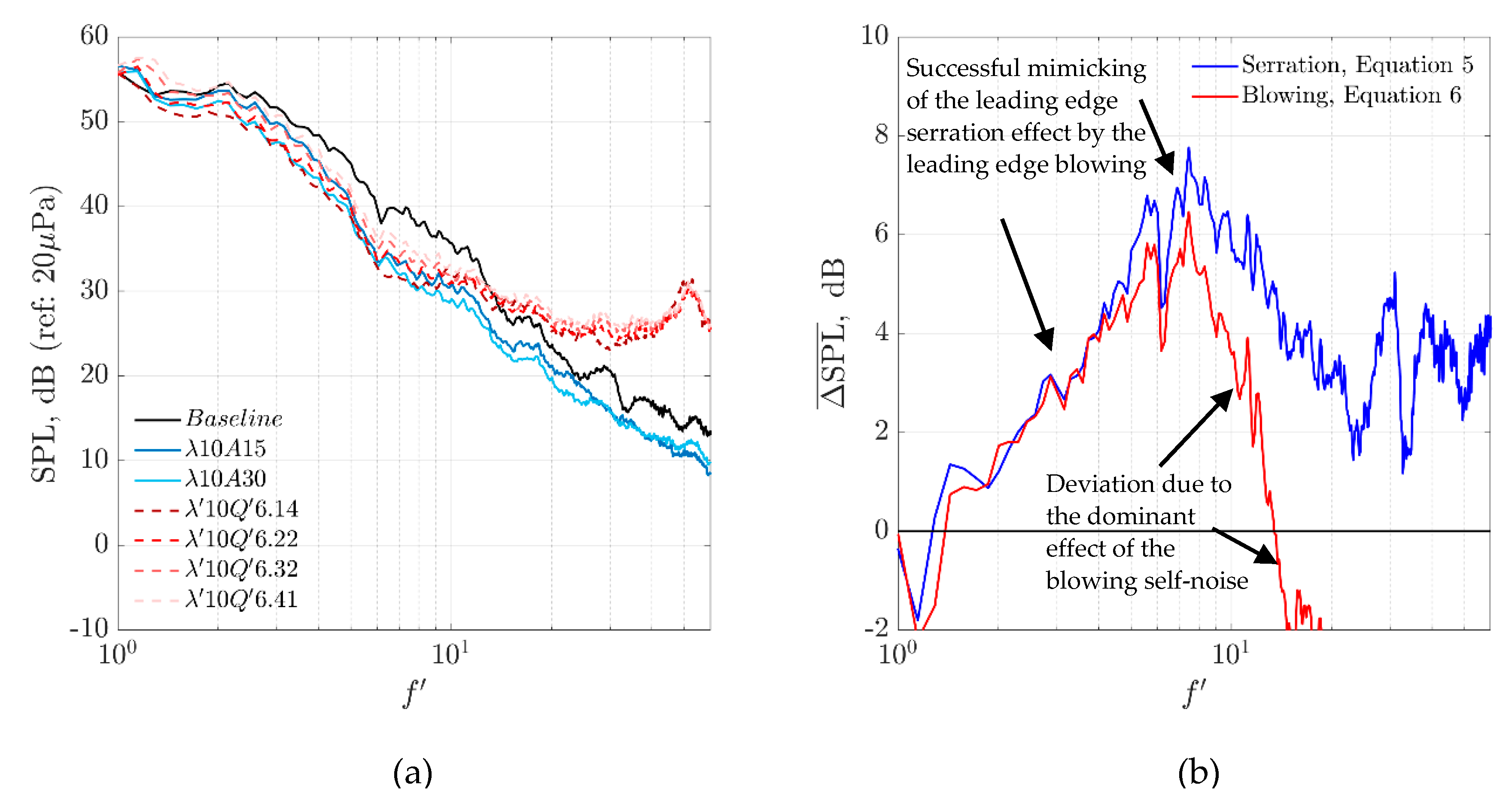
This section will show the acoustical results when the leading edge of the aerofoil is subjected to both the serration and blowing treatments, respectively. By examining the Sound Pressure Level SPL as a function of non-dimensional frequency
f ‘ (=
fC/
U, where
C is the aerofoil chord length) generated by the baseline aerofoil in
Figure 7a, the mostly broadband nature of the spectrum at the low to medium frequency is related to the turbulence–leading edge interaction noise. It is also clear that the elevated freestream
Tu has triggered a bypass transition on the aerofoil surface, as there is no evidence of the Tollmien-Schlichting instability tonal noise in the acoustic spectrum.
Here, ΔSPL is defined as the difference in SPL between the acoustic spectra generated by the baseline and treated leading edges (either serration or blowing). A positive ΔSPL denotes noise reduction by the treated aerofoil, while a negative ΔSPL denotes noise increase. The following discussion focuses on the aeroacoustical performances by the serrated leading edge only. As demonstrated in
Figure 7a,b, the most effective serration configuration for the turbulence–leading edge broadband noise reduction is the combination of the smallest
λ and largest
A, although a slight noise increase at high frequency can also be detected. The
A exerts a more dominant factor on the noise reduction compared to the
λ, which has also been reported in [
14,
15]. Repeating the same set of serrated leading edges across a wider range of
U essentially returns the same positive outcomes, as shown in
Figure 8.
The next discussion concerns one of the most important outcomes of this paper. Facilitating different levels of Q ‘ on the leading edge could produce very interesting aeroacoustical performances. The turbulence–leading edge broadband noise reduction by leading edge blowing can indeed be achieved. In some cases, ΔSPL as high as 10 dB can be achieved by one of the leading edge blowing configurations. However, it is important to stress that the noise reduction can only be achieved over a rather narrow range of blowing rate Q ‘. When the blowing rate is outside of this optimal range, no significant noise reduction can be observed.
From the acquired dataset, a selection of the acoustic spectra subjected to leading edge blowing within the range of 6.14 ≤
Q ‘ ≤ 6.41 L/minute is presented here.
Figure 9a shows the acoustic spectra produced by the leading edge blowing for the
λ’10
Q ‘6.14,
λ’10
Q ‘6.22,
λ’10
Q ‘6.32, and
λ’10
Q ‘6.41 at
U = 45 ms
−1. Acoustic spectra produced by the
λ10
A15 and
λ10
A30 serrated leading edges are also included for comparison. Note that the comparison between the serrated and blowing leading edges is based on the matching value of
λ and
λ’, respectively. In order to provide a clearer picture of the comparison, the mean-difference in the SPL level between the baseline and treated aerofoil is defined below:
Similarly, a positive value in the denotes that noise reduction is achieved against the baseline, and vice versa.
An examination of
Figure 9b can easily identify strong similarities in the noise reduction trend at
f ‘ < 8. This is a clear evidence that the leading edge blowing can indeed mimic the serrated leading edge. Above this frequency, however, cumulative jet noise produced by the orifices becomes dominant and overtakes the aerofoil noise radiation. As a result, negative value of
(i.e., noise increase) can be produced. It should also be noted that the optimised
Q ‘ values listed above for the broadband noise reduction are slightly higher than the optimised
Q ‘ in the C
L distributions (see
Figure 5), which was performed under different
U and
Tu domains. The different levels of sensitivity for
Q ‘ in producing the aeroacoustics and aerodynamic performances are expected due to the different physical mechanisms involved.
The effective margin of the leading edge blowing volume flow rate is so narrow that a small deviation from the optimised Q ‘, which ultimately relates to the exit jet velocity, can produce a large difference in the aeroacoustics performance. The concept of the leading edge blowing is to minimise the interaction of an incoming turbulent flow with the leading edge of the aerofoil. Through blowing, the leading edge jet continuously opposes, and possibly dissipates the incoming turbulent eddies by either displacing the leading edge stagnation point of the aerofoil, or creating a “buffer zone” over the vicinity of the aerofoil leading edge. It seems that one, or possibly both of these mechanisms could be very sensitive to the Q ‘.