Influence of Crushed Rock Properties on the Productivity of a Hydraulic Excavator
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods of Field Research
3. Calculation of the excavator’s Productivity
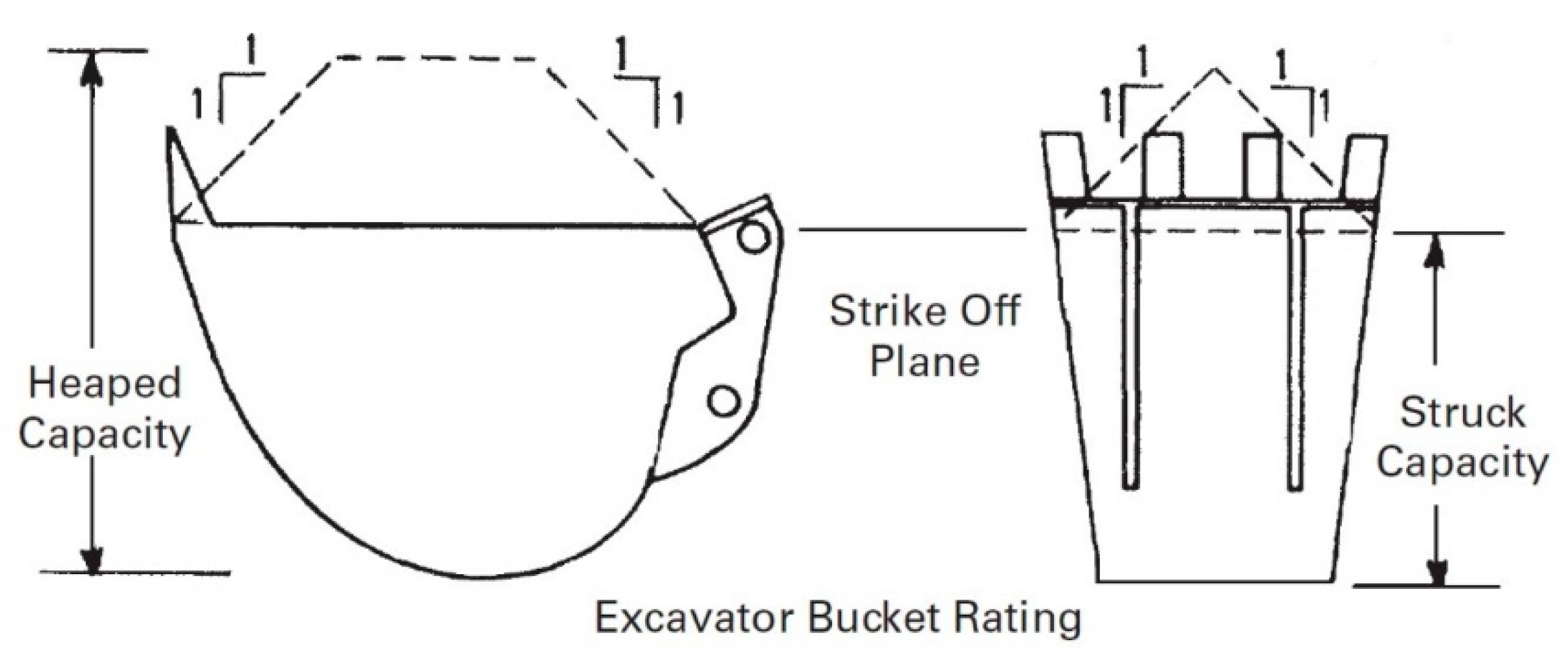
Geometrical Volume of the excavator’s Bucket
4. Results and Discussion
4.1. Factors Influencing Excavator Productivity
4.2. Analysis of the excavator Productivity Determinants
5. Limitations and Future Directions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rodríguez, R.; Bascompta, M. Vibration Analysis and Empirical Law Definition for Different Equipment in a Civil Construction. Appl. Sci. 2020, 10, 4689. [Google Scholar] [CrossRef]
- Sobko, B.; Lozhnikov, O.; Levytskyi, V.; Skyba, G. Conceptual Development of the Transition from Drill and Blast Excavation to Non-Blasting Methods for the Preparation of Mined Rock in Surface Mining. RGN Zb. 2019, 34, 21–28. [Google Scholar] [CrossRef]
- Sobolevskyi, R.; Korobiichuk, V.; Levytskyi, V.; Pidvysotskyi, V.; Kamskykh, O.; Kovalevych, L. Optimization of the Process of Efficiency Management of the Primary Kaolin Excavation on the Curved Face of the Conditioned Area. RGN Zb. 2020, 35, 123–138. [Google Scholar] [CrossRef]
- Graham, L.D.; Smith, S.D. A Method for Effectively Implementing Construction Process Productivity Estimation Models. Available online: https://www.arcom.ac.uk/-docs/proceedings/ar2004-1043-1052_Graham_and_Smith.pdf (accessed on 20 February 2021).
- Schabowicz, K.; Hola, B. Mathematical-neural model for assessing productivity of earthmoving machinery. J. Civ. Eng. Manag. 2007, 13, 47–54. [Google Scholar] [CrossRef]
- Smith, S.D. Earthmoving productivity estimation using linear regression techniques. J. Constr. Eng. Manag. 1999, 125, 133–141. [Google Scholar] [CrossRef]
- Smith, S.D.; Osborne, J.R.; Forde, M.C. Analysis of earth moving systems using discrete event simulation. J. Constr. Eng. Manag. 1999, 121, 388–396. [Google Scholar] [CrossRef]
- Ercelebi, S.G.; Bascetin, A. Optimization of shovel-truck system for surface mining. J. S. Afr. Inst. Min. Metall. 2009, 109, 433–439. [Google Scholar]
- Park, S.; Choi, Y.; Park, H.S. Simulation of Shovel-Truck Haulage Systems in Open-pit Mines by Considering Breakdown of Trucks and Crusher Capacity. Tunn. Undergr. Space 2014, 24, 1–10. [Google Scholar] [CrossRef]
- Edwards, D.J.; Holt, G.D. ESTIVATE: A model for calculating excavator productivity and output costs. Eng. Constr. Archit. Manag. 2000, 7, 52–62. [Google Scholar] [CrossRef]
- Edwards, D.J.; Griffiths, I.J. An artificial intelligent approach to calculating hydraulic excavator cycle time and productivity output. Trans. Inst. Min. Metall. 2000, 109, A23–A29. [Google Scholar] [CrossRef]
- Tam, C.M.; Tong, T.K.L.; Tse, S.L. Artificial neural networks model for predicting excavator productivity. Eng. Constr. Archit. Manag. 2002, 9, 446–452. [Google Scholar] [CrossRef]
- Hola, B.; Schabowciz, K. Estimation of earthworks execution time and cost by means of artificial neural networks. Autom. Constr. 2010, 19, 570–579. [Google Scholar] [CrossRef]
- Edwards, D.J.; Holt, G.D.; Robinson, B. An artificial intelligence approach for improving plant operator maintenance proficiency. J. Qual. Maint. Eng. 2002, 8, 239–252. [Google Scholar] [CrossRef]
- Holt, G.D.; Edwards, D.J. Analysis of interrelationships among excavator productivity modifying factors. Int. J. Product. Perform. Manag. 2015, 64, 853–869. [Google Scholar] [CrossRef]
- Ha, Q.P.; Nguyen, Q.H.; Rye, D.C.; Durrant-Whyte, H.F. Impedance control of a hydraulically actuated robotic excavator. Autom. Constr. 2000, 9, 421–435. [Google Scholar] [CrossRef]
- Michaud, P.R.; Blanchet, J.Y. Establishing a Quantitative Relation between Post Blast Fragmentation and Mine Productivity: A Case Study. In Proceedings of the 5th International Symposium Rock Fragmentation by Blasting, Montreal, QC, Canada, 23–24 August 1996; Franklin, J.A., Katsabanis, P.D., Eds.; Balkema: Rotterdam, The Nederland, 1996; pp. 389–396. [Google Scholar]
- Klanfar, M.; Herceg, V.; Kuhinek, D.; Sekulić, K. Construction and testing of the measurement system for excavator productivity. RGN Zb. 2019, 34, 51–58. [Google Scholar] [CrossRef]
- Lindgren, M. Excavation in Moraine and Dense Non-Cohesive Soil—Numerical Analysis of Soil Behavior. Licentiate Thesis, Royal Institute of Technology, Stockholm, Sweden, 2012. [Google Scholar]
- Singh, S.P.; Yalcin, T. Effects of Muck Size Distribution on Scooping Operations. In Proceedings of the 28th Annual Conference Explosives and Blasting Techniques, Las Vegas, NV, USA, 10–13 February 2002; International Society of Explosives Engineers: Cleveland, OH, USA, 2002; pp. 315–325. [Google Scholar]
- Singh, S.P.; Narendrula, R. Factors Affecting Productivity of Loaders in Surface Mines. Int. J. Min. Reclam. Environ. 2006, 20, 20–32. [Google Scholar] [CrossRef]
- Segarra, P.; Sanchidrián, J.A.; López, L.M.; Querol, E. On the Prediction of Mucking Rates in Metal Ore Blasting. J. Min. Sci. 2010, 46, 167–176. [Google Scholar] [CrossRef]
- Tosun, A.; Konak, G. Estimation of Loader Capacity Based on the Heap Size Distribution Calculated by Using Numerical Models. J. Min. Sci. 2013, 49, 441–449. [Google Scholar] [CrossRef]
- Cunningham, C.V.B. The Kuz-Ram Model for Prediction of Fragmentation from Blasting. In Proceedings of the 1st International Symposium Rock Fragmentation by Blasting, Lulea, Sweden, 22–26 August 1983; Holmberg, R., Rustan, A., Eds.; Lulea Tekniska Universitet: Lulea, Sweden, 1983; pp. 439–453. [Google Scholar]
- Osanloo, M.; Hekmat, A. Prediction of Shovel Productivity in Gol-E-Gohar Iron Mine. J. Min. Sci. 2005, 41, 177–184. [Google Scholar] [CrossRef]
- Taksuk, M.; Erarslan, K. Factors affecting loading performance of the excavators in Garp lignite enterprise. In Proceedings of the Ninth International Symposium on Mine Planning and Equipment Selection, Athens, Greece, 6–9 November 2000; Panagiotou, G.N., Michalakopoulos, T.N., Eds.; Balkema: Rotterdam, The Nederland, 2000; pp. 685–689. [Google Scholar]
- Ng, F.; Harding, A.J.; Glass, J. An eco-approach to optimise efficiency and productivity of a hydraulic excavator. J. Clean. Prod. 2016, 112, 3966–3976. [Google Scholar] [CrossRef]
- Fuglevand, P.F.; Webb, R.S. Water Management during Mechanical Dredging of Contaminated Sediment. In Proceedings of the WEDA XXVI Annual Meeting and 38th TAMU Dredging Seminar, San Diego, CA, USA, 25–28 June 2006; Randell, R.E., Ed.; Texas A&M University: College Station, TX, USA, 2006; pp. 461–467. [Google Scholar]
- Klanfar, M.; Kujundžić, T.; Vrkljan, D. Calculation analysis of bulldozer’s productivity in gravitational transport on open pits. Tech. Gaz. 2014, 21, 517–523. [Google Scholar]
- SAE Standard J296—Excavator Hoe Bucket Rating. In SAE Handbook 1990; Customer Service SAE: Warrendale, PA, USA, 1990; Volume 4.
- ISO 7451:2007. Earth-Moving Machinery—Volumetric Ratings for Hoe-Type and Grab-Type Buckets of Hydraulic Excavators and Backhoe Loaders; International Organization for Standardization: Geneva, Switzerland, 2007. [Google Scholar]
- Caterpillar Inc. Caterpillar Performance Handbook, 43rd ed.; Caterpillar Inc.: Peoria, IL, USA, 2013. [Google Scholar]
- Church, H.K. Excavation Handbook; McGraw-Hill: New York, NY, USA, 1981; p. A-3. [Google Scholar]
- Hartman, H.L. SME Mining Engineering Handbook, 2nd Ed. ed; Society for Mining, Metallurgy and Exploration, Inc.: Littleton, CO, USA, 1992; Volume 2, pp. 259–262. [Google Scholar]
- Peele, R. Mining Engineers’ Handbook, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1961; p. 1314. [Google Scholar]
- APAO. Construction Aggregates Consumers’ Guide; Aggregate Producers’ Association of Ontario: Mississauga, ON, Canada, 2000. [Google Scholar]
- Du Pont, E.I. Blaster’s Handbook, 16th ed.; E. I. Du Pont de Nemours & Co. Inc.: Wilmington, DE, USA, 1980; p. 494. [Google Scholar]
- Earthworks. Available online: http://www.dur.ac.uk/~des0www4/cal/roads/earthwk/earthwk.html (accessed on 7 February 2015).
- Evenfallstudios.com. Available online: http://www.evenfallstudios.com/metrology/earthworkweights.html (accessed on 7 February 2015).
- McNally, G. Soil and Rock Construction Materials; CRC Press: London, UK, 2002; pp. 291–310. [Google Scholar]
- Popescu, C.M.; Phaobunjong, K.; Ovararin, N. Estimating Building Costs—Civil and Environmental Engineering, 1st ed.; CRC Press: Boca Raton, FL, USA, 2003; pp. 120–143. [Google Scholar]
- Muir, B.G. Observations on wind-blown superphosphate in native vegetation. West. Aust. Nat. 1979, 14, 128–130. [Google Scholar]
- Komatsu Inc. Komatsu Specifications and Applications Handbook, 30th ed.; Komatsu Inc.: Tokyo, Japan, 2009. [Google Scholar]
- Litvin, O.; Litvin, Y. Evaluation of Effect of the Excavator Cycle Duration on its Productivity. In E3S Web of Conferences Proceedings of the 5th International Innovative Mining Symposium, Kemerovo, Russia, 19–21 October 2020; EDP Sciences: Paris, France, 2020; Volume 174, p. 01010. [Google Scholar] [CrossRef]


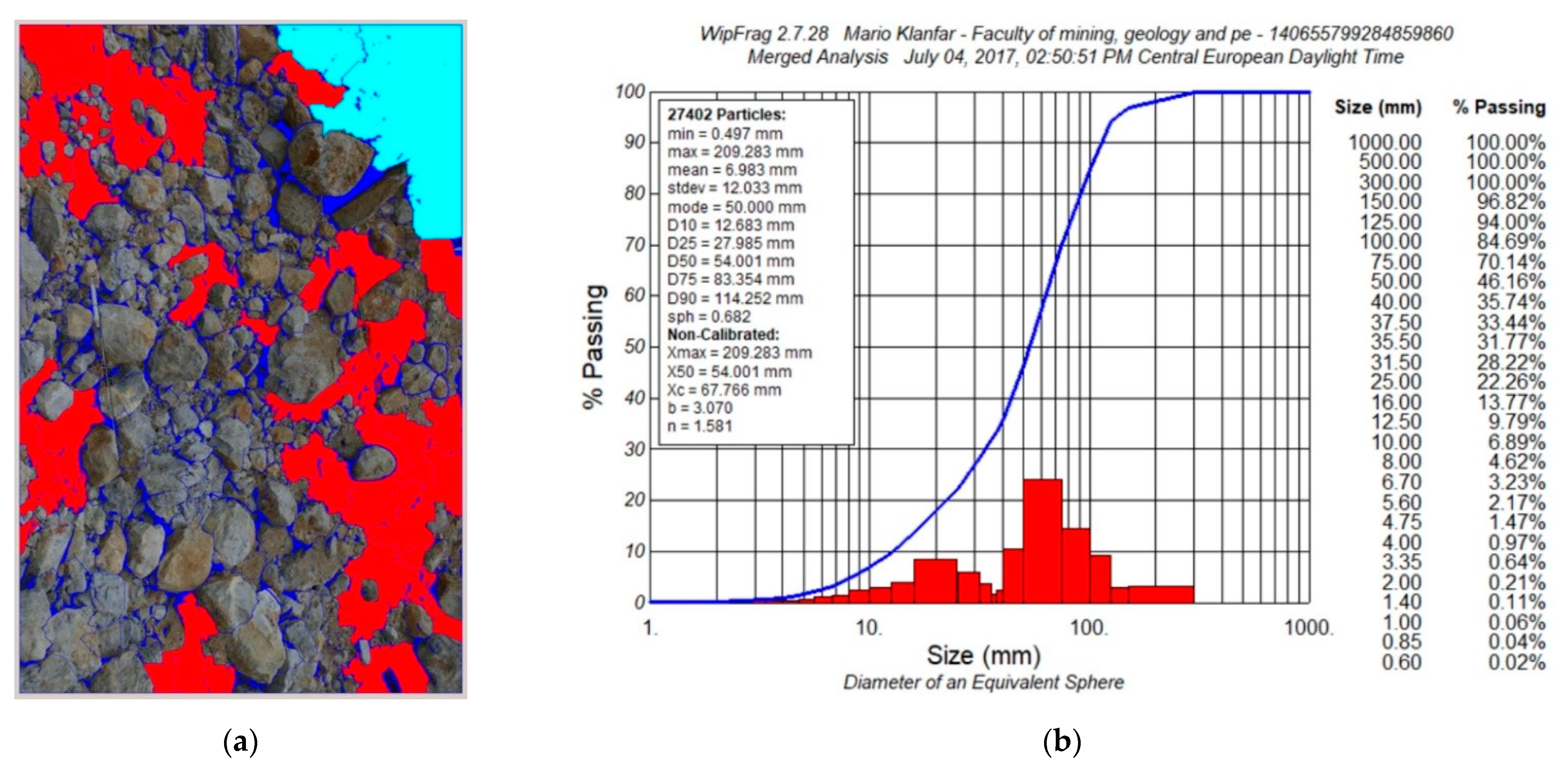
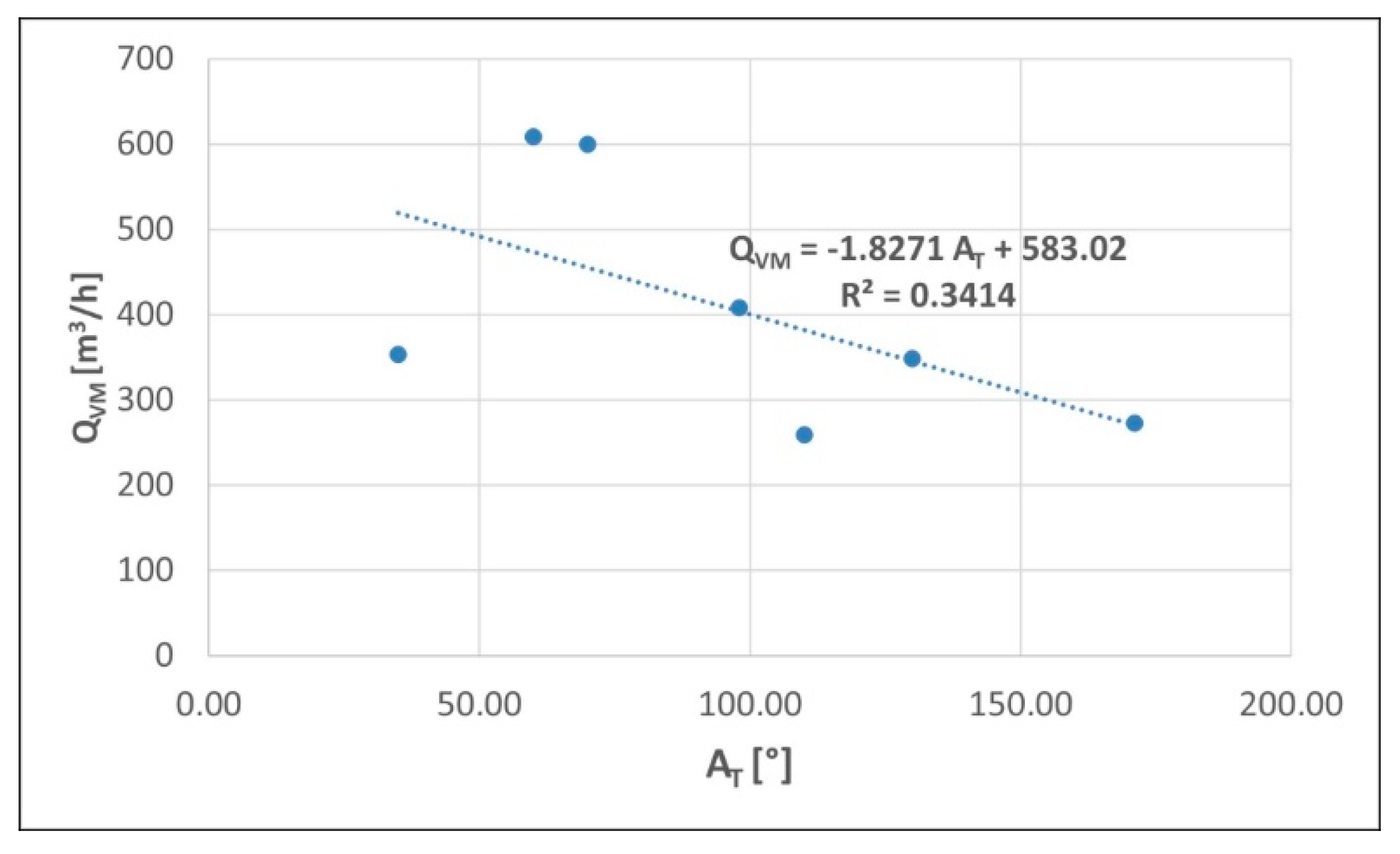
| Quarry | Excavator | Material | Task | AT [°] | Vm [m3] | Ar [°] | Tc [s] | n | Xc [mm] | d50 [mm] | d80 [mm] |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Žervanjska | Liebherr R944C | Overburden (wet) | Heap shifting | 70 | 2.37 | 49 | 14.23 | 6.59 | 30.1 | 29.07 | 32 |
| Zaprešićki Ivanec | Fiat—Hitachi EX355 | Blasted dolomite rock (wet) | Heap shifting | 60 | 2.28 | 48.6 | 13:49 | 3.87 | 1.305 | 1.242 | 1.3 |
| Gradna | Renders RKE 2600 | Blasted dolomite rock (wet) | Truck- shovel | 35 | 2.23 | 44.0 | 22.70 | 1.51 | 34.024 | 25.7 | 50 |
| Škrobotnik | Komatsu PC 340 NLC | Blasted dolomite rock (wet) | Crusher- shovel | 130 | 1.95 | 23.5 | 20.14 | 1.274 | 128.984 | 96.08 | 280 |
| Hruškovec | CAT 330D | Blasted diabase rock (wet) | Truck- shovel | 171 | 2.09 | 39.5 | 27.62 | 1.318 | 91.896 | 67.6 | 152 |
| Špica | CAT 336E | Blasted limestone rock (dry) | Truck- shovel | 98 | 2.05 | 29.2 | 18.09 | 1.485 | 217.461 | 162.4 | 295 |
| Očura | Liebher R944C | Blasted dolomiterock (dry) | Truck- shovel | 110 | 2.03 | 44.1 | 28.21 | 1.581 | 67.766 | 54 | 92 |
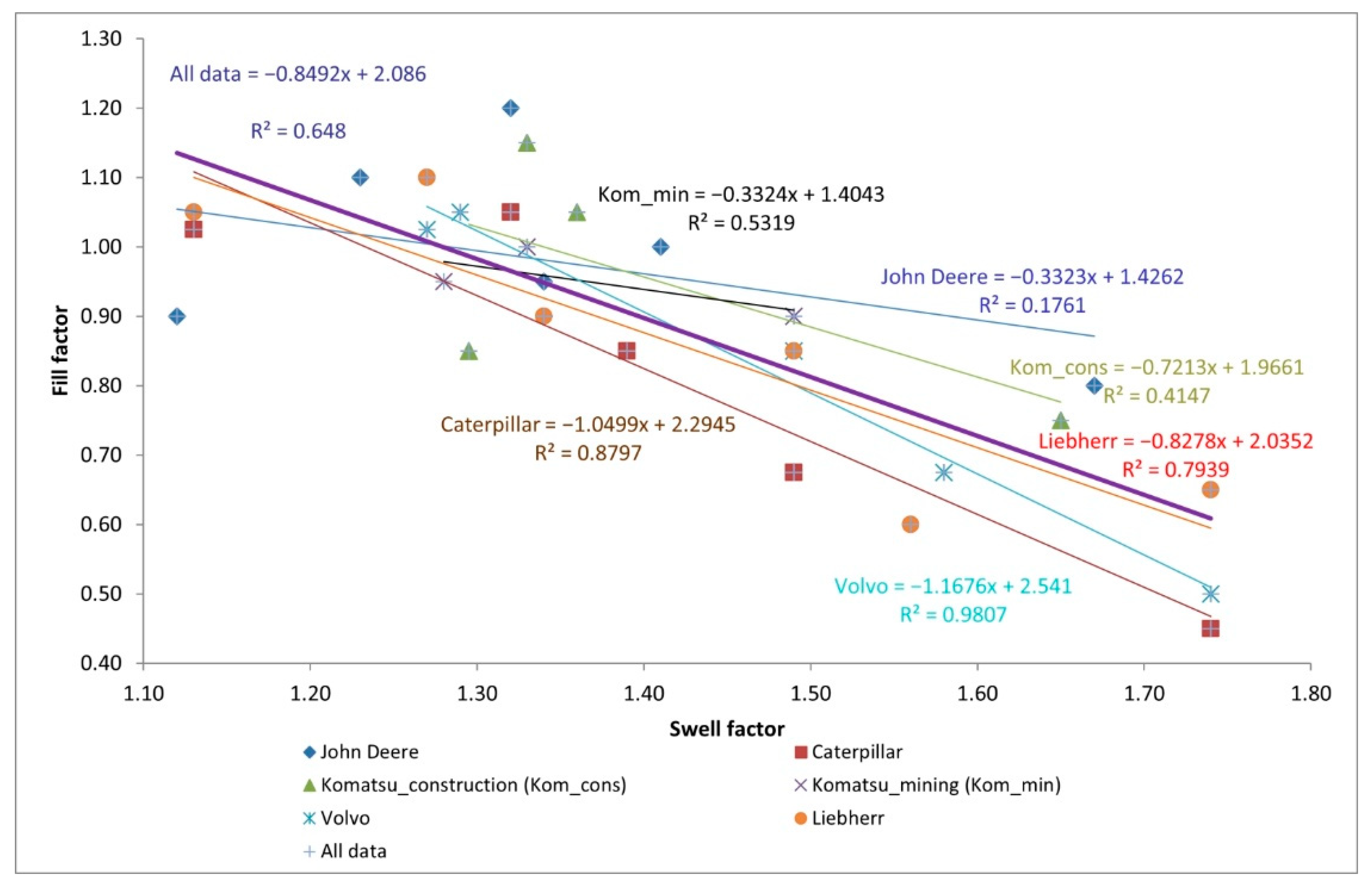
| Source | Material | Fill Factor | Swell Factor |
|---|---|---|---|
| John Deere | Wet Earth, Loam, Sandy Clay Loam | 1.2 | 1.2–1.43 |
| Natural Bed Clay, Damp Sand, Sand & Clay, Lime Rock w/Fines | 1.1 | 1.05–1.33 | |
| Rock and Earth--25%/75%, Dry Clay, Dry Earth, Topsoil | 1.0 | 1.25–1.56 | |
| Rock and Earth--50%/50% | 0.95 | 1.29–1.38 | |
| Rock and Earth--75%/25% | 0.9 | 1.25–1.42 | |
| Dry Sand | 0.9 | 1.11–1.13 | |
| Broken limestone | 0.8 | 1.63–1.70 | |
| Caterpillar | Moist loam or sandy clay | 1.0–1.1 | 1.2–1.43 |
| Sand and Gravel | 0.95–1.1 | 1.11–1.15 | |
| Hard, Tough Clay | 0.8–0.9 | 1.34–1.43 | |
| Rock—Well Blasted | 0.6–0.75 | 1.49 | |
| Rock—Poorly Blasted | 0.4–0.5 | 1.67–1.80 | |
| Komatsu | construction application | ||
| Excavating natural ground of clayey soil, clay, or soft soil | 1.1–1.2 | 1.22–1.43 | |
| Excavating natural ground of soil such as sandy soil and dry soil | 1.0–1.1 | 1.25–1.46 | |
| Excavating natural ground of sandy soil with gravel | 0.8–0.9 | 1.18–1.41 | |
| Loading blasted rock | 0.7–0.8 | 1.49–1.80 | |
| mining application | |||
| Excavating natural ground of clayey soil, clay, or soft soil | 1.0 | 1.22–1.43 | |
| Excavating natural ground of soil such as sandy soil and dry soil | 0.95 | 1.25–1.46 | |
| Excavating natural ground of sandy soil with gravel, Loading blasted rock | 0.9 | 1.18–1.80 | |
| Volvo | Earth/Sandy Clay | 1.0–1.1 | 1.2–1.375 |
| Hard and Compacted Clay, Sand/Gravel | 0.95–1.1 | 1.11–1.43 | |
| Rock—well blasted | 0.75–0.95 | 1.49 | |
| Rock—averagely blasted | 0.6–0.75 | 1.58 | |
| Rock—poorly blasted | 0.4–0.6 | 1.67–1.80 | |
| Liebherr | Clay and sticky material, clay, sandy loam, moist material | 1.1 | 1.1–1.43 |
| Sand, sand gravel mixture, moist | 1.0–1.1 | 1.1–1.15 | |
| Hard dry clay | 0.9 | 1.24–1.43 | |
| Rock, well blasted | 0.85 | 1.49 | |
| Rock, poorly blasted | 0.6–0.7 | 1.67–1.8 | |
| Rock, deteriorated, layered shale, not blasted | 0.5–0.7 | 1.33–1.79 | |
| Underwater digging of sand, gravel & sand-gravel mixtures | 0.85 | - |
| Quarry | Excavator | Material | Vm [m3] | V [m3] | kf | kl |
|---|---|---|---|---|---|---|
| Žervanjska | Liebherr R944C | Overburden (wet) | 2.37 | 1.89 | 0.9 | 1.39 |
| Zaprešićki Ivanec | Fiat—Hitachi EX355 | Blasted dolomite rock (wet) | 2.28 | 1.77 | 0.8 | 1.61 |
| Gradna | Renders RKE 2600 | Blasted dolomite rock (wet) | 2.23 | 1.73 | 0.8 | 1.61 |
| Škrobotnik | Komatsu PC 340 NLC | Blasted dolomite rock (wet) | 1.95 | 1.46 | 0.8 | 1.67 |
| Hruškovec | CAT 330D | Blasted diabase rock (wet) | 2.09 | 1.72 | 0.8 | 1.52 |
| Špica | CAT 336E | Blasted limestone rock (dry) | 2.05 | 1.71 | 0.8 | 1.50 |
| Očura | Liebher R944C | Blasted dolomite rock (dry) | 2.03 | 1.83 | 0.8 | 1.39 |
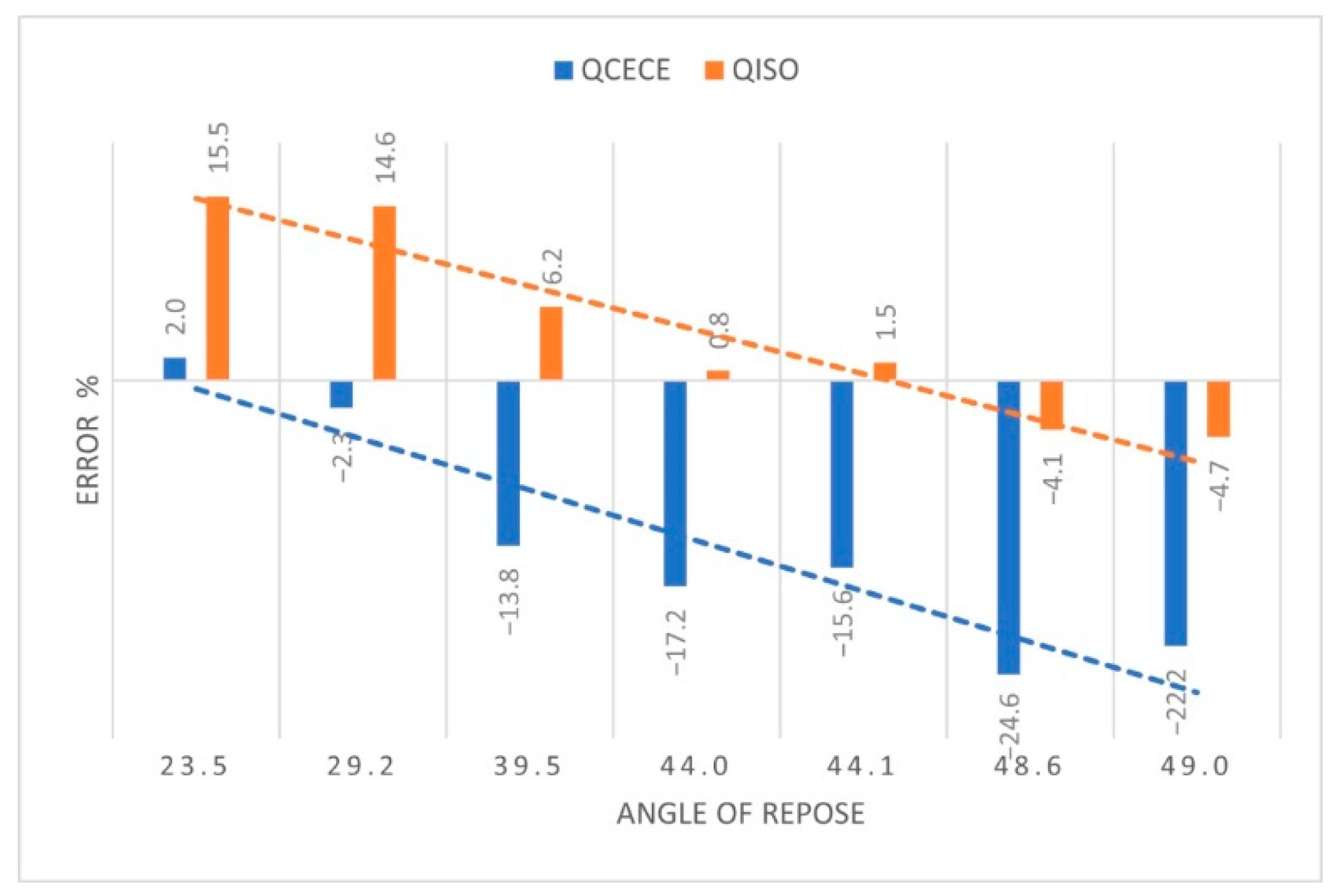
| Quarry | Excavator | AT [°] | Ar [°] | QVm [m3/h] | QISO [m3/h] | QCECE [m3/h] |
|---|---|---|---|---|---|---|
| Žervanjska | Liebherr R944C | 70 | 49 | 600 | 573 | 491 |
| Zaprešićki Ivanec | Fiat—Hitachi EX355 | 60 | 48.6 | 608 | 584 | 488 |
| Gradna | Renders RKE 2600 | 35 | 44 | 354 | 357 | 302 |
| Škrobotnik | Komatsu PC 340 NLC | 130 | 23.5 | 349 | 413 | 356 |
| Hruškovec | CAT 330D | 171 | 39.5 | 272 | 290 | 239 |
| Špica | CAT 336E | 98 | 29.2 | 408 | 478 | 399 |
| Očura | Liebher R944C | 110 | 44.1 | 259 | 263 | 224 |
| AT | Ar | n | Xc | d50 | d80 | |
| AT | 1 | −0.5 | −0.43 | 0.47 | −0.31 | 0.57 |
| Ar | −0.5 | 1 | 0.61 | −0.85 | 0.32 | −0.97 |
| n | −0.43 | 0.61 | 1 | −0.53 | 0.25 | −0.59 |
| Xc | 0.47 | −0.85 | −0.53 | 1 | −0.39 | 0.95 |
| d50 | −0.31 | 0.32 | 0.25 | −0.39 | 1 | −0.39 |
| d80 | 0.57 | −0.97 | −0.59 | 0.95 | −0.39 | 1 |
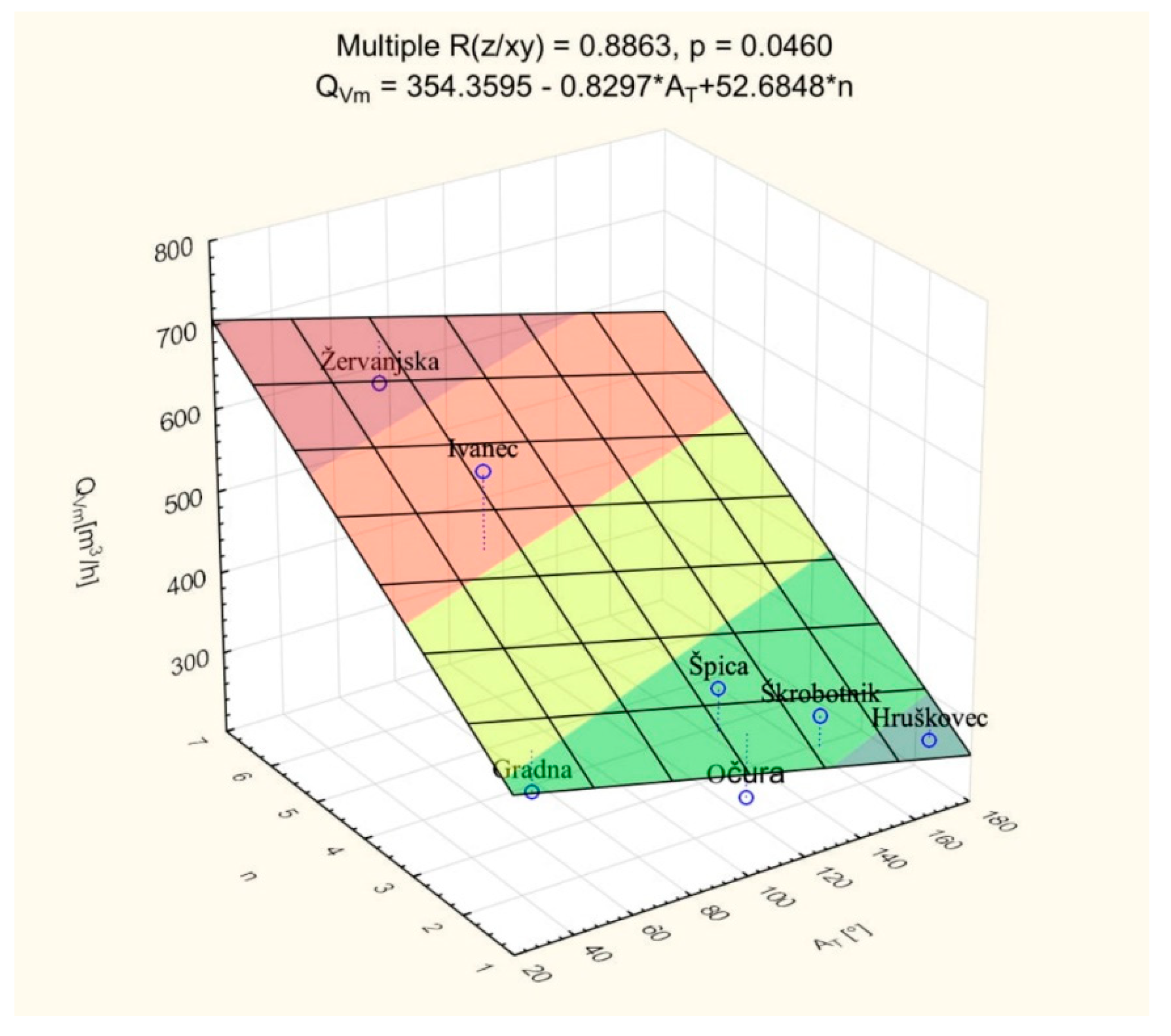
| N = 7 | R = 0.88628382; R2 = 0.78549901; Adjusted R2 = 0.67824851; F (2,4) = 7.324 P < 0.04601; Std. Error of estimate: 81.529 | |||||
|---|---|---|---|---|---|---|
| b * | Std.Err. of b * | b | Std.Err. of b | t (4) | p−Value | |
| Intercept | 354,3595 | 110.2472 | 3.21423 | 0.032458 | ||
| AT [°] | −0.265315 | 0.256894 | −0.8297 | 0.8034 | −1.03278 | 0.360057 |
| n | 0.738543 | 0.256894 | 52.6848 | 18.3258 | 2.87490 | 0.045245 |
| Mark Equation | Regression Summary for Dependent Variable: Excavator Productivity in Loose State of Material Qvm (m3/h) | Mean abs. Deviation (m3/h) |
|---|---|---|
| (7) | R = 0.886284; R2 = 0.785499; Adjusted R2 = 0.678249; F (2,4) = 7.324; p < 0.04601; Std. Error of estimate: 81.529 | 54.75 |
| (8) | R=0.909546; R2=0.8272741; Adjusted R2= 0.6545482; F (3,3) = 4.7895; p < 0.11534; Std. Error of estimate: 84.479 | 44.98 |
| (9) | R = 0.910839; R2 = 0.829628; Adjusted R2 = 0.488884; F (4,2) = 2.4348; p < 0.31172; Std. error of estimate: 102.76 | 47.19 |
| (10) | R = 0.999665; R2 = 0.999331; Adjusted R2 = 0.995984; F (5,1) = 298.63; p < 0.0439; Std. error of estimate: 9.1082 | 2.82 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kujundžić, T.; Klanfar, M.; Korman, T.; Briševac, Z. Influence of Crushed Rock Properties on the Productivity of a Hydraulic Excavator. Appl. Sci. 2021, 11, 2345. https://doi.org/10.3390/app11052345
Kujundžić T, Klanfar M, Korman T, Briševac Z. Influence of Crushed Rock Properties on the Productivity of a Hydraulic Excavator. Applied Sciences. 2021; 11(5):2345. https://doi.org/10.3390/app11052345
Chicago/Turabian StyleKujundžić, Trpimir, Mario Klanfar, Tomislav Korman, and Zlatko Briševac. 2021. "Influence of Crushed Rock Properties on the Productivity of a Hydraulic Excavator" Applied Sciences 11, no. 5: 2345. https://doi.org/10.3390/app11052345
APA StyleKujundžić, T., Klanfar, M., Korman, T., & Briševac, Z. (2021). Influence of Crushed Rock Properties on the Productivity of a Hydraulic Excavator. Applied Sciences, 11(5), 2345. https://doi.org/10.3390/app11052345







