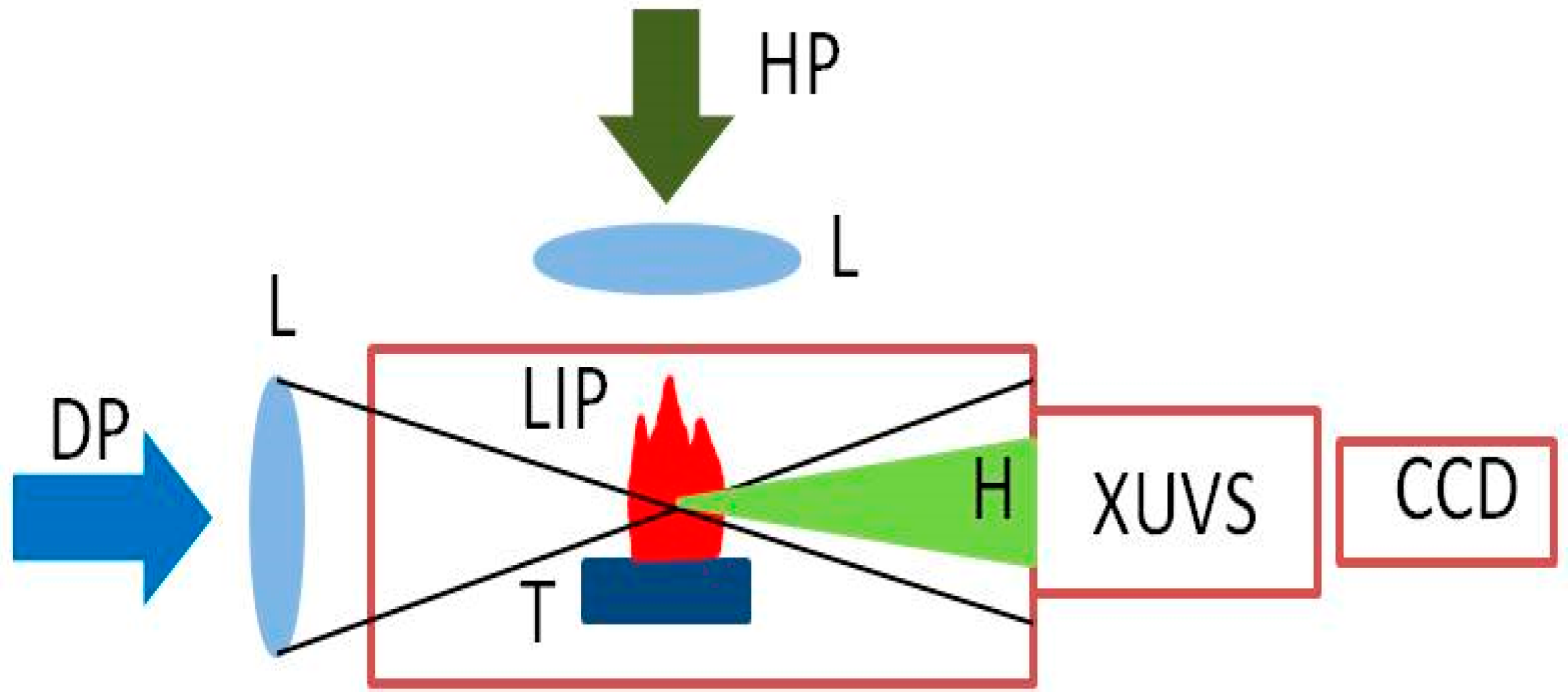
3. Results
The first set of our measurements was aimed at the analysis of plasma emission from the ablated species. The plasma emission spectra in the 30–100 nm wavelength range for the six targets are presented in
Figure 2.
Plasma emission was recorded at heating pulse parameters (pulse energy and fluence) larger than the optimal ablation characteristics for harmonics generation. The fluence of heating pulses during these studies was equal to 15 J cm
−2. We did not average the plasma spectra from these samples but instead used a single shot collection. The emission lines were determined using the NIST database [
21]. The positions of the 806 nm radiation harmonics from the bulk carbon starting from 9th (H9) to 23rd (H23) orders are shown as the red curves. The harmonic profiles shown in this figure were included for demonstration of the closeness with some ionic transitions.
For the bulk C plasma produced by HP with the energy of E
HP = 3 mJ, we can see the presence of intense CI and CII lines corresponding to the transitions in neutral and singly charged ions of carbon in the spectral region between 55 and 100 nm, as well as the presence of CIII lines below 55 nm. The density of free electrons in bulk C plasma was estimated to be ~5 × 10
16 cm
−3, which is similar to the estimates at the same laser parameters presented in [
22]. The particle density was estimated in [
23] to be in the range ~10
18 –10
19 cm
−3 for comparable laser fluencies. The contribution of continuum emission decreased the contrast of emission lines.
In the case of the targets comprising nanostructured materials, the shift of emission to larger presence of the lines attributed to CII and CIII transitions was observed, except for CNF and DN. A pattern similar to the above-described spectrum was observed in the case of CNF (E
HP = 3 mJ) and GR (E
HP = 3 mJ). However, contrary to bulk C plasma, the continuum emission was localized in the shorter wavelength region below 65 nm. In the case of C
60 (E
HP = 2 mJ) and MW CNT (E
HP = 2 mJ), the relative intensities of CIII lines significantly increased, while additional strong CIV transitions appeared in the plasma spectra. A similar pattern was observed in the case of all nanostructure-containing plasmas, except CNF. In the case of C
60, this behavior confirms the earlier reported observations that, under similar experimental conditions, the plasma from fullerenes reaches much higher ionization states than in the case of bulk graphite ablation [
24]. This statement is valid for all nanostructured materials, while at the same time, we observed a decrease in the relative intensity of CI (85.9 nm) line corresponding to the transition in neutral carbon.
In DN (EHP = 4 mJ) case, the plasma spectrum contained less emission lines and a smaller continuum despite the stronger excitation of the target. The different applied HP energies for different samples are explained by the different optimal conditions for plasma formation suitable for HHG. The term “optimal conditions” refers here to the maximal harmonic yield from each ablated sample, which depends on the fluence of HP on the target surface at similar geometry of the focusing conditions. Additionally, the pressed tablets were destroyed at higher fluencies of HP due to their fragility. For example, the harmonic yield from GR and DN LIPs was more than twice as small as from other targets due to weaker ablation at which the pressed tablets remain intact. Correspondingly, we could not increase the HP fluence on those fragile surfaces.
As shown below, the ablation corresponded to the formation of low-ionized plasma using suitable fluence of HPs provided the conditions for efficient HHG. It is important to note that higher densities of free electrons cause the phase mismatch between the driving and harmonics waves for overheated and strongly ionized plasmas, which plays a destructive role in HHG. The moderate fluencies of nanosecond pulses also increased the lifetime of the targets and provided better survival of the original nanostructures being ablated and spread in the plasma plume without their destruction. It was demonstrated that, in the case of laser ablation of C
60, MW CNT, CNF, and DN [
25] at the experimental conditions similar to ours, the transmission electron microscopy analysis of deposited debris has shown that laser-produced plumes contained the original nanostructures.
Figure 3 shows the harmonic spectra in different plasmas at variable delays between heating and driving pulses in the 100–600 ns range. The dependences of the harmonic yield on the delay are plotted in
Figure 4a.
The left column of
Figure 3 compares the harmonics generated from 9th to 25th order from bulk C (blue curve) and C
60 (red curve). The maximal harmonic yields for both samples were observed at ~200 ns delay from the beginning of the ablation. Meanwhile, the delay dependence for C
60 (
Figure 4a, red line with empty squares) demonstrates higher integrated harmonics signal, as well as it is extended up to longer delays (~1
µs). In the case of bulk C (
Figure 4a, black line with filled squares) we observed a pronounced single maximum at 200 ns, which can be interpreted as the moment of arriving of the largest amount of elemental emitters to the interaction area with DP. The estimation for the velocity of the main part of emitters shows that it equals 1.2 × 10
3 m/s, which is close to our HHG-based measurements in the case of DP propagation at 0.2 mm distance from the target surface (~(1–2) × 10
3 m/s). The delay dependence in the case of C
60 (
Figure 4a) demonstrates a weak decay between 200 and 600 ns, which can be interpreted as a gradual passing of C
60 and its different fragments through the interaction area at the velocities slightly varying from 1 × 10
3 m/s. As one can see (left column of
Figure 3), in the case of harmonic spectrum from C
60 their yield gradually increased and maintained almost equal for the 9th to 17th orders in the range of 200 to 500 ns delays.
Figure 4b shows the saturated images of harmonics collected by CCD camera from the phosphorous screen of the microchannel plate of XUV spectrometer at the optimal delays of each studied sample. The images are shown in log scale and normalized to 1. The purpose of such presentation of harmonics distribution is to define the maximal order of generated harmonics, i.e., harmonic cutoff, and better view the difference in harmonic intensities from various species. In this figure, an emission is observable on the right side of 9H in the first five spectra, which is a second-order diffraction related with strong emission from 17th order. One can also see the weak second-order diffraction related to the 19H (see third panel from the top in the case of MW CNT), which is seen on the left side of 9H. Similar pattern is seen in some panels of
Figure 3 showing the lineouts of the harmonic spectra.
For bulk C and C60 we notice a difference in the harmonic cutoffs. From all six samples, ablated bulk C allowed the generation of the highest cutoff at similar conditions of experiments (25th order; we also observed very weak 27th harmonic, however, its signal was close to the sensitivity limit of our detection system). Harmonics generating in C60 LIP showed the smallest cutoff position (21th order).
4. Discussion
Table 1 comprises the optimal conditions of ablation for different targets. Note that earlier studies have demonstrated that neither pulse energy nor pulse intensity can be considered as the definitive parameters responsible for the optimization of plasma formation to produce maximal yield of harmonics. The most important parameter here is the fluence, or energy density, of the heating pulses on the target surface. In this table, we include the optimal fluencies for each studied sample.
It was demonstrated in [
23,
25,
26] by time-of-flight mass spectroscopy (TOFMS) that LIPs from the graphite surface contain, along with neutral carbon atoms and its ions, different C
n clusters and their ions. The number of carbon atoms in such clusters varies from
n = 2 up to
n = 20, and for strong excitation
n could even reach 100.
Earlier, in the case of C
60 ablation at conditions similar to ours, TOFMS demonstrated the presence of preferably C
26+ fragments and smaller amount of C
60+ ions, alongside the neutral nanoparticles, in LIP [
25]. In order to provide a qualitative explanation of the obtained HHG results we use the semiclassical model of HHG in isotropic medium [
27]. According to this model, the HHG cutoff is defined by the expression
Nc ≈ (
Ip + 3.2
Up)/
ω, where
Ip is the ionization potential of elemental emitter,
ω is the laser field frequency,
Up =
Il/(4
ω2) is the pondermotive potential, and
Il is the laser field intensity. The ionization potential of carbon atom is
Ip (Bulk C) = 11.26 eV [
28], while the ionization potential for small-sized carbon molecules varies from
Ip (C
2) = 11.35 eV,
Ip (C
3) = 11.5 eV to
Ip (C
9) = 9.4 eV [
26] with the tendency to decrease toward bigger molecules. For C
60, the ionization potential is correspondingly lower compared to smaller-sized molecules (
Ip (C
60) = 7.6 eV [
29]). The application of our experimental parameters in expression for harmonic cutoff gives
Nc (bulk C) = 31 and
Nc (C
60) = 29. Note that in the present work the 25th and 21st harmonics cutoffs from those species were observed. Thus, we attribute the observed peculiarities of HHG spectra in pair “bulk C–C
60” to the presence of mostly C
60 and its large fragments in the plasma plume, which was indirectly confirmed by our plasma emission spectra (
Figure 2, C
60 panel), where the relative intensity of the CI transition line is lower than that of CIII and CIV lines. Larger harmonics cutoff in bulk C targets can be attributed to the presence of mostly neutral and small-sized carbon molecules in LIP. The presence of highly charged ions does not provide sufficient contribution to the extension of HHG cutoff, since the HHG conversion efficiency quickly reduces with increasing ionization potential.
Returning to the model [
27], harmonics generation is described as a process where the first step is the formation of the electron wave packet by tunneling ionization and the second step includes a classical mechanics description of released electron in laser field. The first step can be described by the Ammosov–Delone–Krainov (ADK) expression for ionization rates
Γion for different ionization potentials [
30] and defines in two-step model the efficiency of conversion. While estimating ADK rates we assumed the laser intensity to be equal to what we measured in the focal plane of the focused driving beam (2 × 10
14 W cm
−2). Direct comparison of ionization rates by ADK formula gives
Γion[
Ip(C) = 11.26 eV]/
Γion[
Ip(C
+) = 24.38 eV]~10
5 higher rate for tunnel ionization in the cases of the neutral and single charged carbon atom. By applying the same approach to evaluate the difference in ionization rates of fullerenes and carbon, one can define the following ratio
Γion[
Ip(C
60) = 7.6 eV]/
Γion[
Ip(C) = 11.26 eV] ≈ 5.
Thus, C
60 molecules can be considered more efficient high harmonics emitters than ordinary carbon atoms or small-sized carbon molecules. Their presence in LIP leads to a stronger enhancement of the low-order part of HHG spectrum comprising the harmonics between 9th and 17th orders. We can conclude that, despite the lower density of C
60 nanoparticles in plasma compared to C atoms and ions originated from graphite ablation, higher HHG efficiency allows the observation of harmonics even at notably larger delays (>1000 ns) compared with the latter species (
Figure 4a). Higher cutoff position in the case of ablated graphite is attributed to the presence of neutral carbon and small-sized C
n (where
n < 20) molecules. Note that the role of different small carbon clusters synthesized during ablation of graphite was analyzed in the studies related to HHG in carbon LIP [
20].
The middle column of
Figure 3 represents HHG spectra obtained from, to some extent, morphologically similar species: multiwalled carbon nanotubes (blue solid lines) and carbon nanofibers (red solid lines). MW CNT plasma dynamics showed the 400 ns optimal delay from the beginning of ablation corresponding to maximal harmonic yield. Simultaneously, the delay dependence (
Figure 4a, blue line with solid circles) had the plateau-like structure between 200 and 400 ns. The harmonic yield in this time scale was equal or slightly higher than in the case of C
60 plasma. The enhanced harmonics from 9th to 17th orders were observed between 100 and 400 ns delays (
Figure 3, middle column). At the same time, the cutoff (25th harmonic) at the optimal delay (400 ns) was slightly higher compared to C
60 plasma (
Figure 4b).
We can assume that the enhanced low-order harmonics were attributed to the presence of small fragments of CNTs in LIP. At the same time, higher cutoff can be attributed to the coherent contribution to HHG from the carbon neutral atoms and small-sized carbon molecules. Notice that the ionization potential of single-walled CNT is in the range of 5–6 eV [
31]. The HHG spectrum in the case of short (100 ns) delay indicates that small-sized components of such plasma can gain, to some extent, larger velocities, thus causing the enhanced harmonic spectra with larger cutoff order. This is what we see in the case of bulk C and MW CNT. At the same time, the large-sized components of LIP responsible for enhancing the lower orders of spectra are expected to appear at larger delays. Summarizing the analysis of HHG in MW CNT, one can conclude that, at the used parameters of HP, MW CNT plasma also contains small carbon particles alongside the fragments of nanotubes.
Meanwhile, the HHG spectrum from CNF was surprisingly similar to C
60. CNF plasma showed optimum delay at 300 ns (
Figure 4a, green line with empty circles) and similar to C
60 cutoff (21st order,
Figure 4b). We assume that plasma from CNF ablation was less fragmented compared to MW CNT despite the higher HP energy used there (3 mJ vs. 2 mJ).
Earlier reported TOFMS spectra have demonstrated the similarities between the MW CNT and CNF, with the presence of small carbon C
n fragments (with
n varied up to 20) and no ions higher than low-sized carbon clusters in the mass spectra up to 5000 mass/charge units [
25]. Additionally, the emission from ablated MW CNT and C
60 targets showed almost similar spectra (
Figure 2), with strong relative lines for CIII and CIV transitions. We can suppose that, in the case of MW CNT, the fragmentation process induces the appearance of small-sized carbon molecules and clusters inducing the larger cutoff, since at short delay (100 ns,
Figure 4a) the integrated harmonic signal from MW CNT plasma exceeds that from bulk C LIP. Plasma spectra for CNF demonstrate the most contradictive result, with strong relative CI transition line, which indirectly points out to the presence of large number of neutral carbon atoms, but without extending the HHG cutoff.
TOFMS is a natural and obvious way to precisely determine the mass-to-charge state of the ablation plume. Notice that the main goal of present research was to study high-order harmonics generation from the plasmas generated on the graphite, fullerenes, carbon nanotubes, carbon nanofibers, diamond nanoparticles, and graphene targets. Meantime, the joint application of HHG and TOFMS facilities in a single set of experiments is hardly to be achieved. Earlier studies, which combined the data revealed from above facilities, were performed separately, which did not allow for a conclusive argument for the similarity of the plasma formation conditions in these two sets of experiments. Meanwhile, we demonstrate that the HHG approach allows for analyzing the dynamics of plasma spreading out from ablated surface thus revealing some interesting peculiarities hardly obtainable in the case of TOFMS approach. Our present research, as well as earlier reported studies of harmonic generation in laser-induced plasmas, enabled a demonstration of the attractive features of the high-order nonlinear spectroscopy of these species.
The HHG spectra generated in the plasmas produced on the graphene sheets and diamond nanoparticles are shown on the right column of
Figure 3. The harmonic yields from GR and DN was multiplied by a factor of 2 to make them more visible and, in order to compare with other spectra. Both plasmas allowed the generation of weaker harmonics compared to the other four samples. The delay dynamics in the case of GR (
Figure 4a, solid pink line with filled rhombuses) indicated the presence of large fragments in LIP, with maximal harmonic yield observed at 300 ns delay. The delay dynamics curve is more flattened with respect to the above-discussed materials, with comparable integrated harmonic yield in the range of 100 ns to 700 ns. We attribute this pattern of delay dynamics to the wide distribution of GR’s pieces possessing different velocities centered at ~1 × 10
3 m/s. The harmonic spectrum changed at optimum delay (
Figure 4b) and showed the cutoff at 23rd order, and the enhanced 11th and 13th harmonics (
Figure 3, left column, black line). We attribute this increase in harmonic yield to the arrival of large-sized fragments of graphene to the interaction area.
Among all studied materials, DNs have the largest crystal lattice energy. This characteristic can explain, to some extent, the better survival of DNs in the plasmas produced by the heating pulses. This may also explain why DNs showed relatively extended optimum delay (500 ns;
Figure 4a, dark yellow line with empty rhombuses). With the increasing of the delay, the 11th to 15th harmonics also enhanced (
Figure 3, right column, red solid lines), while up to 500 ns delay the harmonic spectral shape and cutoff located at 25th order remained the same (
Figure 4b). The observed peculiarities of HHG spectra from GR and DN plasmas can be explained by the presence of the small-sized carbon molecules and clusters having uniform distribution of velocities. The latter assumption can explain the flattened delay curves with the same HHG cutoffs (23rd and 25th orders).
The cutoff positions for all studied samples were, to some extent, close to each other except for graphene (
Figure 3). Though the ionization potentials were almost similar, the studied plasmas were distinguished from each other by the harmonic yield rather than by cutoff energy.
Below, we address the importance of considering the above delay-dependent experiments for understanding the dynamics of plasma propagation. The signature, indicating the presence of specific emitters, is the increase in the output of harmonics at certain specific delays from the beginning of ablation. We can assume that the same average kinetic energy E = mv2/2 could characterize all plasma components containing the same basic atom, in our case carbon. Accordingly, the same average arrival time could be expected for carbon clusters of different sizes. The duration for cluster propagation from the target surface to the optical axis of the femtosecond pulse propagation corresponds to the optimal delay between HP and DP. Our results show that small carbon clusters enter the area of interaction with the femtosecond beam much earlier than expected, assuming only kinetic consideration when it is assumed that the components reach thermodynamic equilibrium during expansion. Alternatively, we can suppose that all carbon clusters acquire the same kinetic energy from the very beginning and propagate from the surface at speed approximately similar to that of a single carbon ablated from bulk material. The arrival times of particles consisting of a single carbon atom, 60 atoms (fullerene), 106 atoms (diamond nanoparticles), 109 atoms (CNT and CNF), and even much larger species, such as parts of graphene sheets, were comparable to each other (200-400 ns). Thus, the role of the cluster’s atomic weight in HHG becomes questionable if only a simple kinetic energy mechanism is considered. In other words, from the very beginning, all the atoms in the clusters acquire the same kinetic energy and propagate from the surface at speed approximately equal to that of a single carbon atom.
When we use the term “heating” for the laser ablation, we do not merely suppose the thermal evaporation of the target. It is not a simple thermal evaporation induced plasma formation. This process depends on the level of target excitation that is used for laser ablation. The creation of nonlinear medium above the target surface is not based on the simple heating of the target surface and steady-state processes of melting, evaporation, and spreading of the particles with the velocities defined from the thermodynamic relations. This relation refers to cw heating. In this case the velocity of the C60 molecule at 1000 K is in the range of 1.5 × 102 m s−1. Correspondingly, during the first few hundred nanoseconds (~200 ns corresponding to our observation of maximal yield of harmonics) the fullerene molecules will move only 30 µm above the surface. Notice that femtosecond driving pulse propagates at the distance of ~0.2 mm above the target’s surface. If one assumes that plasma creation by laser pulses is defined by this slow process, then no harmonics at all should be observed in such experimental configuration for any of our targets, be it C60, CNT, CNF, graphene, or DN. In the meantime, laser ablation of any of the above targets creates a very efficient plasma medium, which generates extreme high harmonics when the femtosecond pulse propagates 200 µm above the target surface.
This contradiction is explained by another model of creation of the cloud of particles, namely, plasma explosion during ablation of the targets. The dynamics of plasma front propagation during laser ablation is studied by few groups (for example [
32] and references therein). The dynamics of plasma formation and spreading can be analyzed by either the time resolved ICCD images or shadowgram technique. A numerical analysis of the generation of such plasmas for the case of single-pulse interaction with the target surface was described in [
33]. Previously, the dynamics of the spatial characteristics of laser plasmas generated from B and Mo targets, measured using the shadowgraphs of the plasma, was reported in [
34]. For Mo, the plasma front spreads with the velocity of ~6 × 10
3 m s
−1. For example, the plasma front reaches 200 µm distance from the target after hundred nanoseconds rather than a few thousand ns, as we can estimate if we assume the steady-state expansion of the plasma particle cloud. Obviously, the formation of “optimal” plasma is not restricted by appearance of the plasma front in the area of femtosecond pulse. We must wait until the density of the particles becomes sufficient for efficient HHG, while the free-electron concentration remains below the level when the impeding processes prevail over the harmonic generation. In our case the velocity of the “optimal” part of carbon nanostructures contained plasma cloud was measured to be 1 × 10
3 m s
−1.
The appearance of continuum points out the strong heating of target surface. The strong incoherent emission of plasma also decreases the overall “quality” of generated XUV radiation when the former emission becomes stronger than coherent emission of harmonics. That is why the determination of “optimal” plasma for HHG [
35] includes various factors playing an important role in amendment and suppression of harmonic yield. Briefly, moderate (10
17 cm
−3) plasma density, a small ionization rate, and correspondingly small electron density (a few units of 10
16 cm
−3) helped achieve the best conversion efficiencies towards the harmonics in the plateau range (10
−5 and higher), which was almost two orders of magnitude higher than in the case of “overheated” targets. The application of “optimal” plasma immediately allowed for the demonstration of such unique properties of HHG in ablated debris like the resonance-induced enhancement of single and group of harmonics, the resonance-induced suppression of some harmonics, the quasi-phase matching of the groups of harmonics in different ranges of XUV, the efficient application of clusters, quantum dots and relatively large nanoparticles for harmonics generation, the application of extended plasmas at the conditions when the coherence length for some harmonics does not exceed the sizes of laser-induced torches, etc. These advanced features of HHG in optimally prepared plasmas cannot be reproduced in the plasmas formed during strong ablation of target surfaces. Moreover, most of above advantages could not be repeated in the gas media commonly used of HHG.
The continuum shown in the emission spectra was produced during the strong excitation of our targets. The motivation to show plasma emission spectra at these conditions is: (a) to demonstrate the similarity in emission lines of different nanostructured materials caused by the presence of carbon in each of these species and (b) to show the closeness of harmonic and plasma emission lines, which does not lead to the resonance-induced enhancement of those harmonics. Moreover, our spectral measurements were carried out at the conditions when we could not distinguish the emission from the target surface and emission from nearby (~0.2 mm above the ablated surface) plasma.
At the moderate ablation conditions (i.e., at the fluence of 2 to 7 J cm−2 on the target surface) the nanostructures are not affected by the temperature of surrounding material (~900 K) but rather safely elevate from the surface. The survival of carbon nanostructures at these conditions of ablation and their presence at the moment of propagating the driving femtosecond pulses through such plasma formations was confirmed by the SEM analysis of the debris deposited on the nearby surfaces.
To summarize, we considered two models: the model of plasma spreading and the model of harmonics generation in the plasmas comprising of the same element (carbon, in our case) either in a single atomic mode or complex morphology state. The first model allowed us to confirm the similarity in the velocities of single-atomic and multi-atomic debris, which corroborates with our observations of the maximal yield of harmonics at approximately same delay between the heating and driving pulses for each of these species. The second model offers the consideration of C and Cn (n refers to the number of atoms in cluster) particles as the harmonic emitters from the point of view of their ionization potentials and harmonic yield. An approximate similarity in the ionization potentials led to similarity, to some extent, of the cutoff harmonics, while a larger number of atoms in nanostructures allowed for increasing the cross section of recombination of the accelerated electron with the parent particle. The latter peculiarity distinguished the harmonic yields from the single-atomic plasma produced from ablated graphite and the multi-atomic plasma produced from other studied carbon-contained species (fullerenes, multiwalled nanotubes, nanofibers, diamond nanoparticles, and graphene). Thus, by combining the analysis of delay dependences of the integrated harmonic signals and HHG spectra in the 30–100 nm wavelength range, the roles played by the carbon monomers, small-sized carbon molecules, and large nanoparticles in the former process were revealed. A search of new approaches in this direction allows for demonstrating the advantages of high-order nonlinear spectroscopy of ablated nanostructured solids.