Abstract
Recently, tunable photonic crystals (PhCs) have received great research interest, thanks to the wide range of applications in which they can be employed, such as light emission and sensing, among others. In addition, the versatility and ease of fabrication of PhCs allow for the integration of a large range of responsive elements that, in turn, can permit active tuning of PhC optical properties upon application of external stimuli, e.g., physical, chemical or even biological triggers. In this work, we summarize the most employed theoretical tools used for the design of optical properties of responsive PhCs and the most used fabrication techniques. Furthermore, we collect the most relevant results related to this field, with particular emphasis on electrochromic devices.
1. Introduction
Photonic crystals (PhCs) represent versatile building blocks in optics, although they are mostly used as passive optical elements. In these systems, the periodic arrangement of materials with different refractive indices gives rise to the so-called photonic band gap (PBG) and, thus, to structural coloration [1,2]. In this context, however, anything that can interfere with either the periodicity or the refractive index contrast can be translated into an active modulation of the PBG. This in fact enables application of PhCs as optical active elements. From conceptualization to fabrication, the simplest photonic crystal is represented by a multilayer that alternates materials with different refractive indices [3,4]. From an application point of view, multilayer photonic crystals, also known as distributed Bragg reflectors (DBRs) or Bragg stacks (BSs), have been used as resonators for distributed feedback lasers [5,6], smart dielectric layers for light-emitting transistors [7] and light-induced tunable filters [8], among others.
In this paper, we will review the latest advancements in the field of responsive 1D PhCs, with particular attention to electro-responsive systems. In particular, this paper will discuss both the theoretical methods that are commonly used to predict the optical properties of 1D PhCs, as well as the most employed fabrication techniques. In addition, we will describe the different approaches utilized to achieve active tuning of the photonic band gap.
2. Theoretical Background
First, we consider a multilayer of materials deposited on a substrate on one side (with refractive index ns) and in contact with air (with refractive index n0 = 1.000277 1) on the other side. The transfer matrix method is exhaustively explained in the literature, such as in reference [9]. The transfer matrix for the kth layer is given by [9]:
with that is the light phase variation passing through the kth layer, nk being the refractive index, dk the thickness of the layer and the parameter that takes into account the light beam propagating through the layer with refractive index nk, related to the angle of incidence ϑ0 (as displayed in Figure 1a) of the light on the structure:
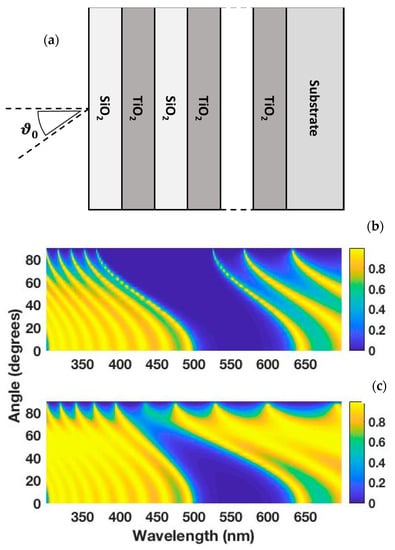
Figure 1.
(a) Sketch of the one-dimensional photonic crystal (ϑ0 is the angle of incidence of the light). Simulation of the angular dependent transmission spectrum of a 5 bilayer TiO2-SiO2 nanoparticle-based photonic crystal for a transverse electric (TE) wave (b) and a transverse magnetic (TM) wave (c). For both the nanoparticle layers, the filling factor is 0.7.
For a transverse electric (TE) wave, the parameter in Equation (1) can be written as , while for a transverse magnetic (TM) wave . The matrix product gives the matrix of the multilayer made of s layers. We can write the transmission coefficient t as
For a transverse electric (TE) wave and , while for a transverse magnetic (TM) wave and . Finally, to calculate the light transmission of the multilayer photonic crystal we can use the following equation:
If, in the spectral range of interest, the refractive index does not show a significant wavelength dependence, its value can be essentially considered as constant. Otherwise, we should consider the refractive index as a function of the wavelength. The refractive indexes of many materials are reported in the literature [10] and can be expressed with a Sellmeier equation. For example, the Sellmeier equation for silicon dioxide, which is widely employed for the fabrication of one-dimensional photonic crystals, is [11]:
For porous materials, we can determine the refractive index by employing the Maxwell–Garnett effective medium approximation [12,13]:
where is the dielectric constant of the material, is the dielectric constant of air and f is the filling factor.
In Figure 1, we show the simulation of the angular dependent transmission of a 1D photonic crystal, consisting of the alternation of five bilayers of TiO2-SiO2 nanoparticles (filling factor = 0.7). The wavelength-dependent refractive index of TiO2 is given by [14]. From these simulations, it is also possible to determine the electric field at the kth interface [15].
3. Fabrication Techniques
Photonic crystals can be fabricated by following two main approaches: (1) top-down methods; and (2) bottom-up methods. In particular, bottom-up techniques can be more conveniently used on the laboratory scale, while top-down approaches rely on the use of microfabrication methods permitting development of microstructures with selected size and shape from bulk materials [16,17]. Besides these advantages, both of them also show some disadvantages. Bottom-up methods usually suffer from a relatively low throughput, whereas top-down techniques require substantial initial investment in terms of money and person hours for dedicated setups. For these reasons, it is thus essential to select the most suitable approach according to the desired goal. Self-assemble techniques are surely the most used bottom-up methods, combining building blocks such as nanoscale structures (e.g., nanoparticles) or block copolymers. These techniques are particularly suitable for the fabrication of responsive photonic crystals as, in this way, one can combine different unitary structures and materials to integrate different functionalities in a one single photonic device. A list of the most used techniques is reported in Table 1.

Table 1.
Main manufacturing techniques of photonic crystals. The type of approach and the most significant advantages are indicated for each technique.
4. Active Tuning of the Photonic Band Gap
Any stimulus that can modify either the periodicity or the refractive index contrast (or both) of the PhC can lead to a shift of the PBG, according to Bragg–Snell’s law:
where λmax is the wavelength of the maximum reflection (photonic band gap) peak, d is the lattice constant, m is the order of diffraction, neff is the effective refractive index and θ is the angle of incidence of the light with respect to the PhC [53]. It is noteworthy that the effective refractive index can be determined with different approaches [54]. A large number of external stimuli that are able to modulate the PBG are reported in the literature. Main examples include chemical, thermal, magnetic, biological, mechanical, light and electrical stimuli.
Table 2 summarizes the main stimuli and tuning mechanisms mentioned in this article.

Table 2.
Summary of main stimuli used for tunable photonic crystals.
4.1. Chemical Stimuli
One of the most used methods to tune the PBG via chemical methods relies on the interaction between a soft structure (e.g., a hydrogel) and a given chemical species. For instance, the interaction with ions can generate a swelling and a shrinkage of the soft structure, which in turn changes the geometrical features of the PhC and leads to a shift of the photonic band gap [45,61,96,97,98]. Furthermore, this approach can be used for the detection H+ ions, and thus for building up pH sensors [45,60,62,99,100]. Another class of chemically tuned PhCs consist in the integration of porous materials in the PhC, in which refractive index modulation is given by infiltration of vapors [30,55,56,101] or solvents [20,29,57,58,59,102,103,104]. Wang et al. fabricated 1D photonic crystals alternating films of poly methyl methacrylate-co-hydroxyethyl methacrylate-co-ethylene glycol dimethacrylate (PMMA-co-PHEMA-co-PEGDMA) and titania nanoparticles by spin-coating, drastically changing its structural color when immersed in different solvents (Figure 2a,b) [32].
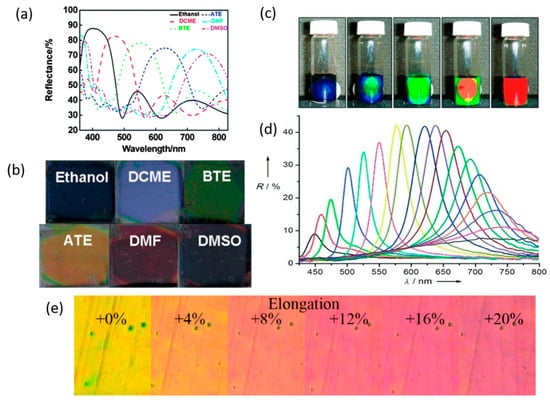
Figure 2.
Different cases of tunable photonic crystals. (a,b) Reflectance spectra and visual effect of PMMA-co-PHEMA-co-PEGDMA) and titania photonic crystals (PhCs) in different solvents. Adapted from reference [32] by permission of The Royal Society of Chemistry. (c,d) Effect of the magnet–sample distance on polyacrylate-capped superparamagnetic magnetite (Fe3O4) colloidal nanocrystal clusters (CNCs). Adapted from reference [110] by permission of John Wiley & Sons. (e) Changing of structural color of grating nanostructured polydimethylsiloxane membrane/TiO2 as the elongation increases. Adapted from reference [31].
4.2. Thermal and Magnetic Stimuli
Photonic crystals fabricated using thermoresponsive materials like polymers or colloidal dispersions can be easily tuned through the application of a temperature gradient [48,62,63,105,106]. Chunfang et al. fabricated a SiO2 PhC and infiltrated the pores with a thermo-sensitive Poly (N-isopropylacrylamide) (PNIPAM) hydrogel. The thermal variation generates a blue shift of the photonic band gap and exhibits a reversible response in the range from 24 °C to 31 °C [64].
Magnetically responsive PhCs are usually fabricated by integrating magnetic nanoparticles in the structure [16]. Herein, an external magnetic field interacts with the active material and changes its optical properties, orienting it according to the direction of the field [65,66,67,68,69,107,108,109]. Ge et al. synthesized some polyacrylate-capped superparamagnetic magnetite (Fe3O4) colloidal nanocrystal clusters (CNCs) with sizes from 30 to 180 nm. These clusters self-assembled into colloidal photonic crystals in solution. In Figure 2c,d, the change in the optical response is visible, as the magnetic field changes by controlling the distance between the sample and an NdFeB magnet [110].
4.3. Biologic Stimuli
Photonic crystals can be easily functionalized with appropriate recognition groups that allow for the detection of specific biomolecules. Due to the change in color, colorimetric detection is quick and easy [16,111]. These sensors change their optical properties not only when in contact with classical biomolecules like sugars, creatinine or glucose [40,112,113], but also larger ones such DNA [42,43,70,71] and proteins [72,73,74,114].
Recently, silver has been integrated inside 1D PhCs in order to exploit its antibacterial properties and detect the presence of bacteria [27,75,115,116,117]. Paternò et al. fabricated a hybrid plasmonic–photonic device applying a silver layer on top of a TiO2/SiO2 PhC. At the Ag/bacteria interface, there is a generation of polarization charges due to a “biodoping” mechanism. This triggers a change in the PBG of the sensor when exposed to Escherichia coli [27].
4.4. Mechanical Stimuli
Mechanically tuned photonic crystals exploit the elastic properties of the constituent materials. In general, they are usually compounded by an elastomeric matrix [17,39,44,47,51] that actively responds to mechanical stimuli. In this case, the mechanical force deforms the polymer and this changes the periodicity of the lattice, thus changing the optical response [16]. Karrock et al. fabricated a 400 nm periodical linear grating made of a nanostructured polydimethylsiloxane membrane by nanoimprinting replication. Subsequently, a high refractive index TiO2 nanoparticle layer was spin-coated, showing a guided-mode resonance. The elastomeric behavior of the membrane allows for a 20% elongation when subjected to stretching, varying the resonance peak position up to ≈80 nm. In Figure 2e, it is possible to see the change of structural colors brought about by the mechanical deformation [31].
4.5. Light Stimuli
Incorporating a photosensitive material [75,118,119,120] or a dye [77,121] inside a photonic crystal structure allows for tuning of its optical properties upon exposure to light stimuli. Light can change the refractive index or lead to a modification of the structural properties. For instance, PhCs can be used like a casing for liquid crystals and they will then be stimulated by light [50,51,76]. Paternò et al. fabricated an optically switchable SiO2/ITO 1D photonic crystal. Through a UV-light photodoping process, it is possible to tune the indium tin oxide (ITO) plasmonic response in the near-infrared range and translate the effect to the visible light range, switching the optical properties of the device [8].
4.6. Electric Stimuli
Electrically tunable photonic crystals represent an incredible opportunity for technological applications, ranging from colorful displays to sensitive claddings and electrochromic windows. Their electrotunability can be triggered in three ways: (1) reorientation of infiltrated liquid crystals; (2) an electrochemical process; and (3) electrophoretic forces in crystalline colloidal arrays. Liquid crystals (LCs) are a class of materials combining the properties of solid crystals and fluids. According to their alignment axis orientation, LCs assume a different distribution inside the liquid, switching from a randomly distributed phase (nematic) to an oriented phase (smectic or chiral). These materials own different refractive indices in different directions, so by changing their phase it is possible tune their optical properties. Thus, it is possible to tune their dielectric constant by applying an external electric field. LCs are usually infiltrated inside a porous structure [78,79,80,81,82,122,123,124]. Criante et al. fabricated a porous silicon dioxide/zirconium dioxide 1D photonic crystal infiltrated with a nematic liquid crystal (Figure 3a). The device is tuned by applying an external electric field and so changing the LC alignment, producing a blue shift (Figure 3b) of the peak of 8 nm at 8 V [83].
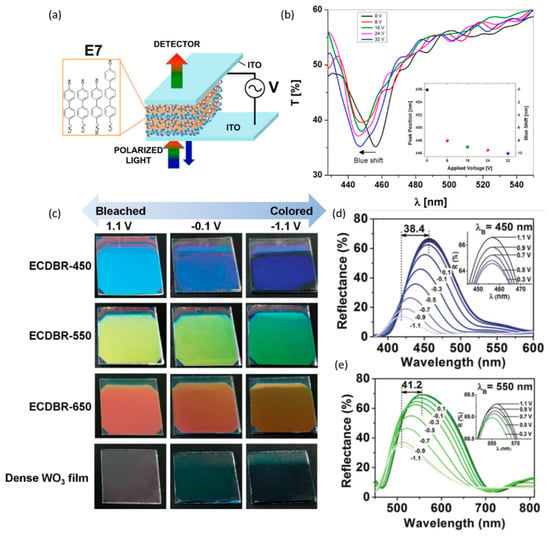
Figure 3.
(a) Schematic representation of a 1D photonic crystal for photonic band gap tuning applying an electric voltage and (b) its transmission spectra after the application of an electric field. Adapted from reference [83] under permission from the American Chemical Society. (c) Optical effect of an electric field application to 4-bilayer photonic crystals and dense WO3 film. (d,e) Changing of reflectance spectra of PhC with peaks at 450 nm and 550 nm. Adapted from reference [26] under permission from John Wiley & Sons.
Electrochemically tuned photonic crystals consist in an electrochemical cell immersed in a liquid electrolyte. By applying an electric field, it is possible to activate an electrolytic process, which promotes an oxidation–reduction effect or an acid–base exchange. The stimulus produces an electrostatic repulsion; thus, the original structure undergoes a destabilization due to a localized charge variation. The consequent reorganization of the structure generates a geometric variation of the sample, which, in accordance with Bragg–Snell’s law, causes a shift of the peak [46,84,85,86,125,126]. In the case of polymers, it is possible to incorporate an electro-responsive material inside the main chain, generating a swelling of the matrix under the application of the field [48,87,127,128,129]. Xiao et al. fabricated a WO3-based electrochromic PhC by a facile, reproducible, one-step room temperature glancing-angle electron-beam evaporation (GLAD). By changing the deposition angle, it is possible to obtain layers with different porosities corresponding to different refractive indices. The PhC is then immersed in 1M LiClO4 in propylene carbonate solution and subjected to an external electric field of −1.1 V (vs. Ag/AgCl). This leads to an electrochromic effect, as reported in Figure 3c. A gradual decrease of the reflectance and a shift of the reflection peak are attributed to colored LixWO3, which decreases the optical thickness (reduces the refractive index) and increases the light absorption (Figure 3d,e). When an anodic potential is applied (+1.1 V), the process is completely reversed [26].
In recent years, the integration of plasmonic nanoparticles in PhCs has attracted the interest of the scientific community. In these systems, quantized carrier oscillations generate localized surface plasmon resonances (LSPRs) that span over a wide range of wavelengths, depending mostly on the charge carrier density and the surrounding refractive environment. For instance, the charge carrier density in heavily doped metal oxide nanocrystals lies in the infrared (IR) region [130,131,132] as it is significantly lower compared with bulk materials (10 21 cm−3 and 10 23 cm−3, respectively). This allows for easy manipulation of this parameter and, hence, of the dielectric function upon application of external electrochemical bias. In particular, by applying an electric field it is possible to induce a capacitive depletion or accumulation and, consequently, a modulation of optical properties [65,132,133]. For these reasons, photonic crystals fabricated with plasmonic materials [27,33,65,88,89,134] have emerged in the in the last decade. Heo et al. exploited these materials to manufacture 1D photonic crystals composed of alternated layers of WO3-x and indium tin oxide (ITO) nanocrystals. In this case, the selected materials show a very similar refractive index in the discharge state (2.19 for ITO and 2.1 for WO3-x in the bulk), while charging leads to a strong modification in the WO3-x refractive index, thus causing a change of the refractive index contrast (Figure 4a–c). Interestingly, the same procedure can be used to deposit the photonic crystals on an ITO-coated flexible polyethylene terephthalate substrate [90].
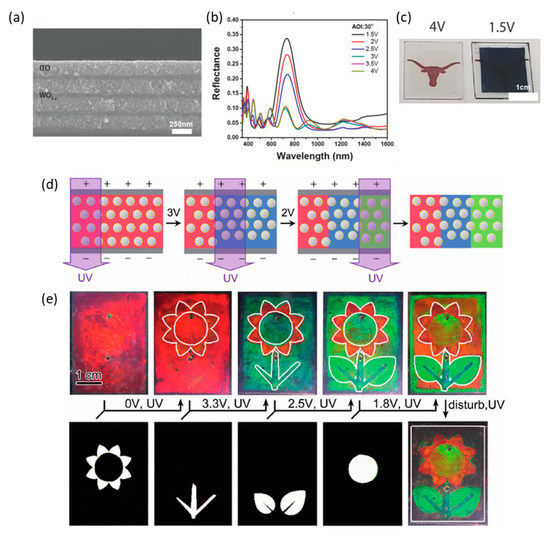
Figure 4.
(a–c) Cross-sectional SEM image, reflectance spectra and optical image of 1D photonic crystals constituted of indium tin oxide (ITO) NCs and WO3-x NC layers (BS1). Adapted from reference [90] under permission from John Wiley & Sons. Effect of an electric tuning and UV curing combination on E-ink. (d) Schematic mechanism and (e) optical example of lithographical printing by photomask covering. Adapted from reference [91] under permission from John Wiley & Sons.
Another approach relies on the immersion of electrotunable PhCs in liquid electrolytes, with the aim to increase the migration of electrons and ions. Despite the relatively high electrotunability achieved in such devices, the electrolyte can lead to a degradation of the samples and restrict the possibilities of their applications [26,90,135]. To address this problem, all solid-state devices have been developed over the past decade, in order to minimize such a detrimental effect [8,49,136] For instance, we have recently proposed a 1D electrolyte-free photonic crystal, combining indium tin oxide nanoparticles with TiO2 nanoparticles on top of a fluorine-doped tin oxide substrate acting as an electrode. The structure was contacted with a top fluorine-doped tin oxide (FTO) substrate and clipped with a paper binder to ensure mechanical stability. By applying a bias to this circuit, charges accumulate at the doped semiconductor/TiO2 interface, leading to an increase of the charge carrier density and an increase of the plasma frequency, according to equation:
where N is the carrier density, e is the electron charge, ε0 is the dielectric constant under vacuum and m* is the effective mass [33].
Tunability of photonic crystals can be also achieved by means of electrophoretic forces, which occurs when an external electric field is applied on a high concentration colloidal system. In this way, the particles are in dynamic equilibrium between packing force and electrostatic repulsive force, leading to a specific interparticle distance and, thus, to a specific optical signal. The applied field generates an electrophoretic force between the particles that are forced to reorganize into a more stable structure. Finally, this lattice modification translates into a shift of the photonic band gap [41,92,93,94,95,137]. For instance, Chen et al. exploited this mechanism to fabricate an electric-field-assisted multicolor printing (Figure 4d,e) based on electrically tunable and photocurable colloidal photonic crystals [91].
5. Conclusions
In this review, we have summarized some notable examples of tunable and stimuli-responsive 1D photonic crystals, with particular emphasis on electrotunable devices. These systems, which can usually be fabricated using easy and low-cost processes, permit the conversion of an external stimulus into an easily recognizable optical response. Given these properties, they have attracted increasing attention from both the scientific community and industry, as they can be employed in a wide range of applications, such as display, sensing and lighting.
Author Contributions
Conceptualization, L.M., G.L., G.M.P. and F.S.; data curation, L.M. and G.M.P.; writing—original draft preparation, L.M., G.M.P. and F.S.; writing—review and editing, L.M., G.M.P. and F.S. All authors have read and agreed to the published version of the manuscript.
Funding
This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement No. [816313]). This work has been supported by Fondazione Cariplo, Grant No. 2018-0979.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- John, S. Strong localization of photons in certain disordered dielectric superlattices. Phys. Rev. Lett. 1987, 58, 2486–2489. [Google Scholar] [CrossRef] [PubMed]
- Yablonovitch, E. Inhibited spontaneous emission in solid-state physics and electronics. Phys. Rev. Lett. 1987, 58, 2059–2062. [Google Scholar] [CrossRef] [PubMed]
- Chiasera, A.; Scotognella, F.; Criante, L.; Varas, S.; Della Valle, G.; Ramponi, R.; Ferrari, M. Disorder in photonic structures induced by random layer thickness. Sci. Adv. Mater. 2015, 7, 1207–1212. [Google Scholar] [CrossRef]
- Bellingeri, M.; Chiasera, A.; Kriegel, I.; Scotognella, F. Optical properties of periodic, quasi-periodic, and disordered one-dimensional photonic structures. Opt. Mater. 2017, 72, 403–421. [Google Scholar] [CrossRef]
- Scotognella, F.; Monguzzi, A.; Meinardi, F.; Tubino, R. DFB laser action in a flexible fully plastic multilayer. Phys. Chem. Chem. Phys. 2010, 12, 337–340. [Google Scholar] [CrossRef] [PubMed]
- Scotognella, F.; Puzzo, D.P.; Zavelani-Rossi, M.; Clark, J.; Sebastian, M.; Ozin, G.A.; Lanzani, G. Two-photon poly(phenylenevinylene) DFB laser. Chem. Mater. 2011, 23, 805–809. [Google Scholar] [CrossRef]
- Natali, M.; Quiroga, S.D.; Passoni, L.; Criante, L.; Benvenuti, E.; Bolognini, G.; Favaretto, L.; Melucci, M.; Muccini, M.; Scotognella, F.; et al. Simultaneous tenfold brightness enhancement and emitted-light spectral tunability in transparent ambipolar organic light-emitting transistor by integration of high-k photonic crystal. Adv. Funct. Mater. 2017, 27, 1605164. [Google Scholar] [CrossRef]
- Paternò, G.M.; Iseppon, C.; D’Altri, A.; Fasanotti, C.; Merati, G.; Randi, M.; Desii, A.; Pogna, E.A.A.; Viola, D.; Cerullo, G.; et al. Solution processable and optically switchable 1D photonic structures. Sci. Rep. 2018, 8, 3517. [Google Scholar] [CrossRef]
- Awasthi, S.K.; Malaviya, U.; Ojha, S.P.; Mishra, N.K.; Singh, B. Design of a tunable polarizer using a one-dimensional nano sized photonic bandgap structure. Prog. Electromagn. Res. B 2008, 5, 133–152. [Google Scholar] [CrossRef][Green Version]
- RefractiveIndex.INFO—Refractive Index Database. Available online: https://refractiveindex.info/ (accessed on 24 December 2020).
- Malitson, I.H. Interspecimen Comparison of the Refractive Index of Fused Silica. J. Opt. Soc. Am. 1965, 55, 1205–1208. [Google Scholar] [CrossRef]
- Mendelsberg, R.J.; Garcia, G.; Li, H.; Manna, L.; Milliron, D.J. Understanding the plasmon resonance in ensembles of degenerately doped semiconductor nanocrystals. J. Phys. Chem. C 2012, 116, 12226–12231. [Google Scholar] [CrossRef]
- Garnett, J.C.M. VII. Colours in metal glasses, in metallic films, and in metallic solutions.—II. Philos. Trans. R. Soc. London. Ser. A 1906, 205, 237–288. [Google Scholar] [CrossRef]
- Scotognella, F.; Chiasera, A.; Criante, L.; Aluicio-Sarduy, E.; Varas, S.; Pelli, S.; Łukowiak, A.; Righini, G.C.; Ramponi, R.; Ferrari, M. Metal oxide one dimensional photonic crystals made by RF sputtering and spin coating. Ceram. Int. 2015, 41, 8655–8659. [Google Scholar] [CrossRef]
- Wiersma, D.S.; Sapienza, R.; Mujumdar, S.; Colocci, M.; Ghulinyan, M.; Pavesi, L. Optics of nanostructured dielectrics. J. Opt. A Pure Appl. Opt. 2005, 7, S190–S197. [Google Scholar] [CrossRef]
- Ge, J.; Yin, Y. Responsive photonic crystals. Angewandte Chemie 2011, 50, 1492–1522. [Google Scholar] [CrossRef]
- Zhang, R.; Wang, Q.; Zheng, X. Flexible mechanochromic photonic crystals: Routes to visual sensors and their mechanical properties. J. Mater. Chem. C 2018, 6, 3182–3199. [Google Scholar] [CrossRef]
- Song, H.; Singer, K.; Lott, J.; Wu, Y.; Zhou, J.; Andrews, J.; Baer, E.; Hiltner, A.; Weder, C. Continuous melt processing of all-polymer distributed feedback lasers. J. Mater. Chem. 2009, 19, 7520–7524. [Google Scholar] [CrossRef]
- Chiasera, A.; Meroni, C.; Scotognella, F.; Boucher, Y.; Galzerano, G.; Lukowiak, A.; Ristic, D.; Speranza, G.; Valligatla, S.; Varas, S.; et al. Coherent emission from fully Er3+ doped monolithic 1-D dielectric microcavity fabricated by rf-sputtering. Opt. Mater. 2019, 87, 107–111. [Google Scholar] [CrossRef]
- Shaban, M.; Ahmed, A.M.; Abdel-Rahman, E.; Hamdy, H. Tunability and sensing properties of plasmonic/1d photonic crystal. Sci. Rep. 2017, 7, 41983. [Google Scholar] [CrossRef]
- Boucher, Y.; Chiasera, A.; Ferrari, M.; Righini, G.C. Extended transfer matrix modeling of an erbium-doped cavity with SiO2/TiO2 Bragg reflectors. Opt. Mater. 2009, 31, 1306–1309. [Google Scholar] [CrossRef]
- Regiński, K.; Muszalski, J.; Bugajski, M.; Ochalski, T.; Kubica, J.; Zbroszczyk, M.; Katcki, J.; Ratajczak, J. MBE growth of planar microcavities with distributed Bragg reflectors. Thin Solid Films 2000, 367, 290–294. [Google Scholar] [CrossRef]
- Rousset, J.-G.; Kobak, J.; Slupinski, T.; Jakubczyk, T.; Stawicki, P.; Janik, E.; Tokarczyk, M.; Kowalski, G.; Nawrocki, M.; Pacuski, W. MBE growth and characterization of a II–VI distributed Bragg reflector and microcavity lattice-matched to MgTe. J. Cryst. Growth 2013, 378, 266–269. [Google Scholar] [CrossRef]
- Passoni, L.; Criante, L.; Fumagalli, F.; Scotognella, F.; Lanzani, G.; Di Fonzo, F. Self-assembled hierarchical nanostructures for high-efficiency porous photonic crystals. ACS Nano 2014, 8, 12167–12174. [Google Scholar] [CrossRef] [PubMed]
- Calvo, M.E.; Colodrero, S.; Hidalgo, N.; Lozano, G.; López-López, C.; Sánchez-Sobrado, O.; Míguez, H. Porous one dimen-sional photonic crystals: Novel multifunctional materials for environmental and energy applications. Energy Environ. Sci. 2011, 4, 4800–4812. [Google Scholar] [CrossRef]
- Xiao, L.; Lv, Y.; Lin, J.; Hu, Y.; Dong, W.; Guo, X.; Fan, Y.; Zhang, N.; Zhao, J.; Wang, Y.; et al. WO3-based electrochromic distributed bragg reflector: Toward electrically tunable microcavity luminescent device. Adv. Opt. Mater. 2018, 6, 6–13. [Google Scholar] [CrossRef]
- Paternò, G.M.; Moscardi, L.; Donini, S.; Ariodanti, D.; Kriegel, I.; Zani, M.; Parisini, E.; Scotognella, F.; Lanzani, G. Hybrid one-dimensional plasmonic–photonic crystals for optical detection of bacterial contaminants. J. Phys. Chem. Lett. 2019, 10, 4980–4986. [Google Scholar] [CrossRef]
- Lova, P.; Manfredi, G.; Boarino, L.; Comite, A.; Laus, M.; Patrini, M.; Marabelli, F.; Soci, C.; Comoretto, D. Polymer distributed Bragg reflectors for vapor sensing. ACS Photonics 2015, 2, 537–543. [Google Scholar] [CrossRef]
- Choi, S.Y.; Mamak, M.; Von Freymann, G.; Chopra, N.; Ozin, G.A. Mesoporous Bragg stack color tunable sensors. Nano Lett. 2006, 6, 2456–2461. [Google Scholar] [CrossRef] [PubMed]
- Bonifacio, L.D.; Lotsch, B.V.; Puzzo, D.P.; Scotognella, F.; Ozin, G.A. Stacking the nanochemistry deck: Structural and compositional diversity in one-dimensional photonic crystals. Adv. Mater. 2009, 21, 1641–1646. [Google Scholar] [CrossRef]
- Karrock, T.; Paulsen, M.; Gerken, M. Flexible photonic crystal membranes with nanoparticle high refractive index layers. Beilstein J. Nanotechnol. 2017, 8, 203–209. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Zhang, J.; Li, J.; Xie, J.; Li, Y.; Liang, S.; Tian, Z.; Li, C.; Wang, Z.; Wang, T.; et al. Colorful detection of organic solvents based on responsive organic/inorganic hybrid one-dimensional photonic crystals. J. Mater. Chem. 2011, 21, 1264–1270. [Google Scholar] [CrossRef]
- Moscardi, L.; Paterno, G.M.; Chiasera, A.; Sorrentino, R.; Marangi, F.; Kriegel, I.; Lanzani, G.; Scotognella, F. Electro-responsivity in electrolyte-free and solution processed Bragg stacks. J. Mater. Chem. C 2020, 8, 13019–13024. [Google Scholar] [CrossRef]
- Smith, A.J.; Wang, C.; Guo, D.; Sun, C.; Huang, J. Repurposing Blu-ray movie discs as quasi-random nanoimprinting templates for photon management. Nat. Commun. 2014, 5, 5517. [Google Scholar] [CrossRef][Green Version]
- Nootchanat, S.; Pangdam, A.; Ishikawa, R.; Wongravee, K.; Shinbo, K.; Kato, K.; Kaneko, F.; Ekgasit, S.; Baba, A. Grating-coupled surface plasmon resonance enhanced organic photovoltaic devices induced by Blu-ray disc recordable and Blu-ray disc grating structures. Nanoscale 2017, 9, 4963–4971. [Google Scholar] [CrossRef]
- Zhang, B.; Cui, J.; Duan, J.; Cui, M. A new fabrication method for nano-gratings based on the high flexibility of PDMS. Opt. Laser Technol. 2017, 92, 206–210. [Google Scholar] [CrossRef]
- Saito, A.T.; Nakajima, M.; Miyamura, Y.; Sogo, K.; Ishikawa, Y.; Hirai, Y. Morpho-blue reproduced by nanocasting lithography. In Proceedings of the Nanoengineering: Fabrication, Properties, Optics, and Devices III, San Diego, CA, USA, 15–17 August 2006. [Google Scholar]
- Nien, C.-K.; Yu, H.H. The applications of biomimetic cicada-wing structure on the organic light-emitting diodes. Mater. Chem. Phys. 2019, 227, 191–199. [Google Scholar] [CrossRef]
- Fudouzi, H.; Sawada, T. Photonic rubber sheets with tunable color by elastic deformation. Langmuir 2006, 22, 1365–1368. [Google Scholar] [CrossRef] [PubMed]
- Ben-Moshe, M.; Alexeev, V.L.; Asher, S.A. Fast responsive crystalline colloidal array photonic crystal glucose sensors. Anal. Chem. 2006, 78, 5149–5157. [Google Scholar] [CrossRef]
- Chen, C.-W.; Li, C.-C.; Jau, H.-C.; Yu, L.-C.; Hong, C.-L.; Guo, D.-Y.; Wang, C.-T.; Lin, T.-H. Electric field-driven shifting and expansion of photonic band gaps in 3D liquid photonic crystals. ACS Photonics 2015, 2, 1524–1531. [Google Scholar] [CrossRef]
- Wang, C.; Li, F.; Bi, Y.; Guo, W. Reversible modulation of 2D photonic crystals with a responsive shape-memory DNA hydrogel film. Adv. Mater. Interfaces 2019, 6, 1900556. [Google Scholar] [CrossRef]
- Li, M.; He, F.; Liao, Q.; Liu, J.; Xu, L.; Jiang, L.; Song, Y.; Wang, S.; Zhu, D. Ultrasensitive DNA detection using photonic crystals. Angewandte Chemie 2008, 120, 7368–7372. [Google Scholar] [CrossRef]
- Chan, E.P.; Walish, J.J.; Thomas, E.L.; Stafford, C.M. Block copolymer photonic gel for mechanochromic sensing. Adv. Mater. 2011, 23, 4702–4706. [Google Scholar] [CrossRef]
- Jia, X.; Wang, K.; Wang, J.; Hu, Y.; Shen, L.; Zhu, J. Full-color photonic hydrogels for pH and ionic strength sensing. Eur. Polym. J. 2016, 83, 60–66. [Google Scholar] [CrossRef]
- Arsenault, A.C.; Puzzo, D.P.; Manners, I.; Ozin, G.A. Photonic-crystal full-colour displays. Nat. Photonics 2007, 1, 468–472. [Google Scholar] [CrossRef]
- Zhang, Z. Proposal and numerical study of a flexible visible photonic crystal defect cavity for nanoscale strain sensors. Opt. Express 2017, 25, 23645. [Google Scholar] [CrossRef]
- Ueno, K.; Matsubara, K.; Watanabe, M.; Takeoka, Y. An electro- and thermochromic hydrogel as a full-color indicator. Adv. Mater. 2007, 19, 2807–2812. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Yeo, L.P.; Ong, A.J.; Zhiwei, W.; Mandler, D.; Magdassi, S.; Tok, A.I.Y. Electrochromic smart glass coating on functional nano-frameworks for effective building energy conservation. Mater. Today Energy 2020, 18, 100496. [Google Scholar] [CrossRef]
- Kubo, S.; Gu, Z.-Z.; Takahashi, K.; Ohko, Y.; Sato, O.; Fujishima, A. Control of the optical band structure of liquid crystal infiltrated inverse opal by a photoinduced nematic−isotropic phase transition. J. Am. Chem. Soc. 2002, 124, 10950–10951. [Google Scholar] [CrossRef] [PubMed]
- Akamatsu, N.; Hisano, K.; Tatsumi, R.; Aizawa, M.; Barrett, C.J.; Shishido, A. Thermo-, photo-, and mechano-responsive liquid crystal networks enable tunable photonic crystals. Soft Matter 2017, 13, 7486–7491. [Google Scholar] [CrossRef]
- Kuai, S.-L.; Bader, G.; Ashrit, P.V. Tunable electrochromic photonic crystals. Appl. Phys. Lett. 2005, 86, 221110. [Google Scholar] [CrossRef]
- Mayonado, G.; Mian, S.M.; Robbiano, V.; Cacialli, F. Investigation of the Bragg-snell law in photonic crystals. In Proceedings of the 2015 Conference on Laboratory Instruction Beyond the First Year; American Association of Physics Teachers (AAPT), College Park, MD, USA, 22–24 July 2015; pp. 60–63. [Google Scholar]
- Niklasson, G.A.; Granqvist, C.G. Optical properties and solar selectivity of coevaporated Co-Al2O3composite films. J. Appl. Phys. 1984, 55, 3382–3410. [Google Scholar] [CrossRef]
- Zhong, K.; Li, J.; Liu, L.; Van Cleuvenbergen, S.; Song, K.; Clays, K. Instantaneous, simple, and reversible revealing of invisible patterns encrypted in robust hollow sphere colloidal photonic crystals. Adv. Mater. 2018, 30, e1707246. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Zhang, J.; Xie, J.; Li, C.; Li, Y.; Liang, S.; Tian, Z.; Wang, T.; Zhang, H.; Li, H.; et al. Bioinspired water-vapor-responsive organic/inorganic hybrid one-dimensional photonic crystals with tunable full-color stop band. Adv. Funct. Mater. 2010, 20, 3784–3790. [Google Scholar] [CrossRef]
- Thomas, M.M.; Chandran, P.R.; Vipin, V.V.; Mohamed, A.P.; Kingshott, P.; Pillai, S. Core-shell based responsive colloidal photonic crystals for facile, rapid, visual detection of acetone. React. Funct. Polym. 2021, 158, 104779. [Google Scholar] [CrossRef]
- Yan, D.; Li, R.; Lu, W.; Piao, C.; Qiu, L.; Meng, Z.-H.; Wang, S. Flexible construction of cellulose photonic crystal optical sensing nano-materials detecting organic solvents. Analyst 2018, 144, 1892–1897. [Google Scholar] [CrossRef] [PubMed]
- Lonergan, A.; Hu, C.; O’Dwyer, C. Filling in the gaps: The nature of light transmission through solvent-filled inverse opal photonic crystals. Phys. Rev. Mater. 2020, 4, 065201. [Google Scholar] [CrossRef]
- Sharma, A.C.; Jana, T.; Kesavamoorthy, R.; Shi, L.; Virji, M.A.; Finegold, A.D.N.; Asher, S.A. A General photonic crystal sensing motif: Creatinine in bodily fluids. J. Am. Chem. Soc. 2004, 126, 2971–2977. [Google Scholar] [CrossRef] [PubMed]
- Nucara, L.; Piazza, V.; Greco, F.; Robbiano, V.; Cappello, V.; Gemmi, M.; Cacialli, F.; Mattoli, V. Ionic strength responsive sulfonated polystyrene opals. ACS Appl. Mater. Interfaces 2017, 9, 4818–4827. [Google Scholar] [CrossRef] [PubMed]
- Honda, M.; Seki, T.; Takeoka, Y. Dual tuning of the photonic band-gap structure in soft photonic crystals. Adv. Mater. 2009, 21, 1801–1804. [Google Scholar] [CrossRef]
- Yan, D.; Lu, W.; Qiu, L.; Meng, Z.; Qiao, Y. Thermal and stress tension dual-responsive photonic crystal nanocomposite hydrogels. RSC Adv. 2019, 9, 21202–21205. [Google Scholar] [CrossRef]
- Li, C.; Xue, Q.; Ji, Z.; Li, Y.; Zhang, H.; Li, D. Construction of photonic crystals with thermally adjustable pseudo-gaps. Soft Matter 2020, 16, 3063–3068. [Google Scholar] [CrossRef] [PubMed]
- Paternò, G.M.; Moscardi, L.; Kriegel, I.; Scotognella, F.; Lanzani, G. Electro-optic and magneto-optic photonic devices based on multilayer photonic structures. J. Photonics Energy 2018, 8, 032201. [Google Scholar] [CrossRef]
- Srivastava, S.K. Magneto tunable defect modes in one-dimensional photonic crystal based on magnetic fluid film. In Recent Trends in Materials and Devices; Springer International Publishing: Cham, Switzerland, 2020; pp. 163–171. [Google Scholar]
- Pourali, N.; Bahador, H. Tunable magneto-optical responses in a photonic crystal containing two plasma defect layers. Phys. Plasmas 2019, 26, 013515. [Google Scholar] [CrossRef]
- Awasthi, S.K.; Panda, R.; Chauhan, P.K.; Shiveshwari, L. Multichannel tunable omnidirectional photonic band gaps of 1D ternary photonic crystal containing magnetized cold plasma. Phys. Plasmas 2018, 25, 052103. [Google Scholar] [CrossRef]
- He, L.; Wang, M.; Ge, J.; Yin, Y. Magnetic assembly route to colloidal responsive photonic nanostructures. Acc. Chem. Res. 2012, 45, 1431–1440. [Google Scholar] [CrossRef]
- Tatsuro, E.; Cheng, X.R.; Endo, T.; Kerman, K. Photonic crystals on copolymer film for label-free detection of DNA hybridization. Biosens. Bioelectron. 2018, 103, 158–162. [Google Scholar] [CrossRef]
- Zhu, K.; Chi, J.; Zhang, D.; Ma, B.; Dong, X.; Yang, J.; Zhao, C.; Liu, H. Bio-inspired photonic crystals for naked eye quantification of nucleic acids. Analyst 2019, 144, 5413–5419. [Google Scholar] [CrossRef]
- Cai, Z.; Sasmal, A.; Liu, X.; Asher, S.A. Responsive photonic crystal carbohydrate hydrogel sensor materials for selective and sensitive lectin protein detection. ACS Sensors 2017, 2, 1474–1481. [Google Scholar] [CrossRef]
- Romano, S.; Lamberti, A.; Masullo, M.; Penzo, E.; Cabrini, S.; Rendina, I.; Mocella, V. Optical biosensors based on photonic crystals supporting bound states in the continuum. Materials 2018, 11, 526. [Google Scholar] [CrossRef]
- El-Aziz, O.A.A.; Elsayed, H.A.; Sayed, M.I. One-dimensional defective photonic crystals for the sensing and detection of protein. Appl. Opt. 2019, 58, 8309–8315. [Google Scholar] [CrossRef]
- Scotognella, F.; Paternò, G.M.; Kriegel, I.; Bonfadini, S.; Moscardi, L.; Criante, L.; Donini, S.; Ariodanti, D.; Zani, M.; Parisini, E.; et al. Ultrafast photochromism and bacteriochromism in one dimensional hybrid plasmonic photonic structures. In Proceedings of the Fiber Lasers and Glass Photonics: Materials through Applications II, 6–10 April 2020. online conference. [Google Scholar]
- Xie, Z.-Y.; Sun, L.-G.; Han, G.-Z.; Gu, Z.-Z. Optical switching of a birefringent photonic crystal. Adv. Mater. 2008, 20, 3601–3604. [Google Scholar] [CrossRef]
- Gu, Z.-Z.; Iyoda, T.; Fujishima, A.; Sato, O. Photo-reversible regulation of optical stop bands. Adv. Mater. 2001, 13, 1295–1298. [Google Scholar] [CrossRef]
- Palto, S.P.; Blinov, L.M.; Barnik, M.I.; Lazarev, V.V.; Umanskii, B.A.; Shtykov, N.M. Photonics of liquid-crystal structures: A review. Crystallogr. Rep. 2011, 56, 622–649. [Google Scholar] [CrossRef]
- Rippa, M.; Mormile, P.; Capasso, R.; Zanella, M.; Petti, L. Electro-optical tuning in photonic crystals—Dispersed liquid crystalline metamaterials. Mol. Cryst. Liq. Cryst. 2013, 573, 18–25. [Google Scholar] [CrossRef]
- Budaszewski, D.; Wolińska, K.; Jankiewicz, B.; Bartosewicz, B.; Woliński, T.R. Spectral properties of photo-aligned photonic crystal fibers infiltrated with gold nanoparticle-doped ferroelectric liquid crystals. Crystals 2020, 10, 785. [Google Scholar] [CrossRef]
- Khalkhali, T.F.; Bananej, A. Tunable complete photonic band gap in anisotropic photonic crystal slabs with non-circular air holes using liquid crystals. Opt. Commun. 2016, 369, 79–83. [Google Scholar] [CrossRef]
- Criante, L.; Scotognella, F. Infiltration of E7 Liquid crystal in a nanoparticle-based multilayer photonic crystal: Fabrication and electro-optical characterization. Mol. Cryst. Liq. Cryst. 2013, 572, 31–39. [Google Scholar] [CrossRef]
- Criante, L.; Scotognella, F. Low-voltage tuning in a nanoparticle/liquid crystal photonic structure. J. Phys. Chem. C 2012, 116, 21572–21576. [Google Scholar] [CrossRef]
- Huang, K.-C.; Hsiao, Y.-C.; Timofeev, I.V.; Zyryanov, V.Y.; Lee, W. Photo-manipulated photonic bandgap devices based on optically tristable chiral-tilted homeotropic nematic liquid crystal. Opt. Express 2016, 24, 25019–25025. [Google Scholar] [CrossRef] [PubMed]
- Kuno, T.; Matsumura, Y.; Nakabayashi, K.; Atobe, M. Electroresponsive structurally colored materials: A combination of structural and electrochromic effects. Angewandte Chemie 2016, 128, 2549–2552. [Google Scholar] [CrossRef]
- Puzzo, D.P.; Arsenault, A.C.; Manners, I.; Ozin, G.A. Electroactive inverse opal: A single material for all colors. Angewandte Chemie 2009, 48, 943–947. [Google Scholar] [CrossRef] [PubMed]
- Walish, J.J.; Kang, Y.; Mickiewicz, R.A.; Thomas, E.L. Bioinspired electrochemically tunable block copolymer full color pixels. Adv. Mater. 2009, 21, 3078–3081. [Google Scholar] [CrossRef]
- Aluicio-Sarduy, E.; Callegari, S.; Del Valle, D.G.F.; Desii, A.; Kriegel, I.; Scotognella, F. Electric field induced structural colour tuning of a silver/titanium dioxide nanoparticle one-dimensional photonic crystal. Beilstein J. Nanotechnol. 2016, 7, 1404–1410. [Google Scholar] [CrossRef]
- Robbiano, V.; Giordano, M.; Martella, C.; Di Stasio, F.; Chiappe, D.; De Mongeot, F.B.; Comoretto, D. Hybrid plasmonic-photonic nanostructures: Gold nanocrescents over opals. Adv. Opt. Mater. 2013, 1, 389–396. [Google Scholar] [CrossRef]
- Heo, S.; Agrawal, A.; Milliron, D.J. Wide dynamic range in tunable electrochromic bragg stacks from doped semiconductor nanocrystals. Adv. Funct. Mater. 2019, 29, 1904555. [Google Scholar] [CrossRef]
- Chen, K.; Fu, Q.; Ye, S.; Ge, J. Multicolor printing using electric-field-responsive and photocurable photonic crystals. Adv. Funct. Mater. 2017, 27, 1702825. [Google Scholar] [CrossRef]
- Manda, R.; Pagidi, S.; Heo, Y.; Lim, Y.J.; Kim, M.; Lee, S.H. Electrically tunable photonic band gap structure in monodomain blue-phase liquid crystals. NPG Asia Mater. 2020, 12, 1–9. [Google Scholar] [CrossRef]
- Chang, H.-K.; Park, J. Flexible all-solid-state electrically tunable photonic crystals. Adv. Opt. Mater. 2018, 6, 1800792. [Google Scholar] [CrossRef]
- Du, X.-W.; Hou, D.-S.; Li, X.; Sun, D.-P.; Lan, J.-F.; Zhu, J.-L.; Ye, W.-J. Symmetric continuously tunable photonic band gaps in blue-phase liquid crystals switched by an alternating current field. ACS Appl. Mater. Interfaces 2019, 11, 22015–22020. [Google Scholar] [CrossRef] [PubMed]
- Han, M.G.; Shin, C.G.; Jeon, S.-J.; Shim, H.; Heo, C.-J.; Jin, H.; Kim, J.W.; Lee, S. Full color tunable photonic crystal from crystalline colloidal arrays with an engineered photonic stop-band. Adv. Mater. 2012, 24, 6438–6444. [Google Scholar] [CrossRef]
- Kang, Y.; Walish, J.J.; Gorishnyy, T.; Thomas, E.L. Broad-wavelength-range chemically tunable block-copolymer photonic gels. Nat. Mater. 2007, 6, 957–960. [Google Scholar] [CrossRef]
- Hong, W.; Hu, X.; Zhao, B.; Zhang, F.; Zhang, D. Tunable photonic polyelectrolyte colorimetric sensing for anions, cations and zwitterions. Adv. Mater. 2010, 22, 5043–5047. [Google Scholar] [CrossRef]
- Asher, S.A.; Sharma, A.C.; Goponenko, A.V.; Ward, M.M. Photonic crystal aqueous metal cation sensing materials. Anal. Chem. 2003, 75, 1676–1683. [Google Scholar] [CrossRef] [PubMed]
- Fei, X.; Lu, T.; Ma, J.; Wang, W.; Zhu, S.; Di Zhang, D. Bioinspired polymeric photonic crystals for high cycling pH-sensing performance. ACS Appl. Mater. Interfaces 2016, 8, 27091–27098. [Google Scholar] [CrossRef]
- Lee, Y.-J.; Braun, P. Tunable inverse opal hydrogel pH sensors. Adv. Mater. 2003, 15, 563–566. [Google Scholar] [CrossRef]
- Colodrero, S.; Ocaña, M.; González-Elipe, A.R.; Míguez, H. Response of nanoparticle-based one-dimensional photonic crystals to ambient vapor pressure. Langmuir 2008, 24, 9135–9139. [Google Scholar] [CrossRef]
- Colodrero, S.; Ocaña, M.; Míguez, H. Nanoparticle-based one-dimensional photonic crystals. Langmuir 2008, 24, 4430–4434. [Google Scholar] [CrossRef]
- Lova, P.; Bastianini, C.; Giusto, P.; Patrini, M.; Rizzo, P.; Guerra, G.; Iodice, M.; Soci, C.; Comoretto, D. Label-free vapor selectivity in poly(p-phenylene oxide) photonic crystal sensors. ACS Appl. Mater. Interfaces 2016, 8, 31941–31950. [Google Scholar] [CrossRef] [PubMed]
- Kuo, W.-K.; Weng, H.-P.; Hsu, J.-J.; Yu, H.H. Photonic crystal-based sensors for detecting alcohol concentration. Appl. Sci. 2016, 6, 67. [Google Scholar] [CrossRef]
- Kanai, T.; Lee, D.; Shum, H.C.; Shah, R.K.; Weitz, D.A. Gel-immobilized colloidal crystal shell with enhanced thermal sensitivity at photonic wavelengths. Adv. Mater. 2010, 22, 4998–5002. [Google Scholar] [CrossRef]
- Sugiyama, H.; Sawada, T.; Yano, H.; Kanai, T. Linear thermosensitivity of gel-immobilized tunable colloidal photonic crystals. J. Mater. Chem. C 2013, 1, 6103. [Google Scholar] [CrossRef]
- Ge, J.; Yin, Y. Magnetically tunable colloidal photonic structures in alkanol solutions. Adv. Mater. 2008, 20, 3485–3491. [Google Scholar] [CrossRef]
- Ge, J.; He, L.; Goebl, J.; Yin, Y. Assembly of magnetically tunable photonic crystals in nonpolar solvents. J. Am. Chem. Soc. 2009, 131, 3484–3486. [Google Scholar] [CrossRef]
- Xu, X.; Friedman, G.; Humfeld, K.D.; Majetich, S.A.; Asher, S.A. Superparamagnetic photonic crystals. Adv. Mater. 2001, 13, 1681–1684. [Google Scholar] [CrossRef]
- Ge, J.; Hu, Y.; Yin, Y. Highly tunable superparamagnetic colloidal photonic crystals. Angewandte Chemie 2007, 46, 7428–7431. [Google Scholar] [CrossRef] [PubMed]
- Paternò, G.M.; Manfredi, G.; Scotognella, F.; Lanzani, G. Distributed Bragg reflectors for the colorimetric detection of bacterial contaminants and pollutants for food quality control. APL Photonics 2020, 5, 080901. [Google Scholar] [CrossRef]
- Asher, S.A.; Alexeev, V.L.; Goponenko, A.V.; Sharma, A.C.; Lednev, I.K.; Wilcox, A.C.S.; Finegold, D.N. Photonic crystal carbohydrate sensors: Low ionic strength sugar sensing. J. Am. Chem. Soc. 2003, 125, 3322–3329. [Google Scholar] [CrossRef]
- Walker, J.P.; Asher, S.A. Acetylcholinesterase-based organophosphate nerve agent sensing photonic crystal. Anal. Chem. 2005, 77, 1596–1600. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, X.; Hu, J.; Xu, M.; Zhao, W.; Sun, L.; Zhu, C.; Xu, H.; Gu, Z. Encoded porous beads for label-free multiplex detection of tumor markers. Adv. Mater. 2008, 21, 569–572. [Google Scholar] [CrossRef] [PubMed]
- Chan, S.; Horner, S.R.; Fauchet, P.M.; Miller, B.L. Identification of gram negative bacteria using nanoscale silicon microcavities. J. Am. Chem. Soc. 2001, 123, 11797–11798. [Google Scholar] [CrossRef]
- Lotsch, B.V.; Knobbe, C.B.; Ozin, G.A. A step towards optically encoded silver release in 1D photonic crystals. Small 2009, 5, 1498–1503. [Google Scholar] [CrossRef]
- Paterno, G.M.; Moscardi, L.; Donini, S.; Ross, A.M.; Pietralunga, S.M.; Vedova, N.D.; Normani, S.; Kriegel, I.; Lanzani, G.; Scotognella, F. Integration of bio-responsive silver in 1D photonic crystals: Towards the colorimetric detection of bacteria. Faraday Discuss. 2020, 223, 125–135. [Google Scholar] [CrossRef]
- Kamenjicki, M.; Lednev, I.; Mikhonin, A.; Kesavamoorthy, R.; Asher, S. Photochemically controlled photonic crystals. Adv. Funct. Mater. 2003, 13, 774–780. [Google Scholar] [CrossRef]
- Maurer, M.K.; Lednev, I.K.; Asher, S.A. Photoswitchable spirobenzopyran-based photochemically controlled photonic crystals. Adv. Funct. Mater. 2005, 15, 1401–1406. [Google Scholar] [CrossRef]
- Gu, Z.-Z.; Fujishima, A.A.; Sato, O. Photochemically tunable colloidal crystals. J. Am. Chem. Soc. 2000, 122, 12387–12388. [Google Scholar] [CrossRef]
- Gu, Z.-Z.; Hayami, S.; Meng, Q.-B.; Iyoda, T.; Fujishima, A.; Sato, O. Control of photonic band structure by molecular aggregates. J. Am. Chem. Soc. 2000, 122, 10730–10731. [Google Scholar] [CrossRef]
- Takeda, H.; Yoshino, K. Tunable refraction effects in two-dimensional photonic crystals utilizing liquid crystals. Phys. Rev. E 2003, 67, 056607. [Google Scholar] [CrossRef]
- Tkachenko, V.; Dyomin, A.A.; Abbate, G.; Sukhoivanov, A.I.; Tkachenko, G.V. Electrical reorientation of liquid crystal molecules inside cylindrical pores for photonic device applications. J. Opt. A: Pure Appl. Opt. 2008, 10, 055301. [Google Scholar] [CrossRef]
- Shimoda, Y.; Ozaki, M.; Yoshino, K. Electric field tuning of a stop band in a reflection spectrum of synthetic opal infiltrated with nematic liquid crystal. Appl. Phys. Lett. 2001, 79, 3627–3629. [Google Scholar] [CrossRef]
- Norton, J.; Han, M.G.; Jiang, P.; Creager, S.; Foulger, S.H. Electrochemical tuning the optical properties of crystalline colloidal arrays composed of poly(3,4-ethylenedioxythiophene) coated silica particles. J. Mater. Chem. 2007, 17, 1149–1153. [Google Scholar] [CrossRef]
- Redel, E.; Mlynarski, J.; Moir, J.; Jelle, A.; Huai, C.; Petrov, S.; Helander, M.G.; Peiris, F.C.; Von Freymann, G.; Ozin, G.A. Electrochromic Bragg mirror: ECBM. Adv. Mater. 2012, 24, OP265–OP269. [Google Scholar] [CrossRef] [PubMed]
- Hwang, K.; Kwak, D.; Kang, C.; Kim, D.; Ahn, Y.; Kang, Y. Electrically tunable hysteretic photonic gels for nonvolatile display pixels. Angewandte Chemie 2011, 50, 6311–6314. [Google Scholar] [CrossRef] [PubMed]
- Ge, J.; Goebl, J.; He, L.; Lu, Z.; Yin, Y. Rewritable photonic paper with hygroscopic salt solution as ink. Adv. Mater. 2009, 21, 4259–4264. [Google Scholar] [CrossRef]
- Lu, Y.; Meng, C.; Xia, H.; Zhang, G.; Wu, C. Fast electrically driven photonic crystal based on charged block copolymer. J. Mater. Chem. C 2013, 1, 6107–6111. [Google Scholar] [CrossRef]
- Garcia, G.; Buonsanti, R.; Runnerstrom, E.L.; Mendelsberg, R.J.; Llordes, A.; Anders, A.; Richardson, T.J.; Milliron, D.J. Dynamically modulating the surface plasmon resonance of doped semiconductor nanocrystals. Nano Lett. 2011, 11, 4415–4420. [Google Scholar] [CrossRef]
- Lounis, S.D.; Runnerstrom, E.L.; Llordés, A.; Milliron, D.J. Defect chemistry and plasmon physics of colloidal metal oxide nanocrystals. J. Phys. Chem. Lett. 2014, 5, 1564–1574. [Google Scholar] [CrossRef]
- Kriegel, I.; Scotognella, F.; Manna, L. Plasmonic doped semiconductor nanocrystals: Properties, fabrication, applications and perspectives. Phys. Rep. 2017, 674, 1–52. [Google Scholar] [CrossRef]
- Agrawal, A.; Cho, S.H.; Zandi, O.; Ghosh, S.; Johns, R.W.; Milliron, D.J. Localized surface plasmon resonance in semicon-ductor nanocrystals. Chem. Rev. 2018, 118, 3121–3207. [Google Scholar] [CrossRef] [PubMed]
- Romanov, S.G.; Korovin, A.V.; Regensburger, A.; Peschel, U. Hybrid colloidal plasmonic-photonic crystals. Adv. Mater. 2011, 23, 2515–2533. [Google Scholar] [CrossRef]
- Shen, L.; Zheng, J.; Xu, C. Enhanced electrochromic switches and tunable green fluorescence based on terbium ion doped WO3 films. Nanoscale 2019, 11, 23049–23057. [Google Scholar] [CrossRef]
- Meng, J.; Li, X.; Qin, M.; Pei, Y.; Yang, S.; Lan, Y.; Wang, R.; Chen, G. Effects of pore size of reverse opal structured PEDOT films on their electrochromic performances. Org. Electron. 2017, 50, 16–24. [Google Scholar] [CrossRef]
- Xia, J.; Ying, Y.; Foulger, S.H. Electric-field-induced rejection-wavelength tuning of photonic-bandgap composites. Adv. Mater. 2005, 17, 2463–2467. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).