Abstract
Monte Carlo Tree Search is one of the main search methods studied presently. It has demonstrated its efficiency in the resolution of many games such as Go or Settlers of Catan and other different problems. There are several optimizations of Monte Carlo, but most of them need heuristics or some domain language at some point, making very difficult its application to other problems. We propose a general and optimized implementation of Monte Carlo Tree Search using neural networks without extra knowledge of the problem. As an example of our proposal, we made use of the Dots and Boxes game. We tested it against other Monte Carlo system which implements specific knowledge for this problem. Our approach improves accuracy, reaching a winning rate of 81% over previous research but the generalization penalizes performance.
1. Introduction
Games are usually considered important benchmarks for artificial intelligence research, being abstract, interesting and challenging for human beings [1,2].
Studies on games can be used as tests to be extended on other contexts such as robotics or chemistry [3]. One of the fields in which artificial intelligence is growing is medicine. For example, hearth disease classification with deep learning techniques [4]. Nevertheless, ethics regarding human health is still an issue to be discussed, although there already are models which try to solve this [5]. That idea leads to the emergence of game theory, which is the study of mathematical models of the interaction strategy between agents who must make decisions [6]. The objective of game theory is to find the optimal solution for each state of the game. Games can be categorized according to its strategy, dynamic of turns, cooperativeness between players and if they are Zero-Sum games. Sohrabi et al. [7] summarize and classify several studies considering classic and modern optimization methods, optimization types, objectives and type of the game theory.
Search algorithms are the key to solve games. For example, Minimax, proposed by Von Neumann [8] is the basis for other methods. It is considered the starting point of game theory, providing conditions that guarantee that the max-min inequality is also an equality. It is a recursive decision method to minimize the maximum expected loss in games with an opponent and with perfect information. The idea is to take the best move for yourself assuming that your opponent will choose the worst move for you. Over the years, multiple variations have emerged, such as Negamax [9].
Alpha-beta pruning [10] is an improvement over Minimax, which tries to reduce the number of nodes that are evaluated in its search tree. It is a technique that is still used in many games such as Tic-tac-toe, Chess or Go. However, it has been overtaken by other techniques when the search space is too wide as is the case with Chess or the Go game. The idea is to stop evaluating a move when it is sure that the movement will be worse than the previous ones.
Although there are many more search methods and alternatives such as NegaScout [11] or MT driver (MTD) [12]. In recent years, the scientific literature is focusing on Monte Carlo (MC) methods. They are based on repeating random simulations to provide approximate solutions to a problem. The main idea is to use randomness to solve problems that are deterministic but too big to be calculated with precision [13]. In addition, the accuracy of MC simulations can be improved using tree-based search, leading to the Monte Carlo Tree Search (MCTS). MCTS is a best-first search algorithm based on heuristics where pseudorandom simulations guide the solution to a problem. The goal is to find optimal decisions in a specific domain of knowledge by generating random samples in the decision space, at the same time that a search tree is generated according to the obtained results [14].
There are also other approaches which combine genetic algorithms and MCTS to get a better response time to play real-time games [15].
MCTS has been successfully applied in different contexts. The most important milestone since its appearance is perhaps the victory of AlphaGo against a Go champion 5-0 by selecting new moves using neural networks ([16,17]) that were trained with supervised learning [18]. Shortly after, AlphaGo Zero won 100-0 against AlphaGo by selecting new moves using neural networks that were trained with reinforcement learning, without human data [19].
Since then, variations of AlphaZero and AlphaGo have been introduced get a better performance such as the contributions made by Grill et al. [20]. MCTS has been used in Settlers of Catan [1] too with reasonable results.
Several contributions have been developed for MCTS to improve accuracy and performance [21,22]. They have been tested in single-player and two-player games such as 8-puzzle, Hanoi, chess or checkers. Walędzik et al. [23] focus their contributions on a knowledge-free heuristic evaluation function which improves results for MCTS on several games.
However, MCTS has also been applied to other areas different from games such as: (1) combinatorial optimization; (2) constraint satisfaction; (3) scheduling problems; (4) sample-based planning; or (5) procedural content generation [14]. An example is to detect intruders in image-based biometrics authentication systems [24].
On the other hand, artificial neural networks can infer the behavior of games been able to replicate good quality movements without implementing each rule.
MCTS and neural networks with Go is an example of good results on a big search space. This recent success led us to use MCTS for our research. In contrast to other algorithms mentioned before, Monte Carlo Tree Search can handle huge search spaces limiting computation through the number of iterations as explained in Section 3. This way, this approach could suit a wide range of games and processes which helps our main objective about generalization of the algorithm.
Due to the background of the previous approaches, we also decided to use MCTS. However, most of the proposed solutions until now, try to speed up the developed system by adding domain-based heuristics which could help to solve the game. The implementation of the heuristics may be complex for certain games or problems or they could not be deeply explored. The main goal of this work is to explore the possibility that the system can learn to solve a problem, without having a data source and without using techniques specific to any problem domain. To that end, we take advantage of the potential of the Monte Carlo Tree Search technique. As part of the work, a case study based on the classic Dots and Boxes game is presented [25] (see Section 2). The system, without using information about the domain of knowledge, and only with the knowledge of the rules of the game, can learn to play.
The rest of this work is structured as follows: In Section 2 we introduce the Dots and Boxes game. In Section 3 we describe Monte Carlo Tree Search algorithm. In Section 4 we present the state of the art related to how to solve the game. In Section 5 we propose our work and contributions to optimize Monte Carlo Tree Search to solve the game. In Section 6 we perform an evaluation of our proposal. Finally, Section 7 deals with the conclusions and future work to be done.
2. Dots and Boxes
To carry out this work, we have chosen as a case study a perfect-information game. Perfect-information games are characterized by the fact that every player has access to all information about the game, such as the position of the board or any configuration depending on the game. Examples of these games are Chess and Tic-tac-toe. A player who follows a strategy better than the others is more likely to win. In addition, there are no random variables which may influence the result [26].
We focus on the perfect-information game Dots and Boxes. It is a combinatorial strategy game for two players popularized between children and adults. The first reference we can find about this game comes from the 19th century in L’Aritmétique amusante written by the mathematician Willian Lucas, who called the game “la pipopipette” [27]. The aim is to reach the end of the game with more closed boxes than the other player.
The Dots and Boxes game is a combinatorial game that represents the group of problems to which MCTS has been most often applied. Combinatorial games have the following properties:
- Two players. There are typically only considered two players, although may not be the case.
- Zero-sum. The gain or loss of a player is exactly balanced by the loss or gain of the other player.
- Perfect information. The state of the game is fully observable to all players.
- Deterministic. There is no randomness in the development of future states.
- Sequential. Players move sequentially in turns.
- Finite. The number of movements must be always finite.
The game board consists of a set of dots displayed as a size matrix. In each turn, the player must link two consecutive dots with a horizontal or vertical line. The strategy to follow is trying to close boxes and trying to avoid the opponent to close his own boxes. To close a box, it must have already three sides, with only one empty side left where the player will place the corresponding line. The turns are alternate, but after closing one box, the player must link another two dots. Movements can be concatenated until there is no possibility of closing any box. When a box is closed, a different mark for each player is written inside. At the end of the game, the score is computed by adding the marks, being the winner the player with the maximum score.
Figure 1 shows the trace of a game played on a board. A corresponds to the boxes closed by P1 (Player 1) and B to the ones closed by P2 (Player 2). M X corresponds to move number Move X. Each square represents the set of moves made by a player before change turn. We can observe that the main strategy followed is to avoid leaving boxes with three sides that could be closed in the next turn by the opponent. Moreover, when there is no other option, the player must minimize the number of closed boxes that the opponent could concatenate in her turn.
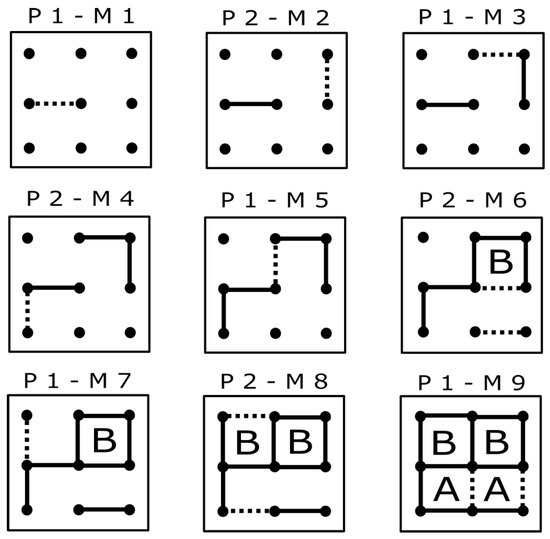
Figure 1.
Dots and Boxes game between two players.
3. Monte Carlo Tree Search Algorithm
Monte Carlo Tree Search algorithm consists of four phases which are iterated for a determined number of times: selection, expansion, simulation and backpropagation. The higher number of iterations, the more the tree grows and the easier is for the results to converge to a meaningful one. A root node must be provided for starting the iterations. The number of iterations will be an important variable in our experiments.
- Selection phase. First, the root node goes through selection phase (Figure 2 and Algorithm 1), where a node is selected based on the biggest Upper Confidence Bounds (UCB) formula value [14]. UCB formula tries to balance exploitation and exploration of the tree thanks to its constant C. This value, according to Browne et al. [14], accomplishes that balance. The way of managing the analysis of a node is characterized by exploitation and exploration. Exploitation of the tree nodes refers to grow the tree in depth from a promising node, while exploration refers to grow the tree in width checking unvisited nodes. UCB formula is composed by two terms which influence the trend of MCTS about exploring or exploiting nodes. We can control and balance it with constant C (the bigger, the more expanded nodes) considering the needed information and computational cost. The adjusted value of C is 1.41 [28].
Algorithm 1 Selection phase function SELECTION(node) while node has children do node = child of node with biggest UCB end whilereturn node end function 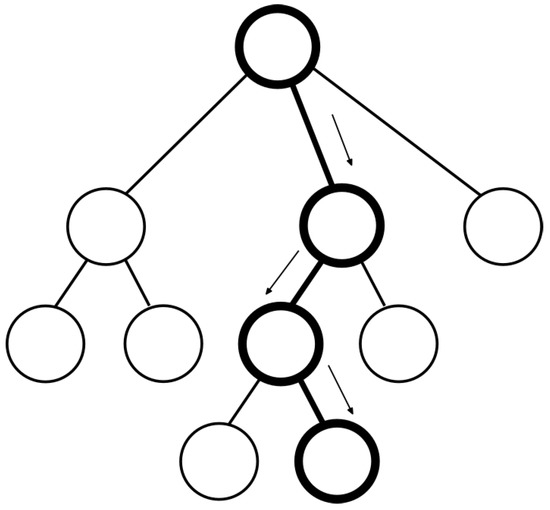 Figure 2. Selection phase in MCTS.
Figure 2. Selection phase in MCTS. - Expansion phase. In expansion phase (Figure 3 and Algorithm 2), if a node has been visited, i.e., it has been simulated, their children (or possible next states) are generated and added to the tree. Otherwise, it continues to the next phase.
Algorithm 2 Expansion phase function EXPANSION(node) if is node visited then generate children of node end if end function 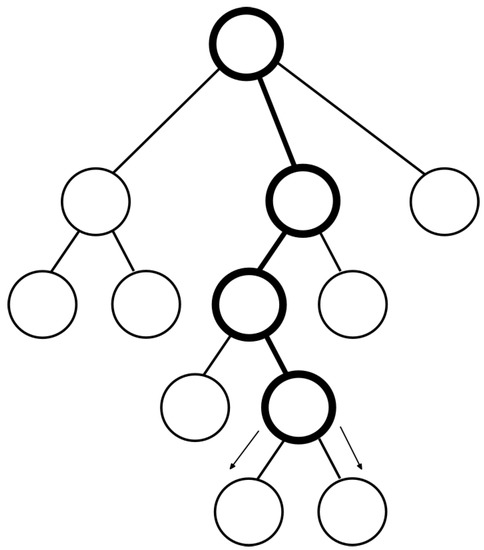 Figure 3. Expansion phase in MCTS.
Figure 3. Expansion phase in MCTS. - Simulation phase. In simulation phase (Figure 4 and Algorithm 3) if selected node is expanded, a random child is taken, else the selected node is taken itself. Then, next states are randomly chosen until it reaches a terminal state. Besides the random technique, it can be used with improved systems. This will be studied in Section 3.1.
Algorithm 3 Simulation phase function SIMULATION(node) while node state is not final do get next node random node = next node end whilereturn node state end function 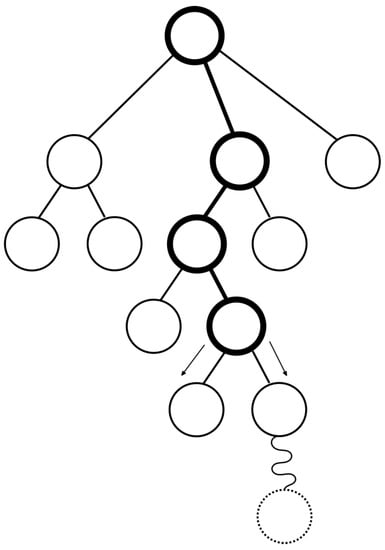 Figure 4. Simulation phase in MCTS.
Figure 4. Simulation phase in MCTS. - Backpropagation phase. In backpropagation phase (Figure 5 and Algorithm 4), the value obtained at simulation phase is propagated from leaves to root of the tree updating the values of the nodes: visits and victories.
Algorithm 4 Backpropagation phase function backpropagation(node) while node is not null do increment node score increment node visits node = parent node end while end function 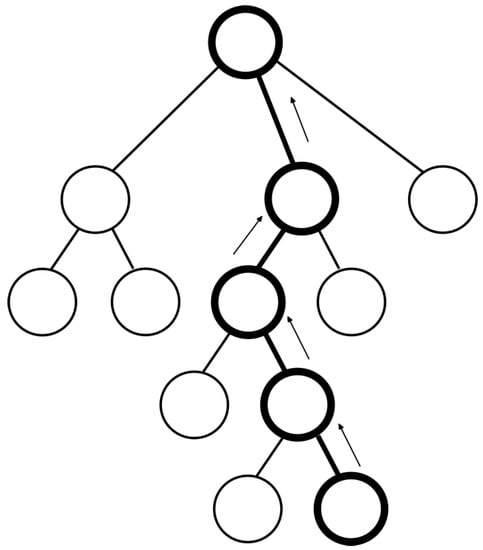 Figure 5. Backpropagation phase in MCTS.
Figure 5. Backpropagation phase in MCTS.
3.1. MCTS and Neural Networks
MCTS simulation phase is characterized by randomness that is optimized focusing on converging the simulations using approaches based on artificial intelligence. AlphaGo is one of the most successful systems that implement this technique, according to Silver et al. [18] it integrates two neural networks in simulation phase:
- Policy network is used to predict if a move corresponds to an expert human move. It was trained with human moves data sets and considers the previous state and the final state after the move. Its output is a probability of belonging to the mentioned data set.
- Value network is used to predict the probability of winning given a certain state. It was trained with game states result of playing again itself, choosing each move with the help of the policy network.
According to Silver et al. [18], policy network is applied after the expansion of a node N0 over every new node Ni. Predicting the probability of move N0 → Ni of being an expert human move. That probability is stored on that node, which will be used on selection phase combined with UCB value to select next node. Value network is applied to the node to be simulated and its prediction is combined with the result of the random simulation giving a final value used to update the tree in backpropagation. Fu [2] suggests a simpler way to use value network: to predict the winner at the beginning of simulation phase, if the result is consistent enough, take that value and jump to backpropagation phase, else perform random simulation. We implement this approximation to build our system.
4. Background
Dots and Boxes problem is challenging because it has a large search space. For a board it has edges, i.e., for a 5 × 5 board it has 60 edges and state space, since any combination of movements is legal. In addition, a naïve search space would generate 60! states, with many of them being duplicates reached from different configurations of the game. This makes infeasible to solve the entire game for larger grids if no specific heuristics are used. In addition, this is a special and interesting game in the sense that despite being impartial (i.e., in Dots and Boxes the possible moves does not depend on the current player), it does not use the normal play convention (i.e., in Dots and Boxes the last player to move not necessarily wins).
Being a classic impartial, combinatorial game, there are many studies about the resolution of Dots and Boxes.
Berlekamp et al. [25,29] explain the game from a mathematical point of view, describing specific strategies to win the game and presenting the problem as NP-hard.
Bossomaier and Knittel [30] describe the evolution of intelligent rule-based agent teams for the Dots and Boxes game. The authors achieve a win rate close to 40% after 3,000,000 games playing against the artificial player Nonie’s Dots and Boxes (http://dsl.ee.unsw.edu.au/dslcdrom/unsw/projects/dots/ (accessed on 9 March 2020)) over a period of approximately 100,000 games. To that end, some structural information about the game space must be included with an artificial economy model.
Since it is a two-player, perfect-information game, researchers try to solve the game, i.e., to discover what can happen if two players are able to play optimally. David Wilson (https://wilson.engr.wisc.edu/boxe/ (accessed on 9 March 2020)) solved the game for a 4 × 4 board in 2020 and some partially completed 5 × 5 games.
Barker and Korf [31] propose a solution that is up to an order-of-magnitude faster than previous works. To achieve that, they apply Alpha-Beta minimax search and different general and problem-specific techniques (based on chains, transposition tables, symmetries and move ordering) to reduce the search space. They can solve a 4 × 5 game, being a tie given optimal play by both players.
Dots and Boxes 5 × 5 has a state space. Algorithms which tend to explore the whole search space would take a big amount of time and most of the computers may not be able to handle that computational cost. An example of this is minimax. As we explained previously, some approaches were developed to reduce the search space, such as Alpha-Beta pruning or MCTS. MCTS makes use of the number of iterations to prune the search space. Also, the introduction of ANN helps to converge the results of the simulations to partially avoid bad quality moves.
Zhuang et al. [32] presents a board presentation specifically designed to solve the Dots and Boxes game. The authors use game-specific knowledge to classify and manage 12 different types of chains and 4 categories of edges. Regarding the strategy to play, authors have used MCTS together with an Artificial Neural Network (ANN) to avoid random movements in the Monte Carlo tree. The ANN has 3 layers (input, hidden and output) with hyperbolic tangent as the activation function and an output that ranges from −1 to 1 which provides a probability of victory or defeat. For a 5 × 5 game, the input only contains 25 elements given their specific representation of the board. Training data for the ANN is generated randomly by generating random states in the middle of the game, applying a minimax search to find the winner when both players play in an optimal way (due to the huge search space it would be impossible to apply that technique from the start of the game). The authors also propose several problem-specific refinements such as (1) the use of UCB1-TUNED [33] instead of the common Upper Confidence bounds applied to Trees (UCT) [34]; (2) auxiliary minimax search; (3) auxiliary greedy policy; (4) exploring order for non-visited nodes; (5) pruning; (6) reusing information of parent nodes; and (7) parallelization. The authors present their implementation in an open-source software called QDab (http://dotsandboxes.tar.xyz/ (accessed on 8 March 2020)). According to their tests, after turn 24 the ANN succeeds to indicate the right move with 66.8% accuracy. After 32 moves the accuracy grows up to 83.8%. QDab was tested with a high success rate against Dabble (https://www.mathstat.dal.ca/~jpg/dabble/ (accessed on 8 March 2020)) and PRsBoxes (http://www.dianneandpaul.net/PRsBoxes/ (accessed on 8 March 2020)).
Lu and Yin [35] combine heuristics with MCTS to avoid MCTS simulations to reach terminal states. The authors obtain an improvement of the performance of the algorithm.
Agrawal and Ziegler [36] explore how controlling different resources (i.e., number of simulations, number of independent learners, amount of information shared among learners, how frequently learners share information), the performance of the game may change by using a parallelized version of MCTS.
Li et al. [37] use convolutional neural networks integrated with MCTS in a value and a policy net inspired by AlphaGo.
Zhang et al. [38] applies AlphaZero algorithm to Dots and Boxes proposing a reinforcement learning method able to improve its ability to play by playing against itself in order avoid the lack of good quality sample data when training a neural network.
Table 1 shows the differences between the contributions of previous studies and ours. We are comparing our approach with Zhuang et al. work, they also play against other systems while other solutions just use their own implementations or humans for testing.

Table 1.
Contribution comparison
In addition to the works cited, there are many other works related to how to solve the game in some aspect, although most of them focus on using game-specific rules and heuristics to take advantage of the domain knowledge. For example, Li et al. [39] work on how to design and implement the board to optimize size and processing time. Bi et al. [40] design an evaluation function with parameters based on a genetic algorithm to optimize them. Allcock [41] gives algorithms for best play in Dots and Boxes consisting of loops and long chains. There are even variations of the game such as Narrow Misère Dots and Boxes by Collette et al. [42], where the goal is to receive the minimum number of points instead of the maximum, reducing the complexity of the original problem. Although Dots and Boxes is a well-studied game, it still lacks a game records database as there may be in other classic games such as Chess or Go. Thus, Gao et al. [43] propose a game records standard format based on JSON to support cross-platform applications and portability.
The main difference of our work with previous proposed works is that our system can learn to play through auto-generated games without any heuristic or extra knowledge added to MCTS. For that, we user Dots and Boxes as a use case.
5. Proposal
The aim of this article is to use an algorithm which implements Monte Carlo Tree Search with neural networks in an efficient way without any domain language. The algorithm will be able to solve the Dots and Boxes game (and be able to beat the current solutions for this game) in a generic way. It will not use any heuristic based on the domain knowledge of the game that could affect MCTS algorithm. In this section we will explain our contributions to classic MCTS described in Section 3. First, we focus on the contributions to MCTS and then on the implementation of our artificial neural network.
5.1. Monte Carlo
In MCTS, each node just uses one counter to sum up number of victories, draws and defeats. We are adding a double counter for each node to solve the problem. In selection phase, a node must be selected according to the greatest UCB value, i.e., to select the next move from the current state. The UCB formula is represented as follows:
where is the mean of wins resulted from node j, nj is the number of visits j node received, n the number of visits for the parent of the node and Cp is a constant. For calculating , we are adding a “win” every time node j reaches a win game status during its simulations. According to Arrington et al. [44] we get a better performance of this formula if the value we assign as winning or losing values in the range [0,1], i.e., normalized. Dots and boxes has three possible game ended status: victory, defeat or draw. Each node has a counter which is updated during backtracking by adding a certain value for victory, defeat or draw.
This value is in UCB formula. If we say that the current move is for Player 1 (P1) and we use just one counter for both players, the next move (next selected node) will be chosen as the best value for P1. This is false for a game with alternative turns. The next move must be the best for the other player, Player 2 (P2) to get a meaningful set of moves. Therefore, we add another counter, this way we have one for saving P1 results and the other for P2 results. When calculating the UCB value for each node, we took the difference between both counters and change the sign, being positive if it is a good option and negative if it is a bad option depending on the current player turn. If it is the turn of Player 1, we do not touch that value, but if it is the turn of Player 2, we place the opposite sign.
Also, if there are several nodes with the same greatest value the system takes a list with all of them and picks one randomly.
5.2. Artificial Neural Network Configuration
One of the objectives of this study is the generalization of the problem. So, we are generating our own data sets to train the artificial neural network by making the system play against itself. This MCTS implementation is configured with an important number of iterations to get good games minimizing incoherent moves. To balance response time and good results, we considered experimentally 100,000 iterations. That number is big enough to reduce meaningless moves and small enough to let us generate games in a reasonable time.
The ANN trains over the moves of the Dots and Boxes board obtained with the previous methodology. The boards are parsed into an array of 85 doubles distinguishing between free and occupied positions (we do not differentiate between moves done by P1 or P2 because the resolution of the game does not depend on who does which move but on the closing of boxes), boxes closed by P1, boxes closed by P2 and free boxes. Table 2 represents all values involved in board, their meaning in the game, their value on the board and their normalized value in the input array of the ANN. 115,000 games are used to train this ANN.

Table 2.
Mapped values from board to neural network.
Artificial neural network configuration is described in Figure 6. It is composed by three layers with 85, 100 and 3 neurons, respectively. Number of neurons of first layer must be the same as the input array size. According to our experiments 100 neurons on layer 2 are effective. Sigmoid activation function (AF) has been proved to be effective in layers 2 and 3. The output is a set of the probabilities of P1 and P2 winning the game and ending on draw.
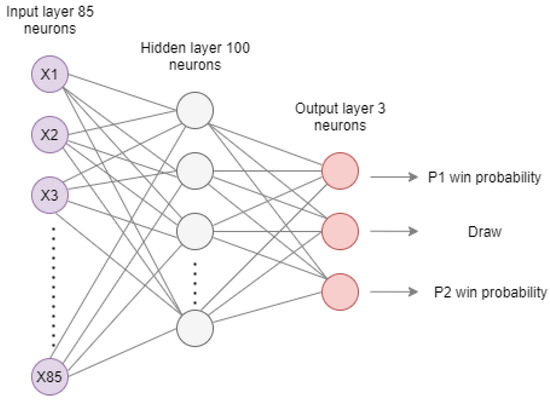
Figure 6.
Artificial neural network configuration.
This ANN is applied in simulation phase in MCTS as shown in Figure 7 and Algorithm 5. Before starting that step, the ANN is called over the node to be simulated, if it returns a probability over a threshold to be determined, it jumps to backpropagation with this win, draw or defeat value, else continues with the random simulation.
| Algorithm 5 ANN applied on MCTS |
| function simulation(node) |
| while node state is not final do |
| probability = ANN(node state) |
| if probability >= threshold then return node state |
| end if |
| get next node random |
| node = next node |
| end whilereturn node state |
| end function |
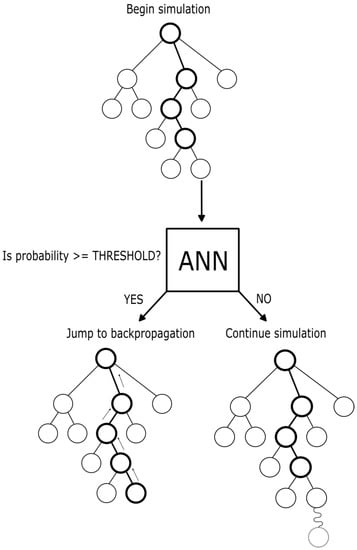
Figure 7.
ANN applied on MCTS.
6. Materials and Methods
6.1. Materials
A program is implemented to make the rival play against our system integrating both movements and being possible to start a game from a determined state. For each set of tests and different parameters, 100 games are played. Tests are done running our system on Windows 10 Pro, 32GB of RAM, AMD Ryzen 7 3700X 8-Core Processor 3.59 GHz and running rival system on Ubuntu Server 18.04 Hyper-V virtual machine and 4 GB of RAM. The virtual machine runs on the host previously specified. Our system is implemented in Java 13 and uses the library Encog Java 3.4 for the neural network.
6.2. Methods
The methodology of the experiments is described in this subsection.
6.2.1. Sets of Tests
The sets of tests taken into account in the experiments are explained below as well as the varying parameters.
- MCTS without ANN and no double counter. The system makes use of MCTS without calling ANN in simulation phase and with a unique counter. We test it varying number of iterations.
- MCTS without ANN. The system makes use of MCTS without calling ANN in simulation phase at all. We test it varying number of iterations.
- MCTS with ANN. The system makes use of MCTS calling ANN in simulation phase. This is the final stage of the system. We test it varying number of iterations and ANN threshold.
6.2.2. System Comparison
We are testing our system against the one implemented by Zhuang et al. [32]. This implementation of Monte Carlo Tree Search also makes use of neural networks, but it makes use of some knowledge of the domain such as heuristics to reorder the candidate nodes to be selected in Monte Carlo selection phase (Source code available at http://dotsandboxes.tar.xyz/). Their board representation is based on the model of Strings-and-Coins explained by Berlekamp and Scott [25,45]. This converts the board in a set of chains joined by edges, which are the remain possible moves, and allows the classification of each edge (candidate move) in a category from 0 to 3, being 0 the safest for the current player and 3 the most dangerous which could end benefiting the other player. At selection phase, they pre-classify the candidate edges (candidate nodes) in these categories and start working with the one from the safer category, reducing the tree search.
They also implement an auxiliary greedy policy to directly select nodes of category 0 if there is one. That makes the system quickly close a box when there is just one move left without starting MCTS. Our system does not require a specific board representation, a matrix representing moves and boxes is used. It neither pre-classifies candidate nodes. When there is a possibility of closing a box, it runs the whole MCTS process instead of using a greedy policy as the rival. This penalizes the performance of our solution for that cases.
Although our board representation consists of 85 elements, their representation allows the translation of the state of the game to a vector of 25 elements, which is the input value of their ANN. Their reduced number of input elements reduces the number of neurons of the input layer of the ANN to 25. Our general representation of the board penalizes the performance of the ANN as the more neurons, the more time it takes. Rival system implements an ANN composed by three layers using the hyperbolic tangent as activation function with 25 and 1 neuron for the input and output layer, respectively. The number of neurons of the hidden layer is unknown as Figure 8 shows.
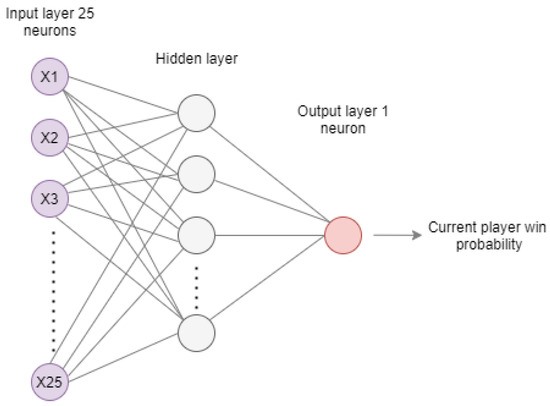
Figure 8.
Rival neural network configuration.
It receives as input a board representation which contains 25 numbers representing several characteristics of the state of the game [32]. It returns a single value with the probability that the current player wins. Their data set is generated by producing games resolved randomly from initial state to the middle of the game and completing the game from there with Minimax search. Our system uses pure MCTS to generate games. For converging to good MCTS results, the ANN is applied in simulation phase for selecting the simulated moves instead of doing it randomly. For balance between execution efficiency and the cost of the ANN, random technique is used at the beginning of the game while ANN is called for the rest. Our system applies ANN to MCTS as described in Section 5.1. Our objective is to prove that Monte Carlo can be used in a generic way without any extra heuristic and be able to get good results. The rival is considered Player 1 (P1) and our system is Player 2 (P2) in the experiments. P1 is configured at maximum difficulty setting its timeout to 70,000.
6.2.3. Selected Games
To reduce the waiting time in the experiments, instead starting to play from initial state, a determined state is used. State S (Figure 9) has been chosen to reduce the tree search, so it has 40 out of 60 moves fixed. The closed boxes number is the same for each player to start the game with the same conditions. This state will be used in each set of experiments.
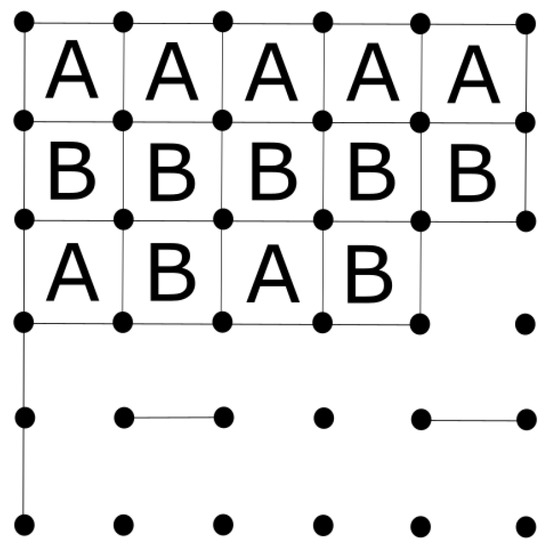
Figure 9.
Starting node State S.
7. Results and Discussion
In this section, results obtained according to the described methodology are shown as well as the evolution of the investigation with the proposed strategies.
7.1. MCTS without ANN and No Double Counter
The need for using double counter instead of unique appeared in early phases of this investigation, where experiments with other games were still going on. Tic-tac-toe was a good game for these experiments because it has few states and it is easy to track them all. When we were debugging the tree for this game generated by MCTS turned into a picture, we realized that the algorithm was not choosing the obvious next move but the more convenient to the player who just moved. Then, we implemented the double counter to prevent the problem described in the Proposal section and check again graphically that the moves were the expected. After the implementation of Dots and Boxes, we run some experiments with this game and unique counter. Table 3 shows how the results would be if instead double counter for each node we used a unique counter and starting at State S.

Table 3.
Results for unique counter.
The results show how determinant is the use of a double counter in our implementation with 0% of victories.
7.2. MCTS without ANN
Table 4 shows the results of the games started at State S. The first column corresponds to the number of iterations done by Monte Carlo algorithm, the next three show the victories for P1, P2 and draws occurred in 100 played games. For the first case, when setting MCTS iterations to 1000, our system won 5 games out of 100.

Table 4.
Results from starting node State S without ANN.
The mean time for the movements of Player 1 and 100,000 MCTS iterations is 300 ms including the sending and response time of the request and some conversions to integrate both systems. We can assume that the time needed to convert the rival response to a move understandable by our system is similar to the time the rival might need to communicate with its own board. Our system measures how long it takes to run MCTS and return a move, this way, we can compare ourselves to that time. Table 4 shows how the time for our system (P2) increases with the number of iterations. With 30,000 iterations we match their time, but with only 35% of victories, while with 100,000 iterations we get 50% of victories but being 2.8 times slower. This is a good result taking into account we are not using domain knowledge of the problem. It also shows that the more MCTS iterations we set, the better results we obtain and the more time it consumes. We start to get good results from 100k iterations, with 50% of victories, although it still takes more time than rival system. Despite the number of generated games, there was no draw case in any of them.
7.3. MCTS with ANN
The main contribution is to be able to use MCTS with ANN in a generic way with acceptable results, so these tests correspond to the final implementation of the system playing from State S.
Table 5 shows the results for MCTS with NN from State S. From left to right: MCTS iterations, good predictions (mean number of times per move the ANN returns a probability above the ANN threshold), number of victories for P1, number of victories for P2, number of draws, mean time per move for P1, mean time per move for P2, number of unique states which are not in data train that appeared along 100 games and times the previous described states appeared along 100 games (certain state not in data train can appear more than once). The ANN threshold has been set experimentally to 0.9.

Table 5.
Results from starting node State S with ANN.
As Table 5 shows, the system reaches the optimal value at 50,000 MCTS iterations with an 81%percent of victories. With 70,000 iterations the system obtains 1% more of victories but with 39.69% more execution time. The good predictions are the 60.82% of the 50,000 iterations. Also, the execution time of the system is 15.40 times bigger than the rival. With 50,000 iterations we obtain 68.75% more victories than with the tests without ANN, so we can say that the use of ANN improves how our system plays. Although our system obtains better game results than the rival, its performance is worse. The generalization of our system, without neither specific representation of the game, which can improve ANN performance, nor heuristics in selection phase nor greedy policy when closing boxes, penalties the average performance. To quantify the time we lose without greedy policy, we assumed that in the best of scenarios, the time taken by the system to close a box with greedy policy is zero. We measure the mean of total moves for Player 2 (Mvs), the mean o moves that close boxes (CB) and the mean time per move for 50,000 MCTS iterations MT. Then, we subtract to TM the number moves that close boxes, obtaining the moves which actually consume time (RMvs), we are calling them real moves.
After that, we calculate the mean time for a complete game (MTG) starting at State S taking into account just the real moves.
Finally, we calculate again the mean time per move with the new mean time per game and the total moves.
For this case, we can say that the absence of a greedy policy in our system increases, at most, a 150% the mean time per move. Although our system presents worse performance, it can be generalized for other problems. Its board representation does not require any knowledge of the game and no domain heuristic modification of MCTS is implemented.
The system we are compared to is called QDab, QDab compares with Dabble, PRsBoxes and MCTS without optimizations. In Table 6 we are showing the winning rate of our system related to QDab and the results of QDab against other systems, these last tests are run taking into account the whole board.

Table 6.
Winning rate comparison.
8. Conclusions and Future Work
Monte Carlo Tree Search can be implemented making use of neural networks in an efficient and generic way. For the game Dots and Boxes, the tests run with a unique counter showed that this approach is not enough to win any game against a MCTS domain-based implementation. Tests with double counter and no ANN indicate an accuracy improvement with 50% of victories but being 2.8 times slower.
Finally, a general implementation of MCTS with ANN, but without any knowledge of the domain, can beat a MCTS implementation with heuristics in the 81% of the cases but takes 15.40 times more execution time.
A general representation of the board and the lack of heuristics over MCTS algorithm penalties performance but allows the application of this system to other problems.
Future work will be focused on the application of generic MCTS to other games as Tic-tac-toe or Chess and prove its effectiveness against systems with domain knowledge. Also, a way of transmitting the self-acquired knowledge of the system to humans could be explored. Works will be carried out on our open-source project JGraphs [46].
Author Contributions
Conceptualization, A.C., V.G.-D., E.R.N.-V., C.G.G. and A.G.; methodology, A.C. and J.C.-W.L.; software, A.C.; validation, A.C., V.G.-D., E.R.N.-V., C.G.G. and A.G.; formal analysis, A.C., V.G.-D., E.R.N.-V., C.G.G. and A.G.; investigation, A.C., V.G.-D., E.R.N.-V., C.G.G. and A.G.; resources, A.C., V.G.-D., E.R.N.-V., C.G.G. and A.G.; data curation, A.C., V.G.-D., E.R.N.-V., C.G.G. and A.G.; writing—original draft preparation, A.C. and V.G.-D.; writing—review and editing, A.C., V.G.-D., E.R.N.-V., C.G.G. and A.G.; visualization, A.C., V.G.-D., E.R.N.-V., C.G.G. and A.G.; supervision, V.G.-D., E.R.N.-V., C.G.G. and A.G.; project administration, A.C., V.G.-D., E.R.N.-V., C.G.G. and A.G.; funding acquisition, A.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Fundación Universidad de Oviedo grant number FI-005-18.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Szita, I.; Chaslot, G.; Spronck, P. Monte Carlo Tree Search in Settlers of Catan. In Advances in Computer Games; Springer: Berlin/Heidelberg, Germany, 2009; pp. 21–32. [Google Scholar]
- Fu, M.C. Alphago and Monte Carlo Tree Search: The simulation optimization perspective. In Proceedings of the 2016 Winter Simulation Conference (WSC) 2016, Washington, DC, USA, 11–14 December 2016; pp. 659–670. [Google Scholar] [CrossRef]
- Risi, S.; Preuss, M. From chess and atari to starcraft and beyond: How game AI is driving the world of AI. KI-Künstliche Intell. 2020, 34, 7–17. [Google Scholar] [CrossRef]
- Muhammad, A.K.Y.K. Cardiac Arrhythmia Disease Classification Using LSTM Deep Learning Approach. Comput. Mater. Contin. 2021, 67, 427–443. [Google Scholar] [CrossRef]
- Reddy, S.; Allan, S.; Coghlan, S.; Cooper, P. A governance model for the application of AI in health care. J. Am. Med. Inform. Assoc. 2019, 27, 491–497. [Google Scholar] [CrossRef]
- Myerson, R.B. Game Theory; Harvard University Press: Harvard, UK, 2013. [Google Scholar]
- Sohrabi, M.K.; Azgomi, H. A survey on the combined use of optimization methods and game theory. Arch. Comput. Methods Eng. 2020, 27, 59–80. [Google Scholar] [CrossRef]
- Neumann, J.V. Zur theorie der gesellschaftsspiele. Math. Ann. 1928, 100, 295–320. [Google Scholar] [CrossRef]
- Althöfer, I. An incremental negamax algorithm. Artif. Intell. 1990, 43, 57–65. [Google Scholar] [CrossRef]
- Knuth, D.E.; Moore, R.W. An analysis of alpha-beta pruning. Artif. Intell. 1975, 6, 293–326. [Google Scholar] [CrossRef]
- Reinefeld, A. Spielbaum-Suchverfahren; Springer: Berlin/Heidelberg, Germany, 2013; Volume 200. [Google Scholar]
- Plaat, A.; Schaeffer, J.; Pijls, W.; De Bruin, A. Best-First Fixed-Depth Minimax Algorithms. Artif. Intell. 1996, 87, 255–293. [Google Scholar] [CrossRef]
- Metropolis, N.; Ulam, S. The Monte Carlo method. J. Am. Stat. Assoc. 1949, 44, 335–341. [Google Scholar] [CrossRef] [PubMed]
- Browne, C.B.; Powley, E.; Whitehouse, D.; Lucas, S.M.; Cowling, P.I.; Rohlfshagen, P.; Tavener, S.; Perez, D.; Samothrakis, S.; Colton, S. A survey of Monte Carlo Tree Search methods. IEEE Trans. Comput. Intell. AI Games 2012, 4, 1–43. [Google Scholar] [CrossRef]
- Kim, M.J.; Ahn, C.W. Hybrid fighting game AI using a genetic algorithm and Monte Carlo tree search. In Proceedings of the Genetic and Evolutionary Computation Conference Companion 2018, Kyoto, Japan, 15–19 July 2018; pp. 129–130. [Google Scholar]
- Bobadilla, J.; Ortega, F.; Gutiérrez, A.; Alonso, S. Classification-based Deep Neural Network Architecture for Collaborative Filtering Recommender Systems. Int. J. Interact. Multimed. Artif. Intell. 2020, 6, 68–77. [Google Scholar] [CrossRef]
- Maheshan, M.; Harish, B.; Nagadarshan, N. A Convolution Neural Network Engine for Sclera Recognition. Int. J. Interact. Multimed. Artif. Intell. 2020, 6, 78–83. [Google Scholar] [CrossRef]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Van Den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484. [Google Scholar] [CrossRef] [PubMed]
- Silver, D.; Schrittwieser, J.; Simonyan, K.; Antonoglou, I.; Huang, A.; Guez, A.; Hubert, T.; Baker, L.; Lai, M.; Bolton, A.; et al. Mastering the game of go without human knowledge. Nature 2017, 550, 354–359. [Google Scholar] [CrossRef]
- Grill, J.B.; Altché, F.; Tang, Y.; Hubert, T.; Valko, M.; Antonoglou, I.; Munos, R. Monte Carlo Tree Search as Regularized Policy Optimization. PMLR 2020, 119, 3769–3778. [Google Scholar]
- Świechowski, M.; Mańdziuk, J. Self-Adaptation of Playing Strategies in General Game Playing. IEEE Trans. Comput. Intell. AI Games 2014, 6, 367–381. [Google Scholar] [CrossRef]
- Świechowski, M.; Mańdziuk, J.; Ong, Y.S. Specialization of a UCT-Based General Game Playing Program to Single-Player Games. IEEE Trans. Comput. Intell. AI Games 2016, 8, 218–228. [Google Scholar] [CrossRef]
- Walędzik, K.; Mańdziuk, J. An Automatically Generated Evaluation Function in General Game Playing. IEEE Trans. Comput. Intell. AI Games 2014, 6, 258–270. [Google Scholar] [CrossRef]
- Tanabe, Y.; Yoshizoe, K.; Imai, H. A study on security evaluation methodology for image-based biometrics authentication systems. In Proceedings of the 2009 IEEE 3rd International Conference on Biometrics: Theory, Applications, and Systems 2009, Washington, DC, USA, 28–30 September 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Berlekamp, E.R. The Dots and Boxes Game: Sophisticated Child’s Play; AK Peters/CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Kuhn, H.W. Classics in Game Theory; Princeton University Press: Princeton, NJ, USA, 1997. [Google Scholar]
- Lucas, W. L’arithmétique amusante. Nature 1895, 53, 79. [Google Scholar] [CrossRef]
- Kocsis, L.; Szepesvári, C.; Willemson, J. Improved Monte Carlo Search. Univ. Tartu Estonia Tech. Rep. 2006, 1. [Google Scholar]
- Berlekamp, E.R.; Conway, J.H.; Guy, R.K. Winning Ways for Your Mathematical Plays; AK Peters/CRC Press: Boca Raton, FL, USA, 2004; Volume 4. [Google Scholar]
- Bossomaier, T.; Knittel, A.; Harre, M.; Snyder, A. An evolutionary agent approach to Dots and Boxes. In Proceedings of the IASTED International Conference on Software Engineering and Applications, Dallas, TX, USA, 13–15 November 2006. [Google Scholar]
- Barker, J.K.; Korf, R.E. Solving Dots and Boxes. In Proceedings of the Twenty-Sixth AAAI Conference on Artificial Intelligence, Toronto, ON, Canada, 22–26 July 2012. [Google Scholar]
- Zhuang, Y.; Li, S.; Peters, T.V.; Zhang, C. Improving Monte Carlo Tree Search for Dots and Boxes with a novel board representation and artificial neural networks. In Proceedings of the 2015 IEEE Conference on Computational Intelligence and Games (CIG), Tainan, Taiwan, 31 August–2 September 2015; pp. 314–321. [Google Scholar]
- Auer, P.; Cesa-Bianchi, N.; Fischer, P. Finite-time analysis of the multiarmed bandit problem. Mach. Learn. 2002, 47, 235–256. [Google Scholar] [CrossRef]
- Coquelin, P.; Munos, R. Bandit Algorithms for Tree Search. CoRR 2007, abs/cs/0703062. [Google Scholar]
- Lu, J.; Yin, H. Using heuristic solver to optimize Monte Carlo Tree Search in Dots and Boxes. In Proceedings of the 2016 Chinese Control and Decision Conference (CCDC), Yinchuan, China, 28–30 May 2016; pp. 4288–4291. [Google Scholar]
- Agrawal, P.; Ziegler, U. Performance of the Parallelized Monte Carlo Tree Search Approach for Dots and Boxes; Western Kentucky University: Bowling Green, KY, USA, 2018. [Google Scholar]
- Li, S.; Zhang, Y.; Ding, M.; Dai, P. Research on integrated computer game algorithm for dots and boxes. J. Eng. 2020, 2020, 601–606. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S.; Xiong, X. A Study on the Game System of Dots and Boxes Based on Reinforcement Learning. In Proceedings of the 2019 Chinese Control And Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; pp. 6319–6322. [Google Scholar]
- Li, S.; Li, D.; Yuan, X. Research and Implementation of Dots and Boxes Game System. JSW 2012, 7, 256–262. [Google Scholar] [CrossRef]
- Bi, F.; Wang, Y.; Chen, W. Adaptive genetic algorithm to optimize the parameters of evaluation function of Dots and Boxes. In Proceedings of the International Conference on Heterogeneous Networking for Quality, Reliability, Security and Robustness, Seoul, Korea, 7–8 July 2016; pp. 416–425. [Google Scholar]
- Allcock, D. Best play in Dots and Boxes endgames. arXiv 2018, arXiv:1811.10747. [Google Scholar]
- Collette, S.; Demaine, E.D.; Demaine, M.L.; Langerman, S. Narrow Misere Dots and Boxes. Games No Chance 4 2015, 63, 57. [Google Scholar]
- Gao, M.; Li, S.; Ding, M.; Kun, M. The Dots and Boxes Records Storing Standard Format for Machine Learning and The Design and Implementation of Its Generation Tool. J. Phys. Conf. Ser. 2019, 1176, 032009. [Google Scholar] [CrossRef]
- Arrington, R.; Langley, C.; Bogaerts, S. Using domain knowledge to improve Monte Carlo Tree Search performance in parameterized poker squares. In Proceedings of the 30th AAAI Conference on Artificial Intelligence, AAAI 2016, Phoenix, AZ, USA, 12–17 February 2016; pp. 4065–4070. [Google Scholar]
- Berlekamp, E.; Scott, K. Forcing Your Opponent to Stay in Control of a Loony Dots and Boxes Endgame. In Proceedings of the MSRI Workshop on Combinatorial Games; 2002. Available online: https://www.semanticscholar.org/paper/Forcing-Your-Opponent-to-Stay-in-Control-of-a-Loony-Berlekamp-Scott/2979cb648924108cb09c5a5cc4599da2a6e4bc02 (accessed on 23 February 2021).
- García-Díaz, V.; Núñez-Valdez, E.R.; García, C.G.; Gómez-Gómez, A.; Crespo, R.G. JGraphs: A Toolset to Work with Monte-Carlo Tree Search-Based Algorithms. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 2020, 28, 1–22. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).