Locomotion of Self-Excited Vibrating and Rotating Objects in Granular Environments
Abstract
1. Introduction
2. Simulation Implementation Details
2.1. Simulation Method
2.2. Simulation Software
2.3. The Simulated System
3. Results and Analysis
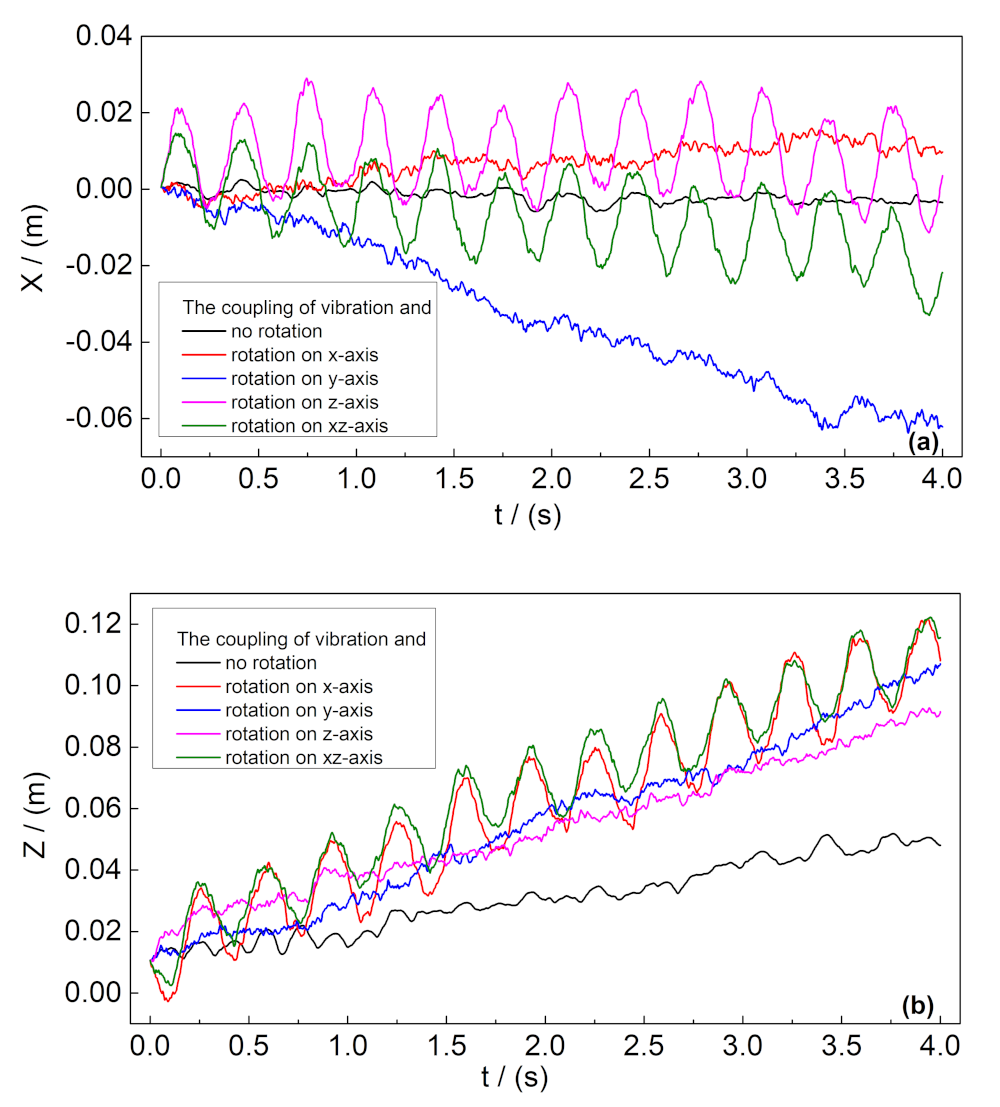
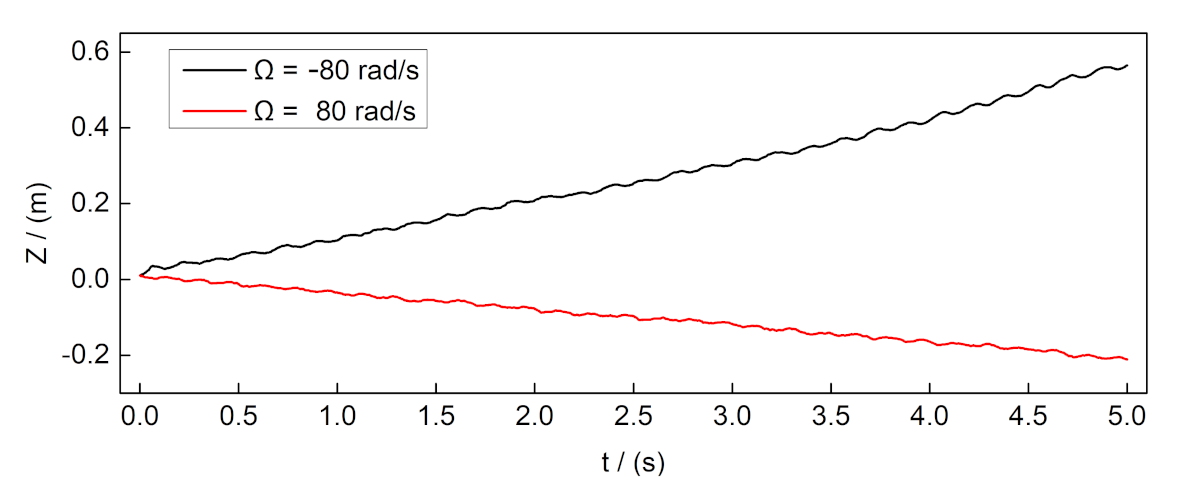
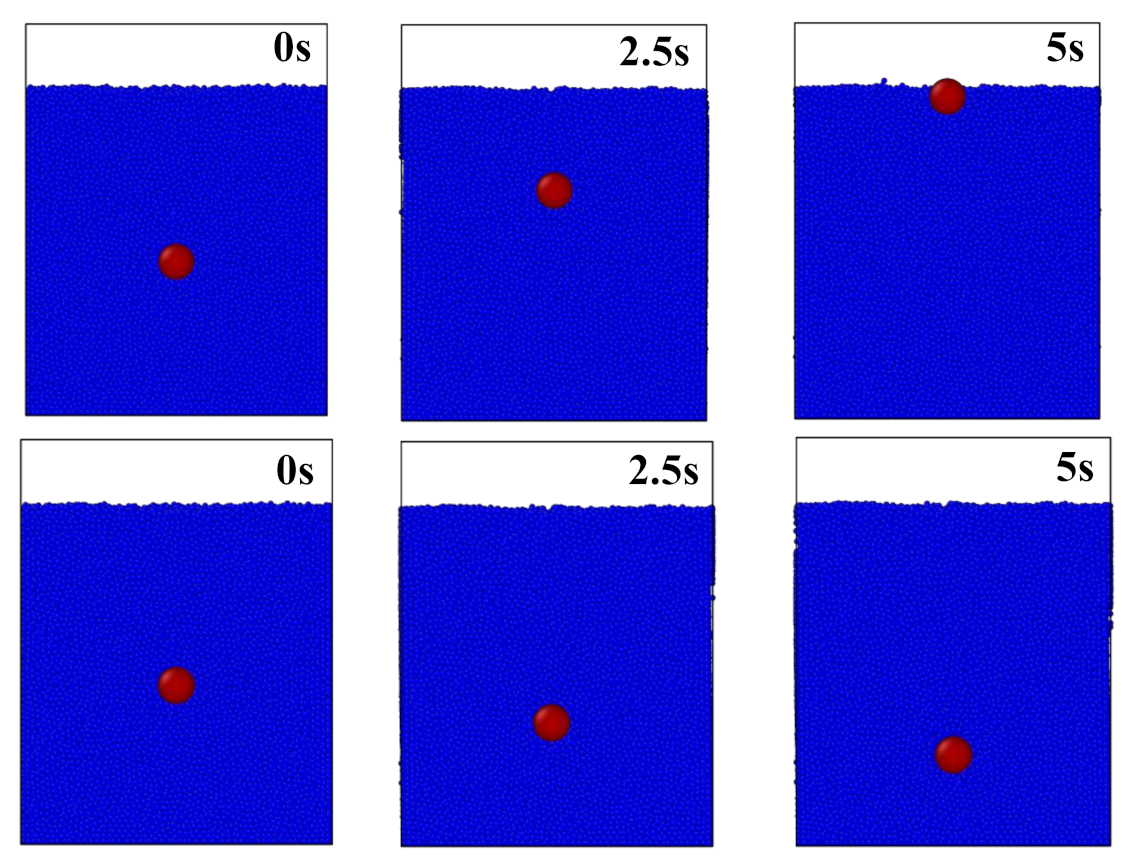
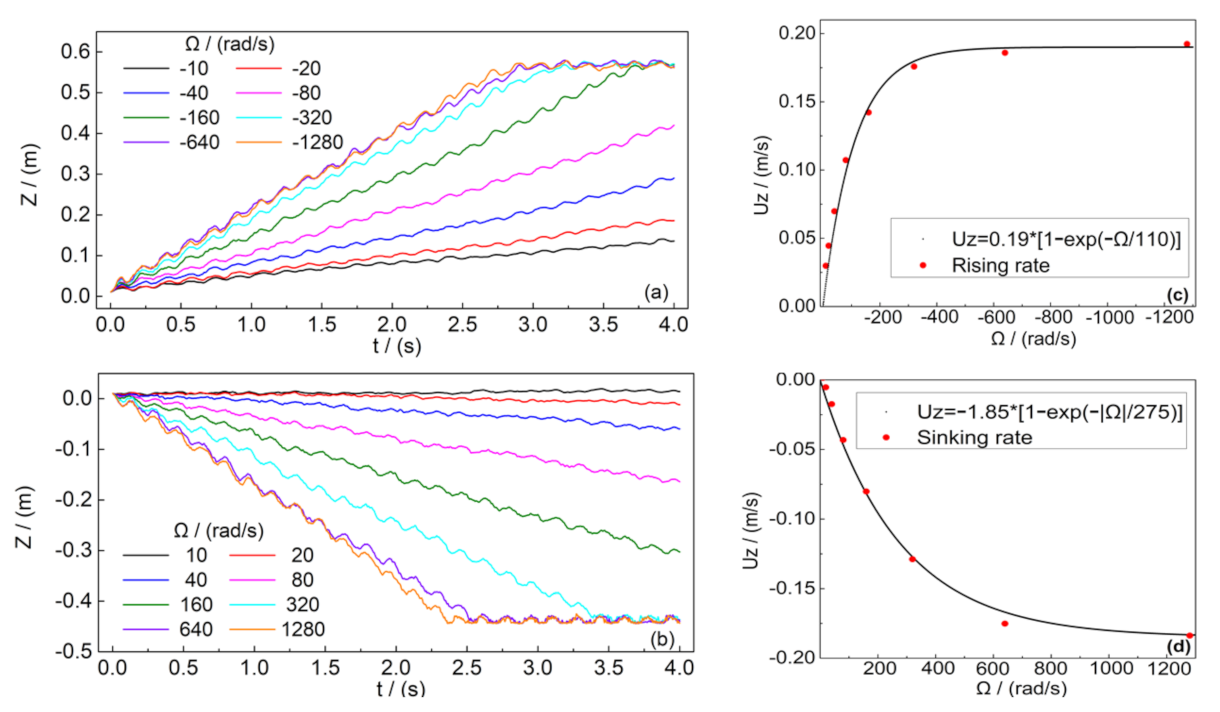
3.1. Coupling Oscillatory Translation and Constant Rotation Speed
- The displacement in the x direction oscillates strongly at frequency f whenever has a component about the z-axis, while otherwise it is relatively smooth.
- The x displacement is vanishingly small except when the rotation is about the y-axis, in which case the SO moves steadily in the direction.
- The displacement in the z direction oscillates strongly at frequency f when has a component about the x-axis, otherwise it is relatively smooth.
- The displacement in the z direction is always upward, with rotation enhancing the rising rate.
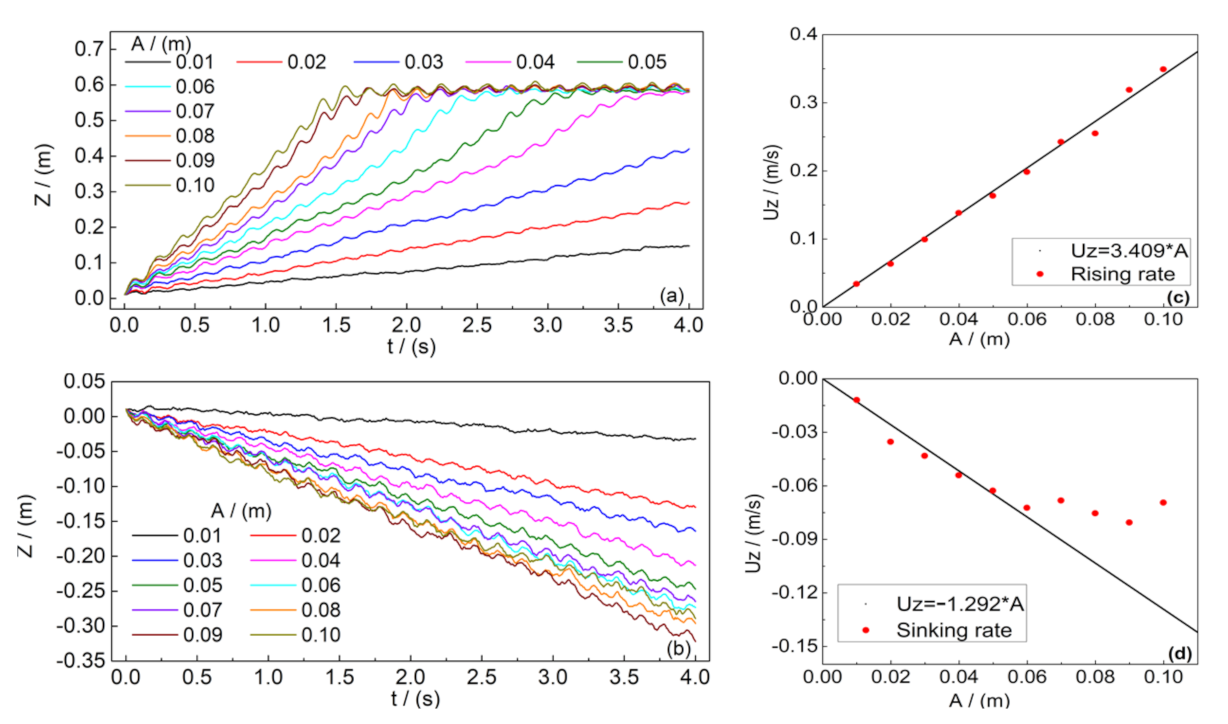
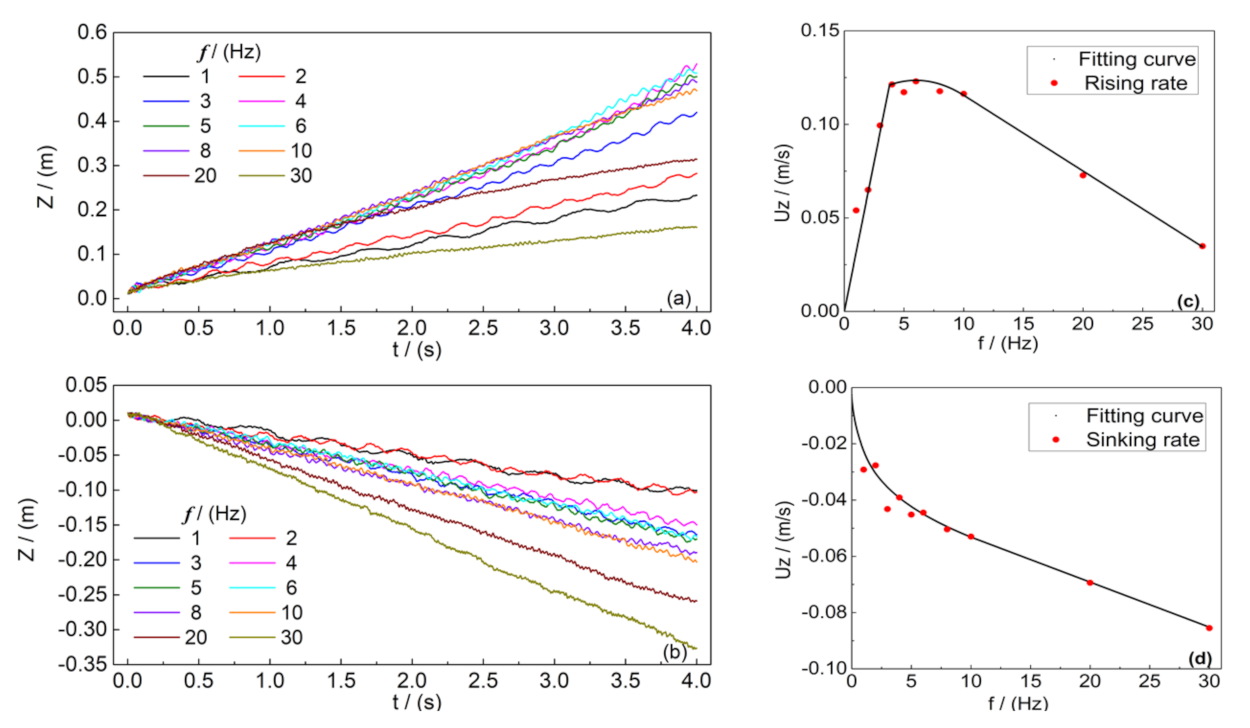
3.2. Coupling Oscillatory Translation and Oscillatory Rotation Speed
3.2.1. The Effect of Rotation Amplitude,
3.2.2. The Effect of the Translational Amplitude, A
3.2.3. The Effect of the Frequency, f
4. Conclusions and Future Research
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jaeger, H.; Nagel, S.; Behringer, R. Granular solids, liquids, and gases. Rev. Mod. Phys. 1996, 68, 1259–1273. [Google Scholar] [CrossRef]
- Nedderman, R.M. Statics and Kinematics of Granular Materials; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics, 2nd ed.; Butterworth-Heinemann, Pergamon Press: Oxford, UK, 1987; Volume 6, pp. 3, 4, 29. [Google Scholar]
- Arnold, E.N. Identifying the effects of history on adaptation: Origins of different sand-diving techniques in lizards. J. Zool. 1995, 235, 351–388. [Google Scholar] [CrossRef]
- Arnold, E.N.; Leviton, A.E. A revision of the lizard genus Scincus. Bull. Br. Mus. Nat. Hist. (Zool.) 1977, 31, 189–248. [Google Scholar]
- Baumgartner, W.; Fidler, F.; Weth, A.; Habbecke, M.; Jakob, P.; Butenweg, C.; Böhme, W. Investigating the locomotion of the sandfish in desert sand using nmr-imaging. PLoS ONE 2008, 3, e3309. [Google Scholar] [CrossRef] [PubMed]
- Maladen, R.D.; Ding, Y.; Li, C.; Goldman, D.I. Undulatory Swimming in Sand: Subsurface Locomotion of the Sandfish Lizard. Science 2009, 325, 314–318. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.; Lutz, C.; Mersch, S.; Thelen, R.; Greiner, C.; Gomard, G.; Hölscher, H. Characterization of the microscopic tribological properties of sandfish (Scincus scincus) scales by atomic force microscopy. Beilstein J. Nanotechnol. 2018, 9, 2618–2627. [Google Scholar] [CrossRef] [PubMed]
- Halloy, M.; Etheridge, R.; Burghardt, G.M. To bury in sand: Phylogenetic relationships among lizard species of the boulengeri group, Liolaemus (Reptilia: Squamata: Tropiduridae), based on behavioral characters. Herpetol. Monogr. 1998, 12, 1–37. [Google Scholar] [CrossRef]
- Luke, C. Convergent evolution of lizard toe fringes. Biol. J. Linn. Soc. 1986, 27, 1–16. [Google Scholar] [CrossRef]
- Evangelista, D.; Hotton, S.; Dumais, J. The mechanics of explosive dispersal and self-burial in the seeds of the filaree, Erodium cicutarium (Geraniaceae). J. Exp. Biol. 2011, 214, 521–529. [Google Scholar] [CrossRef]
- Jung, W.; Choi, S.M.; Kim, W.; Kim, H.Y. Reduction of granular drag inspired by self-burrowing rotary seeds. Phys. Fluids 2017, 29, 041702. [Google Scholar] [CrossRef]
- Vogela, R.; Stark, H. Force-extension curves of bacterial fagella. Eur. Phys. J. E 2010, 33, 259–271. [Google Scholar] [CrossRef]
- Darbois Texier, B.; Ibarra, A.; Melo, F. Helical locomotion in a granular medium. Phys. Rev. Lett. 2017, 119, 068003.1–068003.5. [Google Scholar] [CrossRef]
- Takashi, S.; Dirk, K.; Troy, S.; Hans, H.J. Swimming in granular media. Phys. Rev. E 2009, 80, 020301. [Google Scholar]
- Gray, J.; Hancock, G.J. The propulsion of sea-urchin spermatozoa. J. Exp. Biol. 1955, 32, 802–814. [Google Scholar]
- Ui, T.J.; Hussey, R.G.; Roger, R.P. Stokes drag on a cylinder in axial motion. Phys. Fluids 1984, 27, 787. [Google Scholar] [CrossRef]
- Ding, Y.; Gravish, N.; Goldman, D.I. Drag induced lift in granular media. Phys. Rev. Lett. 2011, 106, 028001. [Google Scholar] [CrossRef]
- Maladen, R.D.; Ding, Y.; Umbanhowar, P.B.; Kamor, A.; Goldman, D.I. Mechanical models of sandfish locomotion reveal principles of high performance subsurface sand-swimming. J. R. Soc. Interface 2011, 8, 1332–1345. [Google Scholar] [CrossRef]
- Percier, B.; Manneville, S.; Mcelwaine, J.N.; Morris, S.W.; Taberlet, N. Lift and drag forces on an inclined plow moving over a granular surface. Phys. Rev. E 2011, 84, 051302. [Google Scholar] [CrossRef]
- Li, C.; Umbanhowar, P.B.; Komsuoglu, H.; Koditschek, D.E.; Goldman, D.I. Sensitive dependence of the motion of a legged robot on granular media. Proc. Natl. Acad. Sci. USA 2009, 106, 3029–3034. [Google Scholar] [CrossRef]
- Maladen, R.D.; Ding, Y.; Umbanhowar, P.B.; Goldman, D.I. Undulatory swimming in sand: Experimental and simulation studies of a robotic sandfish. Int. J. Robot. Res. 2011, 30, 793–805. [Google Scholar] [CrossRef]
- Katsuragi, H. Physics of soft impact and cratering. J. Phys. Condens. Matter. 2015, 6, 977. [Google Scholar]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Kishino, Y. Disc model analysis of the granular media. Micromech. Granul. Mater. 1988, 20, 143–152. [Google Scholar]
- Kishino, Y. Computer analysis of dissipation mechanism in granular media. In Powders and Grains; Balkema: Montpellier, France, 1989; pp. 323–330. [Google Scholar]
- Radjai, F.; Jean, M.; Moreau, J.J.; Roux, S. Force distributions in dense two-dimensional granular systems. Phys. Rev. Lett. 1996, 77, 274–277. [Google Scholar] [CrossRef]
- Cundall, P.A.; Hart, R. Numerical modeling of discontinua. J. Eng. Comp. 1992, 9, 101–113. [Google Scholar] [CrossRef]
- Cook, B.K.; Jensen, R.P. Discrete element methods: Numerical modeling of discontinua. In Proceedings of the Third International Conference on Discrete Element Methods, Santa Fe, NW, USA, 23–25 September 2002; American Society of Civil Engineers: Reston, VA, USA, 2002. [Google Scholar]
- Vango, M.; Feilmayr, C.; Pirker, S.; Lichtenegger, T. Data-assisted CFD modeling of transient blast furnace tapping with a dynamic deadman. Appl. Math. Model. 2019, 73, 210–227. [Google Scholar] [CrossRef]
- Kloss, C.; Goniva, C.; Hager, A.; Amberger, S.; Pirker, S. Models, algorithms and validation for opensource dem and cfd-dem. Prog. Comput. Fluid Dyn. 2012, 12, 140–152. [Google Scholar] [CrossRef]
- Podlozhnyu, A.; Pirker, S.; Kloss, C. Efficient implementation of superquadric particles in discrete element method within an open-source framework. Comput. Part. Mech. 2016, 4, 101–118. [Google Scholar] [CrossRef]
- Silbert, L.; Ertas, D.; Grest, G.; Halsey, T.; Levine, D.; Plimpton, S. Granular flow down an inclined plane: Bagnold scaling and rheology. Phys. Rev. E 2001, 64, 051302. [Google Scholar] [CrossRef] [PubMed]
- Plimpton, S.J. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comp. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Huang, L.; Ran, X.; Blumenfeld, R. Vertical dynamics of a horizontally oscillating active object in a two-dimensional granular medium. Phys. Rev. E 2016, 94, 062906. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Q.; Ran, X.; Liu, P.; Tang, W.; Blumenfeld, R. Numerical simulation of a spinning sphere moving in granular matter. Acta Phys. Sin. 2018, 67, 014702. [Google Scholar]
- Mosauer, W. Adaptive convergence in the sand reptiles of the Sahara and of California: A study in structure and behavior. Copeia 1932, 72–78. [Google Scholar] [CrossRef]
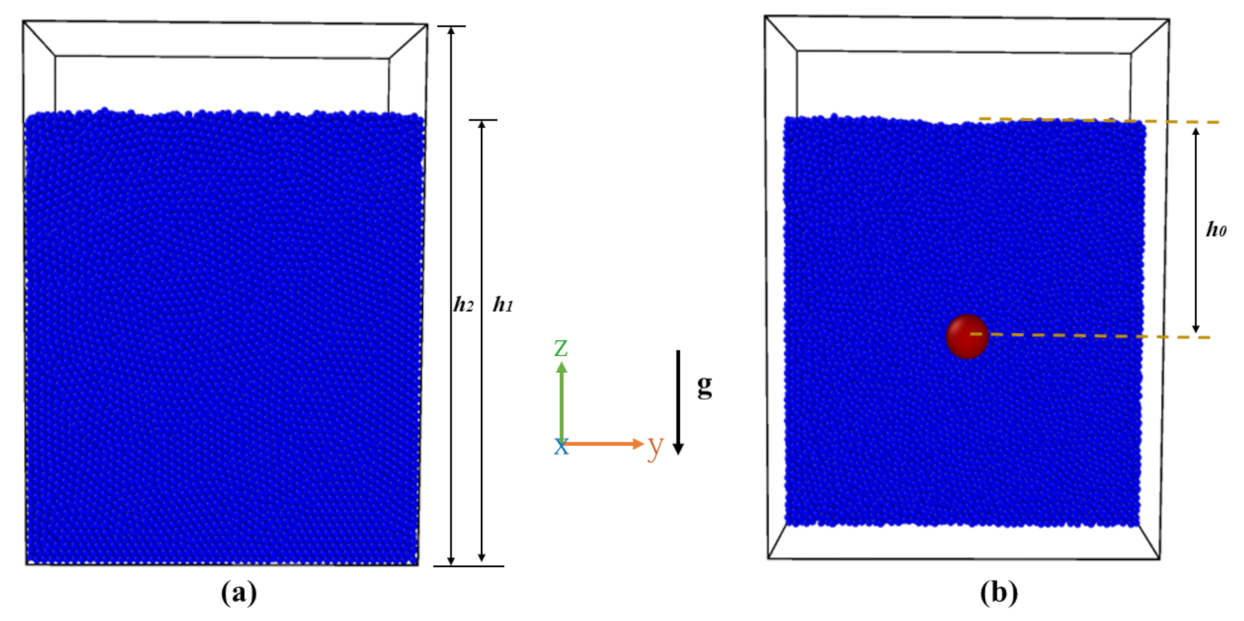
| Parameter | Unit | Bed Particle | SO |
|---|---|---|---|
| Shape | No unit | Spherical | Spherical |
| Diameter | m | 0.02 | 0.12 |
| Density | kg/m | 2500 | 2500 |
| Young’s Modulus | Pa | ||
| Coefficient of Restitution | No unit | 0.9 (bed particle-bed particle) | 0.5 (SO-bed particle) |
| Coefficient of Friction | No unit | 0.45 (bed particle-bed particle) | 0.5 (SO-bed particle) |
| Poisson Ratio | No unit | 0.25 | 0.25 |
| Gravity Acceleration | m/s | 9.81 | 9.81 |
| T (s) | t = 0 | t = T/4 | t = T/2 | t = 3T/4 | t = T |
|---|---|---|---|---|---|
| Displacement y (m) | y = 0 | y = A | y = 0 | y = −A | y = 0 |
| Rotation velocity (rad/s) |
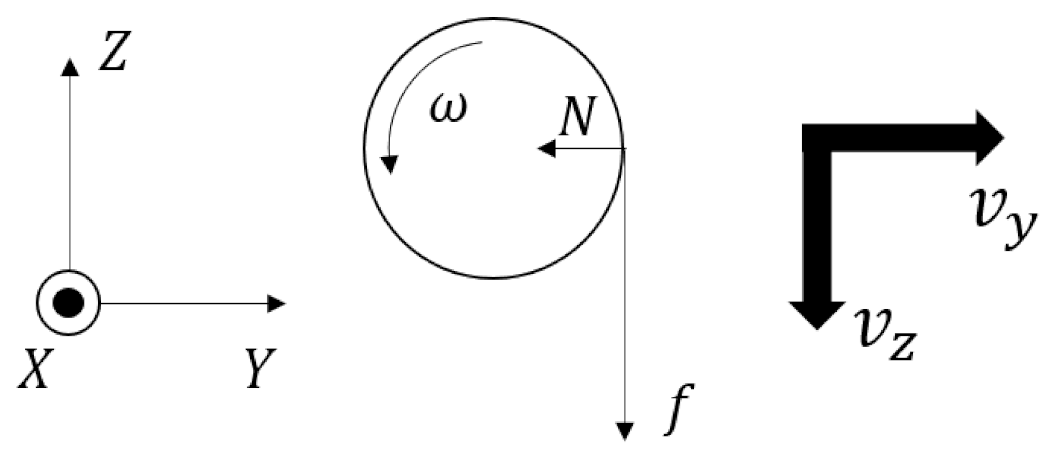
| Region | (t = 0 → t = T/4) | (t = T/4 → t = T/2) | (t = T/2 → t = 3T/4) | (t = 3T/4 → t = T) |
|---|---|---|---|---|
| Vibration direction | direction | direction | direction | direction |
| Rotation direction | clockwise | counter-clockwise | counter-clockwise | clockwise |
| Resultant friction direction | direction | direction | direction | direction |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, P.; Ran, X.; Cheng, Q.; Tang, W.; Zhou, J.; Blumenfeld, R. Locomotion of Self-Excited Vibrating and Rotating Objects in Granular Environments. Appl. Sci. 2021, 11, 2054. https://doi.org/10.3390/app11052054
Liu P, Ran X, Cheng Q, Tang W, Zhou J, Blumenfeld R. Locomotion of Self-Excited Vibrating and Rotating Objects in Granular Environments. Applied Sciences. 2021; 11(5):2054. https://doi.org/10.3390/app11052054
Chicago/Turabian StyleLiu, Ping, Xianwen Ran, Qi Cheng, Wenhui Tang, Jingyuan Zhou, and Raphael Blumenfeld. 2021. "Locomotion of Self-Excited Vibrating and Rotating Objects in Granular Environments" Applied Sciences 11, no. 5: 2054. https://doi.org/10.3390/app11052054
APA StyleLiu, P., Ran, X., Cheng, Q., Tang, W., Zhou, J., & Blumenfeld, R. (2021). Locomotion of Self-Excited Vibrating and Rotating Objects in Granular Environments. Applied Sciences, 11(5), 2054. https://doi.org/10.3390/app11052054






