A Study on Liquid Leak Rates in Packing Seals
Abstract
:1. Introduction
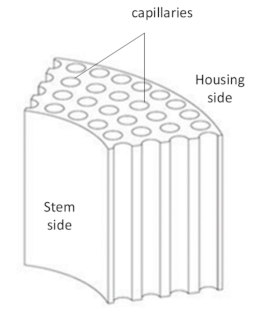
2. Theoretical Model
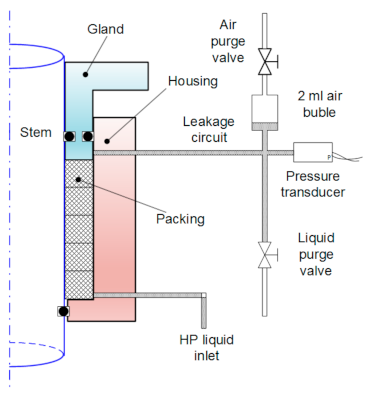
3. Experimental Testing
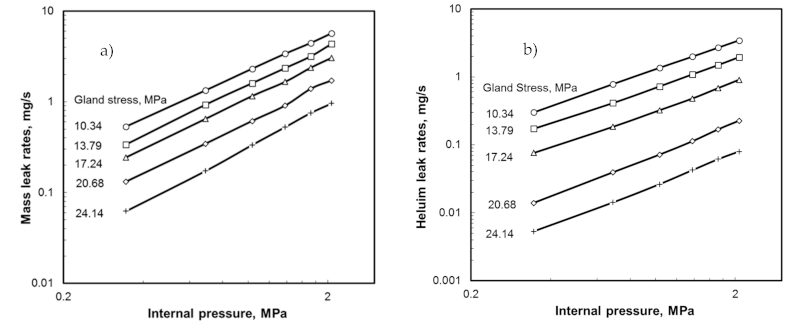
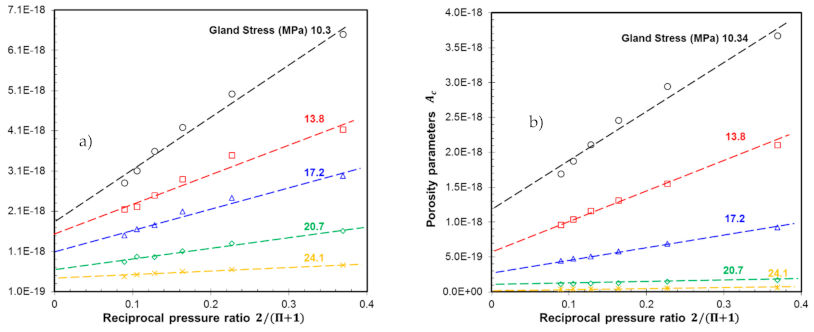
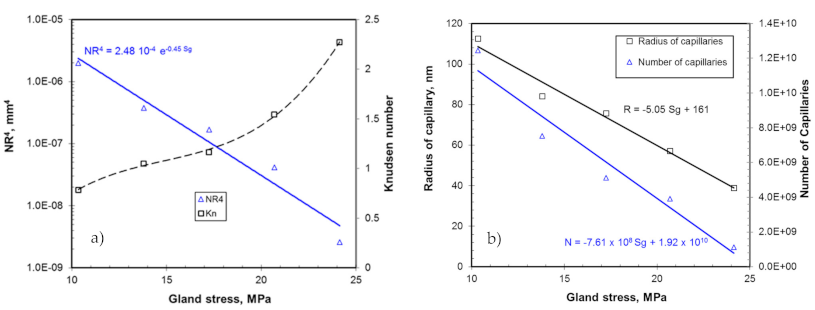
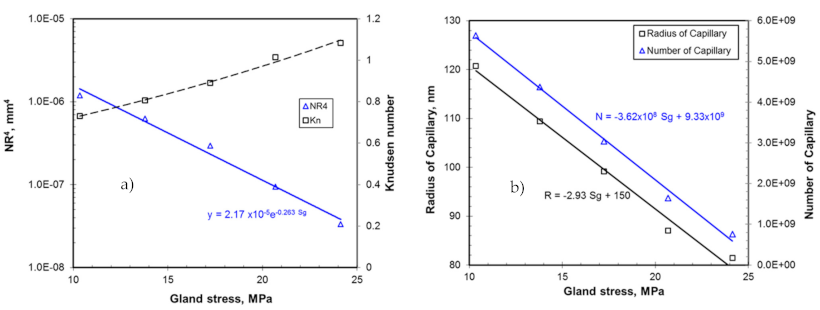
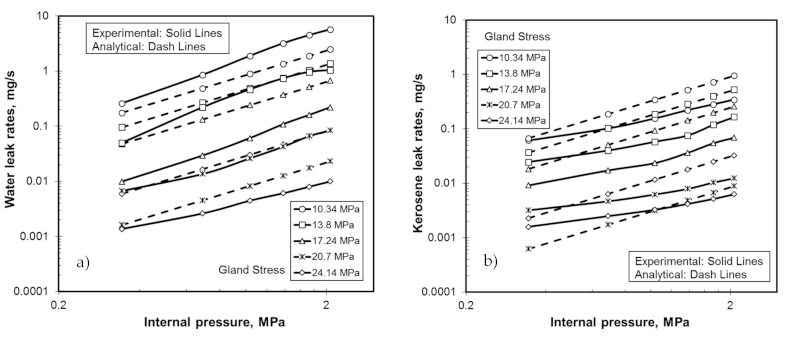
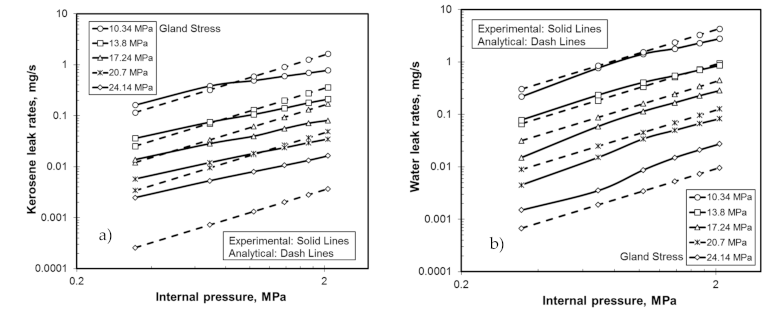
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| K | Lateral pressure coefficient | ||
| Kn | Knudsen number | ||
| L | Leak rate, kg/s | ||
| ℓ | Total axial length of packing rings, m | ||
| Ls | Slip flow in liquids, µm | ||
| N | Number of capillaries | ||
| NR4 | Porosity Parameters for tapered capillary, m4 | ||
| P | Pressure, Pa | ||
| R | Pore radius at distance z, m | ||
| R | Radial direction, m | ||
| T | Temperature, K | ||
| U | Axial velocity, m/s | ||
| Z | Capillary axial direction, m | ||
| Greek Letters | |||
| λ | Mean free path, m | ||
| μ | Dynamic viscosity, Pa s | ||
| ρ | Density, kg/m³ | ||
| σ | Tangential momentum accommodation coefficient | ||
| Π | Inlet to outlet pressure ratio | ||
| ℜ | Specific gas constant, J/kg K | ||
| ΔP | Pressure difference between upstream and downstream, Pa | ||
| Subscripts or Superscripts | |||
| I | Inlet or upstream | ||
| O | Outlet or downstream | ||
References
- Chambers, A.K.; Strosher, M.; Wootton, T.; Moncrieff, J.; McCready, P. Direct Measurement of Fugitive Emissions of Hydrocarbons from a Refinery. J. Air Waste Manag. Assoc. 2008, 58, 1047–1056. [Google Scholar] [CrossRef] [PubMed]
- ASME PCC1. Guidelines for Pressure Boundary Bolted Flange Joint Assembly; American Society of Mechanical Engineers: New York, NY, USA, 2010. [Google Scholar]
- Shabtai, A.; Elovici, Y.; Rokach, L. A Survey of Data Leakage Detection and Prevention Solutions; Springer: New York, NY, USA, 2012. [Google Scholar]
- Payne, J.R. PVRC Flanged Joint User Survey. Weld. Res. Counc. 1985, 306, 1–45. [Google Scholar]
- American Petroleum Industries. API-622—Type Testing of Process Valve Packing for Fugitive Emissions; API Publishing Services: Washington, DC, USA, 2018. [Google Scholar]
- American Petroleum Industries. API-624—Type Testing of Rising Stem Valves Equipped with Flexible Graphite Packing for Fugitive Emissions; API Publishing Services: Washington, DC, USA, 2014. [Google Scholar]
- International Standard Organization. ISO-15848—Industrial Valves—Measurement, Test and Qualification Procedures for Fugitive Emissions; ISO: Geneva, Switzerland, 2015. [Google Scholar]
- Bayreuther, D. Fugitive Emission Testing and Certification of Valves: What Next? Valve Manufacturers Association of America. 2016. Available online: https://www.valvemagazine.com/web-only/categories/technical-topics/7476-fugitive-emission-testing-and-certification-of-valves-what-next.html (accessed on 12 October 2020).
- Ergun, S. Fluid Flow through Packed Columns. Chem. Eng. Prog. 1952, 48, 89–94. [Google Scholar]
- Macdonald, I.; El-Sayed, M.; Mow, K.; Dullien, F. Flow through Porous Media—The Ergun Equation Revisited. Ind. Eng. Chem. Fundam. 1979, 18, 199–208. [Google Scholar] [CrossRef]
- Masi, V.; Bouzid, A.; Derenne, M. Correlation between Gases and Mass Leak Rate of Gasketing Materials. In Proceedings of the 1998 ASME/JSME Joint Pressure Vessels and Piping Conference, San Diego, CA, USA, 26–30 July 1998; Volume 367, pp. 17–24. [Google Scholar]
- Beskok, A.K. Report: A Model for Flows in Channels, Pipes, and Ducts at Micro and Nano Scales. Microscale. Eng. 1999, 3, 43–77. [Google Scholar]
- Xue, H.; Fan, Q.; Shu, C. Prediction of Micro-Channel Flows Using Direct Simulation Monte Carlo. Probabilistic Eng. Mech. 2000, 15, 213–219. [Google Scholar] [CrossRef]
- Asahina, M. Estimation of Sealability with Compressed Fibers Sheet Gaskets for Liquid and Gas Fluid. In Proceedings of the 1998 ASME/JSME Joint Pressure Vessels and Piping Conference, San Diego, CA, USA, 26–30 July 1998; Volume 367, pp. 25–34. [Google Scholar]
- Grine, L.; Bouzid, A. Liquid Leak Predictions in Micro-and Nanoporous Gaskets. ASME J. Press. Vessel. Technol. 2011, 133, 051402-(6). [Google Scholar] [CrossRef]
- Hsieh, S.S.; Lin, C.Y.; Huang, C.F.; Tsai, H. Liquid Flow in a Micro-Channel. J. Micromech. Microeng. 2004, 14, 436–446. [Google Scholar] [CrossRef]
- Koo, J.; Kleinstreuer, C. Liquid Flow in Microchannels: Experimental Observations and Computational Analyses of Microfluidics Effects. J. Micromech. Microeng. 2003, 13, 568–579. [Google Scholar] [CrossRef]
- Marchand, L.; Derenne, M.; Masi, V. Predicting Gasket Leak Rates Using a Laminar-Molecular Flow Model. In Proceedings of the ASME Pressure Vessels and Piping Conference–2005, Denver, CO, USA, 17–21 July 2005; pp. 87–96. [Google Scholar]
- Grine, L.; Bouzid, A. Correlation of Gaseous Mass Leak Rates through Micro-and Nanoporous Gaskets. ASME J. Press. Vessel. Technol. 2011, 133, 021402-(6). [Google Scholar] [CrossRef]
- Sbragaglia, M.; Succi, S. Analytical Calculation of Slip Flow in Lattice Boltzmann Models with Kinetic Boundary Conditions. Phys. Fluids 2005, 17, 093602. [Google Scholar] [CrossRef]
- Dongari, N.; Agrawal, A.; Agrawal, A. Analytical Solution of Gaseous Slip Flow in Long Microchannels. Int. J. Heat Mass Transf. 2007, 50, 3411–3421. [Google Scholar] [CrossRef]
- Maurer, J.; Tabeling, P.; Joseph, P.; Willaime, H. Second-Order Slip Laws in Microchannels for Helium and Nitrogen. Phys. Fluids 2003, 15, 2613–2621. [Google Scholar] [CrossRef]
- Diany, M.; Bouzid, A.H. An Experimental-Numerical Procedure for Stuffing Box Packing Characterization and Leak Tests. J. Tribol. 2011, 133, 012201-(8). [Google Scholar] [CrossRef]
- Kazeminia, M.; Bouzid, A. Leak Prediction through Porous Compressed Packing Rings: A Comparison Study. Int. J. Press. Vessel. Pip. 2018, 166, 1–8. [Google Scholar] [CrossRef]
- Aweimer, A.S.O.; Bouzid, A. Evaluation of Interfacial and Permeation Leaks in Gaskets and Compression Packing. J. Nucl. Eng. Radiat. Sci. 2019, 5, 011013-(9). [Google Scholar] [CrossRef]
- Diany, M.; Bouzid, A. Analytical Evaluation of Stresses and Displacements of Stuffing-Box Packing Based on a Flexibility Analysis. Tribol. Int. 2009, 42, 980–986. [Google Scholar] [CrossRef]
- Ochonski, W. Radial Stress Distribution and Friction Forces in a Soft-Packed Stuffing-Box Seal. Tribol. Int. 1988, 21, 31–38. [Google Scholar] [CrossRef]
- Pengyun, S.; Kuangmin, C.; Zongyun, D. Theoretical Analysis of the Lateral Pressure Coefficients in a Soft-Packed Stuffing-Box Seal. Tribol. Int. 1997, 30, 759–765. [Google Scholar] [CrossRef]
- Hoa, X.J.; Saulot, A.; Busquet, M.; Berthier, Y.; Torrance, A.A.; Hersant, D. Tribological investigation of packing friction along the stem of a valve. Tribol. Int. 2013, 65, 354–362. [Google Scholar] [CrossRef]
- Choi, C.H.; Westin, K.J.A.; Breuer, K.S. Apparent Slip Flows in Hydrophilic and Hydrophobic Microchannels. J. Phys. Fluids 2003, 15, 2897–2902. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bouzid, A.-H. A Study on Liquid Leak Rates in Packing Seals. Appl. Sci. 2021, 11, 1936. https://doi.org/10.3390/app11041936
Bouzid A-H. A Study on Liquid Leak Rates in Packing Seals. Applied Sciences. 2021; 11(4):1936. https://doi.org/10.3390/app11041936
Chicago/Turabian StyleBouzid, Abdel-Hakim. 2021. "A Study on Liquid Leak Rates in Packing Seals" Applied Sciences 11, no. 4: 1936. https://doi.org/10.3390/app11041936
APA StyleBouzid, A.-H. (2021). A Study on Liquid Leak Rates in Packing Seals. Applied Sciences, 11(4), 1936. https://doi.org/10.3390/app11041936




