ECG Signal Denoising and Reconstruction Based on Basis Pursuit
Abstract
1. Introduction
- (1)
- In view of the phenomenon of large errors in signal reconstruction, the compressed sensing BP signal reconstruction algorithm is adopted. We constructed the measurement matrix and established the basis pursuit denoising (BPDN) mode considering the characteristics of ECG signals.
- (2)
- This paper proposes the BP-ADMM algorithm, which overcomes the problems of low reconstruction accuracy. This method introduces dual variables, reduces constraint conditions, and achieves the purpose of optimizing the original variable and the dual variable at the same time through alternate optimization.
- (3)
- A low-pass filter matrix is constructed for baseline wander correction and denoising through a zero-phase filter. The results show that the issue of the peak underestimation of the ECG signal is effectively improved, and the performance of the algorithm is systematically proposed.
- (4)
- The rest of this paper is organized as follows. The related techniques and mathematical methods are presented in Section 2. Section 3 introduces the system model. Section 4 shows the algorithm set-up process as well as the ECG signal denoising and reconstruction process. A detailed description of the simulation results under various algorithms is provided in Section 5, and Section 6 is the conclusion.
2. Technical Background
2.1. Basis Pursuit
2.2. Review of the ADMM Method
3. System Model
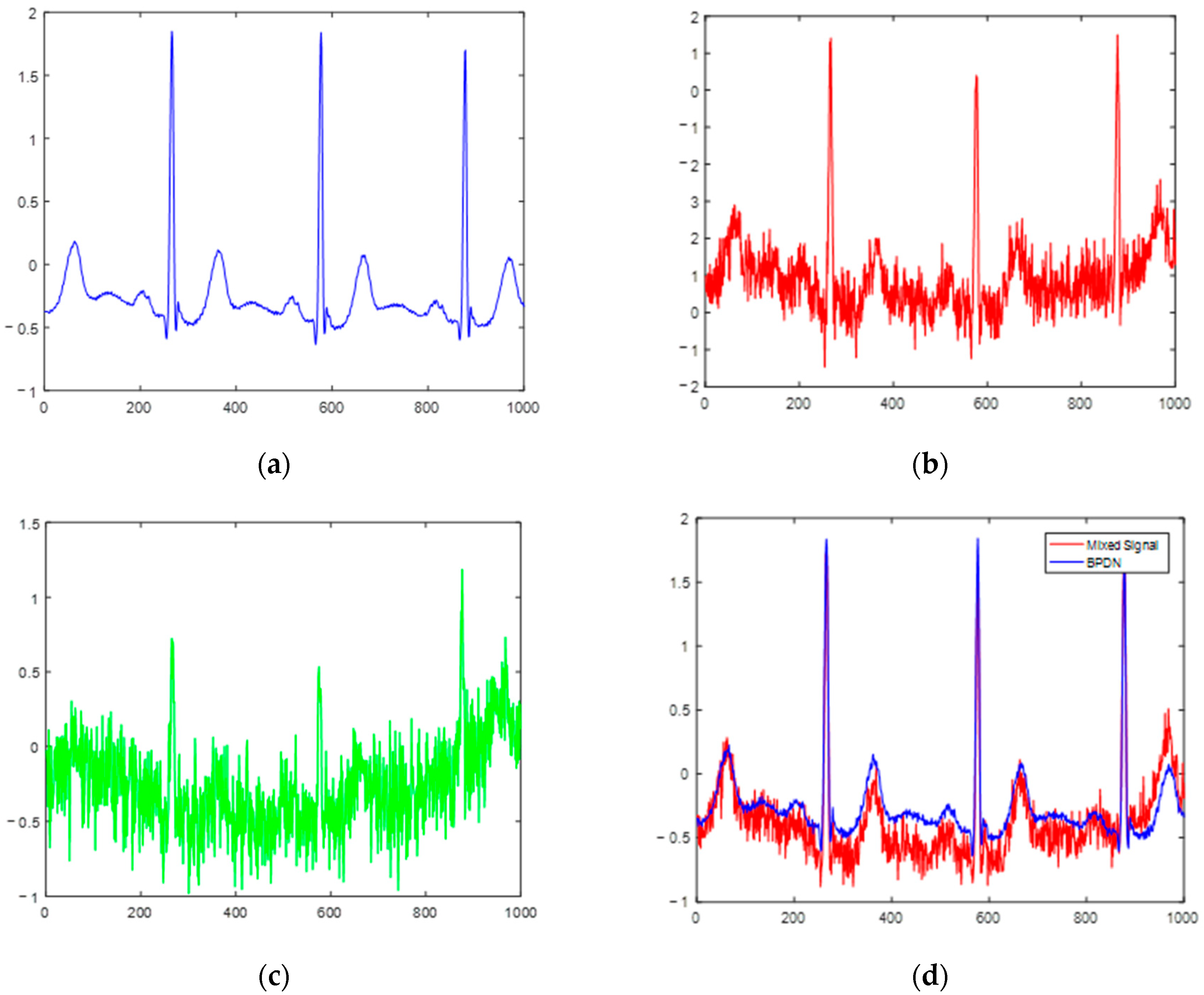
4. Denoising Methods
4.1. BP Denoising
4.2. Low-Pass Filter MATRIX Construction
4.3. BP-ADMM Methods
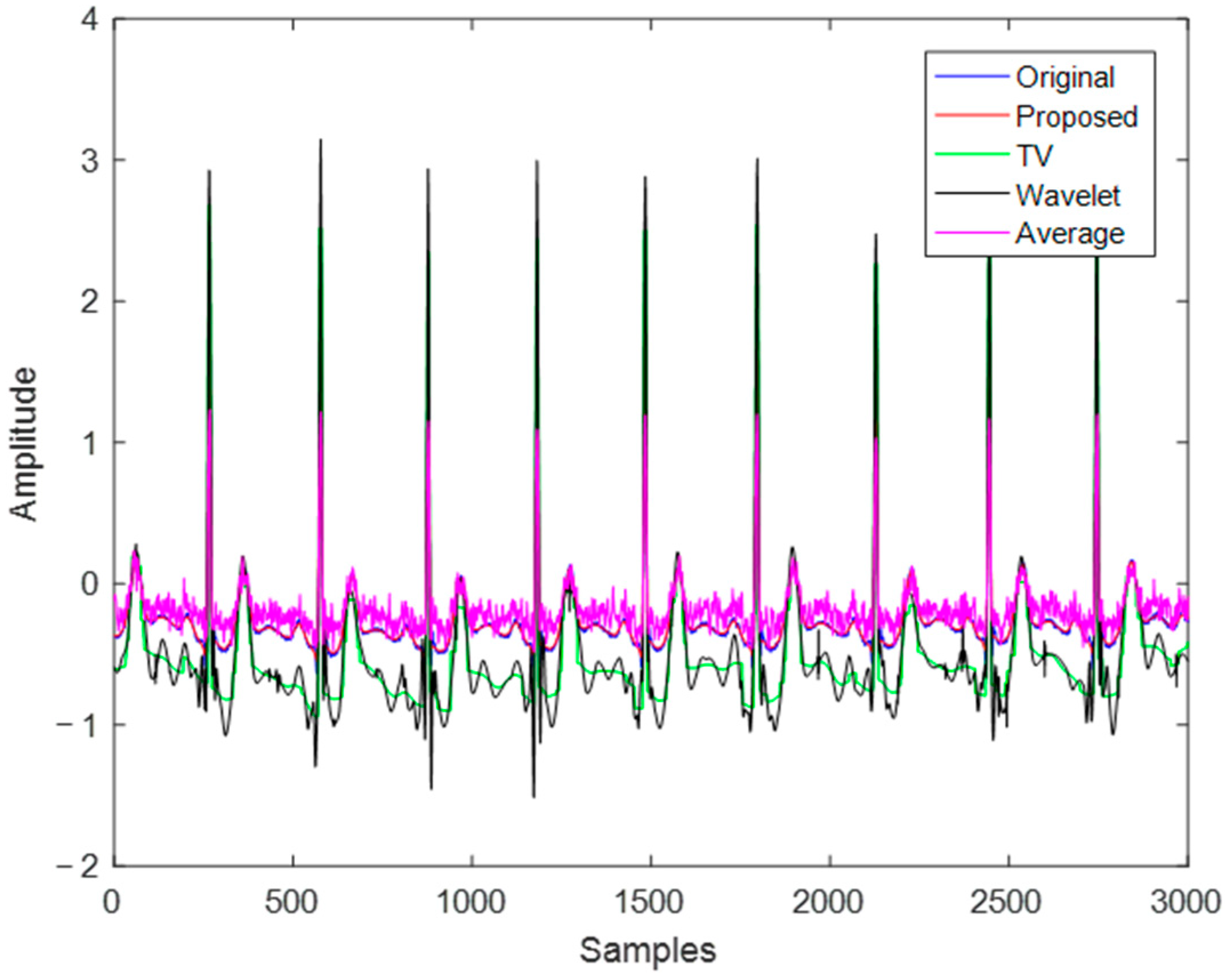
5. Denoising Experiments
5.1. ECG Database
5.2. Performance Analysis
5.3. Simulation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Roonizi, E.K.; Sassi, R. A Signal Decomposition Model-Based Bayesian Framework for ECG Components Separation. IEEE Trans. Signal Process. 2016, 64, 665–674. [Google Scholar] [CrossRef]
- Chiang, H.T.; Hsieh, Y.Y.; Fu, S.W.; Hung, K.H.; Tsao, Y.; Chien, S.Y. Noise Reduction in ECG Signals Using Fully Convolutional Denoising Autoencoders. IEEE Access 2019, 7, 60806–60813. [Google Scholar] [CrossRef]
- Xiong, P.; Wang, H.; Liu, M.; Zhou, S.; Hou, Z.; Liu, X. ECG signal enhancement based on improved denoising auto-encoder. Eng. Appl. Artif. Intell. 2016, 52, 194–202. [Google Scholar] [CrossRef]
- Chandrakar, C.; Kowar, M.K. Denoising ECG signals using adaptive filter algorithm. Int. J. Soft Comput. Eng. 2012, 2, 120–123. [Google Scholar]
- Oster, J.; Behar, J.; Sayadi, O.; Nemati, S.; Johnson, A.E.; Clifford, G.D. Semi-supervised ECG ventricular beat classification with novelty detection based on switching Kalman filters. IEEE Trans. Biomed. Eng. 2015, 62, 2125–2134. [Google Scholar] [CrossRef] [PubMed]
- Rahman, M.Z.U.; Shaik, R.A.; Reddy, D.V.R.K. Efficient and simplified adaptive noise cancelers for ECG sensor based remote health monitoring. IEEE Sens. J. 2012, 12, 566–573. [Google Scholar] [CrossRef]
- Liu, S.; Li, Y.; Hu, X.; Liu, L.; Hao, D. A novel thresholding method in removing noises of electrocardiogram based on wavelet transform. J. Inf. Comput. Sci. 2013, 10, 5031–5041. [Google Scholar] [CrossRef]
- Rakshit, M.; Das, S. An efficient ECG denoising methodology using empirical mode decomposition and adaptive switching mean filter. Biomed. Signal Proc. Control 2018, 40, 140–148. [Google Scholar] [CrossRef]
- Von Gladiss, A.; Ahlborg, M.; Knopp, T.; Buzug, T.M. Compressed Sensing of the System Matrix and Sparse Reconstruction of the Particle Concentration in Magnetic Particle Imaging. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Lustig, M.; Donoho, D.; Pauly, J.M. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn. Reason. Med. 2007, 58, 1182–1195. [Google Scholar] [CrossRef] [PubMed]
- Candès, E.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Donoho, D. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Lopes, M.E. Unknown Sparsity in Compressed Sensing: Denoising and Inference. IEEE Trans. Inf. Theory 2016, 62, 5145–5166. [Google Scholar] [CrossRef]
- Baraldi, R.; Kumar, R.; Aravkin, A. Basis Pursuit Denoise with Nonsmooth Constraints. IEEE Trans. Signal Process. 2019, 67, 5811–5823. [Google Scholar] [CrossRef]
- Mitra, D.; Zand, H.; Rajan, S. Investigation of Kronecker-based Recovery of Compressed ECG Signal. IEEE Trans. Instrum. Meas. 2020, 69, 3642–3653. [Google Scholar] [CrossRef]
- Christian, K.; Wolfgang, E.; Mandy, A.; Patryk, S.; Tobias, K.; Buzug, T.M. Non-Equispaced System Matrix Acquisition for Magnetic Particle Imaging Based on Lissajous Node Points. IEEE Trans. Med. Imaging 2016, 35, 2476–2485. [Google Scholar]
- Zayyani, H.; Korki, M.; Marvasti, F. Dictionary Learning for Blind One Bit Compressed Sensing. IEEE Signal Process. Lett. 2015, 23. [Google Scholar] [CrossRef]
- Van den Berg, E.; Friedlander, M.P. Probing the pareto frontier for basis pursuit solutions. SIAM J. Sci. Comput. 2008, 31, 890–912. [Google Scholar] [CrossRef]
- Chen, S.S.; Donoho, D.L.; Saunders, M.A. Atomic decomposition by basis pursuit. SIAM Rev. 2001, 43, 129–159. [Google Scholar] [CrossRef]
- Lorenz, D.A. Constructing Test Instances for Basis Pursuit Denoising. IEEE Trans. Signal Process. 2012, 61, 1210–1214. [Google Scholar] [CrossRef]
- Mota, J.F.C.; Xavier, J.M.F.; Aguiar, P.M.Q.; Puschel, M. Distributed Basis Pursuit. IEEE Trans. Signal Process. 2012, 60, 1942–1956. [Google Scholar] [CrossRef]
- Wang, Y.; Yin, W.; Zeng, J. Global convergence of ADMM in nonconvex nonsmooth optimization. J. Sci. Comput. 2019, 78, 29–63. [Google Scholar] [CrossRef]
- Zhang, X.; Khalili, M.M.; Liu, M. Recycled ADMM: Improve privacy and accuracy with less computation in distributed algorithms. In Proceedings of the 2018 56th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 2–5 October 2018; pp. 959–965. [Google Scholar]
- Liu, Q.; Shen, X.; Gu, Y. Linearized ADMM for Nonconvex Nonsmooth Optimization with Convergence Analysis. IEEE Access 2019, 7, 76131–76144. [Google Scholar] [CrossRef]
- Nedic, A.; Ozdaglar, A. Distributed subgradient methods for multiagent optimization. IEEE Trans. Autom. Control 2009, 54, 48–61. [Google Scholar] [CrossRef]
- Shi, W.; Ling, Q.; Yuan, K.; Wu, G.; Yin, W. On the linear convergence of the ADMM in decentralized consensus optimization. IEEE Trans. Signal Process. 2014, 62, 1750–1761. [Google Scholar] [CrossRef]
- Bras, N.B. An Alternating Direction Algorithm for Total Variation Reconstruction of Distributed Parameters. IEEE Trans. Image Process. 2012, 21, 3004–3016. [Google Scholar] [CrossRef]
- Wang, L.; Wu, W.; Chen, Y.; Liu, C. An ADMM-net solution to inverse problem of electrocardiology. In Proceedings of the 2018 5th International Conference on Systems and Informatics (ICSAI), Nanjing, China, 10–12 November 2018. [Google Scholar]
- Nguyen, H.Q.; Bostan, E.; Unser, M. Learning Convex Regularizers for Optimal Bayesian Denoising. IEEE Trans. Signal Process. 2018, 66, 1093–1105. [Google Scholar] [CrossRef]
- Chan, S.H. Performance Analysis of Plug-and-Play ADMM: A Graph Signal Processing Perspective. IEEE Trans. Comput. Imaging 2018, 5, 274–286. [Google Scholar] [CrossRef]
- Aviyente, S. Compressed sensing framework for eeg compression. In Proceedings of the 14th IEEE Workshop on SSP, Madison, WI, USA, 26–29 August 2007; pp. 181–184. [Google Scholar]
- Van den Berg, E.; Friedlander, M.P. Sparse optimization with least- squares constraints. SIAM J. Optim. 2011, 21, 1201–1229. [Google Scholar] [CrossRef]
- Selesnick, W.; Chen, P.-Y. Group-sparse signal denoising: Non-convex regularization, convex optimization. IEEE Trans. Signal Process. 2014, 62, 3464–3478. [Google Scholar]
- Yang, J.; Zhang, Y. Alternating direction algorithms for L1-problems in compressive sensing. SIAM J. Sci. Comput. 2011, 33, 250–278. [Google Scholar] [CrossRef]
- Shen, C.; Chang, T.H.; Wang, K.Y.; Qiu, Z.; Chi, C.Y. Distributed robust multi-cell coordinated beamforming with imperfect CSI: An ADMM approach. IEEE Trans. Signal Process. 2011, 60, 2988–3003. [Google Scholar] [CrossRef]
- Almeida, M.S.; Figueiredo, M. Deconvolving images with unknown boundaries using the alternating direction method of multipliers. IEEE Trans. Image Process. 2013, 22, 3074–3086. [Google Scholar] [CrossRef] [PubMed]
- Liavas, A.P.; Sidiropoulos, N.D. Parallel algorithms for constrained tensor factorization via alternating direction method of multipliers. IEEE Trans. Signal Process. 2014, 63, 5450–5463. [Google Scholar] [CrossRef]
- Zhong, F.; Zhang, J.; Li, D. Discriminant Locality Preserving Projections Based on L1-Norm Maximization. IEEE Trans. Neural Netw. Learn. Syst. 2017, 25, 2065–2074. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Jung, T.P.; Makeig, S.; Rao, B.D. Compressed sensing for energy-efficient wireless telemonitoring of noninvasive fetal ECG via block sparse Bayesian learning. IEEE Trans Biomed Eng. 2012, 60, 300–309. [Google Scholar] [CrossRef]
- Wang, D.; Li, L.; Ji, Y.; Yan, Y. Model recovery for Hammerstein systems using the auxiliary model based orthogonal matching pursuit method. Appl. Math. Model. 2018, 54, 537–550. [Google Scholar] [CrossRef]
- Toth, R.; Sanandaji, B.M.; Poolla, K.; Vincent, T.L. Compressive system identification in the linear time-invariant framework. In Proceedings of the IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; pp. 783–790. [Google Scholar]
- You, J.; Liu, Y. Iterative identification for multivariable systems with time-delays based on basis pursuit de-noising and auxiliary model. Algorithms 2018, 11, 180. [Google Scholar] [CrossRef]
- Marcos, R.J.; Paredes, J.L. Robust transforms based on the weighted median operator. IEEE Signal Process. Lett. 2014, 22, 120–124. [Google Scholar]
- Shmaliy, Y.S. An unbiased FIR filter for TIE model of a local clock in applications to GPS-based timekeeping. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2006, 53, 862–869. [Google Scholar] [CrossRef] [PubMed]
- Jin, Z.; Dong, A.; Shu, M.; Wang, Y. Sparse ECG Denoising with Generalized Minimax Concave Penalty. Sensors 2019, 19, 1718. [Google Scholar] [CrossRef]
- Feng, C.; Xu, H.; Li, B. An alternating direction method approach to cloud traffic management. IEEE Trans. Parallel Distrib. Syst. 2017, 28, 2145–2158. [Google Scholar] [CrossRef]
- Moody, W.E.M.G.B.; Mark, R.G. A noise stress test for arrhythmia detectors. Comput. Cardiol. 1984, 11, 381–384. [Google Scholar]
- Zhan, C.; Yeung, L.F.; Yang, Z. A wavelet-based adaptive filter for removing ECG interference in EMGdi signals. J. Electromyogr. Kinesiol. 2010, 20, 542–549. [Google Scholar] [CrossRef]





| MIT-BIH No. | 100 | 103 | 213 | ||
|---|---|---|---|---|---|
| BP-ADMM | 5 dB | SNR | 14.71 | 14.86 | 13.92 |
| MSE | 0.003 | 0.004 | 0.024 | ||
| 15 dB | SNR | 15.13 | 16.02 | 14.37 | |
| MSE | 0.002 | 0.002 | 0.003 | ||
| Wavelet | 5 dB | SNR | 5.3124 | 4.85 | 7.49 |
| MSE | 0.0248 | 0.086 | 0.127 | ||
| 15 dB | SNR | 9.7863 | 5.14 | 8.22 | |
| MSE | 0.1002 | 0.082 | 0.107 | ||
| Average | 5 dB | SNR | 2.3397 | 2.3837 | 3.0389 |
| MSE | 0.5093 | 0.5177 | 1.1896 | ||
| 15 dB | SNR | 3.2910 | 3.3011 | 3.4347 | |
| MSE | 0.2667 | 0.3071 | 0.9611 | ||
| TV | 5 dB | SNR | 4.6338 | 4.8580 | 9.2792 |
| MSE | 0.3025 | 0.3064 | 0.2838 | ||
| 15 dB | SNR | 10.7101 | 11.2702 | 12.7509 | |
| MSE | 0.0481 | 0.0483 | 0.0706 |
| Wavelet | Average | TV | BP-ADMM | |
|---|---|---|---|---|
| mitdb/105 | 5.476 | 2.4294 | 4.9172 | 6.3297 |
| mitdb/106 | 5.5671 | 2.433 | 5.4115 | 5.8936 |
| mitdb/107 | 11.3446 | 3.2118 | 11.6603 | 11.6715 |
| mitdb/108 | 4.4446 | 2.2665 | 4.2473 | 4.8901 |
| mitdb/109 | 7.798 | 2.8677 | 7.6668 | 8.1662 |
| mitdb/111 | 3.0188 | 1.8348 | 2.7679 | 3.6756 |
| mitdb/112 | 11.7158 | 3.2256 | 11.432 | 12.0141 |
| mitdb/113 | 6.647 | 2.7342 | 6.4469 | 6.7013 |
| mitdb/114 | 2.9079 | 1.739 | 2.5118 | 3.5163 |
| mitdb/115 | 7.785 | 2.8554 | 7.5518 | 7.9067 |
| mitdb/116 | 13.2353 | 3.3241 | 13.0733 | 13.6521 |
| mitdb/117 | 11.2684 | 3.1911 | 10.6218 | 11.8165 |
| mitdb/118 | 12.1504 | 3.2713 | 11.8001 | 13.1671 |
| mitdb/119 | 12.4043 | 3.2694 | 11.8452 | 12.9172 |
| mitdb/200 | 6.3196 | 2.6159 | 6.0043 | 6.7027 |
| mitdb/201 | 3.6453 | 1.9371 | 3.2885 | 4.0273 |
| mitdb/202 | 2.9598 | 1.7462 | 2.4286 | 3.7509 |
| mitdb/203 | 6.0959 | 2.6427 | 5.8747 | 6.9253 |
| mitdb/205 | 5.8739 | 2.4731 | 5.322 | 6.0851 |
| mitdb/207 | 5.0551 | 2.405 | 4.8458 | 5.6361 |
| mitdb/208 | 7.4163 | 2.821 | 7.4943 | 8.1552 |
| mitdb/209 | 3.6206 | 1.9473 | 3.2982 | 4.7622 |
| mitdb/210 | 3.5107 | 2.0053 | 3.2245 | 4.1386 |
| mitdb/212 | 4.753 | 2.2869 | 4.5983 | 5.126 |
| mitdb/231 | 3.9913 | 2.0872 | 3.6602 | 4.5625 |
| mitdb/232 | 3.0207 | 1.7841 | 2.2933 | 3.6549 |
| mitdb/233 | 8.7804 | 2.9848 | 8.5975 | 9.2172 |
| mitdb/234 | 4.0129 | 2.1281 | 3.6201 | 4.5516 |
| Mean SNR | 6.6006 | 2.5185 | 6.3037 | 7.129 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, R.; Shu, M.; Chen, C. ECG Signal Denoising and Reconstruction Based on Basis Pursuit. Appl. Sci. 2021, 11, 1591. https://doi.org/10.3390/app11041591
Liu R, Shu M, Chen C. ECG Signal Denoising and Reconstruction Based on Basis Pursuit. Applied Sciences. 2021; 11(4):1591. https://doi.org/10.3390/app11041591
Chicago/Turabian StyleLiu, Ruixia, Minglei Shu, and Changfang Chen. 2021. "ECG Signal Denoising and Reconstruction Based on Basis Pursuit" Applied Sciences 11, no. 4: 1591. https://doi.org/10.3390/app11041591
APA StyleLiu, R., Shu, M., & Chen, C. (2021). ECG Signal Denoising and Reconstruction Based on Basis Pursuit. Applied Sciences, 11(4), 1591. https://doi.org/10.3390/app11041591







