Cyber Attack Detection Scheme for a Load Frequency Control System Based on Dual-Source Data of Compromised Variables
Abstract
1. Introduction
2. Modeling of Compromised LFC System and False Data Injection Attacks
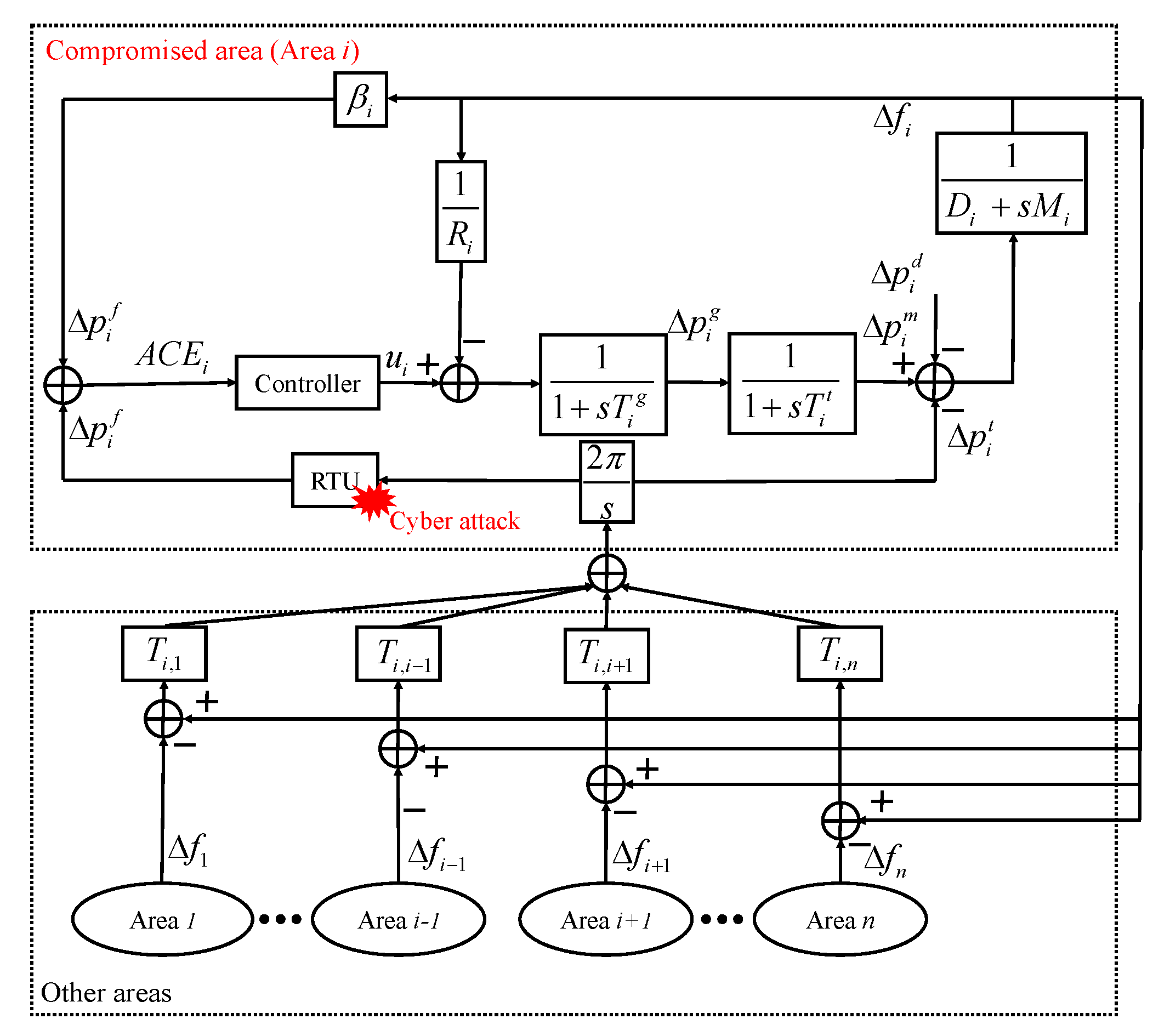
2.1. Basics of a Compromised LFC System
2.2. Attack Templates of FDI Attacks on LFC
- Exogenous attack:where represents the value of the data injection added to the measurements of tie-line power.
- Scaling attack:where is the scaling attack parameter.
3. Design of an Observer for Detecting Tie-Line Power Considering Uncertainties
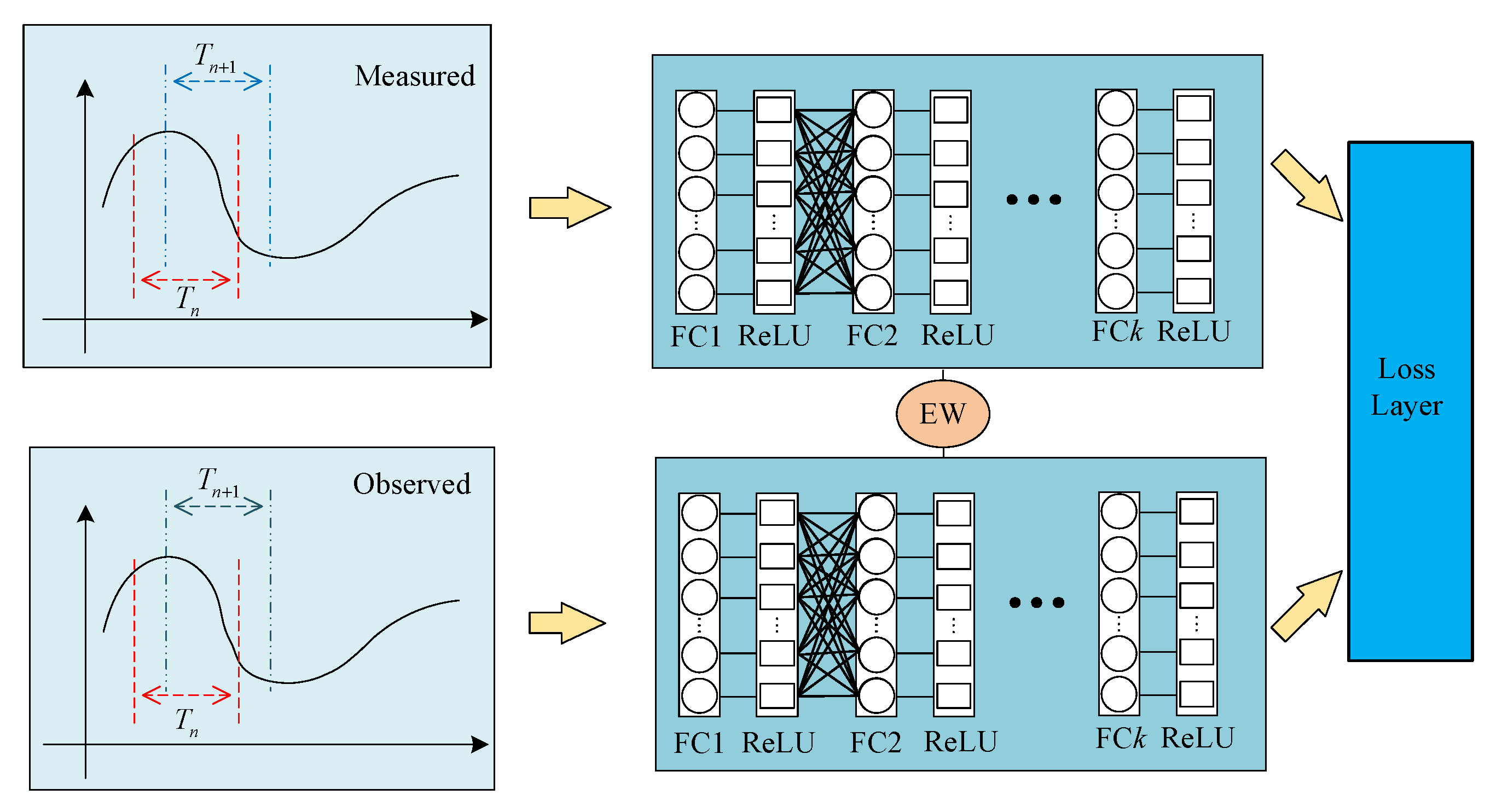
4. Siamese-Network-Based Attack Detection for FDI Attacks on LFC
4.1. Network Structure
4.2. Cluster-Based Loss Function
4.3. Attack Detection Scheme for FDI Attacks on LFC
- Step 2: Transfer the training data in the form of data pairs to the Siamese network for training.
- Step 3: Using the high dimensional features obtained by FC layers to calculate the similarity between observed data and measured data. Loss function is used to make positive pairs compact and negative pairs far away from the positive pairs.
- Step 4: Sample the incoming data pair, which could be compromised potentially or normal load disturbance. By checking the high dimensional features of the data pairs, the status of the RTU for tie-line power can be identified.
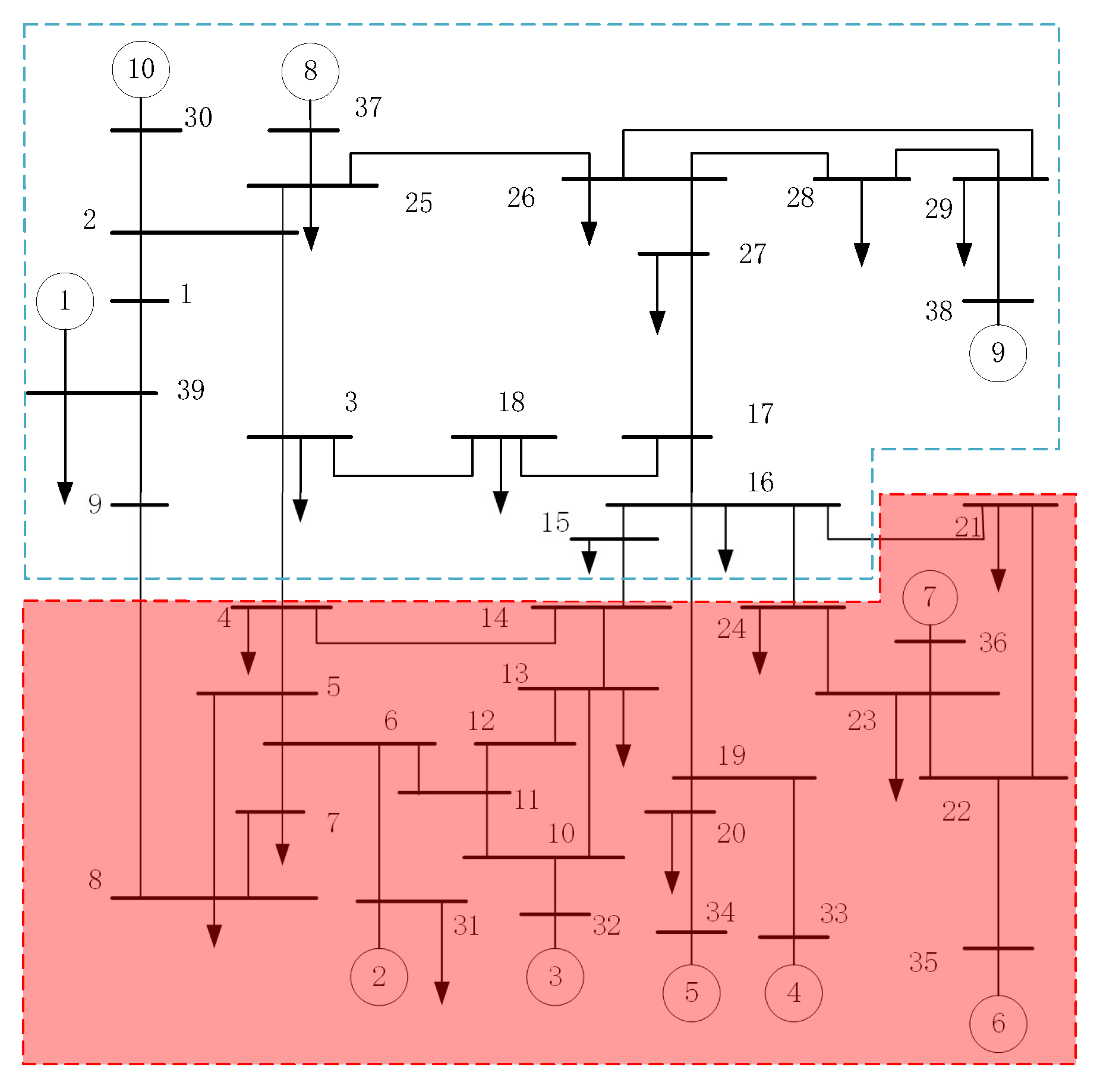
5. Simulations and Analysis
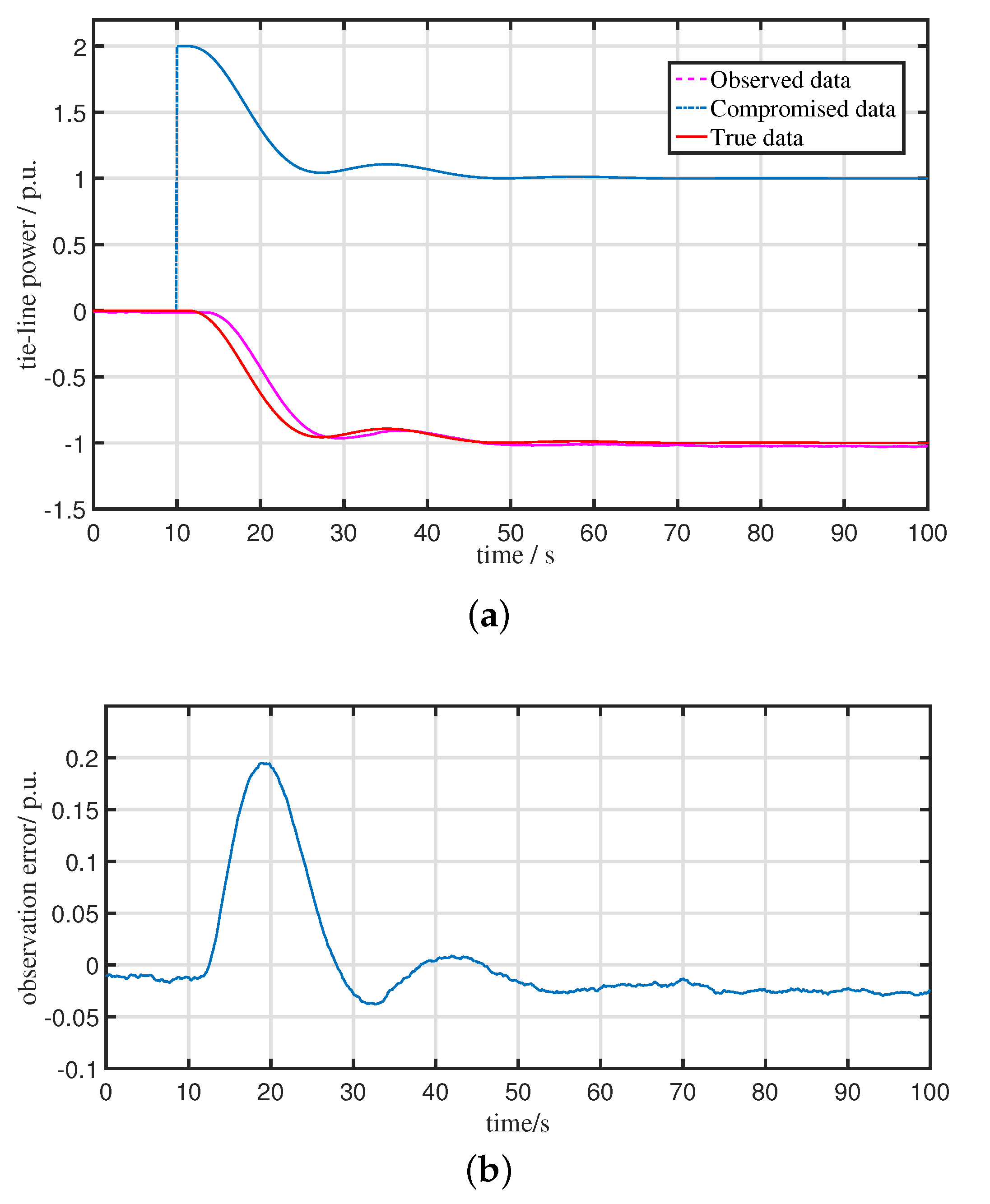
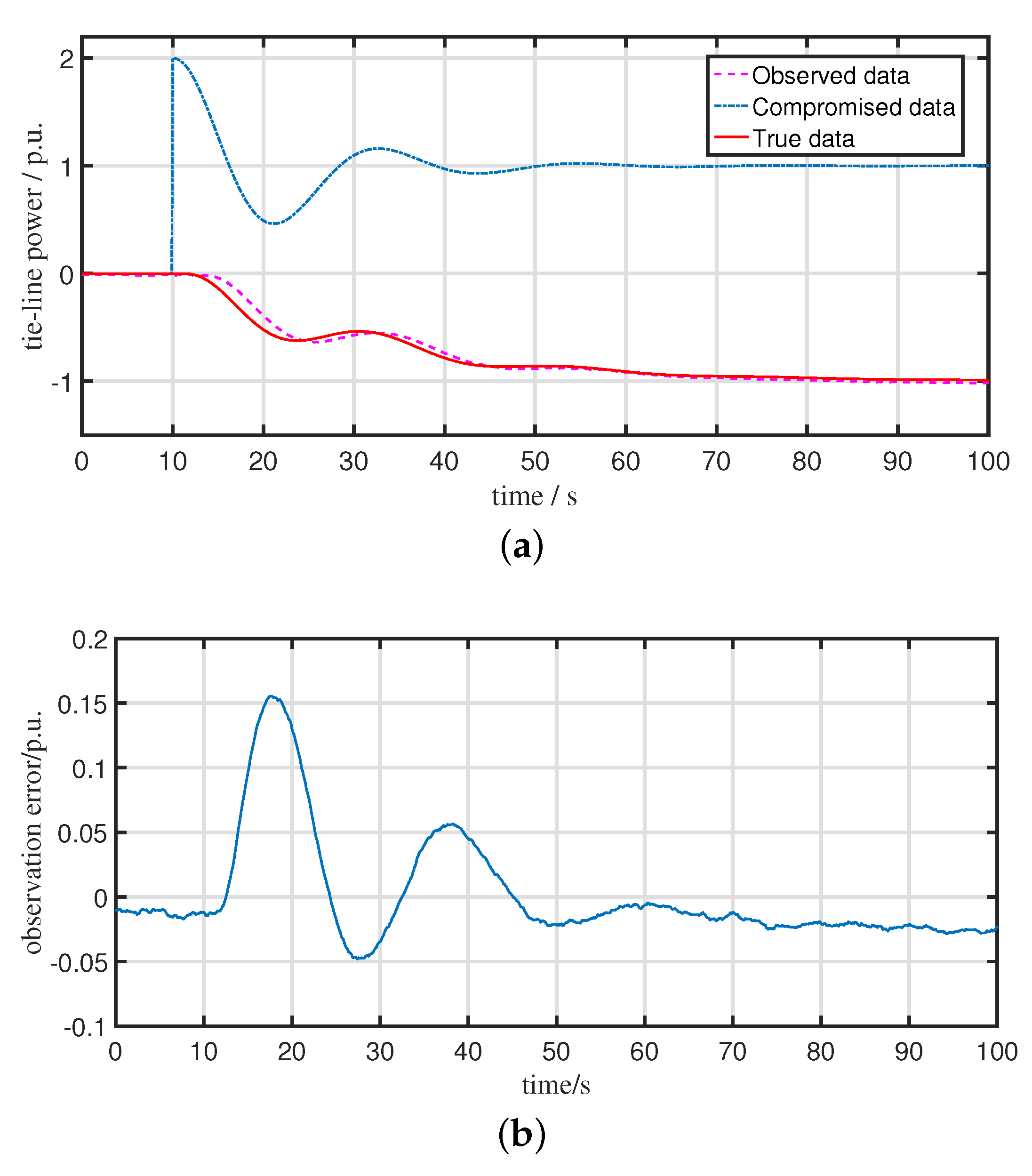
5.1. Performance of the Observer for the Compromised LFC System
5.2. Performance of the Proposed Attack Detection Scheme
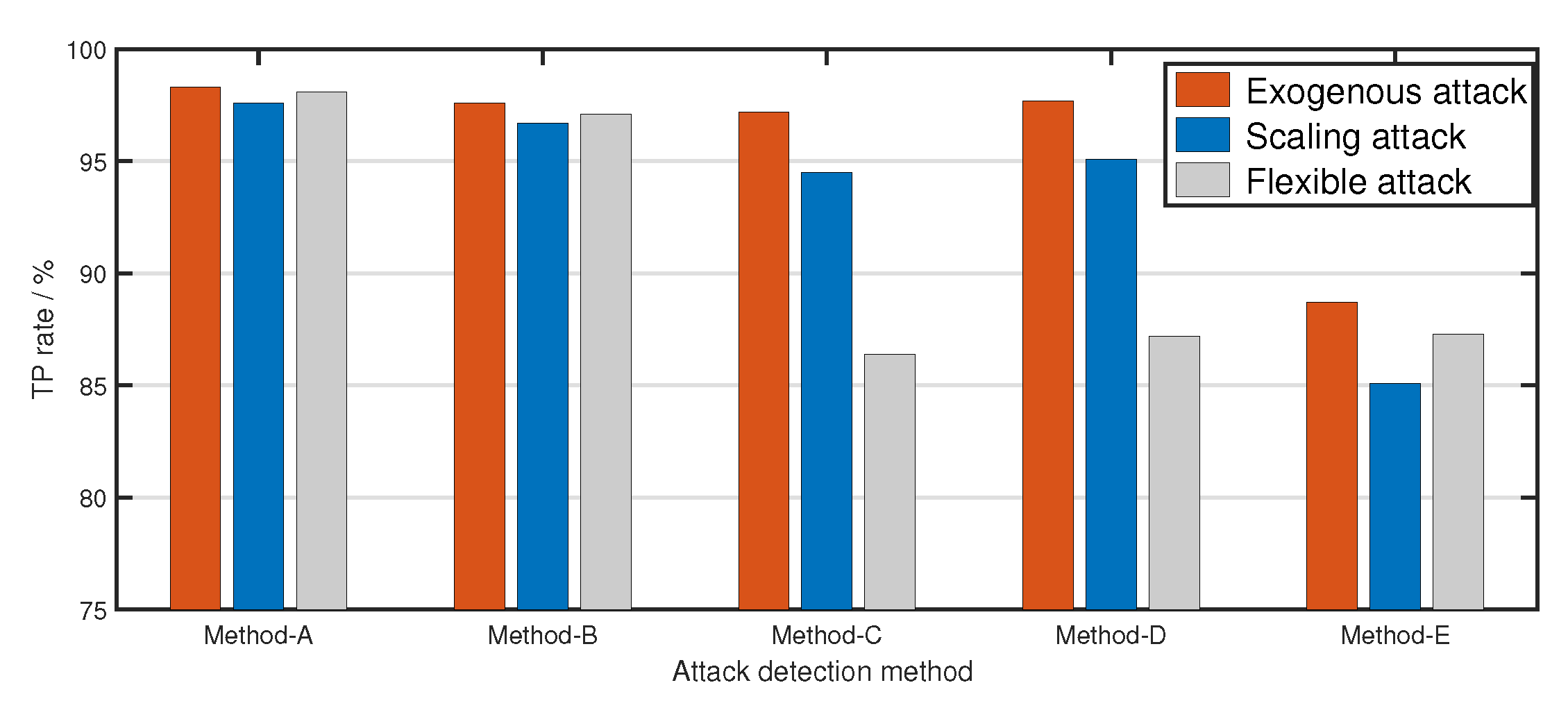
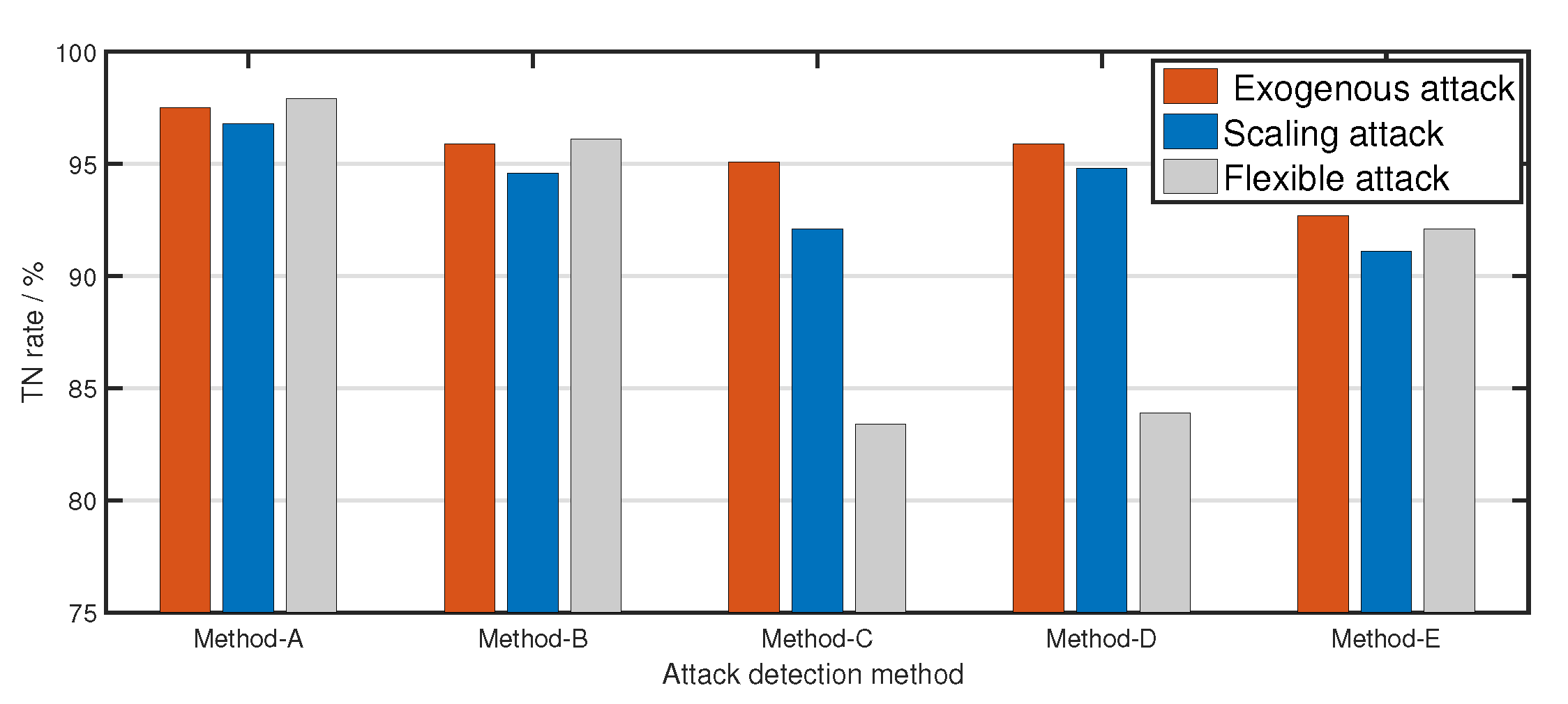
5.3. Reliability of the Proposed Attack Detection Scheme
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Peng, C.; Sun, H.; Yang, M.; Wang, Y.L. A survey on security communication and control for smart grids under malicious cyber attacks. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 1554–1569. [Google Scholar] [CrossRef]
- Deng, R.L.; Zhuang, P.; Liang, H. CCPA: Coordinated Cyber-Physical Attacks and Countermeasures in Smart Grid. IEEE Trans. Smart Grid 2017, 8, 2420–2430. [Google Scholar] [CrossRef]
- Peng, C.; Li, J.; Fei, M. Resilient Event-Triggering H_infinity Load Frequency Control for Multi-Area Power Systems With Energy-Limited DoS Attacks. IEEE Trans. Power Syst. 2016, 32, 4110–4118. [Google Scholar] [CrossRef]
- Liu, Y.; Ning, P.; Reiter, M.K. False data injection attacks against state estimation in electric power grids. ACM Trans. Inf. Syst. Secur. (TISSEC) 2011, 14, 1–33. [Google Scholar] [CrossRef]
- Huang, Y.; Esmalifalak, M.; Nguyen, H.; Zheng, R.; Han, Z.; Li, H.; Song, L. Bad data injection in smart grid: Attack and defense mechanisms. IEEE Commun. Mag. 2013, 51, 27–33. [Google Scholar] [CrossRef]
- Hong, J.; Nuqui, R.F.; Kondabathini, A.; Ishchenko, D.; Martin, A. Cyber attack resilient distance protection and circuit breaker control for digital substations. IEEE Trans. Ind. Inform. 2018, 15, 4332–4341. [Google Scholar] [CrossRef]
- Teixeira, A.; Dán, G.; Sandberg, H.; Johansson, K.H. A cyber security study of a SCADA energy management system: Stealthy deception attacks on the state estimator. IFAC Proc. Vol. 2011, 44, 11271–11277. [Google Scholar] [CrossRef]
- Taha, A.F.; Qi, J.; Wang, J.; Panchal, J.H. Risk mitigation for dynamic state estimation against cyber attacks and unknown inputs. IEEE Trans. Smart Grid 2016, 9, 886–899. [Google Scholar] [CrossRef]
- Luo, X.; Wang, X.; Pan, X.; Guan, X. Detection and isolation of false data injection attack for smart grids via unknown input observers. IET Gener. Transm. Distrib. 2019, 13, 1277–1286. [Google Scholar] [CrossRef]
- Befekadu, G.K.; Gupta, V.; Antsaklis, P.J. Risk-sensitive control under Markov modulated denial-of-service (DoS) attack strategies. IEEE Trans. Autom. Control 2015, 60, 3299–3304. [Google Scholar] [CrossRef]
- Zhang, H.; Cheng, P.; Shi, L.; Chen, J. Optimal denial-of-service attack scheduling with energy constraint. IEEE Trans. Autom. Control 2015, 60, 3023–3028. [Google Scholar] [CrossRef]
- De Persis, C.; Tesi, P. Input-to-state stabilizing control under denial-of-service. IEEE Trans. Autom. Control 2015, 60, 2930–2944. [Google Scholar] [CrossRef]
- Peng, C.; Yang, T.C. Event-triggered communication and H-infinity control co-design for networked control systems. Automatica 2013, 49, 1326–1332. [Google Scholar] [CrossRef]
- Peng, C.; Han, Q.L. On designing a novel self-triggered sampling scheme for networked control systems with data losses and communication delays. IEEE Trans. Ind. Electron. 2015, 63, 1239–1248. [Google Scholar] [CrossRef]
- Sridhar, S.; Govindarasu, M. Model-based attack detection and mitigation for automatic generation control. IEEE Trans. Smart Grid 2014, 5, 580–591. [Google Scholar] [CrossRef]
- Tan, R.; Nguyen, H.H.; Foo, E.Y.; Dong, X.; Yau, D.K.; Kalbarczyk, Z.; Iyer, R.K.; Gooi, H.B. Optimal false data injection attack against automatic generation control in power grids. In Proceedings of the 2016 ACM/IEEE 7th International Conference on Cyber-Physical Systems (ICCPS), Vienna, Austria, 11–14 April 2016; pp. 1–10. [Google Scholar]
- Chen, C.; Zhang, K.; Yuan, K.; Zhu, L.; Qian, M. Novel detection scheme design considering cyber attacks on load frequency control. IEEE Trans. Ind. Inform. 2017, 14, 1932–1941. [Google Scholar] [CrossRef]
- Bi, W.; Chen, C.; Zhang, K. Optimal Strategy of Attack-Defense Interaction Over Load Frequency Control Considering Incomplete Information. IEEE Access 2019, 7, 75342–75349. [Google Scholar] [CrossRef]
- Cheng, Z.; Yue, D.; Hu, S.; Huang, C.; Dou, C.; Chen, L. Resilient load frequency control design: DoS attacks against additional control loop. Int. J. Electr. Power Energy Syst. 2020, 115, 105496. [Google Scholar] [CrossRef]
- Hou, Y.; Zhu, F.; Zhao, X.; Guo, S. Observer design and unknown input reconstruction for a class of switched descriptor systems. IEEE Trans. Syst. Man Cybern. Syst. 2017, 48, 1411–1419. [Google Scholar] [CrossRef]
- Luo, X.; Wang, X.; Zhang, M.; Guan, X. Distributed detection and isolation of bias injection attack in smart energy grid via interval observer. Appl. Energy 2019, 256, 113703. [Google Scholar] [CrossRef]
- Niu, H.; Bhowmick, C.; Jagannathan, S. Attack detection and approximation in nonlinear networked control systems using neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 235–245. [Google Scholar] [CrossRef]
- Liao, K.; Xu, Y. A robust load frequency control scheme for power systems based on second-order sliding mode and extended disturbance observer. IEEE Trans. Ind. Inform. 2017, 14, 3076–3086. [Google Scholar] [CrossRef]
- Su, X.; Liu, X.; Song, Y.D. Fault-tolerant control of multiarea power systems via a sliding-mode observer technique. IEEE/ASME Trans. Mechatronics 2017, 23, 38–47. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, K.; Yuan, K.; Gao, Z.; Teng, X.; Ding, Q. Disturbance rejection-based LFC for multi-area parallel interconnected AC/DC system. IET Gener. Transm. Distrib. 2016, 10, 4105–4117. [Google Scholar] [CrossRef]
- Chen, J.; Patton, R.J.; Zhang, H.Y. Design of unknown input observers and robust fault detection filters. Int. J. Control 1996, 63, 85–105. [Google Scholar] [CrossRef]
- Canizares, C.; Fernandes, T.; Geraldi, E.; Gerin-Lajoie, L.; Gibbard, M.; Hiskens, I.; Kersulis, J.; Kuiava, R.; Lima, L.; DeMarco, F.; et al. Benchmark Models for the Analysis and Control of Small-Signal Oscillatory Dynamics in Power Systems. IEEE Trans. Power Syst. 2017, 32, 715–722. [Google Scholar] [CrossRef]
- Athay, T.; Podmore, R.; Virmani, S. A Practical Method for the Direct Analysis of Transient Stability. IEEE Trans. Power Appar. Syst. 1979, PAS-98, 573–584. [Google Scholar] [CrossRef]
- Qu, F.; Liu, J.; Liu, X.; Jiang, L. A Multi-Fault Detection Method with Improved Triplet Loss Based on Hard Sample Mining. IEEE Trans. Sustain. Energy 2021, 12, 127–137. [Google Scholar] [CrossRef]
- Zheng, H.; Hou, M.; Wang, Y. An efficient hybrid clustering-PSO algorithm for anomaly intrusion detection. J. Softw. 2011, 6, 2350–2360. [Google Scholar] [CrossRef]

| Exogenous attack | 9.3 dB | 10.9 dB | 13.1 dB |
| Scaling attack | 9.5 dB | 11.2 dB | 13.1 dB |
| Flexible attack | 9.8 dB | 11.2 dB | 13.1 dB |
| Exogenous attack | 6.7 s | 5.1 s | 3.2 s |
| Scaling attack | 7.0 s | 4.9 s | 3.2 s |
| Flexible attack | 6.9 s | 5.0 s | 3.1 s |
| Exogenous attack | 45 | 55 | 70 |
| Scaling attack | 45 | 55 | 70 |
| Flexible attack | 60 | 65 | 75 |
| Exogenous attack | 0.6 | 0.8 | 0.9 |
| Scaling attack | 0.6 | 0.8 | 0.9 |
| Flexible attack | 0.6 | 0.8 | 0.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bi, W.; Zhang, K.; Chen, C. Cyber Attack Detection Scheme for a Load Frequency Control System Based on Dual-Source Data of Compromised Variables. Appl. Sci. 2021, 11, 1584. https://doi.org/10.3390/app11041584
Bi W, Zhang K, Chen C. Cyber Attack Detection Scheme for a Load Frequency Control System Based on Dual-Source Data of Compromised Variables. Applied Sciences. 2021; 11(4):1584. https://doi.org/10.3390/app11041584
Chicago/Turabian StyleBi, Wenjun, Kaifeng Zhang, and Chunyu Chen. 2021. "Cyber Attack Detection Scheme for a Load Frequency Control System Based on Dual-Source Data of Compromised Variables" Applied Sciences 11, no. 4: 1584. https://doi.org/10.3390/app11041584
APA StyleBi, W., Zhang, K., & Chen, C. (2021). Cyber Attack Detection Scheme for a Load Frequency Control System Based on Dual-Source Data of Compromised Variables. Applied Sciences, 11(4), 1584. https://doi.org/10.3390/app11041584







