A Guideline for Implementing a Robust Optimization of a Complex Multi-Stage Manufacturing Process
Abstract
Featured Application
Abstract
1. Introduction
2. Materials
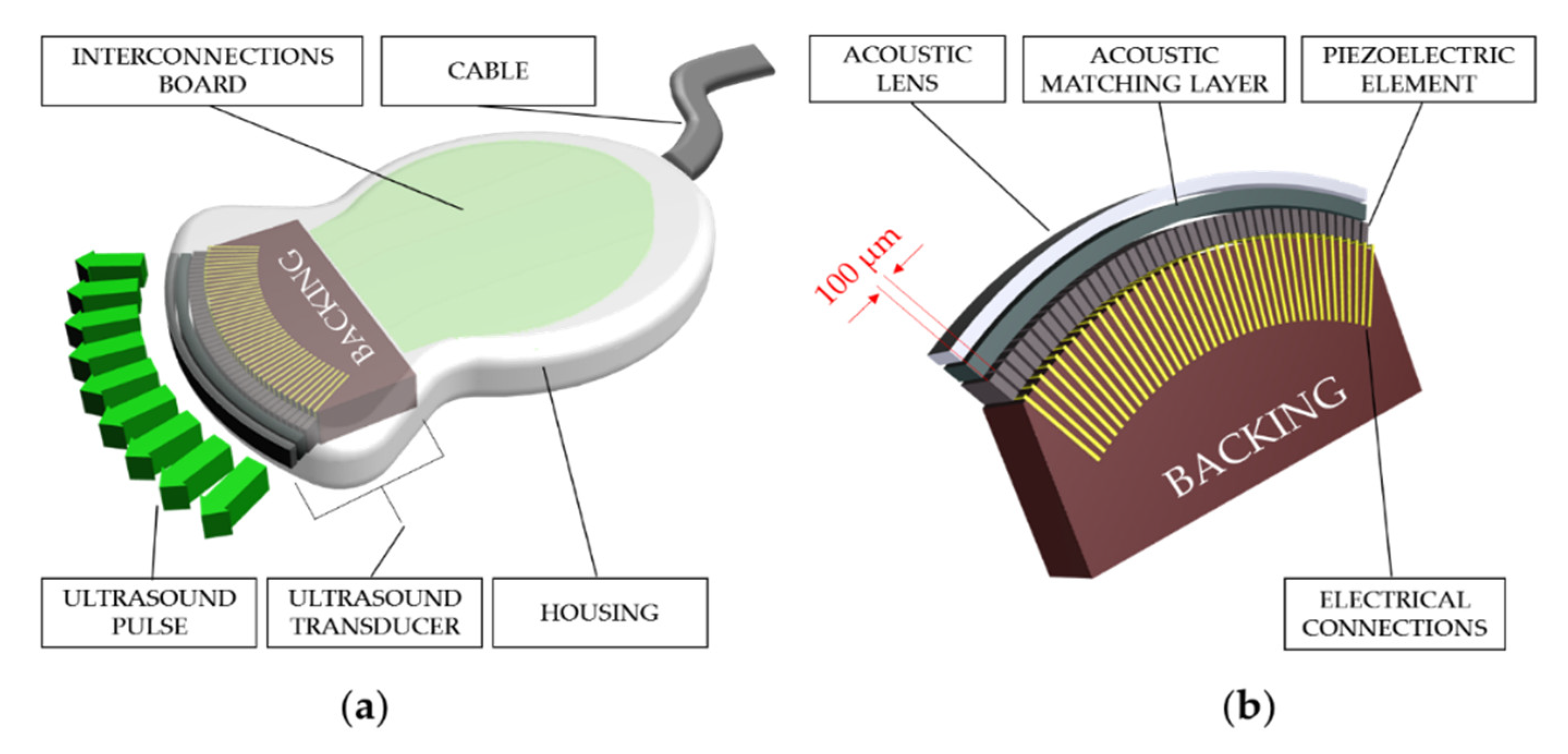
2.1. Ultrasound Probe for Medical Imaging
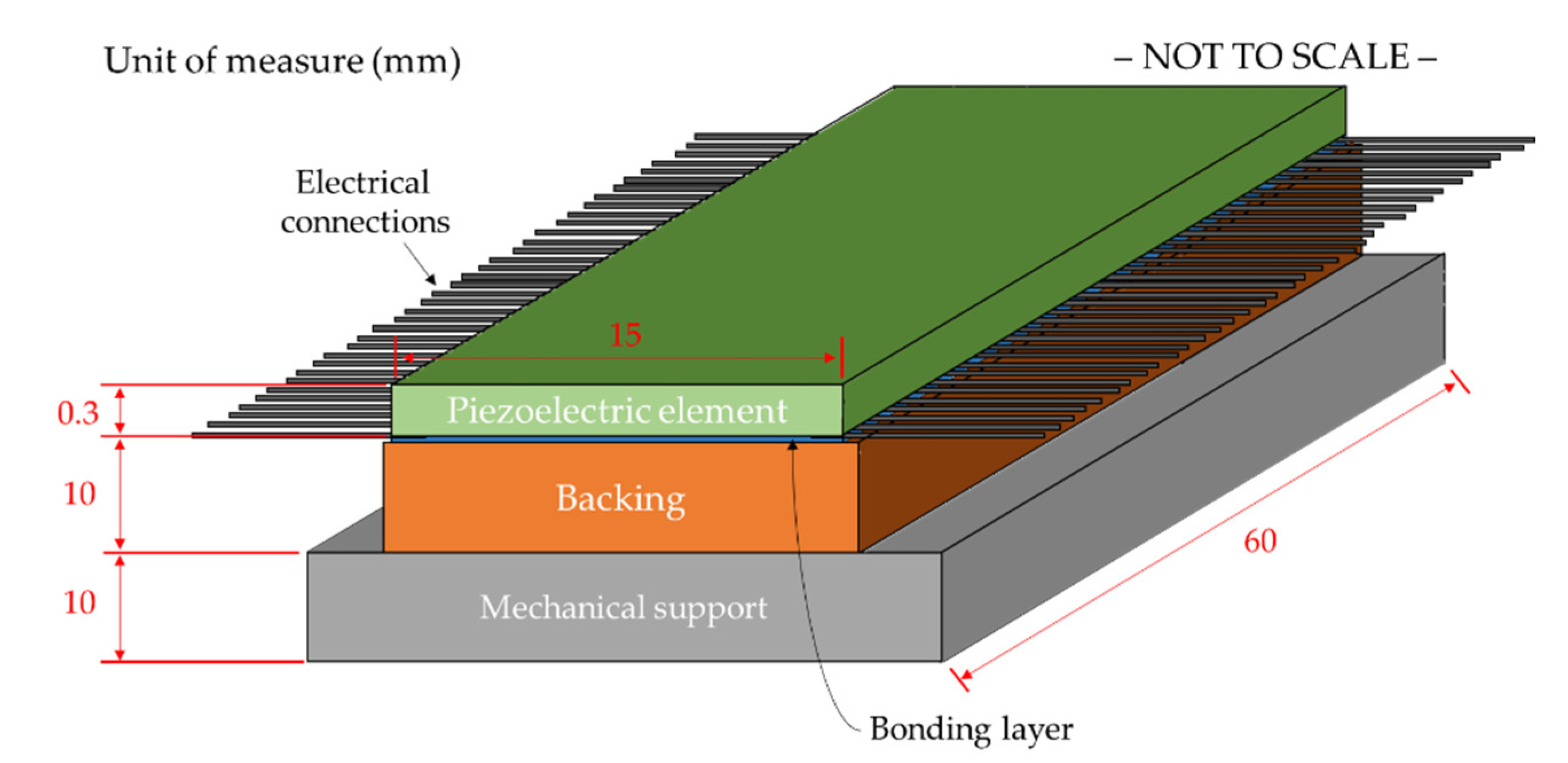
2.2. The Manufacturing Process
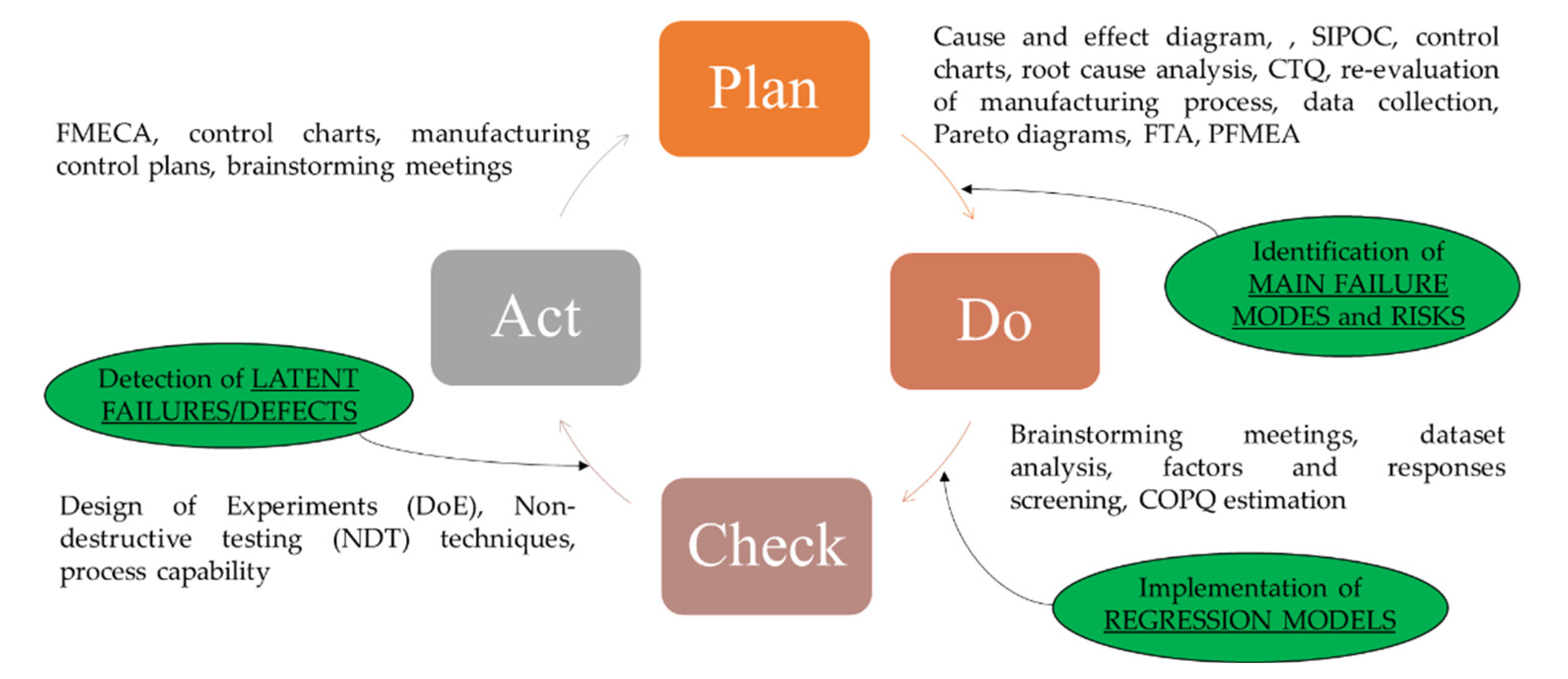
3. The Methodology for Continuous Improvement: Robust Process Optimization
3.1. The PDCA Cycle Implementation
3.2. The Statistical Modeling
The Logit Model
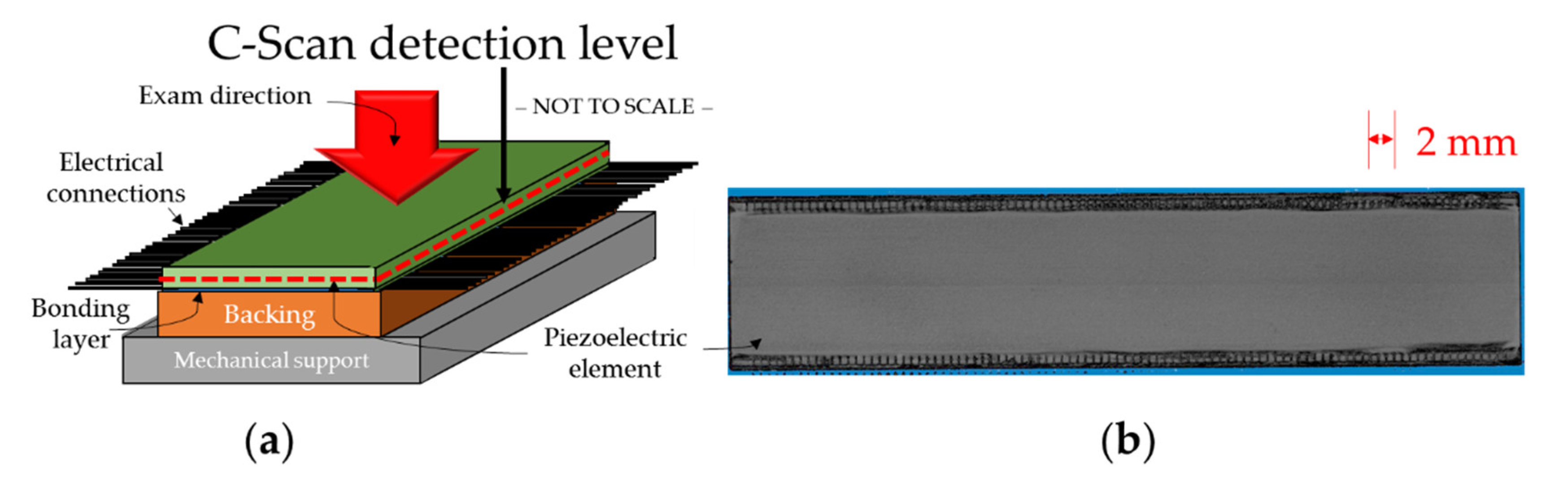
3.3. The Scanning Acoustic Microscopy (SAM) Inspection
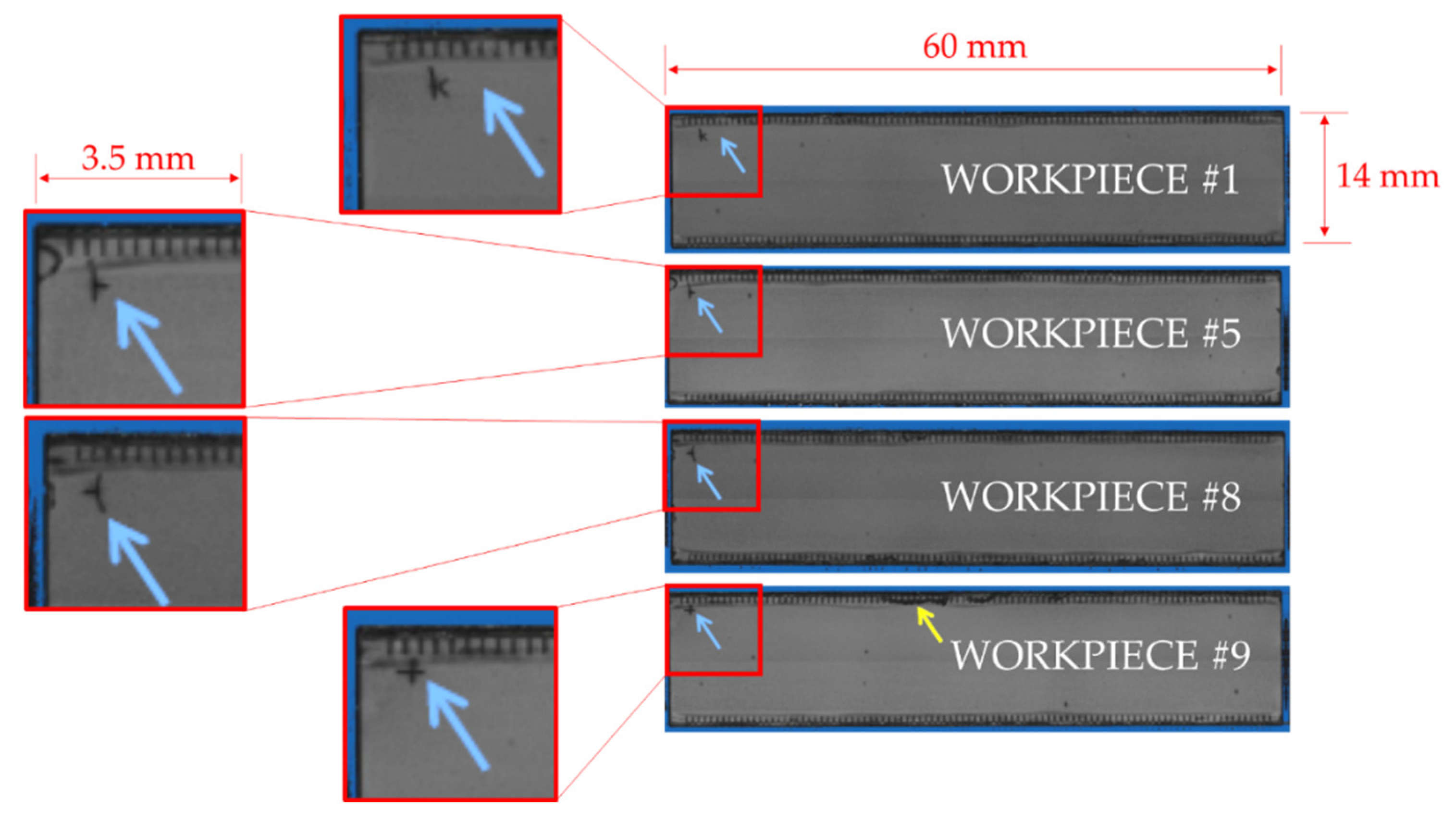
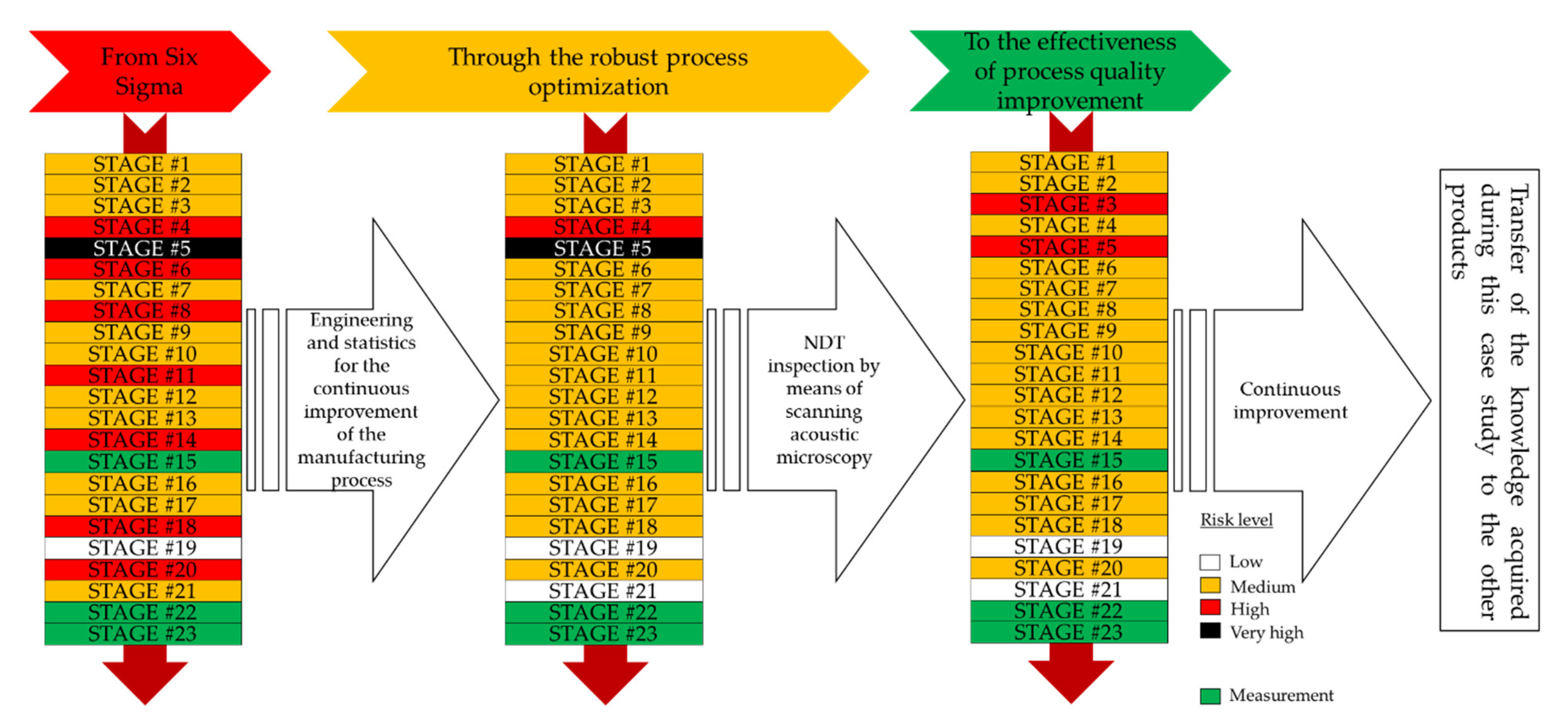
4. Statistical Modeling and Non-Destructive Testing Results
j = 1,2,3; l = 1,2,3,4; s = 1,2; t = 1,2,3,4,5;
j = 1,2,3; l = 1,2,3,4; t = 1,2,3,4,5;
5. Discussion
- The re-examination of each ultrasound probe manufacturing phase under strong critical point of view;
- Need to add electrical and mechanical in-process measurements (several factors, several responses);
- The identification and the analysis of factors, never evaluated by engineering, that can influence the variability of the production process;
- The management and the analysis by considering 36 difference factors and 38 response variables (both qualitative and quantitative); and
- The distinction between systematic, noise, and block effects for defining and planning the design of experiment [70].
- Significant effects of the process factors;
- The operators involved in the manufacturing play a key role in the variability of the production process;
- The need to implement a DoE (design of experiments) in the early stages of the production process for a better screening of the principal critical factors.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Baud-Lavigne, B.; Bassetto, S.; Agard, B. A method for a robust optimization of joint product and supply chain design. J. Intell. Manuf. 2014, 27, 741–749. [Google Scholar] [CrossRef]
- Antuñano, M.A.Z.; Cruz-Salinas, J.; Rodríguez-Reséndiz, J.; González-Gutiérrez, C.A.; Lozano, N.E.M.; Paredes-García, W.J.; Altamirano-Corro, J.A.; Gaytán-Díaz, J.A. Statistical Analysis and Data Envelopment Analysis to Improve the Efficiency of Manufacturing Process of Electrical Conductors. Appl. Sci. 2019, 9, 3965. [Google Scholar] [CrossRef]
- Kahng, S.-J.; Kim, J.-H.; Chung, J.-H. Nanostructured Tip-Shaped Biosensors: Application of Six Sigma Approach for Enhanced Manufacturing. Sensors 2016, 17, 17. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.-N.; Chiu, P.-C.; Cheng, I.-F.; Huang, Y.-F. Contamination Improvement of Touch Panel and Color Filter Production Processes of Lean Six Sigma. Appl. Sci. 2019, 9, 1893. [Google Scholar] [CrossRef]
- Gijo, E.V.; Scaria, J. Process improvement through Six Sigma with Beta correction: A case study of manufacturing company. Int. J. Adv. Manuf. Technol. 2014, 71, 717–730. [Google Scholar] [CrossRef]
- Thakore, R.; Dave, R.; Parsana, T.; Solanki, A. A Review: Six Sigma Implementation Practice in Manufacturing Industries. Int. J. Eng. Res. Appl. 2014, 4, 63–69. [Google Scholar]
- Frizziero, L.; Donnici, G.; Dhaimini, K.; Liverani, A.; Caligiana, G. Advanced Design Applied to an Original Multi-Purpose Venitlator Achievable by Additivie Manufacturing. Appl. Sci. 2018, 8, 2635–2658. [Google Scholar] [CrossRef]
- Jirasukprasert, P.; Garza-Reyes, J.A.; Kumar, V.; Lim, M.K. A Six Sigma and DMAIC application for the reduction of defects in a rubber gloves manufacturing process. Int. J. Lean Six Sigma 2014, 5, 2–21. [Google Scholar] [CrossRef]
- Box, G.E.P.; Hunter, W.G.; Hunter, S.J. Statistics for Experimenters: An Introduction to Design, Data Analysis and Model Building, 1st ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1978. [Google Scholar]
- Khuri, A.I. Response Surface Models with Mixed Effects. J. Qual. Technol. 1996, 28, 177–186. [Google Scholar] [CrossRef]
- Del Castillo, E. Process Optimization, 1st ed.; Springer: New York, NY, USA, 2007. [Google Scholar]
- Vining, G.G. A Compromise Approach to Multiresponse Optimization. J. Qual. Technol. 1998, 30, 309–313. [Google Scholar] [CrossRef]
- Park, G.-J.; Lee, T.-H.; Lee, K.H.; Hwang, K.-H. Robust Design: An Overview. AIAA J. 2006, 44, 181–191. [Google Scholar] [CrossRef]
- Taguchi, G.; Phadke, M.S. Quality Engineering through Design Optimization; Springer Nature: New York, NY, USA, 1989; pp. 77–96. [Google Scholar]
- Kackar, R.N. Off-Line Quality Control, Parameter Design, and the Taguchi Method. J. Qual. Technol. 1985, 17, 176–188. [Google Scholar] [CrossRef]
- Logothetis, N.; Wynn, H.P. Quality Through Design, Experimental Design, Off-Line Quality Control and Taguchi’s Contributions, 1st ed.; Clarendon Press: Oxford, UK, 1989. [Google Scholar]
- Nair, V.N. Taguchi’s Parameter Design: A panel discussion. Technometrics 1992, 30, 127–161. [Google Scholar] [CrossRef]
- Phadke, M.S.; Kackar, R.N.; Speeney, D.V.; Grieco, M.J. Off-Line Quality Control in Integrated Circuit Fabrication Using Experimental Design. Bell Syst. Tech. J. 1983, 62, 1273–1309. [Google Scholar] [CrossRef]
- Parnianifard, A.; Azfanizam, A.; Ariffin, M.; Ismail, M.I.S. An overview on robust design hybrid metamodeling: Advanced methodology in process optimization under uncertainty. Int. J. Ind. Eng. Comput. 2018, 9, 1–32. [Google Scholar] [CrossRef]
- Robinson, T.J.; Pintar, A.L.; Anderson-Cook, C.M.; Hamada, M. A Bayesian Approach to the Analysis of Split-Plot Combined and Product Arrays and Optimization in Robust Parameter Design. J. Qual. Technol. 2012, 44, 304–320. [Google Scholar] [CrossRef]
- Guiras, Z.; Turki, S.; Rezg, N.; Dolgui, A. Optimization of Two-Level Disassembly/Remanufacturing/Assembly System with an Integrated Maintenance Strategy. Appl. Sci. 2018, 8, 666. [Google Scholar] [CrossRef]
- Qi, Q.; Dong, Q.; Xin, Y. Robust optimization design of structures based on the specular reflection algorithm. Adv. Mech. Eng. 2019, 11. [Google Scholar] [CrossRef]
- Sreedharan, V.R.; Rajasekar, S.; Kannan, S.S.; Arunprasad, P.; Rajeev, T. Defect reduction in an electrical parts manufacturer: A case study. TQM J. 2018, 30, 650–678. [Google Scholar] [CrossRef]
- Mariajayaprakash, A.; Senthilvelan, T. Failure detection and optimization of sugar mill boiler using FMEA and Taguchi method. Eng. Fail. Anal. 2013, 30, 17–26. [Google Scholar] [CrossRef]
- Pech, M.; Vaněček, D. Methods of Lean Production to Improve Quality in Manufacturing. Qual. Innov. Prosper. 2018, 22, 1–15. [Google Scholar] [CrossRef]
- Marodin, G.A.; Frank, A.G.; Tortorella, G.L.; Netland, T.H. Lean product development and lean manufacturing: Testing moderation effects. Int. J. Prod. Econ. 2018, 203, 301–310. [Google Scholar] [CrossRef]
- Realyvasquez-Vargas, A.; Arredondo-Soto, K.C.; Carrillo-Gutiérrez, T.; Ravelo, G. Applying the Plan-Do-Check-Act (PDCA) Cycle to Reduce the Defects in the Manufacturing Industry. A Case Study. Appl. Sci. 2018, 8, 2181. [Google Scholar] [CrossRef]
- Smith, G.; Poteat-Godwin, A.; Harrison, L.M.; Randolph, G.D. Applying Lean Principles and Kaizen Rapid Improvement Events in Public Health Practice. J. Public Health Manag. Pract. 2012, 18, 52–54. [Google Scholar] [CrossRef]
- Iwao, S. Revisiting the existing notion of continuous improvement (Kaizen): Literature review and field research of Toyota from a perspective of innovation. Evol. Inst. Econ. Rev. 2017, 14, 29–59. [Google Scholar] [CrossRef]
- Peng, Q.-Y.; Chinese Critical Care Ultrasound Study Group (CCUSG); Wang, X.-T.; Zhang, L.-N. Findings of lung ultrasonography of novel corona virus pneumonia during the 2019–2020 epidemic. Intensiv. Care Med. 2020, 46, 849–850. [Google Scholar] [CrossRef] [PubMed]
- Consoli, L.; Bendotti, V.; Cicchinelli, S.; Gaioni, F.; Prandolini, P.; Bettonagli, M.; Terragnoli, P. 2019 novel coronavirus (COVID-19) pneumonia complications: The importance of lung ultrasound. J. Ultrasound 2020, 1–4. [Google Scholar] [CrossRef]
- Ultrasound Systems. Available online: https://www.esaote.com/ultrasound/ultrasound-systems/p/interventional-mylab-eight-exp/probe-type/transducers/#product-probes (accessed on 19 November 2020).
- McKeighen, R.E. Design guidelines for medical ultrasonic arrays. Med. Imaging 1998, 98, 2–18. [Google Scholar] [CrossRef]
- Gelly, J.F.; Mills, D.M.; Lanteri, F.; Baumgartner, C.E.; Calisti, S.G. Method for Optimized Dematching Layer Assembly in an Ultrasound Transducer. U.S. Patent 7,621,028 B2, 24 November 2009. [Google Scholar]
- Fuegl, M.; Mackh, G.; Meissner, E.; Frey, L. Assessment of dicing induced damage and residual stress on the mechanical and electrical behavior of chips. In Proceedings of the 2015 IEEE 65th Electronic Components and Technology Conference (ECTC), San Diego, CA, USA, 26–29 May 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 214–219. [Google Scholar]
- McCann, S.; Sato, Y.; Sundaram, V.; Tummala, R.R.; Sitaraman, S.K. Prevention of Cracking from RDL Stress and Dicing Defects in Glass Substrates. IEEE Trans. Device Mater. Reliab. 2015, 16, 43–49. [Google Scholar] [CrossRef]
- Bertocci, F.; Grandoni, A. Corrosion of Tin-Indium Solder during the Manufacturing Process of Biomedical Ultrasound Transducers. In Proceedings of the 2019 22nd European Microelectronics and Packaging Conference & Exhibition (EMPC), Pisa, Italy, 16–19 September 2019; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Ganganallimath, M.M.; Patil, S.D.; Gijo, E.V.; Math, R.B.; Hiremath, V. Application of Taguchi-based Six Sigma method to reduce defects in green sand casting process: A case study. Int. J. Bus. Sys. Res. 2019, 13, 226–246. [Google Scholar] [CrossRef]
- Benešová, A.; Hirman, M.; Steiner, F.; Tupa, J. Determination of Changes in Process Management within Industry 4.0. Proc. Manuf. 2019, 38, 1691–1696. [Google Scholar] [CrossRef]
- Krishnaiyer, K.; Chen, F.F.; Burgess, B.; Bouzary, H. D3S Model for Sustainable Process Excellence. Proc. Manuf. 2018, 26, 1441–1447. [Google Scholar] [CrossRef]
- Sayid-Mia, S.M.A.; Nur-E-Alam, M.; Ahmad, F.; Kamal-Uddin, M. Footwear Industry in Bangladesh: Implementation of Six Sigma Methodology. Ind. Eng. Manag. 2017, 6, 211. [Google Scholar] [CrossRef]
- Prashar, A. Adoption of Six Sigma DMAIC to reduce cost of poor quality. Int. J. Prod. Perform. Manag. 2014, 63, 103–126. [Google Scholar] [CrossRef]
- Silva, A.S.; Medeiros, C.F.; Vieira, R.K. Cleaner Production and PDCA cycle: Practical application for reducing the Cans Loss Index in a beverage company. J. Clean. Prod. 2017, 150, 324–338. [Google Scholar] [CrossRef]
- Khorshidi, H.A.; Gunawan, I.; Ibrahim, M.Y. Data-Driven System Reliability and Failure Behavior Modeling Using FMECA. IEEE Trans. Ind. Inform. 2015, 12, 1253–1260. [Google Scholar] [CrossRef]
- Sharma, G.V.S.S.; Rao, P.S.; Babu, B.S. Process capability improvement through DMAIC for aluminum alloy wheel machining. J. Ind. Eng. Int. 2017, 14, 213–226. [Google Scholar] [CrossRef]
- Aslam, M.; Azam, M.; Khan, N.; Jun, C.-H. A mixed control chart to monitor the process. Int. J. Prod. Res. 2015, 53, 4684–4693. [Google Scholar] [CrossRef]
- Weissman, S.A.; Anderson, N.G. Design of Experiments (DoE) and Process Optimization. A Review of Recent Publications. Org. Process. Res. Dev. 2015, 19, 1605–1633. [Google Scholar] [CrossRef]
- Sharif, M.M.; Anwar, Z.; Ayub, Y.; Abbas, A.; Ahmed, M. Optimization in MIG Welding by Using Six Sigma Tools. Ind. Eng. Manag. 2019, 8, 1–9. [Google Scholar]
- Raut, R.; Attar, P.R. Optimization of process capability in an automobile industry: A case study. Int. Res. J. Eng. Tech. 2016, 3, 289. [Google Scholar]
- IEC 61508-1:2010. Functional Safety of Electrical/Electronic/Programmable Electronic Safety-Related Systems—Part 1: General Requirements; International Electrotechnical Commission: London, UK, 2012. [Google Scholar]
- Shafiee, M.; Enjema, E.; Kolios, A. An Integrated FTA-FMEA Model for Risk Analysis of Engineering Systems: A Case Study of Subsea Blowout Preventers. Appl. Sci. 2019, 9, 1192. [Google Scholar] [CrossRef]
- IEC 61025:2006. Fault Tree Analysis (FTA); International Electrotechnical Commission: London, UK, 2007. [Google Scholar]
- SAE J1739: 2009. Potential Failure Mode and Effects Analysis in Design (Design FMEA), Potential Failure Mode and Effects Analysis in Manufacturing and Assembly Processes (Process FMEA); John Wiley & Sons: New York, NY, USA, 2014. [Google Scholar]
- Catelani, M.; Scarano, V.L.; Bertocci, F. Implementation and Characterization of a Medical Ultrasound Phased Array Probe with New Pb-Free Soldering Materials. IEEE Trans. Instrum. Meas. 2010, 59, 2522–2529. [Google Scholar] [CrossRef]
- Box, G.E.P.; Draper, N.R. Empirical Model-Building and Response Surfaces, 1st ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1987. [Google Scholar]
- Khuri, A.I.; Cornell, J.A. Response Surfaces, 2nd ed.; Marcel Dekker: New York, NY, USA, 1996. [Google Scholar]
- Vining, G.G.; Myers, R.H. Combining Taguchi and Response Surface Philosophies: A Dual Response Approach. J. Qual. Technol. 1990, 22, 38–45. [Google Scholar] [CrossRef]
- Myers, R.H.; Khuri, A.I.; Vining, G. Response Surface alternatives to the Taguchi robust parameter design approach. Am. Stat. 1992, 46, 131–139. [Google Scholar]
- Robinson, T.J.; Wulff, S.S.; Montgomery, D.C.; Khuri, A.I. Robust Parameter Design Using Generalized Linear Mixed Models. J. Qual. Technol. 2006, 38, 65–75. [Google Scholar] [CrossRef]
- Box, G.; Jones, S. Split-plot designs for robust product experimentation. J. Appl. Stat. 1992, 19, 3–26. [Google Scholar] [CrossRef]
- Cramer, J.S. Logit Models from Economics and Other Fields; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Casella, G.; Berger, R.L. Statistical Inference, 2nd ed.; Wadsworth, Inc.: Belmont, CA, USA, 1990. [Google Scholar]
- Aryan, P.; Sampath, S.; Kim, K. An Overview of Non-Destructive Testing Methods for Integrated Circuit Packaging Inspection. Sensors 2018, 18, 1981. [Google Scholar] [CrossRef] [PubMed]
- Yunus, M.; Srihari, K.; Pitarresi, J.; Primavera, A. Effect of voids on the reliability of BGA/CSP solder joints. Microelectron. Reliab. 2003, 43, 2077–2086. [Google Scholar] [CrossRef]
- Cheng, Z.; Chen, L.; Wang, G.; Xie, X.; Zhang, Q. The effects of underfill and its material models on thermomechanical behaviors of flip chip package. In Proceedings of the International Symposium on Electronic Materials and Packaging (EMAP2000) (Cat. No.00EX458), Hong Kong, China, 30 November–2 December 2000; IEEE: Piscatway, NJ, USA, 2002; pp. 232–239. [Google Scholar]
- Qiu, Y.; Zhang, S. Study on the pin delamination of plastic encapsulated microcircuits using scanning acoustic microscope. In Proceedings of the 2017 Prognostics and System Health Management Conference, PHM, Harbin, China, 9–12 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–5. [Google Scholar]
- Lee, C.S.; Zhang, G.M.; Harvey, D.M.; Qi, A. Characterization of micro-crack propagation through analysis of edge effect in acoustic micro-imaging of microelectronic packages. NDT & E Int. 2016, 79, 1–6. [Google Scholar]
- Oberhoff, S.; Goetz, K.; Trojan, K.; Zoeller, M.; Glueck, J. Application of high frequency scanning acoustic microscopy for the failure analysis and reliability assessment of MEMS sensors. Microelectron. Reliab. 2016, 64, 656–659. [Google Scholar] [CrossRef]
- Bertocci, F.; Grandoni, A.; Djuric-Rissner, T. Scanning Acoustic Microscopy (SAM): A Robust Method for Defect Detection during the Manufacturing Process of Ultrasound Probes for Medical Imaging. Sensors 2019, 19, 4868. [Google Scholar] [CrossRef] [PubMed]
- Berni, R.; Bertocci, F.; Nikiforova, N.D.; Vining, G.G. A tutorial on randomizing versus not randomizing Split-Plot experiments. Qual. Eng. 2019, 32, 25–45. [Google Scholar] [CrossRef]
- InsightScan-350. Available online: http://www.insightkk.co.jp/index.php/en/acoustic-microsopes/is-350 (accessed on 19 November 2020).
- ISO 13485:2016. Design and Development Validation and Verification; ISO: Geneva, Switzerland, 2020. [Google Scholar]



| Parameter | Symbol | Estimate | St. Error | p-Value (t Test) |
|---|---|---|---|---|
| Intercept | β0 | 373.19 | 40.33 | <0.0001 |
| Worker-St1-#1 | β11 | 1.84 | 17.88 | 0.9194 |
| Worker-St1-#2 | β12 | 6.30 | 13.08 | 0.6364 |
| Worker-St1-#3 | β13 | 0.0 | ||
| Worker-St9-#1 | β21 | −19.57 | 20.51 | 0.3535 |
| Worker-St9-#2 | β22 | −29.87 | 39.17 | 0.4561 |
| Worker-St9-#3 | β23 | −54.51 | 26.77 | 0.0576 |
| Worker-St9-#4 | β24 | 0.0 | ||
| Worker-St11-#1 | β3l | −41.22 | 29.42 | 0.1791 |
| Worker-St11-#2 | β32 | −18.45 | 27.47 | 0.5109 |
| Worker-St11-#3 | β33 | 3.49 | 24.15 | 0.8867 |
| Worker-St11-#4 | β34 | 0.0 | ||
| Dicing-Saw-1 | β4l | −11.53 | 6.88 | 0.1117 |
| Dicing-Saw-2 | β42 | 0.0 | ||
| #Blade-usage-1 | β5l | 5.38 | 10.15 | 0.6031 |
| #Blade-usage-2 | β52 | −7.11 | 10.56 | 0.5098 |
| #Blade-usage-3 | β53 | −9.42 | 9.59 | 0.3397 |
| #Blade-usage-4 | β54 | 5.89 | 9.66 | 0.5502 |
| #Blade-usage-5 | β55 | 0.0 | ||
| #days-St2–3 | β6 | 0.97 | 4.94 | 0.8466 |
| #days-St5–6 | β7 | 0.13 | 7.15 | 0.9858 |
| #days-St8–9 | β8 | −0.59 | 3.14 | 0.8513 |
| #days-St10–11 | β9 | 11.67 | 5.94 | 0.0660 |
| Trn-Flateness-St5 | β10 | 4.30 | 3.28 | 0.2072 |
| Kapton®-St4 | β11,1 | −28.32 | 33.45 | 0.4090 |
| Kapton®-St4 | β11,2 | 0.0 |
| Variable Description | Symbol | Estimate | St. Error | p-Value (Wald’s Test) |
|---|---|---|---|---|
| Intercept | θ0 | −11.50 | 4.63 | 0.0131 |
| #blade-usage-1 | θ11 | 0.0 | ||
| #blade-usage-2 | θ12 | −0.39 | 0.86 | 0.6525 |
| #blade-usage-3 | θ13 | 0.92 | 0.89 | 0.3061 |
| #blade-usage-4 | θ14 | 1.90 | 1.12 | 0.0907 |
| #blade-usage-5 | θ15 | −2.81 | 2.08 | 0.1782 |
| Dicing-Saw-1 | θ21 | 0.0 | ||
| Dicing-Saw-3 | θ22 | 3.01 | 2.56 | 0.2401 |
| Dicing-Saw-4 | θ23 | 2.79 | 2.59 | 0.2820 |
| Worker-St9-#1 | θ31 | 0.0 | ||
| Worker-St9-#2 | θ32 | 3.46 | 1.86 | 0.0631 |
| Worker-St9-#3 | θ33 | −2.66 | 1.76 | 0.1302 |
| Worker-St9-#4 | θ34 | 4.10 | 1.86 | 0.0282 |
| Worker-St11-#1 | θ41 | 0.0 | ||
| Worker-St11-#2 | θ42 | 4.89 | 2.29 | 0.0325 |
| Worker-St11-#3 | θ43 | 4.81 | 2.28 | 0.0349 |
| #days-St5–6 | θ5 | −0.36 | 0.21 | 0.0792 |
| #days-St10–11 | θ6 | 3.56 | 1.42 | 0.0125 |
| Epoxy resin-St3 | θ7 | 1.23 | 0.97 | 0.1976 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bertocci, F.; Grandoni, A.; Fidanza, M.; Berni, R. A Guideline for Implementing a Robust Optimization of a Complex Multi-Stage Manufacturing Process. Appl. Sci. 2021, 11, 1418. https://doi.org/10.3390/app11041418
Bertocci F, Grandoni A, Fidanza M, Berni R. A Guideline for Implementing a Robust Optimization of a Complex Multi-Stage Manufacturing Process. Applied Sciences. 2021; 11(4):1418. https://doi.org/10.3390/app11041418
Chicago/Turabian StyleBertocci, Francesco, Andrea Grandoni, Monica Fidanza, and Rossella Berni. 2021. "A Guideline for Implementing a Robust Optimization of a Complex Multi-Stage Manufacturing Process" Applied Sciences 11, no. 4: 1418. https://doi.org/10.3390/app11041418
APA StyleBertocci, F., Grandoni, A., Fidanza, M., & Berni, R. (2021). A Guideline for Implementing a Robust Optimization of a Complex Multi-Stage Manufacturing Process. Applied Sciences, 11(4), 1418. https://doi.org/10.3390/app11041418






