Abstract
The development of biofilms and the related changes in porous media in the subsurface cannot be directly observed and evaluated. The primary reason that the mechanism of biofilm clogging in porous media cannot be clearly demonstrated is due to the opacity and structural complexity of three-dimensional pore space. Interest in exploring methods to overcome this limitation has been increasing. In the first part of this review, we introduce the underlying characteristics of biofilm in porous media. Then, we summarize two approaches, non-invasive measurement methods and mathematical simulation strategies, for studying fluid–biofilm–porous medium interaction with spatiotemporal resolution. We also discuss the advantages and limitations of these approaches. Lastly, we provide a perspective on opportunities for in situ monitoring at the field site.
1. Introduction
Biofilms are usually defined as the coexistence of microbes and extracellular polymeric substances (EPS) [1,2,3]. Microbial populations secrete vast quantities of EPS and are embedded in the viscous EPS matrix, which has a highly self-organizing heterogeneous structure and can protect the biofilm from virulence and stripping [4,5,6,7,8]. Their potent sorptive capacity enables biofilms to grow even in environments extremely lacking in nutrition [3]. Secretion of EPS is therefore conducive to the adsorption and degradation of pollutants in subsurface porous media such as soil and rock. Biofilms are involved in environmental restoration and protection applications such as remediation of toxic metals, radionuclides, oil spill, and microplastics [9,10,11,12,13,14,15]. The growth of biofilms can be artificially stimulated to promote the degradation of pollutants or to prevent further infiltration of subsurface contaminant plume. However, biofilms growing in the subsurface can clog the porous media and even reduce its permeability, which may have negative effects near groundwater recharge wells, oil recovery water injection wells, or deep geothermal systems [16,17,18].
Therefore, it is essential to evaluate the degree of clogging and analyze the spatial and temporal distribution of biofilms in porous media. Measurement and simulation of the biofilm formation process in porous media are essential for understanding the associated mechanisms that can provide a theoretical foundation for monitoring, qualitative and quantitative prediction, and data interpretation. Understanding the mechanisms that can promote or reduce biofilm growth in porous media is therefore important in the modeling and design of in situ biostimulating and/or alleviation of bioclogging schemes. Related experimental mechanism studies tend to use columns packed with typical porous media (e.g., soil sample or aquifer materials), which make the system opaque and thus not available for direct observation [1]. The invasive examination methods often damage the sample at the cost of terminating of the experiment. Hence, non-invasive and in situ methods are imperative to implement direct imaging or to provide spatiotemporal information of biofilm-mediated processes and the related impacts within the porous media [19,20]. The modeling methods are restricted by the limited knowledge about such processes in three-dimensional (3D) pore space, and the long computational time for model resolution, whereas the existing experimental methods are restricted by the progress of instrumental performance.
This review summarizes methods dealing with the relationships of the growth of biofilms, fluid hydrodynamics, and mass transport in porous media. To facilitate future work and promote advances in field site monitoring, we focus our attention on providing an overview of the non-invasive and in situ measurement methods as well as the mathematical simulation methods. We also discuss the application scope and provide our perspective on opportunities for in situ monitoring at field sites.
2. Characteristics of Biofilm Growth in Porous Media
The morphology and structure of biofilms as well as the factors influencing the structure of biofilms in fluid have been widely studied. The interaction of fluid hydrodynamics and mass transport contributes to the diverse heterogeneous structure of biofilms. Biofilm development is a dynamic process that involves the surface adsorption and proliferation of microbes, the secretion of EPS, and the partial desorption of biofilms into the fluid [2,21,22]. Under an environment that suffers from shear force, detachment of bacterial cells and EPS fragments occurs during each process. The processes are more complicated when biofilms develop on a surface in a porous aqueous environment due to the complexity of pore networks in porous media and the variety of pores sizes and shapes within porous media. The related processes of biofilm evolution in a pore are split into four main stages as shown in the schematic in Figure 1.
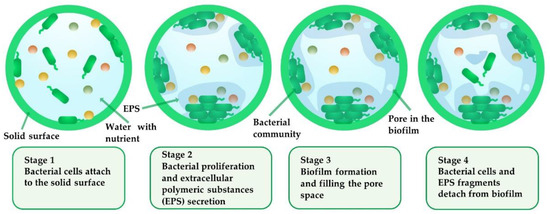
Figure 1.
Biofilm development processes in a pore.
There are common descriptions of characteristics for the biofilm development either in pure fluids or porous media. Microscopic observations have revealed that biofilms are heterogeneous and have structures such as pores, voids, and cavities [4,10,23,24]. Therefore, biofilms can introduce an additional pore structure to porous media. We infer that this is one of the reasons for the lowest permeability in bioclogging porous system. As shown in Figure 2, the microscopic morphology and the adhesion of mature biofilm are affected by the substrate composition and flowing condition [24,25,26,27,28]. For example, the biofilms under high shear condition are ribbon-like, have stronger adhesion, and are more homogeneous with lower porosity [26,27], whereas the biofilm under low shear stress is mound-like [26,29].

Figure 2.
Images of biofilm structures in three flow regimes: (a) laminar, (b) transient, and (c) turbulent by confocal scanning laser microscopy (CLSM), which are more homogeneous in turbulent fluid (reproduced with permission from [27], Copyright John Wiley and Sons, 2010); under three substrate loading rates (d) low, (e) medium and (f) high, by optical coherence tomography (OCT) (reproduced with permission from [24], Copyright Elsevier, 2004), where a low substrate loading leads to low biofilm density [25].
Researchers have found that biofilms formed under non-flow are significantly thicker than those formed under shear stress [30]. The porosity and density of biofilms are also affected by the concentration and loading rate of the substrate (Figure 2) [24,25,31]. Local detachment occurs when the substrates are almost completely consumed or the fluid shear stress is satisfied [21,32,33,34,35]. Furthermore, there are many gaps and flow channels in the biofilm matrix, so the flow in the matrix will form pressure or resistance which is responsible for the detachment of biofilms [29]. With microbe desorption into the fluid, the biomass will be redistributed.
There are still some differences in the characteristics for biofilm growth in porous media. For instance, the biomass distribution is likely to be concentrated at sites of nutrient injection [9,36,37] and depends on the concentration of the inoculated microbe, nutrient injection rate, and pore distributions. The development of biofilms will clog the pore space and reduce the permeability of the porous media [17,38]. The detached biofilm segments induced by shear stress may accelerate the clogging of the pore space. Furthermore, the thickness of the final biofilm was found to be directly influenced by the size of the pore space and has no obvious relationship with the pore structure [37]. In addition, it has been proved that the clogging of pore space will give rise to the local mass transport abnormity [39]. The fluid hydrodynamics and mass transport influence the structure of biofilms. The growth and rough surface of biofilms also lead to heterogeneity of the local fluid field, which results in distribution of local substrates concentration inhomogeneity [17,40,41,42,43,44,45,46]. Therefore, the structure and distribution of biofilm in porous media is the net result of the interaction between biofilm accumulation and fluid hydrodynamics.
3. Non-Invasive and In Situ Measurement of Mass Transport and Fluid Hydrodynamics of Bioclogging System in Porous Media
Many analytical methods have been employed to identify the biofilm-related mechanisms (biomass formation and distribution, permeability reduction, substrate use, hydrodynamic dispersivity, etc.) since it has been proven to be the major cause of clogging of most water-immersed porous material [9,17,47,48]. Early estimation and examination methods that were used were invasive or destructive. The column was dismantled to identify the spatial distribution of the final biofilm by bacterial organic carbon (BOC) assay [17]. Clogging in the porous media can be determined by measuring the permeability and biomass parameters of the effluent, and the existence of biofilm can be confirmed by electron microscopy at the cost of destroying the bioclogging system as the evolution of biofilm cannot be observed at spatiotemporal resolution [9,10,47,48,49,50]. Consequently, the glass micromodels with two-dimensional pore network structures were successfully used to visualize the biofilm growth experiments based on direct optical imaging [49,51,52,53]. For example, the cessation (due to nutrient depletion) and subsequent shedding (due to shear force) of biofilm growth were observed directly, which simultaneously confirmed the presence of the critical shear stress [49]. Once the shear stress exceeds this critical value, biofilm shedding occurs. The pressure drop of the porous media in the plug region increased with the biofilm’s development. Once a maximum pressure drop was reached, a flow channel appeared, along which the nutrients traveled to the next area and then clogged up the area, creating new flow channels [51]. This was further demonstrated in another study, which further indicated that the stability of the plug depends on the location of the plug and the distribution of the pore size [52].
However, the mechanism involved in biofilm clogging in porous media still cannot be clearly demonstrated due to the opacity and structural complexity of three-dimensional (3D) pore space. Thus, using imaging techniques is one of the optimal choices to implement noninvasive visualization at different spatial scales. According to the available information, the application of imaging technologies in this field is still evolving. Therefore, in this section, we summarize the existing imaging techniques and their applicability in monitoring biofilm development and the related changes in porous media. Table 1 lists the porous materials and the relevant grain sizes.

Table 1.
Methods and materials.
3.1. X-ray Tomography Technology
X-ray tomography, as a nondestructive and in situ method, has already been used to obtain 3D images and characterize the structure of porous media as well as the distribution of fluids at the pore scale for decades [64,65,66,67]. However, this technology has not been used to image biofilms in porous media until 2010, due to the significant challenge also ailing conventional contrast agents in distinguishing the biofilm from the fluid phase [54].
In an application for imaging the structure of biofilms in porous media, X-ray beams perpendicularly penetrate the column. The transmitted X-rays are then converted to visible light and a photograph is taken to obtain a two-dimensional (2D) grayscale map [65]. A large number of these 2D images at different depths can be used to reconstruct a 3D structure of biofilms in pore space [55,65]. Since materials with different atomic mass absorb different degrees of X-rays, the water and the porous media can be distinguished because of their different atomic masses [65]. However, since there are more than 90% of water molecules in biofilms [3], a contrast agent is needed for dividing these two kinds of materials.
Within the last decade, to divide the biofilm from bulk fluid, researchers have made progress towards determine contrast agents suitable for biofilm imaging in porous media [20,54,55,56,57]. Iltis et al. [54] first used hollow silver-coated microspheres as a contrast agent to generate realistic 3D representations of biofilm grown in a glass bead pack. They further tried other contrast agents—a mixture of micrometer-sized barium sulfate and potassium iodide—to visualize the biofilms in polyamide and expanded-polystyrene-beads-modeled porous media [55]. The images are restricted to the external structure of biofilm since the agent particles have full coverage over the biofilm surface. Nevertheless, the obtained 3D images of biofilm structure may provide new ideas and experimental bases for studying the heterogeneity of mass transport and pore space caused by biomass growth. 1-Chloronaphtalene was used as a contrast agent to prevent the drawbacks of classical agents, such as fast sedimentation and heterogeneous distribution [20]. Characteristics (for example, partial pore clogging), especially at the sites of nutrient entry, can be observed by imaging experiment. A quantitative analysis on the microstructure (volume fractions and specific surface area) of the biofilm developed in columns of clay beads is also proposed based on the 3D images obtained in that study. The methods mentioned above share another trait in that the agents are potentially destructive to the biofilm morphology. Accordingly, iron sulfate (FeSO4) was chosen as a nontoxic inorganic compound and added to the feed solution during biofilm growth [56]. In the contrasting experiment, barium sulfate was used, and more than 50% of biofilms were washed out due to abrasion and shear detachment, emphasizing the importance of nondestructive contrast agents (Figure 3). The oxidation of Fe (II) to Fe (III), which is less soluble and tends to form colloids, was observed quickly after the startup of the system, complicating the biofilm-filled system.

Figure 3.
X-ray tomography images for biofilm structures in pore space with two types of contrast agents (a) barium sulfate and (b) iron sulfate. The obtained volumetric fraction of biofilms (green area) is much smaller by using barium sulfate as a contrast agent due to the long injection time.
Recently, 3D particle tracking velocimetry (3D-PTV) and X-ray computed microtomography were used together to investigate the effect of hydrodynamics on the structure and distribution of biofilms at the pore scale [57]. 3D-PTV measurements were conducted independently to get velocity and acceleration data along flow trajectories. The wall shear stresses were calculated from these data. Barium sulfate particles were used as a contrast agent at an extremely low injection volumetric flow rate compared to the growth flow rate for more than 12 h to minimize biofilm–contrast agent interactions. Since the experimental study is concerned with the wall surface stress of the biofilm caused by flow, it is assumed that the biofilm is not permeable. The results show that biofilms are formed more in areas with low shear stress and less in areas with high shear stress. However, the results obtained by Stoodley et al. [26] were different, and high shear stress was beneficial in promoting the formation of biofilm with a stronger adhesion force. By comparing the conditions of the two experiments, it can be found that the non-stripping biofilm took longer to grow (14 days) [26], while Carrel et al.’s [57] biofilm cultivation experiment lasted for only 36 h, which is the reason why no biofilms formed at the high shear stress area.
To provide references for improving future experiments, the main disadvantages for contrast agents that are mentioned in this review are listed in Table 2. The advantages for contrast agents are not listed in the table as these agents are bold attempts of the researchers and are proven to have excellent performance on imaging biofilm structure. Shortcomings of a contrast agent can be weakened by other processes in a study, such as the reduction in agent injection rate [57]. In addition, the use of contrast agents and exposure to X-ray may inhibit or kill the growth of microorganisms [54,55]. Consequently, it is impossible to measure biofilm evolution and the interactions with hydrodynamics at the time scale. The exquisite structure information resulting from X-ray microtomography may offer sufficiently high resolution and accuracy for numerical simulation strategies.

Table 2.
The disadvantages of contrast agents used in this review.
3.2. Nuclear Magnetic Resonance Measurement
Nuclear magnetic resonance (NMR) T2 imaging of biofilms in porous media is a direct measurement of the number and state of 1H nuclei in the biofilm matrix and pore space. After being excited by a radio frequency (RF) pulse, the nuclei relax to their initial equilibrium. The spin–lattice relaxation time T1 and spin–spin relaxation time T2 can be used to characterize such relaxation progress. They are both affected by the physical and chemical environment (e.g., pore size and paramagnetic ions). The amplitude of the obtained NMR relaxation signal is directly proportional to the amount of water molecules that are contained in biofilms and pore space. The phase shift of the measured signal can be used to determine the displacement that arises from the fluid flow, which is the basis for NMR velocity imaging. More details about NMR imaging can be find in many articles [68,69,70].
There are many studies involving NMR measurement of biofilms such as those investigating hydrodynamic dispersion, mass transfer, and transport processes in porous biosystems as well as the structure of biofilms in a porous bioreactor. The growth of biofilm in fluids and the flow anomalies associated with this process have been measured by NMR imaging. In an NMR T2 image (Figure 4a), the light area with high T2 values represents the bulk water, while the darker area with low T2 values represents the biofilm [43]. Contrast agents without any effects on the growth of the biofilms were added to the feed to decrease the experiment time or to enhance the boundary between the biofilm and the bulk water. Through NMR T2 imaging, the non-uniform structure of biofilms growing with time can be monitored nondestructively [43,45,46]. The internal structure of biofilm matrix, such as holes, can also be detected [45,46]. NMR velocity measurement is different from PTV measurement mentioned in X-ray method. PTV measurement is a detection for track of flowing tracer particles [57], whereas NMR velocity measurement is a measurement for residual phase shift of nuclear spins varying with time [46]. Through NMR velocity imaging, fluid velocity redistribution induced by the growth of biofilm development can be obtained as well as the local shear stress [43,45,46]. The change of velocity field leads to the change of mass concentration field, which affects the mass transport from bulk to biofilm [71,72]. Therefore, the measurement of velocity field is crucial to the analysis of mass transport between biofilm and fluid.
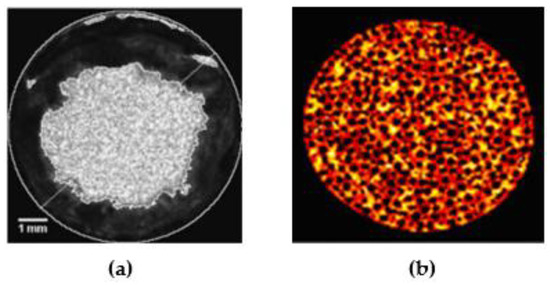
Figure 4.
2D NMR imaging for biofilm in (a) a tube bioreactor with a diameter of 7.7 mm (reproduced with permission from [43], Copyright John Wiley and Sons, 2003) and (b) monodisperse beads in a cylinder with a diameter of 5 mm, (reproduced with permission from [59], Copyright Advances in Water Resources, 2007). NMR imaging can be used to confirm biofouling at any area of a porous media but has a lower resolution on the biofilm structure in contrast to X-ray imaging.
When the NMR technique is used to map the growth of biofilm in porous media, the problem becomes complicated. The spatial resolution restricts the NMR instrument’s capacity to structure images of biofilms in pore space. Brian et al. [58] performed biofilm growth experiments in a transparent parallel plate reactor and a bioreactor with glass beads in it, and employed the nuclear magnetic resonance imaging technique to identify and image biofilm growth. The diameter of the glass beads used to model the porous media were between 1 and 1.5 mm. As a result, the distance between particles (glass beads) was large (if the beads are packed tightly, the distance can reach a maximum value of 1000 μm, while the thickness of the biofilm is about 300 μm at most) [4,73,74,75], leading to the early success in imaging. This was further proved in magnetic resonance experiments conducted by Joseph et al. [39,59], who applied velocity imaging and magnetic-relaxation-weighted imaging methods to study biofouling of a homogeneous model porous media with 241 μm diameter monodisperse polystyrene beads.
Although the morphology of the biofilm cannot be visualized, the results of NMR velocity imaging and NMR T2 imaging can still reflect the heterogeneity induced by biofilm growth in porous media (Figure 4b). In an NMR velocity map of porous media, nonflow regions represent the biofilm clogging area and high-velocity regions represent where no biofilm exists [39]. The degree to which the velocity is reduced coupled to the slice of different position can indicate the space distribution of biofilms. The measured propagators during biofilm growth in porous media can be used to quantify the transition of macroscale transport dynamics and, thus, indicate the transition of pore space [59].
In conclusion, nuclear magnetic resonance (NMR) technology can provide information with spatial temporal resolution in three dimensional (3D) porous media and can be used to study the mass transfer and flow abnormalities caused by the growth of microorganisms in porous media in a nondestructive and in situ manner. Even though the NMR imaging method is less sensitive than optical methods and X-ray methods, it avoids the opacity losses and ionizing radiation.
3.3. Confocal Laser Scanning Microscopy
A confocal laser scanning microscopy (CLSM) with UV and visible lasers can be utilized for the non-invasive investigation of 3D biofilm structure and composition under varying hydrodynamics and substrate loading rate [42,76,77,78,79]. CLSM imaging records the intensity of fluorescence signals in biofilms. Biofilm structure can be quantified using such parameters from CLSM studies as surface area, volume, porosity, etc.
However, the CLSM method has optical penetration depth limitations, which leads to small sample loading. In the only study made by Kim et al. [62], the total volume of the container was 160 μL. Biofilm were cultivated in glass beads at different Darcy velocities and substrate concentrations, and were then stained with fluorescent nucleic acid stain. Fluorescence images for biofilm (Figure 5) were taken, and the water conductivity and biomass flowing out of the system were measured. The results showed that the high flow rate led to rapid shedding of the biofilm. The detached fragments were then captured by the narrow pore neck, resulting in a rapid blockage. However, under the low flow rate, both the speed of biofilm growth and the blockage of the narrow pore neck slowed down. The biofilm was hard enough that it did not slough easily. This result can reflect the influences of both the flow rate and the substrate concentration on the morphology of the biofilm growing in the porous media. The conclusions can be used to verify the problems about mass transport and fluid flow proposed by the mathematical models.
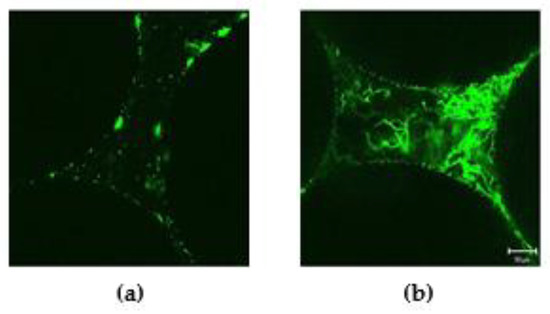
Figure 5.
Gray-scale CLSM images for biofilm structures formed under different Darcy velocities: (a) q = 1.25 mm/min; (b) q = 7.5 mm/min (reproduced with permission from [62], Copyright Water Research, 2010). The dark areas represent the glass beads and pore space, the green color indicates stained biomass (bacteria and EPS) attached on the glass bead surfaces.
3.4. Charge-Coupled Device (CCD) Camera
In addition to the above methods, an optical method was tried in terms for realizing a nondestructive monitor of bioclogging on a time scale. Kone et al. [63] designed a transparent glass flow unit loaded with quartz sand (internal volume 10 cm × 10 cm × 0.5 cm) to visualize the plug caused by biomass growth through imaging acquisition with a charge-coupled device (CCD) camera. The effect of biomass growth on mass transport in a porous media was studied by a tracer experiment through visible light transmission method. Two different conservative tracers were injected throughout the system to characterize biomass distribution (Brilliant Blue) and solute dispersivity (Blue Dextran) in porous media. The decay in gray-level intensity of the obtained images represents the coverage degree of the porous media that is covered by the biomass. Based on Beer–Lambert law, the raw images were converted into the concentration field. The results analyzing from these images showed that with the process of biofilm cultivation, the gray value around the nutrient injection orifice decreased to its minimum. The biomass was densely distributed, while the solute plume was not evenly distributed. The results indicate that biomass accumulation clogs the inlet and affects the mass transfer property.
4. Mathematical Simulations of Biofilm Evolution in Porous Media
As described in the second section of this review, the formation of biofilms is a complex process that involves microbial interactions with both the fluid flow and the medium’s surface. The evolution of biofilms and its surroundings are influenced by many factors such as the nutrient limitations induced by microbial metabolism and shear stress induced by fluid flow. Except for laboratory experiments cultivating biofilm in modeled porous media, it is necessary to establish mathematical models considering these impacts to elucidate the underlying mechanisms and predict the behavior of these complex processes.
Models describing biofilm development in porous media typically include descriptions of the porous media examined, the fluid hydrodynamic, mass transport and the accumulation and decay of biofilm. It is therefore necessary to propose several hypotheses (such as the uniformity of the biofilm matrix, flow condition, and properties of the porous media) to simplify models according to different research purposes (output). Pore-scale models usually originate from the actual structures of porous media including the microfluidic flow cell [80,81,82,83,84], glass pore network models [52,85], and others [86,87,88,89,90,91]. Fluid flow and mass transport are modeled using continuous strategies based on Darcy’s law and conservation laws.
Models describing the evolution of biofilms are the key to solving problems involving fluid hydrodynamics and mass transfer in bioclogged porous media. Figure 6 provides a schematic for the modeling strategies of biofilm development in a pore. Strategies for modeling biomass evolution are divided into three types: individual-based biomass models (IbMs), discrete biomass-based models (DbMs), and continuum biomass-based models (CbMs) [92]. CbMs use differential equations to express biomass expansion. There are no internal structures (e.g., pores and holes) in the modeled biomass. DbMs use rectangular elements (cubes or squares) moving in the finite number of lattice directions to represent biomass behavior. The pattern of biomass growth is defined based on a series of simple rules. Biomass spread process is discrete in time, space, and state. DbMs can simulate the impacts of fluid flow (detachment, captured by narrow pores, etc.). IbMs use individual solid spheres to represent biomass. Each sphere has a variable volume and a variable mass. The biomass evolution is defined explicitly with a set of rules that mimic the behavior of individual bacterial cells, and is continuous in time and space. More details with respect to modeling rules can be found in other reviews [92,93,94].
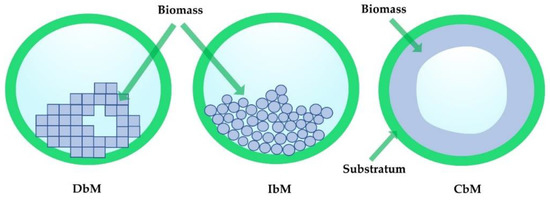
Figure 6.
Schematic of the modeling strategies of biofilm development in a pore. Discrete biomass-based models (DbMs) can be established through cellular automaton (CA) in 2D and 3D space with discrete distribution directions and discrete displacement. Individual-based biomass models (IbMs) treat individual microbes as basic units, allowing cell variation and movement in a continuous direction and distance. In continuum biomass-based models (CbMs), the development process of biofilm growth is represented by differential equations.
Several models have been used to investigate mechanisms relating to biofilm development in fluid bioreactors. The morphology of biofilm [95,96,97], biofilm detachment [98,99,100], and removal of contaminants [101,102] can be well simulated regardless of being in 2D or 3D as well as the mass transfer between biofilm and fluid [103,104]. However, biofilm development in a porous media involves interactions between the biomass, porous media, and fluid flow, which adds complexity and difficulty to the calculation. Two-dimensional models thus constitute most developed models of the biofouling porous system. If the interaction between biofilm development and fluid dynamics in porous media is studied on the microscale, a 2D model could be selected. A 3D model is more practical on a larger scale at the cost of more computational time, especially when the degree of biofouling, porosity, and water conductivity of the entire system are considered.
Model strategies presented here focus on solving problems as follows: (1) effects of biofilm formation on permeability; (2) interactions between fluid flow and biofilm development; (3) multispecies biofilm formation. Subsequently, several examples are introduced.
4.1. Effects of Biofilm Formation on Permeability
The reduction in permeability is one of the most striking features of biofouling in porous media. The first 3D numerical pore-scale model of biofilm growth in porous media was presented by Schulenburg et al. [89] based on a lattice Boltzmann simulation platform complemented with an individual-based biofilm model (LB-IbM). The numerical model can calculate parameters such as the velocity, pressure, nutrient concentration fields, biomass distribution, and porous media’s permeability. By comparing the simulation results in 2D and 3D space, it was found that pore space clogging caused by biofilm growth was slower in 3D space because of the greater connectivity between pores. The LB-IbM method was applied by the same research group to achieve optimum reduction of permeability through biofilm growth in porous media in a 2D space [88]. Critical biofilm strength was observed when the separation of biomass was considered. This study also indicates that the detachment of biofilm is of significance in the study of blockage events, which was also verified in another modeling study [86]. They further extended this simulation method to consider the permeability of biofilms and explored how the permeability of biofilms influence their growth rate in 3D space [105]. As shown in Figure 7, a higher magnitude of biofilm permeability accelerated the biomass accumulation. With the increase of biofilm permeability, the velocities of biofilm-occupied regions increased (areas within white box), but the velocities in the free pore space decreased (areas within red box).
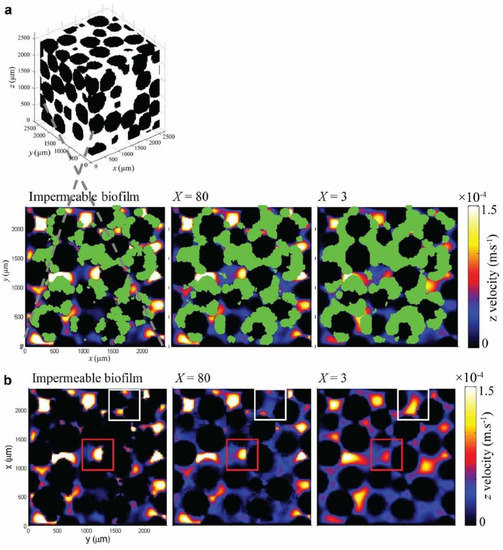
Figure 7.
After 27 h development of biomass, velocity maps at slice z = 600 μm for impermeable biofilms (X = ∞) and permeable biofilms (X = 80 and X = 3) are shown in (a) with biomass (green areas) and (b) biomass omitted, (reproduced with permission from [105], Copyright John Wiley and Sons, 2012).
In addition, a modeling study showed that the permeability of the biofilm has an effect on the permeability of the porous system [91]. It was revealed that the model would underestimate the permeability of the biofouling porous system if the permeability value of biofilm was not taken into account. Furthermore, solute transport in porous media is also an important factor for permeability reduction. A 3D continuum biomass model for simulating the relationship between solute transport and biofilm growth in porous media was developed by Chao-Zhong et al. [36]. The pore was saturated with water and the homogenous biofilm accumulation was uniform. The results revealed that biofilm clogging occurred at the inlet region when the solute supply was insufficient, which resulted in the fast reduction of the porous media’s permeability. When the solute supply was sufficient, biofilm would grow uniformly throughout the pore network. The results also indicated that there is no unique relationship between permeability and porosity in the pore network of biofilm growth.
4.2. Interactions between Fluid Flow and Biofilm Development
There are two ways in which flow fields in pore space affect the distribution of biofilm: mass transport and shear stress. The growth of biofilm increases the heterogeneity of flow velocity in porous media which, in turn, leads to the heterogeneity of both local mass transport and shear stress, resulting in the redistribution of biofilms in porous media.
In George et al.’s [86] study, biofilm was considered as a heterogeneous porous material, and the spatiotemporal evolution of biofilms in the pore space of a 2D granular media was simulated. Biofilm growth was described with a DbM approach. The formation of preferential flow paths within the granular porous media induced by the biofilm growth was also simulated. Since the stripped biofilm fragments were considered in the modeling process, it was found that even small fragments can affect the dynamic behavior of the entire system. Simona et al. [106] also discussed the issues of preferential flow paths using a two-dimensional pore-scale numerical model. The system was represented by a rectangular domain, which was divided into three different domains: the grains, the fluid, and the biofilm. The porous media was assumed to be uniform. The biofilm was considered homogeneous and described by an extended DbM method. Based on different assumptions, they simulated flow path dynamics in biofilm-forming porous media under shear forces. The results showed that considering the biomass decay or not results in different flow paths, and the flow paths will change due to the substrate redistribution. We can conclude from these two simulations that whether the biofilm as well as solid grains are homogeneous or not does not affect the generation of preferential flow paths.
During biofilm evolution in porous media, breakthrough channels recur due to shear stress and nutrient deprivation forming preferential flow paths, which are thus inferred as another cause of the existence of the lowest permeability discovered in early laboratory simulation studies [17,37].
4.3. Multispecies Biofilm Formation
Most biofilm models only take the formation of single-species biofilm into account, through microorganisms often exist in the form of multiple species in a natural environment. Hence, the population competition can be considered within the modeling rules. For example, in Youneng et al.’s work [83], a pore-scale model was used to simulate microfluidic flow cell and a cellular automaton-based method was used to simulate the biofilm development. This model simulates not only the multispecies biofilm formation at pore-scale, but also the biomass distribution and the contaminant removal rate. Most recently, a LB-DbM method was used to investigate the competition of biofilm growth in a bioreactor at the pore scale [84]. The effects of different nutrient ratios on population cooperation and competition were studied at constant flow rates and concentrations of species in 2D space.
The establishment of models concerned with multispecies will provide significant understanding of the mechanisms of biofilm-mediated activities in natural porous media.
5. Opportunities for In Situ Monitoring at Field Sites
Field monitoring of biofilm development in situ is still in its infancy, and more mechanisms and experimental studies are needed. Research on geophysical signal response of biofilm development provides opportunities for monitoring subsurface bioclogging in situ in applications of biofilm in biological barriers [61,107], underground carbon dioxide sequestration [108] and bioremediation [109,110].
In a biofilm growth experiment, the polarization response was proven to be directly derived from the biofilm formation process. This study suggested that the imaginary conductivity could be used as a proxy for microbial growth and biofilm formation in porous media [111]. Gamal and Abdel [112] analyzed the results of hydraulic conductivity measurement, cell count, and environmental scanning electron microscopy (SEM). They concluded that the changes in complex conductivity correspond to different stages of microbial plugging. The growth of biofilms not only changed the electrical properties but also changed the acoustic properties of the porous media [19,50]. For example, a study by Davis [19] indicated that the measured heterogeneity of the elastic experimental sand column was originated from the morphology and structure differences of biofilms in the porous media. Studies on the acoustic and electrical properties of biofilms in porous media so far remain within a laboratory setting. Further research on the mechanism of these signal changes caused by the development of biofouling is needed.
In addition, NMR technology as a biosensor has been used to detect the presence and development of biofilms in porous media due to its excellent performance in oil exploration and water resource search at subsurface [113,114,115,116,117]. Sarah et al. [60] investigated the applicability of 2D NMR relaxation techniques (T2, T1–T2, and T2–T2 measurements) by measuring pore and surface changes caused by biofilm growth in different porous media (different bead packs and natural Berea sandstone). However, under high field intensity, the measurement result cannot be used to accurately describe the pore size distribution of the porous media. The narrow range of the uniform field leads to the narrow measurement range, which is a disadvantage in researching the growth of biofilms in natural porous media. Therefore, Alexis et al. [118] subsequently studied the sensitivity of low-field NMR to the growth of biofilms in a porous media. Catherine [61] further studied the applicability of in situ NMR logging techniques to the growth of microorganisms at the subsurface. The two studies implied that low-field NMR is sensitive to microbial growth in the porous media, that is, microbial growth corresponds to the abnormalities of T2 relaxation signal and can even be detected in the field site. However, the test results cannot be completely explained by the existing low-field NMR technology, so a more detailed and targeted analysis of the NMR relaxation signals of microorganisms in porous media is still needed.
These studies focused on the relationship between biofilm growth in unconsolidated porous media (silica sands) and the geophysical signals. Further study should cultivate biofilm in porous media from the subsurface and design experiments to evaluate how the biofilm development process affects the geophysical signals. In addition, since the NMR T2 relaxation measurement is a direct response of biofilms and water in the porous media, efforts could be made on to determine the permeability reduction induced by biofilm formation in the subsurface by NMR logging.
6. Conclusions
Biofilm evolution in porous media involves a huge variety of involving physical, chemical, and biological reactions. An overview of the existing methods with respect to the relationships of the evolution of biofilms, fluid hydrodynamics, and mass transport in porous media focused on non-invasive, in situ, and mathematical simulation methods is presented to facilitate the future work and promote advances in field site monitoring. We think that the sophisticated and ingenious experimental design coupled with the improvement of instrumental performance, such as sample volume capacity and spatiotemporal resolution, will promote further understanding of interactions between biofilms and their surrounding environments in subsurface. The mathematical simulation models of biofilm evolution in porous media still cannot provide comprehensive scientific inferences and need to be further improved and validated with the progress of advanced scientific experiments.
Author Contributions
Selection of papers, Y.Z., C.F. and A.X.; investigation, Y.Z., A.X. and X.L.; writing—original draft preparation, Y.Z.; writing—review and editing, Y.Z., X.L., A.X. and Q.W.; drawing and modification of figures, Y.Z., Q.W. and C.F.; modifying, C.F. and J.L.; funding acquisition, J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Key Foundation for Exploring Scientific Instrument of China (2011YQ030133).
Conflicts of Interest
The authors declare no conflict of interest.
References
- O’Toole, G.; Kaplan, H.B.; Kolter, R. Biofilm formation as microbial development. Annu. Rev. Microbiol. 2000, 54, 49–79. [Google Scholar] [CrossRef] [PubMed]
- Stoodley, P.; Sauer, K.; Davies, D.G.; Costerton, J.W. Biofilms as complex differentiated communities. Annu. Rev. Microbiol. 2002, 56, 187–209. [Google Scholar] [CrossRef] [PubMed]
- Flemming, H.C.; Wingender, J.; Szewzyk, U.; Steinberg, P.; Rice, S.A.; Kjelleberg, S. Biofilms: An emergent form of bacterial life. Nat. Rev. Microbiol. 2016, 14, 563–575. [Google Scholar] [CrossRef]
- Beer, D.D.; Stoodley, P.; Roe, F.; Lewandowski, Z. Effects of biofilm structures on oxygen distribution and mass transport. Biotechnol. Bioeng. 1993, 43, 1131–1138. [Google Scholar] [CrossRef] [PubMed]
- Palmer, R.J.J.; White, D.C. Developmental biology of biofilms: Implications for treatment and control. Trends Microbiol. 1997, 5, 435–440. [Google Scholar] [CrossRef]
- Shafahi, M.; Vafai, K. Synthesis of biofilm resistance characteristics against antibiotics. Int. J. Heat Mass Transf. 2010, 53, 2943–2950. [Google Scholar] [CrossRef]
- Ahmed, U.; Vafai, K. Analysis of biofilm growth in the presence of osmotic pressure and temperature effects. Int. J. Heat Mass Transf. 2012, 55, 5709–5721. [Google Scholar] [CrossRef][Green Version]
- Hauser, M.; Vafai, K. Analysis of the multidimensional effects in biofilms. Int. J. Heat Mass Transf. 2013, 56, 340–349. [Google Scholar] [CrossRef][Green Version]
- Vandevivere, P.; Baveye, P. Effect of bacterial extracellular polymers on the saturated hydraulic conductivity of sand columns. Appl. Environ. Microbiol. 1992, 58, 1690–1698. [Google Scholar] [CrossRef]
- Massol-Deyá, A.A.; Whallon, J.; Hickey, R.F.; Tiedje, J.M. Channel structures in aerobic biofilms of fixed-film reactors treating contaminated groundwater. Appl. Environ. Microbiol. 1995, 61, 769–777. [Google Scholar] [CrossRef]
- Pal, A.; Paul, A.K. Microbial extracellular polymeric substances central elements in heavy metal bioremediation. Indian J. Microbiol. 2008, 48, 49–64. [Google Scholar] [CrossRef] [PubMed]
- Tufenkji, N. Modeling microbial transport in porous media: Traditional approaches and recent developments. Adv. Water Resour. 2007, 30, 1455–1469. [Google Scholar] [CrossRef]
- Rummel, C.D.; Jahnke, A.; Gorokhova, E.; Kühnel, D.; Schmitt-Jansen, M. Impacts of biofilm formation on the fate and potential effects of microplastic in the aquatic environment. Environ. Sci. Technol. Lett. 2017, 4, 258–267. [Google Scholar] [CrossRef]
- Guan, J.; Qi, K.; Wang, J.; Wang, W.; Wang, Z.; Lu, N.; Qu, J. Microplastics as an emerging anthropogenic vector of trace metals in freshwater: Significance of biofilms and comparison with natural substrates. Water Res. 2020, 184, 116205. [Google Scholar] [CrossRef]
- Shafahi, M.; Vafai, K. Biofilm affected characteristics of porous structures. Int. J. Heat Mass Transf. 2009, 52, 574–581. [Google Scholar] [CrossRef]
- Baveye, P.; Vandevivere, P.; Hoyle, B.L.; DeLeo, P.C.; de Lozada, D.S. Environmental impact and mechanisms of the biological clogging of saturated soils and squifer materials. Crit. Rev. Environ. Sci. Technol. 1998, 28, 123–191. [Google Scholar] [CrossRef]
- Taylor, S.W.; Jaffé, P.R. Biofilm growth and the related changes in the physical properties of a porous medium 1. Experimental investigation. Water Resour. Res. 1990, 26, 2153–2159. [Google Scholar]
- Bouwer, H. Artificial recharge of groundwater: Hydrogeology and engineering. Hydrogeol. J. 2002, 10, 121–142. [Google Scholar] [CrossRef]
- Davis, C.A.; Pyrak-Nolte, L.J.; Atekwana, E.A.; Werkema, D.D.; Haugen, M.E. Acoustic and electrical property changes due to microbial growth and biofilm formation in porous media. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Rolland du Roscoat, S.; Martins, J.M.; Sechet, P.; Vince, E.; Latil, P.; Geindreau, C. Application of synchrotron X-ray microtomography for visualizing bacterial biofilms 3D microstructure in porous media. Biotechnol. Bioeng. 2014, 111, 1265–1271. [Google Scholar] [CrossRef]
- Trulear, M.G.; Characklis, W.G. Dynamics of biofilm processes. J. WPCF 1982, 54, 1288–1301. [Google Scholar]
- Stoodley, P.; Boyle, J.D.; DeBeer, D.; Lappin-Scott, H.M. Evolving perspectives of biofilm structure. Biofouling 1999, 14, 75–90. [Google Scholar] [CrossRef]
- Eighmy, T.T.; Maratea, D.; Bishop, P.L. Electron microscopic examination of wastewater biofilm formation and structural components. Appl. Environ. Microbiol. 1983, 45, 1921–1931. [Google Scholar] [CrossRef] [PubMed]
- Wijeyekoon, S.; Mino, T.; Satoh, H.; Matsuo, T. Effects of substrate loading rate on biofilm structure. Water Res. 2004, 38, 2479–2488. [Google Scholar] [CrossRef] [PubMed]
- Lecuyer, S.; Rusconi, R.; Shen, Y.; Forsyth, A.; Vlamakis, H.; Kolter, R.; Stone, H.A. Shear stress increases the residence time of adhesion of Pseudomonas aeruginosa. Biophys. J. 2011, 100, 341–350. [Google Scholar] [CrossRef] [PubMed]
- Stoodley, P.; Cargo, R.; Rupp, C.J.; Wilson, S.; Klapper, I. Biofilm material properties as related to shear-induced deformation and detachment phenomena. J. Ind. Microbiol. Biotechnol. 2002, 29, 361–367. [Google Scholar] [CrossRef]
- Wagner, M.; Taherzadeh, D.; Haisch, C.; Horn, H. Investigation of the mesoscale structure and volumetric features of biofilms using optical coherence tomography. Biotechnol. Bioeng. 2010, 107, 844–853. [Google Scholar] [CrossRef]
- Yang, J.; Cheng, S.; Li, C.; Sun, Y.; Huang, H. Shear stress affects biofilm structure and consequently current generation of bioanode in microbial electrochemical systems (MESs). Front. Microbiol. 2019, 10, 398. [Google Scholar] [CrossRef] [PubMed]
- Stoodley, P.; Dodds, I.; Boyle, J.D.; Lappin-Scott, H.M. Influence of hydrodynamics and nutrients on biofilm structure. J. Appl. Microbiol. 1999, 85, S19–S28. [Google Scholar] [CrossRef]
- Mukherjee, P.K.; Chand, D.V.; Chandra, J.; Anderson, J.M.; Ghannoum, M.A. Shear stress modulates the thickness and architecture of Candida albicans biofilms in a phase-dependent manner. Mycoses 2009, 52, 440–446. [Google Scholar] [CrossRef]
- Chen, M.J.; Zhang, Z.; Bott, T.R. Effects of operating conditions on the adhesive strength of Pseudomonas fluorescens biofilms in tubes. Colloids Surf. B Biointerfaces 2005, 43, 61–71. [Google Scholar] [CrossRef]
- Wagner, M.; Manz, B.; Volke, F.; Neu, T.R.; Horn, H. Online assessment of biofilm development, sloughing and forced detachment in tube reactor by means of magnetic resonance microscopy. Biotechnol. Bioeng. 2010, 107, 172–181. [Google Scholar] [CrossRef] [PubMed]
- Gjermansen, M.; Ragas, P.; Sternberg, C.; Molin, S.; Tolker-Nielsen, T. Characterization of starvation-induced dispersion in Pseudomonas putida biofilms. Environ. Microbiol. 2005, 7, 894–906. [Google Scholar] [CrossRef]
- Guillemot, G.; Vaca-Medina, G.; Martin-Yken, H.; Vernhet, A.; Schmitz, P.; Mercier-Bonin, M. Shear-flow induced detachment of Saccharomyces cerevisiae from stainless steel: Influence of yeast and solid surface properties. Colloids Surf. B Biointerfaces 2006, 49, 126–135. [Google Scholar] [CrossRef]
- Gjermansen, M.; Nilsson, M.; Yang, L.; Tolker-Nielsen, T. Characterization of starvation-induced dispersion in Pseudomonas putida biofilms: Genetic elements and molecular mechanisms. Mol. Microbiol. 2010, 75, 815–826. [Google Scholar] [CrossRef]
- Qin, C.-Z.; Hassanizadeh, S.M. Pore-network modeling of solute transport and biofilm growth in porous media. Transp. Porous Media 2015, 110, 345–367. [Google Scholar] [CrossRef]
- Cunningham, A.B.; Characklls, W.G.; Abedeen, F.; Crawford, D. Influence of biofilm accumulation on porous media hydrodynamics. Environ. Sci. Technol. 1991, 25, 1305–1311. [Google Scholar] [CrossRef]
- Kirk, M.F.; Santillan, E.F.U.; McGrath, L.K.; Altman, S.J. Variation in hydraulic conductivity with decreasing pH in a biologically-clogged porous medium. Int. J. Greenh. Gas. Control 2012, 11, 133–140. [Google Scholar] [CrossRef]
- Seymour, J.D.; Gage, J.P.; Codd, S.L.; Gerlach, R. Anomalous fluid transport in porous media induced by biofilm growth. Phys. Rev. Lett. 2004, 93, 198103. [Google Scholar] [CrossRef]
- Stoodley, P.; Debeer, D.; Lewandowski, Z. Liquid flow in biofilm systems. Appl. Environ. Microbiol. 1994, 60, 2711–2716. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Lewandowski, Z. Measurement of local mass transfer coefficient in biofilms. Biotechnol. Bioeng. 1995, 48, 737–744. [Google Scholar] [CrossRef] [PubMed]
- Tolker-Nielsen, T.; Brinch, U.C.; Ragas, P.C.; Andersen, J.B.; Jacobsen, C.S.; Molin, S. Development and dynamics of Pseudomonas sp. biofilms. J. Bacteriol. 2000, 182, 6482–6489. [Google Scholar] [CrossRef] [PubMed]
- Manz, B.; Volke, F.; Goll, D.; Horn, H. Measuring local flow velocities and biofilm structure in biofilm systems with magnetic resonance imaging (MRI). Biotechnol. Bioeng. 2003, 84, 424–432. [Google Scholar] [CrossRef] [PubMed]
- Klausen, M.; Aaes-Jorgensen, A.; Molin, S.; Tolker-Nielsen, T. Involvement of bacterial migration in the development of complex multicellular structures in Pseudomonas aeruginosa biofilms. Mol. Microbiol. 2003, 50, 61–68. [Google Scholar] [CrossRef]
- Seymour, J.D.; Codd, S.L.; Gjersing, E.L.; Stewart, P.S. Magnetic resonance microscopy of biofilm structure and impact on transport in a capillary bioreactor. J. Magn. Reson. 2004, 167, 322–327. [Google Scholar] [CrossRef] [PubMed]
- Gjersing, E.L.; Codd, S.L.; Seymour, J.D.; Stewart, P.S. Magnetic resonance microscopy analysis of advective transport in a biofilm reactor. Biotechnol. Bioeng. 2005, 89, 822–834. [Google Scholar] [CrossRef] [PubMed]
- Vandevivere, P.; Baveye, P. Saturated hydraulic conductivity reduction caused by aerobic bacteria in sand columns. Soil Sci. Soc. Am. J. 1992, 56, 1–13. [Google Scholar] [CrossRef]
- Vandevivere, P.; Baveye, P. Relationship between transport of bacteria and their clogging efficiency in sand columns. Appl. Environ. Microbiol. 1992, 58, 2523–2530. [Google Scholar] [CrossRef]
- Kim, D.-S.; Fogler, H.S. Biomass evolution in porous media and its effects on permeability under starvation conditions. Biotechnol. Bioeng. 2000, 69, 47–56. [Google Scholar] [CrossRef]
- Davis, C.A.; Pyrak-Nolte, L.J.; Atekwana, E.A.; Werkema, D.D.; Haugen, M.E. Microbial-induced heterogeneity in the acoustic properties of porous media. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Stewart, T.L.; Fogler, H.S. Biomass plug development and propagation in porous media. Biotechnol. Bioeng. 2000, 72, 353–363. [Google Scholar] [CrossRef]
- Stewart, T.L.; Scott Fogler, H. Pore-scale investigation of biomass plug development and propagation in porous media. Biotechnol. Bioeng. 2002, 77, 577–588. [Google Scholar] [CrossRef] [PubMed]
- Dunsmore, B.C.; Bass, C.J.; Lappin-Scott, H.M. A novel approach to investigate biofilm accumulation and bacterial transport in porous matrices. Environ. Microbiol. 2004, 6, 183–187. [Google Scholar] [CrossRef] [PubMed]
- Iltis, G.C.; Armstrong, R.T.; Jansik, D.P.; Wood, B.D.; Wildenschild, D. Imaging biofilm architecture within porous media using synchrotron-based X-ray computed microtomography. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Davit, Y.; Iltis, G.; Debenest, G.; Veran-Tissoires, S.; Wildenschild, D.; Gerino, M.; Quintard, M. Imaging biofilm in porous media using X-ray computed microtomography. J. Microsc. 2011, 242, 15–25. [Google Scholar] [CrossRef] [PubMed]
- Carrel, M.; Beltran, M.A.; Morales, V.L.; Derlon, N.; Morgenroth, E.; Kaufmann, R.; Holzner, M. Biofilm imaging in porous media by laboratory X-ray tomography: Combining a non-destructive contrast agent with propagation-based phase-contrast imaging tools. PLoS ONE 2017, 12, e0180374. [Google Scholar] [CrossRef]
- Carrel, M.; Morales, V.L.; Beltran, M.A.; Derlon, N.; Kaufmann, R.; Morgenroth, E.; Holzner, M. Biofilms in 3D porous media: Delineating the influence of the pore network geometry, flow and mass transfer on biofilm development. Water Res. 2018, 134, 280–291. [Google Scholar] [CrossRef]
- Hoskins, B.C.; Fevang, L.; Majors, P.D.; Sharma, M.M.; Georgiou, G. Selective imaging of biofilms in porous media by NMR relaxation. J. Magn. Reson. 1999, 139, 67–73. [Google Scholar] [CrossRef]
- Seymour, J.D.; Gage, J.P.; Codd, S.L.; Gerlach, R. Magnetic resonance microscopy of biofouling induced scale dependent transport in porous media. Adv. Water Resour. 2007, 30, 1408–1420. [Google Scholar] [CrossRef]
- Codd, S.L.; Vogt, S.J.; Hornemann, J.A.; Phillips, A.J.; Maneval, J.E.; Romanenko, K.R.; Hansen, L.; Cunningham, A.B.; Seymour, J.D. NMR relaxation measurements of biofouling in model and geological porous media. Org. Geochem. 2011, 42, 965–971. [Google Scholar] [CrossRef][Green Version]
- Kirkland, C.M.; Herrling, M.P.; Hiebert, R.; Bender, A.T.; Grunewald, E.; Walsh, D.O.; Codd, S.L. In situ detection of subsurface biofilm using low-field NMR: A field study. Environ. Sci. Technol. 2015, 49, 11045–11052. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.W.; Choi, H.; Pachepsky, Y.A. Biofilm morphology as related to the porous media clogging. Water Res. 2010, 44, 1193–1201. [Google Scholar] [CrossRef]
- Kone, T.; Golfier, F.; Orgogozo, L.; Oltéan, C.; Lefèvre, E.; Block, J.C.; Buès, M.A. Impact of biofilm-induced heterogeneities on solute transport in porous media. Water Resour. Res. 2014, 50, 9103–9119. [Google Scholar] [CrossRef]
- Nakashima, Y.; Nakano, T.; Nakamura, K.; Uesugi, K.; Tsuchiyama, A.; Ikeda, S. Three-dimensional diffusion of non-sorbing species in porous sandstone: Computer simulation based on X-ray microtomography using synchrotron radiation. J. Contam. Hydrol. 2004, 74, 253–264. [Google Scholar] [CrossRef]
- Werth, C.J.; Zhang, C.; Brusseau, M.L.; Oostrom, M.; Baumann, T. A review of non-invasive imaging methods and applications in contaminant hydrogeology research. J. Contam. Hydrol. 2010, 113, 1–24. [Google Scholar] [CrossRef] [PubMed]
- San José Martínez, F.; Muñoz Ortega, F.J.; Caniego Monreal, F.J.; Peregrina, F. Morphological functions with parallel sets for the pore space of X-ray CT images of soil columns. Pure Appl. Geophys. 2014, 173, 995–1009. [Google Scholar] [CrossRef]
- Zhou, H.; Mooney, S.J.; Peng, X. Bimodal soil pore structure investigated by a combined soil water retention curve and X-Ray computed tomography approach. Soil Sci. Soc. Am. J. 2017, 81, 1270–1278. [Google Scholar] [CrossRef]
- Kutsovsky, Y.E.; Scriven, L.E.; Davis, H.T.; Hammer, B.E. NMR imaging of velocity profiles and velocity distributions in bead packs. Phys. Fluids 1996, 8, 863–871. [Google Scholar] [CrossRef]
- Dijk, P.; Berkowitz, B.; Bendel, P. Investigation of flow in water-saturated rock fractures using nuclear magnetic resonance imaging (NMRI). Water Resour. Res. 1999, 35, 347–360. [Google Scholar] [CrossRef]
- Neu, T.R.; Manz, B.; Volke, F.; Dynes, J.J.; Hitchcock, A.P.; Lawrence, J.R. Advanced imaging techniques for assessment of structure, composition and function in biofilm systems. FEMS Microbiol. Ecol. 2010, 72, 1–21. [Google Scholar] [CrossRef]
- Eberl, H.J.; Picioreanu, C.; Heijnen, J.J.; Loosdrecht, M.C.M.V. A three-dimensional numerical study on the correlation of spatial structure, hydrodynamic conditions, and mass transfer and conversion in biofilms. Chem. Eng. Sci. 2000, 55, 6209–6222. [Google Scholar] [CrossRef]
- Stoodley, P.; Yang, S.; Lappin-Scott, H.; Lewandowski, Z. Relationship between mass transfer coefficient and liquid flow velocity in heterogenous biofilms using microelectrodes and confocal microscopy. Biotechnol. Bioeng. 1997, 56, 681–688. [Google Scholar] [CrossRef]
- Stewart, P.S.; Peyton, B.M.; Drury, W.J.; Murga, R. Quantitative observations of heterogeneities in Pseudomonas aeruginosa biofilms. Appl.Environ. Microbiol. 1993, 59, 327–329. [Google Scholar] [CrossRef] [PubMed]
- Murga, R.; Stewart, P.; Daly, D. Quantitative analysis of biofilm thickness variability. Biotechnol. Bioeng. 1994, 45, 503–510. [Google Scholar] [CrossRef]
- Heydorn, A.; Nielsen, A.T.; Hentzer, M.; Sternberg, C.; Givskov, M.; Ersbøll, B.K.; Molin, S. Quantification of biofilm structures by the novel computer program COMSTAT. Microbiology 2000, 146, 2395–2407. [Google Scholar] [CrossRef] [PubMed]
- Hentzer, M.; Teitzel, G.M.; Balzer, G.J.; Heydorn, A.; Molin, S.; Givskov, M.; Parsek, M.R. Alginate overproduction affects Pseudomonas aeruginosa biofilm structure and function. J. Bacteriol. 2001, 183, 5395–5401. [Google Scholar] [CrossRef]
- Garny, K.; Horn, H.; Neu, T.R. Interaction between biofilm development, structure and detachment in rotating annular reactors. Bioprocess Biosyst. Eng. 2008, 31, 619–629. [Google Scholar] [CrossRef]
- Kim, S.R.; Oh, H.S.; Jo, S.J.; Yeon, K.M.; Lee, C.H.; Lim, D.J.; Lee, C.H.; Lee, J.K. Biofouling control with bead-entrapped quorum quenching bacteria in membrane bioreactors: Physical and biological effects. Environ. Sci. Technol. 2013, 47, 836–842. [Google Scholar] [CrossRef]
- Rodriguez-Melcon, C.; Alonso-Hernando, A.; Riesco-Pelaez, F.; Garcia-Fernandez, C.; Alonso-Calleja, C.; Capita, R. Biovolume and spatial distribution of foodborne Gram-negative and Gram-positive pathogenic bacteria in mono- and dual-species biofilms. Food Microbiol. 2021, 94, 103616. [Google Scholar] [CrossRef]
- Knutson, C.E.; Werth, C.J.; Valocchi, A.J. Pore-scale simulation of biomass growth along the transverse mixing zone of a model two-dimensional porous medium. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Zhang, C.; Kang, Q.; Wang, X.; Zilles, J.L.; Muller, R.H.; Werth, C.J. Effects of pore-scale heterogeneity and transverse mixing on bacterial growth in porous media. Environ. Sci. Technol. 2010, 44, 3085–3092. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Valocchi, A.J.; Werth, C.J.; Liu, H. An improved pore-scale biofilm model and comparison with a microfluidic flow cell experiment. Water Resour. Res. 2013, 49, 8370–8382. [Google Scholar] [CrossRef]
- Tang, Y.; Liu, H. Modeling multidimensional and multispecies biofilms in porous media. Biotechnol. Bioeng. 2017, 114, 1679–1687. [Google Scholar] [CrossRef] [PubMed]
- Aghajani Delavar, M.; Wang, J. Pore-scale modeling of competition and cooperation of multispecies biofilms for nutrients in changing environments. AIChE J. 2020, 66. [Google Scholar] [CrossRef]
- Stewart, T.L.; Kim, D.-S. Modeling of biomass-plug development and propagation in porous media. Biochem. Eng. J. 2004, 17, 107–119. [Google Scholar] [CrossRef]
- Kapellos, G.E.; Alexiou, T.S.; Payatakes, A.C. Hierarchical simulator of biofilm growth and dynamics in granular porous materials. Adv. Water Resour. 2007, 30, 1648–1667. [Google Scholar] [CrossRef]
- Golfier, F.; Wood, B.D.; Orgogozo, L.; Quintard, M.; Buès, M. Biofilms in porous media: Development of macroscopic transport equations via volume averaging with closure for local mass equilibrium conditions. Adv. Water Resour. 2009, 32, 463–485. [Google Scholar] [CrossRef]
- Pintelon, T.R.; Graf von der Schulenburg, D.A.; Johns, M.L. Towards optimum permeability reduction in porous media using biofilm growth simulations. Biotechnol. Bioeng. 2009, 103, 767–779. [Google Scholar] [CrossRef]
- Graf von der Schulenburg, D.A.; Pintelon, T.R.R.; Picioreanu, C.; Van Loosdrecht, M.C.M.; Johns, M.L. Three-dimensional simulations of biofilm growth in porous media. AIChE J. 2009, 55, 494–504. [Google Scholar] [CrossRef]
- Ebigbo, A.; Helmig, R.; Cunningham, A.B.; Class, H.; Gerlach, R. Modelling biofilm growth in the presence of carbon dioxide and water flow in the subsurface. Adv. Water Resour. 2010, 33, 762–781. [Google Scholar] [CrossRef]
- Deng, W.; Cardenas, M.B.; Kirk, M.F.; Altman, S.J.; Bennett, P.C. Effect of permeable biofilm on micro- and macro-scale flow and transport in bioclogged pores. Environ. Sci. Technol. 2013, 47, 11092–11098. [Google Scholar] [CrossRef] [PubMed]
- Picioreanu, C.; Loosdrecht, M.C.M.V. Use of mathematical modelling to study biofilm development and morphology. In Biofilms in Medicine, Industry and Environmental Biotechnology: Characteristics, Analysis and Control; Lens, P., Moran, A.P., Mahony, T., Stoodley, P., O’Flaherty, V., Eds.; IWA: London, UK, 2003; pp. 413–438. [Google Scholar]
- Loosdrecht, M.C.M.V.; Heijnen, J.J.; Eberl, H.; Kreft, J.; Picioreanu, C. Mathematical modelling of biofilm structures. Anton. Van Leeuw. Int. J. G 2002, 81, 245–256. [Google Scholar] [CrossRef] [PubMed]
- Mattei, M.R.; Frunzo, L.; D’Acunto, B.; Pechaud, Y.; Pirozzi, F.; Esposito, G. Continuum and discrete approach in modeling biofilm development and structure: A review. J. Math. Biol. 2018, 76, 945–1003. [Google Scholar] [CrossRef]
- Hermanowicz, S.W. A simple 2D biofilm model yields a variety of morphological features. Math. Biosci. 2000, 169, 1–14. [Google Scholar] [CrossRef]
- Hunt, S.M.; Werner, E.M.; Huang, B.; Hamilton, M.A.; Stewart, P.S. Hypothesis for the role of nutrient starvation in biofilm detachment. Appl. Environ. Microbiol. 2004, 70, 7418–7425. [Google Scholar] [CrossRef]
- Acemel, R.D.; Govantes, F.; Cuetos, A. Computer simulation study of early bacterial biofilm development. Sci. Rep. 2018, 8, 5340. [Google Scholar] [CrossRef]
- Luna, E.; Dominguez-Zacarias, G.; Ferreira, C.P.; Velasco-Hernandez, J.X. Detachment and diffusive-convective transport in an evolving heterogeneous two-dimensional biofilm hybrid model. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2004, 70, 061909. [Google Scholar] [CrossRef]
- Klapper, I.; Rupp, C.J.; Cargo, R.; Purvedorj, B.; Stoodley, P. Viscoelastic fluid description of bacterial biofilm material properties. Biotechnol. Bioeng. 2002, 80, 289–296. [Google Scholar] [CrossRef]
- Chambless, J.D.; Stewart, P.S. A three-dimensional computer model analysis of three hypothetical biofilm detachment mechanisms. Biotechnol. Bioeng. 2007, 97, 1573–1584. [Google Scholar] [CrossRef]
- Cunningham, J.A.; Mendoza-Sanchez, I. Equivalence of two models for biodegradation during contaminant transport in groundwater. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- D’Acunto, B.; Esposito, G.; Frunzo, L.; Mattei, M.R.; Pirozzi, F. Mathematical modeling of heavy metal biosorption in multispecies biofilms. J. Environ. Eng. 2016, 142. [Google Scholar] [CrossRef]
- Picioreanu, C.; Loosdrecht, M.C.M.V.; Heijnen, J.J. Effect of diffusive and convective substrate transport on biofilm structure formation: A two-dimensional modeling study. Biotechnol. Bioeng. 2000, 69, 504–515. [Google Scholar] [CrossRef]
- Taherzadeh, D.; Picioreanu, C.; Horn, H. Mass transfer enhancement in moving biofilm structures. Biophys. J. 2012, 102, 1483–1492. [Google Scholar] [CrossRef]
- Pintelon, T.R.; Picioreanu, C.; Loosdrecht, M.C.; Johns, M.L. The effect of biofilm permeability on bio-clogging of porous media. Biotechnol. Bioeng. 2012, 109, 1031–1042. [Google Scholar] [CrossRef]
- Bottero, S.; Storck, T.; Heimovaara, T.J.; van Loosdrecht, M.C.; Enzien, M.V.; Picioreanu, C. Biofilm development and the dynamics of preferential flow paths in porous media. Biofouling 2013, 29, 1069–1086. [Google Scholar] [CrossRef]
- Komlos, J.; Cunningham, A.B.; Camper, A.K.; Sharp, R.R. Biofilm barriers to contain and degrade dissolved trichloroethylene. Environ. Prog. 2004, 23, 69–77. [Google Scholar] [CrossRef]
- Mitchell, A.C.; Phillips, A.J.; Hiebert, R.; Gerlach, R.; Spangler, L.H.; Cunningham, A.B. Biofilm enhanced geologic sequestration of supercritical CO2. Int. J. Greenh. Gas. Con. 2009, 3, 90–99. [Google Scholar] [CrossRef]
- Abdel Aal, G.Z.; Atekwana, E.A. Spectral induced polarization (SIP) response of biodegraded oil in porous media. Geophys. J. Int. 2014, 196, 804–817. [Google Scholar] [CrossRef]
- Lu, L.; Huggins, T.; Jin, S.; Zuo, Y.; Ren, Z.J. Microbial metabolism and community structure in response to bioelectrochemically enhanced remediation of petroleum hydrocarbon-contaminated soil. Environ. Sci. Technol. 2014, 48, 4021–4029. [Google Scholar] [CrossRef]
- Davis, C.A.; Atekwana, E.; Atekwana, E.; Slater, L.D.; Rossbach, S.; Mormile, M.R. Microbial growth and biofilm formation in geologic media is detected with complex conductivity measurements. Geophys. Res. Lett. 2006, 33, L18403. [Google Scholar] [CrossRef]
- Abdel Aal, G.Z.; Atekwana, E.A.; Atekwana, E.A. Effect of bioclogging in porous media on complex conductivity signatures. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Godefroy, S.; Korb, J.P.; Fleury, M.; Bryant, R.G. Surface nuclear magnetic relaxation and dynamics of water and oil in macroporous media. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2001, 64, 021605. [Google Scholar] [CrossRef]
- Heij, E.J.L.; Kerkhof, P.J.A.M.; Kopinga, K.; Pel, L. Determining expression porosity profiles during filtration and of sewage sludge by NMR imaging. AIChE J. 1996, 42, 953–959. [Google Scholar] [CrossRef]
- Bryar, T.R.; Knight, R.J. NMR relaxation measurements to quantify immiscible organic contaminants in sediments. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Dlubac, K.; Knight, R.; Song, Y.-Q.; Bachman, N.; Grau, B.; Cannia, J.; Williams, J. Use of NMR logging to obtain estimates of hydraulic conductivity in the High Plains aquifer, Nebraska, USA. Water Resour. Res. 2013, 49, 1871–1886. [Google Scholar] [CrossRef]
- Parsekian, A.D.; Grosse, G.; Walbrecker, J.O.; Müller-Petke, M.; Keating, K.; Liu, L.; Jones, B.M.; Knight, R. Detecting unfrozen sediments below thermokarst lakes with surface nuclear magnetic resonance. Geophys. Res. Lett. 2013, 40, 535–540. [Google Scholar] [CrossRef]
- Sanderlin, A.B.; Vogt, S.J.; Grunewald, E.; Bergin, B.A.; Codd, S.L. Biofilm detection in natural unconsolidated porous media using a low-field magnetic resonance system. Environ. Sci. Technol. 2013, 47, 987–992. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).