Advanced Chirp Transform Spectrometer with Novel Digital Pulse Compression Method for Spectrum Detection
Abstract
1. Introduction
2. Chirp Transform Spectrometer
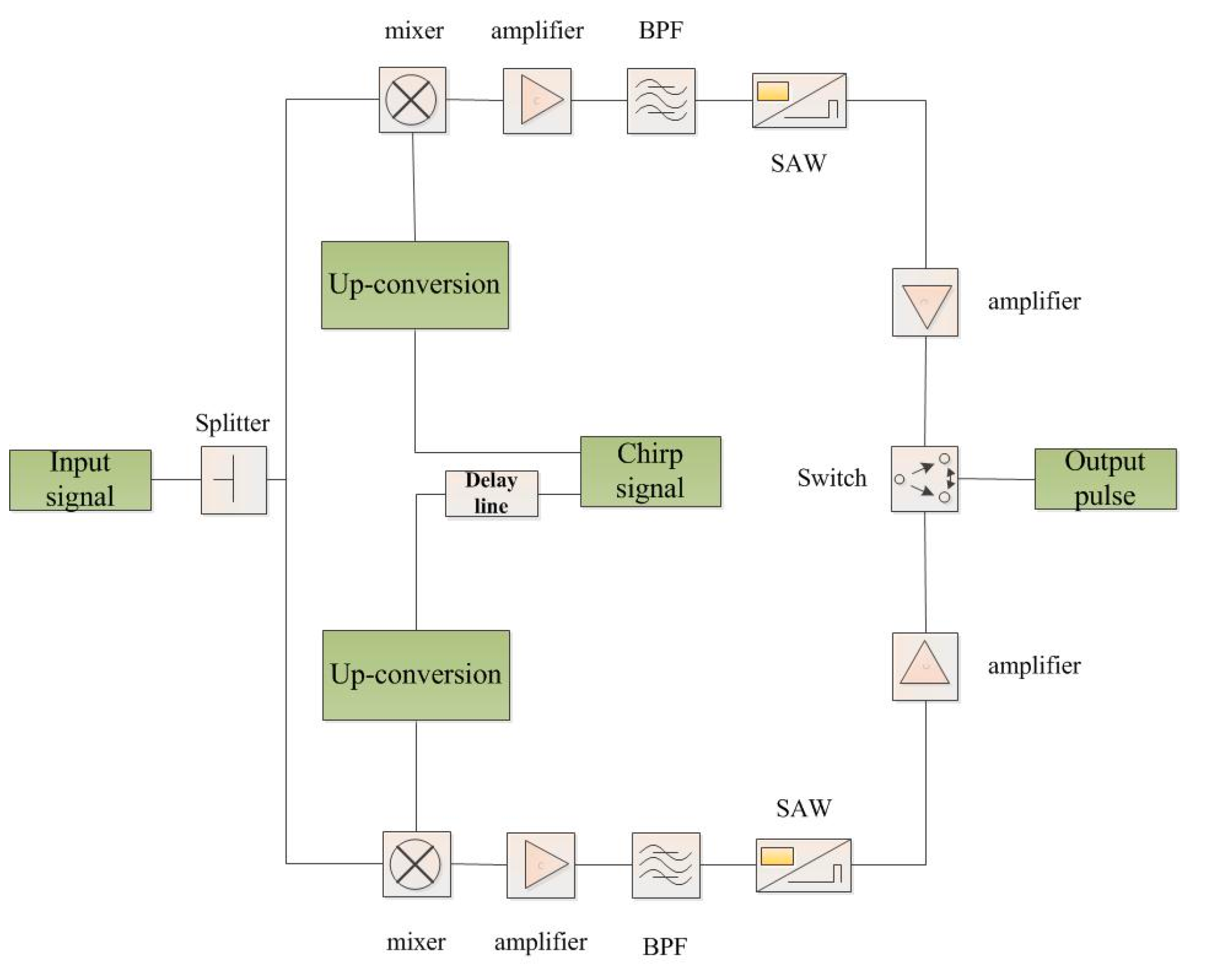
2.1. Functional Principle of CTS (Chirp Transform Spectrometer)
2.2. Pulse Compression in CTS System
- Influenced by the large insertion loss of the SAW convolution filters, which is usually larger than 40 dB, the operation bandwidth and dynamic range are both limited and cannot be very large. Therefore, the corresponding system performance, i.e., frequency resolution and sensitivity, are degraded.
- Imperfect manufacturing of the SAW convolution filter will cause deviations from the ideal dispersion characteristics, which will degrade the system performance, e.g., frequency resolution and power spectral density accuracy.
- The dispersive characteristic match between the generated expander chirp signal and the SAW filter behaving as the compressor/convolver need to be carefully considered. It is very hard to fabricate two SAW filters with perfectly matched dispersion characteristics.
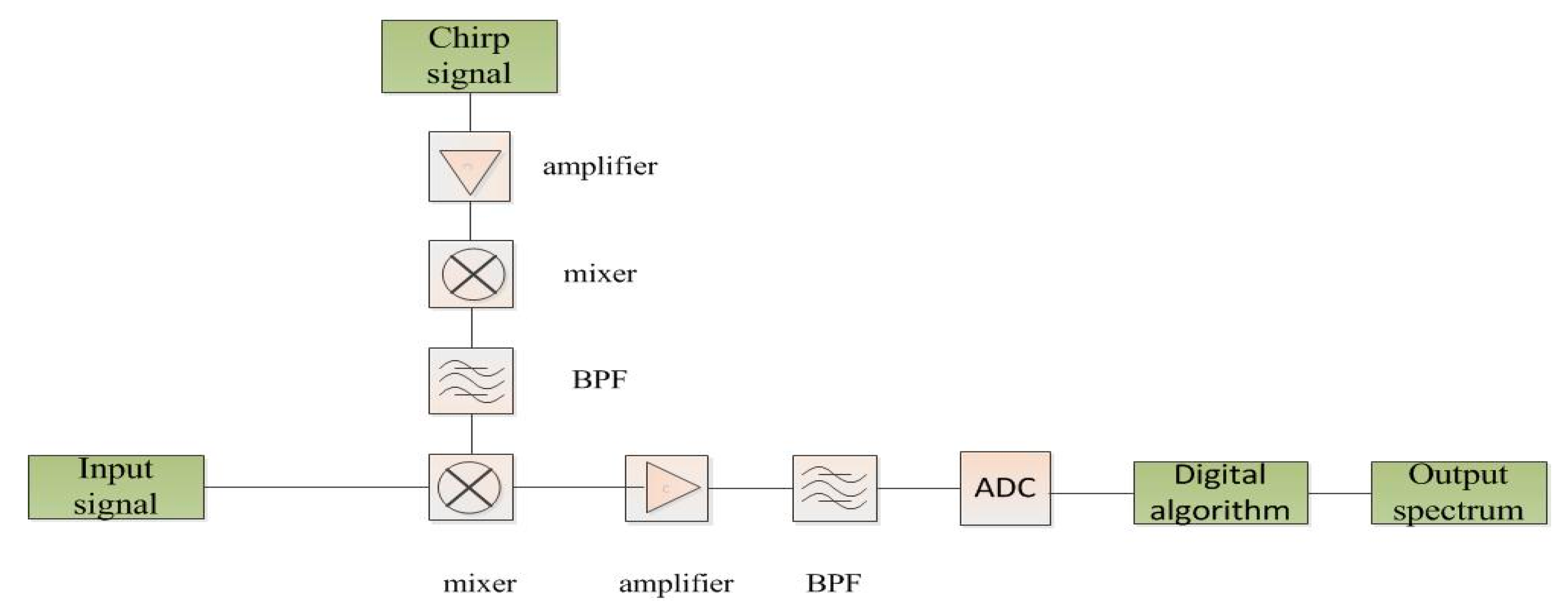
3. Digital Pulse Compression
3.1. Classical Digital Pulse Compression Methods
3.1.1. Pulse Compression in Time Domain
3.1.2. Pulse Compression in Frequency Domain
3.2. Linear Phase Sampling and Accumulating Method for Fast Pulse Compression
- 1.
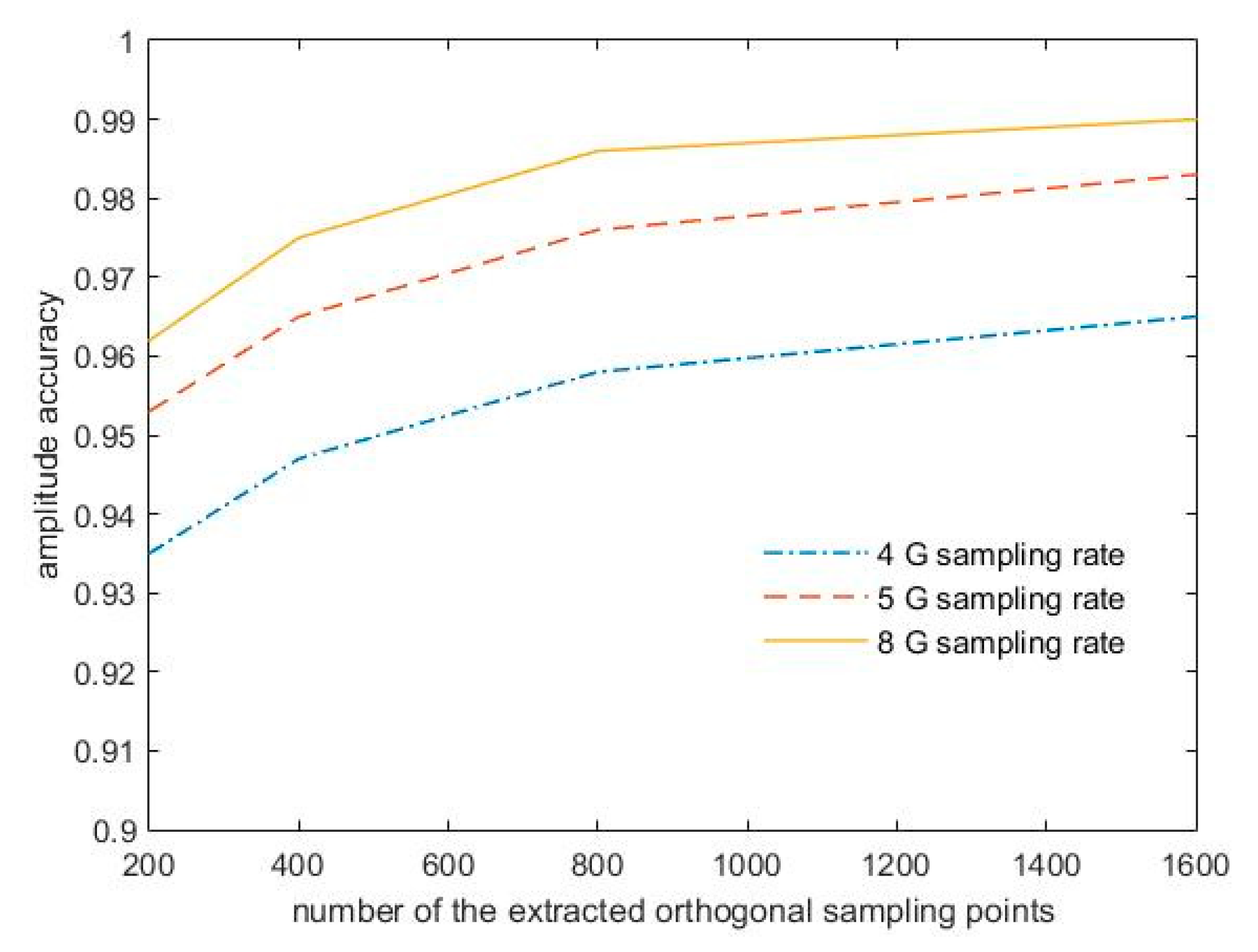
- Quantifying the IF chirp signalDifferent from Nyquist sampling, in the presented fast pulse compression method, the higher sampling rate will yield more suitable and precise orthogonal sampling points, whose phases satisfy (16) and (17), leading to higher amplitude accuracy of the output pulses.
- 2.
- Selecting two sets of mutually orthogonal sampling pointsDue to the sampling, the ideal orthogonal sampling points that satisfy (16) and (17) may not exist; therefore, adjacent points can be used as alternative orthogonal points. Thus, the phases of the nonideal orthogonal sampling points satisfy the following approximation formulas:where N is the total number of the selected sampling points, which depends on the sampling rate, the characteristic of the IF chirp signal and the compression time. The notation p denotes the approximation factor, which influences the amplitude accuracy of the output pulses. A higher sampling rate allows a smaller approximation factor to be used, leading to higher amplitude accuracy.
- 3.
- Spectrum detection under low frequency resolutionBased on the relationship between the compression time and the frequency resolution, the compression time can be determined for a certain low frequency resolution. The orthogonal sampling points that satisfy (31) can be determined. Subsequently, the i-th IF chirp component can be compressed by summing the orthogonal sampling points from the starting time , and other chirp components can also be compressed by shifting the starting time. This procedure can first obtain the spectrum distribution under a low frequency resolution with a modest amount of computation.
- 4.
- Spectrum subdivision under high frequency resolutionAfter the third procedure, the spectrum was measured under low frequency resolution. Setting an amplitude threshold, the channels with amplitudes below the threshold can be seen as noise channels, while those with amplitudes above it need to be further subdivided. Similarly, a longer compression time needs to be determined according to the high frequency resolution. Then, the corresponding orthogonal sampling points can be determined. Finally, the spectrum under high frequency resolution can be measured by the LPSA method. As analyzed in Section 3.2, for the signal with a relatively low dynamic range, the number of the orthogonal sampling points can be properly reduced due to the linear sampling, which can further reduce the required number of calculations.
4. Simulation and Analysis
4.1. Modeling of the CTS System
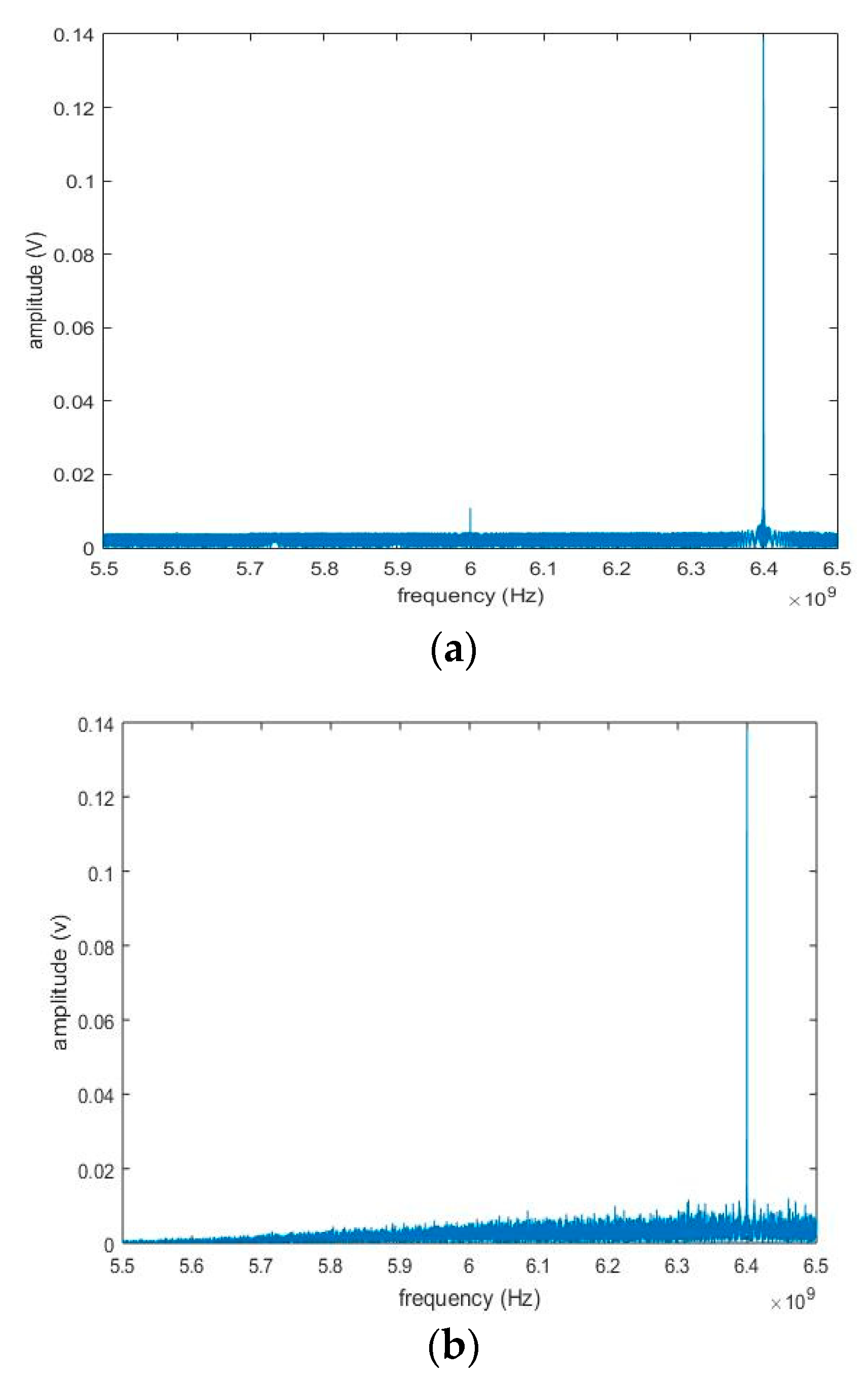
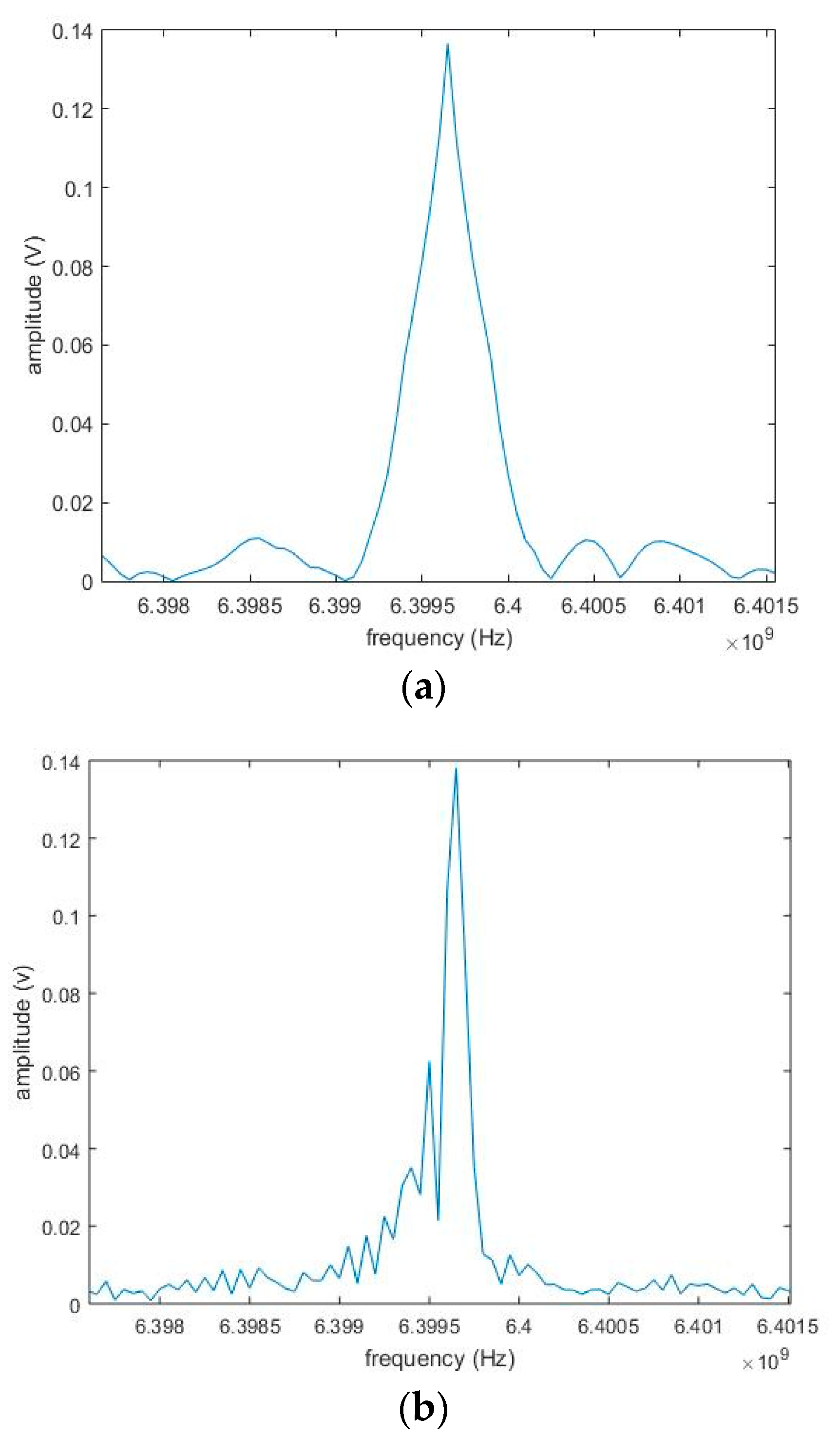
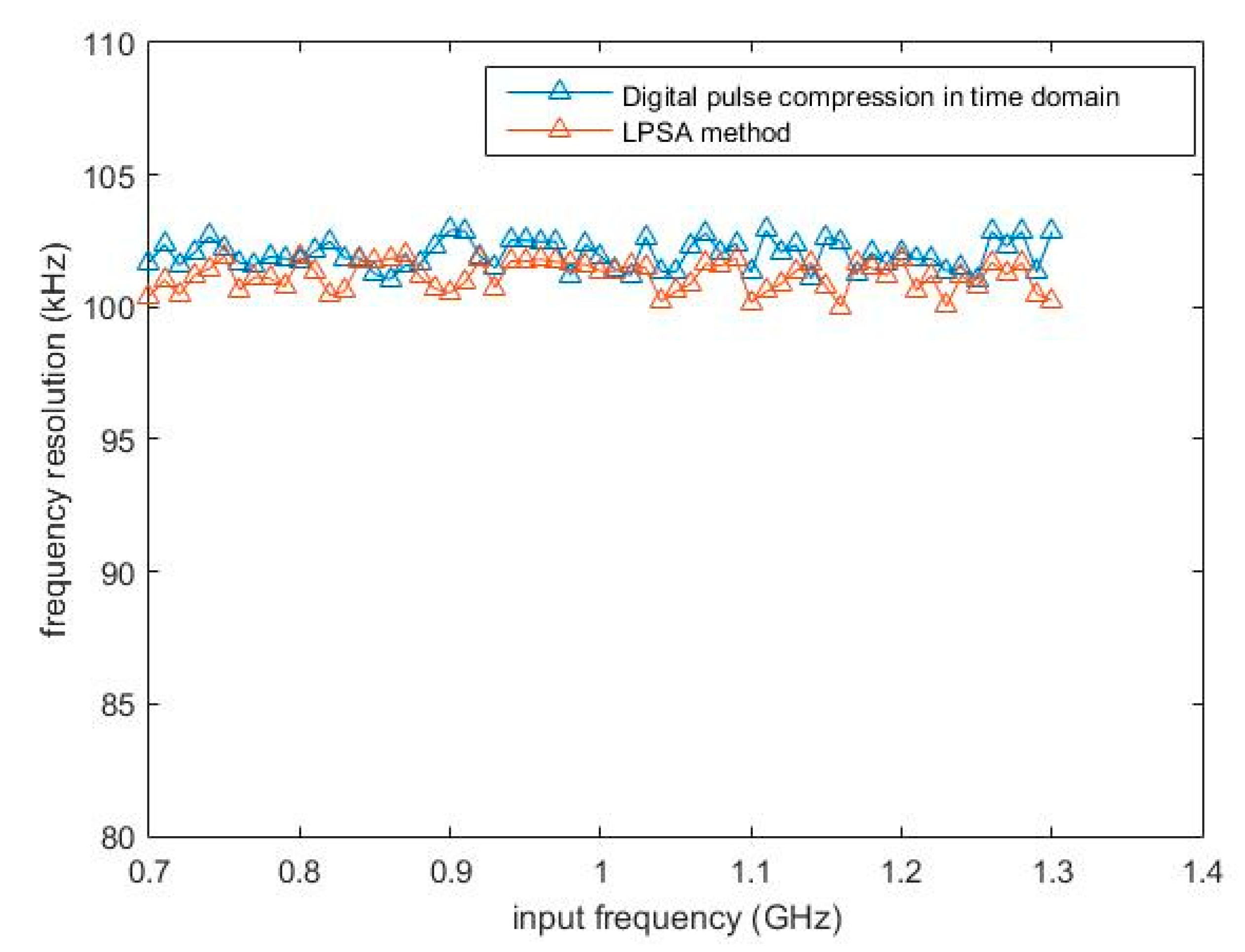
4.2. Simulation Results and Analysis
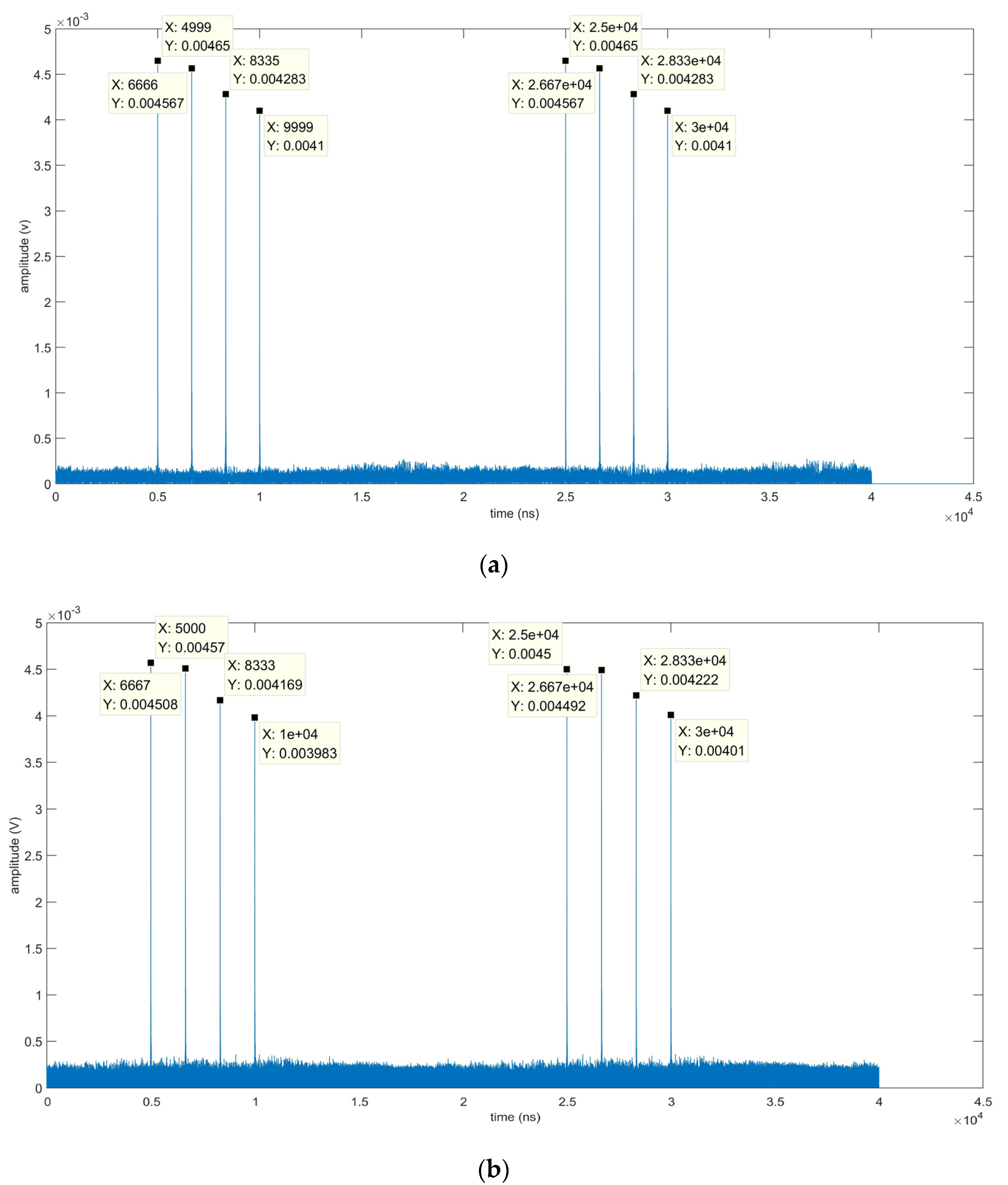
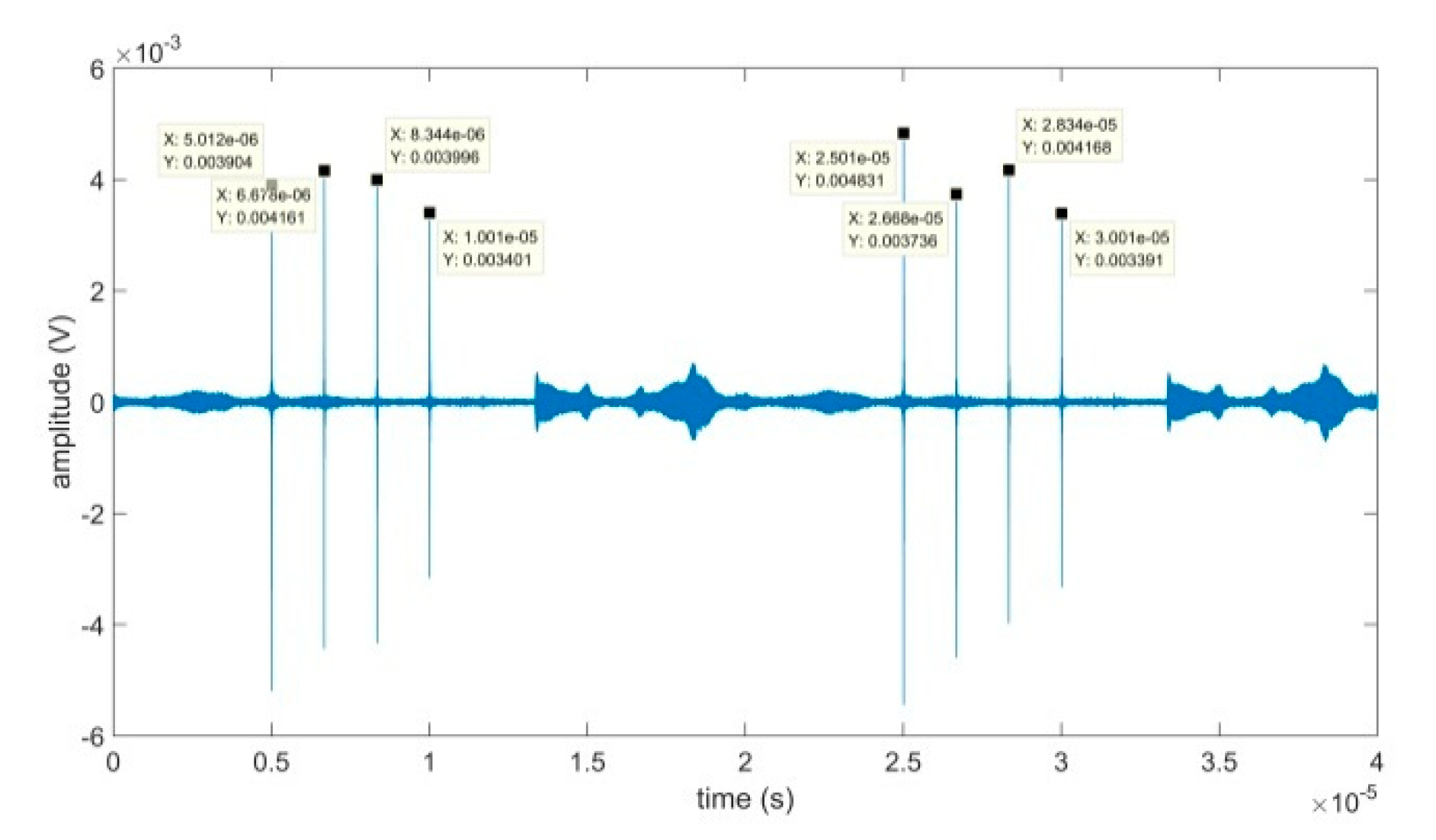
4.3. Analysis of Computational Complexity
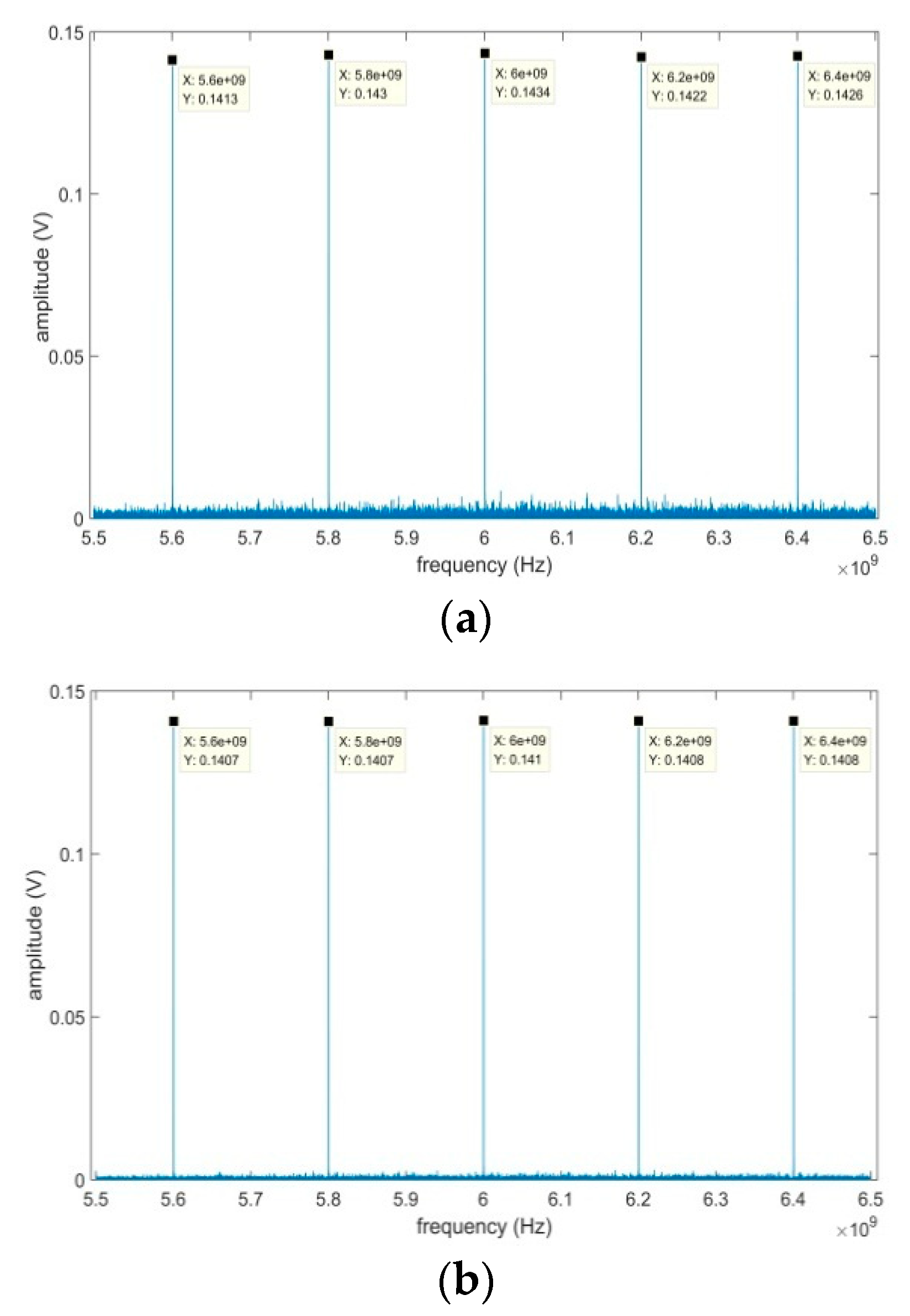
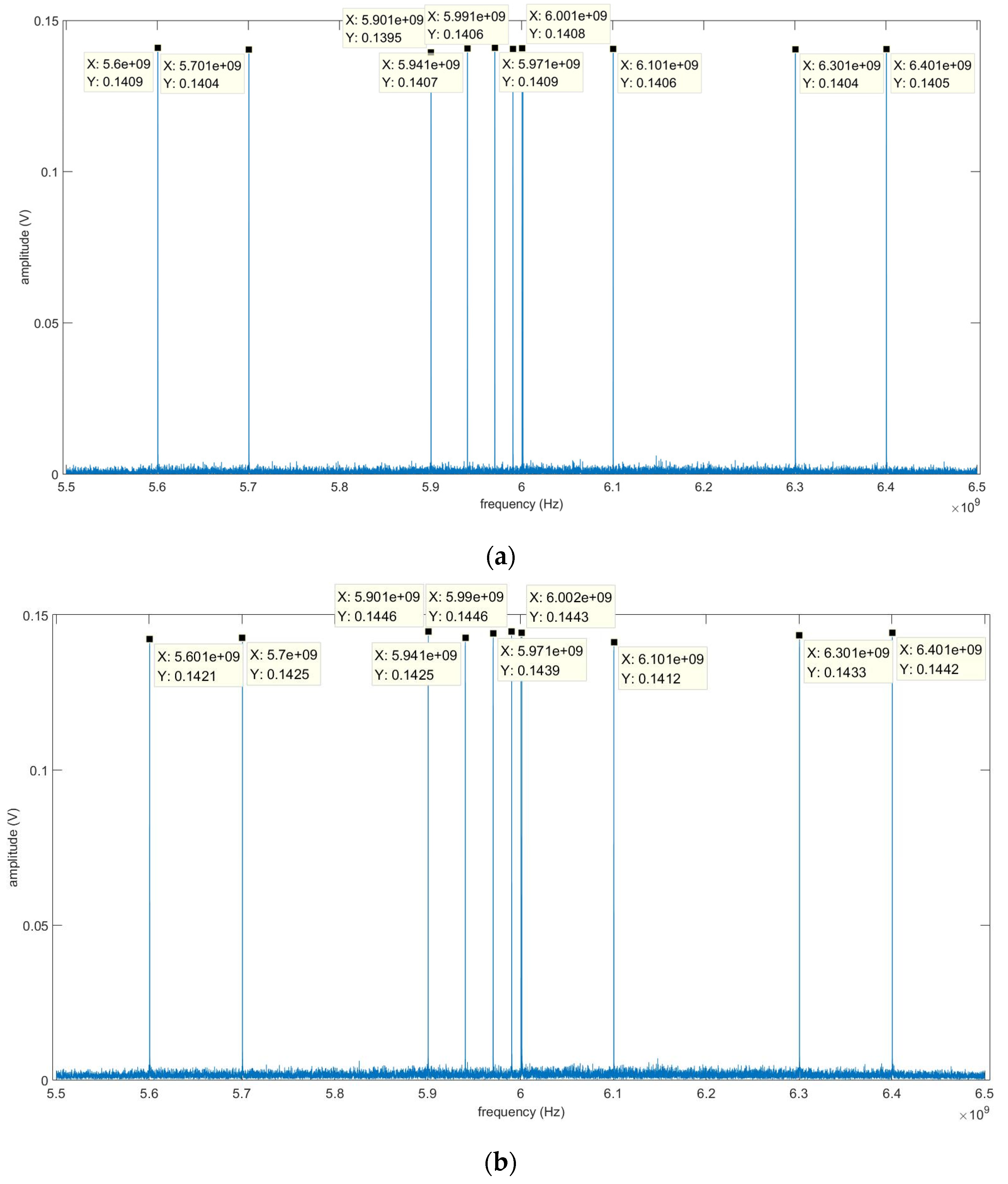
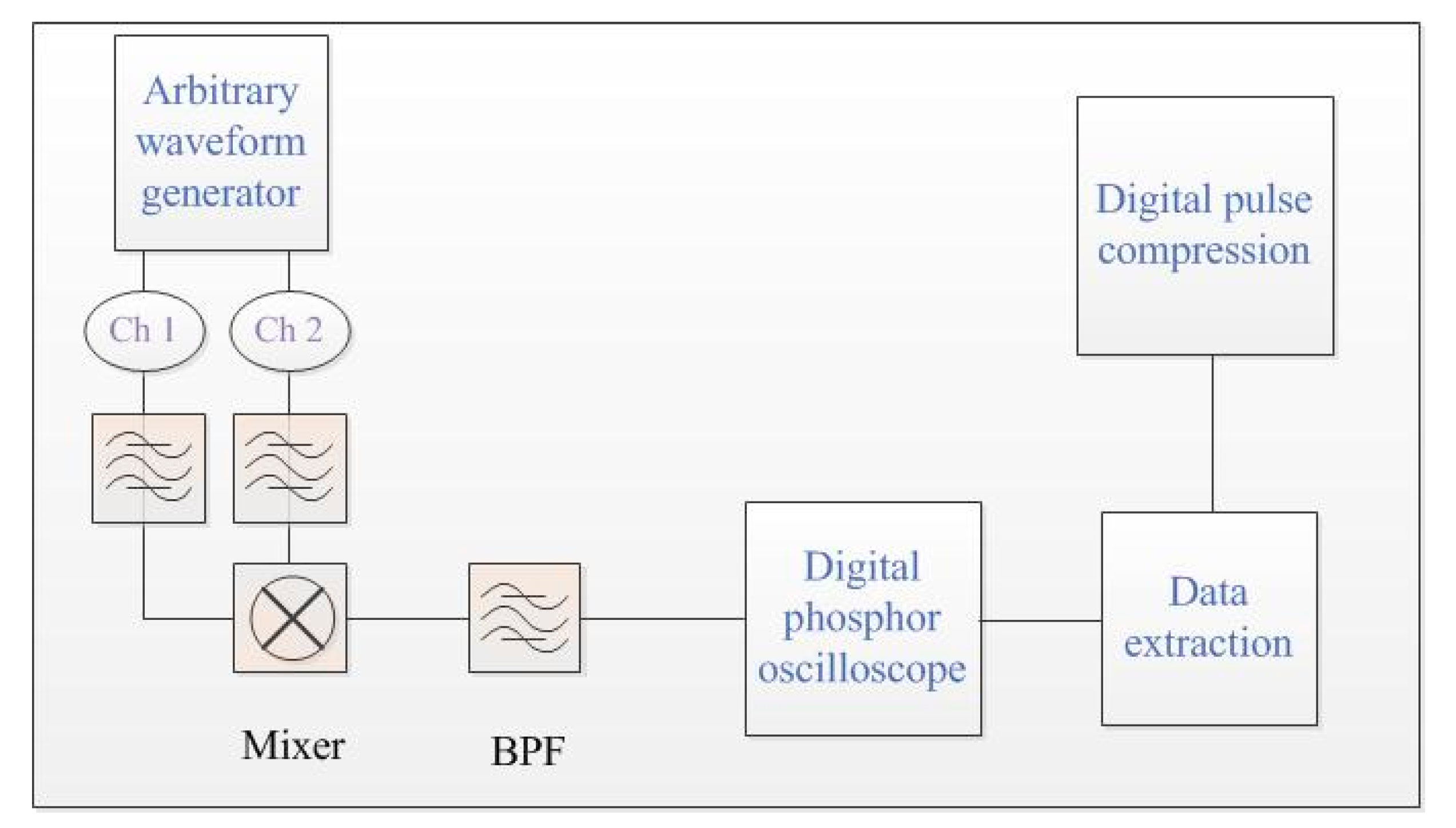
5. Experimental Verification and Analysis
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schwaab, G.W. Heterodyne spectrometer. Infrared Phys. Technol. 1999. [Google Scholar] [CrossRef]
- Stanko, S.; Klein, B.; Kerp, J. A Field Programmable Gate Array Spectrometer for Radio Astronomy. Astron. Astrophys. 2005, 436, 391–395. [Google Scholar] [CrossRef]
- Klein, B.; Philipp, S.D.; Güsten, R.; Krämer, I.; Samtleben, D. A new generation of spectrometer for radio astronomy: Fast Fourier Transform Spectrometer. Proc. Spie 2006, 6275, 627511. [Google Scholar]
- Klein, B.; Hochgurtel, S.; Kramer, I.; Bell, A.; Meyer, K.; Gusten, R. High-resolution wide-band Fast Fourier Transform spectrometers. Astron. Astrophys. 2012, 542, L3. [Google Scholar] [CrossRef]
- Weintroub, S. Pulse Compression and Radar. Nature 1967, 216, 409. [Google Scholar] [CrossRef]
- Klauder, J.R.; Price, A.C.; Darlington, S.; Albersheim, W.J. The theory and design of chirp radars. Bell Syst. Technol. J. 1960, 39, 745–808. [Google Scholar] [CrossRef]
- Darlington, S. Demodulation of wideband, low-power fm signals. Bell Syst. Technol. J. 2014, 43, 339–374. [Google Scholar] [CrossRef]
- Hartogh, P.; Hartmann, G. A high-resolution chirp transform spectrometer for microwave measurements. Meas. Sci. Technol. 1990, 1, 592–595. [Google Scholar] [CrossRef]
- Hartogh, P.; Hartmann, G.K.; Heimesaat, G. The Use of Chirp Transform Spectrometers for Real Time Fourier Transform of Stochastic Signals; Technical Report; Max-Planck-Institut fr Aeronomie: Katlenburg-Lindau, Germany, 1989. [Google Scholar]
- Lis, D.C.; Biver, N.; Bockeleemorvan, D.; Bockelée-Morvan, D.; Hartogh, P.; Bergin, E.A.; Blake, G.A.; Crovisier, J.; de Val-Borro, M.; Jehin, E.; et al. A herschel study of D/H in water in the jupiter-family comet 45p/honda-mrkos-pajdusakova and prospects for D/H measurements with CCAT. Astrophys. J. Lett. 2013, 774, L3. [Google Scholar] [CrossRef]
- Villanueva, G.L.; Mumma, M.J.; Novak, R.E.; Käufl, H.U.; Hartogh, P.; Encrenaz, T.; Tokunaga, A.; Khayat, A.; Smith, M.D. Strong water isotopic anomalies in the martian atmosphere: Probing current and ancient reservoirs. Science 2015, 348, 218–221. [Google Scholar] [CrossRef] [PubMed]
- Hartogh, P. A fast, high resolution chirp transform spectrometer for atmospheric remote sensing from space. IEEE Int. Geosci. Remote Sens. Symp. 1991, 979–982. [Google Scholar]
- Zhao, Q.; Tong, L.; Bo, G. A Novel Single-channel Arrangement in Chirp Transform Spectrometer for High-resolution Spectrum Detection. Appl. Sci. 2020, 10, 4896. [Google Scholar]
- Zhao, Q.; Tong, L.; Bo, G. Spectral Analysis of Stationary Signals Based on Two Simplified Arrangement of Chirp Transform Spectrometer. Electronics 2020, 10, 65. [Google Scholar] [CrossRef]
- Villanueva, G.L.; Hartogh, P.; Reindl, L.M. A digital dispersive matching network for SAW devices in chirp transform spectrometers. IEEE Trans. Microw. Theory Technol. 2006, 54, 1415–1424. [Google Scholar] [CrossRef]
- Li, X.Y.; Reindl, L.; Weimann, T.; Plessky, V.; Hartogh, P. Duty cycle weighting using e-beam lithography in RACs with constant groove depth for Chirp Transform Spectrometers. Adv. Geosci. 2010. [Google Scholar] [CrossRef]
- Qu, X.J.; Ma, C.M.; Zhang, S.X.; Lian, S.T. High real-time design of digital pulse compression based on FPGA. Math. Probl. Eng. 2015, 1–8. [Google Scholar] [CrossRef]
- Golubicic, Z.; Simic, S.; Zejak, A.J. Design and FPGA implementation of digital pulse compression for band-pass radar signals. J. Electr. Eng.-Elektrotechnicky Cas. 2013, 64, 191–195. [Google Scholar]
- Villanueva, G. The High Resolution Spectrometer for Sofia-Great: Instrumentation, Atmospheric Modeling and Observations. Ph.D. Thesis, Albert Ludwig University, Freiburg, Germany, 2004. [Google Scholar]
- Hofstadter, M.D.; Hartogh, P.; Mcmullin, J.P.; Martin, R.N.; Peters, W. A search for variability in the HCN to H2CO Ratio on Comet Hale-Bopp. Earth Moon Planets 1997, 78, 53–61. [Google Scholar] [CrossRef]
- Hartogh, P. High-resolution chirp transform spectrometer for middle atmospheric microwave sounding. In Satellite Remote Sensing of Clouds & the Atmosphere II; International Society for Optics and Photonics: Lindua, Germany, 1998. [Google Scholar]
- Hartogh, P.; Fujisada, H. Present and future chirp transform spectrometers for microwave remote sensing. IEEE Trans. Microw. Theory Tech. 1997, 3221, 328–339. [Google Scholar]
- Paganini, L. Power Spectral Density Accuracy in Chirp Transform Spectrometers. Ph.D. Thesis, Albert Ludwig University, Freiburg, Germany, 2008. [Google Scholar]
| Method | Classical Time-Domain Pulse Compression | Linear Phase Sampling and Accumulation |
|---|---|---|
| sampling rate | >2 GHz | 8 GHz |
| amplitude accuracy | >99% | >98% |
| frequency resolution | 101.6 kHz | 99.8 kHz |
| multiplication | ||
| addition |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Q.; Tong, L.; Gao, B. Advanced Chirp Transform Spectrometer with Novel Digital Pulse Compression Method for Spectrum Detection. Appl. Sci. 2021, 11, 960. https://doi.org/10.3390/app11030960
Zhao Q, Tong L, Gao B. Advanced Chirp Transform Spectrometer with Novel Digital Pulse Compression Method for Spectrum Detection. Applied Sciences. 2021; 11(3):960. https://doi.org/10.3390/app11030960
Chicago/Turabian StyleZhao, Quan, Ling Tong, and Bo Gao. 2021. "Advanced Chirp Transform Spectrometer with Novel Digital Pulse Compression Method for Spectrum Detection" Applied Sciences 11, no. 3: 960. https://doi.org/10.3390/app11030960
APA StyleZhao, Q., Tong, L., & Gao, B. (2021). Advanced Chirp Transform Spectrometer with Novel Digital Pulse Compression Method for Spectrum Detection. Applied Sciences, 11(3), 960. https://doi.org/10.3390/app11030960






