A Bacterial Chemotaxis-Inspired Coordination Strategy for Coverage and Aggregation of Swarm Robots
Abstract
1. Introduction
2. Bacteria Inspiration
2.1. Bacteria Behavior
2.2. Applications
3. Problem Statements and Preliminary
3.1. Problem Statements
- (1)
- Environment. The environment E ⊂ R2 is unobstructed and bounded. The size denotes L × L. L is the number of units for the length of horizontal (ordinate) range. There are no chemical signals in the environment.
- (2)
- Robots. The robot i is labeled as ri, i ∈ N, N = {1, 2, …, n}. Each robot is omnidirectional and can move in any direction. The physical structure of the robot is ignored. The robot can only sense the presence of other robots within a sense radius. The robots can collaborate with each other only by using the position information of their neighbors.
- (3)
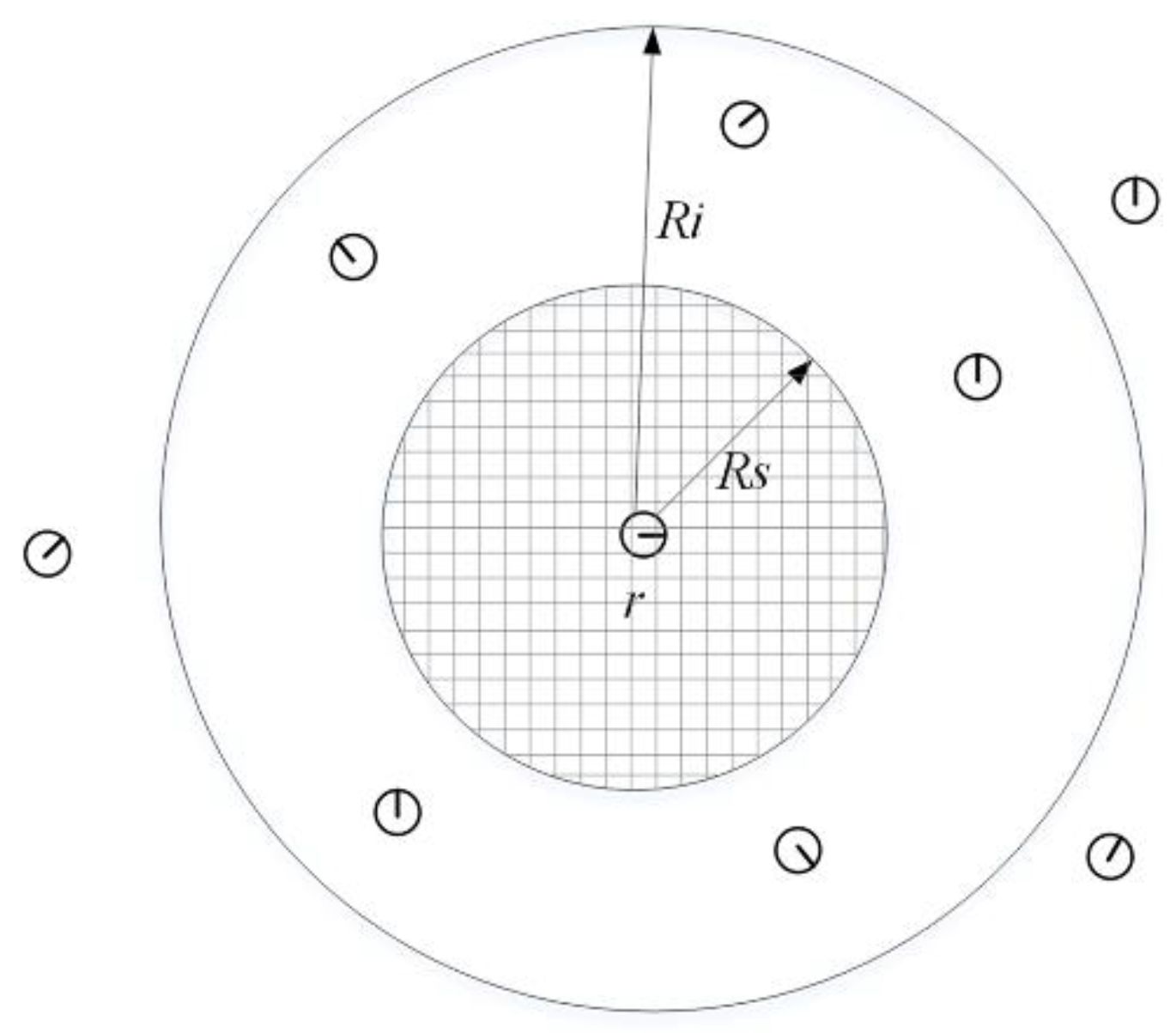
- Radius. As shown in Figure 3, we define Rs and Ri as the covered radius and sense radius, respectively, in which Ri = 2Rs. The robot can cover circular areas with a radius smaller than Rs. The robot can sense others within the Ri. Given robot i, the set of its neighbors is defined is the position of the robot. Ni follows the conditions: (i) ; (ii) ; (iii) .
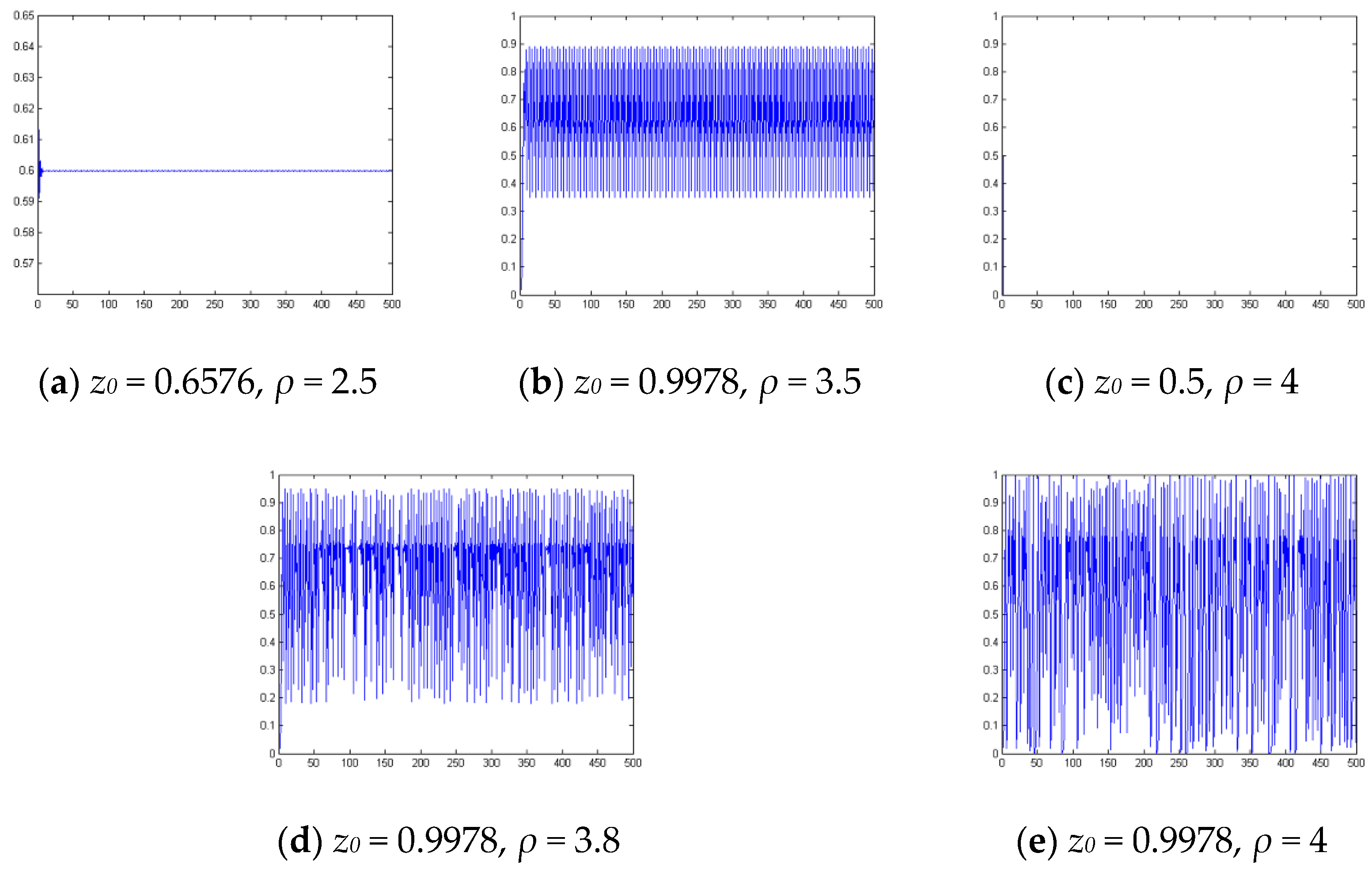
3.2. Chaotic Model
4. Proposed Method
- (1)
- Construct the fitness function, which is available for coverage and aggregation.
- (2)
- Compare the current fitness function value with previous ones.
- (3)
- The robot makes running or rotating depending on the comparison result in list (2).
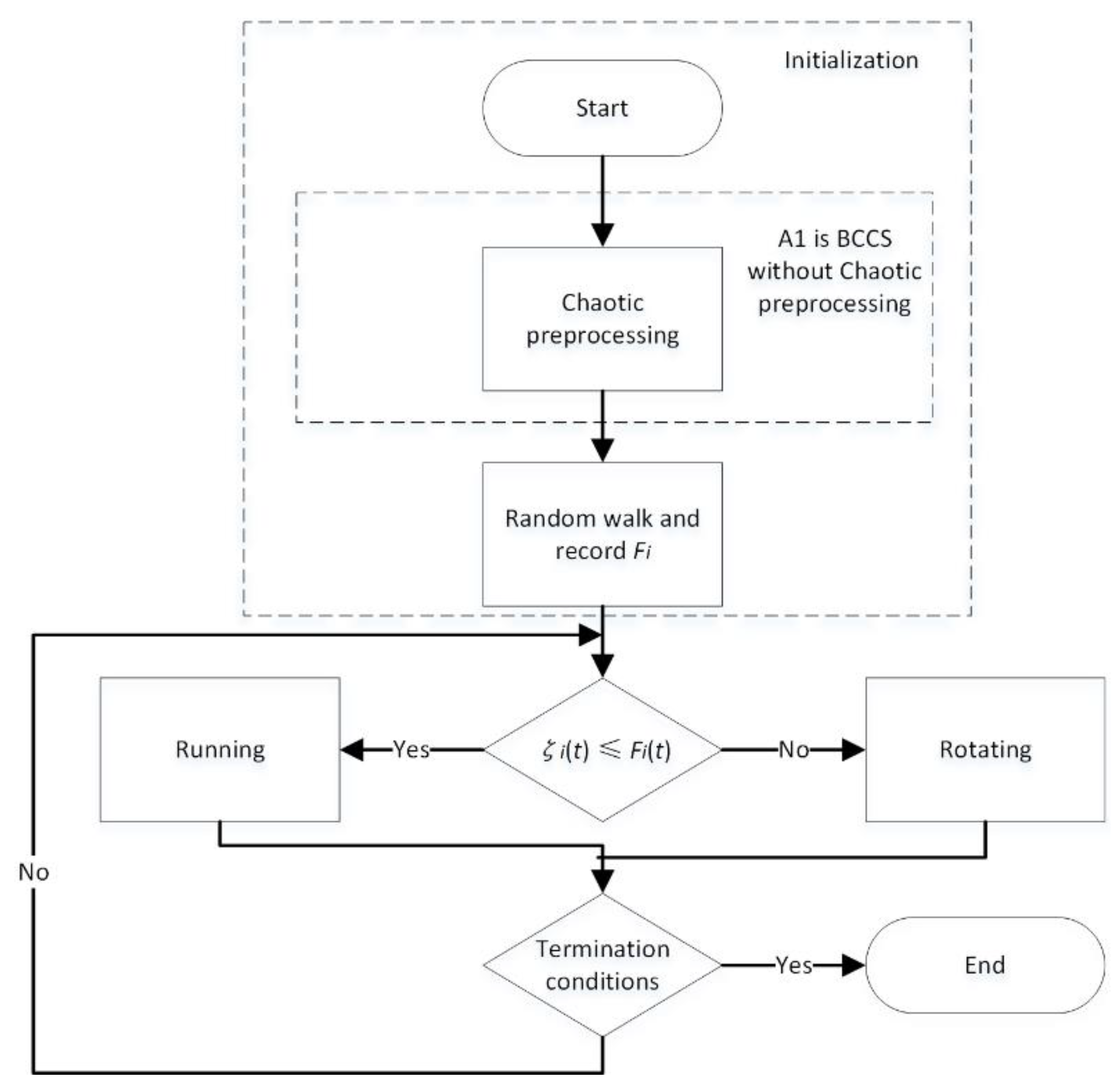
4.1. The BCCS for Coverage
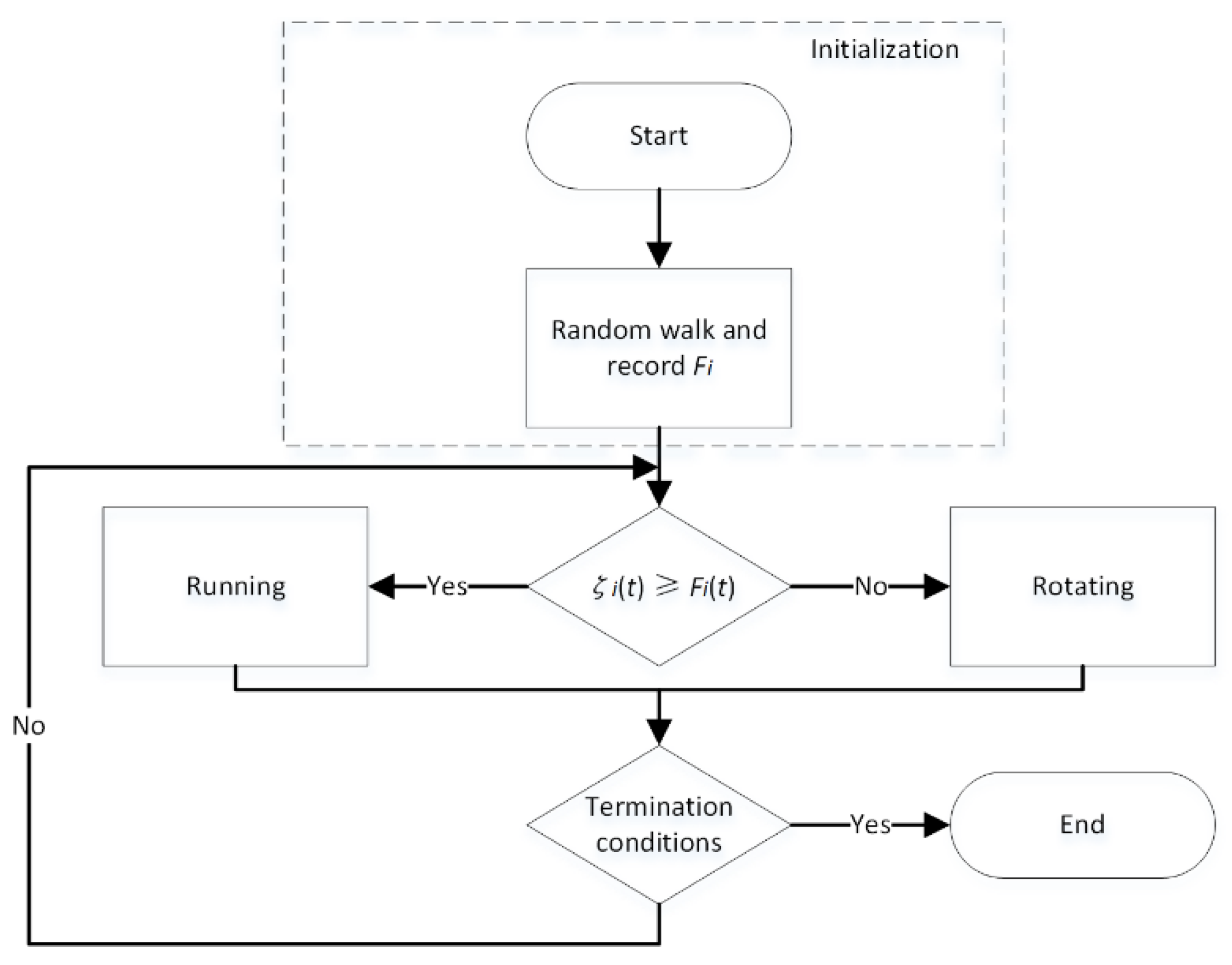
4.2. The BCCS for Aggregation
5. Simulations and Discussion
5.1. Simulations Setup
5.2. Evaluation Criteria
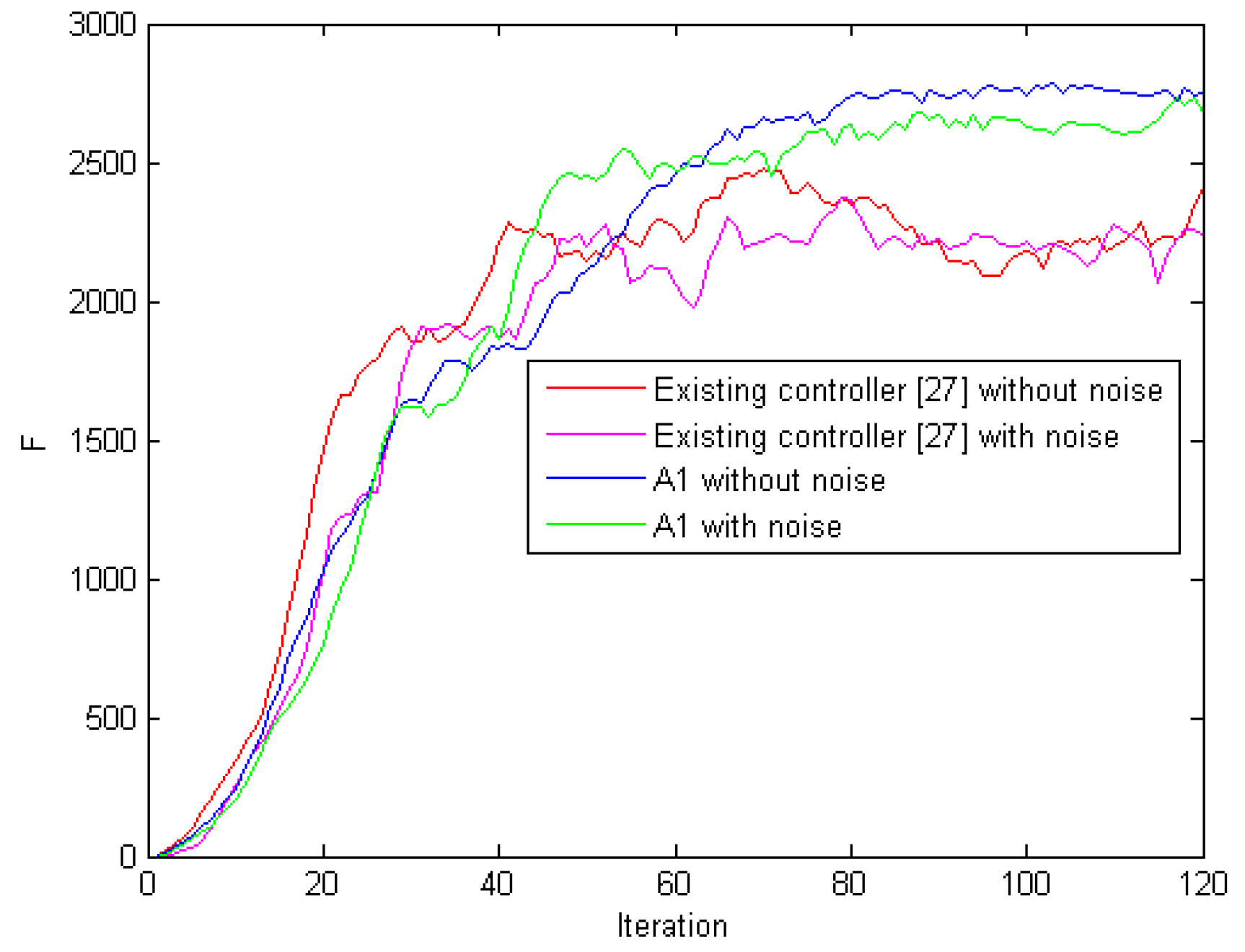
5.3. Comparison for Coverage
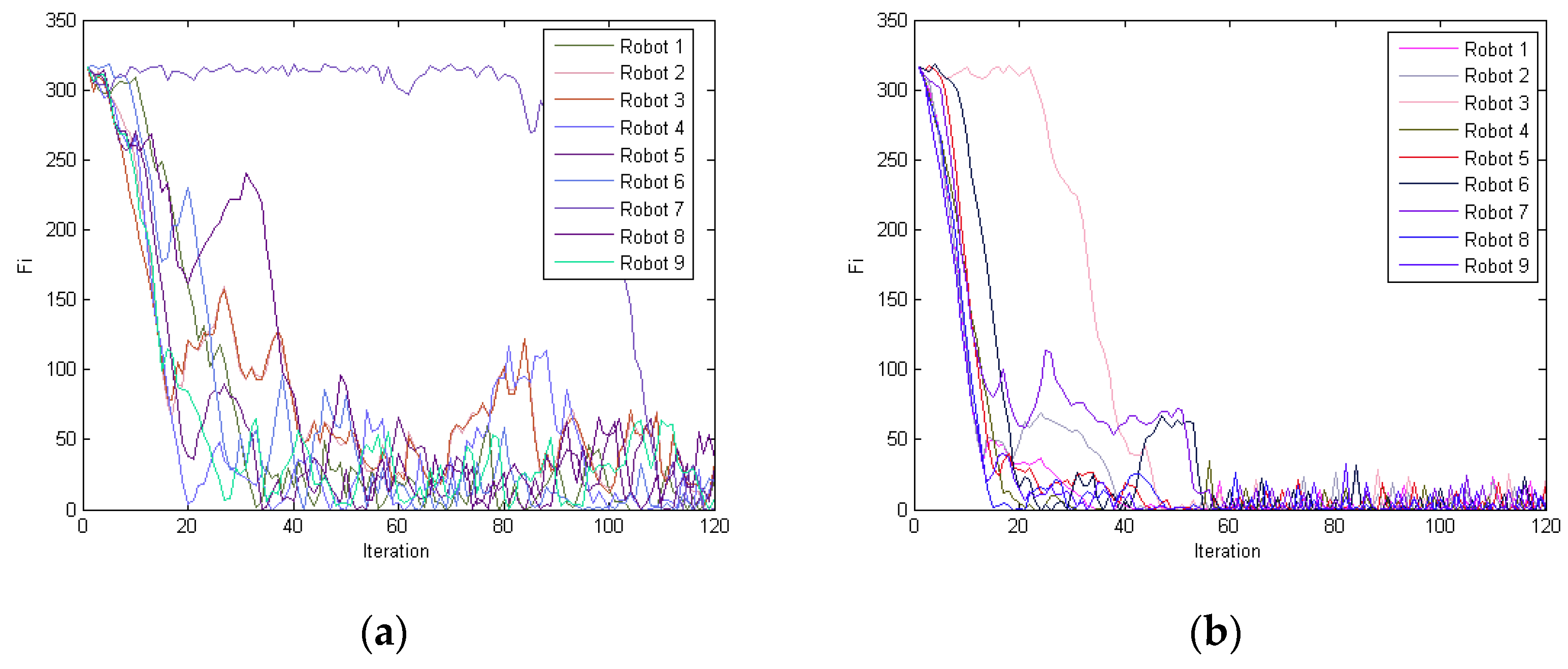
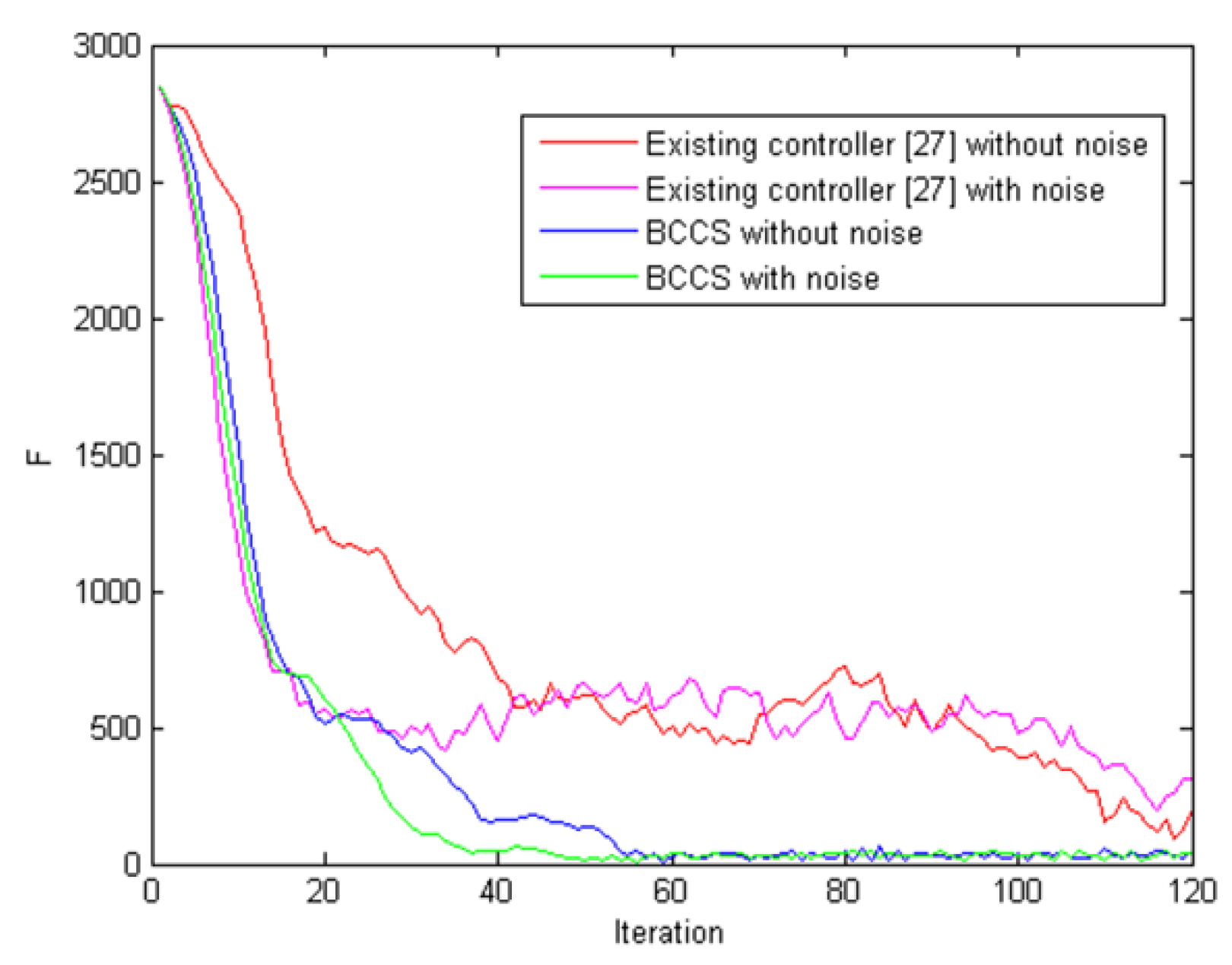
5.4. Comparison for Aggregation
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dadgar, M.; Jafari, S.; Hamzeh, A. A PSO-Based multi-robot cooperation method for target searching in unknown environments. Neurocomputing 2016, 177, 62–74. [Google Scholar] [CrossRef]
- Tang, H.; Sun, W.; Yu, H.; Lin, A.; Xue, M.; Song, Y. A novel hybrid algorithm based on PSO and FOA for target searching in unknown environments. Appl. Intell. 2019, 49, 2603–2622. [Google Scholar] [CrossRef]
- Aguilar, G.; Bravo, L.; Ruiz, U.; Murrieta-Cid, R.; Chavez, E. A Distributed Algorithm for Exploration of Unknown Environments with Multiple Robots. J. Intell. Robot. Syst. 2019, 95, 1021–1040. [Google Scholar] [CrossRef]
- De Rango, F.; Palmieri, N.; Yang, X.; Marano, S. Swarm robotics in wireless distributed protocol design for coordinating robots involved in cooperative tasks. Soft Comput. 2018, 22, 4251–4266. [Google Scholar] [CrossRef]
- Oyekan, J.; Hu, H.; Gu, D. Exploiting bacteria swarms for pollution mapping. In Proceedings of the 2009 IEEE International Conference on Robotics and Biomimetics (ROBIO), Gui Lin, China, 19–23 December 2009; pp. 39–44. [Google Scholar]
- Oyekan, J.; Gu, D.B.; Hu, H.S. Visual Imaging of Invisible Hazardous Substances Using Bacterial Inspiration. IEEE Trans. Syst. Man Cybern. Syst. 2013, 43, 1105–1115. [Google Scholar] [CrossRef]
- Oyekan, J.; Gu, D.B.; Hu, H.S. A model for using self-organized agents to visually map environmental profiles. Ecol. Complex. 2014, 19, 68–79. [Google Scholar] [CrossRef][Green Version]
- Sourjik, V.; Wingreen, N.S. Responding to Chemical Gradients: Bacterial Chemotaxis. Curr. Opin. Cell Biol. 2012, 24, 262–268. [Google Scholar] [CrossRef]
- Bakhale, M.; Hemalatha, V.; Dhanalakshmi, S.; Kumar, R.; Jain, M.S. A Dynamic Inertial Weight Strategy in Micro PSO for Swarm Robots. Wirel. Pers. Commun. 2020, 110, 573–592. [Google Scholar] [CrossRef]
- Martel, S.; Mohammadi, M. Using a swarm of self-propelled natural microrobots in the form of flagellated bacteria to perform complex micro-assembly tasks. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation (ICRA), Anchorage, AK, USA, 3–8 May 2010; pp. 500–505. [Google Scholar]
- Servant, A.; Qiu, F.; Mazza, M.; Kostarelos, K.; Nelson, B.J. Controlled In Vivo Swimming of a Swarm of Bacteria-Like Microrobotic Flagella. Adv. Mater. 2015, 27, 2981–2988. [Google Scholar] [CrossRef]
- Yigit, B.; Alapan, Y.; Sitti, M. Programmable Collective Behavior in Dynamically Self Assembled Mobile Microrobotic Swarms. Adv. Sci. 2019, 6, 1801837. [Google Scholar] [CrossRef]
- Nurzaman, S.G.; Matsumoto, Y.; Nakamura, Y.; Koizumi, S.; Ishiguro, H. “Yuragi”-Based adaptive mobile robot search with and without gradient sensing: From bacterial chemotaxis to a Levy walk. Adv. Robot. 2011, 25, 2019–2037. [Google Scholar] [CrossRef]
- Nurzaman, S.G.; Matsumoto, Y.; Nakamura, Y.; Shirai, K.; Ishiguro, H. Bacteria-Inspired underactuated mobile robot based on a biological fluctuation. Adapt. Behav. 2012, 20, 225–236. [Google Scholar] [CrossRef]
- Shirai, K.; Matsumoto, Y.; Nakamura, Y.; Koizumi, S.; Ishiguro, H. Noise-Based Underactuated Mobile Robot Inspired by Bacterial Motion Mechanism. In Proceedings of the 2009 IEEE-RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 11–15 October 2009; pp. 1043–1048. [Google Scholar]
- Davison, T.; Nguyen, H.; Nickels, K.; Frasch, D.; Basagaoglu, H. Localization of chemical sources using E. coli chemotaxis. In Proceedings of the Conference on Bioinspiration, Biomimetics and Bioreplication, Las Vegas, NV, USA, 21–22 May 2016; p. 9797. [Google Scholar]
- Russell, R.A.; Bab-Hadiashar, A.; Shepherd, R.L.; Wallace, G.G. A comparison of reactive robot chemotaxis algorithms. Robot. Auton. Syst. 2003, 45, 83–97. [Google Scholar] [CrossRef]
- Nickels, K.; Nguyen, H.; Frasch, D.; Davison, T. Effective Exploration Behavior for Chemical-Sensing Robots. BIOMIM 2019, 4, 69. [Google Scholar] [CrossRef] [PubMed]
- Hossain, M.A.; Ferdous, I. Autonomous robot path planning in dynamic environment using a new optimization technique inspired by bacterial foraging technique. Robot. Auton. Syst. 2014, 64, 137–141. [Google Scholar] [CrossRef]
- Jimenez, F.; Gonzalez-Herrera, F.; Lara-Alvarez, C. A Coordinated Wilderness Search and Rescue Technique Inspired by Bacterial Foraging Behavior. In Proceedings of the 2018 IEEE International Conference on Robotics and Biomimetics, Kuala Lumpur, Malaysia, 12–15 December 2018; pp. 318–324. [Google Scholar]
- Sharma, S.; Sur, C.; Shukla, A.; Tiwari, R. Multi Robot Path Planning for Known and Unknown Target Using Bacteria Foraging Algorithm. In Proceedings of the 5th International Conference on Swarm, Evolutionary and Memetic Computing, Bhubaneswar, India, 18–20 December 2015; pp. 674–685. [Google Scholar]
- Liang, X.D.; Li, L.Y.; Wu, J.G.; Chen, H.N. Mobile robot path planning based on adaptive bacterial foraging algorithm. J. Cent. South Univ. 2013, 20, 3391–3400. [Google Scholar] [CrossRef]
- Cortes, J.; Martinez, S.; Karatas, T.; Bullo, F. Coverage control for mobile sensing networks. IEEE Trans. Robot. Autom. 2004, 20, 243–255. [Google Scholar] [CrossRef]
- Bayindir, L. A review of swarm robotics tasks. Neurocomputing 2016, 172, 292–321. [Google Scholar] [CrossRef]
- Garnier, S.; Jost, C.; Gautrais, J.; Asadpour, M.; Caprari, G.; Jeanson, R.; Grimal, A.; Theraulaz, G. The embodiment of cockroach aggregation behavior in a group of micro-robots. Artif. Life 2008, 14, 387–408. [Google Scholar] [CrossRef]
- Caratozzolo, M.; Carnazza, S.; Fortuna, L.; Frasca, M.; Guglielmino, S.; Gurrieri, G.; Marletta, G. Self-Organizing models of bacterial aggregation states. Math. Biosci. Eng. 2008, 5, 75–83. [Google Scholar]
- Izumi, S.; Azuma, S.I.; Sugie, T. Multi-Robot Control Inspired by Bacterial Chemotaxis: Coverage and Rendezvous via Networking of Chemotaxis Controllers. IEEE Access 2020, 8, 124172–124184. [Google Scholar] [CrossRef]
- Izumi, S.; Azuma, S.I. Chemotaxis-Inspired Control for Multi-Agent Coordination: Formation Control by Two Types of Chemotaxis Controllers. New Gener. Comput. 2020, 38, 303–324. [Google Scholar] [CrossRef]
- Marques, L.; Nunes, U.; de Almeida, A. Olfaction-Based mobile robot navigation. Thin Solid Films 2001, 418, 51–58. [Google Scholar] [CrossRef]
- Shklarsh, A.; Ariel, G.; Schneidman, E.; Ben-Jacob, E. Smart Swarms of Bacteria-Inspired Agents with Performance Adaptable Interactions. PLoS Comput. Biol. 2011, 7, e1002177. [Google Scholar] [CrossRef]
- Rashid, S.; Long, Z.C.; Singh, S.; Kohram, M.; Vashistha, H.; Navlakha, S.; Salman, H.; Oltvai, Z.N.; Bar-Joseph, Z. Adjustment in tumbling rates improves bacterial chemotaxis on obstacle-laden terrains. Proc. Natl. Acad. Sci. USA. 2019, 116, 11770–11775. [Google Scholar] [CrossRef]
- Rashid, S.; Singh, S.; Navlakha, S.; Bar-Joseph, Z. A bacterial based distributed gradient descent model for mass scale evacuations. Swarm Evol. Comput. 2019, 46, 97–103. [Google Scholar] [CrossRef]
- Kurdi, H.; AlDaood, M.F.; Al-Megren, S.; Aloboud, E.; Aldawood, A.S.; Youcef-Toumi, K. Adaptive task allocation for multi-UAV systems based on bacteria foraging behavior. Appl. Soft. Comput. 2019, 83, 105643. [Google Scholar] [CrossRef]
- Pang, B.; Song, Y.; Zhang, C.J.; Wang, H.L.; Yang, R.T. A Swarm Robotic Exploration Strategy Based on an Improved Random Walk Method. J. Robot. 2019, 2019, 6914212. [Google Scholar] [CrossRef]
- Yang, B.; Ding, Y.S.; Jin, Y.C.; Hao, K.R. Self-Organized swarm robot for target search and trapping inspired by bacterial chemotaxis. Robot. Auton. Syst. 2015, 72, 83–92. [Google Scholar] [CrossRef]
- Yuan, X.F.; Zhang, T.; Xiang, Y.Z.; Dai, X.S. Parallel chaos optimization algorithm with migration and merging operation. Appl. Soft. Comput. 2015, 35, 591–604. [Google Scholar] [CrossRef]












| Related Works | Coverage | Aggregation | Multitask | |
|---|---|---|---|---|
| Related bacteria chemotaxis-inspired control strategies | [5] | ✓ | ||
| [6] | ✓ | |||
| [34] | ✓ | |||
| [35] | ✓ | ✓ | ||
| [27] | ✓ | ✓ | ✓ | |
| This paper | ✓ | ✓ | ✓ |
| Parameter | Value |
|---|---|
| Environments, E | 60 units × 60 units, 80 units × 80 units, 100 units × 100 units |
| Cell size, k | 1 unit × 1 unit |
| Number of robots, n | 9, 16, 25 |
| Velocity of robot, v | 1 unit/iteration |
| Maximum iterations, Imax | 2L |
| Covered radius, Rs | 10 units |
| Sense radius, Ri | 20 units |
| Logistic equation iterations, Ic | 500 |
| Rotation range, θ | 0–360° |
| The Controller in Reference [27] | A1 | BCCS | #Robots | #Environment | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Avg | Std | Succ (%) | Avg | Std | Succ (%) | Avg | Std | Succ (%) | (Unit × Unit) | |
| 84 | 10.88 | 93.33 | 73 | 9.35 | 100 | 55 | 8.81 | 100 | 9 | 60 × 60 |
| 117 | 17.19 | 76.67 | 98 | 13.17 | 93.33 | 71 | 8.47 | 100 | 16 | 80 × 80 |
| 162 | 15.88 | 60.00 | 126 | 19.55 | 90.00 | 108 | 22.88 | 100 | 25 | 100 × 100 |
| Robot | xi,1 | xi,2 |
|---|---|---|
| 1 | 10 | 10 |
| 2 | 30 | 10 |
| 3 | 50 | 10 |
| 4 | 10 | 30 |
| 5 | 30 | 30 |
| 6 | 50 | 30 |
| 7 | 10 | 50 |
| 8 | 30 | 50 |
| 9 | 50 | 50 |
| The Controller in Reference [27] | BCCS | #Robots | #Environment | ||||
|---|---|---|---|---|---|---|---|
| Avg | Std | Succ (%) | Avg | Std | Succ (%) | (Unit × Unit) | |
| 104 | 8.53 | 46.67 | 56 | 9.85 | 100 | 9 | 60 × 60 |
| 137 | 8.26 | 30.00 | 100 | 14.67 | 100 | 16 | 80 × 80 |
| 178 | 10.36 | 23.33 | 125 | 7.76 | 100 | 25 | 100 × 100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, L.; Mo, H.; Tian, P. A Bacterial Chemotaxis-Inspired Coordination Strategy for Coverage and Aggregation of Swarm Robots. Appl. Sci. 2021, 11, 1347. https://doi.org/10.3390/app11031347
Jiang L, Mo H, Tian P. A Bacterial Chemotaxis-Inspired Coordination Strategy for Coverage and Aggregation of Swarm Robots. Applied Sciences. 2021; 11(3):1347. https://doi.org/10.3390/app11031347
Chicago/Turabian StyleJiang, Laihao, Hongwei Mo, and Peng Tian. 2021. "A Bacterial Chemotaxis-Inspired Coordination Strategy for Coverage and Aggregation of Swarm Robots" Applied Sciences 11, no. 3: 1347. https://doi.org/10.3390/app11031347
APA StyleJiang, L., Mo, H., & Tian, P. (2021). A Bacterial Chemotaxis-Inspired Coordination Strategy for Coverage and Aggregation of Swarm Robots. Applied Sciences, 11(3), 1347. https://doi.org/10.3390/app11031347




