PSOFuzzer: A Target-Oriented Software Vulnerability Detection Technology Based on Particle Swarm Optimization
Abstract
1. Introduction
- (1)
- We theoretically analyze the feasibility of introducing the PSO algorithm to generate samples in the fuzzing process.
- (2)
- We use format constraint technology to build a fuzzing system based on the PSO algorithm that can be used for target-oriented vulnerability detection.
- (3)
- We experimentally verify the effectiveness of the PSO algorithm in fuzzing.
2. Related Work
2.1. Coverage-Oriented Fuzzing
2.2. Target-Oriented Fuzzing
2.3. Non-Oriented Fuzzing
3. Particle Swarm Optimization and Fuzzing
3.1. Principle of Particle Swarm Optimization
3.2. The Relationship between Fuzzing and Particle Swarm Optimization
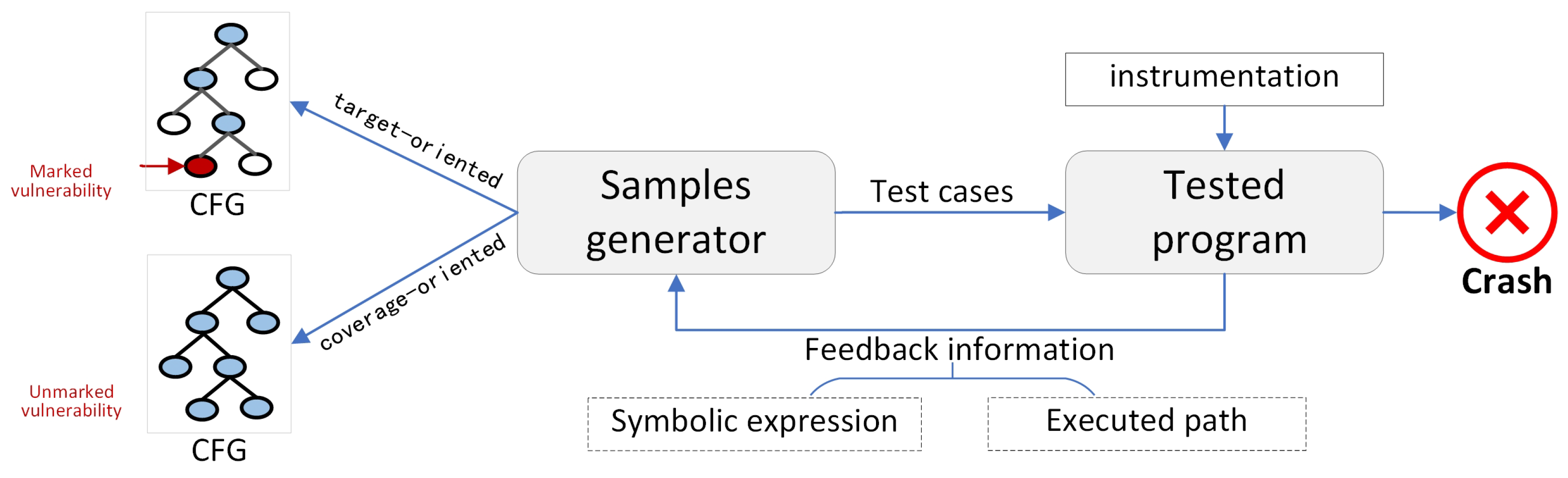
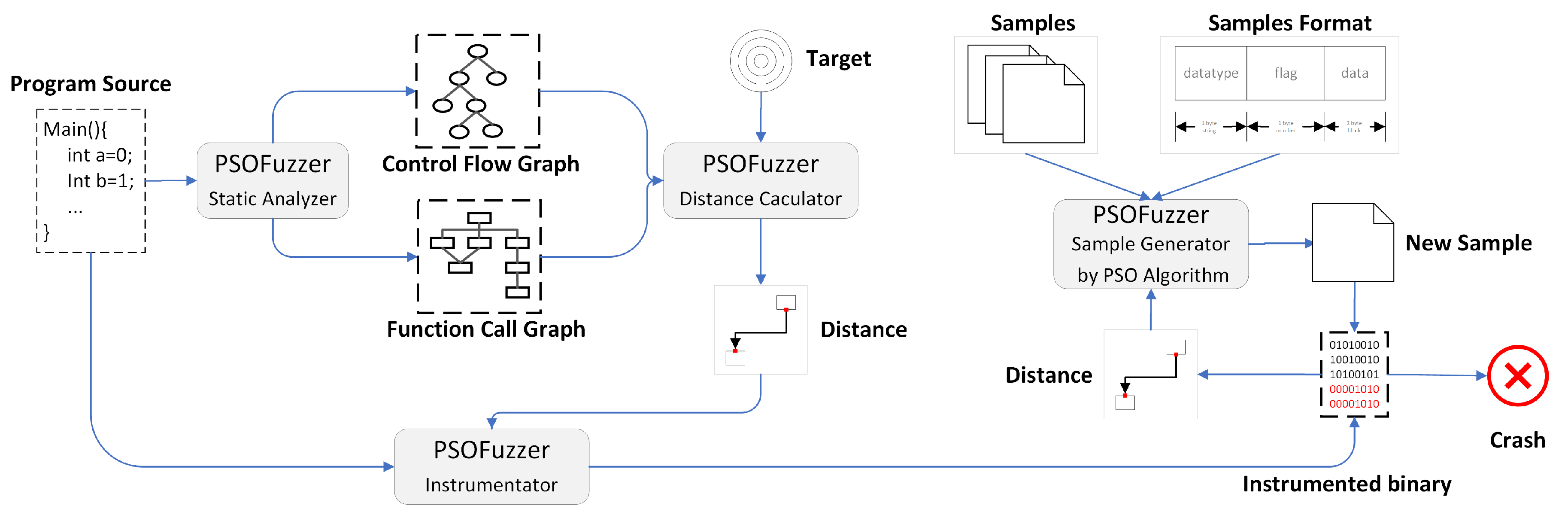
4. Fuzzing System Design
4.1. A Measurement of the Distance between a Seed Input and Target Point
4.2. Mapping Fuzzing to Particle Swarm
4.3. Sample Normalization
4.4. Fuzzing Based on the PSO Algorithm
- Update the local optimal particle: compare the fitness value of the current sample with the optimal fitness value of this sample in history . If , then update to . The fitness function f is used to obtain the distance between the current sample and the target point.
- Update the global optimal particle: compare each evaluation value of the local optimal samples with the evaluation value of the global optimal sample g. If , update g with .
- Generate samples: map the current sample into the template, establish the relationship between sample and vector, and then generate new sample based on Formulas (4) and (5). At this time, the sample has good guidance but lacks enough destructiveness to trigger vulnerabilities. PSOFuzzer uses mutation algorithms applied to different types of data fields under a certain probability to improve the effect of mutation. The mutation algorithms the PSOFuzzer used are shown in Table 1.
| Algorithm 1 PSO Algorithm. |
|
5. Experiment
5.1. Experimental Preparation
5.2. Results
5.3. Discussions
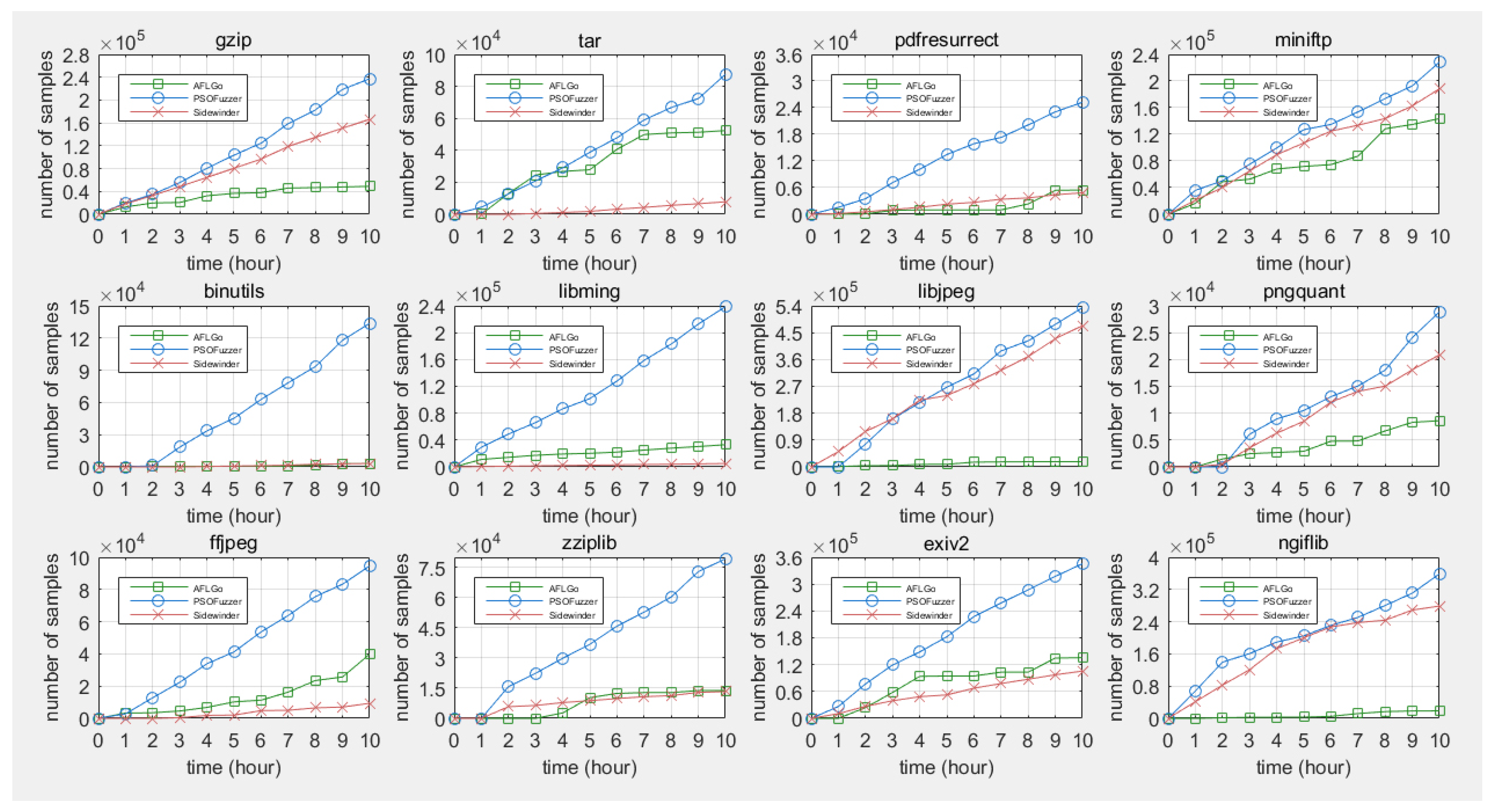
5.3.1. Capability of Generating High-Quality Samples
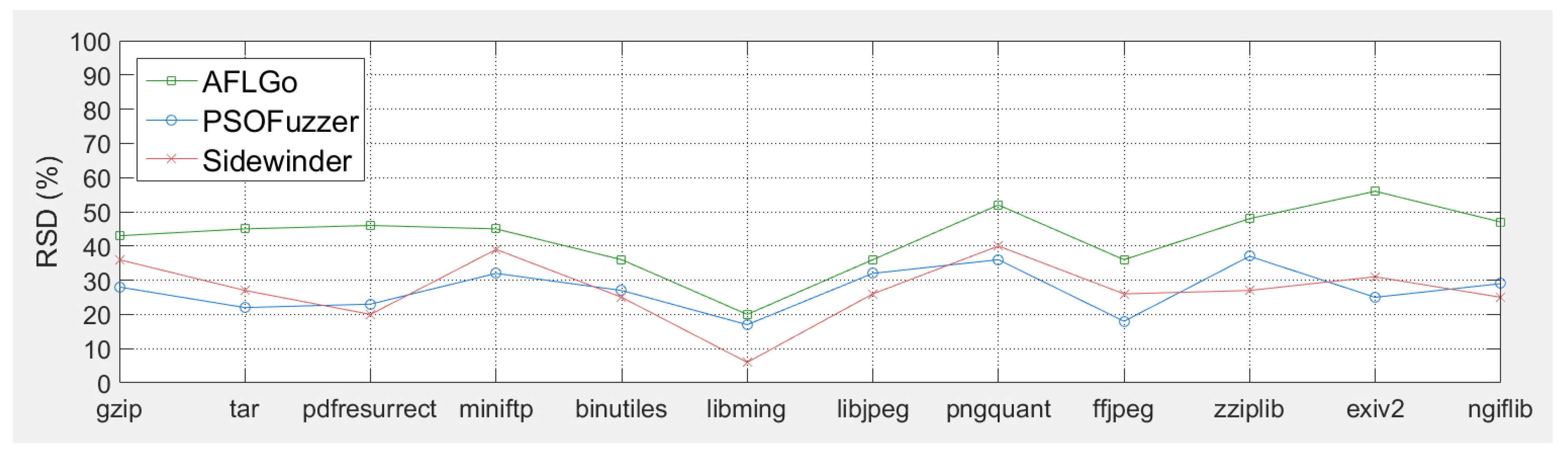
5.3.2. Stability of Generating High-Quality Samples
5.3.3. Capability of Triggering Vulnerabilities
6. Challenges/Limitations
- (1)
- The parameters and specified mutation algorithms that are employed in the swarm intelligence algorithm are mainly selected randomly, which cannot be adjusted by real-time test information. Thus, random selection may degrade the performance of the test.
- (2)
- PSOFuzzer uses format constraint technology, which relies on known sample format information. In the absence of sample format information, the sample mutation is blind, which reduces the probability of triggering vulnerabilities.
- (3)
- PSOFuzzer needs to specify the suspected vulnerability points in advance, which will increase the probability of false negatives when the suspected vulnerability points are inaccurate.
7. Future Directions
- (1)
- Optimize the strategy for choosing the mutation algorithms and PSO parameters by changing the value of the sample distance to the target to further improve the efficiency of fuzzing.
- (2)
- Collect the execution path by modifying a sample byte by byte and analyze the characteristics of the paths before and after modification. The sample format can be obtained in reverse to improve the adaptability of PSOFuzzer to the program without sample format information.
- (3)
- By analyzing the relevant elements in the code that hide vulnerability and extracting them as the input data to train the graph embedding model, the trained model can be employed to identify and locate vulnerabilities in the software.
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Miller, B.P.; Fredriksen, L.; So, B. An Empirical Study of the Reliability of Unix Utilities. Commun. ACM 1990, 33, 32–44. [Google Scholar] [CrossRef]
- Zzuf Fuzzer. Available online: https://github.com/samhocevar/zzuf (accessed on 9 February 2020).
- Peach Fuzzer. Available online: http://www.peachfuzzer.com/products/peach-platform (accessed on 9 February 2020).
- Spike Fuzzer Platform. Available online: http://resources.infosecinstitute.com/fuzzer-automation-with-spike/ (accessed on 28 August 2019).
- Röning, J.; Laakso, M.; Takanen, A.; Kaksonen, R. PROTOS-Systematic Approach to Eliminate Software Vulnerabilities. In Proceedings of the Invited Presentation at Microsoft Research, Seattle, WA, USA, 17 September 2002. [Google Scholar]
- Kamel, N.; Lanet, J.L. Analysis of HTTP Protocol Implementation in Smart Card Embedded Web Server. Int. J. Inf. Netw. Secur. 2013, 2, 417. [Google Scholar] [CrossRef]
- Alimi, V.; Vernois, S.; Rosenberger, C. Analysis of Embedded Applications by Evolutionary Fuzzing. In Proceedings of the International Conference on High Performance Computing & Simulation (HPCS), Bologna, Italy, 21–25 July 2014; pp. 551–557. [Google Scholar]
- Van, F.; Hond, B.; Torres, A.C. Security Testing of GSM Implementations. In Proceedings of the International Symposium on Engineering Secure Software and Systems, Munich, Germany, 26–28 February 2014; pp. 179–195. [Google Scholar]
- American Fuzzy Lop. Available online: https://github.com/mirrorer/afl (accessed on 9 February 2020).
- Böhme, M.; Pham, V.T.; Roychoudhury, A. Coverage-based greybox fuzzing as markov chain. IEEE Trans. Softw. Eng. 2017, 45, 489–506. [Google Scholar] [CrossRef]
- Gan, S.; Zhang, C.; Qin, X.; Tu, X.; Li, K.; Pei, Z.; Chen, Z. Collafl: Path sensitive fuzzing. In Proceedings of the 2018 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 21–23 May 2018; pp. 679–696. [Google Scholar]
- She, D.; Pei, K.; Epstein, D.; Yang, J.; Ray, B.; Jana, S. NEUZZ: Efficient fuzzing with neural program smoothing. In Proceedings of the IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 19–23 May 2019; pp. 803–817. [Google Scholar]
- Lyu, C.; Ji, S.; Zhang, C.; Li, Y.; Lee, W.H.; Song, Y.; Beyah, R. MOPT: Optimized Mutation Scheduling for Fuzzers. In Proceedings of the 28th USENIX Security Symposium, Santa Clara, CA, USA, 14–16 August 2019; pp. 1949–1966. [Google Scholar]
- Cadar, C.; Dunbar, D.; Engler, D.R. KLEE: Unassisted and Automatic Generation of High-coverage Tests for Complex Systems Programs. In Proceedings of the USENIX Symposium on Operating Systems Design and Implementation (OSDI), San Diego, CA, USA, 8–10 December 2008; Volume 8, pp. 209–224. [Google Scholar]
- Chipounov, V.; Kuznetsov, V.; Candea, G. S2E: A platform for in-vivo multi-path analysis of software systems. ACM Sigplan Not. 2011, 46, 265–278. [Google Scholar] [CrossRef]
- Cha, S.K.; Avgerinos, T.; Rebert, A.; Brumley, D. Unleashing Mayhem on Binary Code. In Proceedings of the IEEE Symposium on Security and Privacy (S&P), San Francisco, CA, USA, 21–23 May 2012; pp. 380–394. [Google Scholar]
- Godefroid, P.; Levin, M.Y.; Molnar, D.A. Automated Whitebox Fuzz Testing. In Proceedings of the Network and Distributed System Security Symposium (NDSS), San Diego, CA, USA, 10–13 February 2008; Volume 8, pp. 151–166. [Google Scholar]
- Stephens, N.; Grosen, J.; Salls, C.; Dutcher, A.; Wang, R.; Corbetta, J.; Shoshitaishvil, Y.; Kruegel, C.; Vigna, G. Driller: Augmenting Fuzzing through Selective Symbolic Execution. In Proceedings of the Network and Distributed System Security Symposium (NDSS), San Diego, CA, USA, 21–24 February 2016. [Google Scholar]
- Yun, I.; Lee, S.; Xu, M.; Jang, Y.; Kim, T. QSYM: A Practical Concolic Execution Engine Tailored for Hybrid Fuzzing. In Proceedings of the USENIX Security Symposium, Baltimore, MD, USA, 15–17 August 2018; pp. 745–761. [Google Scholar]
- Huang, H.; Yao, P.; Wu, R.; Shi, Q.; Zhang, C. PANGOLIN: Incremental Hybrid Fuzzing with Polyhedral Path Abstraction. In Proceedings of the Symposium on Security and Privacy (SP), San Francisco, CA, USA, 18–21 May 2020; pp. 1613–1627. [Google Scholar]
- Kim, K.; Jeong, D.R.; Kim, C.H.; Jang, Y.; Shin, I.; Lee, B. HFL: Hybrid Fuzzing on the Linux Kernel. In Proceedings of the Network and Distributed System Security Symposium (NDSS), San Diego, CA, USA, 23–26 February 2020. [Google Scholar]
- Chen, C.; Cui, B.; Ma, J.; Wu, R.; Guo, J.; Liu, W. A systematic review of fuzzing techniques. Comput. Secur. 2018, 75, 118–137. [Google Scholar] [CrossRef]
- Rawat, S.; Jain, V.; Kumar, A.; Cojocar, L.; Giuffrida, C.; Bos, H. VUzzer: Application-aware Evolutionary Fuzzing. In Proceedings of the Network and Distributed System Security Symposium (NDSS), San Diego, CA, USA, 26 February–1 March 2017. [Google Scholar]
- Ispoglou, K.; Austin, D.; Mohan, V. FuzzGen: Automatic Fuzzer Generation. In Proceedings of the 29th USENIX Security Symposium, Boston, MA, USA, 12–14 August 2020; pp. 2271–2287. [Google Scholar]
- Yue, T.; Wang, P.; Tang, Y.; Wang, E.; Yu, B.; Lu, K.; Zhou, X. EcoFuzz: Adaptive Energy-Saving Greybox Fuzzing as a Variant of the Adversarial Multi-Armed Bandit. In Proceedings of the 29th USENIX Security Symposium, Boston, MA, USA, 12–14 August 2020; pp. 2307–2324. [Google Scholar]
- Chen, H.; Guo, S.; Xue, Y.; Sui, Y.; Zhang, C.; Li, Y.; Wang, H.; Liu, Y. MUZZ: Thread-aware Grey-box Fuzzing for Effective Bug Hunting in Multithreaded Programs. In Proceedings of the 29th USENIX Security Symposium, Boston, MA, USA, 12–14 August 2020; pp. 2325–2342. [Google Scholar]
- Aschermann, C.; Schumilo, S.; Abbasi, A.; Holz, T. Ijon: Exploring Deep State Spaces via Fuzzing. In Proceedings of the IEEE Symposium on Security and Privacy (S&P), San Francisco, CA, USA, 18–21 May 2020; pp. 1597–1612. [Google Scholar]
- Fioraldi, A.; Maier, D.; Eifeldt, H.; Heuse, M. AFL++: Combining Incremental Steps of Fuzzing Research. Available online: https://www.usenix.org/conference/woot20/presentation/fioraldi (accessed on 25 January 2021).
- Haller, I.; Slowinska, A.; Neugschwandtner, M.; Bos, H. Dowsing for Overflows: A Guided Fuzzer to Find Buffer Boundary Violations. In Proceedings of the USENIX Security Symposium, Washington, DC, USA, 14–16 August 2013; pp. 49–64. [Google Scholar]
- Neugschwandtner, M.; Milani Comparetti, P.; Haller, I.; Bos, H. The BORG: Nanoprobing Binaries for Buffer Overreads. In Proceedings of the 5th ACM Conference on Data and Application Security and Privacy, San Antonio, TX, USA, 2–4 March 2015; pp. 87–97. [Google Scholar]
- Böhme, M.; Pham, V.T.; Nguyen, M.D.; Roychoudhury, A. Directed Greybox Fuzzing. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, Dallas, TX, USA, 30 October 2017; pp. 2329–2344. [Google Scholar]
- Embleton, S.; Sparks, S.; Cunningham, R. Sidewinder: An Evolutionary Guidance System for Malicious Input Crafting. Available online: http://www.blackhat.com/presentations/bh-usa-06/BH-US-06-Embleton.pdf (accessed on 9 February 2020).
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE ICNN’95-International Conference on Neural Networks, Perth, Australia, 27 November 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Shaukat, K.; Luo, S.; Varadharajan, V.; Hameed, I.A.; Chen, S.; Liu, D.; Li, J. Performance Comparison and Current Challenges of Using Machine Learning Techniques in Cybersecurity. Energies 2020, 13, 2509. [Google Scholar] [CrossRef]
- Dar, K.S.; Luo, S.; Varadharajan, V.; Hameed, I.A.; Xu, M. A Survey on Machine Learning Techniques for Cyber Security in the Last Decade. IEEE Access 2020, 8, 222310–222354. [Google Scholar]
- Pailoor, S.; Aday, A.; Jana, S. MoonShine: Optimizing OS Fuzzer Seed Selection with Trace Distillation. In Proceedings of the 27th USENIX Security Symposium (Security), Baltimore, MD, USA, 15–17 August 2018; pp. 729–743. [Google Scholar]
- Syzkaller. Available online: https://github.com/google/syzkaller (accessed on 20 September 2020).
- Gzip. Available online: http://mirror.keystealth.org/gnu/gzip/ (accessed on 20 September 2020).
- Goahead. Available online: http://mirror.keystealth.org/gnu/tar/ (accessed on 20 September 2020).
- Pdfresurrect. Available online: https://github.com/enferex/pdfresurrect/ (accessed on 20 September 2020).
- Miniftp. Available online: https://github.com/skyqinsc/MiniFtp/ (accessed on 20 September 2020).
- Binutils. Available online: http://mirror.keystealth.org/gnu/binutils/ (accessed on 20 September 2020).
- Libming. Available online: https://github.com/libming/libming (accessed on 20 September 2020).
- Libjpeg. Available online: http://www.ijg.org/ (accessed on 20 September 2020).
- Pngquant. Available online: https://github.com/kornelski/pngquant (accessed on 20 September 2020).
- Ffjpeg. Available online: https://github.com/rockcarry/ffjpeg (accessed on 20 September 2020).
- Zziplib. Available online: https://enterprise.dejacode.com/packages/public/d9018a4f-2e88-498d-8cb9-d52680be48f5/ (accessed on 20 September 2020).
- Exiv2. Available online: https://www.exiv2.org/archive.html (accessed on 20 September 2020).
- Ngiflib. Available online: https://github.com/miniupnp/ngiflib (accessed on 20 September 2020).


| Data Type | Mutation Algorithms |
|---|---|
| Blob | Flips part of total bits in a blob |
| Slides a Double Word (DWORD) through the blob | |
| Grows the blob | |
| Shrinks the blob | |
| String | Changes the case of a string |
| Generates a string using the string in the dictionary | |
| Generates bad UTF-8 strings | |
| Injects Byte-order mark (BOM) markers into longer strings | |
| Generates bad long UTF-8 three-byte strings | |
| Array | Changes the length of arrays to numerical edge cases |
| Randomizes the order of the array | |
| Reverses the order of the array | |
| Changes the length of arrays from count −N to count +N | |
| Number | Produces random numbers for each element |
| Produces values that are unrelated to the default Value | |
| Produces defaultValue −N to defaultValue +N | |
| Changes the length of sized data to numerical edge cases | |
| Changes the length of sizes to numerical edge cases |
| Software | Type | Version Number | CVE ID | Vulnerability Position |
|---|---|---|---|---|
| gzip | compressor | 1.2.4 | 2009–2624 | inflate.c line 763 |
| tar | compressor | 1.14 | 2007–4476 | safer_name_suffix.c line 1046 |
| pdfresurrect | pdf analyzer | 0.15 | 2019–14,267 | pdf.c line 237 |
| miniftp | file transfer | 1.0 | - | parseconf.c line 62 |
| binutils | binary utilities | 2.32 | 2019–14,444 | readelf.c line 13347 |
| libming | flash library | 0.4.8 | 2019–9113 | decompile.c line 381 |
| libjpeg | jpeg library | 9a | 2018–11,213 | rdppm.c line 153 |
| pngquant | png compressor | 2.7.0 | 2016–5735 | rwpng_read_image24_libpng.c line 238 |
| ffjpeg | encoder | 24 February 2020 | 2020–13,438 | jfif.c line 748 |
| zziplib | decoder | 0.13.67 | 2018–6381 | mmapped.c line 685 |
| exiv2 | metadata library | 0.26 | 2018–5772 | image.c line 468 |
| ngiflib | gif decoder | 0.4 | 2018–10,677 | ngiflib.c line 808 |
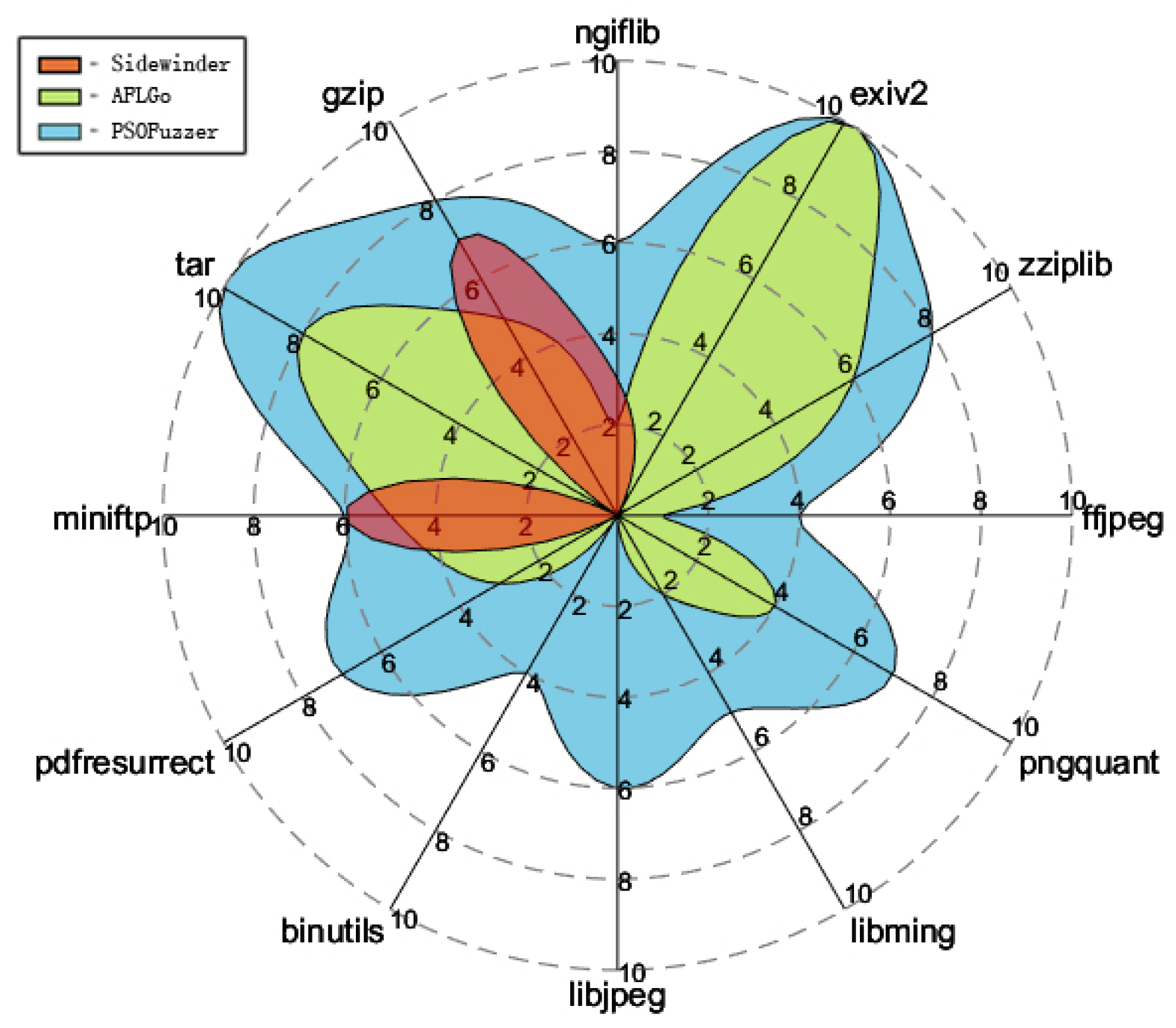
| Gzip | Tar | Miniftp | Pdfresurrect | Binutils | Libjpeg | Libming | Pngquant | Ffjpeg | Zziplib | Exiv2 | Ngiflib | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AFLGo | 5 | 8 | 5 | 3 | 0 | 0 | 2 | 4 | 1 | 6 | 10 | 2 |
| PSOFuzzer | 8 | 10 | 6 | 7 | 4 | 6 | 5 | 7 | 4 | 8 | 10 | 6 |
| Sidewinder | 7 | 0 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Xu, H.; Cui, B. PSOFuzzer: A Target-Oriented Software Vulnerability Detection Technology Based on Particle Swarm Optimization. Appl. Sci. 2021, 11, 1095. https://doi.org/10.3390/app11031095
Chen C, Xu H, Cui B. PSOFuzzer: A Target-Oriented Software Vulnerability Detection Technology Based on Particle Swarm Optimization. Applied Sciences. 2021; 11(3):1095. https://doi.org/10.3390/app11031095
Chicago/Turabian StyleChen, Chen, Han Xu, and Baojiang Cui. 2021. "PSOFuzzer: A Target-Oriented Software Vulnerability Detection Technology Based on Particle Swarm Optimization" Applied Sciences 11, no. 3: 1095. https://doi.org/10.3390/app11031095
APA StyleChen, C., Xu, H., & Cui, B. (2021). PSOFuzzer: A Target-Oriented Software Vulnerability Detection Technology Based on Particle Swarm Optimization. Applied Sciences, 11(3), 1095. https://doi.org/10.3390/app11031095





