Time Domain Spherical Harmonic Processing with Open Spherical Microphones Recording
Abstract
Featured Application
Abstract
1. Introduction
2. Problem Formulation
2.1. Spherical Harmonic Decomposition of Sound Field in Frequency-Space Domain
2.2. Equivalent Spherical Harmonic Decomposition of a Sound Field in Time-Space Domain
3. Filter Design for Obtaining Time Domain Spherical Coefficients
3.1. Stability of Ideal Inverse Filter
3.2. Modified Inverse Filter
3.3. Practical Considerations of Filter Implementation
3.4. Error Analysis
4. A Filter Design Example
4.1. Effect of Frequency Truncation of
4.2. Choice of Filter Length of
5. Simulation Results and Analysis
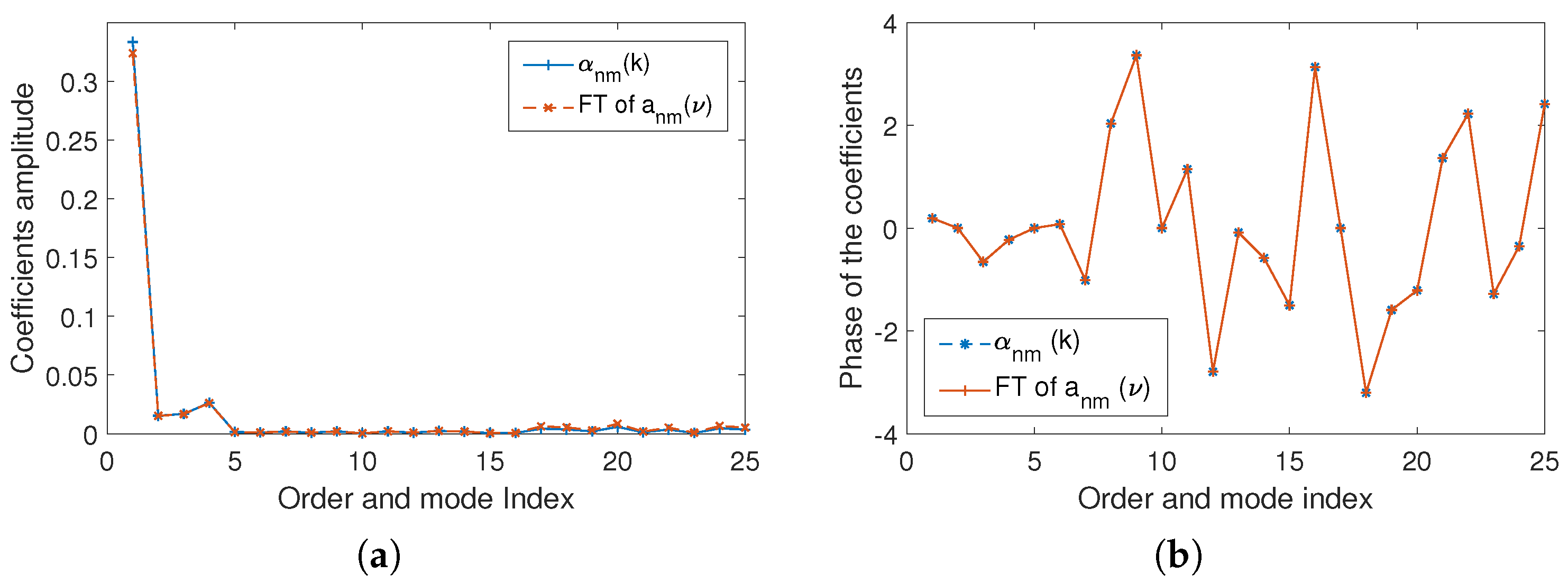
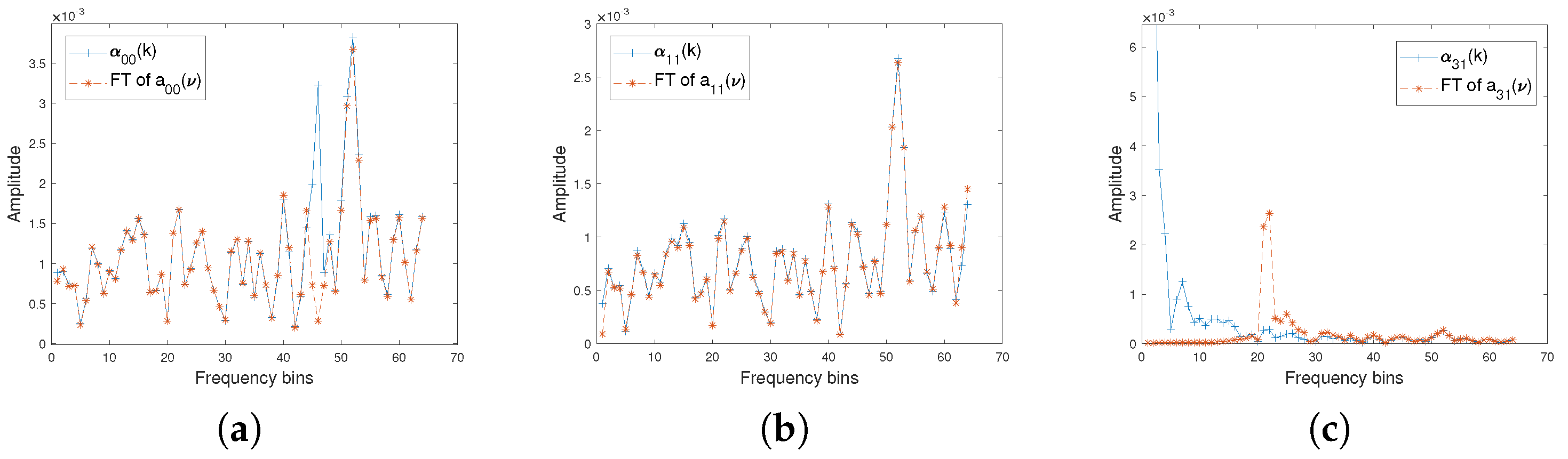
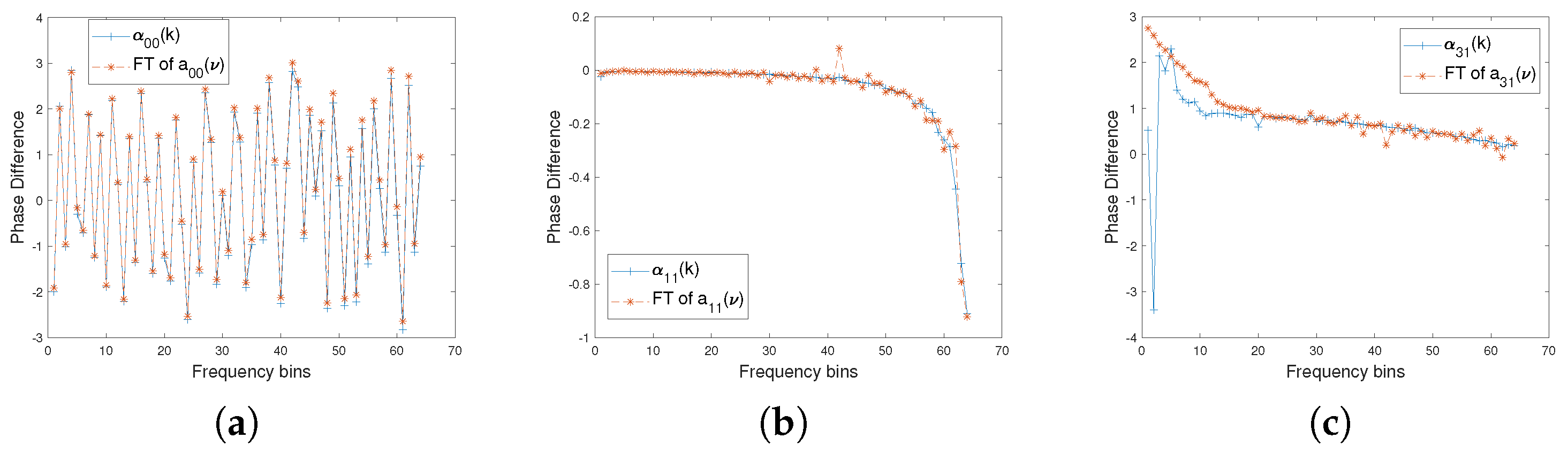
5.1. Comparison between the Time Domain and the Frequency Domain Spherical Harmonic Coefficients
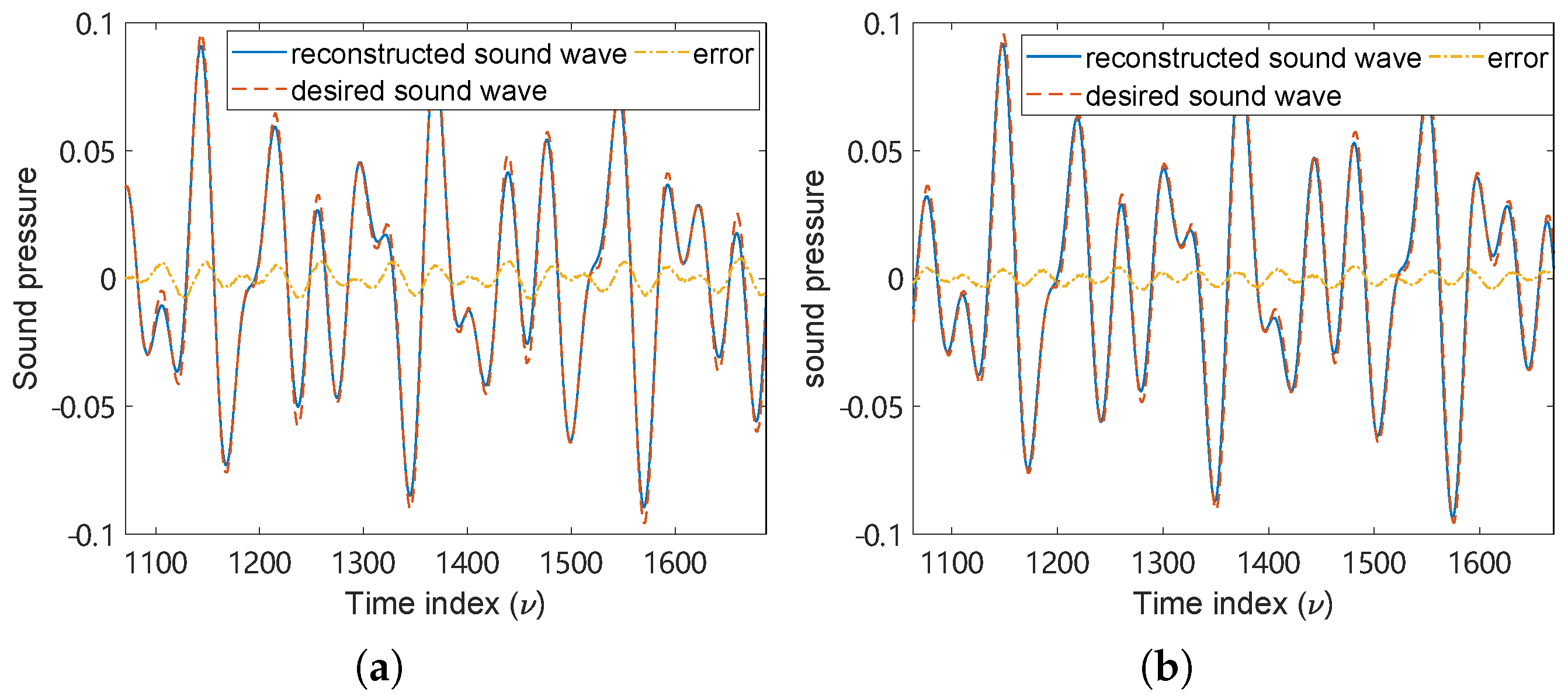
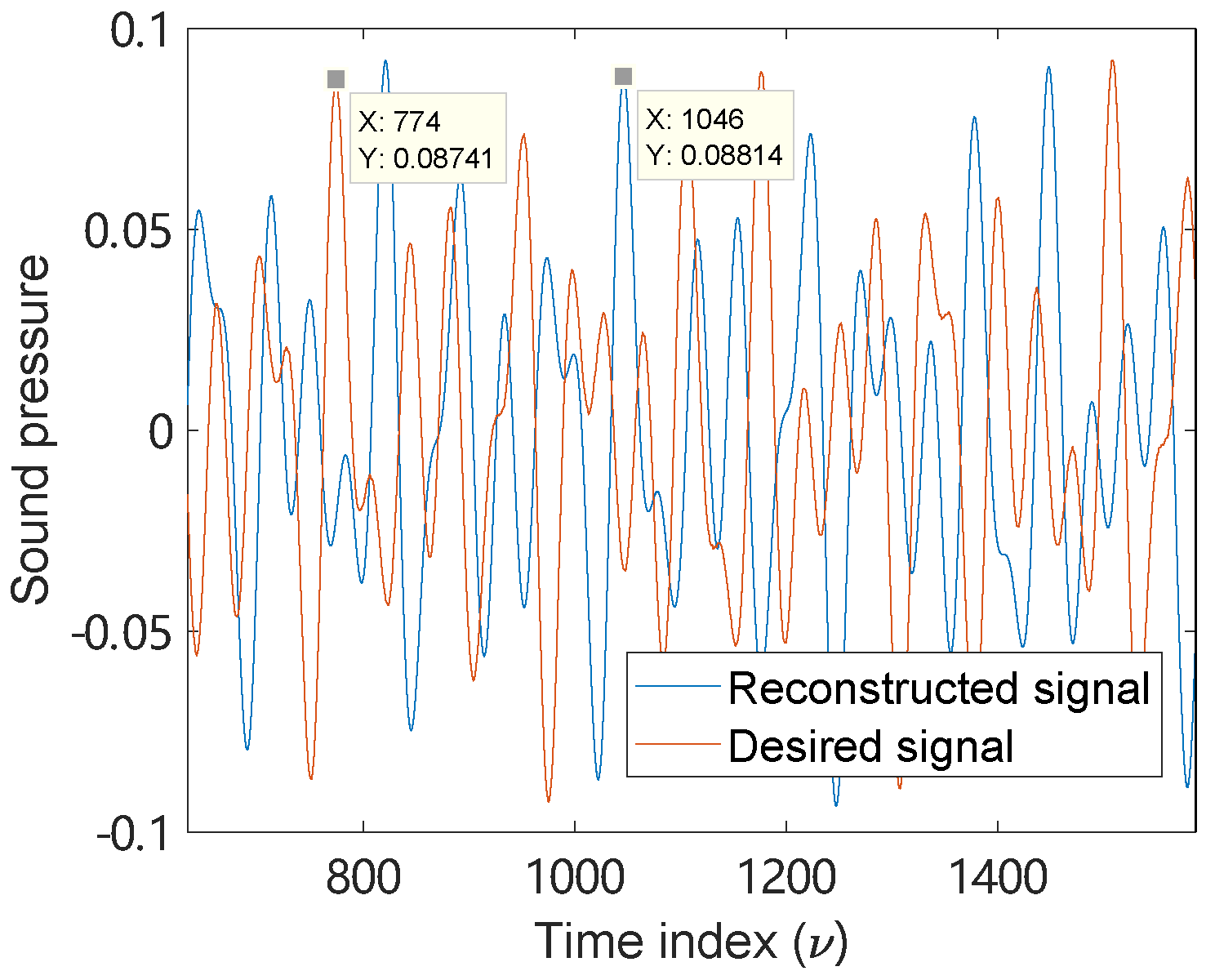
5.2. Sound Pressure Comparison at a Point Of Interest
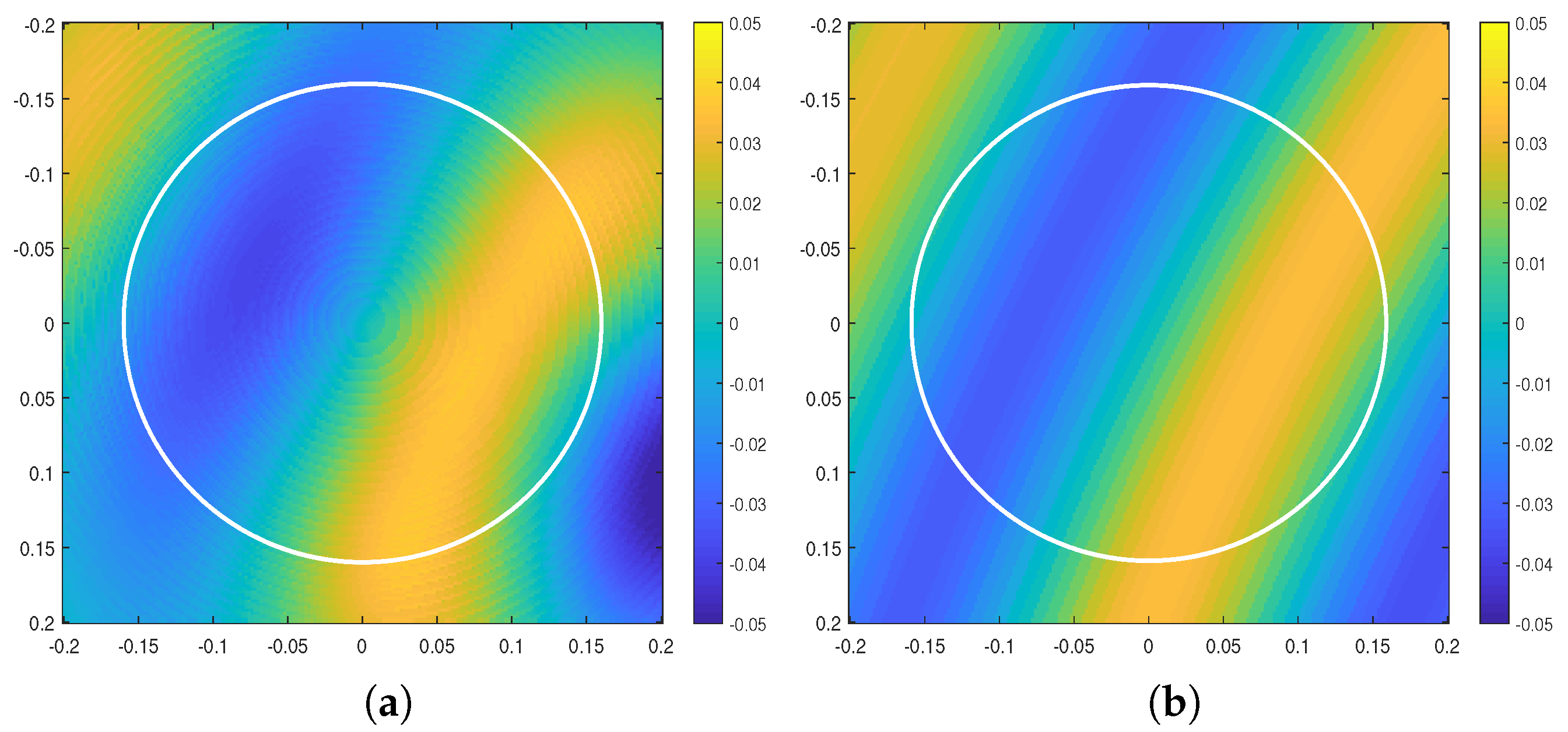
5.3. Sound Field Comparison over a Plane
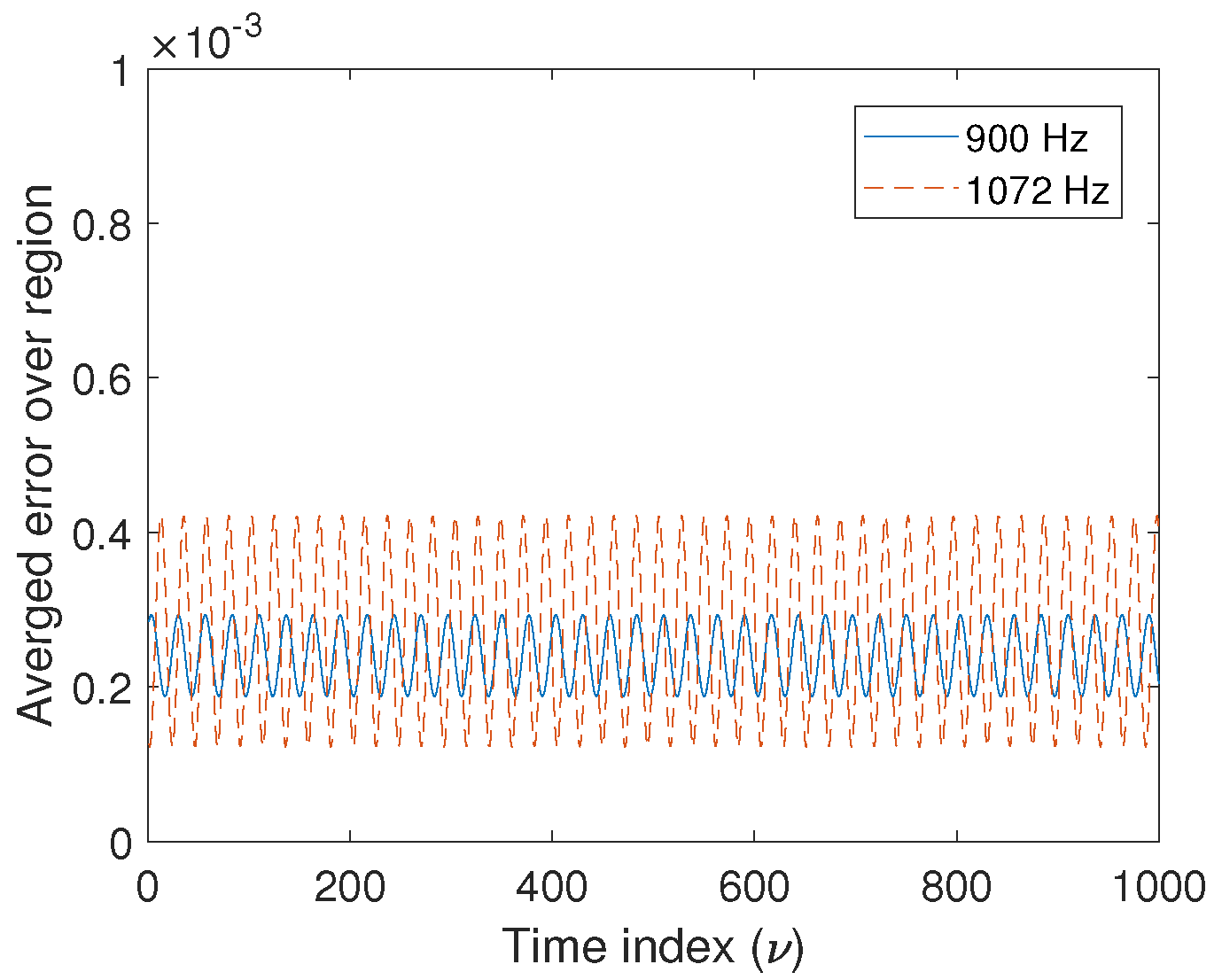
5.4. Sound Field Error Estimation over The Region
5.5. Processing Delay Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANC | Active noise control |
| 3D | Three-dimensional |
| IFFT | Inverse fast fourier transform |
| FIR | Finite impulse response |
| SNR | Signal to noise ratio |
Appendix A. Proof of Equation (9)
References
- Ward, D.B.; Abhayapala, T.D. Reproduction of a plane-wave sound field using an array of loudspeakers. IEEE Trans. Speech Audio Process. 2001, 9, 697–707. [Google Scholar] [CrossRef]
- Abhayapala, T.D.; Ward, D.B. Theory and design of high order sound field microphones using spherical microphone array. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Orlando, FL, USA, 13–17 May 2002; Volume 2, pp. 1949–1952. [Google Scholar]
- Rafaely, B. Analysis and design of spherical microphone arrays. IEEE Trans. Speech Audio Process. 2004, 13, 135–143. [Google Scholar] [CrossRef]
- Park, M.; Rafaely, B. Sound-field analysis by plane-wave decomposition using spherical microphone array. J. Acoust. Soc. Am. 2005, 118, 3094–3103. [Google Scholar] [CrossRef]
- Zuo, H.; Samarasinghe, P.N.; Abhayapala, T.D.; Dickins, G. Spatial sound intensity vectors in spherical harmonic domain. J. Acoust. Soc. Am. 2019, 145, EL149–EL155. [Google Scholar] [CrossRef] [PubMed]
- Epain, N.; Jin, C.T. Spherical harmonic signal covariance and sound field diffuseness. IEEE/ACM Trans. Audio Speech Lang. Process. (TASLP) 2016, 24, 1796–1807. [Google Scholar] [CrossRef]
- Koretz, A.; Rafaely, B. Dolph–Chebyshev beampattern design for spherical arrays. IEEE Trans. Signal Process. 2009, 57, 2417–2420. [Google Scholar] [CrossRef]
- Gover, B.N.; Ryan, J.G.; Stinson, M.R. Microphone array measurement system for analysis of directional and spatial variations of sound fields. J. Acoust. Soc. Am. 2002, 112, 1980–1991. [Google Scholar] [CrossRef] [PubMed]
- Argentieri, S.; Danes, P.; Soueres, P. Modal analysis based beamforming for nearfield or farfield speaker localization in robotics. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 866–871. [Google Scholar]
- Birnie, L.; Abhayapala, T.D.; Chen, H.; Samarasinghe, P.N. Sound Source Localization in a Reverberant Room Using Harmonic Based Music. In Proceedings of the ICASSP 2019–2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 651–655. [Google Scholar]
- Spors, S.; Buchner, H. An approach to massive multichannel broadband feedforward active noise control using wave-domain adaptive filtering. In Proceedings of the IEEE Workshop on Applications of Signal Processing to Audio and Acoustics, New Paltz, NY, USA, 21–24 October 2007; pp. 171–174. [Google Scholar]
- Zhang, J.; Abhayapala, T.D.; Zhang, W.; Samarasinghe, P.N.; Jiang, S. Active Noise Control Over Space: A Wave Domain Approach. IEEE/ACM Trans. Audio Speech Lang. Process. (TASLP) 2018, 26, 774–786. [Google Scholar] [CrossRef]
- Cassina, L.; Fredianelli, L.; Menichini, I.; Chiari, C.; Licitra, G. Audio-visual preferences and tranquillity ratings in urban areas. Environments 2018, 5, 1. [Google Scholar] [CrossRef]
- Kuo, S.M.; Morgan, D.R. Active Noise Control Systems: Algorithms and DSP Implementations; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1995. [Google Scholar]
- Baumgartner, R.; Pomberger, H.; Frank, M. Practical implementation of radial filters for ambisonic recordings. In Proceedings of the ICSA 2011, Detmold, Germany, 10–13 November 2011. [Google Scholar]
- Moreau, S.; Daniel, J.; Bertet, S. 3D sound field recording with higher order ambisonics–Objective measurements and validation of a 4th order spherical microphone. In Proceedings of the 120th Convention of the AES, Paris, France, 20–23 May 2006; pp. 20–23. [Google Scholar]
- Zotter, F. A linear-phase filter-bank approach to process rigid spherical microphone array recordings. In Proceedings of the 5th International Conference on Electrical, Electronic and Computing Engineering, Palić, Serbia, 11–14 June 2018. [Google Scholar]
- Sun, H.; Abhayapala, T.D.; Samarasinghe, P.N. Time Domain Spherical Harmonic Analysis for Adaptive Noise Cancellation over a Spatial Region. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 516–520. [Google Scholar]
- Chen, H.; Abhayapala, T.D.; Zhang, W. Theory and design of compact hybrid microphone arrays on two-dimensional planes for three-dimensional soundfield analysis. J. Acoust. Soc. Am. 2015, 138, 3081–3092. [Google Scholar] [CrossRef]
- Abhayapala, T.D.; Gupta, A. Spherical harmonic analysis of wavefields using multiple circular sensor arrays. IEEE Trans. Audio Speech Lang. Process. 2010, 18, 1655–1666. [Google Scholar] [CrossRef]
- Sun, H.; Abhayapala, T.D.; Samarasinghe, P.N. Active Noise Control Over 3D Space with Multiple Circular Arrays. In Proceedings of the 2019 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA), New Paltz, NY, USA, 20–23 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 135–139. [Google Scholar]
- Bilbao, S.; Ahrens, J.; Hamilton, B. Incorporating source directivity in wave-based virtual acoustics: Time-domain models and fitting to measured data. J. Acoust. Soc. Am. 2019, 146, 2692–2703. [Google Scholar] [CrossRef] [PubMed]
- Farina, A.; Capra, A.; Chiesi, L.; Scopece, L. A spherical microphone array for synthesizing virtual directive microphones in live broadcasting and in post production. In Proceedings of the Audio Engineering Society Conference: 40th International Conference: Spatial Audio: Sense the Sound of Space, Tokyo, Japan, 8–10 October 2010; Audio Engineering Society: New York, NY, USA, 2010. [Google Scholar]
- Mabande, E.; Schad, A.; Kellermann, W. A time-domain implementation of data-independent robust broadband beamformers with lowfilter order. In Proceedings of the 2011 Joint Workshop on Hands-free Speech Communication and Microphone Arrays, Edinburgh, UK, 30 May–1 June 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 81–85. [Google Scholar]
- Simón Gálvez, M.F.; Elliott, S.J.; Cheer, J. Time domain optimization of filters used in a loudspeaker array for personal audio. IEEE/ACM Trans. Audio Speech Lang. Process. (TASLP) 2015, 23, 1869–1878. [Google Scholar] [CrossRef]
- Nelson, P.A.; Elliott, S.J. Active Control of Sound; Academic Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Long, G.; Ling, F.; Proakis, J.G. The LMS algorithm with delayed coefficient adaptation. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 1397–1405. [Google Scholar] [CrossRef]
- Long, G.; Ling, F.; Proakis, J.G. Corrections to ‘The LMS algorithm with delayed coefficient adaptation’. IEEE Trans. Signal Process. 1992, 40, 230–232. [Google Scholar] [CrossRef]
- Lösler, S.; Zotter, F. Comprehensive radial filter design for practical higher-order Ambisonic recording. In Proceedings of the Fortschritte der Akustik DAGA, Nuremberg, Germany, 16–19 March 2015; pp. 452–455. [Google Scholar]
- Jin, C.T.; Epain, N.; Parthy, A. Design, optimization and evaluation of a dual-radius spherical microphone array. IEEE/ACM Trans. Audio Speech Lang. Process. 2013, 22, 193–204. [Google Scholar] [CrossRef]
- Politis, A.; Gamper, H. Comparing modeled and measurement-based spherical harmonic encoding filters for spherical microphone arrays. In Proceedings of the 2017 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA), New Paltz, NY, USA, 15–18 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 224–228. [Google Scholar]
- Balmages, I.; Rafaely, B. Open-sphere designs for spherical microphone arrays. IEEE Trans. Audio Speech Lang. Process. 2007, 15, 727–732. [Google Scholar] [CrossRef]
- Chardon, G.; Kreuzer, W.; Noisternig, M. Design of spatial microphone arrays for sound field interpolation. IEEE J. Sel. Top. Signal Process. 2015, 9, 780–790. [Google Scholar] [CrossRef]
- Ueno, N.; Koyama, S.; Saruwatari, H. Sound field recording using distributed microphones based on harmonic analysis of infinite order. IEEE Signal Process. Lett. 2017, 25, 135–139. [Google Scholar] [CrossRef]
- Poletti, M.; Abhayapala, T.D.; Teal, P.D. Time domain description of spatial modes of 2D and 3D free-space greens functions. In Proceedings of the Audio Engineering Society Conference: 2016 AES International Conference on Sound Field Control, Guildford, UK, 18–20 July 2016; Audio Engineering Society: New York, NY, USA, 2016. [Google Scholar]
- Winter, F.; Hahn, N.; Spors, S. Time-domain realisation of model-based rendering for 2.5 D local wave field synthesis using spatial bandwidth-limitation. In Proceedings of the 2017 25th European Signal Processing Conference (EUSIPCO), Kos, Greece, 28 August–2 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 688–692. [Google Scholar]
- Hahn, N.; Spors, S. Time-Domain Representations of a Plane Wave with Spatial Band-Limitation in the Spherical Harmonics Domain. In Proceedings of the Meeting of the German Acoustical Society (DAGA), Rostock, Germany, 18–21 March 2019. [Google Scholar]
- Yan, S.; Sun, H.; Ma, X.; Svensson, U.P.; Hou, C. Time-domain implementation of broadband beamformer in spherical harmonics domain. IEEE Trans. Audio Speech Lang. Process. 2010, 19, 1221–1230. [Google Scholar]
- Ren, W.; Chen, H.; Gao, W. On the design of time-domain implementation structure for steerable spherical modal beamformers with arbitrary beampatterns. Appl. Acoust. 2017, 122, 146–151. [Google Scholar] [CrossRef]
- Arfken, G.B.; Weber, H.J. Mathematical Methods for Physicists; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Williams, E.G. Fourier Acoustics: Sound Radiation and Nearfield Acoustical Holography; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Homeier, H.H.H.; Steinborn, E.O. Some properties of the coupling coefficients of real spherical harmonics and their relation to Gaunt coefficients. J. Mol. Struct. THEOCHEM 1996, 368, 31–37. [Google Scholar] [CrossRef]
- Oppenheim, A.V. Discrete-Time Signal Processing; Pearson Education India: Tamil Nadu, India, 1999. [Google Scholar]
- Langrenne, C.; Bavu, E.; Garcia, A. A linear phase IIR filterbank for the radial filters of ambisonic recordings. In Proceedings of the EAA Spatial Audio Signal Processing Symposium, Paris, France, 6–7 September 2019. [Google Scholar]
- Chang, H.P.; Sarkar, T.K.; Pereira-Filho, O.M. Antenna pattern synthesis utilizing spherical Bessel functions. IEEE Trans. Antennas Propag. 2000, 48, 853–859. [Google Scholar] [CrossRef]
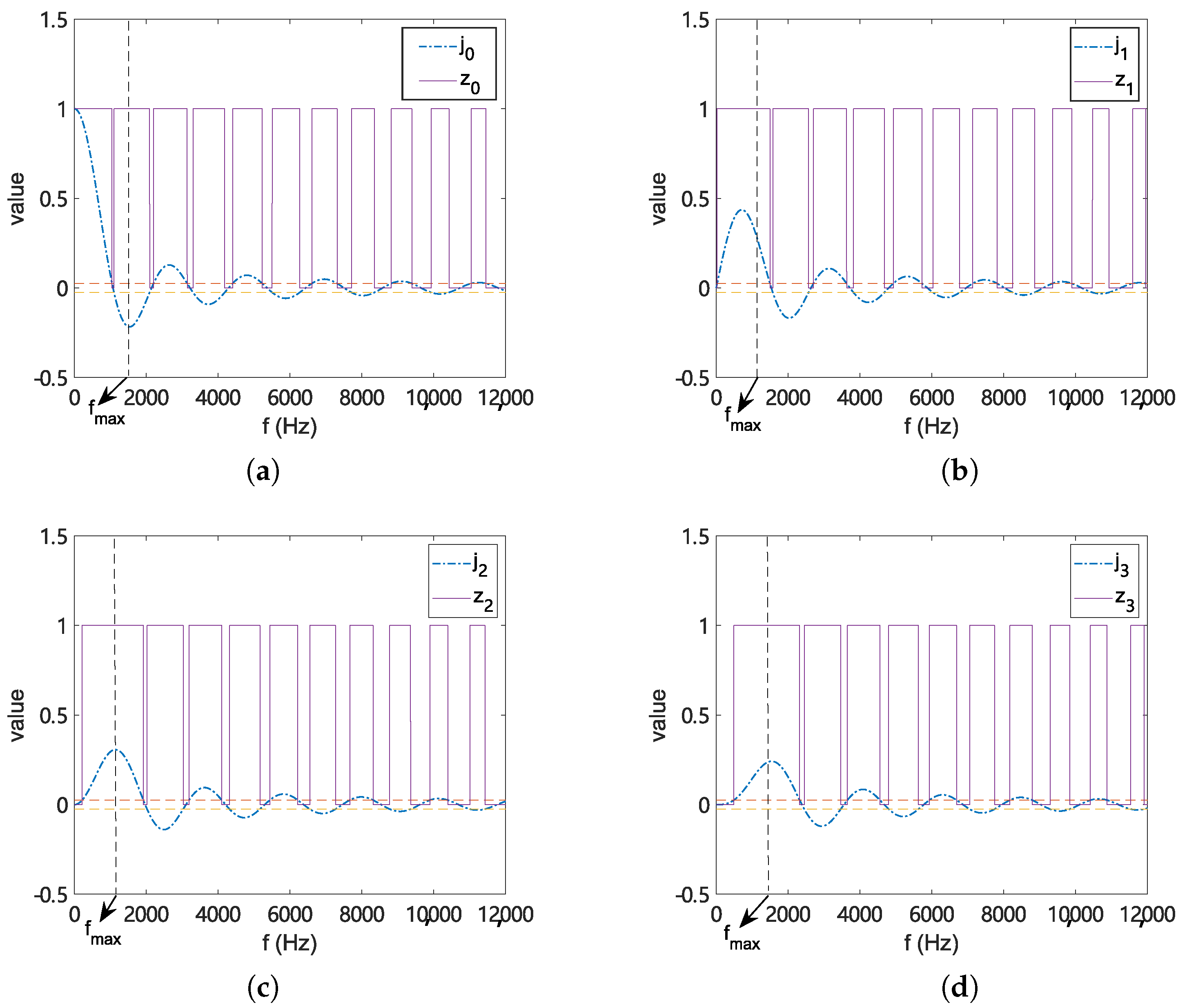
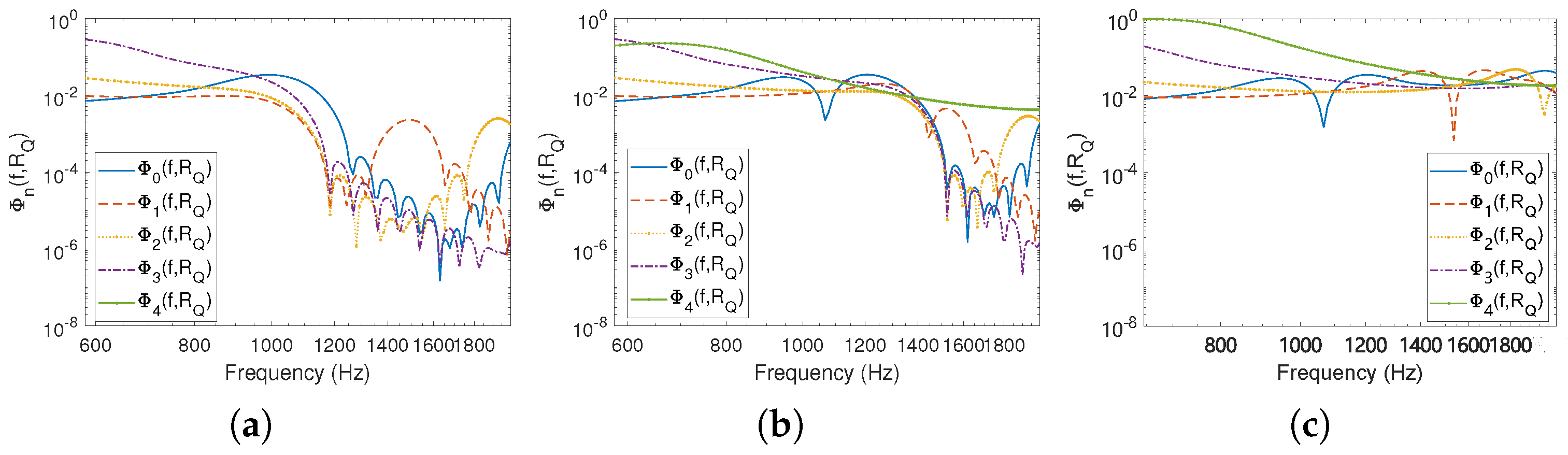
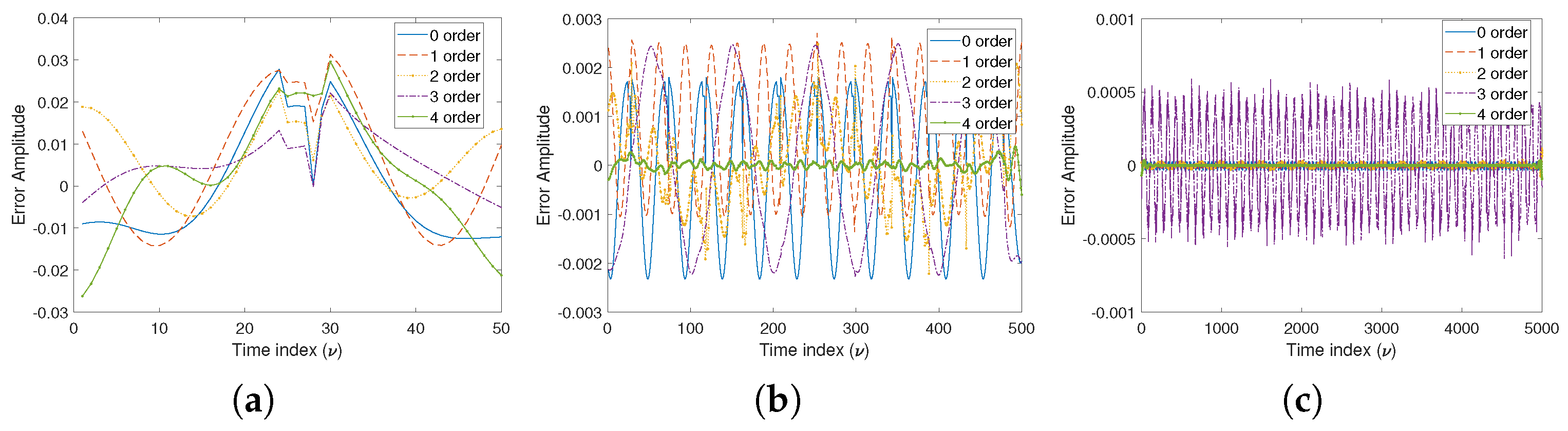
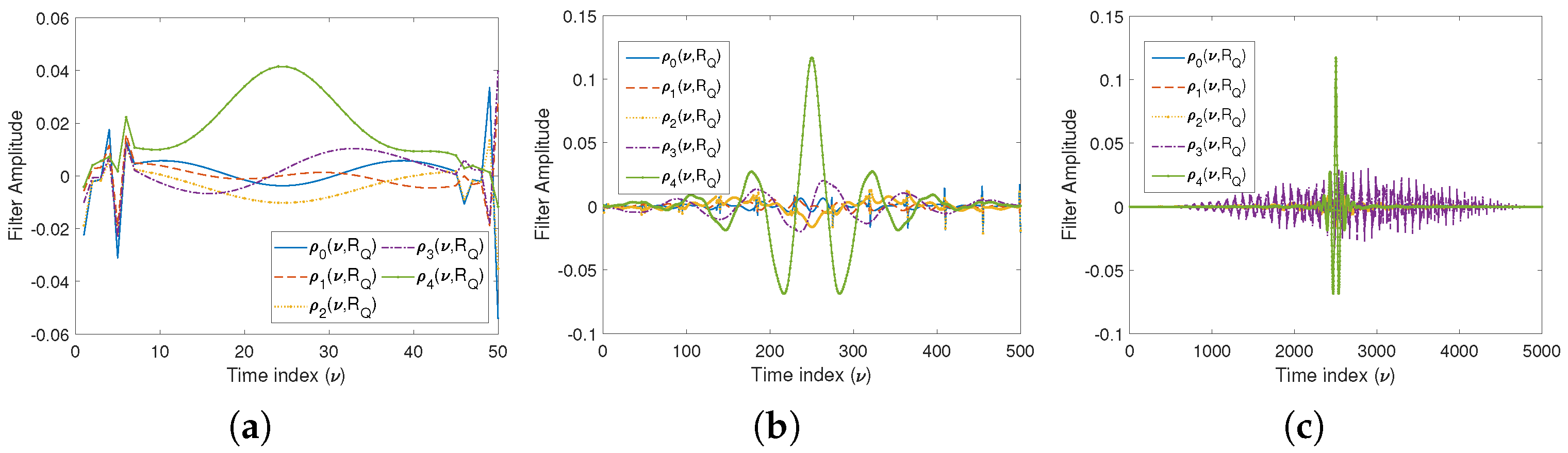
| n (Order) | w | w | w | w |
|---|---|---|---|---|
| 0 | 0.0009 | 0.1369 | 0.1439 | 0.2680 |
| 1 | 0.0033 | 0.1957 | 0.2059 | 0.2680 |
| 2 | 0.0276 | 0.2509 | 0.3643 | 0.2680 |
| 3 | 0.0640 | 0.2680 | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, H.; Abhayapala, T.D.; Samarasinghe, P.N. Time Domain Spherical Harmonic Processing with Open Spherical Microphones Recording. Appl. Sci. 2021, 11, 1074. https://doi.org/10.3390/app11031074
Sun H, Abhayapala TD, Samarasinghe PN. Time Domain Spherical Harmonic Processing with Open Spherical Microphones Recording. Applied Sciences. 2021; 11(3):1074. https://doi.org/10.3390/app11031074
Chicago/Turabian StyleSun, Huiyuan, Thushara D. Abhayapala, and Prasanga N. Samarasinghe. 2021. "Time Domain Spherical Harmonic Processing with Open Spherical Microphones Recording" Applied Sciences 11, no. 3: 1074. https://doi.org/10.3390/app11031074
APA StyleSun, H., Abhayapala, T. D., & Samarasinghe, P. N. (2021). Time Domain Spherical Harmonic Processing with Open Spherical Microphones Recording. Applied Sciences, 11(3), 1074. https://doi.org/10.3390/app11031074





