Expansion of the Laser Beam Wavefront in Terms of Zernike Polynomials in the Problem of Turbulence Testing
Abstract
:1. Introduction
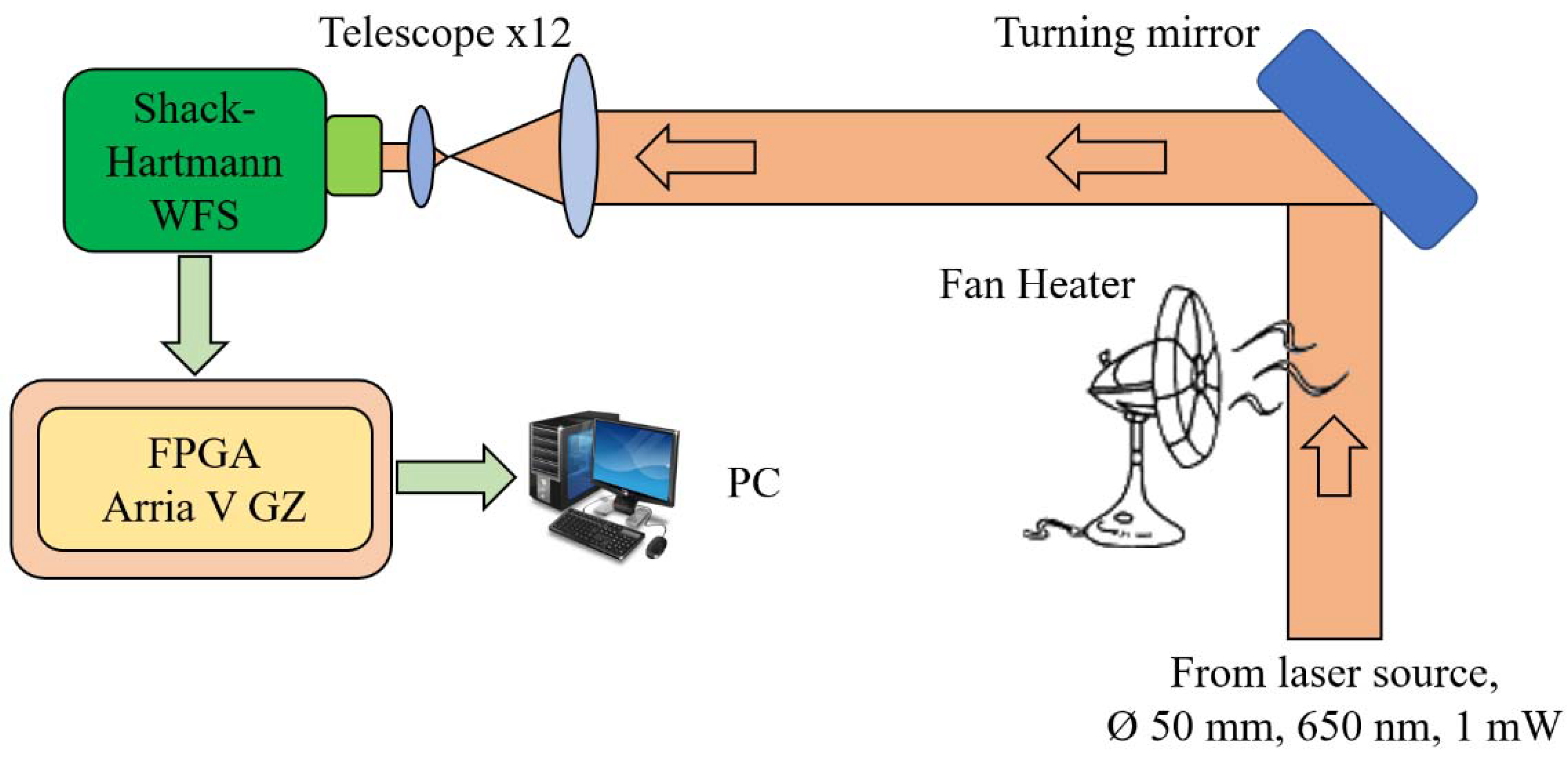
2. Materials and Methods (Obtaining Experimental Data)
- by solving the system of equations:
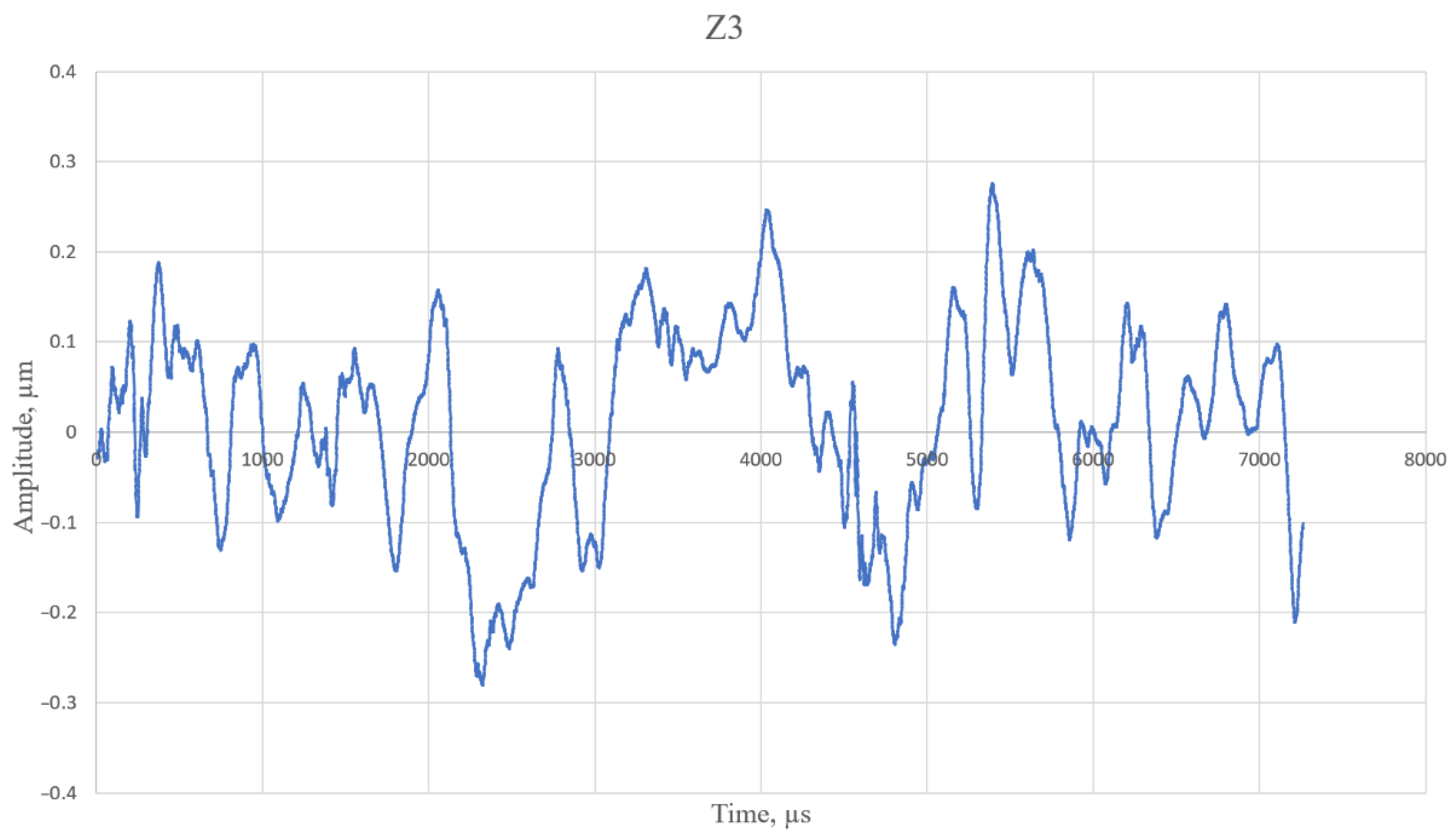
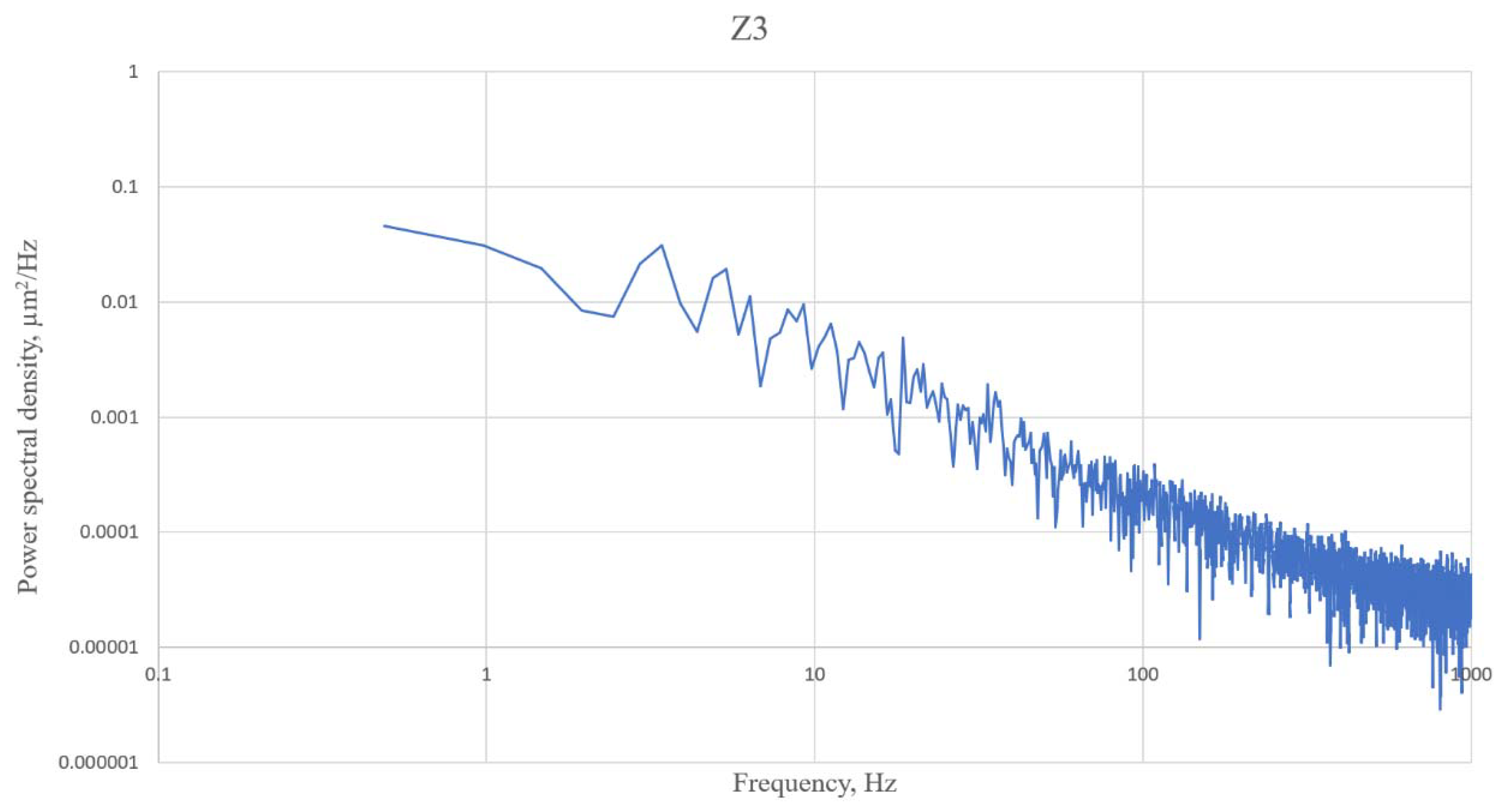
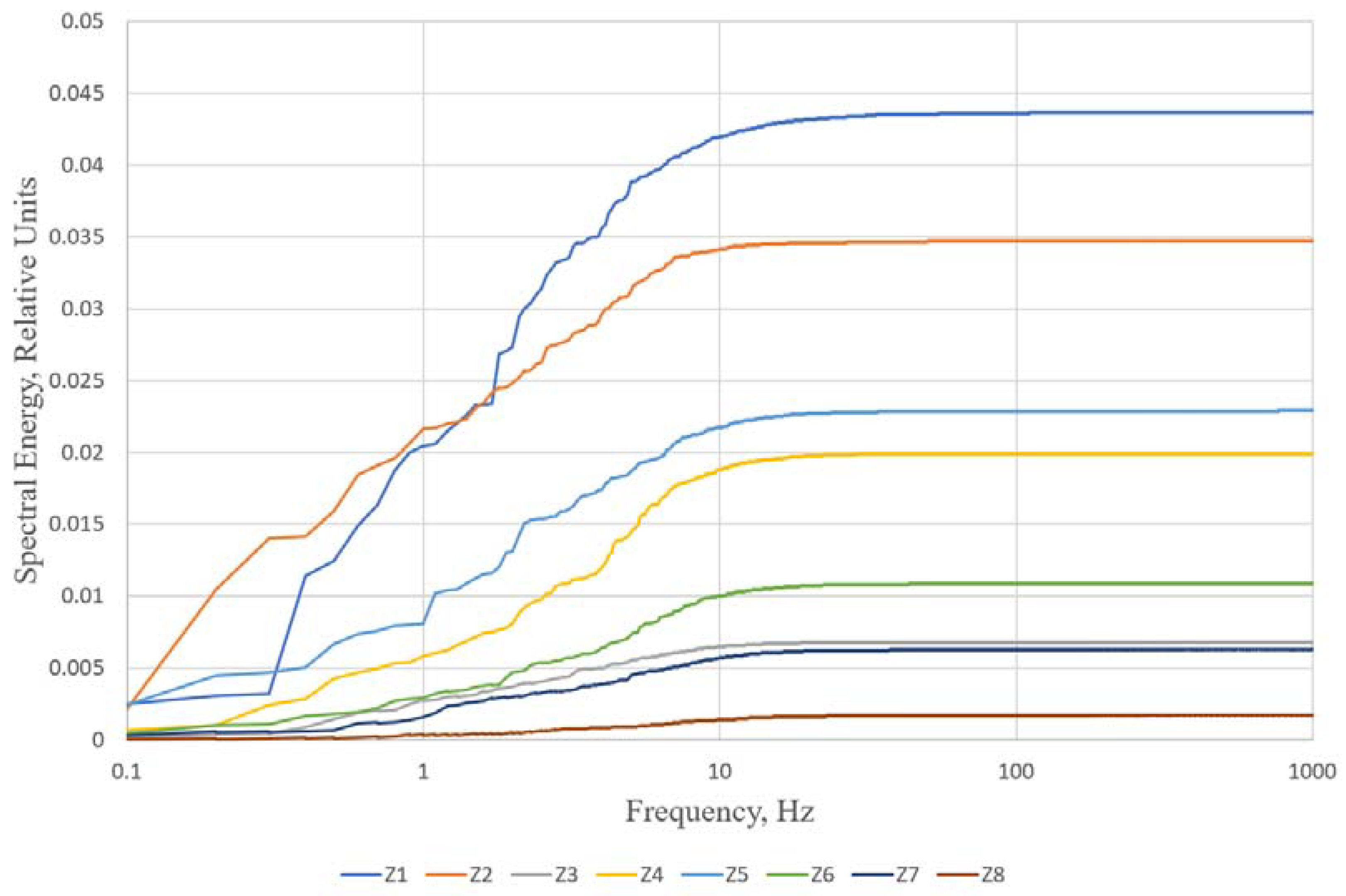
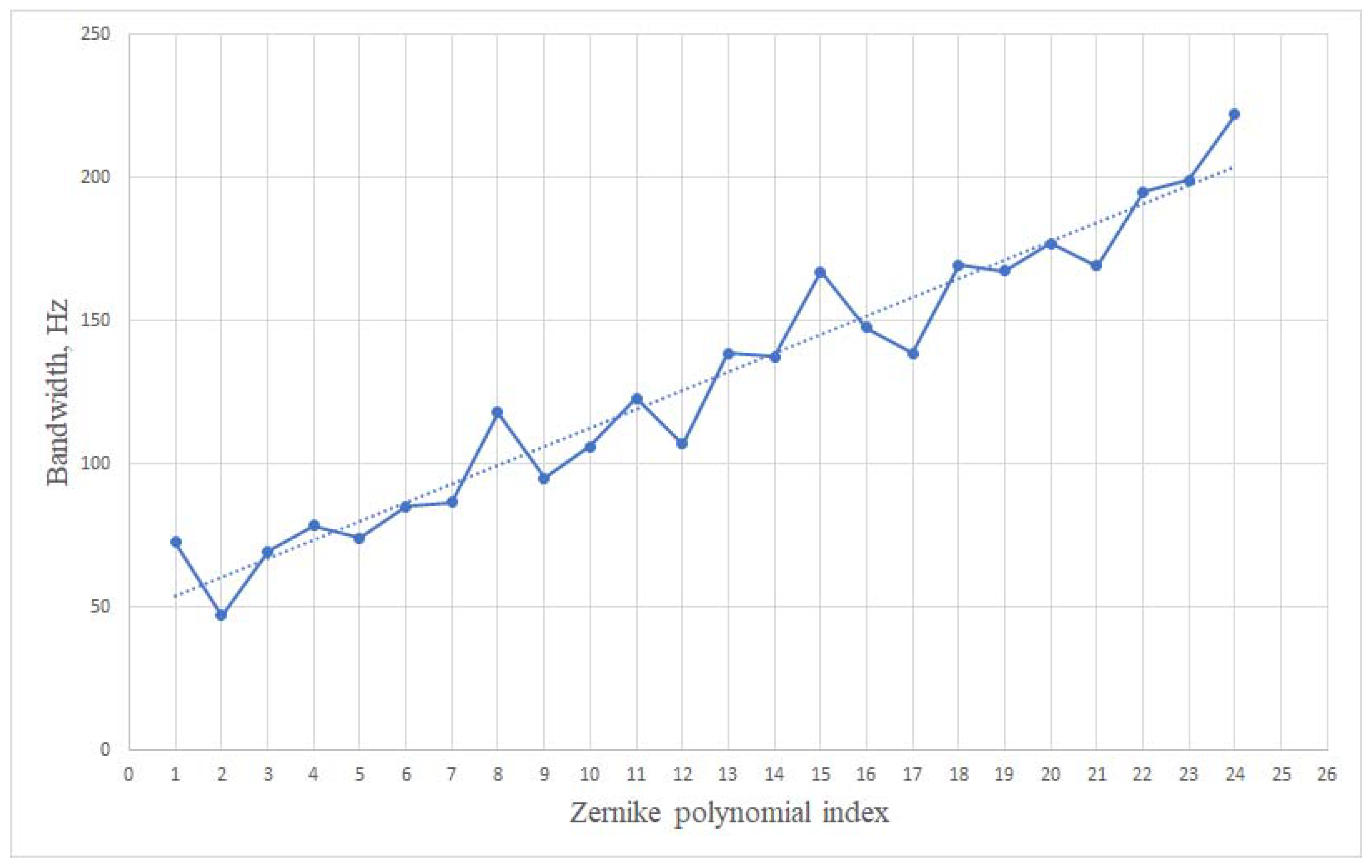
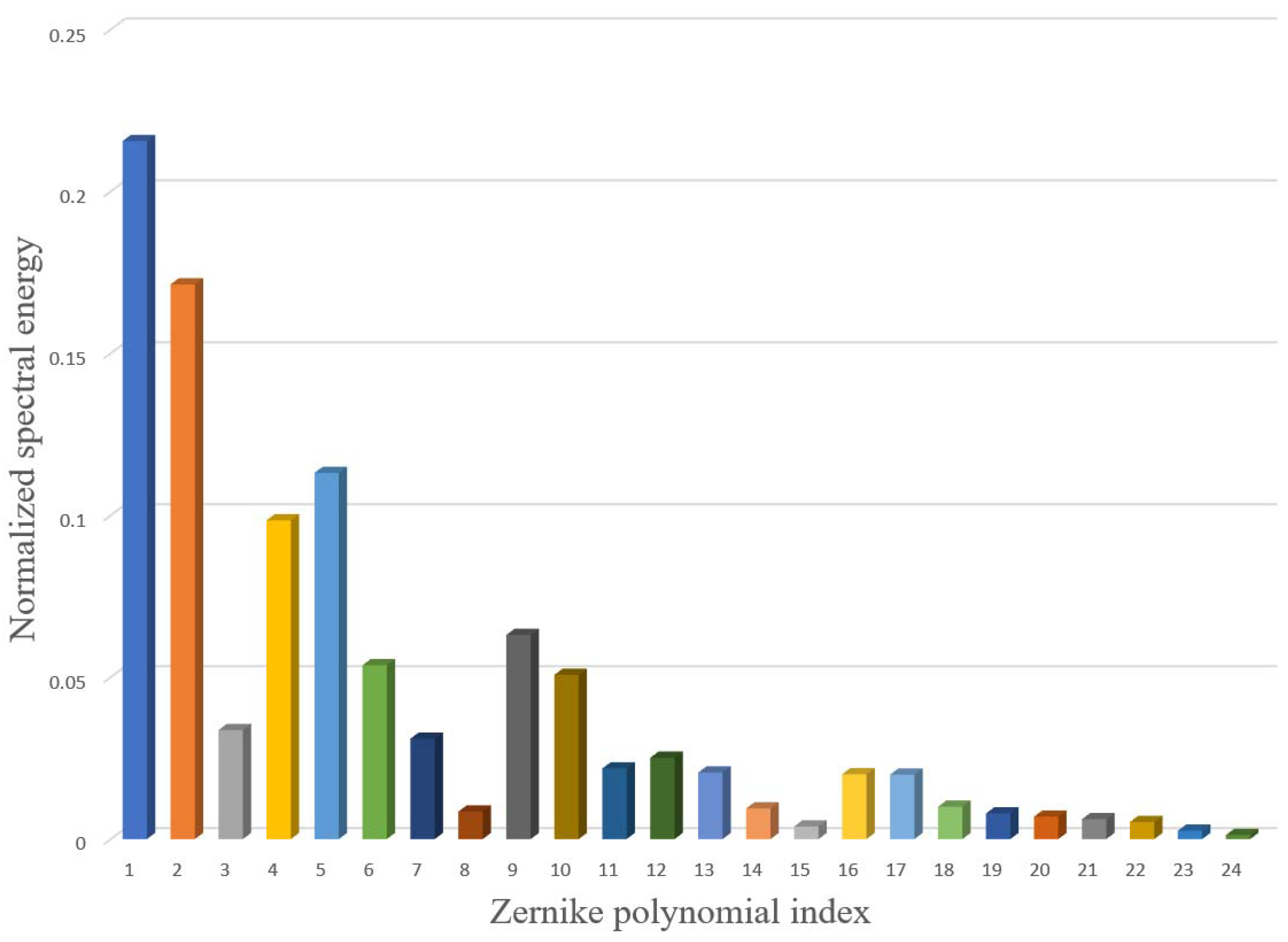
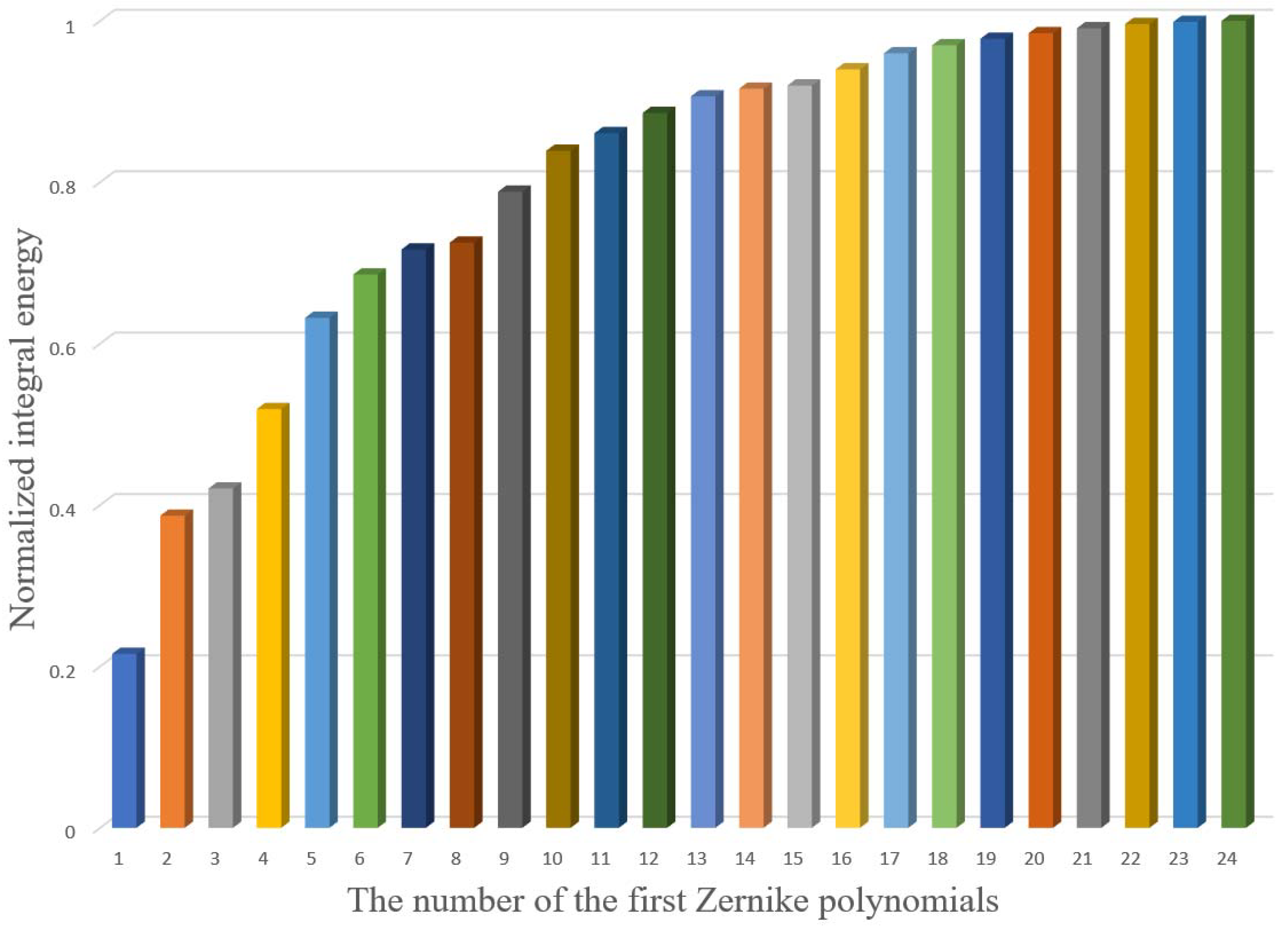
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Huang, Q.; Liu, D.; Chen, Y.; Wang, Y.; Tan, J.; Chen, W.; Liu, J.; Zhu, N. Secure free-space optical communication system based on data fragmentation multipath transmission technology. Optics Express 2018, 26, 13536–13542. [Google Scholar] [CrossRef]
- Vorontsov, M.; Weyrauch, T.; Carhart, G.; Beresnev, L. Adaptive optics for free space laser communications. In Lasers, Sources and Related Photonic Devices; OSA Technical Digest Series (CD); LSMA1; Optical Publishing Group: Washington, DC, USA, 2010. [Google Scholar] [CrossRef]
- Lu, M.; Bagheri, M.; James, A.P.; Phung, T. Wireless charging techniques for UAVs: A review, reconceptualization, and extension. IEEE Access 2018, 6, 29865–29884. [Google Scholar] [CrossRef]
- Landis, G.A.; Westerlund, H. Laser Beamed Power—Satellite Demonstration Applications; NASA Contractor Report 190793; IAF-92-0600; NASA: Washington, DC, USA, 1992. [Google Scholar]
- Bennet, F.; Conan, R.; D’Orgeville, C.; Dawson, M.; Paulin, N.; Price, I.; Rigaut, F.; Ritchie, I.; Smith, C.; Uhlendorf, K. Adaptive optics for laser space debris removal. Proc. SPIE 2012, 8447, 844744. [Google Scholar] [CrossRef] [Green Version]
- Tatarskii, V.I. Wave Propagation in a Turbulent Medium; McGraw-Hill: New York, NY, USA, 1961; 304p. [Google Scholar]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation through Random Media, 2nd ed.; SPIE Press: Bellingham, WA, USA, 2005; 782p. [Google Scholar] [CrossRef]
- Conan, J.; Rousset, G.; Madec, P. Wave-front temporal spectra in high-resolution imaging through turbulence. J. Opt. Soc. Am. A 1995, 12, 1559–1570. [Google Scholar] [CrossRef]
- Rukosuev, A.L.; Kudryashov, A.V.; Lylova, A.N.; Samarkin, V.V.; Sheldakova, Y.V. Adaptive optical system for real-time wavefront correction. Atmos. Ocean. Opt. 2015, 28, 381–386. [Google Scholar] [CrossRef]
- Rukosuev, A.L.; Nikitin, A.N.; Sheldakova, Y.V.; Kudryashov, A.V.; Belousov, V.N.; Bogachev, V.A.; Volkov, M.V.; Garanin, S.G.; Starikov, F.A. Smart adaptive optical system for correcting the laser wavefront distorted by atmospheric turbulence. Quantum Electron. 2020, 50, 707–709. [Google Scholar] [CrossRef]
- Malacara, D. Optical Shop Testing, 3rd ed.; Wiley-Interscience, A John Wiley & Sons Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Neal, D.R. Shack-Hartmann sensor engineered for commercial measurement applications. In Robert Shannon and Roland Shack: Legends in Applied Optics; SPIE Press: Bellingham, WA, USA, 2004. [Google Scholar]
- Kaya Instruments. Available online: https://kayainstruments.com/ (accessed on 10 November 2021).
- Nikitin, A.; Rukosuev, A.; Sheldakova, J.; Belousov, V.; Galaktionov, I.; Samarkin, V.; Kudryashov, A. FPGA-based 2 kHz closed-loop adaptive optical system with stacked actuator deformable mirror. Proc. SPIE 2020, 11508, 115080K. [Google Scholar] [CrossRef]
- Nikitin, A.; Starikov, F.; Volkov, V.; Bogachev, V.; Khlebnikov, A.; Rukosuev, A. Dynamic correction of the laser beam distortion by 2000 Hz FPGA-based adaptive optical system. Proc. SPIE 2020, 11506, 1150607. [Google Scholar] [CrossRef]
- Kudryashov, A.; Rukosuev, A.; Nikitin, A.; Galaktionov, I.; Sheldakova, J. Real-time 1.5 kHz adaptive optical system to correct for atmospheric turbulence. Opt. Express 2020, 28, 37546–37552. [Google Scholar] [CrossRef] [PubMed]
- Southwell, W.H. Wave-front estimation from wave-front slope measurements. J. Opt. Soc. Am. 1980, 70, 998–1006. [Google Scholar] [CrossRef]
- Cubalchini, R. Modal wave-front estimation from phase derivative measurements. J. Opt. Soc. Am. 1979, 69, 972–977. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light, 1st ed.; Pergamon Press: London, UK; New York, NY, USA; Paris, France, 1959; 986p. [Google Scholar]
- Goodwin, E.P.; Wyant, J.C. Field Guide to Interferometric Optical Testing; SPIE Field Guide Series; SPIE Press: Bellingham, WA, USA, 2006; Volume FG10, 114p. [Google Scholar]
- Brigham, E.O. The Fast Fourier Transform and Its Applications; Prentice Hall: Upper Saddle River, NJ, USA, 1988; 448p. [Google Scholar]
- Taylor, G.I. The Spectrum of Turbulence. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1938, 164, 476–490. [Google Scholar] [CrossRef] [Green Version]
- Toporovskiy, V.; Kudryashov, A.; Samarkin, V.; Sheldakova, J.; Rukosuev, A.; Skvortsov, A.; Pshonkin, D. Bimorph deformable mirror with a high density of electrodes to correct for atmospheric distortions. Appl. Opt. 2019, 58, 6019–6026. [Google Scholar] [CrossRef] [PubMed]
- Toporovskii, V.V.; Skvortsov, A.A.; Kudryashov, A.V.; Samarkin, V.V. Sheldakova, Y.V.; Pshonkin, D.E. Flexible bimorphic mirror with high density of control electrodes for correcting wavefront aberrations. J. Opt. Technol. 2019, 86, 32–38. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rukosuev, A.; Nikitin, A.; Belousov, V.; Sheldakova, J.; Toporovsky, V.; Kudryashov, A. Expansion of the Laser Beam Wavefront in Terms of Zernike Polynomials in the Problem of Turbulence Testing. Appl. Sci. 2021, 11, 12112. https://doi.org/10.3390/app112412112
Rukosuev A, Nikitin A, Belousov V, Sheldakova J, Toporovsky V, Kudryashov A. Expansion of the Laser Beam Wavefront in Terms of Zernike Polynomials in the Problem of Turbulence Testing. Applied Sciences. 2021; 11(24):12112. https://doi.org/10.3390/app112412112
Chicago/Turabian StyleRukosuev, Alexey, Alexander Nikitin, Vadim Belousov, Julia Sheldakova, Vladimir Toporovsky, and Alexis Kudryashov. 2021. "Expansion of the Laser Beam Wavefront in Terms of Zernike Polynomials in the Problem of Turbulence Testing" Applied Sciences 11, no. 24: 12112. https://doi.org/10.3390/app112412112
APA StyleRukosuev, A., Nikitin, A., Belousov, V., Sheldakova, J., Toporovsky, V., & Kudryashov, A. (2021). Expansion of the Laser Beam Wavefront in Terms of Zernike Polynomials in the Problem of Turbulence Testing. Applied Sciences, 11(24), 12112. https://doi.org/10.3390/app112412112








