Thermally Constrained Conceptual Deep Geological Repository Design under Spacing and Placing Uncertainties

Abstract

The temperature evolution within a deep geological repository (DGR) is a key design consideration for the safe and permanent storage of the high-level radioactive waste contained inside used nuclear fuel containers (UFCs). Due to the material limitations of engineered components with respect to high temperature tolerance, the Nuclear Waste Management Organization of Canada requires the maximum temperature within a future Canadian DGR to be less than 100 °C. Densely placing UFCs within a DGR is economically ideal, but greater UFC placement density will increase the maximum temperature reached in the repository. This paper was aimed to optimize (i) the separation between UFCs, (ii) the distance between container placement rooms, and (iii) the locations of the age-dependent UFCs in the placement rooms for a conceptual DGR constructed in crystalline rock. Surrogate-based optimization reduced the amount of computationally expensive evaluations of a COMSOL Multiphysics model used to study the temperature evolution within the conceptual DGR and determined optimal repository design points. Via yield optimization, nominal design points that considered uncertainties in the design process were observed. As more information becomes available during the design process for the Canadian DGR, the methods employed in this paper can be revisited to aid in selecting a UFC placement plan and to mitigate risks that may cause repository failure.

1. Introduction

In accordance with international scientific consensus, the best solution for the final disposal of Canadian high-level radioactive waste, which is predominantly produced by the country’s operation of nuclear power plants running CANDU reactors, is to isolate it within a deep geological repository (DGR) that will prevent radionuclide release into the biosphere for at least one million years. Designing and implementing such a repository are the responsibilities of the Nuclear Waste Management Organization (NWMO), and they have devised a plan for a DGR that will utilize a multiple-barrier system. It will employ five engineered and natural barriers for the isolation of the used nuclear fuel, as shown in Figure 1. The used CANDU fuel bundles (durable ceramic UO2 fuel pellets and the Zircaloy cladding that house them) provides the initial two barriers. The remaining three layers of the multiple-barrier system will be copper-coated carbon steel used fuel containers (UFCs) that consolidate 48 used fuel bundles per UFC, highly compacted bentonite buffer boxes for encasing the UFCs, and the host rock environment of the future repository approximately 500–800 m below ground surface.

As a critical component for the containment of used nuclear fuel, the integrity of the UFCs is the focus of many research programs at NWMO. The copper coating of the UFCs has been designed to be 3 mm thick, more than double the expected corrosion allowances for uniform corrosion, under-deposit corrosion, and microbially induced corrosion over one million years [1,2,3]. These phenomena are partially influenced by the presence of groundwater and the dissolved chemical species it would contain at the final DGR site. Although the copper coating on the UFCs should outperform its design life, it is still best to limit the transport of corrosive species towards the containers. Bentonite is an excellent material to help achieve this because it swells when exposed to water, meaning it will resist flow and can act as a sealing material. However, these desired properties of bentonite are lost if it is subjected to elevated temperatures—it converts to illite, a non-swelling clay, at around 140 °C [4]. Furthermore, at around 125 °C, the electrochemical properties of copper change such that corrosion kinetics become more rapid [4]. Furthermore, elevated temperatures will increase diffusive transport through the engineered barriers [5]. In consideration of these drawbacks, NWMO has chosen the maximum temperature within Canada’s DGR to be below 100 °C.

The conceptual DGR designed by NWMO thus far has UFCs stacked into two staggered layers, organized in a series of parallel placement rooms [4]. The temperature evolution within the DGR will be caused by the heat generated during the radioactive decay of the used nuclear fuel. As such, the maximum evolved temperature will be directly affected by the emplacement density of the UFCs inside the repository. Previous computer modelling studies on DGRs, including the one proposed by NWMO, have determined the thermal evolution within an infinite DGR through modeling a unit cell within a placement room [7,8,9]. Others have further studied the minimum combinations of UFC spacing and placement room spacings to meet maximum temperature requirements [10,11]. However, these studies were highly conservative, as the heat output of all UFCs was assumed to be identical at a maximum value. Should a UFC inventory of various ages (i.e., the time since the fuel they contain was discharged from a nuclear power reactor) be considered instead, the placement density of UFCs may be increased. This would be economically beneficial because for a given number of UFCs because a higher placement density would decrease the DGR footprint, thus requiring less material, land space, construction time, etc.

In this paper, the arrangement of UFCs into a conceptual DGR in a crystalline rock environment, detailed by NWMO in [4], is studied. Arrangement refers to spacing and UFC age, specifically: (i) the separation between containers within a placement room, (ii) the distance between placement rooms, and (iii) the locations of the age-dependent UFCs in the placement room. Here, these design variables are, respectively, denoted as UFC spacing, room spacing, and UFC age. For UFC inventories assumed to be stored in the DGR, optimal combinations of the design variables describing various arrangements were determined through surrogate-based optimization. Additionally, yield optimization was performed under assumptions of arbitrary design variable distributions as a means for incorporating risk into the design process.

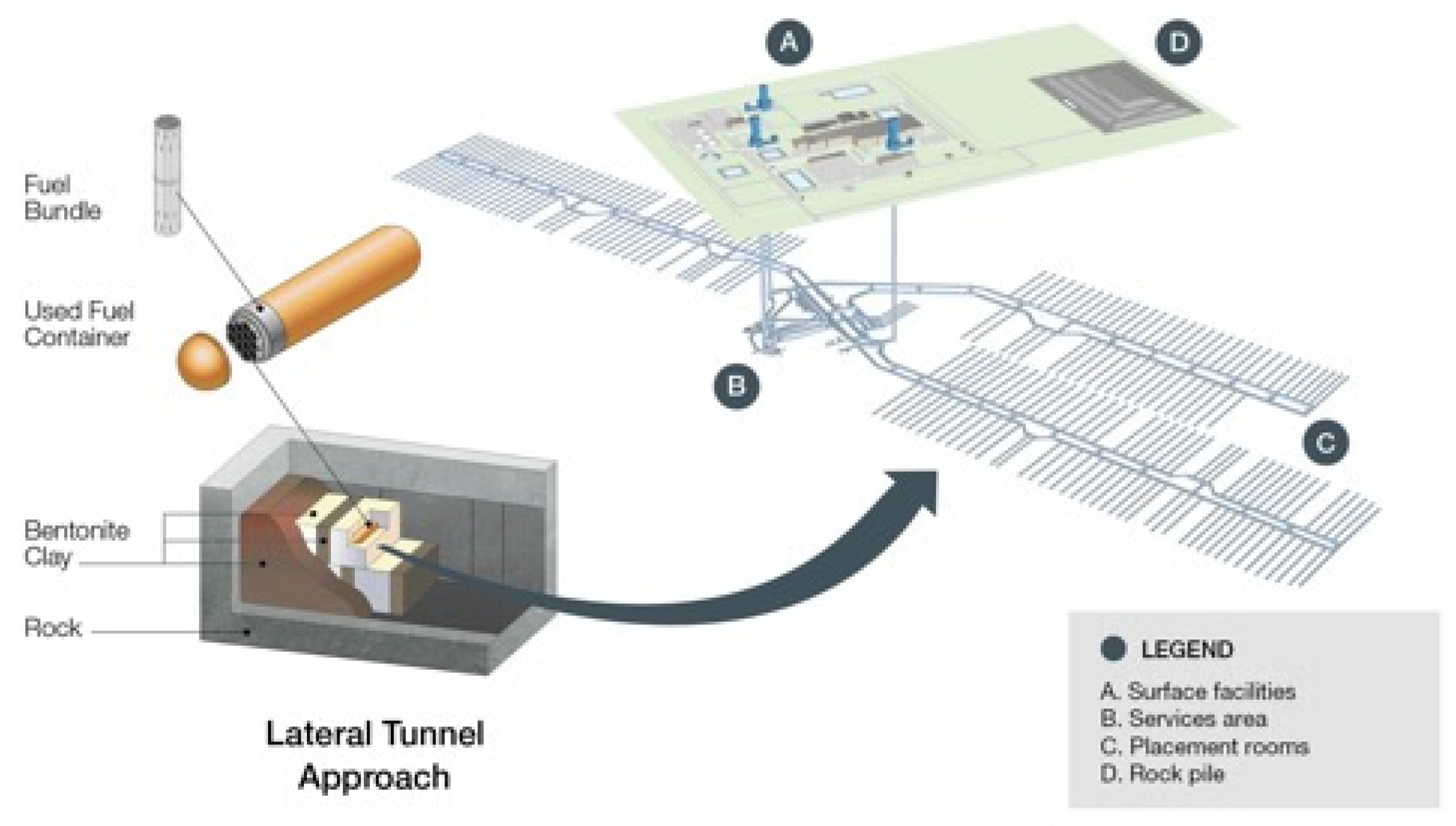
2. Finite Element Modeling of the Deep Geological Repository

The finite element analysis software COMSOL Multiphysics (COMSOL) was used to determine the maximum temperature that would occur for various DGR designs specified by the three design variables. The model built was based on the description of NWMO’s conceptual DGR in crystalline rock in [4], and it is a modification of the model developed in [7]. To consider UFC age, a unit cell that represents one repeating section inside a placement room could not be modeled, as was done in prior studies. Instead, half the length of a placement room (140.75 m) was modeled as a unit cell (Figure 2a); thus, UFC age was assumed to be symmetric from the room center. Further dimensional details of the conceptual DGR in crystalline rock by NWMO are illustrated in [12].

The model components were UFCs, buffer boxes, spacer blocks, gap-fill, and the host rock. Buffer boxes encased UFCs, spacer blocks distanced the boxes, and gap-fill lined the placement room walls (Figure 2b). Like buffer boxes, the spacer blocks and gap-fill material were bentonite-based components. Since the number of UFCs that could be placed in a placement room depends on the UFC spacing, the model placed an enlarged spacer block and highly compacted bentonite block at the end of the room to fill any voids due to unused space (Figure 2c). In this way, the model only considered conductive heat transfer. The depth of the modeled host rock was 5000 m based on the observation in [7] in which the temperature rise at this depth was negligible. The main dimensions of the model are shown in Figure 2, with the room spacing and UFC spacing design variables identified in Figure 2a,b, respectively.

An infinite repository was modeled through the application of adiabatic boundary conditions on the unit cell’s boundaries perpendicular to the horizontal dimensions, which act as symmetry axes. The top and bottom boundaries of the model were based on assumptions for a constant ground surface temperature of 5 °C and a geothermal gradient of 12 °C/km, respectively [13]. These adiabatic and isothermal boundaries are marked in Figure 2a. The initial temperature of the model was specified using the geothermal gradient.

The thermal properties of the model components were those specified in [7,12], which are summarized in

Table 1. Thermal properties of model components.

Component	Bulk Density [kg/m3]	Thermal Conductivity [W/m/K]	Specific Heat Capacity [J/kg/K]
UFC	7800	60.5	434
Buffer Box	1955	1.0	1280
Spacer Block	2276	2.0	1060
Gap-Fill	1439	0.4	870
Host Rock	2700	3.0	845

. All modeled UFCs were assumed to be discharged from a CANDU reactor for a minimum of 30 years by the time of repository placement, as per NWMO’s specifications [12]. Additionally, every UFC was assumed to contain used fuel that had been irradiated at a burnup of 220 MWh/kg. The heat output of one container under this assumption was estimated in [14] and is shown in

Table 2. Heat output of a UFC with 220 MWh/kg of fuel burnup.

Time Out-of-Reactor [a]	Heat Output [W]	Time Out-of-Reactor [a]	Heat Output [W]
30	169.092	150	46.108
35	155.232	160	44.075
40	142.296	200	38.716
45	131.208	300	32.802
50	121.968	500	26.888
55	112.728	1000	18.665
60	105.336	2000	12.751
70	91.568	5000	9.240
75	85.932	10,000	6.644
80	80.850	20,000	3.844
90	72.257	35,000	2.097
100	65.327	50,000	1.321
110	59.783	100,000	0.380
135	49.988	1,000,000	0.137

.

Using the described infinite repository model, a simulation for one million years using COMSOL would result in a maximum temperature profile that exhibits two peaks. The profile would represent the maximum temperature within the DGR at each specific time. The first peak in the maximum temperature would occur within 100 years after UFC placement into the DGR, while the second peak would occur at approximately 1550 years [7]. The occurrence of a second peak would be due to the use of adiabatic boundary conditions, and for a finite repository, it would be an overestimation of the DGR’s temperature. A method was developed in [7] to correct a temperature profile resulting from the use of an infinite repository to model a finite repository. The results of the method indicated that the first peak in the temperature profile for an infinite repository is representative of the peak in the temperature profile for the finite repository it represents. Thus, the maximum temperatures here were found by determining the value of the first peak occurring within the first few hundred years of simulation. An example of a maximum temperature profile that has a peak temperature of 84 °C is shown in Figure 3 for a model with a UFC spacing of 1.5 m, a room spacing of 25 m, and all UFC ages being 30 years.

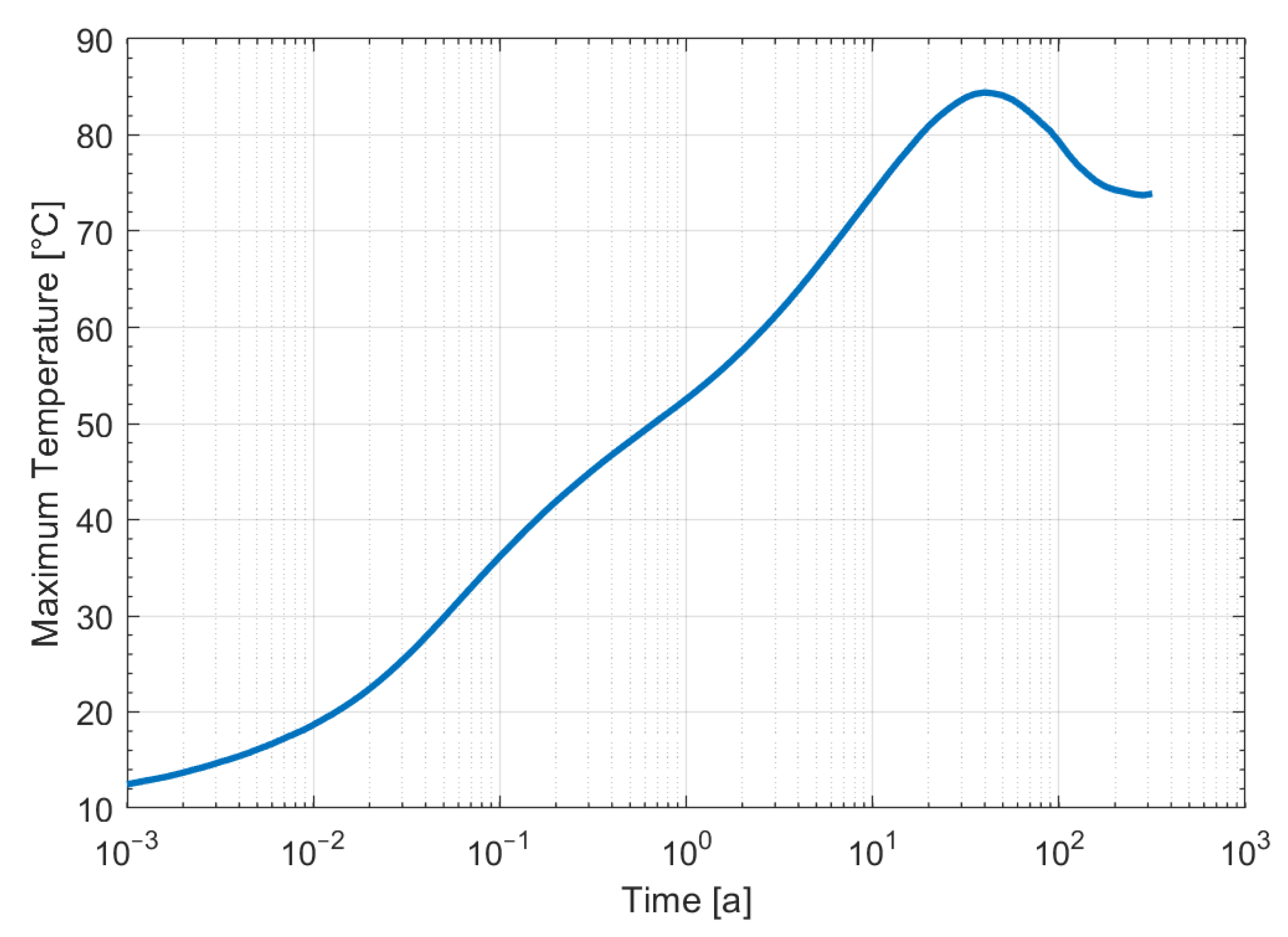
3. Maximum Temperatures of UFC Arrangements in the Repository

To densely place UFCs into the DGR, the maximization problem that needs to be solved is:

$$\begin{array}{cc}\hfill \underset{\mathit{x}}{\max }& T_{\max }\left(\mathit{x}\right)\hfill \\ \hfill \mathrm{subject} \mathrm{to}& T_{\max }\left(\mathit{x}\right)\le 100\hfill \\ & x_i^L\le x_i\le x_i^U, i=1,2,3\end{array}$$

(1)

where $T_{\max }\left(\mathit{x}\right)$ is the maximum temperature reached inside the DGR in [°C]; $\mathit{x}=\left[x_1,x_2,x_3\right]$ is the design variable vector with indices ordered as UFC spacing in [m], room spacing in [m], and UFC age in [a]; and superscripts $L$ and $U$ denote lower and upper bounds, respectively. The discrete values of the considered spacing design variables followed those in [10]. Specifically, they were $x_1=\{1.0,1.1,\dots ,2.0\}$ and $x_2=\{10,11,\dots ,40\}$. The value $x_1=1.0$ reflected the absence of spacer blocks (Figure 2b) in the DGR, and it was the minimum UFC spacing possible because the buffer boxes were one meter wide. Regarding the UFC age design variable, two UFC inventory cases were studied. The first case was an inventory with identical UFC ages of 30 years ($x_3=30$), which is comparable to previous studies and is a worst-case scenario as per the minimum UFC age specification by NWMO. The second case considered inventories with assorted UFC ages ranging from 30 to 60 years. This assumed that initially placed UFCs were of 30 years of age and were 60 years of age by the end of a 30-year repository operation. This length of operation was reduced from an estimated repository operation time of about 38 years in [15] to obtain more conservative designs, as younger UFCs would have higher heat output.

3.1. Feasible UFC Arrangements

Excluding design variable bounds, the maximum temperature constraint in Equation (1) was the only criterion that had to be satisfied. Approximating the constraint at equality would determine a boundary that separates feasible and infeasible DGR design points, and design points resulting in maximum temperatures at or just below the 100 °C threshold could then be quickly identified. These would identify the solutions to Equation (1). Thus, the following minimization problem was solved instead:

$$\begin{array}{cc}\hfill \underset{\mathit{x}}{\min }& \left|T_{\max }\left(\mathit{x}\right)-100\right|\hfill \\ \hfill \mathrm{subject} \mathrm{to}& x_i^L\le x_i\le x_i^U, i=1,2,3\hfill \end{array}$$

(2)

3.2. Parameterization of UFC Age Arrangement

The study of the second case of assorted UFC ages was limited to a selection of age arrangements through the application of single parameter shape functions. Shape functions designated an age value for each container location within a placement room under the assumption that there would be sufficient inventory to do so. This method was opposed to specifying various UFC inventories and finding the optimal permutation of the UFC age at each placement room location, which might lead to excessively strict design specifications. Two shape functions were considered; they were based on a cosine function and a Kumaraswamy probability density function (PDF).

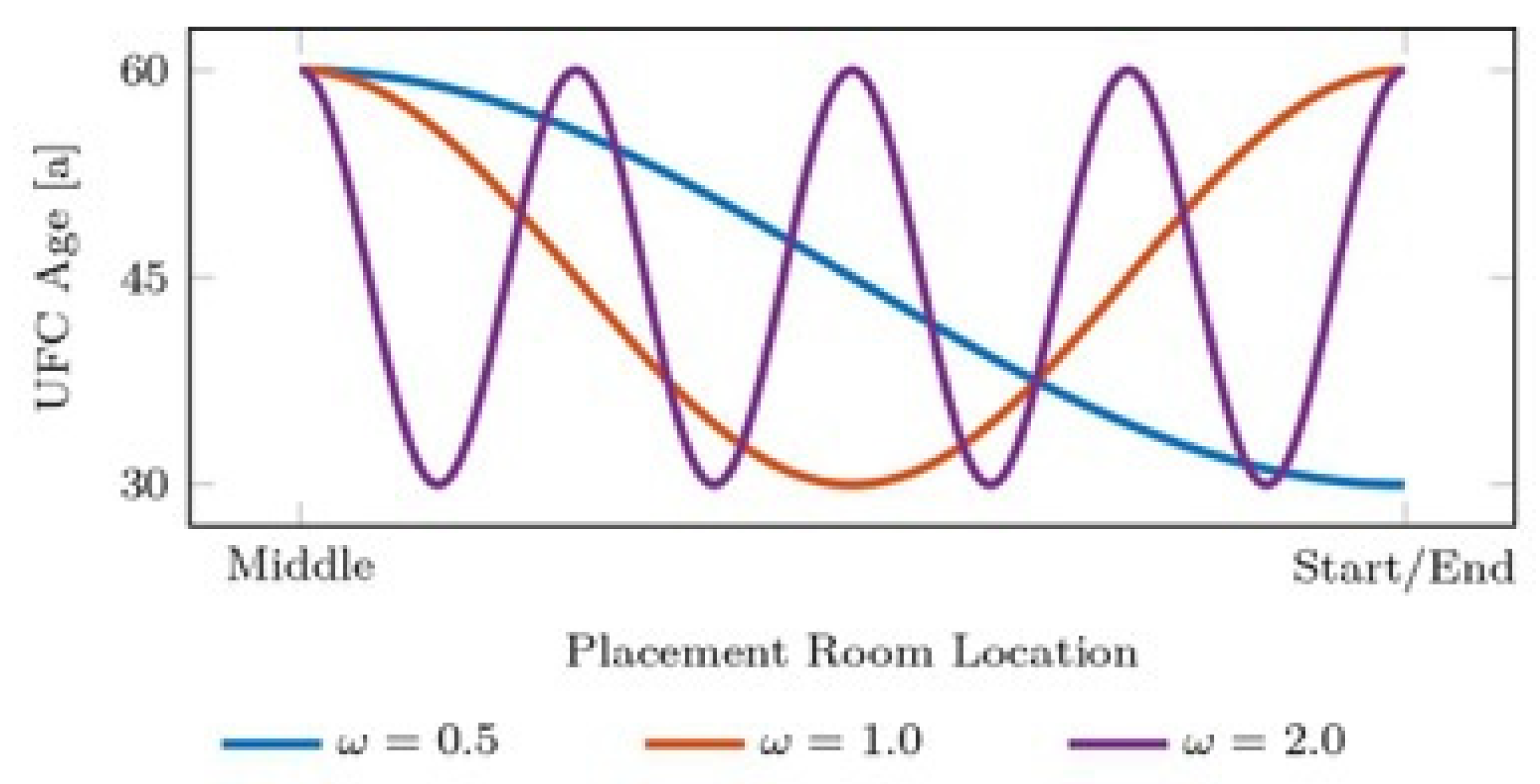
3.2.1. Cosine-Based Shape Function

Using a cosine-based shape function would organize UFC ages in arrangements that alternate between the youngest and oldest (30–60 years), with frequency being dependent on one parameter, $\omega$. The shape function that designated the UFC ages to locations from the center of the placement room ($u=0$) to the start/end of the room ($u=140.75$) in this way was:

$$x_{3,\cos }\left(u;\omega \right)=15\cos \left(\omega \frac{u}{140.75}\right)+45, u\in \left[0,140.75\right]$$

(3)

The considered values of the shape parameter in Equation (3) were $w=\{0.5,1.0,\dots ,10\}$, representing UFC arrangements that alternate 1–20 times over the span of an entire placement room. A few values of $\omega$ are shown in Figure 4.

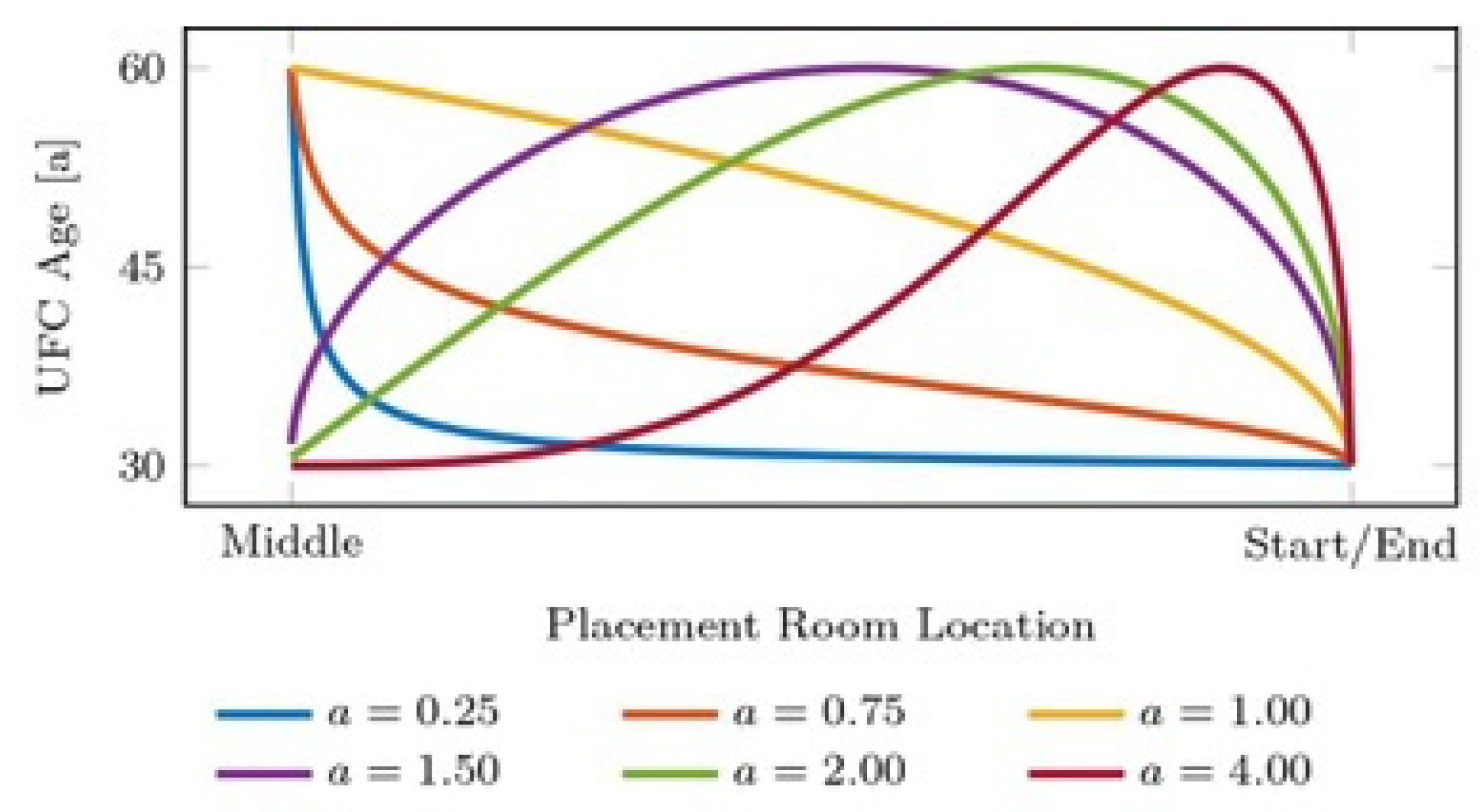
3.2.2. Kumaraswamy PDF-Based Shape Function

The definition of a Kumaraswamy PDF is [16]:

$$f\left(x;a,b\right)=ab{x}^{a-1}{\left(1-x^a\right)}^{b-1}, x\in \left(0,1\right)$$

(4)

Depending on the values of $a$ and $b$ in Equation (4), the Kumaraswamy PDF takes on various shapes [16]. A Kumaraswamy PDF-based shape function allows for the consideration of a variety of UFC age arrangements. To limit possibilities and keep the scope of the age arrangements relatively small, shape parameter values $a=\{0.25,0.50,\dots ,4.00\}$ were considered, while the other parameter was kept constant at $b=1.5$ . The corresponding shape function was:

$$x_{3,\mathrm{KPDF}}\left(u;a\right)=\frac{30\left(1.5\right)}{\max x_{3,\mathrm{KPDF}}^{\prime }\left(u;a\right)}{\left(\frac{0.99u}{140.75}+0.01\right)}^{a-1}{\left(1-{\left(\frac{0.99u}{140.75}+0.01\right)}^a\right)}^{b-1}, u\in \left[0,140.75\right]$$

(5)

where $x_{3,\mathrm{KPDF}}^{\prime }\left(u;a\right)=30\left(1.5\right){\left(\frac{0.99u}{140.75}+0.01\right)}^{a-1}{\left(1-{\left(\frac{0.99u}{140.75}+0.01\right)}^a\right)}^{b-1}$. The constants 0.99 and 0.01 in the equation were due to the mapping of $x\in \left[0.01,1\right]$ from Equation (4) to $u\in \left[0,140.75\right]$ in Equation (5). This was required because the Kumaraswamy PDF tends to infinity for values $0<a<1$ when $b=1.5$. The shape function in Equation (5) for several values of $a$ is illustrated in Figure 5.

The parameterization of the UFC age arrangement using the shape functions in Equations (3) and (5) implied that the UFC age design variable would be expressed as:

$$x_3\left(u;\alpha \right)=\{\begin{array}{cc}{x}_{3,\cos }\left(u;\omega \right)\hfill & \mathrm{if} \cos \mathrm{ine}\text{-}\mathrm{based}\hfill \\ x_{3,\mathrm{KPDF}}\left(u;a\right)\hfill & \mathrm{if} \mathrm{Kumaraswamy} \mathrm{PDF}\text{-}\mathrm{based}\hfill \end{array}$$

(6)

Thus, the general shape parameter $\alpha$ became the third design variable to be optimized for the assorted UFC age case.

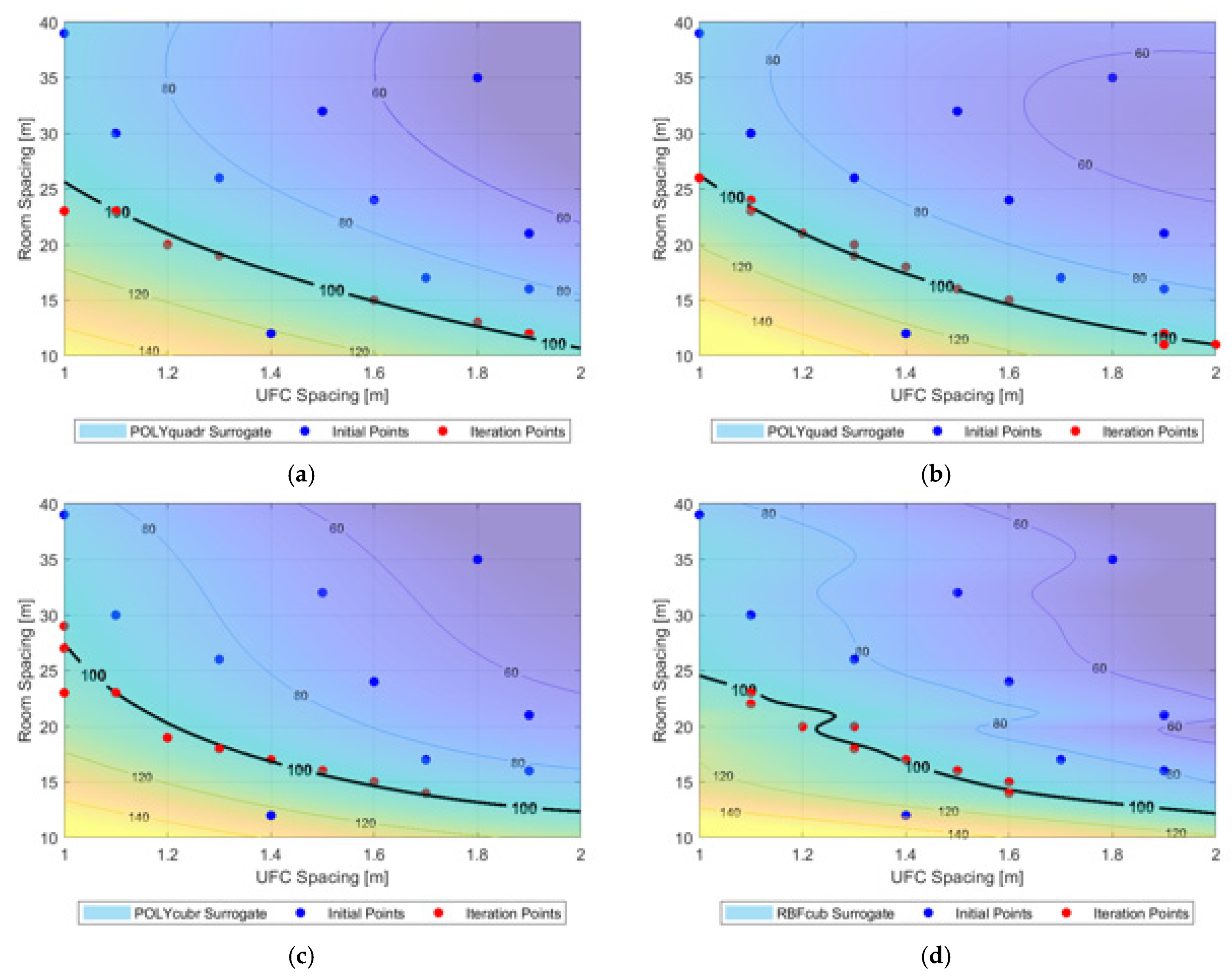
4. Surrogate-Based Optimization

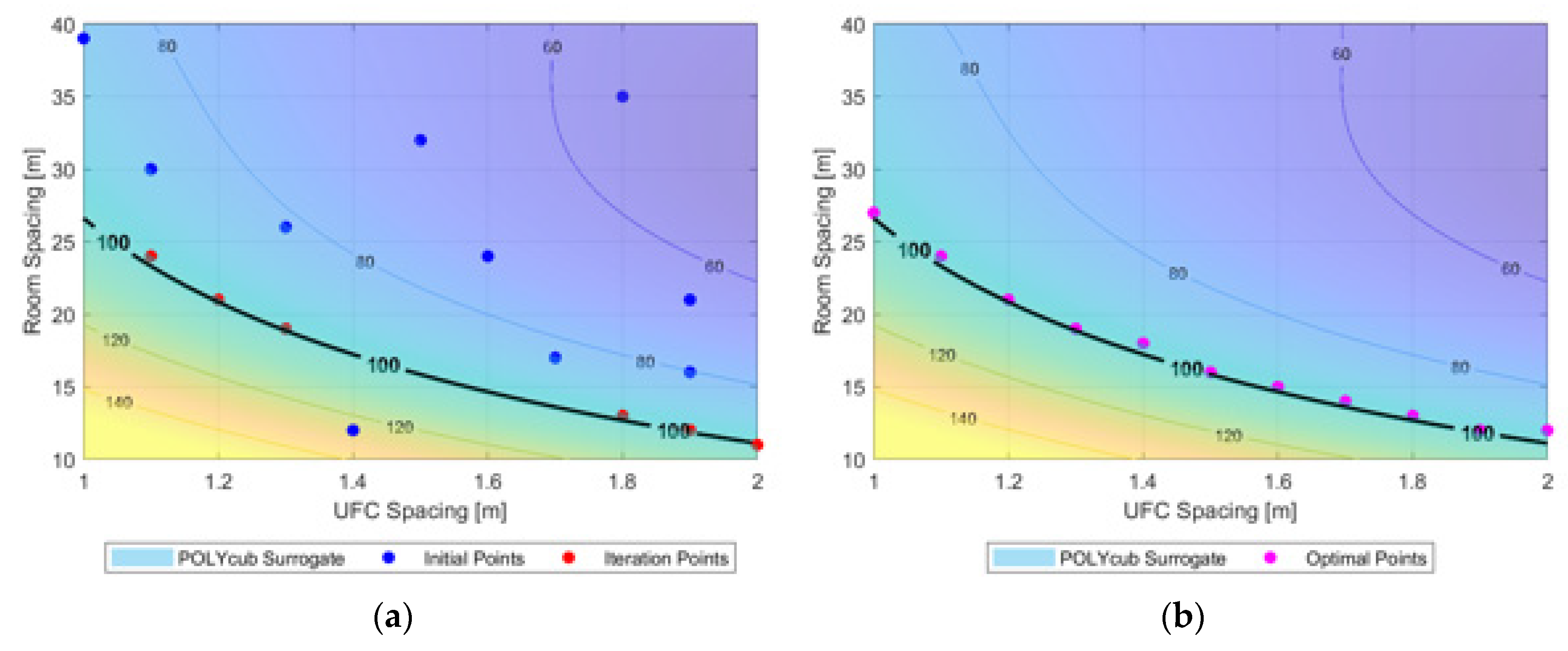
4.1. Method

The COMSOL model described in Section 2 used to compute the maximum temperature inside the DGR, $T_{\max }\left(\mathit{x}\right)$, was regarded as a high-fidelity model and a black-box function since the maximum temperature cannot be easily predicted given a particular UFC arrangement. The direct optimization of the objective function in Equation (2) to determine optimal repository designs would be computationally expensive due to many high-fidelity model evaluations being required. Hence, we employed surrogate-based optimization, which approximated the objective function with surrogate models that used computationally cheaper functions. Two types of surrogate functions were used, namely polynomial and radial basis function (RBF) surrogate functions. An RBF is a function that calculates the distance of a point from the origin or a specified center.

The steps of the used surrogate-based optimization are summarized below [17]:

• Initially ($k≔0$), a set of ten design points, ${\mathit{S}}_0$, were chosen through Latin hypercube sampling [18]. These were then evaluated using the high-fidelity model to determine their corresponding maximum temperatures.
• A surrogate model, ${\mathit{s}}_k$, was fitted to the available data, $\left\{\left(\mathit{x},T_{\max }\left(\mathit{x}\right)\right)|\mathit{x}\in {\mathit{S}}_k\right\}$.
• A maximin point from evaluated points, ${\mathit{S}}_k$, was identified through surface-minimum point sampling (using random selection to break ties) and evaluated using the high-fidelity model.
• The predicted maximum temperature from $s_k$ was compared to the true value from the high-fidelity model. If the difference exceeded 0.5 °C, the process was repeated from Step 2 after updating ${\mathit{S}}_k$; otherwise, the optimization converged.

The toolbox MATSuMoTo provided MATLAB functions for constructing surrogate models using polynomial functions and RBFs [19].

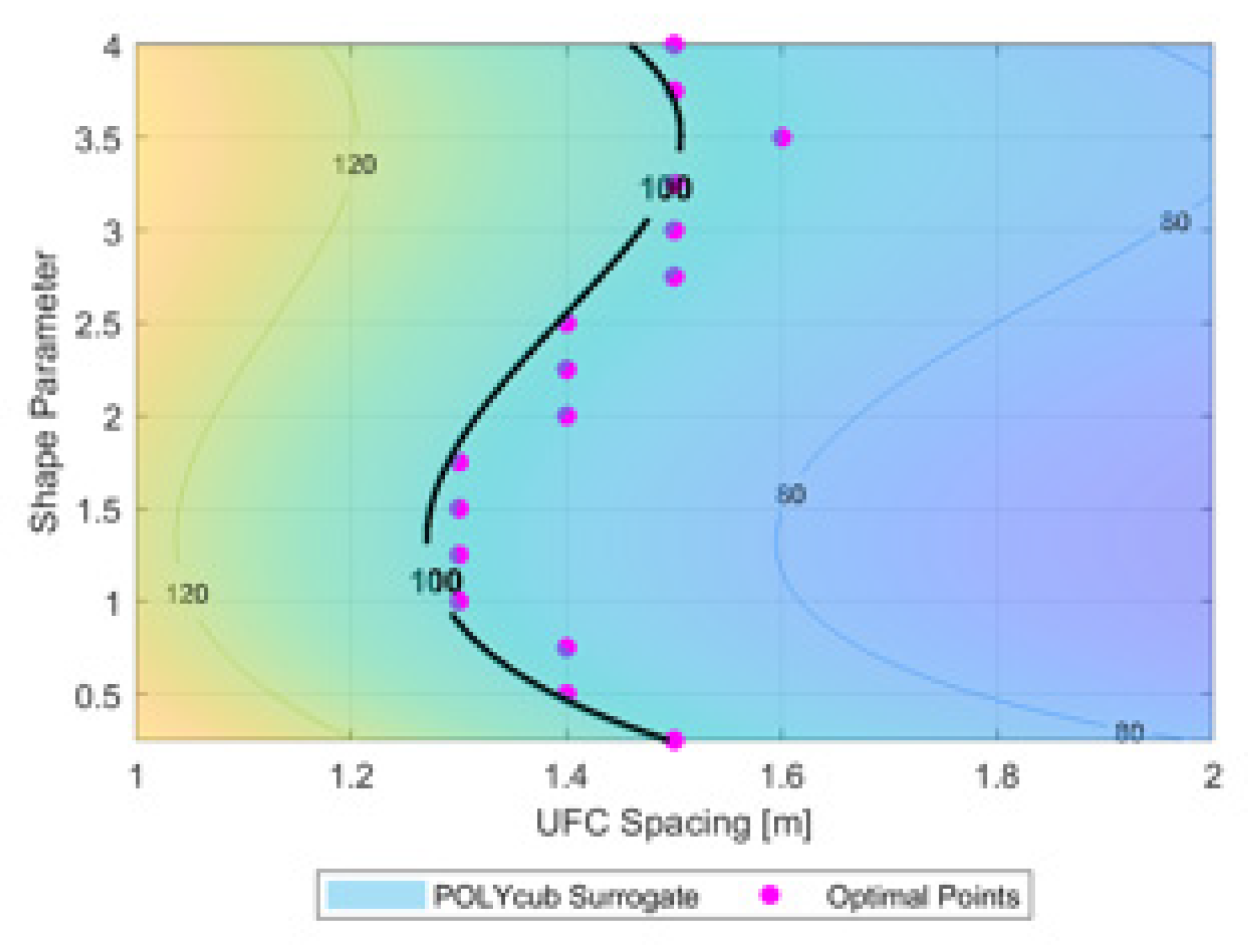
4.2. Optimal Arrangements for an Inventory with Identical UFC Age

For the case of an inventory with identical UFC age ($x_3=30$), the maximum temperature within the DGR was found to be a function of the spacing design variables, i.e., $T_{\max }=T_{\max }\left(x_1,x_2\right)$. The surrogate-based optimization of Equation (2) when a cubic polynomial surrogate function was used resulted in the determination of the black boundary in Figure 6a, which approximated the combinations of UFC and room spacings that would result in maximum temperatures of 100 °C. Including the design variable bounds, the feasible region in Figure 6a is the region above the black boundary.

Recalling Equation (1), the optimal design points are those closest to and above the black boundary. For a UFC inventory assumed to be identical in age, the discrete optimal combinations of UFC and room spacings are indicated in Figure 6b. The results reveal that if spacer blocks are not used in the DGR (i.e., $x_1=1.0$), the minimum room spacing required to keep the maximum temperature below 100 °C is 27 m. If spacer blocks are at their widest considered width of 2 m (i.e., $x_1=2.0$), the room spacing can be reduced to 12 m.

The use of surrogate-based optimization lessened the burden of evaluating many design points using the high-fidelity model. A total of 16 high-fidelity model evaluations can be seen in Figure 6a, which is a fraction of the total number of possible discrete design points (341 for the considered values of $x_1$ and $x_2$). Surrogate-based optimization reduced the computation time by a factor of about 21 based on a convergence criterion of 0.5 °C if it was assumed that model simulations at all the remaining design points would converge in comparable times. Considering that the 16 high-fidelity model evaluations were completed in 32 h on a machine with an Intel Core i5-3230M CPU at 2.60 GHz using two cores in one socket with 8 GB of RAM, up to 650 h or 95% of computation time were saved. This highlights the benefits of surrogate-based optimization, with the applicability reducing computational requirements of even more complex objective functions such as those within Section 4.3 that consider UFC age distributions via shape functions.

Looking at functions that can adequately approximate given objective, black-box functions would be ideal surrogate candidates to employ with surrogate-based optimization as the most reductions in model evaluations, and computation time would be attained due to accelerated convergence. The performance of the cubic polynomial surrogate function in Figure 6a can be compared against other polynomial and RBF surrogate functions in Figure A1 of Appendix A. Of the investigated surrogate functions, the fewest iterations were required when using the cubic polynomial surrogate function when starting from the same initial design points. For the given design case of an inventory with identical UFC age, the thin-plate spline RBF surrogate function would have been a poor choice because it required a total of 28 high-fidelity model evaluations—nearly double the 16 evaluations, i.e., double the computation time, required when using the cubic polynomial surrogate function.

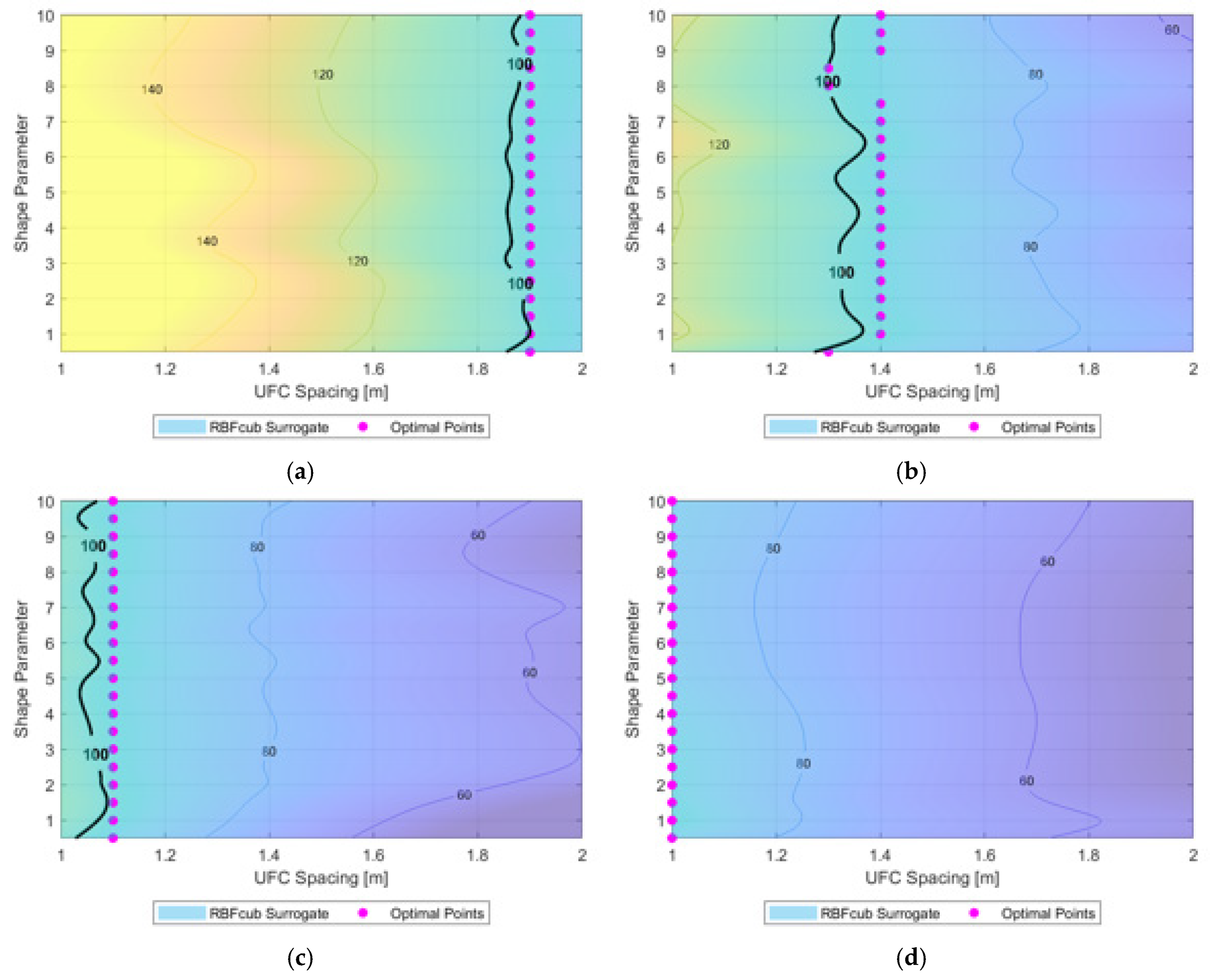
4.3. Optimal Arrangements for Inventories with Assorted UFC Ages

Although studies of UFC arrangements for inventories with assorted ages could have been conducted with all three design variables (UFC spacing, room spacing, and shape parameter) using surrogate-based optimization, optimization performed at fixed values of room spacing (i.e., $T_{\max }=T_{\max }\left(x_1,\alpha \right)$) was used here for simplicity of interpretation. It can be seen in Figure 6b that designs with room spacings above 27 m did not have maximum temperatures that exceeded 100 °C, so we limited the values of room spacing for which the optimization was performed to $x_2=\{10,15,20,25\}$.

Unlike in the previous case, cubic RBF surrogate functions were employed during optimization instead of cubic polynomial surrogate functions. While it may be apparent that a decrease in UFC spacing would require an increase in room spacing to remain on the maximum temperature contour (and thus a simple polynomial surrogate was adequate in Figure 6 where $T_{\max }=T_{\max }\left(x_1,x_2\right)$), here it was expected that $T_{\max }=T_{\max }\left(x_1,\alpha \right)$ would have nonlinearity characteristics that would be better captured by cubic RBFs. A polynomial surrogate is limited to a set of monomials; however, an RBF surrogate linearly combines many RBFs using evaluated data points as their origins.

4.3.1. Cosine-Based Shape Function

The surrogate-based optimization results of Equation (2) for UFC ages arranged using a cosine-based shape function at room spacings $x_2=\{10,15,20,25\}$ and the optimal design points as per Equation (1) are given in Figure 7. It can be seen that when UFC ages are arranged sinusoidally in a placement room within the studied values of $\omega$, the frequency of alternating between the minimum age of 30 years and the maximum age of 60 years does not affect the required UFC spacing. For this age arrangement, the minimum UFC spacings required at room spacings of 10, 15, and 20 m were found to be 1.9, 1.4, and 1.1 m, respectively. Figure 7d shows that no spacer blocks ($x_1=1.0$) would be required at a room spacing of 25 m to achieve maximum temperatures below 100 °C. Recall that $x_1=1.0$ was the minimum UFC spacing possible as even if spacer blocks were entirely removed, the size of the buffer boxes were still separated the UFCs by one meter center-to-center (Figure 7b).

4.3.2. Kumaraswamy PDF-Based Shape Function

In contrast to those shown in Figure 7, the results of the surrogate-based optimization in Figure 8 varied with different values of the shape parameter $a$ when UFC ages were arranged using a Kumaraswamy PDF-based shape function. Thus, for a given room spacing, the UFC spacing necessary can be quite different depending on how one wishes to arrange UFCs by age. By using a shape function and parameterizing the UFC age arrangement, the UFC spacings required for many arrangements (within one family of functions) were able to be studied. To our knowledge, this method has not yet been used in the design process of the DGR.

Based on the nature of the 100 °C contour in Figure 8b, the choice of cubic RBF surrogate functions was justified because polynomial surrogates would not have been able to produce such a curve. This can be seen if Figure 8b is compared to Figure A2 of Appendix A, which shows the results from using a cubic polynomial surrogate function.

The results in Figure 8 demonstrate that the largest UFC spacings are required for shape parameter values of $a\to 0.25$ and $a\to 4.00$, while smaller UFC spacings are allowed for shape parameter values in between those values. These results agree with the age distribution examples depicted in Figure 5. Shape parameter values $a\to 0.25$ and $a\to 4.00$ would place the greatest number of young, high heat-generating UFCs together (at the start/end and middle of the placement rooms, respectively); thus, more distance between the containers would be required to keep the temperature around them manageable.

For this age arrangement at a room spacing of 10 m, only shape parameter values $0.75\le a\le 2.50$ can lead to maximum temperatures below 100 °C (Figure 8a). From another perspective, Figure 8 shows that the largest required UFC spacings should have age arrangements that follow a Kumaraswamy PDF-based shape function. At room spacings of 15, 20, and 25 m, the largest required UFC spacings are 1.6, 1.3, and 1.1 m, respectively. This can be concluded as shape parameter values of $a\to 0.25$ and $a\to 4.00$ most unfavorably place UFCs by age. Should there be deviations from the age arrangements specified by these values, the young and high heat-generating UFCs can only be further dispersed from their alike peers.

5. Yield Optimization

The optimal repository designs determined in Section 4.2 and Section 4.3 via surrogate-based optimization were deterministic, as they assumed that the construction of the DGR could be done precisely to the UFC arrangement specifications. In practice, slight variations in the intended dimensions may exist (e.g., DGR walls will be textured due to drill and blast excavation techniques), and it is important to understand the effect of such variations on the maximum achieved temperature. Performing yield optimization is a way to analyze the effect of certain design deviations (given uncertainty information) on the maximum DGR temperature to ensure that temperatures will not exceed 100 °C. This section is intended to illustrate the practicality of determining yield and subjecting it to optimization using assumptive calculations, as applied to the conceptual DGR by NWMO.

5.1. Method

Yield optimization is a method for reducing the risk/probability of system failure by aiming to center a tolerance box in the design space such that the probability mass of the random variables inside the feasible region is at a maximum [20]. When used, it adds a stochastic consideration to a design process. Here, system failure is defined as the maximum DGR temperature exceeding 100 °C.

Yield optimization comprises three steps: feasible region approximation, joint cumulative distribution approximation, and yield maximization [21]. Their details are as follows, provided here for readers’ better understanding.

• For a feasible/acceptability region of $m$ design variables defined by $k$ constraints:

  $$R_A=\left\{\mathit{x}\in {ℝ}^m\right|h_i\ge 0,i=1,\dots ,k\}$$

  (7)

  a polyhedral approximation is performed to obtain the constraints in the form [21]:

  $$h_i\left(\mathit{x}\right)\approx h_i\left({\mathit{x}}^{*}\right)+{\mathit{g}}_i{\left({\mathit{x}}^{*}\right)}^{\mathrm{T}}\left(\mathit{x}-{\mathit{x}}^{*}\right)$$

  (8)

  where ${\mathit{g}}_i\left({\mathit{x}}^{*}\right)$ is the gradient vector of constraint $h_i\left({\mathit{x}}^{*}\right)$ and ${\mathit{x}}^{*}$ is an expansion point that lies on the surface of $h_i\left({\mathit{x}}^{*}\right)=0$ and is closest to the center of the design’s tolerance box. This leads to a polytope that approximates the feasible region [21]:

  $$R_P=\left\{\mathit{x}\right|\mathit{A}\mathit{x}\ge \mathit{c},{\mathit{x}}^L\le \mathit{x}\le {\mathit{x}}^U\}$$

  (9)

  where vector ${\left({\mathit{g}}_i^{*}\right)}^{\mathrm{T}}={\left[\frac{\partial h_i}{\partial x_1},\dots ,\frac{\partial h_i}{\partial x_m}\right]}_{{\mathit{x}}_i^{*}}$ and scalar ${\left({\mathit{g}}_i^{*}\right)}^{\mathrm{T}}{\mathit{x}}_i^{*}$ make up the $i$th row of $\mathit{A}$ and $\mathit{c}$, respectively. Superscripts $L$ and $U$ denote lower and upper bounds on the design variables, respectively.
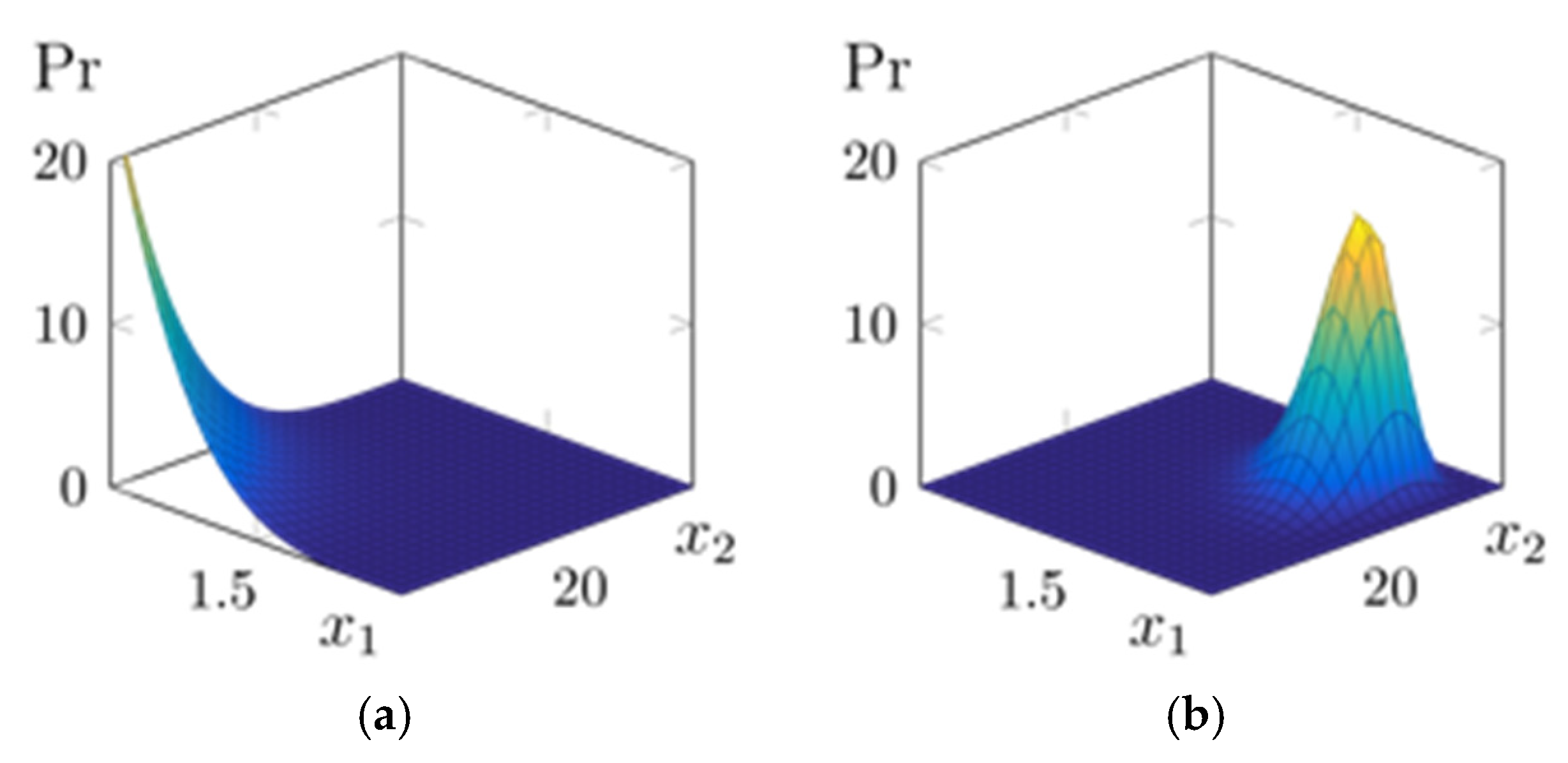
• If unknown, the true distributions of the random variables (design variables) are approximated by arbitrary distributions. A closed-form cumulative distribution function (CDF) is ideal for the next step. Thus, for algebraic simplicity, the authors of [21] used the Kumaraswamy distribution, which has the following CDF [16]:

  $$\begin{array}{cc}F\left(x;a,b\right)=1-{\left(1-x^{\widehat{a}}\right)}^{\widehat{b}},& x\in \left(0,1\right)\end{array}$$

  (10)

  where parameters $\widehat{a}$ and $\widehat{b}$ are those in the Kumaraswamy PDF described earlier in Equation (4). Additionally, recall that the Kumaraswamy PDF is useful in that it can represent many distributions (Figure 5) depending on its two shape parameters. Here, we use $\widehat{a}$ and $\widehat{b}$ to denote the shape parameters for the distribution of random variables, while the previous $a$ and $b$ continue to denote the shape parameters that define the UFC age arrangement.
• Yield maximization proceeds by determining the location of a maximum yield box that is strictly located within the approximated feasible region, $R_P$. This containment requirement is [21]:

  $${\mathit{A}}^{+}{\mathit{x}}^u-{\mathit{A}}^{-}{\mathit{x}}^l\le \mathit{c}$$

  (11)

  where ${\mathit{A}}_{ij}^{+}=\max \left\{0,A_{ij}\right\}$ and ${\mathit{A}}_{ij}^{-}=\max \left\{0,-A_{ij}\right\}$. Superscripts $l$ and $u$ denote lower and upper bounds on the optimum maximum yield box, respectively. The maximum yield box is contained inside the design’s tolerance box, which has dimensions specified by $\mathit{t}$. The yield maximization problem that must be solved is therefore [21]:

  $$\begin{array}{cc}\hfill \underset{{\mathit{x}}^r,{\mathit{x}}^l,{\mathit{x}}^u}{\max }& \mathrm{Yield}\left({\mathit{x}}^r,{\mathit{x}}^l,{\mathit{x}}^u\right)\hfill \\ \hfill \mathrm{subject} \mathrm{to}& {\mathit{A}}^{+}{\mathit{x}}^u-{\mathit{A}}^{-}{\mathit{x}}^l\le \mathit{c}\hfill \\ & {\mathit{x}}^u\le {\mathit{x}}^r+\mathit{t}\hfill \\ & {\mathit{x}}^r\le {\mathit{x}}^l\le {\mathit{x}}^u\hfill \end{array}$$

  (12)

  where ${\mathit{x}}^r$ is a reference point corresponding to the lower bounds of the tolerance box. Using the Kumaraswamy CDF in Equation (10) and assuming variable independence, yield is simply calculated [21]:

  $$\mathrm{Yield}\left({\mathit{x}}^r,{\mathit{x}}^l,{\mathit{x}}^u\right)={\displaystyle \prod }_{j=1}^m\left[F\left(\frac{x_j^u-x_j^r}{t_j}\right)-F\left(\frac{x_j^l-x_j^r}{t_j}\right)\right]$$

  (13)

The solution to the maximization problem in Equation (12) determines the optimal design point as ${\mathit{X}}_0={\mathit{x}}^r+0.5\mathit{t}$.

The steps above assume that the feasible region is convex. If it is nonconvex, the nominal design point, ${\mathit{X}}_0$, can be used as the expansion point, ${\mathit{x}}^{*}$, in Equation (8) in a subsequent iteration [21].

5.2. Designs with Failure Allowance

In this section, yield optimization for determining a nominal DGR design point is exemplified by assuming that the UFC spacing ($x_1$) and room spacing ($x_2$) of the repository are random variables with arbitrary tolerances and distributions. Due to a single variable representing the UFC spacing between all containers and the COMSOL model portraying an infinite repository, the interpretation of the results should consider that the realized values of the random variables represent that of the entire repository.

Because the bounds considered on UFC and room spacings would result in a large feasible region (e.g., see Figure 6), yield optimization would always give 100% yield designs for any reasonably sized tolerance box on the two random variables, regardless of their distributions. However, should some failure probability be allowed such that a portion of the design’s tolerance box can extend across the feasible boundary, the distributions of the random variables would then be significant. Thus, for demonstration, we studied failure probabilities of 1% and 5% for the specific case of an assorted UFC age inventory arranged using a Kumaraswamy PDF-based shape function with shape parameter values of $a=0.25$ and $b=1.5$. Note that earlier in Section 4.3.2 and Figure 8, it was shown that the largest UFC spacings are required for shape parameter values of $a\to 0.25$ because this would mean like-aged UFCs being densely placed. Therefore, the subsequent calculations can be considered as designing for unfavorable or high-risk cases.

To obtain the feasible region required to start yield optimization, $R_A$ in Equation (7), surrogate-based optimization was first performed for $T_{\max }=T_{\max }\left(x_1,x_2\right)$ with $a=0.25$.

The objective function in Equation (12) was modified to incorporate failure probability. Additionally, a penalty term that discouraged large UFC spacings and room spacings was included for reducing the DGR construction cost; otherwise, optimization would place the tolerance box in the center of the large feasible region, thus leading to no failures but a huge cost to construct the DGR. The yield optimization problem became:

$$\begin{array}{cc}\hfill \underset{{\mathit{x}}^r,{\mathit{x}}^l,{\mathit{x}}^u}{\max }& \begin{array}{c}\mathrm{Yield}\left({\mathit{x}}^r,{\mathit{x}}^l,{\mathit{x}}^u\right)-\frac{1}{100}\left(\frac{\theta \left(X_{0,1}-x_1^L\right)}{x_1^U-x_1^L}+\frac{\left(1-\theta \right)\left(X_{0,2}-x_2^L\right)}{x_2^U-x_2^L}\right)\hfill \end{array}\\ \hfill \mathrm{subject} \mathrm{to}& \mathrm{Yield}\left({\mathit{x}}^r,{\mathit{x}}^l,{\mathit{x}}^u\right)\le 1-F^T\hfill \\ & {\mathit{A}}^{+}{\mathit{x}}^u-{\mathit{A}}^{-}{\mathit{x}}^L\le \mathit{c}\hfill \\ & {\mathit{x}}^u\le {\mathit{x}}^r+\mathit{t}\hfill \\ & {\mathit{x}}^r\le {\mathit{x}}^l\le {\mathit{x}}^u\hfill \end{array}$$

(14)

where $\theta$ is an arbitrary weighting parameter, ${\mathit{X}}_0$ is the nominal design point, and $F^T$ is a target failure probability. The constant $1/100$ scales the penalty term down so that maximizing yield is of higher priority. The arbitrary weighting parameter determines whether tighter UFC spacing or room spacing is more important. Since larger UFC spacing increases the DGR footprint and the amount of host rock excavated for more placement rooms while larger room spacing only increases the DGR footprint, preference was given to smaller UFC spacings by assigning the parameter a value of 0.8 so that designs that reduce the overall cost of the repository would be identified (compare the excavation cost in [22] and land cost in [23]). The modification of including the target failure probability could lead to inaccurate results because the predicted yield only approximates the actual portion of the tolerance box within/beyond the feasible region. However, for small failure probabilities, the approximation should be reasonable.

Tolerances and Distributions

The tolerances on UFC and room spacings were, respectively, assumed to be 0.2 and 3 m (i.e., $x_1\pm 0.1$ and $x_2\pm 1.5$). Two arbitrary distributions were considered for both of the random variables using the Kumaraswamy distribution, namely a tail distribution towards smaller UFC spacings and room spacings ($\hat{a}=[1,1]$, $\hat{b}=[5,5]$) and a kurtotic distribution towards larger UFC spacings and room spacings ($\hat{a}=[8,8]$, $\hat{b}=[8,8]$). Under the assumption of variable independence, the two corresponding joint PDFs are visualized in Figure 9.

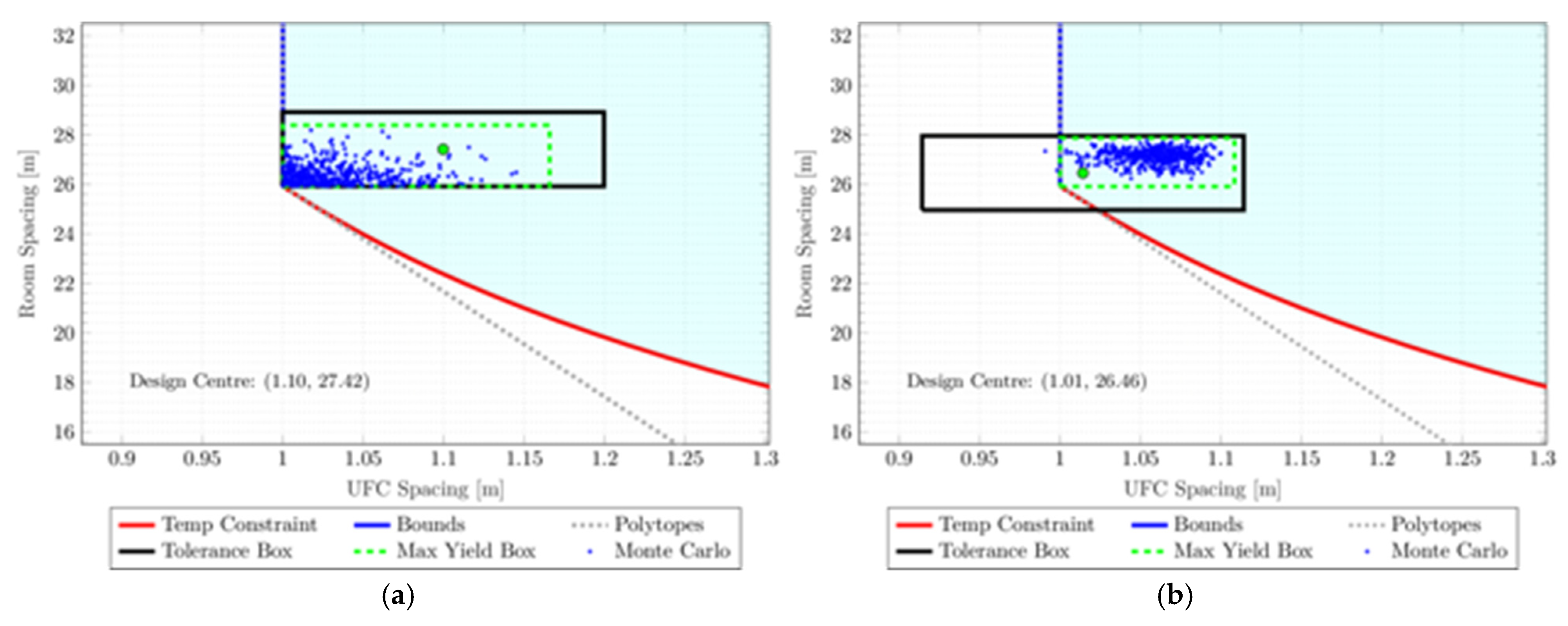
5.3. Failure Allowance of 1%

The nominal design points for when 1% failure probability was allowed under tail and kurtotic distributions are illustrated in Figure 10. Monte Carlo simulation points are included to depict the distributions, and these were determined by applying the inverse Kumaraswamy CDF transformation with relevant shape parameter values to uniformly distributed random numbers generated by the MATLAB rand() function. As is shown, depending on the distributions assigned to the random variables, the optimal design point for the DGR changes. If the distributions of the UFC and room spacings are such that smaller values are more likely to be realized, then larger nominal values need to be specified for the DGR design to ensure the maximum temperature does not exceed 100 °C, e.g., see Figure 10a. If the opposite is true, then smaller nominal values that are closer to the boundary of the feasible region can be chosen without an unfavorable increase in system failure, e.g., see Figure 10b. The tail and kurtotic distributions are quite extreme cases, and they were considered to demonstrate the need for either larger or smaller nominal UFC and room spacings within the DGR. Regardless of what the actual distributions for UFC and room spacings may be, yield optimization can provide insight for specifying an appropriate DGR design—with accuracy dependent on available information in Figure 9.

5.4. Failure Allowance of 5%

In contrast to a 1% failure probability, Figure 11 shows that a 5% failure probability allows for nominal design points to shift closer to their feasible region boundary. The increased failure probability incorporated higher risk into the repository design. However, if the assigned random variable distributions were appropriate, the nominal points determined through yield optimization would be more robust than the points in Section 4.2 and Section 4.3 because those deterministic results did not take uncertainty into account for the design variables. In Figure 11b, it can be seen that depending on the distribution, an optimal design point found through yield optimization might even lie outside the feasible region but, at the same time, still have a small probability for system failure.

6. Summary and Conclusions

In this paper, UFC arrangements for a Canadian DGR in a crystalline rock environment conceptualized by NWMO were studied. UFC spacing, room spacing, and UFC age were considered as the design variables that affected the maximum temperature inside the repository, which could not exceed 100 °C.

Surrogate-based optimization was used to optimize a high-fidelity COMSOL model of the DGR, reducing the number of computationally expensive evaluations required to reach optimal results. By using shape functions to specify the UFC age arrangement within the repository’s placement room, many arrangements were considered. Their results could be useful for the actual placement of UFCs in the future DGR as used nuclear fuel inventory information becomes available and finalized. Cosine-based and Kumaraswamy PDF-based shape functions were used, but more arrangements using other functions can be studied via the presented approach.

Yield optimization was exemplified as a means to incorporate risk into the design process. Considering UFC and room spacings as random variables, optimal DGR design points with an allowed failure probability (i.e., a target yield) were determined through the application of arbitrary tolerances and distributions. Should more information regarding DGR processes that inherently vary become known, such as manufacturing or construction limitations, the demonstrated method can be refined or even applied to other design variables to determine robust nominal design points that serve to prevent repository system failure.