Applying Infinite Petri Nets to the Cybersecurity of Intelligent Networks, Grids and Clouds
Abstract
:1. Introduction
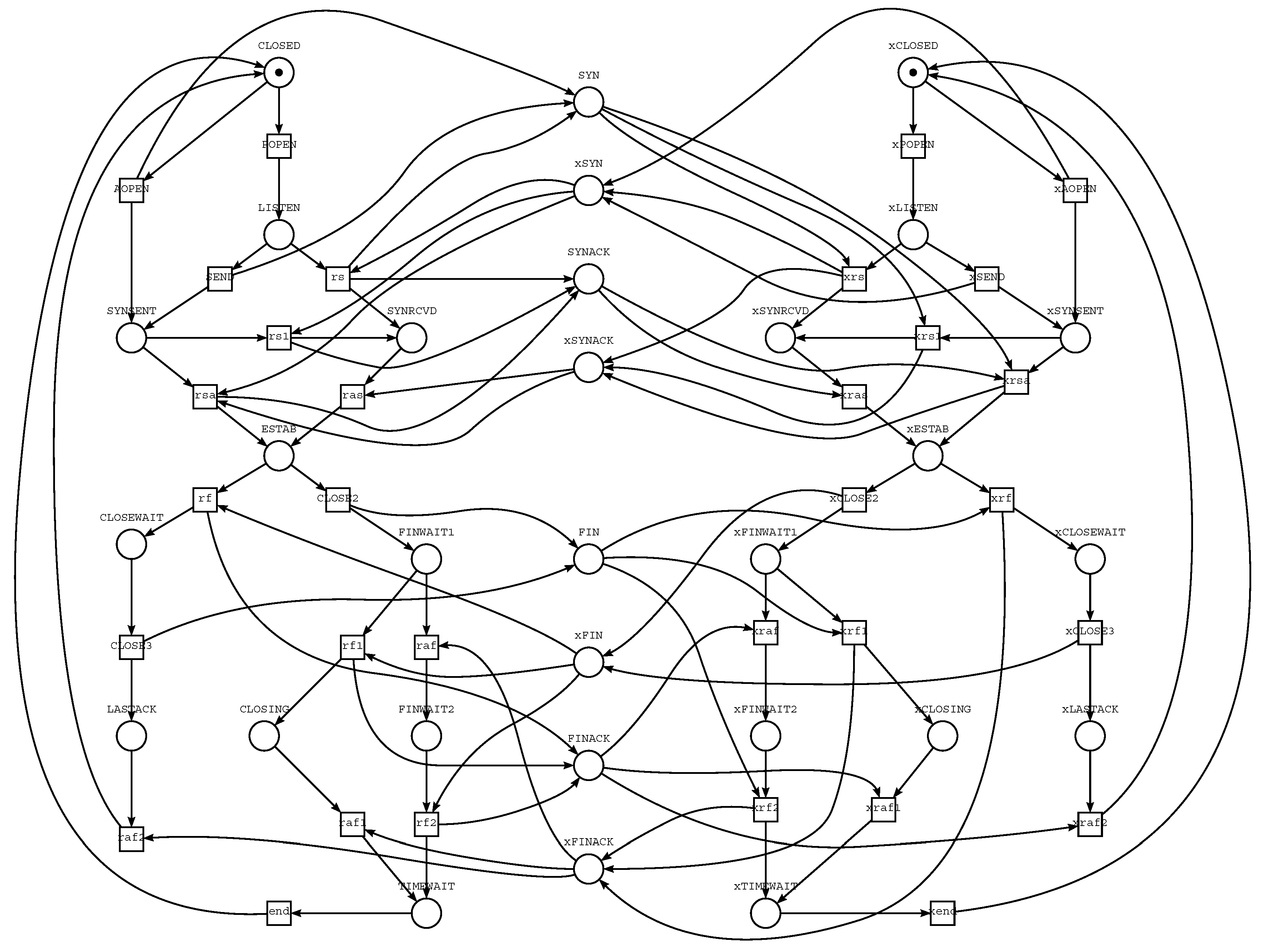
2. Modern Trends in Verification of Networking Protocols
3. Getting Familiar with Petri Nets
4. Infinite Petri Net of First Kind: A Single Infinite Structure
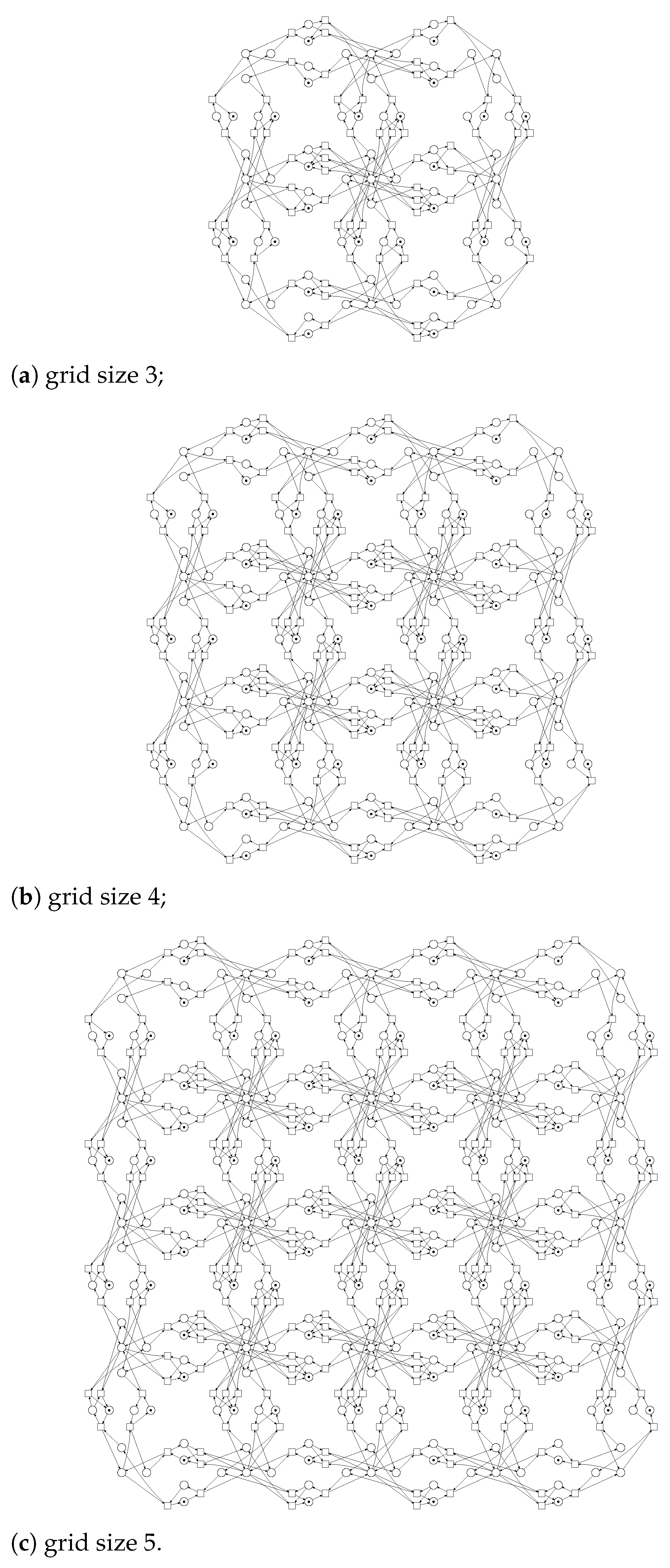
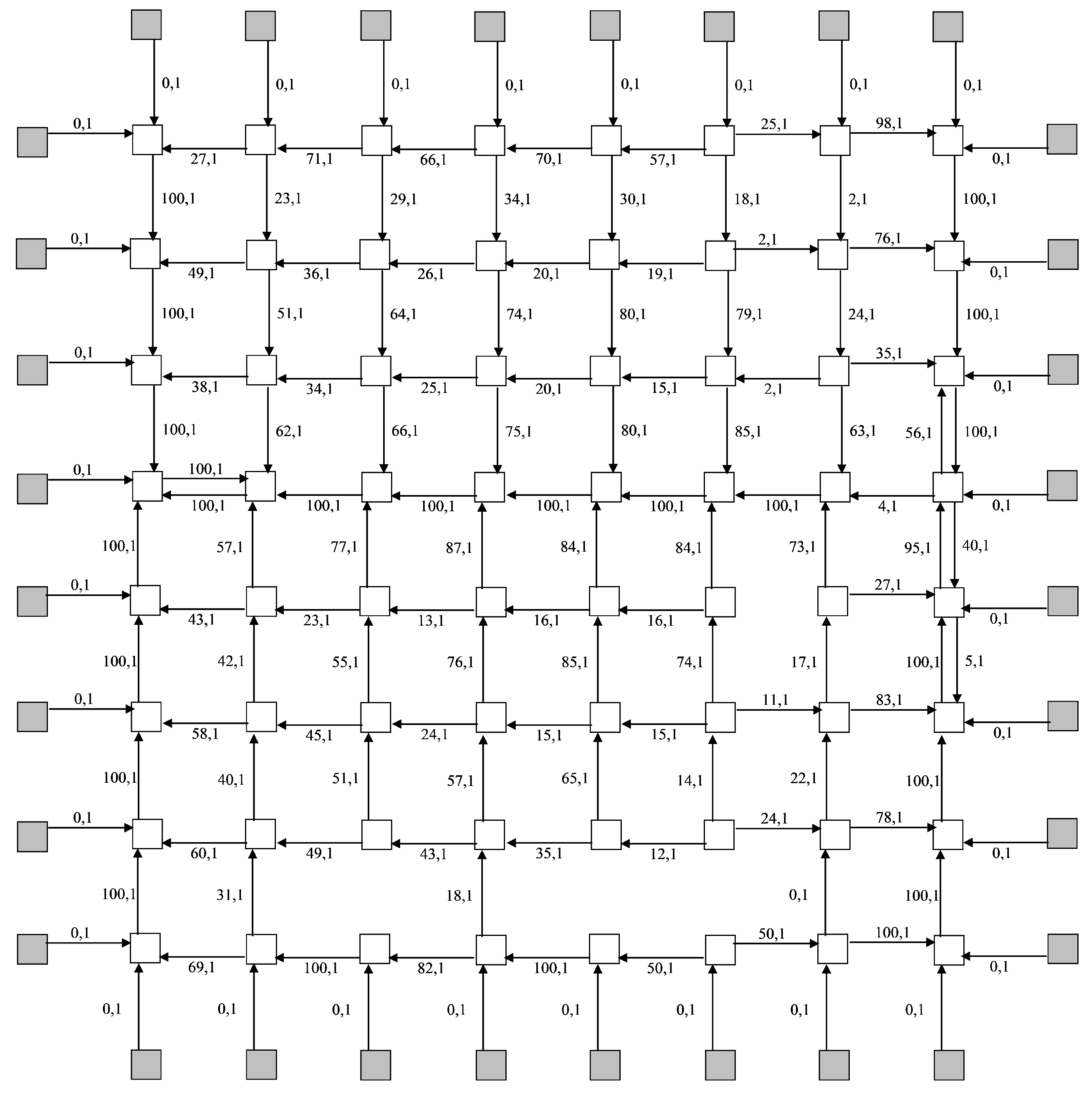
5. Infinite Petri Net of Second Kind: An Infinite Set of Finite Structures
6. Specifying and Analysing Infinite Petri Nets
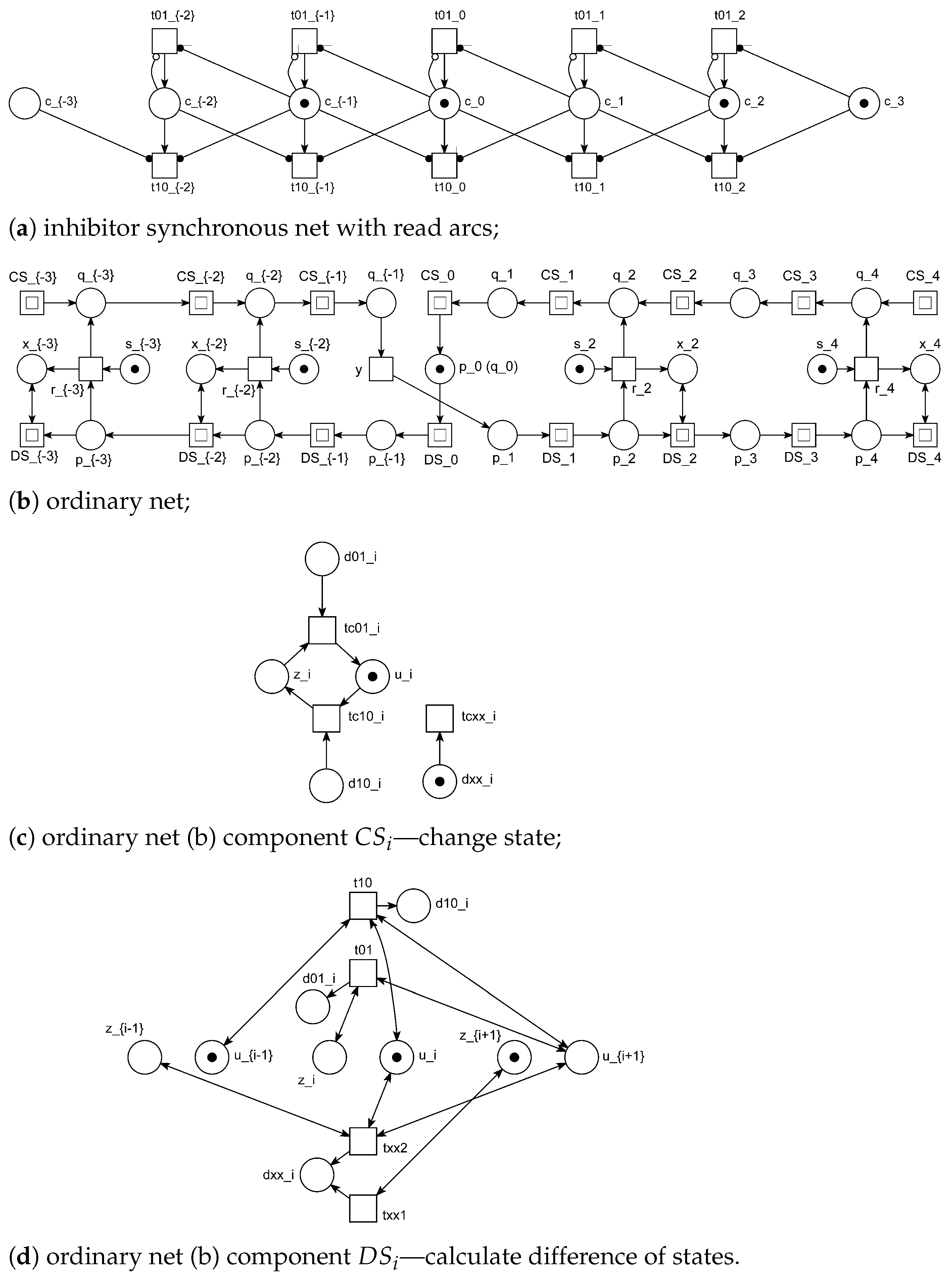
6.1. Finite Specification of Infinite Petri Net
6.2. Solving Infinite Linear Systems in Parametric Form
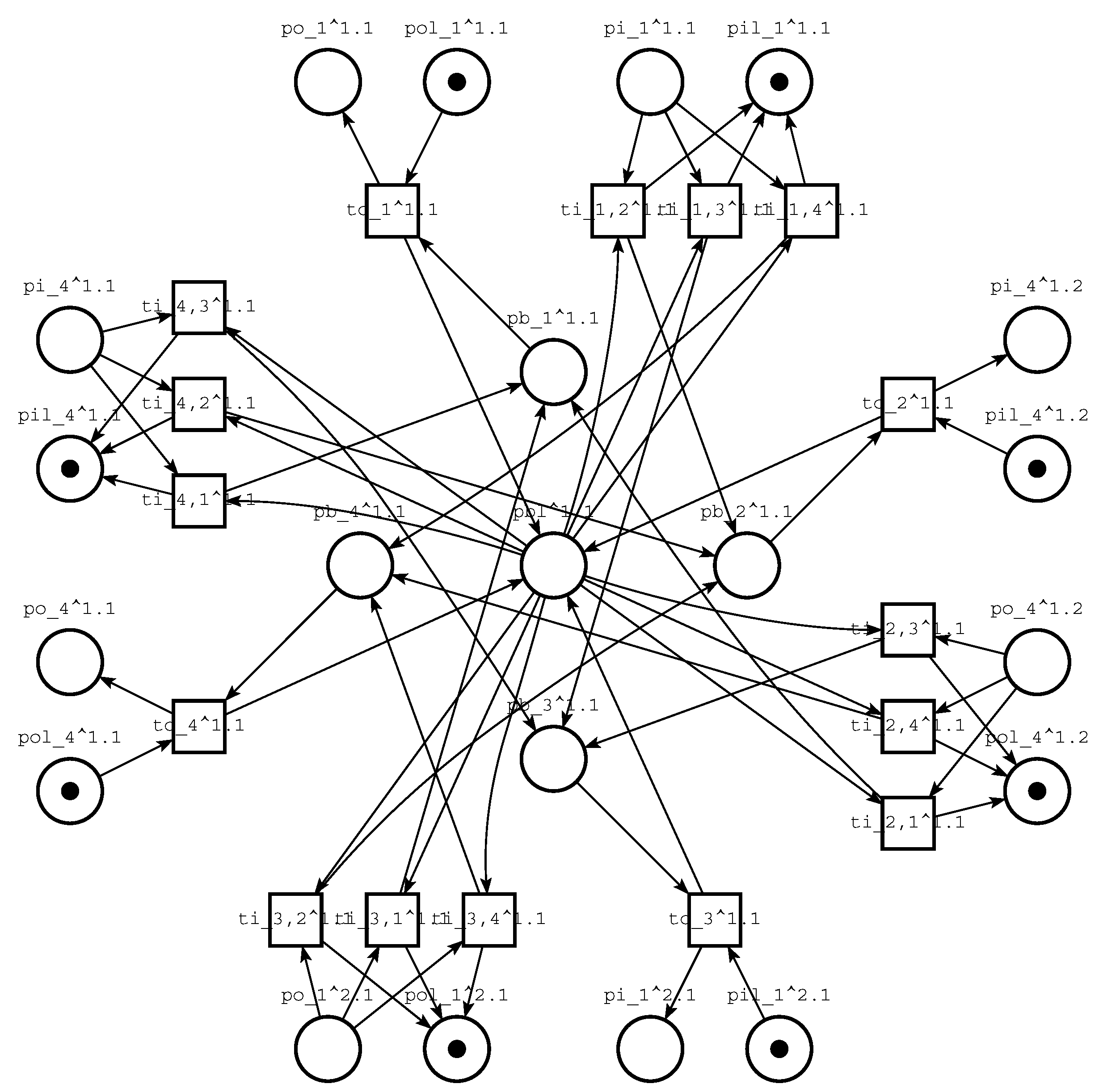
6.3. Complex Deadlocks within Computing Grid Models
6.4. Generalization of Obtained Results
7. Open Problems
- A general method for solving infinite systems of Diophantine linear algebraic equations, especially in non-negative numbers.
- Methods to find siphons and traps of infinite Petri nets to solve tasks of liveness and liveness-enforcing.
- Composition methods on infinite Petri nets, say composition of clans.
- Representation and application of reachability and coverability tree for infinite Petri nets.
- Composing and analyzing infinite Petri nets built of a few repeated components.
- An algorithm of mutual transformation for direct and dual specification of infinite Petri nets.
- Recognition of disguised attacks via induced deadlocks and corresponding countermeasures.
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Diaz, M. Modelling and Analysis of Communication and Cooperation Protocols Using Petri Net Based Model. Comput. Netw. 1982, 6, 419–441. [Google Scholar]
- Berthelot, G.; Terrat, R. Petri Nets Theory for the Correctness of Protocols. IEEE Trans. Commun. 1982, 30, 2497–2505. [Google Scholar] [CrossRef]
- Jasiul, B.; Szpyrka, M.; Śliwa, J. Detection and Modeling of Cyber Attacks with Petri Nets. Entropy 2014, 16, 6602–6623. [Google Scholar] [CrossRef] [Green Version]
- Bland, J.A.; Petty, M.D.; Whitaker, T.S.; Maxwell, K.P.; Cantrell, W.A. Machine Learning Cyberattack and Defense Strategies. Comput. Secur. 2020, 92, 101738. [Google Scholar] [CrossRef]
- Petty, M.D.; Whitaker, T.S.; Bland, J.A.; Cantrell, W.A.; Mayfield, K.P. Modeling Cyberattacks with Petri Nets: Research Program Overview and Status Report. In Proceedings of the 2019 International Conference on Modeling, Simulation, and Visualization Methods, Simulation, and Visualization Methods, Las Vegas, NV, USA, 29 July–1 August 2019; pp. 27–33. [Google Scholar]
- Sheldon, F.T.; Greiner, S.; Benzinger, M. Specification, Safety and Reliability Analysis Using Stochastic Petri Net Models. In Proceedings of the Tenth International Workshop on Software Specification and Design, San Diego, CA, USA, 7 November 2000. [Google Scholar]
- Henry, M.H.; Layer, R.M.; Snow, K.Z.; Zaret, D.R. Evaluating the risk of cyber attacks on scada systems via petri net analysis with application to hazardous liquid loading operations. In Proceedings of the 2009 IEEE Conference on Technologies for Homeland Security, HST 2009, Waltham, MA, USA, 11–12 May 2009; pp. 607–614. [Google Scholar]
- Szpyrka, M.; Jasiul, B. Evaluation of cyber security and modelling of risk propagation with Petri nets. Symmetry 2017, 9, 32. [Google Scholar] [CrossRef]
- Mayfield, K.; Petty, M. Petri Nets with Players, Strategies and Cost: A Formalism for Modelling Cyberattacks. In Proceedings of the 2018 International Conference on Security and Management, SAM’18, Las Vegas, NV, USA, 30 July–2 August 2018; pp. 237–244. [Google Scholar]
- Zhu, Q.; Qin, Y.; Zhao, Y.; Zhou, C. A hierarchical colored Petri net–based cyberattacks response strategy making approach for critical infrastructures. Int. J. Distrib. Sens. Netw. 2020, 16. [Google Scholar] [CrossRef]
- Almutairi, L.; Hong, L.; Shetty, S. Security analysis of multiple SDN controllers based on Stochastic Petri Nets. In Proceedings of the 2019 Spring Simulation Conference, SpringSim-ANSS, Tucson, AZ, USA, 29 April–2 May 2019; Volume 51. No. 1. [Google Scholar]
- Zaitsev, D.A.; Zaitsev, I.D.; Shmeleva, T.R. Infinite Petri Nets: Part 2, Modeling Triangular, Hexagonal, Hypercube and Hypertorus Structures. Complex Syst. 2017, 26, 341–371. [Google Scholar] [CrossRef] [Green Version]
- Zaitsev, D.A.; Zaitsev, I.D.; Shmeleva, T.R. Infinite Petri Nets: Part 1, Modeling Square Grid Structures. Complex Syst. 2017, 26, 157–195. [Google Scholar] [CrossRef]
- Chen, T.M.; Sanchez-Aarnoutse, J.C.; Buford, J. Petri Net Modeling of Cyber-Physical Attacks on Smart Grid. IEEE Trans. Smart Grid 2011, 2, 741–749. [Google Scholar] [CrossRef] [Green Version]
- Bhuyan, M.H.; Bhattacharyya, D.K.; Kalita, J.K. Network Traffic Anomaly Detection and Prevention: Concepts, Techniques, and Tools; Springer: Berlin/Heidelberg, Germany, 2017; 263p. [Google Scholar]
- Wang, Z.; Sun, L.; Zhu, H. Defining Social Engineering in Cybersecurity. IEEE Access 2020, 8, 85094–85115. [Google Scholar] [CrossRef]
- Blum, D. Rational Cybersecurity for Business: The Security Leaders’ Guide to Business Alignment; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Forshaw, J. Attacking Network Protocols: A Hacker’s Guide to Capture, Analysis, and Exploitation; No Starch Press: San Francisco, CA, USA, 2018. [Google Scholar]
- Lai, R.; Jirachiefpattana, A. Communication Protocol Specification and Verification; Springer: Boston, MA, USA, 2012. [Google Scholar]
- Groote, J.F.; Mousavi, M.R. Modeling and Analysis of Communicating Systems; MIT Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Diaz, M. Petri Nets: Fundamental Models, Verification and Applications; John Wiley and Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Popovic, M. Communication Protocol Engineering; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Zaitsev, D.A. Clans of Petri Nets: Verification of Protocols and Performance Evaluation of Networks; LAP LAMBERT Academic Publishing: Chisinau, Moldova, 2013. [Google Scholar]
- Burdett, D. Internet Open Trading Protocol, Internet Standard, IETF, RFC 2801. April 2000. Available online: https://datatracker.ietf.org/doc/html/rfc2801 (accessed on 29 June 2021).
- Raj, P.; Koteeswaran, S. Novel Practices and Trends in Grid and Cloud Computing; IGI Global: Hershey, PA, USA, 2019. [Google Scholar]
- Jerger, N.E.; Krishna, T.; Peh, L.S. On-Chip Networks; Morgan & Claypool Publishers: San Rafael, CA, USA, 2017. [Google Scholar]
- Reisig, W. Understanding Petri Nets: Modeling Techniques, Analysis Methods, Case Studies; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Cambronero, M.E.; Macià, H.; Valero, V.; Orozco-Barbosa, L. Modeling and Analysis of the 1-Wire Communication Protocol Using Timed Colored Petri Nets. IEEE Access 2018, 6, 27356–27372. [Google Scholar] [CrossRef]
- Kacem, I.; Sait, B.; Mekhilef, S.; Sabeur, N. A New Routing Approach for Mobile Ad Hoc Systems Based on Fuzzy Petri Nets and Ant System. IEEE Access 2018, 6, 65705–65720. [Google Scholar] [CrossRef]
- Ding, Z.; Yang, R. Modeling and Analysis for Mobile Computing Systems Based on Petri Nets: A Survey. IEEE Access 2018, 6, 68038–68056. [Google Scholar] [CrossRef]
- Postel, J. Transmission Control Protocol, Internet Standard, IETF, RFC 793. September 1981. Available online: https://datatracker.ietf.org/doc/html/rfc793 (accessed on 29 June 2021).
- Berthomieu, B.; Ribet, O.-P.; Vernadat, F. The tool TINA—Construction of abstract state space for Petri nets and Time Petri nets. Int. J. Prod. Res. 2004, 42, 2741–2756. Available online: http://www.laas.fr/tina (accessed on 15 February 2021). [CrossRef]
- Marsan, M.A.; Chiola, G.; Fumagalli, A. An accurate performance model of CSMA/CD bus LAN. In Advances in Petri Nets 1987; APN 1986; Rozenberg, G., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1987; Volume 266. [Google Scholar]
- Shmeleva, T.R. Automated Composition of Petri Net Models for Cellular Structures. In Proceedings of the Electrical and Computer Engineering (UKRCON) 2017: Transactions of IEEE First Ukraine Conference, Kyiv, Ukraine, 29 May–2 June 2017; pp. 1019–1024. [Google Scholar] [CrossRef]
- Ajima, Y.; Sumimoto, S.; Shimizu, T. Fujitsu Tofu: A 6D Mesh/Torus Interconnect for Exascale Computers. Computer 2009, 42, 36–40. [Google Scholar] [CrossRef]
- Medhi, D.; Ramasamy, K. Network Routing Algorithms, Protocols, and Architectures; Morgan Kaufmann: Burlington, MA, USA, 2018; 1018p. [Google Scholar]
- Cheng, S.; Zhong, W.; Isaacs, K.E.; Mueller, K. Visualizing the Topology and Data Traffic of Multi-Dimensional Torus Interconnect Networks. IEEE Access 2018, 6, 57191–57204. [Google Scholar] [CrossRef]
- Wolfram, S. A New Kind of Science; Wolfram Media Place: Champaign, IL, USA, 2002. [Google Scholar]
- Li, X.; Wu, J.; Li, X. Theory of Practical Cellular Automaton; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Morita, K. Theory of Reversible Computing; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Zaitsev, D.A. Simulating Cellular Automata by Infinite Petri Nets. J. Cell. Autom. 2018, 13, 121–144. [Google Scholar]
- Zaitsev, D.A. Universality in Infinite Petri Nets. In Proceedings of the 7th International Conference, MCU 2015, Famagusta, North Cyprus, 9–11 September 2015; Volume 9288, pp. 180–197. [Google Scholar]
- Zaitsev, D.A. A generalized neighborhood for cellular automata. Theor. Comput. Sci. 2017, 666, 21–35. [Google Scholar] [CrossRef]
- Zaitsev, D.A.; Shmeleva, T.R.; Groote, J.F. Verification of Hypertorus Communication Grids by Infinite Petri Nets and Process Algebra. IEEE/CAA J. Autom. Sin. 2019, 6, 733–742. [Google Scholar] [CrossRef]
- Shmeleva, T.R.; Zaitsev, D.A.; Zaitsev, I.D. Verification of square communication grid protocols via infinite Petri nets. In Proceedings of the MESM 2009—10th Middle Eastern Simulation Multiconference, Beirut, Lebanon, 27–29 September 2009; pp. 53–59. [Google Scholar]
- Chen, H.; Wu, N.; Zhou, M.C. A novel method for deadlock prevention of AMS by using resource-oriented petri nets. Inf. Sci. 2016, 363, 178–189. [Google Scholar] [CrossRef]
- Bistarelli, S.; Cervesato, I.; Gabriele, L.; Fabio, M. Relating Multiset Rewriting and Process Algebras for Security Protocol Analysis. J. Comput. Secur. 2005, 13, 3–47. [Google Scholar] [CrossRef] [Green Version]
- Zaitsev, D.A. Verification of Computing Grids with Special Edge Conditions by Infinite Petri Nets. Autom. Control Comput. Sci. 2013, 47, 403–412. [Google Scholar] [CrossRef]
- Zaitsev, D.A.; Shmeleva, T.R.; Retschitzegger, W.; Pröll, B. Security of grid structures under disguised traffic attacks. Clust. Comput. 2016, 19, 1183–1200. [Google Scholar] [CrossRef]
- Zaitsev, D.A.; Shmeleva, T.R. Verification of hypercube communication structures via parametric Petri nets. Cybern. Syst. Anal. 2010, 46, 105–114. [Google Scholar] [CrossRef]
- Shmeleva, T.R. Analysis of a Hypertorus Grid. Electronics and Nanotechnology ELNANO-2018. In Proceedings of the IEEE 38th International Conference, Kyiv, Ukraine, 24–26 April 2018; NTUU, Igor Sikorsky Kyiv Polytechnic Institute: Kyiv, Ukraine, 2018; pp. 56–59. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaitsev, D.A.; Shmeleva, T.R.; Probert, D.E. Applying Infinite Petri Nets to the Cybersecurity of Intelligent Networks, Grids and Clouds. Appl. Sci. 2021, 11, 11870. https://doi.org/10.3390/app112411870
Zaitsev DA, Shmeleva TR, Probert DE. Applying Infinite Petri Nets to the Cybersecurity of Intelligent Networks, Grids and Clouds. Applied Sciences. 2021; 11(24):11870. https://doi.org/10.3390/app112411870
Chicago/Turabian StyleZaitsev, Dmitry A., Tatiana R. Shmeleva, and David E. Probert. 2021. "Applying Infinite Petri Nets to the Cybersecurity of Intelligent Networks, Grids and Clouds" Applied Sciences 11, no. 24: 11870. https://doi.org/10.3390/app112411870
APA StyleZaitsev, D. A., Shmeleva, T. R., & Probert, D. E. (2021). Applying Infinite Petri Nets to the Cybersecurity of Intelligent Networks, Grids and Clouds. Applied Sciences, 11(24), 11870. https://doi.org/10.3390/app112411870





