Vacuum Leak Detection Method Using Index Regression and Correction for Semiconductor Equipment in a Vacuum Chamber

Abstract

In semiconductor manufacturing, fault detection is an important method for monitoring equipment condition and examining the potential causes of a fault. Vacuum leakage is considered one of the major faults that can occur in semiconductor processing. An unnecessary O₂ and N₂ mixture, a major component of the atmosphere, creates unexpected process results and hence drops in yield. Vacuum leak detection systems that are currently available in the vacuum industry are based on helium mass spectrometers. They are used for detecting the vacuum leakage at the sole isolation condition where the chamber is fully pumped but cannot be used for in situ detection while the process is ongoing in the chamber. In this article, a chamber vacuum leak detection method named Index Regression and Correction (IRC) is presented, utilizing common data which were gathered during normal chamber operation. This method was developed by analyzing a simple list of data, such as pressure, the temperature of the chamber body, and the position of the auto pressure control (APC), to detect any leakages in the vacuum chamber. The proposed method was experimentally verified and the results showed a high accuracy of up to 97% when a vacuum leak was initiated in the chamber. The proposed method is expected to improve the process yield of the chamber by detecting even small vacuum leakages at very early stages of the process.

1. Introduction

Over the past few decades, the worldwide semiconductor industry has maintained an average growth of 15% per year. This steady growth is the result of a continuous reduction in the cost per function of 25–30% per year [1,2,3].

Semiconductor manufacturing involves a highly complex and lengthy wafer fabrication process, with 300–500 process steps and a large number of interrelated variables [4,5,6]. To obtain substantial benefits, the semiconductor industry focuses on features related to manufacturing technology that are required in order to maintain the high reliability and effectiveness of the manufacturing process, such as reducing gate length, increasing wafer size and improving yield [7,8,9]. However, manufacturing technology has already reached its limit. Thus, it has been recognized that factory productivity should also be improved in order to maintain growth while reducing the production cost [10,11]. In semiconductor manufacturing, some process steps need to be performed continuously, without any interruption in the process flow, such as etching, ashing, deposition, and lithography. The sequence of continuous steps is called a ”run” and is performed on individual manufacturing equipment. Even though a fault may occur during any step of the run, it can only be detected after the entire run has been completed by performing wafer metrology [12,13,14].

As a result, data-driven fault detection has become a significant topic in the semiconductor industry and is expected to provide an efficient method for predictive maintenance that allows companies to save time and money [15,16,17,18,19,20]. Vacuum leakage is considered to be one of the major drawbacks in semiconductor processing and its final yield. An unnecessary O₂ and N₂ mixture, a major component of the atmosphere, creates unanticipated process outcomes and, consequently, drops in yield [21,22,23].

In this article, a new chamber vacuum leak detection method named index regression and correction is presented, utilizing common data gathered during normal chamber operation. This method was developed by analyzing a simple list of data, such as pressure, the temperature of the chamber body, and the position of the APC, to detect any changes in the sustained vacuum of the vacuum chamber system.

The remainder of this paper is organized as follows. Section 2 introduces a review of related work in real-word leak detection methods and data-driven methods. Section 3 presents the experimental setting and data acquisition from a real semiconductor facility. Section 4 presents the vacuum leak modeling by applying the ideal gas equation. Section 5 presents proof of the Section 4 modeling with experimental results. Section 6 introduces the proposed new leak detection method named IRC. Section 7 presents the experimental results using the actual process data, comparing our proposed method with the Auto Regressive Integrated Moving Average (ARIMA) model. Lastly, Section 8 concludes the paper by listing its contributions and discussing future research directions.

2. Related Work

Leak detection equipment has been developed over the past few decades following the ever-increasing demands of the industry. The current real-world vacuum leak detection method in the semiconductor industry is based on mass spectrometers. In theory, every kind of mass spectrometer can be used for leak detection. In many situations, it is more practical to use mass spectrometers that are devoted to leak detection by using helium tracer gas [24,25], which require the chamber to be in an isolated state with full pumping and make it unsuitable for in situ vacuum leak detection during the ongoing process [26]. Moreover, the cost of the He vacuum leak detector and He gas is too high, which makes the whole detection system not cost effective. Therefore, it is important and necessary to create a leak detection system that does not require high cost measurement tools, such as a helium leak detector.

To overcome this problem, data-driven anomaly detection has been extensively studied. Wise and Gallagher proposed a partial least squares (PLS) method [27]. PLS is a regression model between predictors and responses in a reduced feature space using orthogonal latent vectors. PLS studies orthogonal latent vectors that best explain the covariance between responses and predictors. The latent vectors serve as new predictors and regress the responses on these new predictors. In fault detection, the tool state features are predictors and the wafer class is the response. Ison et al. [28] proposed a decision tree classification model to detect faults in dry etch equipment. The model was built from the five sensor signal data. Goodlin et al. [29] proposed to build a specific control chart for detecting specific types of faults. They collected tool state data directly from the etcher. These data consisted of 19 variables. Spitzlsperger et al. [30] proposed a technique based on the statistical method. They adapted the multivariate control chart method to maintain changes in the mean and standard deviation coefficients by remodeling the technique.

3. Experimental Details and Data Acquisition

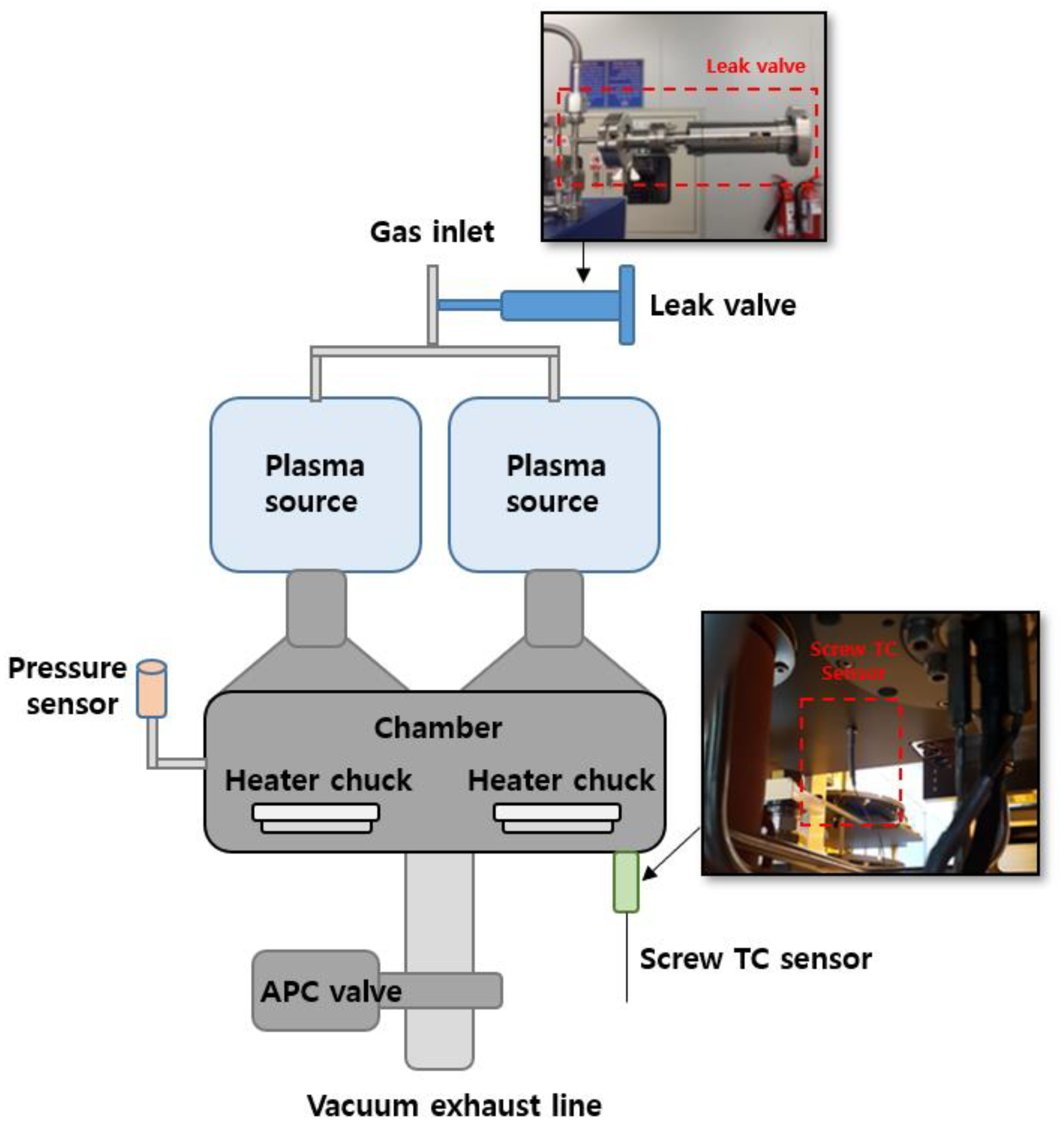
Figure 1 shows the schematic description for the process module of 300 mm dry asher (SUPRA, PSK). The process module consisted of the plasma sources, a chamber, and a vacuum exhauster. The PSK dry ashing tool contained two plasma sources in one chamber called the peanut chamber, which shared a supply of gas and a vacuum exhaust line for these two sources. Thus, each wafer was processed under the same conditions. The plasma source used was ferrite core inductively coupled plasma (FCIP R3, MKS). The chamber body was made of aluminum. The maximum temperature set point for the aluminum heater chucks was 350 °C. The chamber pressure was monitored using a capacitance gauge (MKS). The chamber pressure was controlled using a butterfly-type automatic pressure control valve (MKS), the open ratio range of which lies between 0 (closed) and 100,000 (fully open) steps.

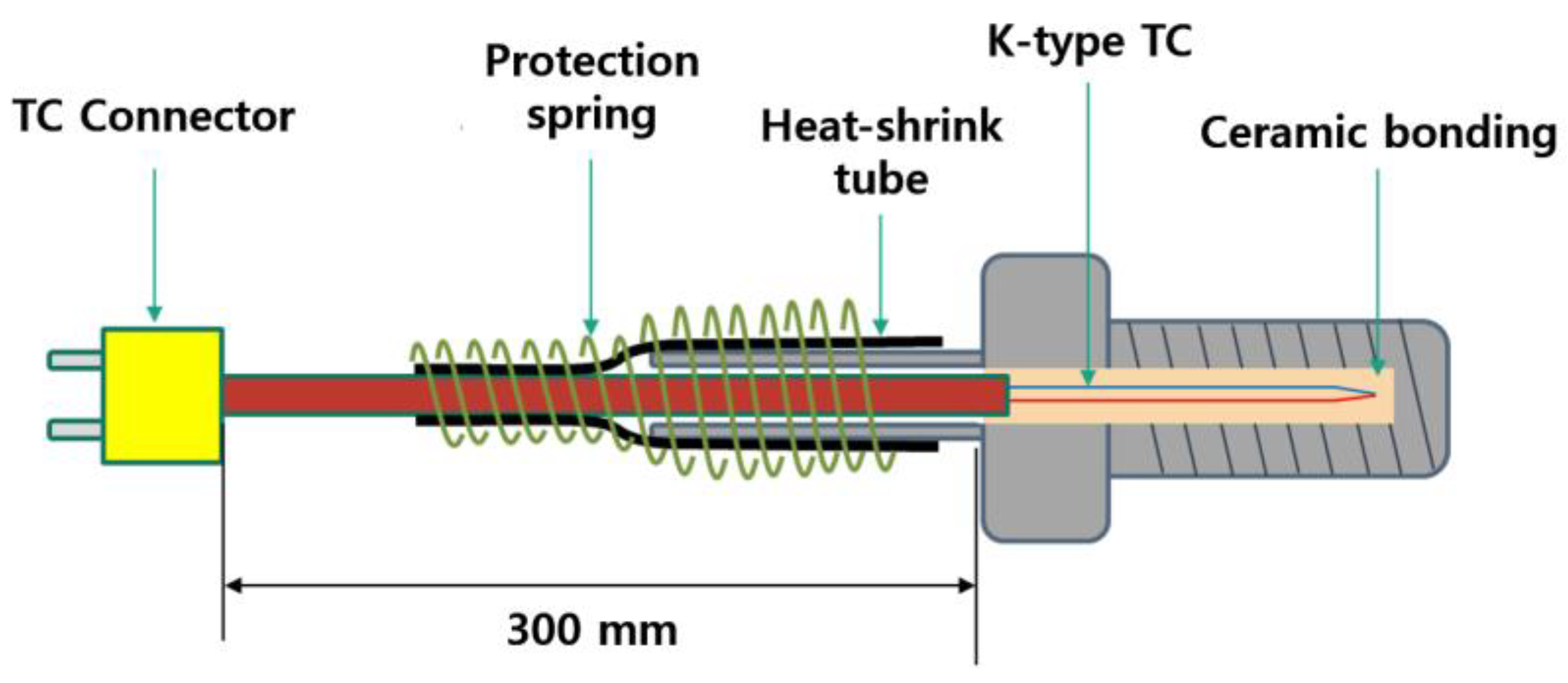
The chamber body temperature was monitored using a screw-type thermal sensor (Figure 2, PSK). In order to minimize the influence of outside air, PSK developed a screw type TC (thermocouple) sensor which uses K-type thermocouples. The temperature measurement point was about 1.5 cm from the chamber body surface. Its temperature measuring range was from −200 °C to 1372 °C. The test error was ±1 °C in −100–1372 °C, without considering the error of the thermocouple. In order to produce a controlled artificial vacuum leak, a micro vacuum leak control valve was installed on the gas inlet (vacuum leak valve series 590, MKS). The control vacuum leak rate was from 10 mT/m to 1000 mT/m. During the process, the plasma source power was fixed at 4400 W and the pressure to 1.4 Torr. The total gas (O₂, N₂) flow was 14,000 sccm. The chuck temperature was set to 250 °C.

All generated sensor data were recorded by the central controller. The APC position value range was from 0 to 100,000 and the sampling time was 100 ms. The chamber body temperature data were recorded to one decimal place and the sampling time interval was set to 1 s. The minimum sampling time of the temperature sensor controller was 1 s. High performance controllers were not applied because it would take more than 10 s for the chamber temperature to change by 0.1 °C.

Data Set Description

The data set was obtained from a real semiconductor ashing process. The process consisted of seven steps, including pumping, gas flow, pressure stabilization, plasma ignition, ashing, over-ashing, and the vent of the chamber.

Table 1. Process values.

Condition	Value
O2–N2 total gas flow rate (sccm)	14,000
Source power (W)	4400
Pressure (mTorr)	1500
Chuck Temperature (°C)	250
Main process time (s)	20

presents the process values for the experiment condition.

The state variable identification (SVID) data collected from the process chamber were as follows: gas1 monitor, gas2 monitor, source power1, source power2, pressure, APC position, chuck Temp.1, chuck Temp.2, and chamber body temp. In this study, only the APC position and chamber body temperature were used. The reason for this will be covered in Section 4 and Section 5. Two data sets were collected; the first data set included 472 normal and 48 leaks and the second data set included 795 normal and 44 leaks. These two data sets were used to study the temperature and APC position relationship in Section 5 and to evaluate the performance of the proposed method in Section 7.

4. Modeling of Process Chamber Vacuum Leakage

The presented in situ vacuum leak detection method follows ideal gas Equation (1) characteristics.

PV = nRT

(1)

Each variable in the equation can be related to the chamber parameters, where: P is the chamber pressure; V is the chamber volume; n is the amount of substance of gas; R is the ideal or universal gas constant; and T is the temperature of the gas. The volume (V) and the gas constant (R) are regarded as constants, and the pressure (P), gas amount (n), and temperature (T) are considered as variables.

P ∞ nT

(2)

Note that P is proportional to n and T (2). In summary, an increase in gas input and chamber temperature causes a rise in pressure inside the process chamber. Based on this relationship, the following hypotheses were drawn:

Hypothesis 1 (H1).

When the chamber body temperature increases, the APC position value increases;

Hypothesis 2 (H2).

When a vacuum leak occurs, the APC position value increases;

Hypothesis 3 (H3).

When a vacuum leak occurs, the chamber body temperature does not change.

In detail, the APC changes its position value by reacting to the current pressure of the chamber to maintain a certain target value. When the chamber pressure rises, due to an increase in chamber body temperature or due to an increase in outside air caused by the chamber vacuum leak, the APC position increases (becomes more open). On the contrary, when the chamber pressure decreases, due to a decrease in chamber body temperature or eliminated chamber vacuum leaks, the APC position decreases (becomes more closed). In addition, the outside air caused by the vacuum leak is considerably smaller than the volume of the chamber and amount of supply gas, meaning that the temperature of the chamber body will be maintained without any changes. The assumption was confirmed through a relationship test between the temperature and APC position.

5. Test of Relationship between Temperature and APC Position

In this section, a simple test with two parameters (APC position and body temperature) empirically proves the proposed conception to be valid. In the equipment idle status, a total of 520 process runs were performed using same values. In those, 472 normal process runs were conducted and 48 faults (vacuum leak valve open) were reproduced. The test results are shown in Figure 3.

The blue circles indicate the APC position as single point values of the stable state before plasma ignition begins, so the obtained values in that section were not affected by other factors of the plasma process. The orange circles indicate the APC position as single point values of the disturbed state where the vacuum leak valve was opened. The red circles belong to the chamber body temperature that was acquired in parallel to the APC position values. The chamber body temperature was keep maintained at 60 °C in the idle state of equipment where the heater chuck temp was 250 °C. As the process continued, the thermal energy generated from the plasma raised the chamber body temperature. The gas supplied to the chamber received thermal energy from the chamber body and the pressure increased. The test results below prove the assumption to be true.

Proof of Hypothesis 1 (H1).

The APC position opens (APC position value increases) more to reduce the elevated pressure. For normal overall data, the correlation coefficient between the APC position and the chamber body temperature is 9.7 with a p-value of 2.37 × 10⁻²³. These results indicate that there is a strong positive correlation. □

Proof of Hypothesis 2 (H2).

When the body temperature is saturated, the APC position value is also saturated. When the vacuum leak valve opened at the end of the test (vacuum leak rate: 300 mT/m), the APC position value was increased. The t-test result for the APC position normal and leak data is −13.0, with a p-value of 4.0 × 10⁻²², at the end of the data (the number of normal data is 44 and leak data is 44). These results indicate that there is a significant mean difference between normal runs and leak runs. □

Proof of Hypothesis 3 (H3).

There is no change in the chamber body temperature at the same time as when vacuum leak valve is opened. At the end of the data (leak area, number of data is 44), the correlation coefficient between the APC position and chamber body temperature is 0.13 with a p-value of 8.34 × 10⁻⁵. These results indicate that there is no correlation. □

The relationship between the chamber body temperature and changes in the APC position during a vacuum leak occurrence was confirmed. Based on this relationship, a sequential check list was developed for vacuum leak detection as shown in Figure 4.

6. Index Regression and Correction

The sensor values of the semiconductor equipment have more deviations, even if the same process is performed under the influence of temperature, humidity, and degradation. Without solving this problem, the prediction accuracy cannot be improved. This section describes how to create an APC temperature index table and correct the error in order to achieve accurate results.

6.1. APC Temperature Index Table

The APC temperature index table was developed so that it can predict the APC position Y from chamber body temperature T. From the previous test results, the relationship between the two quantities is inferred as:

$$\widehat{Y}={\alpha }_0+{\alpha }_1{T}_i, i=1,\dots ,472$$

(3)

where ${\alpha }_0$ and ${\alpha }_1$ are estimated by the least square method:

$${\alpha }_0=\widehat{Y}-{\alpha }_1\overline{T}$$

(4)

$${\alpha }_1=\frac{{{\displaystyle \sum }}_{i=1}\left(y_i-\overline{y}\right)\left(T_i-\overline{T}\right)}{{{\displaystyle \sum }}_{i=1}{\left(T_i-\overline{T}\right)}^2}$$

(5)

The calculated coefficient ${\alpha }_1$ between the chamber body temperature and APC value was 11.76 and the intercept ${\alpha }_0$ was 30,000.68. The temperature and APC data are plotted on the T-Y axis, respectively, as shown in Figure 5. If there is more than one APC value accumulated from the same chamber body temperature, then the average value is used as the index value, which is indicated by red circles in Figure 5 and in

Table 2. A part of the APC–chamber body temperature table (33 of 472).

Temperature [°C]	APC Position	Temperature [°C]	APC Position	Temperature [°C]	APC Position
67.8	30,726	74.5	30,880	81.9	30,964
68.4	30,786	75.3	30,887	82.5	30,965
68.8	30,798	76	30,910	83	30,965
69.3	30,804	76.7	30,916	83.5	30,977
69.9	30,824	77.4	30,920	84.1	30,989
70.5	30,836	78.1	30,929	84.6	30,995
71.1	30,848	78.8	30,950	85	31,000
71.8	30,867	79.4	30,940	85.5	31,010
72.5	30,870	80.1	30,945	85.9	31,005
73.2	30,877	80.7	30,960	86.4	31,010
73.9	30,880	81.3	30,955	86.8	31,025

. However, it is inevitable that the use of averages as the index values implies that the prediction deviates further from the actual APC position value. In order to improve this error, the error update method of the Kalman filter is implemented.

6.2. Correction: Error Update

6.2.1. Kalman Filter

The filter is named after Rudolf E. Kalman (19 May 1930–2 July 2016). In 1960, Kalman published his famous paper describing a recursive solution to the discrete data linear filtering problem. The Kalman filter has been widely applied in fault detection [31,32,33,34,35,36,37,38]. Chinniah et al. [39] showed that the bulk modulus and the viscous damping coefficient of a hydrostatic actuation system could be correctly estimated, in sequence, using EKF. Liniger et al. [40] showed the feasibility and advantage of applying an EKF-based algorithm that describes the development and application of a model-based scheme for detecting the early signs of coil failure in solenoid valves over other existing techniques. Additionally, the Kalman filter provides a prediction of the future system state, based on the past estimations. The Kalman filter algorithm consists of two stages: prediction and update. Note that the terms “prediction” and “update” are often called “propagation” and “correction” [41,42,43]. The predicted state estimate is evolved from the updated previous state estimate. These two terms form a loop with each other and make predictions by reflecting on previous prediction errors. The update term has an error value between the measured value and the predicted value. Therefore, it is unnecessary to hold the entire past data, which guarantees faster operation and makes it suitable for real-time time series prediction.

A prediction method was developed to reduce errors by applying the prediction–update loop idea of the Kalman filter.

6.2.2. Correction

Predictions and updates can be expressed as equations, as follows:

$${\widehat{Y}}^{\prime }=\beta \cdot \widehat{Y}+\left(1-\beta \right)E,$$

(6)

$$E=\gamma {\widehat{Y}}^{\prime }{}_{t-1}+\left(1-\gamma \right)M_{t-1}.$$

(7)

where ${\widehat{Y}}^{\prime }$ is a re-estimated value for the APC position; $\widehat{Y}$ is obtained from (3); $E$ is a correction of the previous prediction; $M$ is a measured value of the APC position; $\alpha$ is the least square estimate in (4) and (5); and $\beta$ and $\gamma$ are the hyper parameters of a gain that is set between 0 and 1, respectively. When the updated term is compensated for in the next prediction, the error of the table can be reduced by the following arguments based on equipment characteristics. If the equipment is in its normal state, the surrounding process APC value has a similar value to the current process APC value. The chamber body temperature is gradually changed. Therefore, the error between the present measurement and the table error is reflected in the next prediction, allowing the error contained in the table to be reduced.

6.3. Evaluation Metrics

Fault detection is a binary classification problem, in which we predict whether the process could be a leak or normal. Therefore, accuracy, precision, recall and F1 score were used to measure the performance of the proposed IRC method. The computation methods of these metrics are given in

Table 3. Classification matrix for predicting leak or normal cases.

	Predicted Class
Actual Class		Class = 1 (Leak)	Class = −1 (Normal)
	Class = 1	True Positive (TP)	False Negative (FN)
	Class = −1	False Positive (FP)	Ture Negative (TN)

.

The accuracy is used to evaluate the correctly predicted samples among the whole data set. The recall or sensitivity is the ratio of correctly predicted samples to the true positive samples. The precision is the proportion of correctly predicted samples out of the predicted positive samples. The F1 score can be utilized as an overall metric by integrating the recall and precision. The accuracy is a ratio of correctly predicted observations to the total observations, which is the most intuitive performance measure. However, the accuracy is not a proper metric due to the severe class imbalance problem in this domain where all faulty processes can be misclassified as a very high accuracy. Thus, we reported precision, recall, and F1 score in addition to the accuracy. The accuracy, precision, recall, and F1 score are calculated as:

$$Accuracy=\frac{TP+TN}{TP+TN+FP+FN}$$

(8)

$$Precision=\frac{TP}{TP+FP}$$

(9)

$$Recall=\frac{TP}{TP+FN}$$

(10)

$$F1 score=\frac{2\times Precision\times Recall}{Precision+Recall}$$

(11)

7. Results

7.1. Effect of Correction

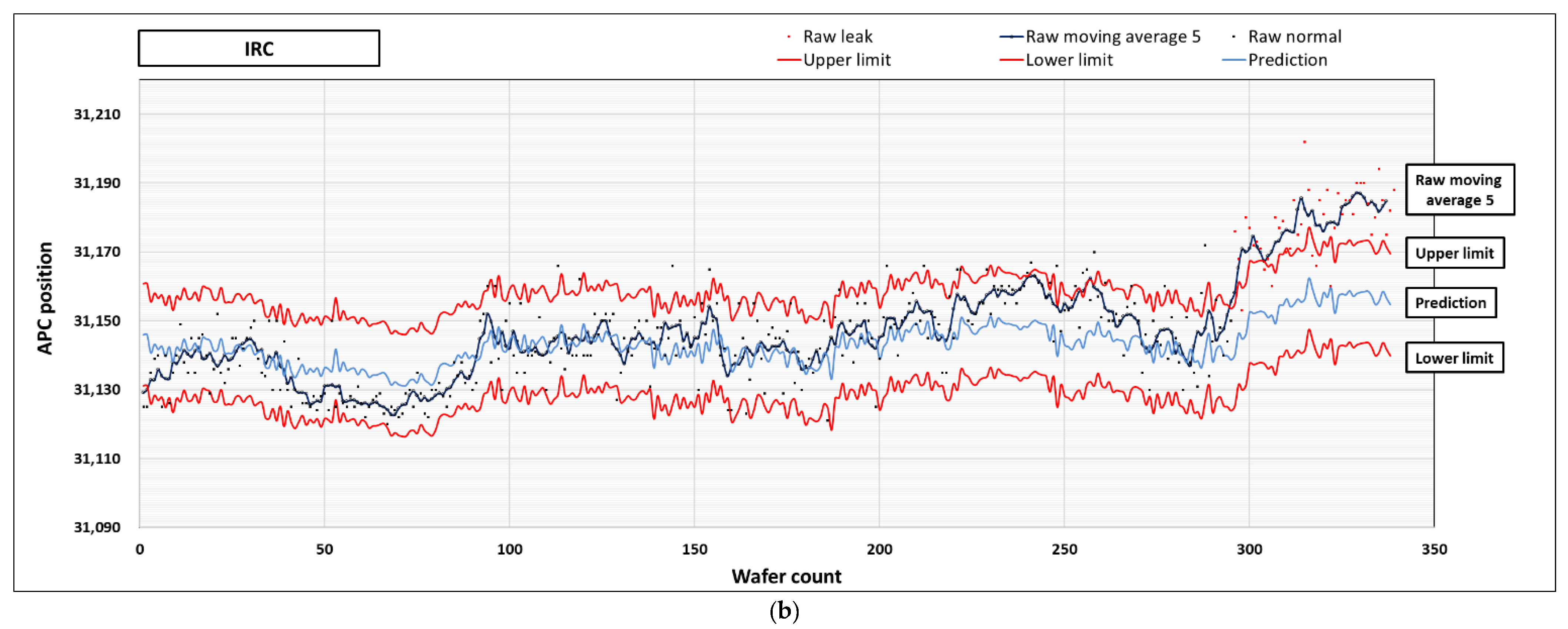
Figure 6 shows the plots for the measured data (actual data) and predicted values. Figure 6a is the result graph without using the update, whereas Figure 6b is the result after using the update. The former demonstrates a larger prediction error compared with the latter case where the update is employed. The bottom plot shows that the predicted values are closer to the measurement data. The results demonstrate that the update is effective in reducing the error.

7.2. Accuracy

The performance test for finding the effectiveness of the vacuum leak detection method proposed in this paper was conducted as follows. In total, 500 consecutive training runs were followed by test runs with and without vacuum leaks (295 and 44 runs, respectively). For performance comparison, the performance index was obtained using the IRC, IRC (no update), and ARIMA. The ARIMA model is one of the widely used statistical methods for predicting time series data. ARIMA, short for ”Auto Regressive Integrated Moving Average”, is actually a class of models that ”explain” a given time series based on its own past values—that is, its own lags and the lagged forecast errors—meaning that an equation can be used to forecast future values [44]. The ARIMA model was adopted for performance comparison because the methods proposed in this study had similar considerations for past data and forecast errors. The best condition result for each parameter was extracted and used from the final results sequence. The best gain of the IRC method was $\beta$ = 0.5 and $\gamma$ = 0.6. For the IRC that did not use the update, the gains were set to $\beta$ = 1 and $\gamma$ = 1. The ARIMA model used best order (1,1,0). The test results are shown in

Table 4. Results of the scores for each method.

	IRC	IRC (No Correction)	ARIMA
Accuracy	0.97	0.91	0.66
Recall	0.93	1.00	0.84
Precision	0.91	0.60	0.25
F1 score	0.92	0.75	0.39

. The F1 score is the harmonic mean of the precision and recall, where it reaches its best value at 1 (perfect precision and recall) and worst value at 0. Therefore, the F1 score is close to 1 when both the recall and precision are high. The accuracy of the IRC model was 0.97 and the F1 score was 0.92. In the performance comparison experiment, the IRC method had the best performance. In the case of the IRC model without using the update, 100% of vacuum leaks were detected but the vacuum leak was misdiagnosed as leaks 29 times as opposed to 4 times, and the equipment had to be checked 25 more times than when the update was used. On the other hand, the proposed model misdiagnosed three out of all vacuum leaks as normal. The ARIMA model test results showed that the vacuum leak detection was excellent, but there were 108 type 1 errors, which judged normal as a vacuum leak, showing a low accuracy of 66%. The root cause of the large error count in the ARIMA model can be attributed to the non-periodicity of the data gathered in the facility.

8. Conclusions

To classify the vacuum leak, the IRC method using an APC–temp table and error update was proposed. As a result of the accuracy comparison evaluation, the excellent performance was confirmed with an accuracy of 0.97 and an F1 score of 0.92. The IRC method was effective in classifying abnormalities by predicting the time series data of the semiconductor facility sensors. For future research, it is necessary to further discover key parameters and improve accuracy through multivariate analysis.