Abstract
The objective of the present work is to investigate the performance of flat-plate solar panels in Saudi Arabia that continuously follow the daily motion of the sun. To that end, the annual energy sums are estimated for such surfaces at 82 locations covering all Saudi Arabia. All calculations use a surface albedo of 0.2 and another one with a near-real value. The variation of the solar energy sums on annual, seasonal, and monthly basis is given for near-real ground albedos; the analysis provides regression equations for the energy sums as function of time. A map of the annual inclined solar energy for Saudi Arabia is derived and presented. The annual energy sums are found to vary between 2159 and 4078 kWhm−2year−1. Finally, a correction factor, introduced in a recent publication, is used; it is confirmed that the linear relationship between the correction factor and the ground-albedo ratio is general enough to be graphically representable as a nomogram. A discussion regarding the differences among solar systems on horizontal, fixed-tilt, 1-axis, and 2-axis systems is presented.
1. Introduction
Installations with tilted solar panels for exploiting the (renewable) energy of the sun have long been available in the market as commercial products. Solar flat-plate panels are nowadays widely used for converting solar energy into electricity (PV installations). These systems consist of solar modules receiving solar radiation by flat-plate surface(s) that (i) operate at a fixed-tilt angle with southward orientation in the northern hemisphere or northward orientation in the southern hemisphere, (ii) continuously track the sun at a fixed-tilt angle rotated on a vertical axis, and (iii) continuously track the sun at a varying tilt angle fixed on a system with two axes (one vertical and one horizontal); this makes the receiving surface to always be normal to the solar rays. Installations of mode (i) are known as fixed-tilt systems and are widely used because of lower cost for the supporting frame. Installations of mode (ii), also known as 1- or single-axis systems, provide higher solar energy on the inclined surface, but have slightly higher cost because of the need to maintain the moving parts. Installations of mode (iii) are considered the most effective and are known as 2-, double-, or dual-axis systems. They provide higher efficiency, but, on the other hand, they are associated with higher maintenance costs because of more moving parts. The first type of solar system is also called stationary or static, while the other two are dynamic, because of their sun-tracking ability. Farahat et al. [1] examined the mode (i) static systems for the performance of fixed-tilt flat-plate solar systems with southward orientation in Saudi Arabia, while Farahat et al. [2] investigated the mode (ii) dynamic systems receiving solar energy on fixed-tilt flat-plate solar panels that rotate on a vertical single-axis structure and track the sun continuously. This work is a continuation of the previous two as it investigates the mode (iii) dynamic systems for the solar energy received by flat-plate solar systems with continuously variable tilt angle of the inclined surface and mounted on 2-axis sun trackers across the country.
Static solar systems are widely used nowadays in solar energy production throughout the world because of their simple construction and low maintenance cost; therefore, they have received major attention from researchers (i.e., for estimating the solar potential or solar availability) at a certain location or region, e.g., [3,4,5]. A second preference has been given to dynamic mode (ii) solar systems because of their relatively higher performance in terms of the solar energy received, e.g., [6]. The dynamic mode (iii) solar systems have started being used in the last 20 years or so because of their higher performance in comparison to that of the other two types, e.g., [7,8]. Much effort has been invested in improving both the moving and electronic parts for the sun-tracking sensors [9,10]. Nevertheless, despite the technology development, the performance of such systems must be evaluated against solar radiation measurements at first hand. However, the scarcity of solar radiation measuring stations around the world has triggered studies to use solar radiation modelling, e.g., [11,12,13], in order to derive the optimum tilt angle and orientation for obtaining maximum solar energy on flat-plate solar panels. Other methods use a combination of ground-based solar data and modelling, e.g., [14], or utilise solar data from international data bases, e.g., [15,16]. Recently, a new method was presented by [17] for Greece and was applied in two recent studies for Saudi Arabia [1,2]. The proposed method [17] is able to find the maximum solar energy received by flat-plate solar systems with southward (northward) orientation in the northern (southern) hemisphere. The idea behind this methodology is applied in the present study for solar modules continuously tracking the sun.
Some studies similar to the present work have already been conducted for Saudi Arabia. El-Sebaii et al. [4] computed the global, direct, and diffuse solar radiation components on horizontal and tilted surfaces at Jeddah. Kaddoura et al. [15] estimated the optimal tilt angle for maximum energy reception by PV installations at 7 sites in the country. They suggested that the PV panels should be adjusted six times in a year for maximum performance, a conclusion that triggers extra installation and maintenance costs because of the moving parts involved. Zell et al. [18] performed solar radiation measurements at 30 stations in Saudi Arabia in the period October 2013–September 2014 (1 year) to assess the solar potential at these sites. The World Bank [19] has derived a Global Solar Atlas, which includes Saudi Arabia. This solar map provides the distribution of the three solar radiation components over the country and is based on calculations during the periods 1994, 1999, and 2007–2018. Finally, Almasoud et al. [20] has provided a study about the economics of solar energy in Saudi Arabia.
From the above, it is clear that no attempt has been made thus far to construct a solar map for Saudi Arabia to show the solar potential on inclined flat-plate surfaces that continuously track the sun. This gap is bridged in the present study and includes two innovations. (i) For the first time, solar maps for Saudi Arabia showing maximum energy on inclined flat-plate surfaces tracking the sun are derived. (ii) The notion of the (ground-albedo) correction factor introduced in [1,2] is also used.
The structure of the paper is as follows. Section 2 describes the data collection and data analysis, Section 3 deploys the results of the study, Section 4 provides a comparison among the various fixed and moving solar systems, Section 5 gives the guidelines for using the results deployed, and Section 6 presents the conclusions and main achievements of the work. Acknowledgements and references follow.
2. Materials and Methods
2.1. Data Collection
Hourly values of Hb,0 (direct horizontal solar irradiance in Wm−2) and Hd,0 (diffuse horizontal solar irradiance in Wm−2) were downloaded from the PV—Geographical Information System (PV-GIS) tool [21] using the latest Surface Solar Radiation Data Set—Heliostat (SARAH) 2005–2016 database (12 years) [22,23]. This platform provides solar radiation data through a user-friendly tool for any location in Europe, Africa, the Middle East including Saudi Arabia, Central and Southeast Asia, and most parts of the Americas. Nevertheless, the platform provides solar maps for Europe, Africa, Turkey, and Central Asia only. The methodologies used for estimation of solar radiation from satellites by the PV-GIS tool are described in various works [24,25,26].
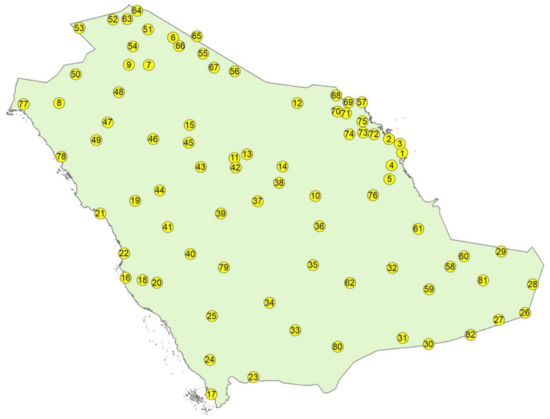
For the purpose of the present work, a set of 82 sites was arbitrarily chosen in order to cover the whole territory of Saudi Arabia. Table 1 provides the names and geographical coordinates of the sites; Figure 1 shows their location in the map of the country. The selection of the sites was based on the “inhabited” criterion (i.e., urban areas, 57 out of 82), while the additional 25 sites out of the 82 are uninhabited and have no name (marked as “unnamed” in Table 1). For this reason, the distribution of the 82 sites is not uniform within Saudi Arabia. It must be mentioned that the downloaded hourly solar horizontal radiation values refer to those for an unobstructed horizon.

Table 1.
The 82 sites arbitrarily selected over Saudi Arabia to cover the whole area of the country; φ is the geographical latitude, and λ the geographical longitude in the WGS84 geodetic system. The “unnamed” sites refer to those away from known locations. This table is a reproduction of Table 1 in [1,2]. N = North, E = East.
2.2. Data Processing and Analysis
To process the data used in this work, we followed the following 5 steps:
Step 1. The downloaded hourly data from the PV-GIS website were transferred from universal time coordinate (UTC) into Saudi Arabian local standard time (LST = UTC + 3 h). It must be mentioned that the PV-GIS solar radiation values were provided at different UTC times for the 82 sites considered, e.g., at hh:48 or hh:09, where hh stands for any hour between 00 and 23.
Step 2. The hourly global horizontal solar radiation, Hg, values were estimated at all sites as the sum Hg = Hb + Hd.
Step 3. The routine SUNAE introduced by Walraven [27] was used to derive the solar azimuths and elevations. The original SUNAE algorithm has, however, been renamed to XRONOS (meaning time in Greek, X is pronounced CH) because of added modifications due to the right ascension and atmospheric refraction effects [28,29]. XRONOS ran for the geographical coordinates of the 82 sites in the period 2005–2016 to derive the solar altitudes, γ, at all LST times calculated in step 1.
Step 4. All solar radiation and solar geometry values were assigned to the nearest LST hour (i.e., values at hh:48 LST or hh:09 LST were assigned to hh:00 LST). This was done in order to have all values in the data base as integer hours.
Step 5. Only those hourly solar radiation values greater than 0 Wm−2 and corresponding to γ ≥ 5° (to avoid the cosine effect) were retained for further analysis. Moreover, the criterion of Hd,0 ≤ Hg,0 was required to be met at the hourly level.
For estimating global solar irradiance on an inclined plane that continuously tracks the sun, Hg,t (in Wm−2), the isotropic model of Liu-Jordan [30] was adopted (the subscript t stands for “tracking”). The isotropic model was used to estimate the ground-reflected radiation from the surrounding surface, Hr,t (in Wm−2), received on the inclined plane. This model was adopted in the present study because of its simplicity and effectiveness in comparison to other anisotropic models in providing the tilted total solar radiation in many parts of the world; the good performance of the isotropic model has been verified by various studies (e.g., [31,32,33,34,35]).
Figure 2 provides a schematic for a tilted surface receiving solar radiation. Deliberately, the tilted surface is not aligned along the direction of the sun in order to show the various angles formed, i.e., the tilt angle of the surface, β; the solar altitude, γ; the solar zenithal angle, θz; the incidence angle, θ (the angle between the normal to the surface and the direction toward the sun); the solar azimuth, ψ; and the azimuth of the tilted plane, ψ’. In this graph, the sun lies in the N-S plane that is normal to the local horizon (therefore, ψ = 180°). In the case of a surface tracking of the sun, it is easy to conclude that θ = 0° (the solar rays are normal to the tilted surface), β = 90° − γ, and ψ = ψ’.
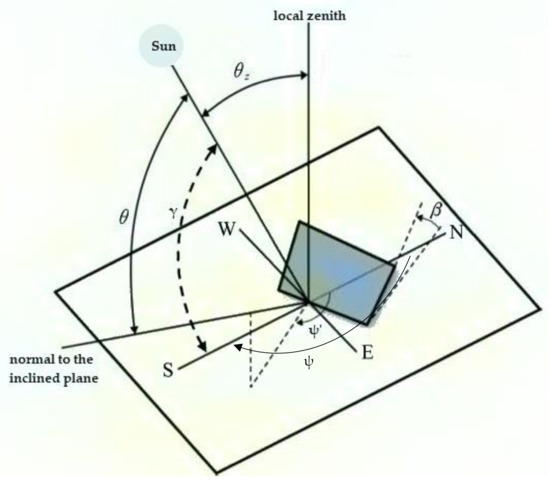
Figure 2.
Inclined surface at a tilt angle β with arbitrary orientation. E, W, N, S denote East, West, North, and South, respectively. Moreover, the solar altitude, γ; the solar azimuth, ψ; the tilted surface’s azimuth, ψ’; and the incidence angle, θ, are shown.
For a sun-tracking surface, the received total solar radiation is given by the following well-known expression:
where the subscript t implies “tracking” the sun by the receiving surface. According to Liu-Jordan (L-J) [30]:
where θ = 0° and β = 90° − γ because the inclined surface is always normal to the solar rays (see Figure 2). Rdi and Rr are the isotropic sky-configuration and ground-inclined plane-configuration factors, respectively. In the L-J model, the ground albedo usually takes the value of ρg0 = 0.2 (Equation (3)). This value was used in the present study. Apart from using ρg0 in the calculations, values of ρg close to reality were also adopted in this study as in [1,2]. To retrieve such values for the 82 sites, we made use of the Giovanni portal [36]; pixels of 0.5° × 0.625° spatial resolution were centered over each of the 82 sites for which monthly mean values of the ground albedo were downloaded in the period 2005–2016. Annual mean ρg values were then computed and were used to re-calculate Hg,t.
Hg,t = Hb,t + Hd,t + Hr,t,
Hd,t = Hd,0·Rdi,
Hr,t = Hg,0·Rr·ρg0, (or Hg,0·Rr·ρg)
Rdi = (1 + cosβ)/2 = (1 + sinγ)/2,
Rr = (1 − cosβ)/2 = (1 − sinγ)/2,
Hb,t = Hb,0 · cosθ/sinγ = Hb,0 · cos0/sinβ = Hb,0/cosγ
For every site, hourly values of Hg,t were estimated twice from Equation (1); the first time by using computations with ρg0 = 0.2 in Equation (3), being considered as reference value in solar modelling, and a second time by using calculations with ρg equal to the ground-albedo value retrieved from the Giovanni platform. From the hourly Hg,t values, annual, seasonal, and monthly solar energy sums (in kWhm−2) under all-sky conditions were estimated for all sites and both ground-albedo values.
3. Results
3.1. Annual Energy Sums
Annual solar energy sums were derived from the appropriate database of each site by utilising both ground albedos, ρg0 and ρg, in Equation (3). The annual solar energy sum (or yield) at each location was estimated by aggregating (summing up) all hourly solar radiation values within the period of 2005–2016. Table 2 shows these annual Hg,t sums. It should be noted here that the reference value of ρg0 is used for grassland areas (and widely used in the L-J model), while surfaces with different vegetation or no vegetation (such as tundra, desert, and snow-covered area) may have different reflectance far from 0.2 [25]. Figure 3 shows the variation of the annual solar energy yields on horizontal as well as on inclined flat-plate surfaces for all three solar system types (static and dynamic) across all 82 sites. The difference in the mean values between the mode (iii) and (ii) systems is only 4.2%, and between the mode (i) and horizontal cases only 6.4%. At first glance, these small differences imply a preference to use mode (ii) solar systems with constant tracking-the-sun ability instead of the more sophisticated mode (iii) ones, or to use horizontal surfaces instead of mode (i) inclined ones with constant tilt towards the South. As shown in Figure 4, the above difference of 4.2% is equivalent to 11,883 kWhm−2year−1, and the second difference of 6.4% to 10,353 kWhm−2year−1. Indeed, the first difference is equal to 3.81 times the average annual solar energy sum for a mode (iii) solar system, i.e., 3.81 × 3120 kWhm−2year−1 = 11,887 kWhm−2year−1, or 3.97 times the average annual solar energy sum for a mode (ii) solar system, i.e., 3.97 × 2994 kWhm−2year−1 = 11,886 kWhm−2year−1. The second difference is equal to 4.27 times the average annual energy sum for a mode (i) solar system, i.e., 4.27 × 2422 kWhm−2year−1 = 10,342 kWhm−2year−1, or 4.55 times the average annual solar energy sum for a horizontal surface, i.e., 4.55 × 2277 kWhm−2year−1 = 10,360 kWhm−2year−1. Therefore, these solar energy differences cannot be ignored as they correspond to sites producing 3.81 (3.97) more energy than mode (iii) ((ii)) solar systems or corresponding to sites deriving 4.27 (4.55) more energy than mode (i) (horizontal) solar systems. On the other hand, it is clear about what type of solar system to use if one has to choose between the first group with modes (ii) and (iii) systems and between the second group with horizontal and mode (i) systems, as the gap between the two groups was found to be rather high (i.e., 707 kWhm−2year−1 = (3120 kWhm−2year−1 - 2994 kWhm−2year−1)/2 − (2422 kWhm−2year−1 − 2277 kWhm−2year−1)/2, see Figure 3). Nevertheless, the choice of the solar system type depends upon the cost-benefit criterion. This criterion is discussed in Section 4.

Table 2.
Maximum annual solar energy sums for the 82 sites in Saudi Arabia for flat-plate solar collectors that are: horizontal (Hg,0), mode (i) static (Hg,β,S/ρg), mode (ii) dynamic (Hg,β,t/ρg), and mode (iii) dynamic (Hg,t/ρg) derived by using a ground albedo of ρg, under all-sky conditions in the period 2005–2016. The Hg values are rounded integers in kWhm−2year−1.
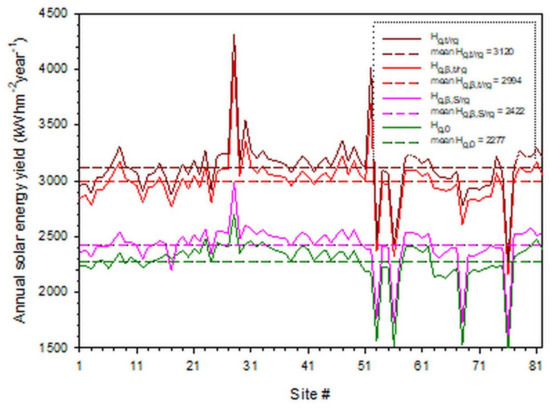
Figure 3.
Variation of the maximum annual solar energy yield across the 82 selected sites in Saudi Arabia on horizontal surface (green lines), on inclined flat-plate surfaces of mode (i) static (purple lines), of mode (ii) dynamic (red lines), and of mode (iii) dynamic (brown lines) systems. The solid lines represent the variation of the annual yield across all sites, while the dashed ones represent the means of the curves.
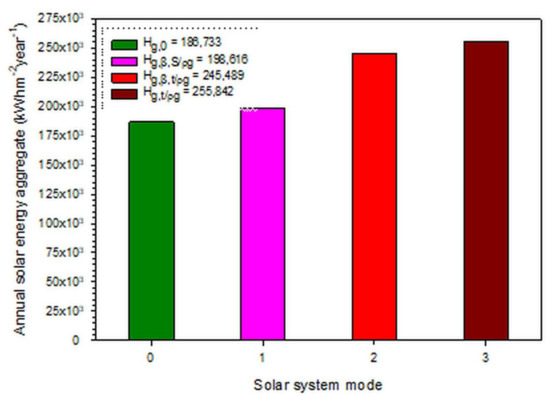
Figure 4.
Annual solar energy aggregate (sum, yield) across all 82 sites in Saudi Arabia for each type of installation; 0: horizontal surface; 1: mode (i) static system; 2: mode (ii) dynamic system; 3: mode (iii) dynamic system.
As a summary, Table 2 reports the total annual solar energy sum per site for all cases of possible installation modes of solar collectors in Saudi Arabia.
Contrary to the recent works by Farahat et al. [1,2], where three solar energy zones (SEZs) with three different tilt angles for the solar installations were defined and adopted, the present work is independent from these SEZs because the tilt angles of the inclined surfaces are not constant but continuously variable. As far as other similar works to the present one are concerned, the study by Zell et al. [18] is worthy of mention. That study divided the country into five geographical regions (central, eastern, southern, western, and western inland) for the purpose of analysing the solar radiation data from [19]. However, the partitioning by Zell et al. did not follow any solar radiation criteria, and, therefore, it is of limited practical value.
Another study by Kaddoura et al. [15] estimated 12 optimal angles β for the 12 months of the year for Tabuk (#8 in Table 1), Al Jawf (#9), Riyadh (#10), Jeddah (#16), and Abha (#24). These angles were derived from modelling and, therefore, have a purely theoretical value, since it is not practical at all to change the tilt angle of the solar panel frame every month. From the international literature, no other work has appeared in relation to modes (ii) or (iii) solar systems for Saudi Arabia.
3.2. Monthly Energy Sums
The intra-annual variation of Hg,t/ρg for all sites is shown in Figure 5. It is seen that the variations of almost all sites are very close to each other, creating a bundle, a zone. There are, however, two sites that present exceptional monthly yields and, therefore, lay above the bundle (i.e., sites #28, and 52). Site #28 lies in the very southeastern part of Saudi Arabia and receives high solar insolation throughout the year. On the contrary, site #52 lies in the very northern part of the country, and lower solar insolation would be expected; this unevenness could probably be attributed to local climatology with very clear skies occurring most time of the year or miscalculation of the ground albedo at the Giovanni platform or inaccurate estimation of solar radiation by the PV-GIS tool or a combination of them. The exceptional performance of solar energy at these two sites is also depicted in Figure 3.
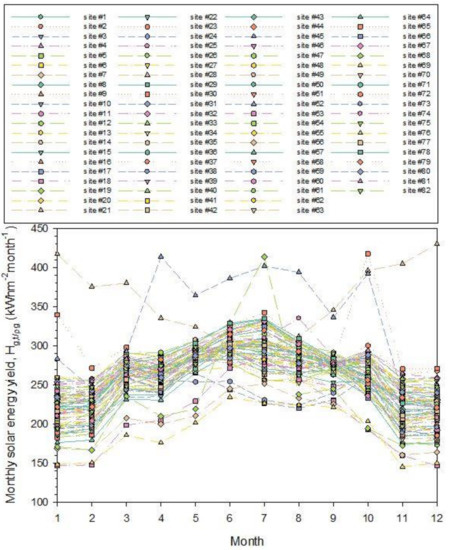
Figure 5.
Intra-annual variation of Hg,t/ρg under all-sky conditions for all 82 sites. The monthly values are sums of the hourly solar radiation ones for each site and averaged over the period 2005–2016. The numbers in the legend correspond to the sites shown in column 1, Table 1.
From Figure 5, one can detect the energy yield per site. Nevertheless, this task is not very informative for solar energy engineers and entrepreneurs, as they would like to have a “compass” that would show them an (even approximate) estimate of the monthly solar energy yield. For this reason, the average monthly energy sums for all sites were estimated, and their intra-annual variation for all Saudi Arabia is shown in Figure 6. It might have been anticipated that all curves (mean and mean ± 1σ) in Figure 6 would be smoother than those actually derived because of the continuous normality of the solar rays on the inclined flat-plate surface. Nevertheless, the differentiation in the ground-albedo values across the whole territory of Saudi Arabia and the variation in local climatology provided the shapes seen in Figure 6. The mean + 1σ curve shows a peak in August and a secondary one in October. Since this statistic is related to the dispersion of the 82 Hg,t values within some limits (i.e., the band of mean ± 1σ), the upper limit (mean + 1σ) corresponds to the dispersion of the higher solar energy values and the lower limit (mean − 1σ) to the dispersion of the lower solar energy values. In other words, the red line in Figure 6 denotes the weighting of the higher values in the whole sample of the 82 Hg,t values, while the blue line is weighted towards the lower values in the same sample. This implies that the upper limit is dominated by the high Hg,t values in the south of the country (i.e., SEZ-A, Figure 3 in [2]), while the lower limit by the low Hg,t values that occurred in the northern part of Saudi Arabia (i.e., SEZ-C, Figure 3 in [2]). Therefore, the upper limit is influenced by a solar energy pattern with maximum in the summer (August), and the lower limit by a solar energy pattern with a main peak in the summer (June, July) and minor peaks in April and September. These observations are justified by Figure 5 in [2]. Table 3 provides the expression for the monthly Hg,t values over all Saudi Arabia as function of the month number, s (s = 1,…,12); the regression equation has a very high R2 equal to 0.96, implying an almost perfect fit to the data.
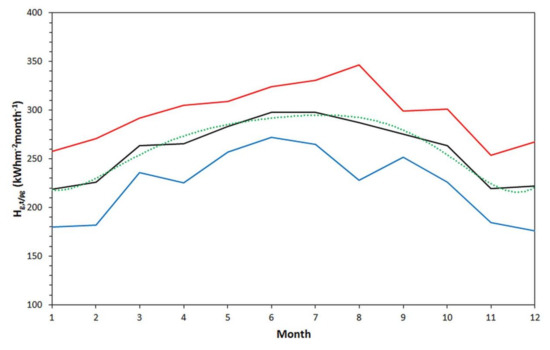
Figure 6.
Intra-annual variation of Hg,t/ρg under all-sky conditions, averaged over all sites and over each month in the period 2005–2016. The black solid line represents the average monthly Hg,t/ρg sums. The red line corresponds to the mean + 1σ curve, and the blue line to the mean − 1σ one. The green dotted line refers to the best-fit curve to the mean one.

Table 3.
Regression equations for the best-fit curves to the monthly (seasonal) mean Hg,t,β/ρg sums averaged over all 82 sites in the period 2005–2016, together with their R2 values; s is month in the range 1–12; 1 = January,…,12 = December (season in the range 1–4; 1 = spring, 2 = summer, 3 = autumn, 4 = winter).
3.3. Seasonal Energy Sums
Minimum and maximum possible energies received by solar energy systems occur during the winter and summer months, respectively, as anticipated. Therefore, this Section is devoted to analszing the seasonal solar energy sums, i.e., during spring (March–April–May), summer (June–July–August), autumn (September–October–November), and winter (December–January–February). The seasonal energy values at each site were calculated by the summation of all hourly solar radiation values in each season.
As in the case of the intra-annual variation of the Hg,t/ρg levels, Figure 7 presents the seasonal variation of the solar energy values; each individual data point in the graph is the average seasonal energy yield for the specific site over the period 2005–2016. To find an overall expression for the received seasonal energy sum in Saudi Arabia, as done for the monthly case, we averaged the energy values for each season from all sites over the period 2005–2016 under all-sky conditions; Figure 8 presents the results. Table 3 provides the regression equation for the curve that best fits the mean seasonal values. The fit is ideal (R2 = 1).
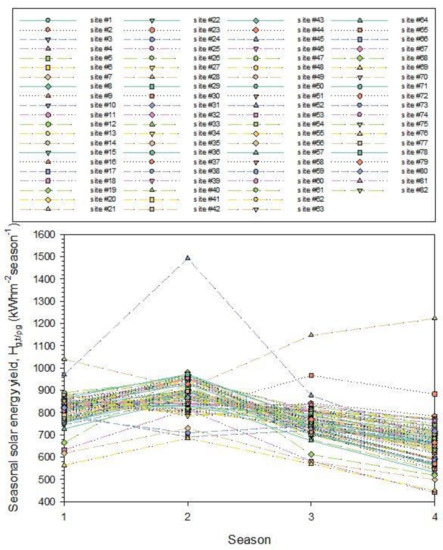
Figure 7.
Seasonal variation of Hg,t/ρg under all-sky conditions for all 82 sites. The seasonal values are sums of the hourly solar radiation ones for each site and averaged over each season in the period 2005–2016. The numbers in the legend correspond to the sites shown in column 1, Table 1. The numbers 1–4 in the x-axis refer to the seasons in the sequence spring to winter.
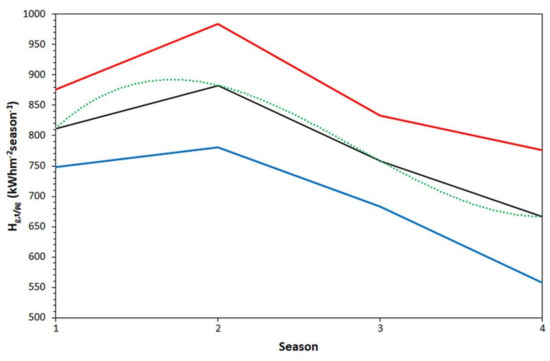
Figure 8.
Seasonal variation of Hg,t/ρg in Saudi Arabia. The black line represents the seasonal mean. The red line refers to the mean + 1σ curve, and the blue one to the mean − 1σ curve, under all-sky conditions. All Hg,t/ρg values were averaged over all 82 sites and over each season in the period 2005–2016. The green dotted line refers to the best-fit curve to the mean one. The numbers 1–4 in the x-axis refer to the seasons in the sequence spring to winter.
3.4. Maps of Annual Energy Sums
Figure 9 shows the solar potential over Saudi Arabia in terms of the annual Hg,t,β/ρg sums. A gradual increase in the annual solar potential in the direction NE–SW for the sun-tracking inclined flat planes is observed. Very similar patterns to that in the present study are given in the Solar Radiation Atlas for Saudi Arabia [37]. The interpretation for this gradient is attributed to two reasons. (i) Latitude: the higher the latitude, the lower the solar radiation levels received on the surface of the earth. (ii) Meteorology: more frequent precipitation is observed in the north-eastern part of the country, which is related to the precipitation occurring in southern Iraq and Iran [38].
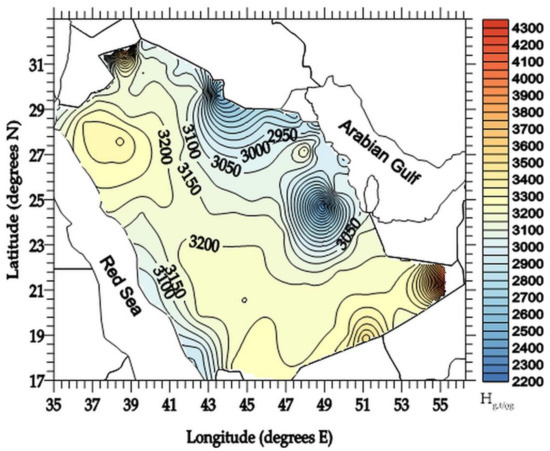
Figure 9.
Distribution of the annual Hg,t/ρg (kWhm−2year−1) sums across Saudi Arabia, averaged over the period 2005–2016, under all-sky conditions.
3.5. Evaluation of the PV-GIS Tool
There have been various validation studies for the solar radiation PV-GIS satellite-derived estimates in the literature (e.g., [24,25,26]). The reported differences between the estimated values and those derived by PV-GIS were found to vary between −14% and +11%. Furthermore, Farahat et al. [1,2] demonstrated such a comparison by taking monthly mean Hg values measured at the Actinometric Station of the National Observatory of Athens (ASNOA, 37.97° N, 23.72° E, 107 m above sea level) and corresponding values from the PV-GIS platform in the period 2005–2011. Figure 10 presents this comparison, which shows an excellent agreement (R2 = 0.99). Although the PV-GIS-estimated values seemed to overestimate the measured Hg ones by +10%, this figure is within the acceptable range (−14%, +11%). For this reason, the PV-GIS data were accepted for use in the present study.
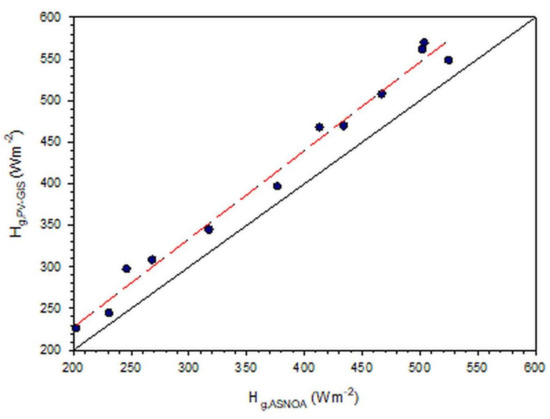
Figure 10.
Comparison of monthly mean solar energy values from PV-GIS, Hg,PV-GIS, to measured ones at ASNOA, Hg,ASNOA, in the period 2005–2011. The red dashed line represents the best fit to the data points and is expressed by the regression equation: Hg,PV-GIS = 1.06Hg,ASNOA + 14.96 (R2 = 0.99). The solid black line is the 1:1 (or y = x) line. This figure is a reproduction of Figure 8 in [1] and Figure 9 in [2].
3.6. The Correction Factor
Farahat et al. [1] introduced the notion of the correction factor, CF, which, for the purpose of the present work, is defined as: CF = Hg,t/ρg/Hg,t/ρg0. CF is, therefore, the ratio of the annual Hg,t sum at each site of the 82, calculated twice, once for ρg0 = 0.2 and a second time for ρg = actual value. The practicality of using CF is that it corrects the solar energy incident on an inclined surface under the influence of a ground albedo equal to 0.2 to that which is under the influence of a near-real ground-albedo value. Despite the variation of CF as function of β for all 82 sites in [1,2], the present analysis of the Hg,t values does not depend on this parameter at all because of the ever varying tilt angle of the receiving flat-plate surface during the operation of a mode (iii) system. Therefore, a different graph was prepared, i.e., a graph of CF as function of the ground-albedo ratio, ρr = ρg0/ρg. Figure 11 shows this dependence, which is linear: CF = 0.0203ρr + 0.9797 with R2 = 0.98 at the 95% confidence level; similar dependence was firstly found by Farahat et al. [1,2]. The two lines CF = 1 and ρr = 1 in Figure 11 cross each other at the site #24, which has a ground albedo ρg = ρg0 = 0.2, and, therefore, Hg,t/ρg = Hg,t/ρg0. The blue and red bands show the confidence and prediction intervals around the best-fit line, respectively. It is seen that many sites are within the blue zone, but most of them are accommodated in the red band. Only four sites lie outside the prediction interval. This observation means that some of the sites (i.e., their CF-ρr data pairs) that lie within the confidence interval are significant at the 95% level, while others that are within the prediction zone will be significant at the 95% level in the future (i.e., they will tend to be significant), and those four sites that are outside the prediction zone will be non-significant at the 95% level anyway.
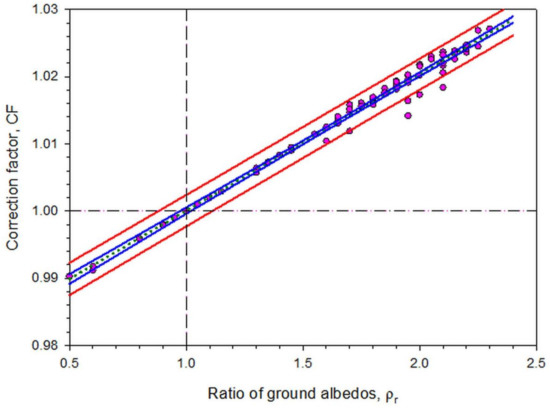
Figure 11.
Variation of the correction factor, CF, as function of the ground-albedo ratio, ρr, under all-sky conditions; both CF and ρr data points are annual averages over each site and over the period 2005–2016. The straight dotted green line expresses the best fit to the data points. The blue and the red zones are the confidence and prediction intervals at the 95% level, respectively. The horizontal black dash-dotted line and the vertical black dashed line indicate the crossing point of CF = 1 and ρr = 1.
Further, by defining the ratio of the annual solar energy sum differences, RΔHg = (Hg,t/ρg − Hg,β,S/ρg)/(Hg,t/ρg − Hg,β,t/ρg), we derived two more plots. Figure 12a shows the dependence of CF on RΔHg, and Figure 12b the dependence of ρr on RΔHg. Both plots show the mean RΔHg (black lines) and the (mean RΔHg + 1σ, mean RΔHg − 1σ) zone; this zone includes most of the 82 sites, a fact that is interpreted as meaning that most of the RΔHg values are statistically significant at the 95% level in relation to those of CF vs. ρr (Figure 11). The other 24 sites outside the band (as #24 for which CF = ρr = 1) can be characterised as reflecting a loose dependence of CF or ρr on RΔHg; this may occur because of the following reasons: (i) inaccurate estimation of ρg at the Giovanni platform, (ii) inaccurate estimation of Hg by the PV-GIS tool, or (iii) both.
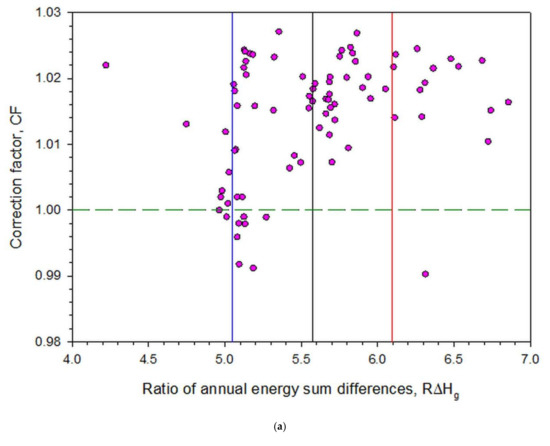
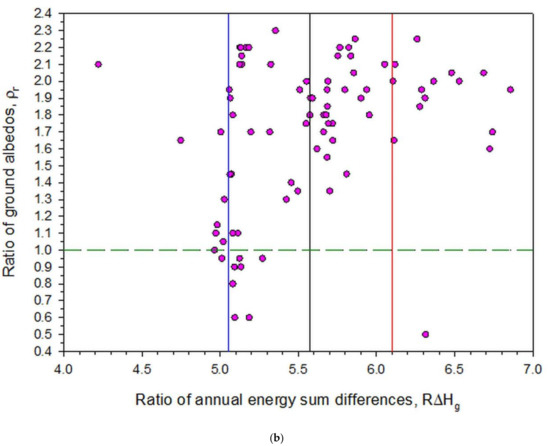
Figure 12.
The correction factor, CF, as function of the ratio of the annual solar energy sum differences, RΔHg (a), and the ground-albedo ratio, ρr, as function of RΔHg (b) for the 82 sites in Saudi Arabia. The data points in the plots are averages over each site and over the period 2005–2016. The green dashed lines represent the values CF = ρr = 1; the vertical black lines are the means of RΔHg; and the red and blue ones are the limits of the (mean + 1σ, mean − 1σ) band, respectively.
4. Comparison of the Three Configuration Modes
This section is devoted to a comparison of static and dynamic solar systems in terms of cost–benefit. To achieve this goal, we searched for works published in the international literature.
A study for the USA by Drury et al. [39] showed that 1-axis tracking systems can increase power generation by 12–25% in relation to fixed-tilt ones, and 2-axis tracking systems by 30–45%. These researchers estimated the installation cost at 0.25 $W−1, 0.82 $W−1, and 1.23 $W−1 for fixed-tilt, 1-axis, and 2-axis systems, respectively. In the same way, their operation and maintenance costs were estimated at 25 $kW−1year−1, 32 $kW−1year−1, and 37.5 $kW−1year−1, respectively.
Another study in Spain by Eke and Senturk [40] concluded that a double-axis solar system may result in an increase in electricity by 30.7% compared to a fixed-tilt system.
Hammad et al. [41] compared the performance and cost between fixed-tilt (static) and double-axis (dynamic) systems in Jordan. They found 31.29% more energy produced by the 2-axis system in comparison with the static one. Further, they estimated the payback period to be 27.6 and 34.9 months for the dynamic and static systems, respectively, with corresponding electricity costs of 0.08 $kWh−1 and 0.10 $kWh−1.
Lazaroiu et al. [42] found a 12–20% increase in the energy produced by a dual-axis solar system in comparison to a fixed-tilt one.
Michaelides et al. [43] studied the performance of solar boilers for Athens, Greece, and Nicosia, Cyprus, by considering 1-axis, seasonal-tilt, and fixed-tilt systems. They found that the solar fractions (the normalised difference between the hot water energy provided by the sun and the auxiliary one supplied by electricity) were 81.4%, 76.2%, and 74.4% for Athens, and 87.6%, 81.6%, and 79.7% for Nicosia in the case of a single-axis, a seasonal-tilt, and a fixed-tilt solar system, respectively.
As far as Saudi Arabia is concerned, the results of the present study (see Figure 3) lead to increases shown in Table 4.

Table 4.
Increase (in %) in the annual solar energy sums from all 82 sites in Saudi Arabia when using horizontal, mode (i) static, and modes (ii) and (iii) dynamic configurations.
5. Discussion
Three innovations appeared in the present study. (i) For the first time, solar maps for Saudi Arabia of the solar energy received on inclined flat surfaces continuously tracking the sun were derived. (ii) A universal curve (nomogram) of CF in relation to ρr was derived for this case, as in [1,2]. (iii) Accommodation of most sites within the mean RΔHg ± 1σ band was found in both relations CF vs. RΔHg and ρr vs. RΔHg; the last two statements remain to be confirmed at other locations in the world to constitute universality.
On the basis of the adopted methodology, we here provide some guidelines for interested solar energy scientists and/or solar energy entrepreneurs. The steps of the guidelines are the following.
- If a solar radiation station exists in the area, hourly or daily values of the solar global horizontal radiation are collected for a climatological period of 10 years at least.
- If no solar radiation exists, then data from relevant websites (e.g., BSRN, GEBA, PV-GIS, ARM) are obtained.
- In the extreme case that this option is not possible, use of a solar energy model can be made to derive the anticipated data from other available variables (e.g., from meteorological parameters as the Meteorological Radiation Model-MRM does [44]).
- Transposition of the selected data from horizontal to inclined planes that track the sun takes place by setting the tilt angle always equal to 90° − γ. The transposition is achieved by selecting the desired model (the L-J model is sufficient). It is recommended that a near-real ground-albedo value is used in these calculations; if knowledge of this value is not available for the site, use of the nomogram of Figure 11 is made to correct the solar energy values derived.
- Annual solar energy sums for the inclined planes are calculated.
- Monthly solar energy sums are estimated, and a regression line can be derived that serves as guideline for estimating the expected solar energy on flat planes.
- The last step is repeated for the seasonal solar energy sums and the derivation of best-fit curves.
The significance of the results of the present study as far as the solar industry and society of Saudi Arabia are concerned can be summarised in the following. The solar engineering society now has a map with fresh knowledge about the solar potential for mode (iii) solar systems across Saudi Arabia. This knowledge may prove useful for designing such systems. On the other hand, actions from governmental policies may have indirect benefits to the society, if these policies promote renewable energy sources in Saudi Arabia (and especially solar energy sources), because of the new knowledge gained through the present work.
6. Conclusions
The present study investigated the solar potential across Saudi Arabia on flat-plate solar panels that vary their tilt angle in order to receive solar radiation normally to their surfaces during the day. The main objective was to find the annual energy available in this configuration type under all-sky conditions. This was achieved by calculating the annual energy sum on flat-plate surfaces with varying tilt angles that track the sun across Saudi Arabia; the solar availability on a horizontal plane was also included for reference purposes. For this reason, hourly solar radiation data in the period 2005–2016 were downloaded from the PV-GIS platform for 82 sites in the country. The calculations for the energy received on the tilted surfaces were performed for a ground albedo equal to 0.2 (as a reference value) and also for a near-real ground albedo. The latter values were retrieved from the Giovanni website.
The main result of the work was that the annual solar energy received by such (dynamic) mode (iii) systems varied between 2267 and 4319 kWhm−2year−1 within Saudi Arabia. Along with the annual energy sums, monthly solar energy values averaged over all locations and over the mentioned period were estimated under all-sky conditions. A regression equation was provided as best-fit curve to the monthly mean energy sums that estimates the solar energy potential at any location in Saudi Arabia with great accuracy (R2 = 0.96). This expression may prove very useful to architects, civil engineers, solar energy engineers, and solar energy system investors in order to assess the solar energy availability in Saudi Arabia for sun-tracking flat-plate solar systems throughout the year.
Seasonal solar energy sums were also calculated. They were averaged over all sites and over the period 2005–2016 under all-sky conditions. A new regression curve that best fits the mean values was estimated with absolute accuracy (R2 = 1). Maximum sums were found in the summer (882 kWm−2), and minimum ones in the winter (667 kWm−2), as expected.
Although unified curves were presented for the monthly and seasonal solar energy yields in all territory of Saudi Arabia numerically expressed in Table 3, individual monthly and seasonal curves for all 82 sites were given in Figure 6 and Figure 8, respectively, in order for the interested scientist or engineer to see the individual solar energy yield variation.
The correction factor, CF, introduced in [1], was also used in this work. A graph of CF as function of ρr showed a linear dependence with increasing CF values as ρr increased. Such a behaviour was claimed to be considered universal (i.e., representable as nomogram). Nevertheless, this universality remains to be confirmed at other locations in the world with different climate and terrain characteristics. Two more plots were also prepared: (i) a graph of CF vs. RΔHg, and (ii) a graph of ρr as function of RΔHg. In both cases, 58 of the 82 sites were found to be accommodated within the ±1σ band around the mean RΔHg value of 5.57. The other 24 sites remained outside the band, thus indicating a loose dependence of CF (ρr) on RΔHg. These two graphs may be used as criteria for a strong (weak) dependence of CF (ρr) on the received solar energy, but this conclusion remains to be confirmed at other sites worldwide with different climate and terrain characteristics.
Author Contributions
Conceptualization, methodology, data collection, data analysis, writing—original draft preparation, H.D.K.; data collection, data analysis, writing—review and editing, A.F.; writing—review and editing, M.A.; writing—review and editing, E.R. All authors have read and agreed to the published version of the manuscript.
Funding
Researchers would like to acknowledge the support provided by the Deanship of Scientific Research (DSR) at the King Fahd University of Petroleum and Minerals (KFUPM) for funding this work through project no. ISSP2103.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The solar radiation data and the ground-albedo data for Saudi Arabia are publicly available and were downloaded from the PV-GIS platform (https://ec.europa.eu/jrc/en/pvgis, accessed on 1 July 2021) and the Giovanni website (https://giovanni.gsfc.nasa.gov/giovanni/, accessed on 1 July 2021), respectively. The ASNOA solar radiation data are available on request to third parties, but they were used on a self-evident permission to the first author as ex member and now emeritus researcher in the institution.
Acknowledgments
The authors are thankful to the Giovanni-platform staff as well the MODIS-mission scientists and associated NASA personnel for the production of the ground-albedo data used in this research. They also thank the personnel of the PV-GIS platform for providing the necessary solar horizontal irradiances over Saudi Arabia. The authors A.F. and E.R. are thankful for the support of the Centre of Research Excellence in Renewable Energy (CORERE), KFUPM.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Farahat, A.; Kambezidis, H.D.; Almazroui, M.; Ramadan, E. Solar Potential in Saudi Arabia for Southward-Inclined Flat-Plate Surfaces. Appl. Sci. 2021, 11, 4101. [Google Scholar] [CrossRef]
- Farahat, A.; Kambezidis, H.D.; Almazroui, M.; Al Otaibi, M. Solar Potential in Saudi Arabia for Inclined Flat-Plate Surfaces of Constant Tilt Tracking the Sun. Appl. Sci. 2021, 11, 7105. [Google Scholar] [CrossRef]
- Demain, C.; Journée, M.; Bertrand, C. Evaluation of Different Models to Estimate the Global Solar Radiation on Inclined Surfaces. Renew. Energy 2013, 50, 710–721. [Google Scholar] [CrossRef]
- El-Sebaii, A.A.; Al-Hazmi, F.S.; Al-Ghamdi, A.A.; Yaghmour, S.J. Global, Direct and Diffuse Solar Radiation on Horizontal and Tilted Surfaces in Jeddah, Saudi Arabia. Appl. Energy 2010, 87, 568–576. [Google Scholar] [CrossRef]
- García, I.; de Blas, M.; Hernández, B.; Sáenz, C.; Torres, J.L. Diffuse Irradiance on Tilted Planes in Urban Environments: Evaluation of Models Modified with Sky and Circumsolar View Factors. Renew. Energy 2021, 180, 1194–1209. [Google Scholar] [CrossRef]
- Akbar, H.S.; Fathallah, M.N.; Raoof, O.O. Efficient Single Axis Sun Tracker Design for Photovoltaic System Applications. IOSR J. Appl. Phys. 2017, 9, 53–60. [Google Scholar] [CrossRef]
- Heslop, S.; MacGill, I. Comparative Analysis of the Variability of Fixed and Tracking Photovoltaic Systems. Sol. Energy 2014, 107, 351–364. [Google Scholar] [CrossRef]
- Abdallah, S.; Nijmeh, S. Two Axes Sun Tracking System with PLC Control. Energy Convers. Manag. 2004, 45, 1931–1939. [Google Scholar] [CrossRef]
- Akbar, H.S. Design of Sun Tracker System for Solar Energy Applications. J. Phys. Res. 2015, 1, 29–34. [Google Scholar]
- Hafez, A.Z.; Yousef, A.M.; Harag, N.M. Solar Tracking Systems: Technologies and Trackers Drive Types—A Review. Renew. Sustain. Energy Rev. 2018, 91, 754–782. [Google Scholar] [CrossRef]
- Altarawneh, I.S.; Rawadieh, S.I.; Tarawneh, M.S.; Alrowwad, S.M.; Rimawi, F. Optimal Tilt Angle Trajectory for Maximizing Solar Energy Potential in Ma’an Area in Jordan. J. Renew. Sustain. Energy 2016, 8, 033701. [Google Scholar] [CrossRef]
- Talebizadeh, P.; Mehrabian, M.A.; Abdolzadeh, M. Prediction of the Optimum Slope and Surface Azimuth Angles Using the Genetic Algorithm. Energy Build. 2011, 43, 2998–3005. [Google Scholar] [CrossRef]
- Evseev, E.G.; Kudish, A.I. The Assessment of Different Models to Predict the Global Solar Radiation on a Surface Tilted to the South. Sol. Energy 2009, 83, 377–388. [Google Scholar] [CrossRef]
- Kambezidis, H.D. The Solar Radiation Climate of Athens: Variations and Tendencies in the Period 1992–2017, the Brightening Era. Sol. Energy 2018, 173, 328–347. [Google Scholar] [CrossRef]
- Kaddoura, T.O.; Ramli, M.A.M.; Al-Turki, Y.A. On the Estimation of the Optimum Tilt Angle of PV Panel in Saudi Arabia. Renew. Sustain. Energy Rev. 2016, 65, 626–634. [Google Scholar] [CrossRef]
- Ohtake, H.; Uno, F.; Oozeki, T.; Yamada, Y.; Takenaka, H.; Nakajima, T.Y. Estimation of Satellite-Derived Regional Photovoltaic Power Generation Using a Satellite-Estimated Solar Radiation Data. Energy Sci. Eng. 2018, 6, 570–583. [Google Scholar] [CrossRef]
- Kambezidis, H.D.; Psiloglou, B.E. Estimation of the Optimum Energy Received by Solar Energy Flat-Plate Convertors in Greece Using Typical Meteorological Years. Part I: South-Oriented Tilt Angles. Appl. Sci. 2021, 11, 1547. [Google Scholar] [CrossRef]
- Zell, E.; Gasim, S.; Wilcox, S.; Katamoura, S.; Stoffel, T.; Shibli, H.; Engel-Cox, J.; Al Subie, M. Assessment of Solar Radiation Resources in Saudi Arabia. Sol. Energy 2015, 119, 422–438. [Google Scholar] [CrossRef] [Green Version]
- ESMAP. Global Solar Atlas 2.0; Technical Report: 2019; World Bank: Washington, DC, USA, 2019. [Google Scholar]
- Almasoud, A.H.; Gandayh, H.M. Future of Solar Energy in Saudi Arabia. J. King Saud. Univ. 2015, 27, 153–157. [Google Scholar] [CrossRef] [Green Version]
- Huld, T.; Müller, R.; Gambardella, A. A New Solar Radiation Database for Estimating PV Performance in Europe and Africa. Sol. Energy 2012, 86, 1803–1815. [Google Scholar] [CrossRef]
- Urraca, R.; Gracia-Amillo, A.M.; Koubli, E.; Huld, T.; Trentmann, J.; Riihelä, A.; Lindfors, A.V.; Palmer, D.; Gottschalg, R.; Antonanzas-Torres, F. Extensive Validation of CM SAF Surface Radiation Products over Europe. Remote Sens. Environ. 2017, 199, 171–186. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Urraca, R.; Huld, T.; Gracia-Amillo, A.; Martinez-de-Pison, F.J.; Kaspar, F.; Sanz-Garcia, A. Evaluation of Global Horizontal Irradiance Estimates from ERA5 and COSMO-REA6 Reanalyses Using Ground and Satellite-Based Data. Sol. Energy 2018, 164, 339–354. [Google Scholar] [CrossRef]
- Mueller, R.W.; Matsoukas, C.; Gratzki, A.; Behr, H.D.; Hollmann, R. The CM-SAF Operational Scheme for the Satellite Based Retrieval of Solar Surface Irradiance—A LUT Based Eigenvector Hybrid Approach. Remote Sens. Environ. 2009, 113, 1012–1024. [Google Scholar] [CrossRef]
- Mueller, R.; Behrendt, T.; Hammer, A.; Kemper, A. A New Algorithm for the Satellite-Based Retrieval of Solar Surface Irradiance in Spectral Bands. Remote Sens. 2012, 4, 622–647. [Google Scholar] [CrossRef] [Green Version]
- Amillo, A.G.; Huld, T.; Müller, R. A New Database of Global and Direct Solar Radiation Using the Eastern Meteosat Satellite, Models and Validation. Remote Sens. 2014, 6, 8165–8189. [Google Scholar] [CrossRef] [Green Version]
- Walraven, R. Calculating the Position of the Sun. Sol. Energy 1978, 20, 393–397. [Google Scholar] [CrossRef]
- Wilkinson, B.J. An Improved FORTRAN Program for the Rapid Calculation of the Solar Position. Sol. Energy 1981, 27, 67–68. [Google Scholar] [CrossRef]
- Kambezidis, H.D.; Papanikolaou, N.S. Solar Position and Atmospheric Refraction. Sol. Energy 1990, 44. [Google Scholar] [CrossRef]
- Liu, B.; Jordan, R.C. The Long-Term Average Performance of Flat-Plate Solar-Energy Collectors. Sol. Energy 1963, 7, 53–74. [Google Scholar] [CrossRef]
- Kambezidis, H.D.; Psiloglou, B.E.; Gueymard, C. Measurements and Models for Total Solar Irradiance on Inclined Surface in Athens, Greece. Sol. Energy 1994, 53. [Google Scholar] [CrossRef]
- Nijmeh, S.; Mamlook, R. Testing of Two Models for Computing Global Solar Radiation on Tilted Surfaces. Renew. Energy 2000, 20, 75–81. [Google Scholar] [CrossRef]
- Jin, Z.; Yezheng, W.; Gang, Y. Estimation of Daily Diffuse Solar Radiation in China. Renew. Energy 2004, 29, 1537–1548. [Google Scholar] [CrossRef]
- Benkaciali, S.; Gairaa, K. Comparative Study of Two Models to Estimate Solar Radiation on an Inclined Surface The Radiometric Station Was Installed on the Roof of Solar Radiation Laboratory Of. Rev. Energies Renouvelables 2012, 15, 219–228. [Google Scholar]
- Pandey, C.K.; Katiyar, A.K. Hourly Solar Radiation on Inclined Surfaces. Sustain. Energy Technol. Assessments 2014, 6, 86–92. [Google Scholar] [CrossRef]
- Acker, J.G.; Leptoukh, G. Online Analysis Enhances Use of NASA Earth Science Data. Eos Trans. Am. Geophys. Union 2007, 88, 14. [Google Scholar] [CrossRef]
- National Renewable Energy Laboratory. Kingdom of Saudi Arabia: Solar Radiation Atlas. Available online: https://digital.library.unt.edu/ark:/67531/metadc690351/ (accessed on 27 September 2021).
- Marey, H.S.; Gille, J.C.; El-Askary, H.M.; Shalaby, E.A.; El-Raey, M.E. Aerosol Climatology over Nile Delta Based on MODIS, MISR and OMI Satellite Data. Atmos. Chem. Phys. 2011, 11, 10637–10648. [Google Scholar] [CrossRef] [Green Version]
- Drury, E.; Lopez, A.; Denholm, P.; Margolis, R. Relative Performance of Tracking versus Fixed Tilt Photovoltaic Systems in the USA. Prog. Photovolt. Res. Appl. 2013, 22, 1302–1315. [Google Scholar] [CrossRef]
- Eke, R.; Senturk, A. Performance Comparison of a Double-Axis Sun Tracking versus Fixed PV System. Sol. Energy 2012, 86, 2665–2672. [Google Scholar] [CrossRef]
- Hammad, B.; Al-Sardeah, A.; Al-Abed, M.; Nijmeh, S.; Al-Ghandoor, A. Performance and Economic Comparison of Fixed and Tracking Photovoltaic Systems in Jordan. Renew. Sustain. Energy Rev. 2017, 80, 827–839. [Google Scholar] [CrossRef]
- Lazaroiu, G.C.; Longo, M.; Roscia, M.; Pagano, M. Comparative Analysis of Fixed and Sun Tracking Low Power PV Systems Considering Energy Consumption. Energy Convers. Manag. 2015, 92, 143–148. [Google Scholar] [CrossRef]
- Michaelides, I.M.; Kalogirou, S.A.; Chrysis, I.; Roditis, G.; Hadjiyianni, A.; Kambezidis, H.D.; Petrakis, M.; Lykoudis, S.; Adamopoulos, A.D. Comparison of Performance and Cost Effectiveness of Solar Water Heaters at Different Collector Tracking Modes in Cyprus and Greece. Energy Convers. Manag. 1999, 40, 1287–1303. [Google Scholar] [CrossRef]
- Kambezidis, H.D.; Psiloglou, B.E.; Karagiannis, D.; Dumka, U.C.; Kaskaoutis, D.G. Meteorological Radiation Model (MRM v6.1): Improvements in Diffuse Radiation Estimates and a New Approach for Implementation of Cloud Products. Renew. Sustain. Energy Rev. 2017, 74, 616–637. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).