An Approximation-Based Design Optimization Approach to Eigenfrequency Assignment for Flexible Multibody Systems
Abstract
:1. Introduction
2. Method Description
2.1. Modal Approximation Model
- and are the mass and stiffness matrices of the assembled finite element matrices of all the flexible links, respectively;
- is the matrix of centrifugal and Coriolis terms;
- is the matrix which represents the relation between velocities at the nodes of the ERLS and the generalized velocities , and is its time derivative;
- is the gravity vector and is the generalized external force vector.
2.2. Iterative Computation of the Taylor Polynomial
2.3. Partial Linearization
2.4. Optimization Problem
3. Results
3.1. Description of a Benchmark Problem
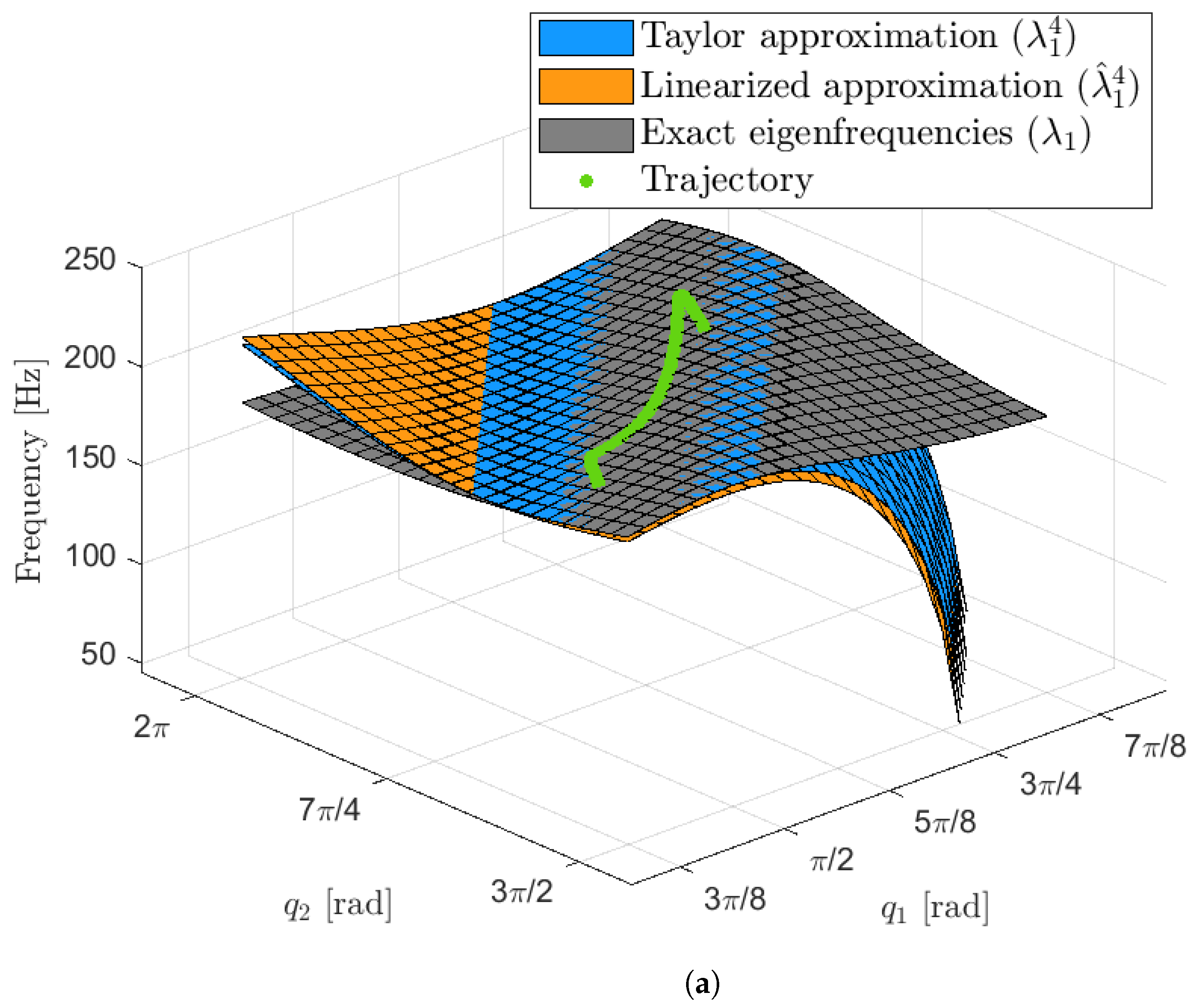
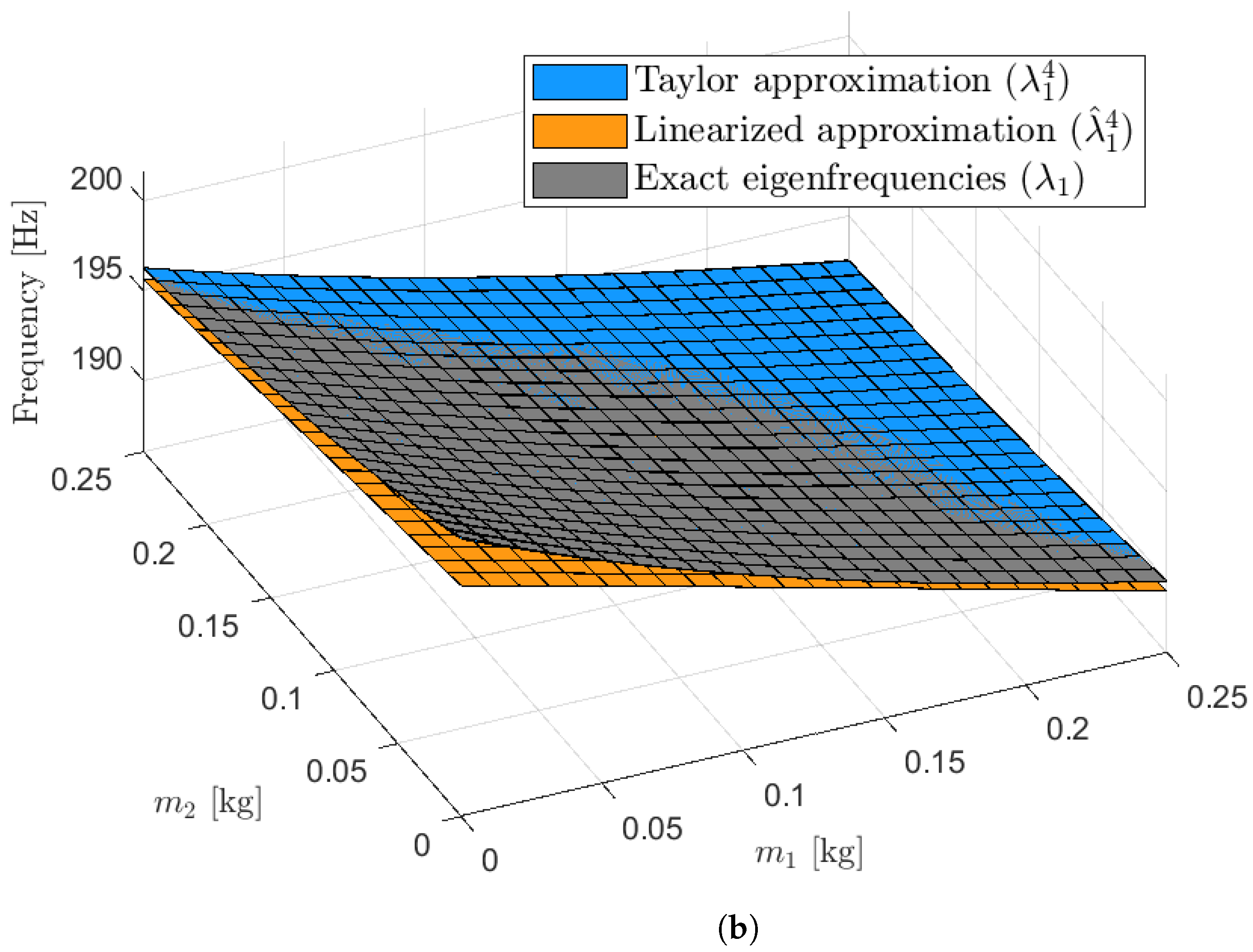
3.2. Parameter Study Results
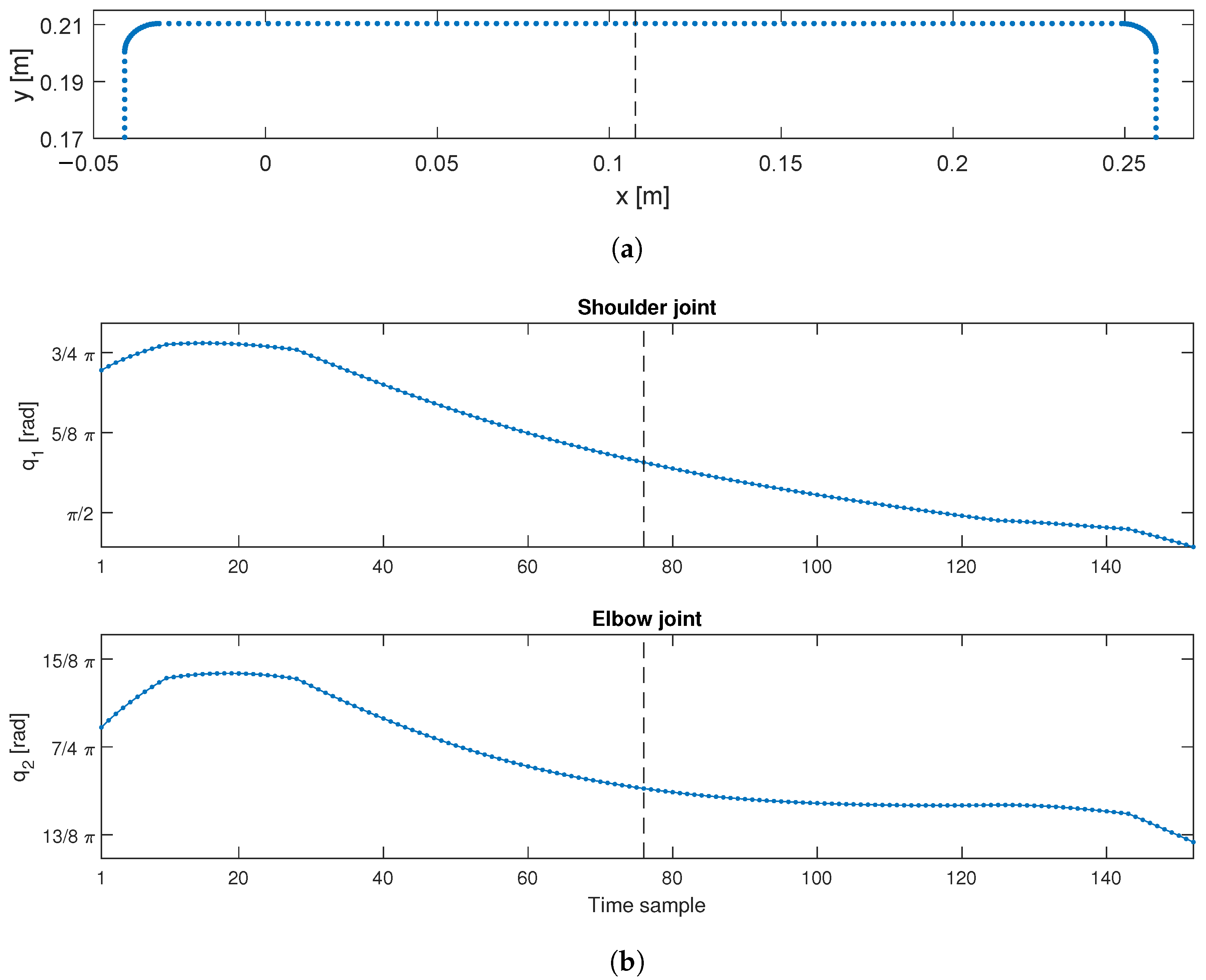
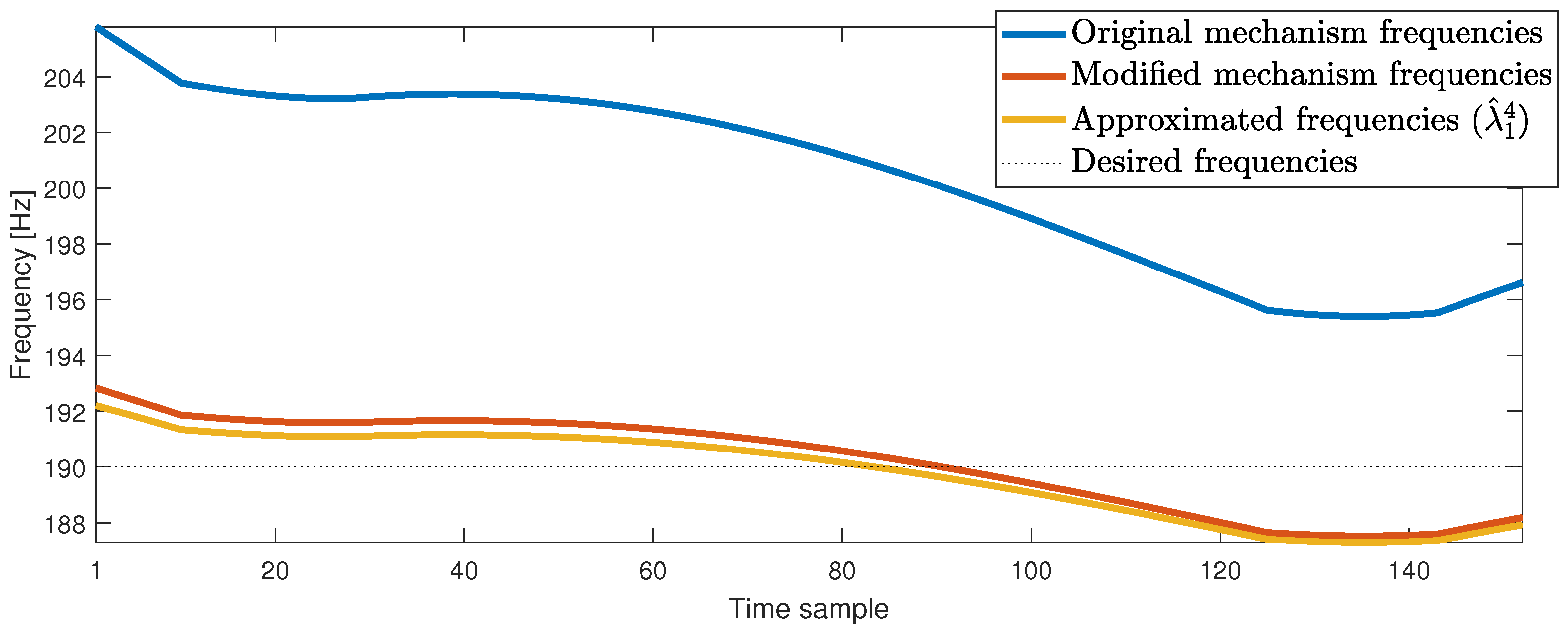
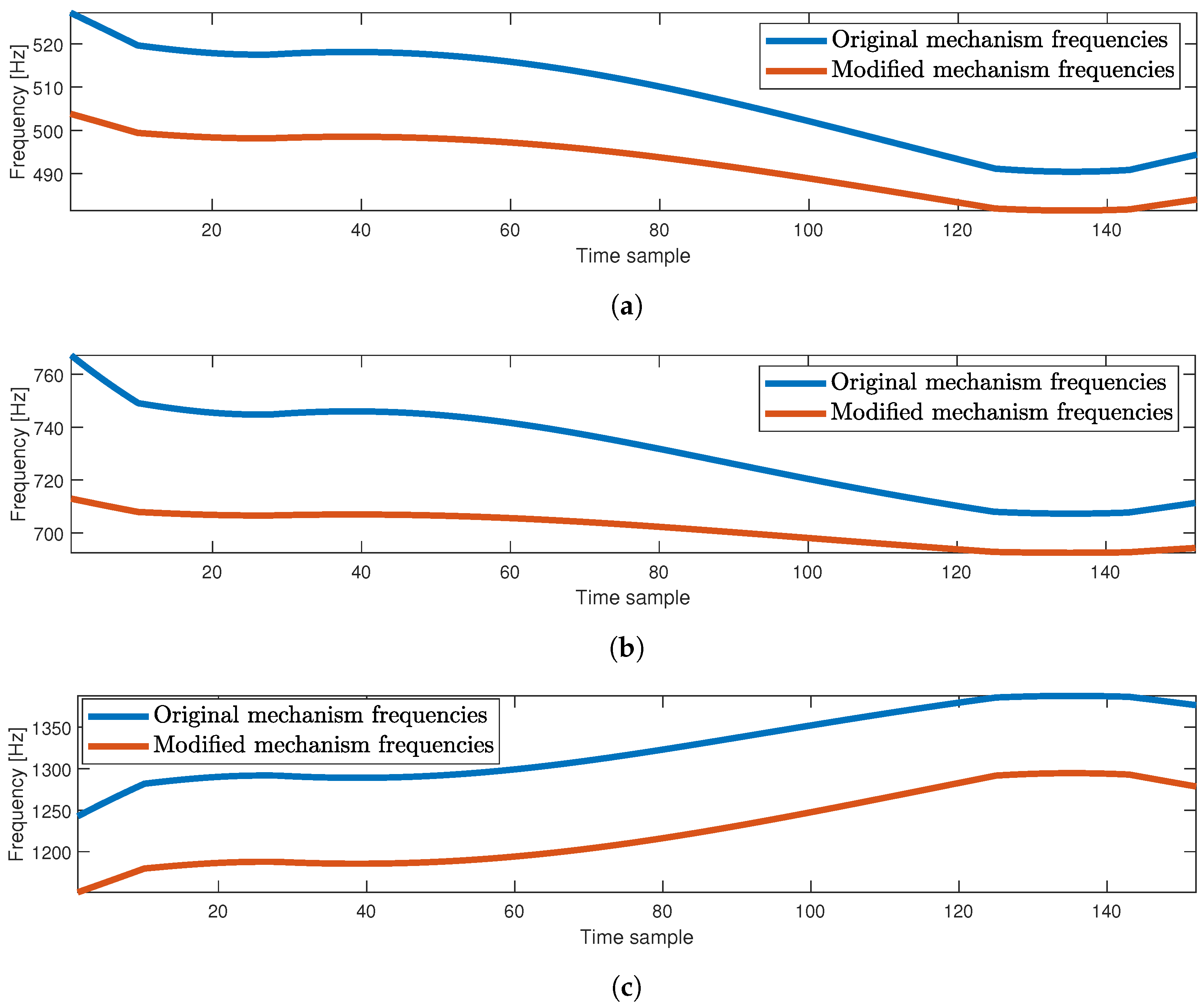
3.3. Optimum Design Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Braun, S.; Ram, Y. Modal modification of vibrating systems: Some problems and their solutions. Mech. Syst. Signal Process. 2001, 15, 101–119. [Google Scholar] [CrossRef]
- Liangsheng, W. Direct Method of Inverse Eigenvalue Problems for Structure Redesign. J. Mech. Des. Trans. ASME 2003, 125, 845–847. [Google Scholar] [CrossRef]
- Gladwell, G.M.L. Inverse Problems in Vibration. Appl. Mech. Rev. 1986, 39, 1013–1018. [Google Scholar] [CrossRef]
- Mottershead, J.; Ram, Y. Inverse eigenvalue problems in vibration absorption: Passive modification and active control. Mech. Syst. Signal Process. 2006, 20, 5–44. [Google Scholar] [CrossRef]
- Belotti, R.; Caracciolo, R.; Palomba, I.; Richiedei, D.; Trevisani, A. An Updating Method for Finite Element Models of Flexible-Link Mechanisms Based on an Equivalent Rigid-Link System. Shock Vib. 2018, 2018, 1797506. [Google Scholar] [CrossRef]
- Richiedei, D.; Tamellin, I.; Trevisani, A. Simultaneous assignment of resonances and antiresonances in vibrating systems through inverse dynamic structural modification. J. Sound Vib. 2020, 485, 115552. [Google Scholar] [CrossRef]
- Richiedei, D.; Tamellin, I.; Trevisani, A. A homotopy transformation method for interval-based model updating of uncertain vibrating systems. Mech. Mach. Theory 2021, 160. [Google Scholar] [CrossRef]
- Palomba, I.; Vidoni, R. Flexible-link multibody system eigenvalue analysis parameterized with respect to rigid-body motion. Appl. Sci. 2019, 9, 5156. [Google Scholar] [CrossRef] [Green Version]
- Turcic, D.A.; Midha, A. Generalized Equations of Motion for the Dynamic Analysis of Elastic Mechanism Systems. J. Dyn. Syst. Meas. Control 1984, 106, 243–248. [Google Scholar] [CrossRef]
- Vidoni, R.; Gallina, P.; Boscariol, P.; Gasparetto, A.; Giovagnoni, M. Modeling the vibration of spatial flexible mechanisms through an equivalent rigid-link system/component mode synthesis approach. JVC/J. Vib. Control. 2017, 23, 1890–1907. [Google Scholar] [CrossRef]
- Myers, R.; Montgomery, D. Response Surface Methodology: Process and Product Optimization Using Designed Experiments, 2nd ed.; Wiley: Hoboken, NJ, USA, 2002. [Google Scholar] [CrossRef]
- Krige, D.G. A statistical Approach to Some Mine Valuations and Allied Problems at the Witwatersrand. Master’s Thesis, University of Witwatersrand, Johannesburg, South Africa, 1951. [Google Scholar]
- Forrester, A.I.; Keane, A.J. Recent advances in surrogate-based optimization. Prog. Aerosp. Sci. 2009, 45, 50–79. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, C. Optimal design of aeroengine turbine disc based on Kriging surrogate models. Comput. Struct. 2011, 89, 27–37. [Google Scholar] [CrossRef]
- Xu, Q.; Wehrle, E.; Baier, H. Adaptive surrogate-based design optimization with expected improvement used as infill criterion. Optimization 2012, 61, 661–684. [Google Scholar] [CrossRef]
- Boursier Niutta, C.; Wehrle, E.J.; Duddeck, F.; Belingardi, G. Surrogate modeling in design optimization of structures with discontinuous responses: A new approach for ill-posed problems in crashworthiness design. Struct. Multidiscip. Optim. 2018, 57, 1857–1869. [Google Scholar] [CrossRef]
- Duddeck, F.; Wehrle, E.J. Recent advances on surrogate modeling for robustness assessment of structures with respect to crashworthiness requirements. In Proceedings of the 10th European LS-DYNA Conference, Wrzburg, Germany, 15–17 June 2015. [Google Scholar]
- Shabana, A.; Zaher, M.; Recuero, A.; Rathod, C. Study of nonlinear system stability using eigenvalue analysis: Gyroscopic motion. J. Sound Vib. 2011, 330, 6006–6022. [Google Scholar] [CrossRef]
- Wittmuess, P.; Henke, B.; Tarin, C.; Sawodny, O. Parametric modal analysis of mechanical systems with an application to a ball screw model. In Proceedings of the 2015 IEEE Conference on Control Applications (CCA), Sydney, Australia, 21–23 September 2015; pp. 441–446. [Google Scholar]
- Palomba, I.; Vidoni, R.; Wehrle, E. Application of a parametric modal analysis approach to flexible-multibody systems. Mech. Mach. Sci. 2019, 66, 386–394. [Google Scholar] [CrossRef]
- Palomba, I.; Wehrle, E.; Vidoni, R.; Gasparetto, A. Parametric eigenvalue analysis for flexible multibody systems. Mech. Mach. Sci. 2019, 73, 4117–4126. [Google Scholar] [CrossRef]
- Floudas, C.A.; Visweswaran, V. Quadratic Optimization. In Handbook of Global Optimization; Springer: Boston, MA, USA, 1995; pp. 217–269. [Google Scholar] [CrossRef]
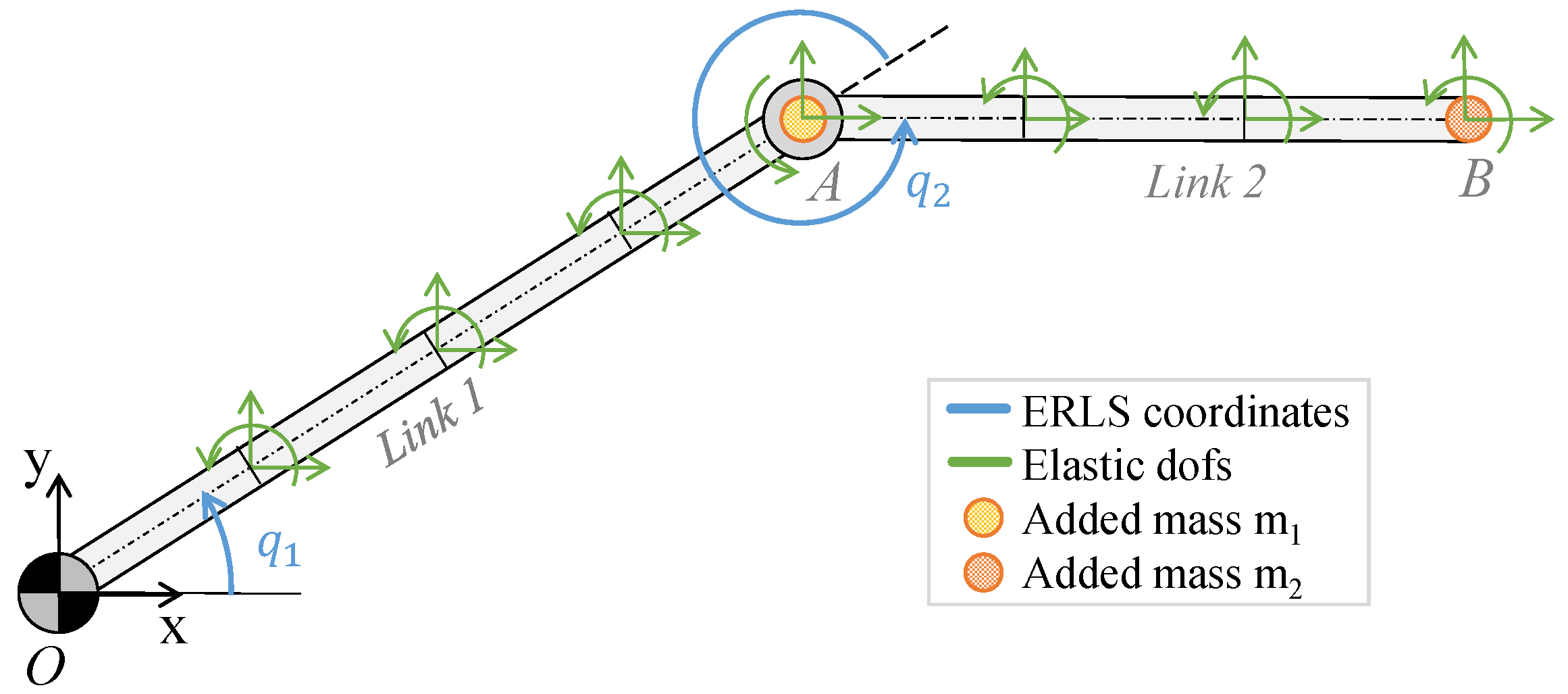
| Parameter | Value |
|---|---|
| Link 1 length | |
| Link 2 length | |
| Linear mass density | 1.9 kg/m |
| Young’s modulus | |
| Bending moment of inertia |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belotti, R.; Palomba, I.; Wehrle, E.; Vidoni, R. An Approximation-Based Design Optimization Approach to Eigenfrequency Assignment for Flexible Multibody Systems. Appl. Sci. 2021, 11, 11558. https://doi.org/10.3390/app112311558
Belotti R, Palomba I, Wehrle E, Vidoni R. An Approximation-Based Design Optimization Approach to Eigenfrequency Assignment for Flexible Multibody Systems. Applied Sciences. 2021; 11(23):11558. https://doi.org/10.3390/app112311558
Chicago/Turabian StyleBelotti, Roberto, Ilaria Palomba, Erich Wehrle, and Renato Vidoni. 2021. "An Approximation-Based Design Optimization Approach to Eigenfrequency Assignment for Flexible Multibody Systems" Applied Sciences 11, no. 23: 11558. https://doi.org/10.3390/app112311558
APA StyleBelotti, R., Palomba, I., Wehrle, E., & Vidoni, R. (2021). An Approximation-Based Design Optimization Approach to Eigenfrequency Assignment for Flexible Multibody Systems. Applied Sciences, 11(23), 11558. https://doi.org/10.3390/app112311558









