Quantum-Inspired Classification Algorithm from DBSCAN–Deutsch–Jozsa Support Vectors and Ising Prediction Model

Abstract

Quantum computing is suggested as a new tool to deal with large data set for machine learning applications. However, many quantum algorithms are too expensive to fit into the small-scale quantum hardware available today and the loading of big classical data into small quantum memory is still an unsolved obstacle. These difficulties lead to the study of quantum-inspired techniques using classical computation. In this work, we propose a new classification method based on support vectors from a DBSCAN–Deutsch–Jozsa ranking and an Ising prediction model. The proposed algorithm has an advantage over standard classical SVM in the scaling with respect to the number of training data at the training phase. The method can be executed in a pure classical computer and can be accelerated in a hybrid quantum–classical computing environment. We demonstrate the applicability of the proposed algorithm with simulations and theory.

1. Introduction

Quantum machine learning [1,2,3] is an emerging field using quantum information processing for machine learning applications. Various quantum machine learning algorithms have been proposed, such as quantum Boltzmann machines [4], supervised quantum autoencoders [5], reinforcement learning using quantum Boltzmann machines [6], quantum circuit learning [7,8] and some quantum methods for linear algebra [9,10,11]. Even though the exponentially large Hilbert space is expected to help tackling the “curse of dimensionality” in machine learning, loading large classical data sets into a small quantum memory is a bottleneck [12,13]. Even though this problem can be circumvented in some settings [14], the available quantum information processors are restricted by the small number of qubits and high operational noise in the current noisy intermediate-scale quantum [15] era. On the other hand, these quantum algorithms have inspired various new classical efficient methods [16,17,18,19]. The dequantizing of quantum algorithms is not only for practical concerns, but also for theoretical interests in complexity theory [20].

The support-vector machine (SVM) is a widely used classification algorithm [21,22,23,24]. There are also newly developed variants of the SVM [25,26] and several quantum versions of the SVM have been proposed [27,28,29]. One proposal is to use the HHL algorithm [9] to invert the kernel matrix [27]. Schuld et al. [28] proposed a QSVM algorithm in which the distance for the kernel classifier is evaluated by single qubit gate circuits. Recently, Havlicek et al. [29] implemented the quantum circuit learning classification and a quantum kernel estimator for the SVM. However, due to the requirements of quantum coherence, the applications of these algorithms to large-scale data sets has not been demonstrated yet.

In this work, we propose a new quantum-inspired algorithm for classification tasks. The support vectors are selected from the data by a principle inspired by the classical clustering algorithm density-based spatial clustering of applications with noise (DBSCAN) [30] and the quantum algorithm Deutsch–Jozsa (DJ) [31]. DBSCAN is a commonly used classical clustering algorithm that determines clusters by considering numbers of data points within some distance parameter $ϵ$. DBSCAN is efficient, noise-resilient and does not require the input of the number of clusters. DJ is a deterministic quantum algorithm that determines a specific property of a given Boolean function $f:{\{0,1\}}^n\to \{0,1\}$ with a single oracle call to the function f. The classical deterministic algorithm to solve the DJ problem requires $O\left(2^n\right)$ calls. We combine DBSCAN and DJ to identify support vectors that are close to the classification boundary. The support vectors are then used for prediction based on an Ising model classifier. The prediction labels are identified as spins in an Ising model and the prediction label is aligned with nearby support vectors through spin–spin interactions. The training time complexity of the proposed algorithm scales according to $O\left(l^{2}d\right)$, where l is the number of training data and d is the feature dimension. This is favorable comparing to $O\left(l^{3}d\right)$ standard kernel support-vector machines, such as LIBSVM, used in scikit-learn [21,22,23,24]. The proposed algorithm can be executed on classical computers, while quantum devices could be used to accelerate several subroutines in the algorithm. The numerical verification is presented. We also provide theoretical evidences for the learnability of the algorithm. We show that the training algorithm is described by an integer linear programming problem. We also derive upper bounds for the VC dimension of the Ising classifier in two special lattices.

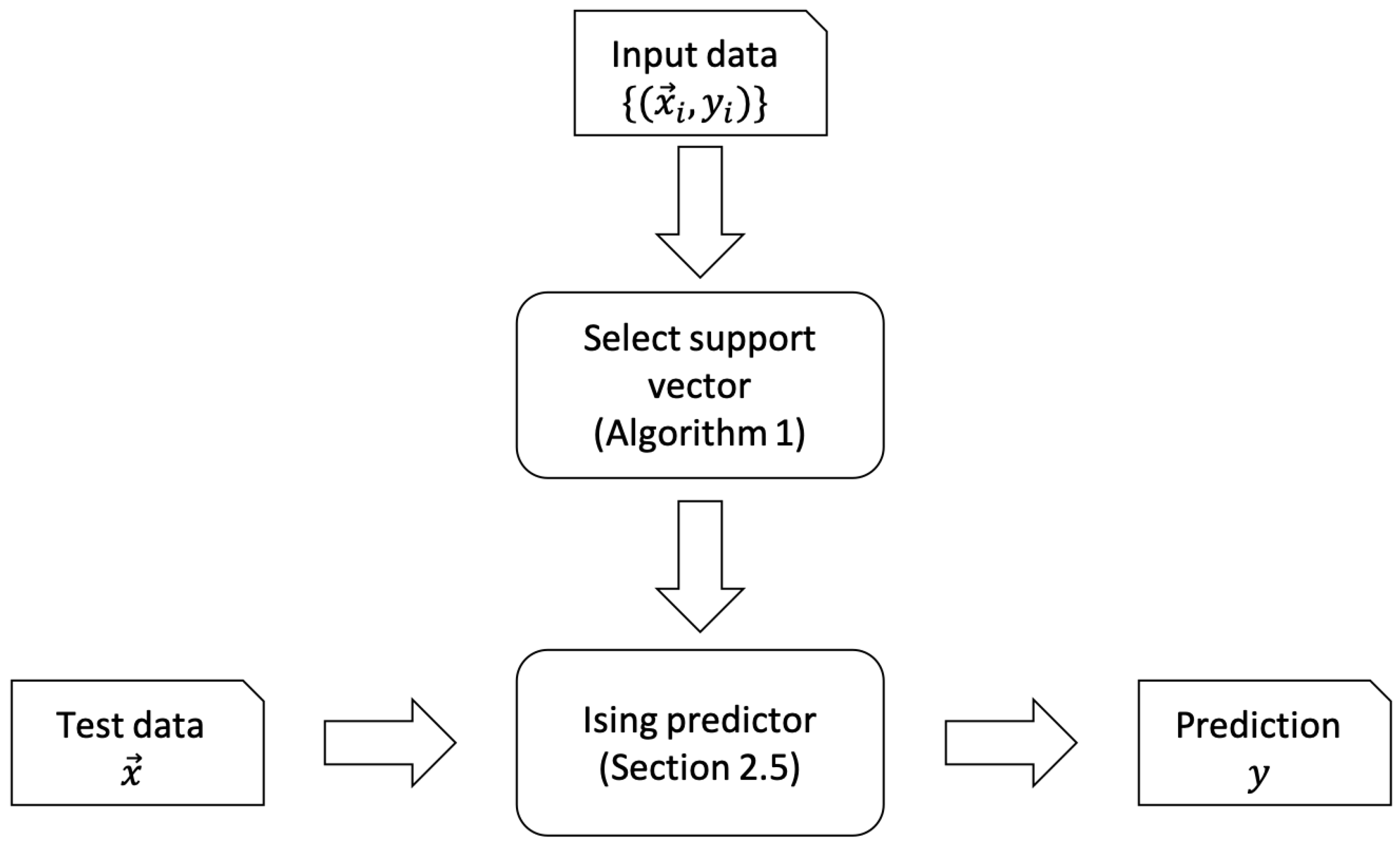
2. The Learning Algorithm

2.1. Hypothesis Set

In this subsection, we briefly illustrate the hypothesis set and training and testing algorithms. The flow chart is illustrated in Figure 1. The details are discussed in the following sections. Given the training data set $\tau =\left\{({\overrightarrow{x}}_i,y_i)\right|i=1,\dots ,l\}$, where $y_i\in \{\pm 1\}$ are the labels for binary classification, the goal of a classification algorithm is to find a hypothesis $f_{\theta }:({\overrightarrow{x}}_1,\dots ,{\overrightarrow{x}}_{n_t})\mapsto {\{-1,+1\}}^{n_t}$ with small prediction error, where $n_t$ is the number of test data. The classification algorithm consists of two parts, training and prediction. A training algorithm finds a hypothesis by minimizing some loss function $L(f_{\theta }\left({\overrightarrow{x}}_i\right),y_i)$. Our hypothesis set consists of the ground states of the Ising model. The hypothesis set is

$$\begin{array}{ccc}\hfill f_{\theta }({\overrightarrow{x}}_1,\dots ,{\overrightarrow{x}}_{n_t})& & =(s_1,\dots ,s_{n_t}),{\overrightarrow{x}}_i\in T\hspace{0.17em}\mathrm{for}\hspace{0.17em}1\le i\le n_t,\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill (s_1,\dots ,s_{n_t+n_{sv}})& & =arg\underset{\left\{s_k\right\}}{min}[-\sum _{\underset{{\overrightarrow{x}}_i,{\overrightarrow{x}}_j\in S\cup T}{i<j}}{J}_{i,j}({\overrightarrow{x}}_i,{\overrightarrow{x}}_j)s_i{s}_j-\sum _{\underset{{\overrightarrow{x}}_i\in S\cup T}{i}}{h}_i{s}_i],\hfill \end{array}$$

(2)

where $S=\left\{\mathrm{support}\hspace{0.17em}\mathrm{vectors}\right\}$ and $T=\left\{\mathrm{test}\hspace{0.17em}\mathrm{data}\right\}$, $n_{sv}=\left|S\right|$, $n_t=\left|T\right|$, $s_i\in \{-1,1\}$. $h_i=y_i$ for ${\overrightarrow{x}}_i\in S$ and $h_i=0$ for ${\overrightarrow{x}}_i\in T$. The free parameters of the model are, in general, $\theta =\left(J_{ij}\right)$. We use a physics-motivated ansatz to efficiently determine the support vectors and $\theta$ from three free parameters, ${\theta }^{\prime }=(\alpha ,\beta ,ϵ)$, as explained in the following subsections. Finally, the training is performed by minimizing the loss function with respect to the remaining three free parameters, $\theta =(\alpha ,\beta ,ϵ)$, with particle swarm optimization (PSO). The loss function is the cross-entropy loss function

$$L(f_{\theta }\left({\overrightarrow{x}}_i\right),y_i)=-(1-q\left({\overrightarrow{x}}_i\right))ln\left(p_{-1}\left({\overrightarrow{x}}_i\right)\right)-q\left({\overrightarrow{x}}_i\right)ln\left(p_{+1}\left({\overrightarrow{x}}_i\right)\right),$$

(3)

where $q\left({\overrightarrow{x}}_i\right)=(1+y_i)/2$; $p_{\pm 1}\left({\overrightarrow{x}}_i\right)$ is the probability that $s_i=\pm 1$ for the Ising ground state.

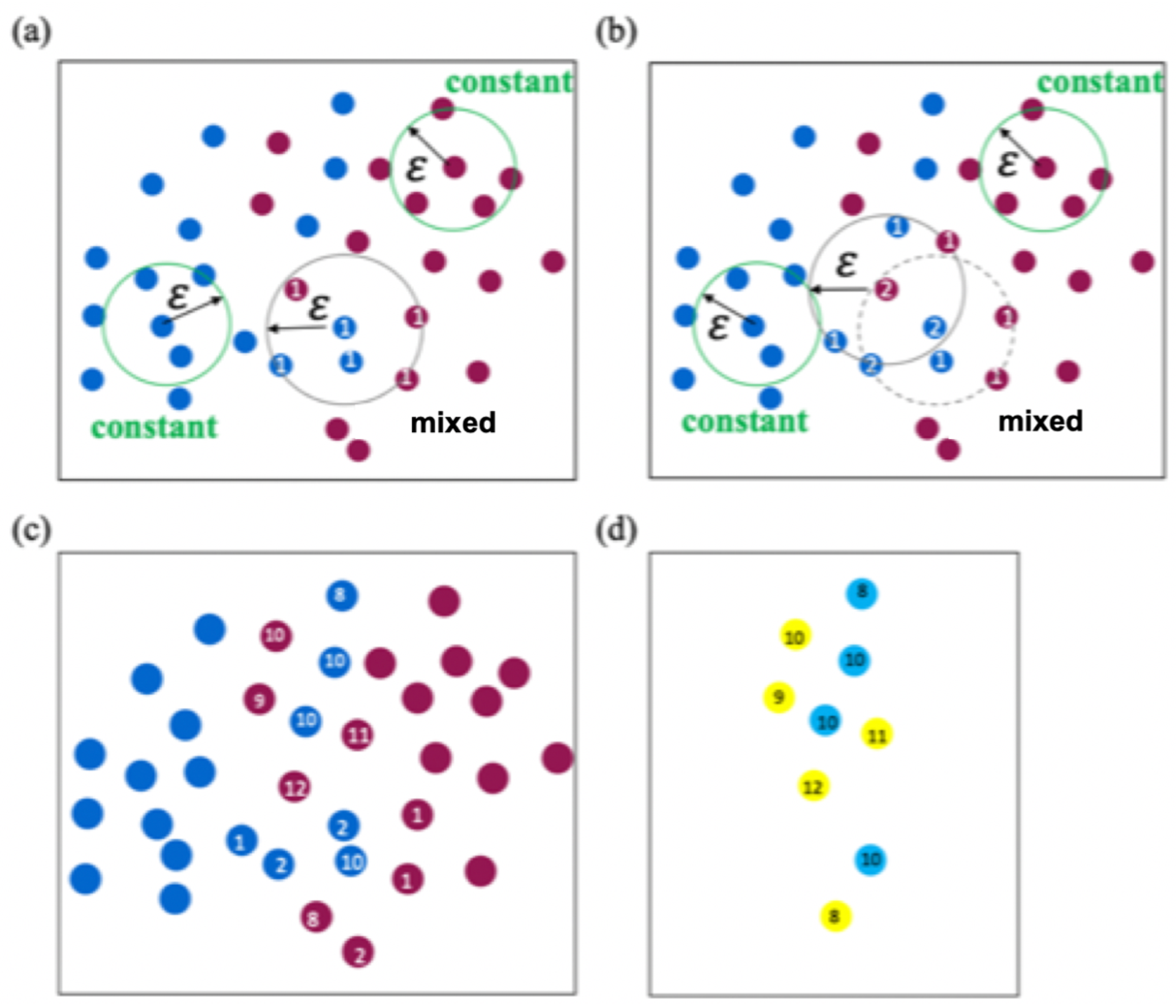
2.2. DBSCAN Algorithm for Determining the Support Vector

The training algorithm is designed by applying the DBSCAN clustering algorithm to a Deutsch–Jozsa decision problem on the training data. The idea is depicted in Figure 2. Let us consider the hypersphere $B_{ϵ}\left({\overrightarrow{x}}_i\right)$ of radius $ϵ$ centered in the data point ${\overrightarrow{x}}_i$. Near the classification boundary, it is more likely that the data in the sphere have two different classification labels. On the other hand, for the data in the interior of each cluster, it is more likely that all the data points in the sphere have the same label. Hence, the classification boundary can be identified by a DBSCAN scanning through all the data points. For each data point, we query a decision problem, namely, whether the data inside the sphere is constant or not. If the number of non-constant spheres around is large for a given data point, we then select this point as a support vector for the prediction algorithm. This decision problem takes the form of a Deutsch–Jozsa problem and the potential use of the quantum DJ algorithm to enhance the training is discussed in Section 2.4.

After selecting the support vectors from the training data, we compute a kernel matrix ${\left(J_{sv}\right)}_{i,j}=J({\overrightarrow{x}}_i,{\overrightarrow{x}}_j)$ for ${\overrightarrow{x}}_i,{\overrightarrow{x}}_j\in \left\{\mathrm{support}\hspace{0.17em}\mathrm{vectors}\right\}$. This kernel matrix will be used in the prediction algorithm. The matrix elements are, in general, some functions of data positions. We choose J to be the inverse of some power-law function of distances between data points:

$$J({\overrightarrow{x}}_i,{\overrightarrow{x}}_j)=\frac{1}{\left|\right|{\overrightarrow{x}}_i-{\overrightarrow{x}}_j{\left|\right|}^{\beta }}.$$

(4)

The training algorithm can be described as the pseudo-code Algorithm 1.

Algorithm 1: The training algorithm to determine support vectors.

2.3. Integer Linear Programming Formulation

We show that the training algorithm is equivalent to solving an integer linear programming problem. We use the following definitions: $B_{ϵ}\left({\overrightarrow{x}}_i\right)$ is the hypersphere of radius $ϵ$ centered in ${\overrightarrow{x}}_i$; $Y_{ij}=\frac{1}{2}(1+y_i{y}_j)$ is the indicator y-correlation matrix of training labels; $K_{ij}^{ϵ}={\kappa }_{ϵ}({\overrightarrow{x}}_i,{\overrightarrow{x}}_j)=\underset{\gamma \to \infty }{lim}\frac{1}{2}[1+tanh(\gamma (ϵ-||{\overrightarrow{x}}_i-{\overrightarrow{x}}_j\left|\right|\left)\right)]=H(ϵ-||{\overrightarrow{x}}_i-{\overrightarrow{x}}_j\left|\right|)$ is the indicator kernel matrix, where $H\left(x\right)$ is the Heaviside step function. The indicator kernel matrix satisfies

$$K_{ij}^{ϵ}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}{\overrightarrow{x}}_j\in B_{ϵ}\left({\overrightarrow{x}}_i\right)\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right..$$

(5)

The indicator y-correlation matrix satisfies

$$Y_{ij}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}{y}_i=y_j\hfill \\ 0,\hfill & \mathrm{if}{y}_i=-y_j\hfill \end{array}\right..$$

(6)

From the definitions, we have

$$\prod _{p=1}^l{Y}_{jp}^{K_{jp}}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}\left\{y_k\right|{\overrightarrow{x}}_k\in B_{ϵ}\left({\overrightarrow{x}}_j\right)\}\mathrm{is}\mathrm{constant}\hfill \\ 0,\hfill & \mathrm{if}\left\{y_k\right|{\overrightarrow{x}}_k\in B_{ϵ}\left({\overrightarrow{x}}_j\right)\}\mathrm{is}\mathrm{mixed}\hfill \end{array}\right..$$

(7)

Then, the counting number returned by the DBSCAN-DJ training procedure is $c_i={\sum }_{j=1}^l{K}_{ij}(1-{\prod }_{p=1}^l{Y}_{jp}^{K_{jp}})$. Since all $c_i>0$, the ranking algorithm selects support vectors that satisfy the solution for the constrained integer linear programming problem:

$$\begin{array}{c}\hfill \underset{{\alpha }_i}{min}\sum _i^l{c}_i{\alpha }_i\end{array}$$

(8)

$$\begin{array}{c}\hfill {\alpha }_i\in \{0,1\}\end{array}$$

(9)

$$\begin{array}{c}\hfill \sum _i^l{\alpha }_i=\lfloor \frac{1}{\alpha }\rfloor ,\end{array}$$

(10)

where ${\alpha }_i=1$ if and only if ${\overrightarrow{x}}_i$ is selected as a support vector. Notice that, if the number of training data is l, the sorting only takes $O(llogl)$ time, while general integer linear programming is NP-complete.

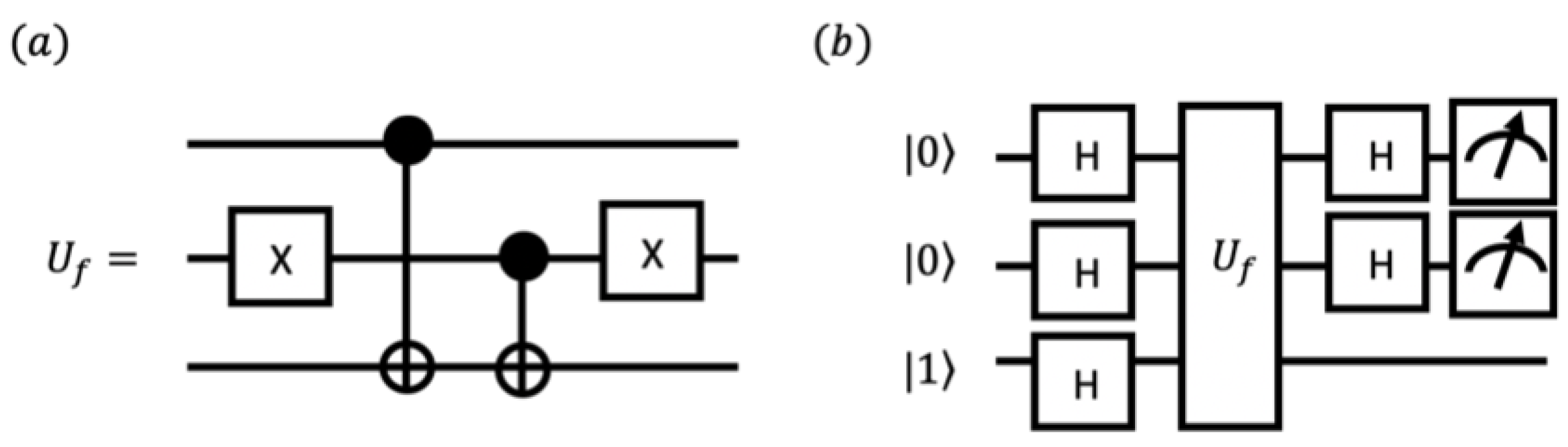
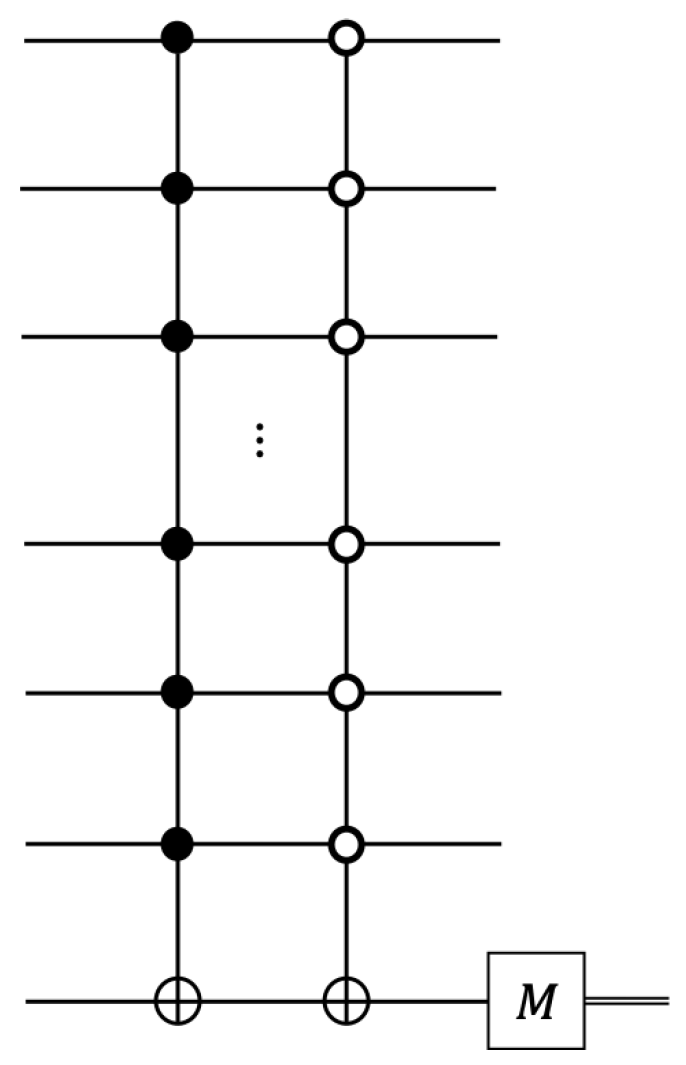
2.4. Quantum-Enhanced Algorithm with DJ

Given a Boolean function $f:{\{0,1\}}^n\to \{0,1\}$, that is guaranteed to be constant or balanced, and its reversible circuit $U_f:|x\rangle |y\rangle \to |x\rangle |y\oplus f\left(x\right)\rangle$, the DJ algorithm determines whether f is constant or balanced with one call to $U_f$. A balanced function means $f\left(x\right)=1$ for half of the possible input string x. The DJ algorithm is conducted using operator $(H^{\otimes n}\otimes 1)U_f{H}^{\otimes (n+1)}$ on the initial state ${|0\rangle }^{\otimes n}|1\rangle$. The probability to measure an all-zero string $x=00\dots 0$ is $P_0={\left|\frac{1}{2^n}{\sum }_x{(-1)}^{f\left(x\right)}\right|}^2$. Hence, if f is constant, the probability to obtain a measurement result $00\dots 0$ is $P_0=1$. If f is balanced, then $P_0=0$. If f is not constant nor balanced, then $1>P_0>0$.

Given the data $\left\{({\overrightarrow{x}}_i,y_i)\right\}$ in a sphere, we construct the reversible circuit for the function $f:{\overrightarrow{x}}_i\to (1+y_i)/2$. This serves as the oracle function in the DJ algorithm. A four-data point example is shown in

Table 1. An example of four training data’s look-up table for function $f\left(x\right)$.

${\mathit{x}}_{\mathit{i}}$	${\mathit{y}}_{\mathit{i}}$	$(1+{\mathit{y}}_{\mathit{i}})/2$
00	−1	0
01	1	1
10	1	1
11	−1	0

and Figure 3. For n data points, the reading of the data and the construction of the oracle $U_f$ take $O\left(n\right)$ time. However, once given the oracle, the DJ algorithm can determine whether the function is constant or balanced with a single call. In the case where the data are not constant, there is some probability to obtain measurement results other than $0\dots 0$. We could repeat the algorithm several times (the number of repetitions is another hyper-parameter that determines the precision) to obtain a reasonable estimation of the probability of how likely that is a constant function. Then, this probability provides an estimation for $c_i$. For an efficient implementation of the $U_f$ circuit, one could utilize the single-step n-Toffoli gate [32] in a quantum computer. While this scheme works in principle, it is difficult to implement and the overhead is large. In our simulation, we take an simplified oracle consisting of one n-Toffoli gate and one n-Toffoli gate with negative control, as shown in Figure 4. Each qubit is encoded in a classical indicator state $(1+y_i)/2\in \{0,1\}$. Then, a single query to the oracle gives the measurement result ${\prod }_i(1+y_i)/2$, which indicates whether the data are constant or not. This approach is simpler to implement, but requires more encoding qubits. In the original DJ, it takes $O(logn)$ for n data points, while, in this simplified approach, it takes $O\left(n\right)$ qubits. However, it has a potential acceleration similar to that of DJ, where a single call to the oracle gives the desired result.

2.5. Annealing Algorithm for Data Prediction

The classical SVM algorithm constructs $\overrightarrow{w}$ and b from the training data and then predicts each test data by computing $\overrightarrow{w}·\overrightarrow{x}+b$. We propose an algorithm such that it is possible to predict multiple test data points with a single run of the prediction algorithm. The prediction is made by finding the ground state of the Ising model:

$$H=-\sum _{i<j}{J}_{i,j}{s}_i{s}_j-\sum _i{h}_i{s}_i.$$

(11)

The number of spins is $N=n_{sv}+n_t$, where $n_{sv}$ is the number of support vectors and $n_t$ is the number of test data. The coupling constants are functions of the data positions $J_{ij}({\overrightarrow{x}}_i,{\overrightarrow{x}}_j)$ defined in Equation (4). We use the notation

$$J_{ij}=\left\{\begin{array}{cc}{\left(J_{sv}\right)}_{ij},\hfill & \mathrm{if}{\overrightarrow{x}}_i,{\overrightarrow{x}}_j\in \left\{\mathrm{support}\mathrm{vectors}\right\}\hfill \\ {\left(J_t\right)}_{ij},\hfill & \mathrm{if}{\overrightarrow{x}}_i,{\overrightarrow{x}}_j\in \left\{\mathrm{testing}\mathrm{data}\right\}\hfill \\ {\left(J_{int}\right)}_{ij},\hfill & \mathrm{if}{\overrightarrow{x}}_i\in \left\{\mathrm{testing}\mathrm{data}\right\},{\overrightarrow{x}}_j\in \left\{\mathrm{support}\mathrm{vectors}\right\}\hfill \end{array}\right..$$

(12)

$J_{sv}$ is an $n_{sv}\times n_{sv}$ matrix, $J_t$ is an $n_t\times n_t$ matrix and $J_{int}$ is an $n_{sv}\times n_t$ matrix. Notice that the $J_{sv}$ matrix is given by the training algorithm and does not need to be computed again. The magnetic field is defined as

$$h_i=\left\{\begin{array}{cc}{y}_i,\hfill & \mathrm{if}{\overrightarrow{x}}_i\in \left\{\mathrm{support}\mathrm{vectors}\right\}\hfill \\ 0,\hfill & \mathrm{if}{\overrightarrow{x}}_i\in \left\{\mathrm{testing}\mathrm{data}\right\}\hfill \end{array}\right..$$

(13)

The prediction result is given by the ground state of the Ising model:

$$y_i=s_i,\mathrm{for}{\overrightarrow{x}}_i\in \left\{\mathrm{testing}\mathrm{data}\right\}.$$

(14)

The configurations $s_i$ of the support vectors are dummy variables and not used for prediction. Intuitively, the model favors parallel spins, since $J_{ij}>0$. Hence, we expect the prediction to have the same spin direction as nearby training data. In principle, the Ising ground state can be calculated by any Ising solver. However, the problem of finding the general Ising model ground state is equivalent to quadratic unconstrained binary optimization (QUBO), which is NP-hard. In this work, we use adiabatic quantum computing implemented on a quantum circuit simulator to find the ground state [33]. The prediction labels are determined by

$$s_i=\left\{\begin{array}{cc}-1,\hfill & \mathrm{if}{p}_{-1}\left({\overrightarrow{x}}_i\right)>p_{+1}\left({\overrightarrow{x}}_i\right)\hfill \\ +1,\hfill & \mathrm{if}{p}_{-1}\left({\overrightarrow{x}}_i\right)<p_{+1}\left({\overrightarrow{x}}_i\right)\hfill \end{array}\right.,$$

(15)

where $p_{\pm }$ is the probability that the point label is predicted to be $\pm 1$.

2.6. The VC Dimension

We further show that the Ising classifier has a finite VC dimension upper bound in two simplified toy models in Figure 5. These simplifications can be regarded as regularization methods. The intuition is that, for $J_{ij}>0$, anti-parallel spin configurations have higher energy and it is difficult that they are a ground state. This difficulty sets a limitation on how many points can be shattered and leads to an upper bound for the VC dimension. The detail derivation is in Appendix A. We use the following definitions: $n_{sv}$ is the number of support vectors; $n_t$ is the number of prediction data points; $N=n_{sv}+n_t$ is the total number of spins in the Ising model; d is the feature space dimension. We assume that $n_{sv}\le n_t$. For the first toy model, we consider a simplification by introducing equal distance constraints to the support vectors and test data. This means $J_{ij}=\frac{1}{\left|\right|{\overrightarrow{x}}_i-{\overrightarrow{x}}_j\left|\right|}=J$ for all $(i,j)$. The Ising prediction model, in this case, is the fully connected infinite-dimensional mean field Ising model:

$$H=-J\sum _{i<j}{s}_i{s}_j.$$

(16)

Notice that this is a strong constraint which requires $N\le d+1$, but there is still one continuous parameter J, so the hypothesis set is still infinite. This model is exactly solvable. The eigenenergy is $E_m=J(-\frac{1}{2}N(N-1)+2m(N-m))$ for eigenstates with m spin up and $N-m$ spin down. If there are two test data, the anti-parallel state $\uparrow \downarrow$ is always an excited state; hence, it is impossible it is part of a ground state. We obtain the result $d_{VC}=1$ in this case.

This upper bound can be relaxed by considering a model with less constraints. Consider a second toy model where all the support vectors form a fully connected equal-distance lattice defined by parameter $J_{sv}$. All the test data form another fully connected equal-distance lattice defined by another parameter, $J_t$. The distance between support vectors and prediction data is parametrized by a different variable $J_{int}$. Hence, there are three continuous variables in the model. The interaction between support vectors and prediction data points is restricted to one-to-one coupling. Let

$$\left\{\begin{array}{cc}\left\{\mathrm{support}\mathrm{vectors}\right\}\hfill & =\{{\overrightarrow{x}}_1,{\overrightarrow{x}}_2,\dots ,{\overrightarrow{x}}_{n_{sv}}\}\hfill \\ \left\{\mathrm{test}\mathrm{data}\right\}\hfill & =\{{\overrightarrow{x}}_{n_{sv}+1},{\overrightarrow{x}}_{n_{sv}+2},\dots ,{\overrightarrow{x}}_{n_{sv}+n_t}\}\hfill \end{array}\right..$$

(17)

Then, the coupling for this model is

$$J_{ij}=\left\{\begin{array}{cc}{J}_{sv},\hfill & \mathrm{if}1\le i<j\le n_{sv}\hfill \\ J_t,\hfill & \mathrm{if}(n_{sv}+1)\le i<j\le (n_{sv}+n_p)\hfill \\ J_{int},\hfill & \mathrm{if}1\le i\le n_{sv}\mathrm{and}j=i+n_{sv}\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right..$$

(18)

For this model, we obtain the result $d_{vc}\le \sqrt{\frac{2J_{int}}{J_t}{n}_{sv}}$. The intuition is that, if there are more support vectors (large $n_{sv}$), the model has more degrees of freedom. If the support vectors are closer to the test data (large $J_{int}$), the model has stronger influences on the test data. Hence, the Ising model can shatter more test data for larger $J_{int}$ and $n_{sv}$. On the other hand, if the distance among test data is small (large $J_t$), then the strong interactions among test data make it difficult to be shattered by the model.

3. Simulation Results

We demonstrate the classification task for two types of teacher data (linear classification boundary and non-linear classification boundary) using the proposed method. The learning of the optimal $(\alpha ,\beta ,ϵ)$ parameters was performed by minimizing the cost function. Since the $(\alpha ,\beta ,ϵ)$ parameters are associated with discrete ranking, we chose gradient-free optimization instead of gradient-based optimization. We implemented the Nelder–Mead method and particle swarm optimization (PSO) algorithms. We observed that PSO generally gives better results; hence, we focused on the results obtained by PSO. The hyperparameter N is the number of particles for PSO. The learned support vectors, classification boundary and learning curves for $N=10,50,100$ are depicted in Figure 6. The learned parameters are shown in

Table 2. Particle swarm optimization results. N is the number of particles and $\beta$ is the hyperparameter being optimized. The optimization is conducted by minimizing the cross-entropy loss function Equation (3). The optimized results are visualized in Figure 6.

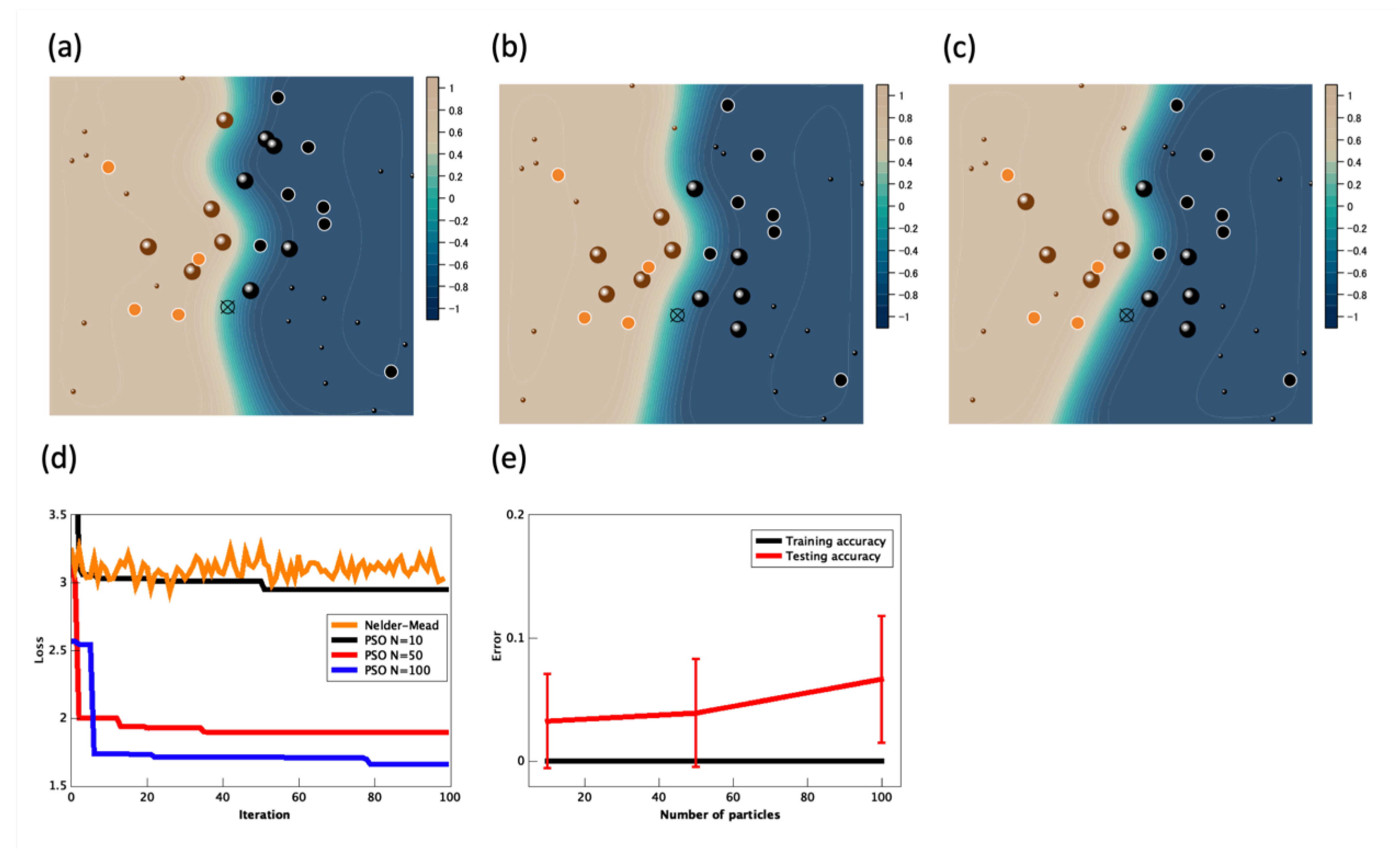
N	$\mathit{\beta }$	Test Accuracy
10	1.128	0.9675
50	0.6356	0.9610
100	0.6157	0.9335

. In all the cases, the total number of support vectors was fixed at $n_{sv}=10$, where five of them belonged to $+1$ and the other five belonged to $-1$. The $\alpha$ and the $ϵ$ parameters were fixed to $\alpha =3$ and $ϵ=0.4$. The optimization was performed by minimizing the loss function Equation (3) for the optimal values of $\beta$. We observed that the classification could be performed in all experiments. We also observed that, for larger values of N, the optimized loss function had a lower value, but the test accuracy was also lower. This suggests possible overfitting for large values of N in PSO optimization.

We now compare the proposed method with scikit-learn SVM. The verification results are shown in Figure 7. We used 28 teacher data (small dots) for each verification. The detail numbers of data used are listed in

Table 3. The number of training and testing data used in the experiment in Figure 7.

Data	Total	+1 Label	$-1$ Label
Linear Training	28	13	15
Linear Testing	12	5	7
Non-linear Training	28	9	19
Non-linear Testing	12	7	5

. The large sphere symbols are the support vectors. In the classification using the proposed algorithm, we set the radius of the scan circle to $ϵ=0.5$ (linear data) and $ϵ=0.6$ (non-linear data). The power of the reciprocal of the distance among data was $\beta =1$ and the criterion for determining the support vectors from the ranking was $\alpha =3$. For the traditional SVM, we used scikit-learn.svm.SVC with default values. From Figure 7, we found that both the linear classification and the non-linear classification performed by the proposed method could give a classification boundary similar to that of scikit-learn. However, if we changed only the positions of teacher data without changing the number of teacher data, there were cases where it could not be classified well. A possible cause is that the number of teacher data was too small. As a result, the number of support vectors was insufficient and the classification accuracy might have been reduced. Therefore, we expected a better classification result by using a larger number of training data. However, we noticed that quantum adiabatic calculations required a number of qubits of $n_{sv}+n_t$, where $n_{sv}$ is the number of support vectors and $n_t$ is the number of test data. Our experiment was limited by this restriction.

4. Computational Complexity

We investigate the efficiency of the proposed algorithm.

Table 4. Worst-case time complexity for the proposed algorithm comparing to the standard kernel SVM [22,23,24]. d is the feature space dimension, l is the number of training data, $n_{sv}$ is the number of support vectors, $n_t$ is the number of test data and $n_b$ is the number of batches for the test data. $T_a$ is the annealing time to find the Ising ground state, which depends on the choice of Ising solver algorithm.

	Training	Prediction
Kernel SVM	$O\left(l^{3}d\right)$	$O\left(n_{sv}{n}_{t}d\right)$
This work	$O\left(l^{2}d\right)$	$O((n_{sv}+\frac{n_t}{n_b})n_{t}d)+T_a$

shows the time complexity of the kernel SVM and the proposed algorithm. The training algorithm is DBSCAN; hence, the worst-case complexity is essentially the same as DBSCAN which takes $O\left(l^2\right)$ time for computing distances among l training data points. This is better than the standard kernel SVM, which takes the worst-case time of $O\left(l^3\right)$ for kernel matrix inversion (empirical scaling is $O\left(l^{2+\delta }\right)$ for some $1>\delta >0$) [22,23]. The training algorithm has also the feature of Deutsch–Jozsa; hence, it can be quantum-enhanced by using an n-Toffoli gate to speed it up. The speed-up does not change the worst-case scaling of the training algorithm’s complexity. The cost of the prediction part is $O\left((n_{sv}+n_t)n_{t}d\right)$ for computing the $J_t$ and $J_{int}$ matrices. This scaling seems to be worse than that of the kernel SVM, but, in practice, this is not an issue. We could divide the test data into $n_b$ batches and run the prediction algorithm one time for each batch. The scaling becomes $O((n_{sv}+\frac{n_t}{n_b})n_{t}d)$ in this case. For example, when $n_b=n_t$ (i.e., we predict one datum at the time, as in the kernel SVM), we recover the same scaling as the kernel SVM. The cost of the prediction part depends on finding the ground state of the Ising model, which is equivalent to solving a QUBO problem. This, in general, could take an exponentially large amount of time, depending on the solver algorithm. However, to make a reasonable prediction, it is not necessary to find the optimal solution. The Ising prediction part can be solved by classical simulated annealing, or other QUBO solver and can be potentially accelerated by using adiabatic quantum computation or quantum annealing [34]. One might question about the possibility to combine the DBSCAN–DJ training algorithm with the kernel SVM prediction. However, since our training algorithm does not produce $\overrightarrow{w}$ and $\overrightarrow{b}$ vectors, it cannot be used for kernel SVM prediction.

5. Conclusions

In this work, we propose a quantum-inspired algorithm for classification. The algorithm has an advantage over the traditional kernel SVM in the training stage. The algorithm can be performed on a pure classical computer and can be enhanced in a hybrid quantum–classical computing environment. We experimentally verify the algorithm and provide theoretical background for the algorithm. The applicability to more general classification problems and possible improvements will be studied in future works. For example, multi-class classifications could be treated by one-versus-rest or one-versus-one approaches [35]. The optimal value for $ϵ$ could be determined by other methods [36].