A Study on Estimating Land Value Distribution for the Talingchan District, Bangkok Using Points-of-Interest Data and Machine Learning Classification
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Dataset
2.2.1. Points-of-Interest Data
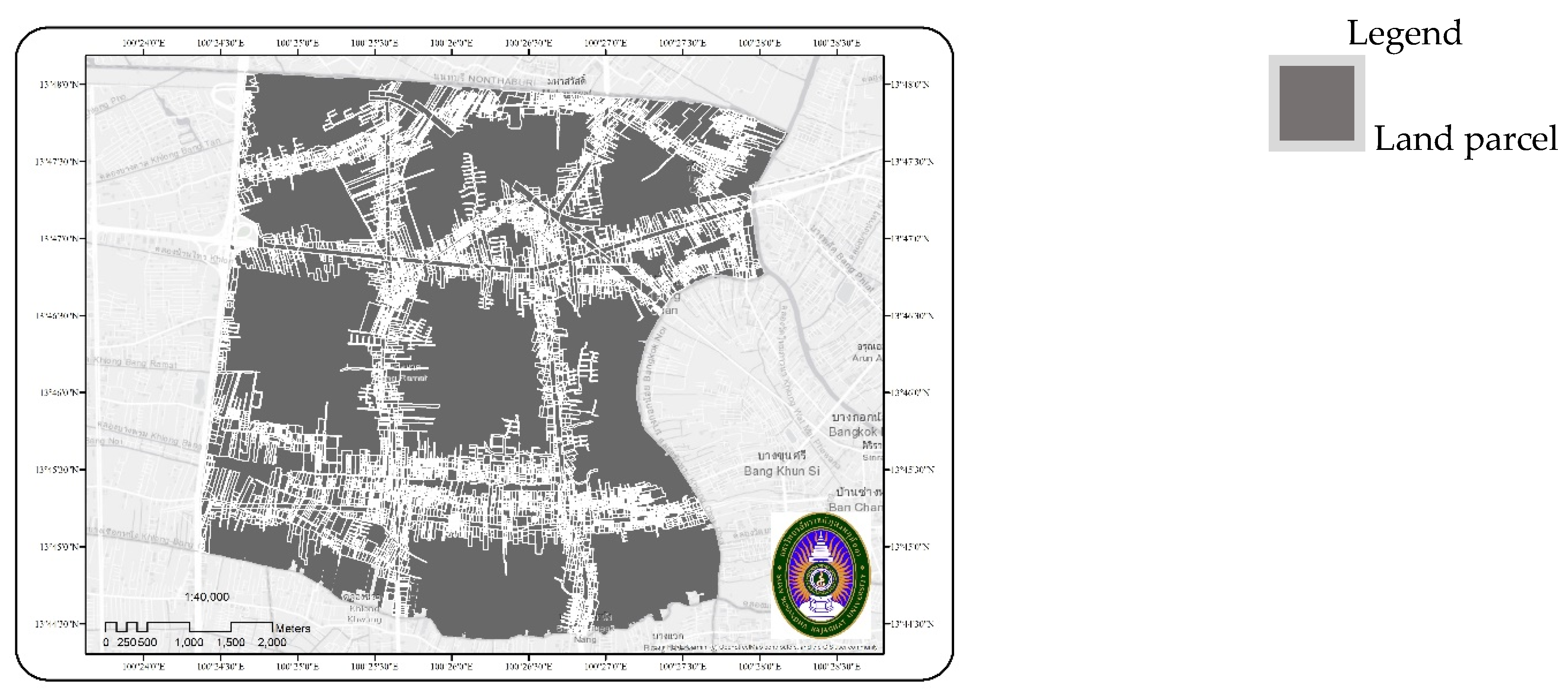
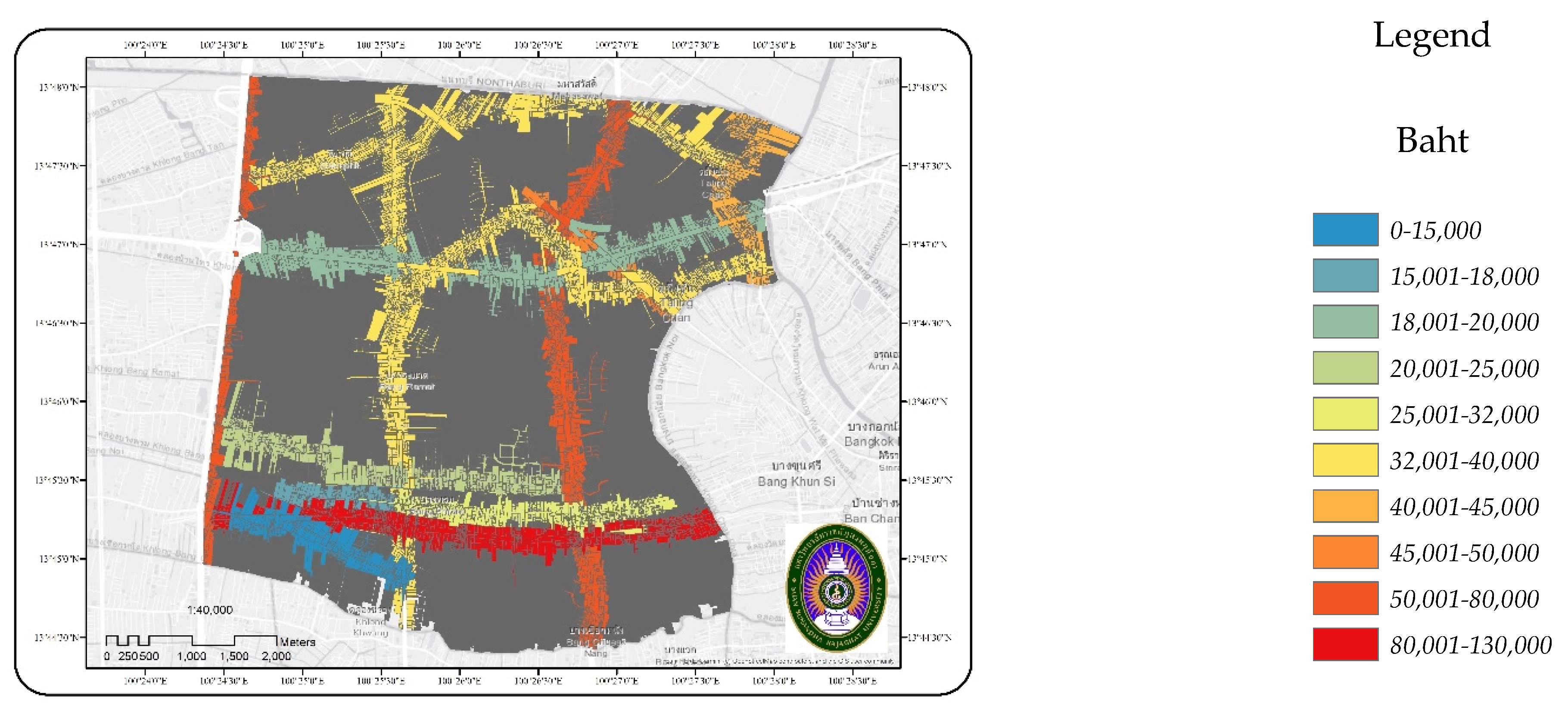
2.2.2. Land Parcel and Land Value Data
2.3. Methods
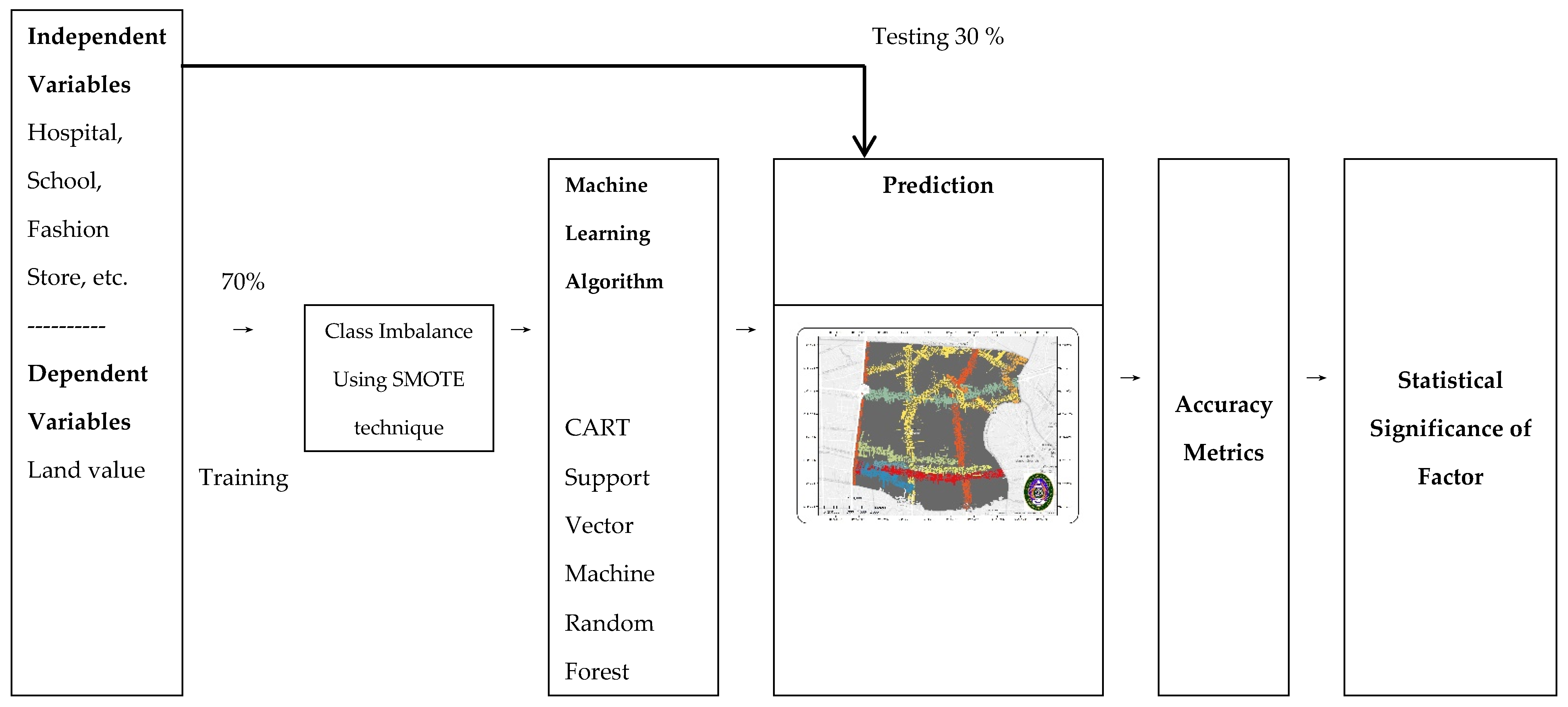
2.3.1. Modeling Framework
2.3.2. Imbalanced Data
2.3.3. Machine Learning Models
2.3.4. Model Evaluation
2.3.5. GINI Index
3. Results
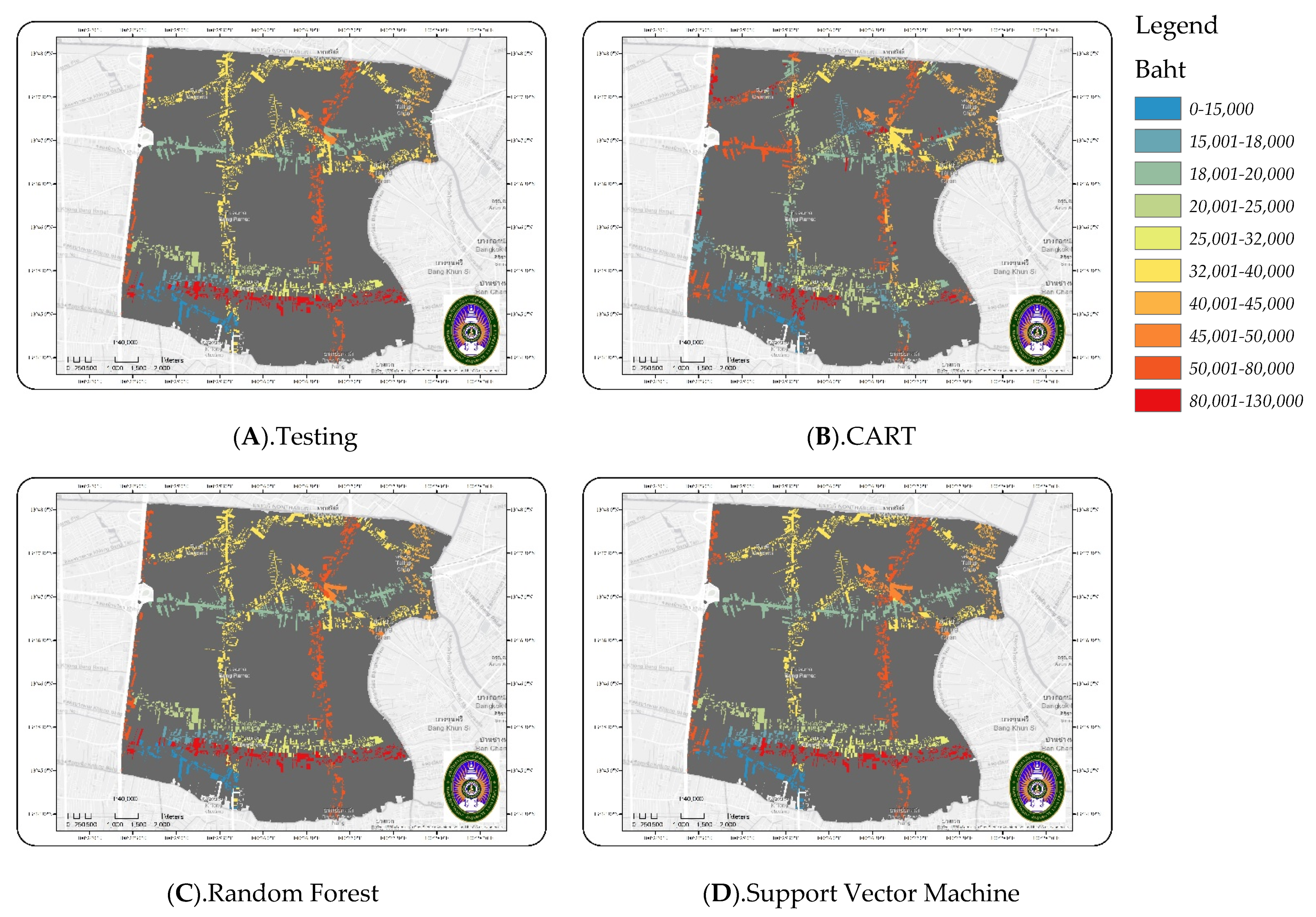
3.1. Validating the Land Value Predictive Value Obtained by Applying the Machine Learning Technique Model
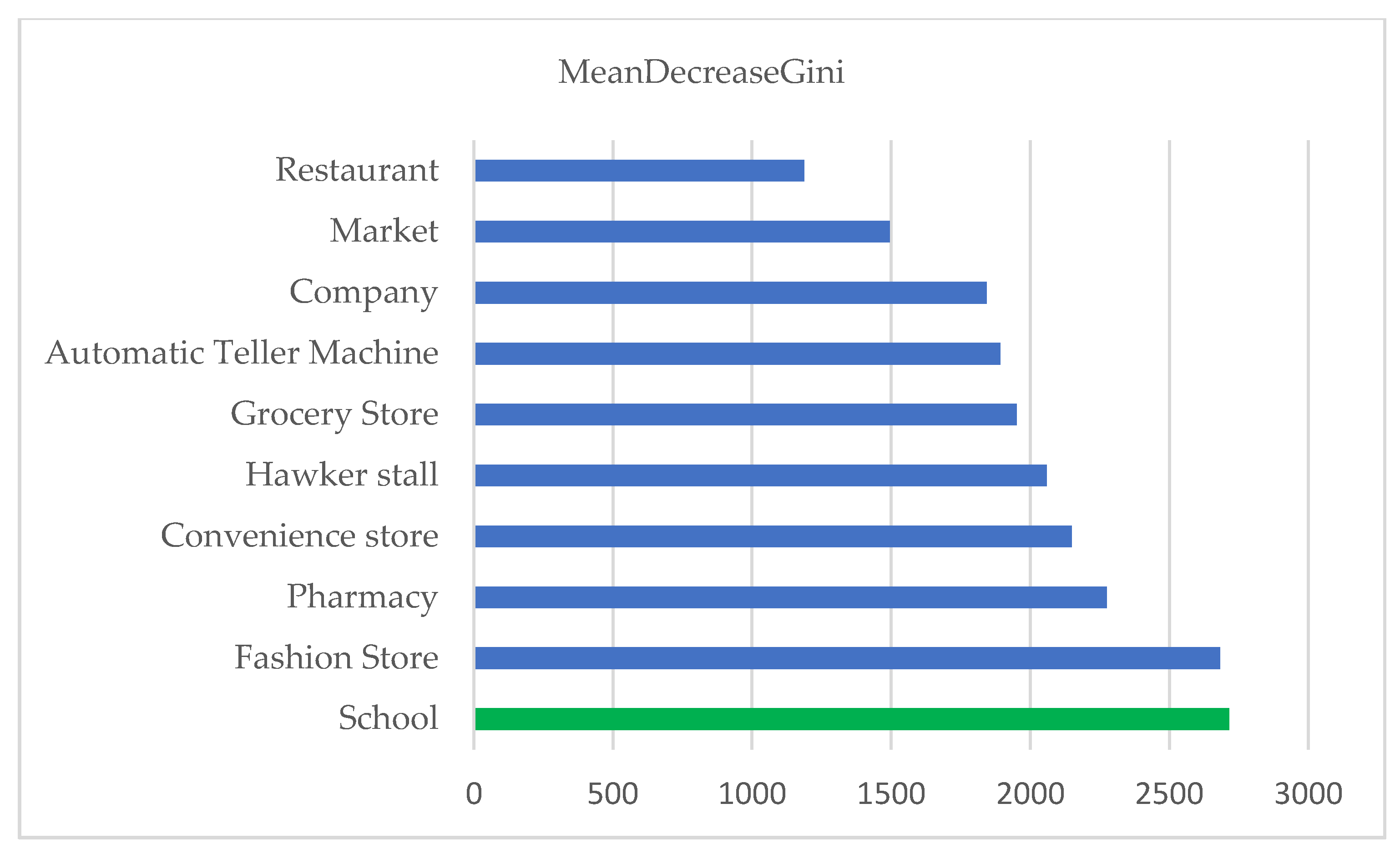
3.2. The Factors That Influence the Land Value Parcel
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pruksanubal, B. Rural-Urban Linkages Pertaining to Rural Trade in Bangkok Mega-Urban Region: A Case Study of Phathumthani Province; Chulalongkorn University: Bangkok, Thailand, 2007. [Google Scholar] [CrossRef]
- Ginsburg, N.S.; Koppel, B.; McGee, T.G.; East-West Environment and Policy Institute. The Extended Metropolis: Settlement Transition Is Asia; University of Hawaii Press: Honolulu, HI, USA, 1991. [Google Scholar]
- Yoonan, M. Forcasting Model for Bangkok CBD Vacant Land Prices Using MLR Methods; Thammasat University: Bangkok, Thailand, 2018. [Google Scholar] [CrossRef]
- Hu, S.; Yang, S.; Li, W.; Zhang, C.; Xu, F. Spatially non-stationary relationships between urban residential land price and impact factors in Wuhan city, China. Appl. Geogr. 2016, 68, 48–56. [Google Scholar] [CrossRef] [Green Version]
- Qu, S.; Hu, S.; Li, W.; Zhang, C.; Li, Q.; Wang, H. Temporal variation in the effects of impact factors on residential land prices. Appl. Geogr. 2020, 114, 102124. [Google Scholar] [CrossRef]
- Davis, M.A.; Oliner, S.D.; Pinto, E.J.; Bokka, S. Residential land values in the Washington, DC metro area: New insights from big data. Reg. Sci. Urban Econ. 2017, 66, 224–246. [Google Scholar] [CrossRef]
- Mendonça, R.; Roebeling, P.; Martins, F.; Fidélis, T.; Teotónio, C.; Alves, H.; Rocha, J. Assessing economic instruments to steer urban residential sprawl, using a hedonic pricing simulation modelling approach. Land Use Policy 2020, 92, 104458. [Google Scholar] [CrossRef]
- Yang, S.; Hu, S.; Wang, S.; Zou, L. Effects of rapid urban land expansion on the spatial direction of residential land prices: Evidence from Wuhan, China. Habitat Int. 2020, 101, 102186. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, X.; Li, X.; Liu, Y.; Xu, X. Mapping the fine-scale spatial pattern of housing rent in the metropolitan area by using online rental listings and ensemble learning. Appl. Geogr. 2016, 75, 200–212. [Google Scholar] [CrossRef]
- Hu, L.; He, S.; Han, Z.; Xiao, H.; Su, S.; Weng, M.; Cai, Z. Monitoring housing rental prices based on social media:An integrated approach of machine-learning algorithms and hedonic modeling to inform equitable housing policies. Land Use Policy 2019, 82, 657–673. [Google Scholar] [CrossRef]
- Glumac, B.; Herrera-Gomez, M.; Licheron, J. A hedonic urban land price index. Land Use Policy 2019, 81, 802–812. [Google Scholar] [CrossRef]
- Wen, H.; Goodman, A.C. Relationship between urban land price and housing price: Evidence from 21 provincial capitals in China. Habitat Int. 2013, 40, 9–17. [Google Scholar] [CrossRef]
- Huang, H.; Yin, L. Creating sustainable urban built environments: An application of hedonic house price models in Wuhan, China. Neth. J. Hous. Environ. Res. 2014, 30, 219–235. [Google Scholar] [CrossRef]
- Burge, G. The capitalization effects of school, residential, and commercial impact fees on undeveloped land values. Reg. Sci. Urban Econ. 2014, 44, 1–13. [Google Scholar] [CrossRef]
- Wen, H.; Xiao, Y.; Hui, E.C.; Zhang, L. Education quality, accessibility, and housing price: Does spatial heterogeneity exist in education capitalization? Habitat Int. 2018, 78, 68–82. [Google Scholar] [CrossRef]
- Cervero, R.; Kang, C.D. Bus rapid transit impacts on land uses and land values in Seoul, Korea. Transp. Policy 2011, 18, 102–116. [Google Scholar] [CrossRef] [Green Version]
- Du, X.; Huang, Z. Spatial and temporal effects of urban wetlands on housing prices: Evidence from Hangzhou, China. Land Use Policy 2018, 73, 290–298. [Google Scholar] [CrossRef]
- Glaesener, M.-L.; Caruso, G. Neighborhood green and services diversity effects on land prices: Evidence from a multilevel hedonic analysis in Luxembourg. Landsc. Urban Plan. 2015, 143, 100–111. [Google Scholar] [CrossRef]
- Kim, H.-S.; Lee, G.-E.; Lee, J.-S.; Choi, Y. Understanding the local impact of urban park plans and park typology on housing price: A case study of the Busan metropolitan region, Korea. Landsc. Urban Plan. 2019, 184, 1–11. [Google Scholar] [CrossRef]
- Liu, Q.; Xu, Q.; Zheng, V.W.; Xue, H.; Cao, Z.; Yang, Q. Multi-task learning for cross-platform siRNA efficacy prediction: An in-silico study. BMC Bioinform. 2010, 11, 181. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schläpfer, F.; Waltert, F.; Segura, L.; Kienast, F. Valuation of landscape amenities: A hedonic pricing analysis of housing rents in urban, suburban and periurban Switzerland. Landsc. Urban Plan. 2015, 141, 24–40. [Google Scholar] [CrossRef]
- Higgins, C.D. A 4D spatio-temporal approach to modelling land value uplift from rapid transit in high density and topographically-rich cities. Landsc. Urban Plan. 2019, 185, 68–82. [Google Scholar] [CrossRef]
- Hu, S.; Cheng, Q.; Wang, L.; Xu, D. Modeling land price distribution using multifractal IDW interpolation and fractal filtering method. Landsc. Urban Plan. 2013, 110, 25–35. [Google Scholar] [CrossRef]
- Chan, T.-H.; Jia, K.; Gao, S.; Lu, J.; Zeng, Z.; Ma, Y. PCANet: A Simple Deep Learning Baseline for Image Classification? IEEE Trans. Image Process. 2015, 24, 5017–5032. [Google Scholar] [CrossRef] [Green Version]
- Worachairungreung, M.; Ninsawat, S.; Witayangkurn, A.; Dailey, M. Identification of Road Traffic Injury Risk Prone Area Using Environmental Factors by Machine Learning Classification in Nonthaburi, Thailand. Sustainability 2021, 13, 3907. [Google Scholar] [CrossRef]
- Chen, W.; Xie, X.; Wang, J.; Pradhan, B.; Hong, H.; Bui, D.T.; Duan, Z.; Ma, J. A comparative study of logistic model tree, random forest, and classification and regression tree models for spatial prediction of landslide susceptibility. Catena 2017, 151, 147–160. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Yu, S.; Échevin, D.; Fan, M. Is poverty predictable with machine learning? A study of DHS data from Kyrgyzstan. Socio-Econ. Plan. Sci. 2021, 101195. [Google Scholar] [CrossRef]
- Park, B.; Bae, J.K. Using machine learning algorithms for housing price prediction: The case of Fairfax County, Virginia housing data. Expert Syst. Appl. 2015, 42, 2928–2934. [Google Scholar] [CrossRef]
- Ma, J.; Cheng, J.C.; Jiang, F.; Chen, W.; Zhang, J. Analyzing driving factors of land values in urban scale based on big data and non-linear machine learning techniques. Land Use Policy 2020, 94, 104537. [Google Scholar] [CrossRef]
- Ho, W.K.; Tang, B.-S.; Wong, S.W. Predicting property prices with machine learning algorithms. J. Prop. Res. 2021, 38, 48–70. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Routledge: Oxfordshire, UK, 1984. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Pal, M.; Mather, P.M. An assessment of the effectiveness of decision tree methods for land cover classification. Remote Sens. Environ. 2003, 86, 554–565. [Google Scholar] [CrossRef]
- Vapnik, V.; Golowich, S.E.; Smola, A. Support vector method for function approximation, regression estimation and signal processing. In Advances in Neural Information Processing Systems 10: Proceedings of the 1997 Conference, Denver, CO, USA, 1–6 December 1997; MIT Press: Cambridge, MA, USA, 1998; pp. 281–287. [Google Scholar]
- Aizerman, M.A. Theoretical Foundations of the Potential Function Method in Pattern Recognition Learning. Autom. Remote Control. 1964, 25, 821–837. [Google Scholar]
- Manliguez, C. Generalized Confusion Matrix for Multiple Classes. 2016. Available online: https://www.researchgate.net/publication/310799885_Generalized_Confusion_Matrix_for_Multiple_Classes (accessed on 11 October 2021). [CrossRef]
- Nichols, T.R.; Wisner, P.M.; Cripe, G.; Gulabchand, L. Putting the Kappa Statistic to Use. Qual. Assur. J. 2010, 13, 57–61. [Google Scholar] [CrossRef]
- Lewis, C.D. Industrial and Business Forecasting Methods: A Practical Guide to Exponential Smoothing and Curve Fitting; Butterworth-Heinemann: Oxford, UK, 1982. [Google Scholar]
- Bae, H.; Chung, I.H. Impact of school quality on house prices and estimation of parental demand for good schools in Korea. KEDI J. Educ. Policy 2013, 10, 43–61. [Google Scholar]
- Wu, R.; Wang, J.; Zhang, D.; Wang, S. Identifying different types of urban land use dynamics using Point-of-interest (POI) and Random Forest algorithm: The case of Huizhou, China. Cities 2021, 114, 103202. [Google Scholar] [CrossRef]
- Wu, M.; Pei, T.; Wang, W.; Guo, S.; Song, C.; Chen, J.; Zhou, C. Roles of locational factors in the rise and fall of restaurants: A case study of Beijing with POI data. Cities 2021, 113, 103185. [Google Scholar] [CrossRef]
- Pai, P.-F.; Wang, W.-C. Using Machine Learning Models and Actual Transaction Data for Predicting Real Estate Prices. Appl. Sci. 2020, 10, 5832. [Google Scholar] [CrossRef]
- Del Giudice, V.; De Paola, P.; Forte, F. Using Genetic Algorithms for Real Estate Appraisals. Buildings 2017, 7, 31. [Google Scholar] [CrossRef] [Green Version]
- Plakandaras, V.; Gupta, R.; Gogas, P.; Papadimitriou, T. Forecasting the U.S. real house price index. Econ. Model. 2015, 45, 259–267. [Google Scholar] [CrossRef] [Green Version]
- Antipov, E.A.; Pokryshevskaya, E.B. Mass appraisal of residential apartments: An application of Random forest for valuation and a CART-based approach for model diagnostics. Expert Syst. Appl. 2012, 39, 1772–1778. [Google Scholar] [CrossRef] [Green Version]
- Kuşan, H.; Aytekin, O.; Özdemir, I. The use of fuzzy logic in predicting house selling price. Expert Syst. Appl. 2010, 37, 1808–1813. [Google Scholar] [CrossRef]
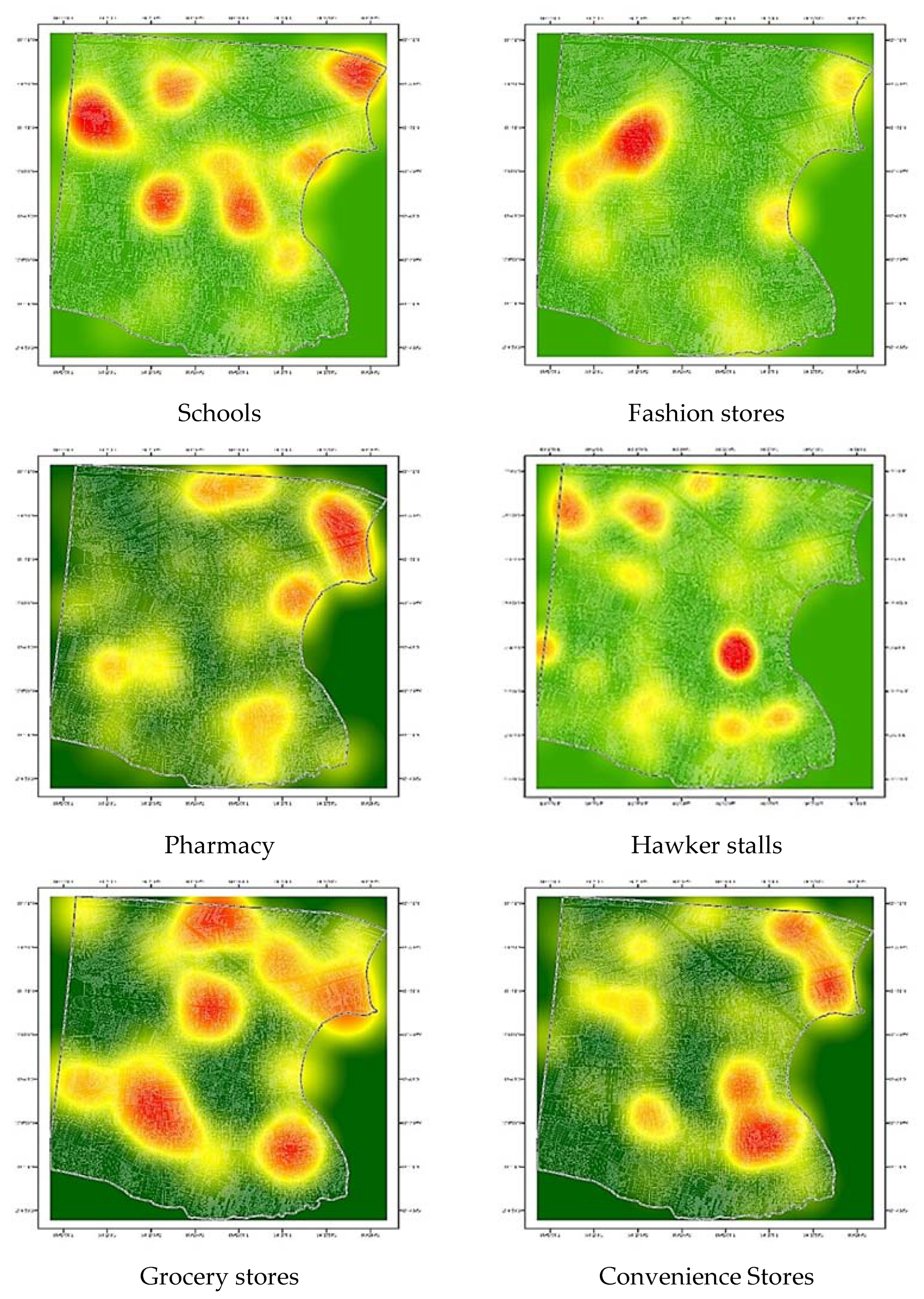
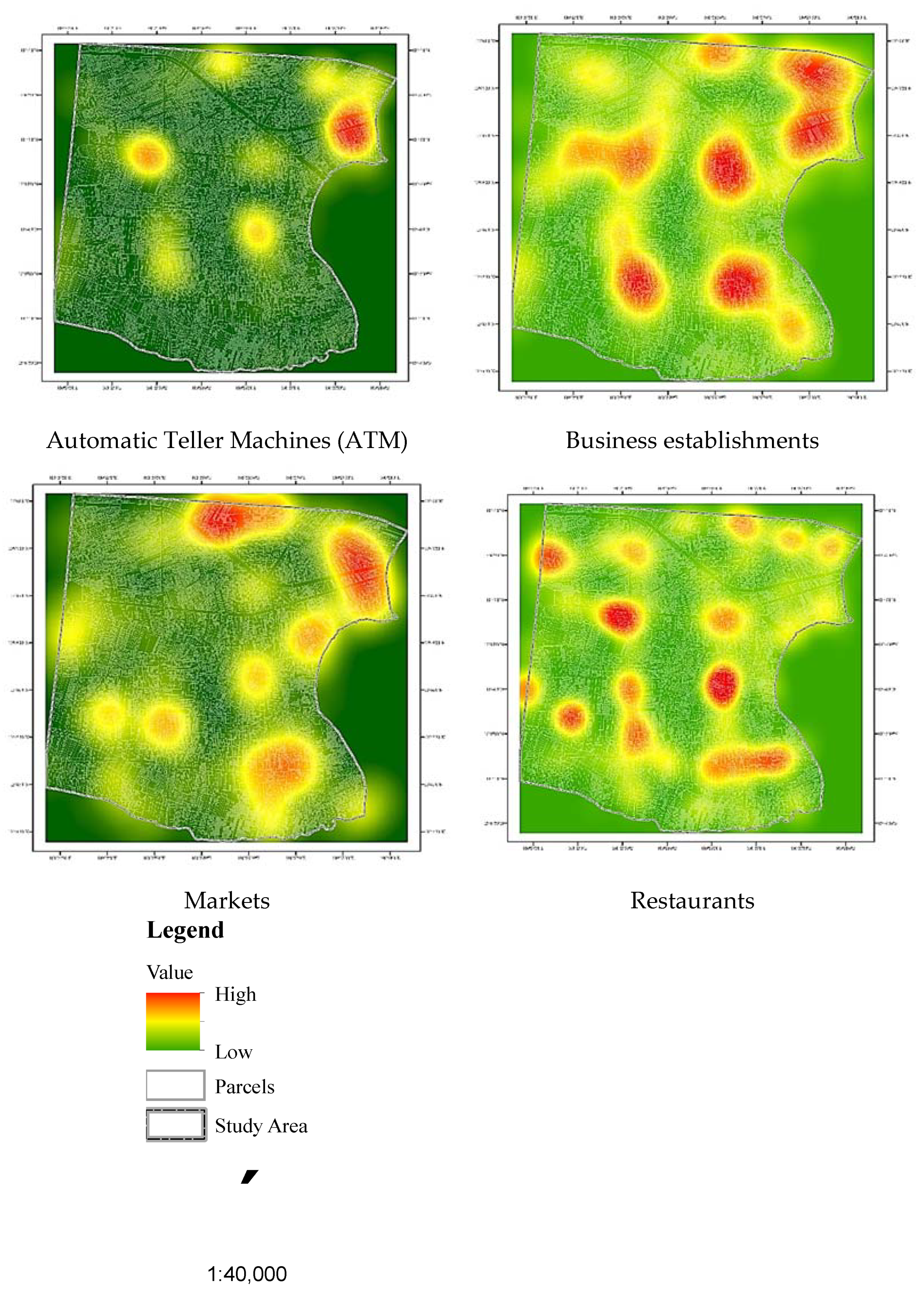

| Point of Interest | Frequency | Percentage | Data Attribute | Data Source |
|---|---|---|---|---|
| School | 175 | 7.22 | Points | Google Places API |
| Fashion Store | 41 | 1.69 | ||
| Pharmacy | 20 | 0.82 | ||
| Restaurant | 116 | 4.78 | ||
| Hawker stall | 599 | 24.70 | ||
| Convenience store | 76 | 3.13 | ||
| Automatic Teller Machine | 434 | 17.90 | ||
| Company | 99 | 4.08 | ||
| Market | 151 | 6.23 | ||
| Grocery Store | 714 | 29.44 | ||
| 2425 | 100.00 |
| Land Value Level THB/wah2 | Frequency | Percentage | Data Attribute | Data Source |
|---|---|---|---|---|
| 0–15,000 | 1148 | 2.55 | Polygons | Land parcel from the Department of Land Parcel value level from the Treasury Department |
| 15,001–18,000 | 886 | 1.97 | ||
| 18,001–20,000 | 3334 | 7.40 | ||
| 20,001–25,000 | 3596 | 7.99 | ||
| 25,001–32,000 | 3011 | 6.69 | ||
| 32,001–40,000 | 22,973 | 51.01 | ||
| 40,001–45,000 | 2091 | 4.64 | ||
| 45,001–50,000 | 993 | 2.21 | ||
| 50,001–80,000 | 3393 | 7.53 | ||
| 80,001–130,000 | 3607 | 8.01 | ||
| 45,032 | 100.00 |
| A | B | C | D | E | F | G | H | I | J | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0– 15,000 | 15,001– 18,000 | 18,001– 20,000 | 20,001– 25,000 | 25,001– 32,000 | 32,001– 40,000 | 40,001– 45,000 | 45,001– 50,000 | 50,000– 80,000 | 80,001– 130,000 | |
| Training | 833 | 529 | 2166 | 2409 | 2253 | 16,084 | 1416 | 584 | 2686 | 2566 |
| SMOTE | 3153 | 3153 | 3153 | 3152 | 3152 | 3153 | 3152 | 3153 | 3153 | 3152 |
| Kappa | Interpretation |
|---|---|
| <0% | No agreement |
| 0.01–20% | Slight |
| 21–40% | Fair |
| 41–60% | Moderate |
| 61–80% | Substantial |
| 81–100% | Perfect |
| Actual Land Value Range (THB/wah2) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Prediction Land Value Range (THB/wah2) | 0– 15,000 | 15,001– 18,000 | 18,001– 20,000 | 20,001– 25,000 | 25,001– 32,000 | 32,001– 40,000 | 40,001– 45,000 | 45,001– 50,000 | 50,000– 80,000 | 80,001– 130,000 | |
| 0– 15,000 | 322 | 2 | 0 | 0 | 0 | 42 | 0 | 0 | 12 | 17 | |
| 15,001– 18,000 | 6 | 205 | 40 | 88 | 42 | 428 | 0 | 0 | 59 | 91 | |
| 18,001– 20,000 | 0 | 0 | 563 | 0 | 44 | 550 | 5 | 2 | 178 | 12 | |
| 20,001– 25,000 | 0 | 9 | 64 | 926 | 117 | 794 | 0 | 0 | 25 | 53 | |
| 25,001– 32,000 | 0 | 8 | 0 | 7 | 733 | 15 | 0 | 0 | 5 | 123 | |
| 32,001– 40,000 | 0 | 0 | 40 | 0 | 11 | 3489 | 12 | 13 | 58 | 0 | |
| 40,001– 45,000 | 0 | 0 | 119 | 0 | 1 | 585 | 589 | 0 | 52 | 0 | |
| 45,001– 50,000 | 0 | 0 | 0 | 0 | 0 | 428 | 0 | 235 | 84 | 0 | |
| 50,000– 80,000 | 18 | 0 | 86 | 11 | 0 | 181 | 0 | 0 | 654 | 69 | |
| 80,001– 130,000 | 11 | 2 | 16 | 0 | 17 | 381 | 0 | 0 | 23 | 734 | |
| Actual Land Value Range (THB/wah2) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Prediction Land Value Range (THB/wah2) | 0– 15,000 | 15,001– 18,000 | 18,001– 20,000 | 20,001– 25,000 | 25,001– 32,000 | 32,001– 40,000 | 40,001– 45,000 | 45,001– 50,000 | 50,000– 80,000 | 80,001– 130,000 | |
| 0– 15,000 | 354 | 0 | 0 | 0 | 0 | 17 | 0 | 0 | 0 | 9 | |
| 15,001– 18,000 | 0 | 221 | 0 | 1 | 14 | 6 | 0 | 0 | 0 | 17 | |
| 18,001– 20,000 | 0 | 0 | 916 | 0 | 0 | 83 | 6 | 0 | 10 | 0 | |
| 20,001– 25,000 | 0 | 0 | 0 | 1029 | 1 | 41 | 0 | 0 | 1 | 0 | |
| 25,001– 32,000 | 0 | 2 | 0 | 0 | 929 | 12 | 0 | 0 | 1 | 15 | |
| 32,001– 40,000 | 1 | 0 | 2 | 1 | 0 | 6619 | 2 | 1 | 4 | 1 | |
| 40,001– 45,000 | 0 | 0 | 2 | 0 | 0 | 29 | 598 | 0 | 0 | 0 | |
| 45,001– 50,000 | 0 | 0 | 1 | 0 | 0 | 23 | 0 | 248 | 12 | 0 | |
| 50,000– 80,000 | 0 | 0 | 7 | 1 | 1 | 42 | 0 | 1 | 1120 | 4 | |
| 80,001– 130,000 | 2 | 3 | 0 | 0 | 20 | 21 | 0 | 0 | 2 | 1053 | |
| Actual Land Value Range (THB/wah2) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Prediction Land Value Range (THB/wah2) | 0– 15,000 | 15,001– 18,000 | 18,001– 20,000 | 20,001– 25,000 | 25,001– 32,000 | 32,001– 40,000 | 40,001– 45,000 | 45,001– 50,000 | 50,000– 80,000 | 80,001– 130,000 | |
| 0– 15,000 | 353 | 0 | 0 | 0 | 0 | 60 | 0 | 0 | 0 | 21 | |
| 15,001– 18,000 | 0 | 223 | 0 | 1 | 48 | 34 | 0 | 0 | 0 | 35 | |
| 18,001– 20,000 | 0 | 0 | 876 | 0 | 0 | 268 | 1 | 0 | 17 | 0 | |
| 20,001– 25,000 | 0 | 3 | 0 | 1029 | 0 | 92 | 0 | 0 | 7 | 0 | |
| 25,001– 32,000 | 0 | 0 | 0 | 1 | 886 | 8 | 0 | 0 | 5 | 27 | |
| 32,001– 40,000 | 0 | 0 | 2 | 0 | 0 | 5887 | 1 | 0 | 3 | 2 | |
| 40,001– 45,000 | 0 | 0 | 22 | 0 | 0 | 70 | 604 | 0 | 0 | 0 | |
| 45,001– 50,000 | 0 | 0 | 14 | 0 | 0 | 337 | 0 | 250 | 35 | 0 | |
| 50,000– 80,000 | 0 | 0 | 14 | 1 | 0 | 91 | 0 | 0 | 1078 | 9 | |
| 80,001– 130,000 | 4 | 0 | 0 | 0 | 31 | 46 | 0 | 0 | 5 | 1005 | |
| Land Value Range (THB/wah2) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 – 15,000 | 15,001 – 18,000 | 18,001 – 20,000 | 20,001 – 25,000 | 25,001 – 32,000 | 32,001 – 40,000 | 40,001 – 45,000 | 45,001 – 50,000 | 50,001 – 80,000 | 80,001 – 130,000 | ||
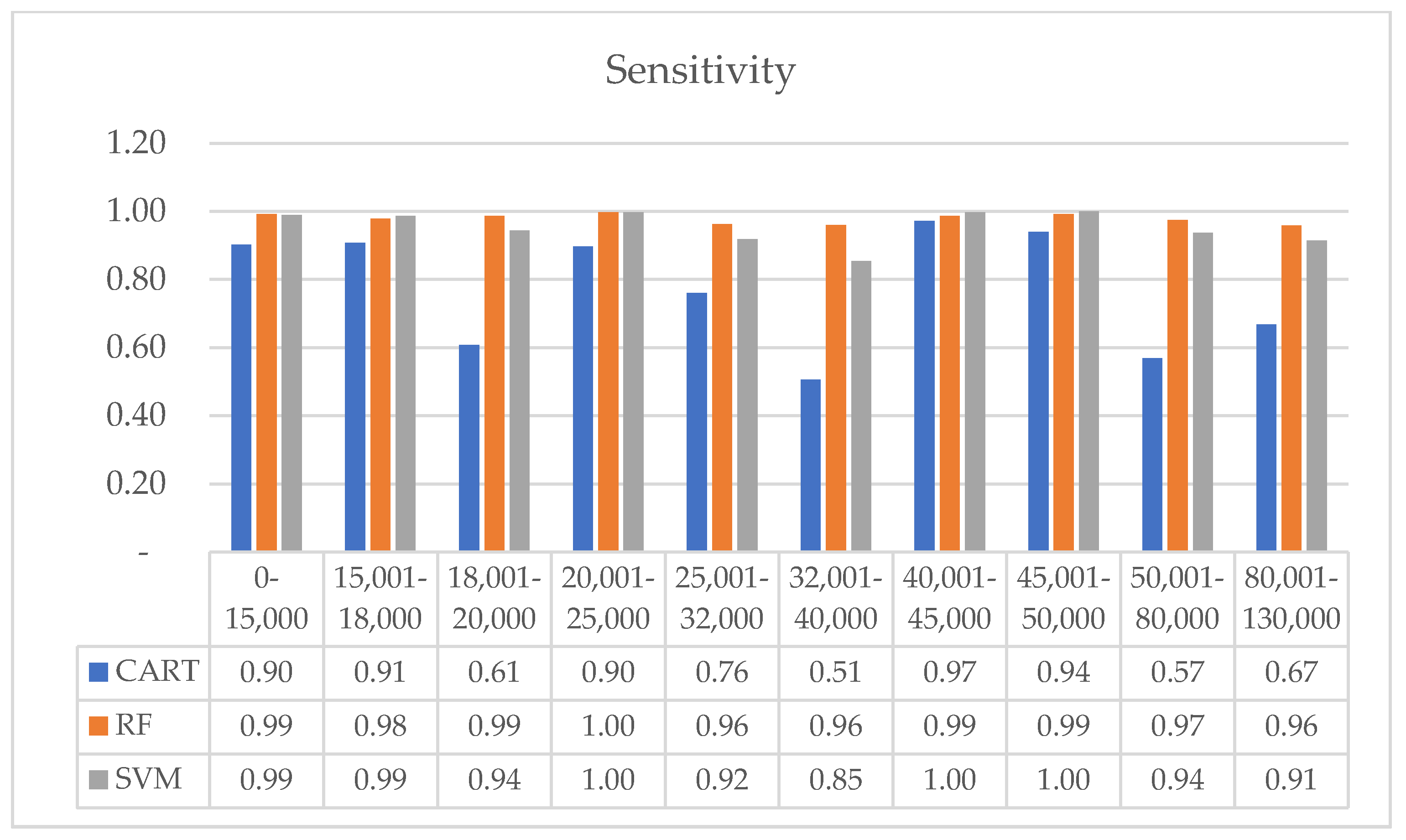
| Sensitivity | CART | 0.902 | 0.907 | 0.607 | 0.897 | 0.760 | 0.506 | 0.972 | 0.940 | 0.569 | 0.668 |
| RF | 0.992 | 0.978 | 0.987 | 0.997 | 0.963 | 0.960 | 0.987 | 0.992 | 0.974 | 0.958 | |
| SVM | 0.989 | 0.987 | 0.944 | 0.997 | 0.918 | 0.854 | 0.997 | 1.000 | 0.937 | 0.914 | |
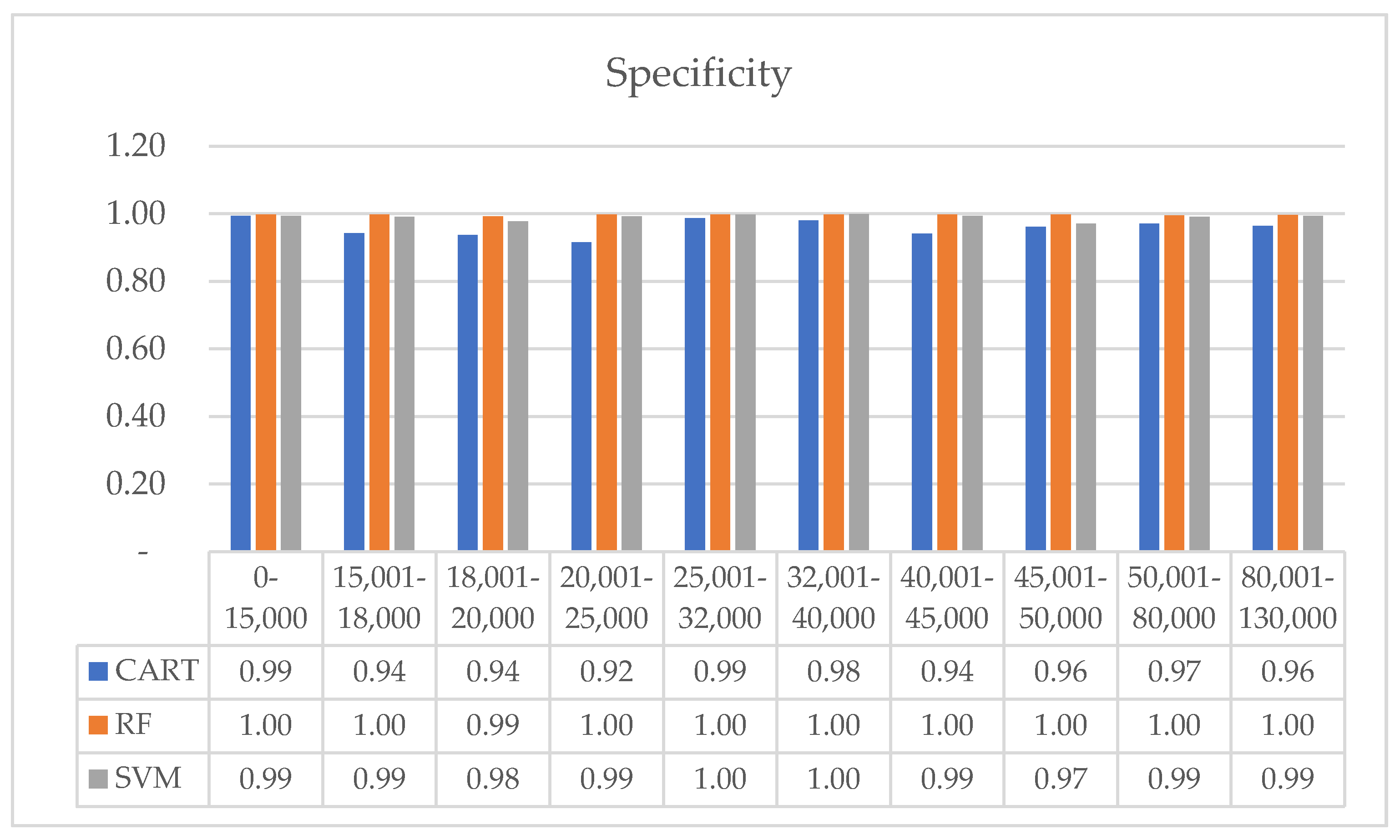
| Specificity | CART | 0.994 | 0.943 | 0.937 | 0.915 | 0.987 | 0.980 | 0.941 | 0.961 | 0.970 | 0.964 |
| RF | 0.998 | 0.997 | 0.992 | 0.997 | 0.998 | 0.998 | 0.998 | 0.997 | 0.995 | 0.996 | |
| SVM | 0.994 | 0.991 | 0.977 | 0.992 | 0.997 | 0.999 | 0.993 | 0.971 | 0.991 | 0.993 | |
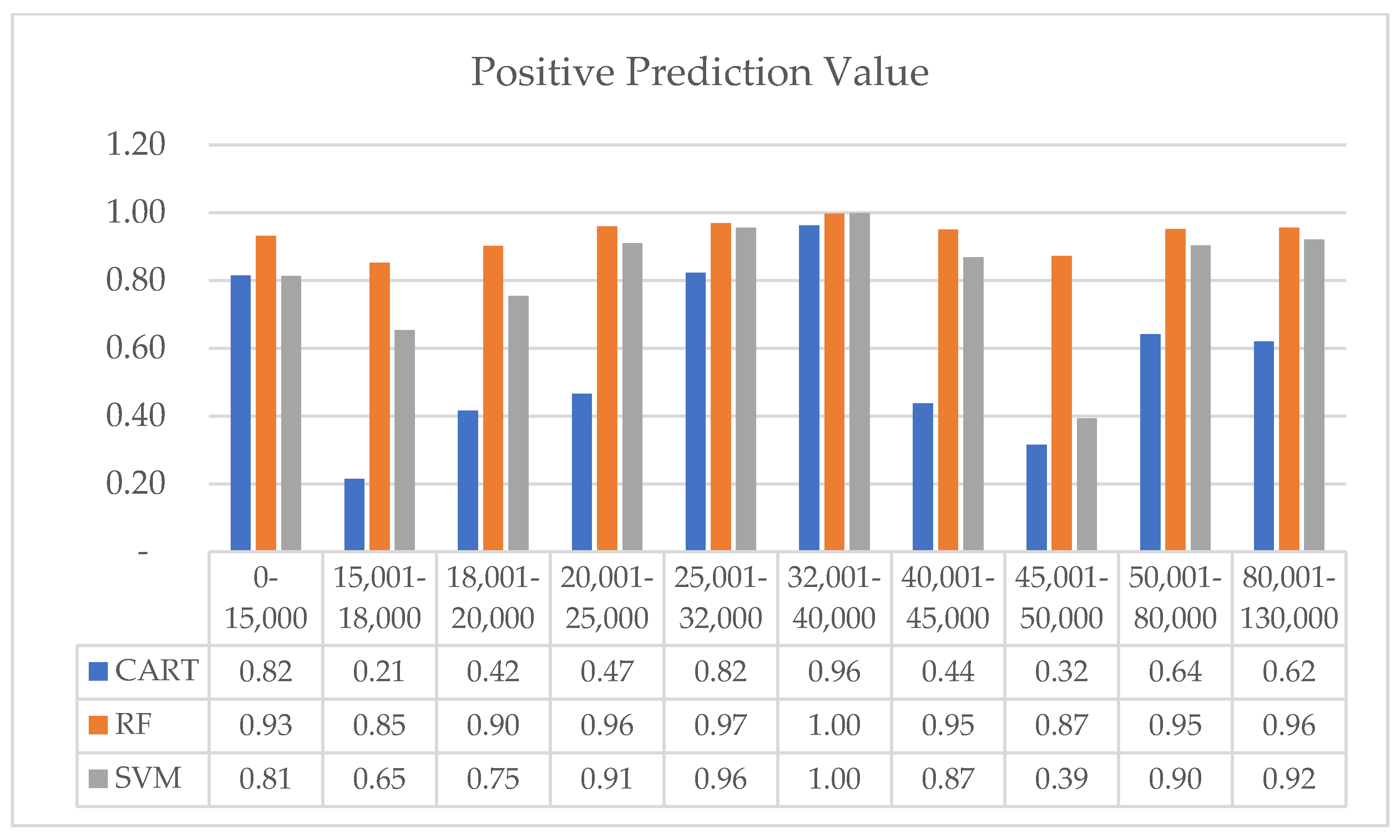
| Pos Pred Value | CART | 0.815 | 0.214 | 0.416 | 0.466 | 0.823 | 0.963 | 0.438 | 0.315 | 0.642 | 0.620 |
| RF | 0.932 | 0.853 | 0.902 | 0.960 | 0.969 | 0.998 | 0.951 | 0.873 | 0.952 | 0.956 | |
| SVM | 0.813 | 0.654 | 0.754 | 0.910 | 0.956 | 0.999 | 0.868 | 0.393 | 0.904 | 0.921 | |
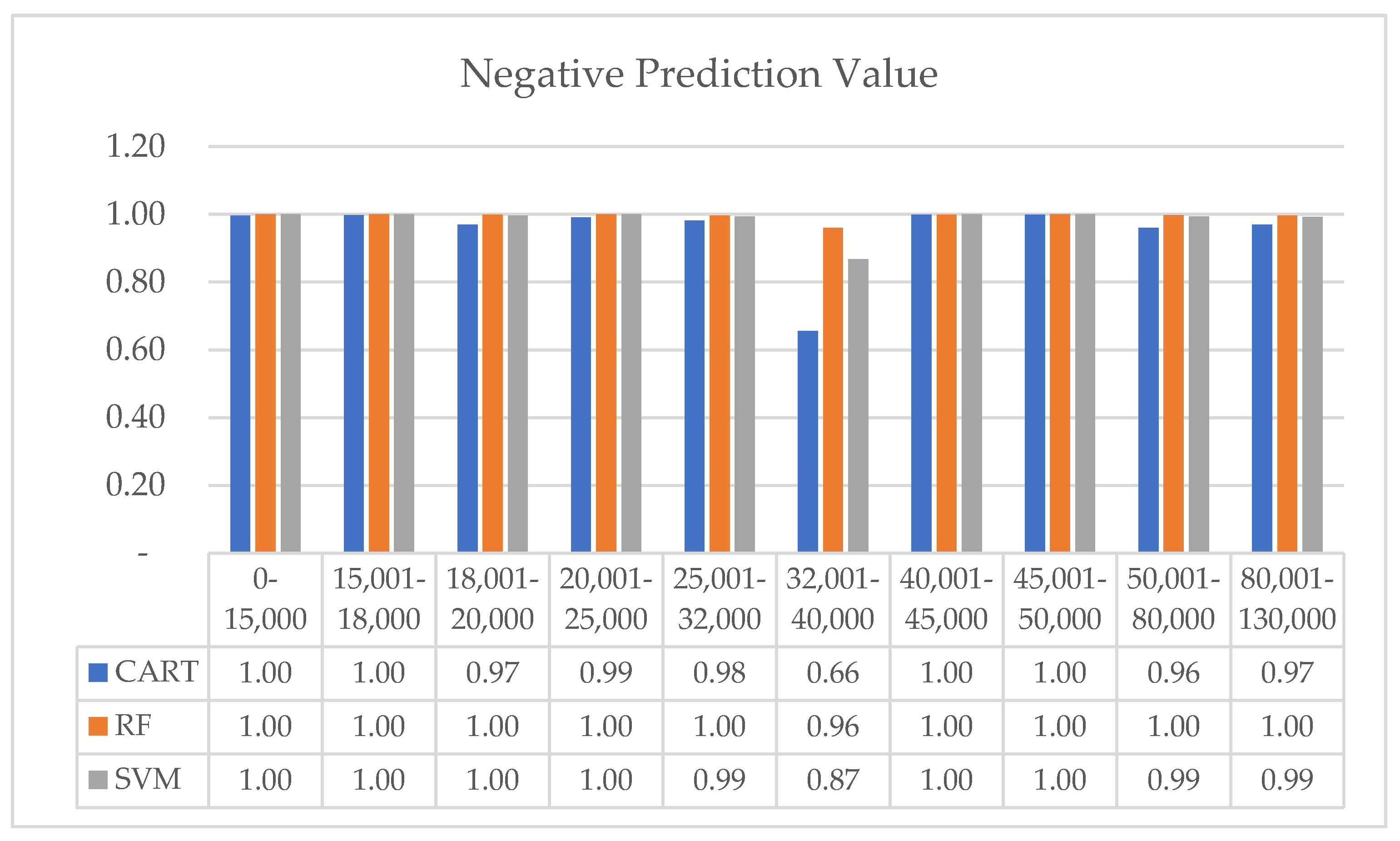
| Neg Pred Value | CART | 0.997 | 0.998 | 0.970 | 0.991 | 0.982 | 0.656 | 0.999 | 0.999 | 0.960 | 0.970 |
| RF | 1.000 | 1.000 | 0.999 | 1.000 | 0.997 | 0.960 | 0.999 | 1.000 | 0.998 | 0.996 | |
| SVM | 1.000 | 1.000 | 0.996 | 1.000 | 0.994 | 0.868 | 1.000 | 1.000 | 0.994 | 0.992 | |
| Models | CART | RF | SVM |
|---|---|---|---|
| MAPE (%) | 20.39105 | 1.906275 | 5.242138 |
| Prediction Models | MAPE (%) |
|---|---|
| Del Giudice et al. [44] | 10.62 |
| Plakandaras et al. [45] | 2.15 |
| Antipov and Pokryshevskaya [46] | 13.95 |
| Kusan et al. [47] | 3.65 |
| Pai et al. [43] models without attribute selection | 1.676 |
| Pai et al. [43] models with attribute selection | 0.228 |
| RF * | 1.906 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Worachairungreung, M.; Thanakunwutthirot, K.; Ninsawat, S. A Study on Estimating Land Value Distribution for the Talingchan District, Bangkok Using Points-of-Interest Data and Machine Learning Classification. Appl. Sci. 2021, 11, 11029. https://doi.org/10.3390/app112211029
Worachairungreung M, Thanakunwutthirot K, Ninsawat S. A Study on Estimating Land Value Distribution for the Talingchan District, Bangkok Using Points-of-Interest Data and Machine Learning Classification. Applied Sciences. 2021; 11(22):11029. https://doi.org/10.3390/app112211029
Chicago/Turabian StyleWorachairungreung, Morakot, Kunyaphat Thanakunwutthirot, and Sarawut Ninsawat. 2021. "A Study on Estimating Land Value Distribution for the Talingchan District, Bangkok Using Points-of-Interest Data and Machine Learning Classification" Applied Sciences 11, no. 22: 11029. https://doi.org/10.3390/app112211029
APA StyleWorachairungreung, M., Thanakunwutthirot, K., & Ninsawat, S. (2021). A Study on Estimating Land Value Distribution for the Talingchan District, Bangkok Using Points-of-Interest Data and Machine Learning Classification. Applied Sciences, 11(22), 11029. https://doi.org/10.3390/app112211029






