Abstract
With the complexity of the task requirement, multiple operating conditions have gradually become the common scenario for equipment. However, the degradation trend of monitoring data cannot be accurately extracted in life prediction under multiple operating conditions, which is because some monitoring data is affected by the operating conditions. Aiming at this problem, this paper proposes an improved similarity trajectory method that can directly use the monitoring data under multiple operating conditions for life prediction. The morphological pattern and symbolic aggregate approximation-based similarity measurement method (MP-SAX) is first used to measure the similarity between the monitoring data under multiple operating conditions. Then, the similar life candidate set, and corresponding weight are obtained according to the MP-SAX. Finally, the life prediction results of equipment under multiple operating conditions can be calculated by aggregating the similar life candidate set. The proposed method is validated by the public datasets from NASA Ames Prognostics Data Repository. The results show that the proposed method can directly and effectively use the original monitoring data for life prediction without extracting the degradation trend of the monitoring data.
1. Introduction
As an important task of condition-based maintenance (CBM), health prognostics has become more and more popular which can predict the remaining useful life (RUL) of equipment according to historical data or observed degradation trend, which can make effective maintenance plan for equipment to improve the reliability of equipment and reduce the loss and safety problems caused by equipment failure [1,2].
With the rapid development of machine learning and deep learning technology, artificial intelligence (AI) based on machine learning and deep learning were gradually applied to fault diagnosis and life prediction [3,4,5,6,7,8]. Such as She et al. [9] proposed a bidirectional gated recurrent unit prediction method based on bootstrap to solve the problem that the uncertainty of the prediction. Wang et al. [10] proposed a new framework named recurrent convolutional neural network to address the limitations of the convolutional neural network, which different degradation states did not consider the temporal dependencies and the prediction results were uncertain. A novel neural network called quantum recurrent encoder-decoder neural network was proposed by Chen et al. [11] to improve the prediction accuracy in the degradation trend prediction of rotating machinery. Figueroa et al. [12] proposed a framework for feature selection embedded in deep neural networks (DNN) for PHM to addresses the accuracy interpretability tradeoff. For turbofan engines, Muneer et al. [13] proposed four data-driven prognostic models based on deep neural networks, and analyzed the influence of its network structure on generalization abilities. Furthermore, Muneer et al. [14] proposed a new attention-based deep convolutional neural network incorporating the time window to predict the RUL of turbofan engines.
However, although the excellent prediction results of equipment can be obtained by the life prediction method based on machine learning and deep learning, the accuracy of prediction results mostly depends on the design of network structure and the selection of parameters. At this time, the similarity trajectory method (STM) based on the case-based reasoning (CBR) which can be regarded as a form of intradomain analogy, and a branch of machine learning shown obvious advantages. CBR can solve the problem of a new instance only by measuring the similarity between a new instance and the historical instance and reusing the information and knowledge of the historical instance [15]. Therefore, STM can realize life prediction without constructing a specific prediction model and selecting parameters, which can reduce the influence of network structure design and parameter selection on the accuracy of prediction results. Therefore, STM has been widely discussed and applied to life prediction since it was proposed by Wang et al. [16]. For example, You et al. [17] pointed out that the traditional Euclidean distance cannot highlight the importance of the recent samples, and on the basis of the Euclidean distance, the decay coefficient was introduced to make the recent degradation samples have a larger weight. Liang et al. [18,19] improved the prediction accuracy of STM by improving the deficiency of degradation indicators construction. Cannarile et al. [20] proposed evidential similarity-based regression for life prediction and related uncertainty based on both complete and incomplete degradation trajectories. Yang et al. [21] proposed an integrated prediction model based on the similarity trajectory method and the differential evolution support vector regression for predicting the tool wear and life. A general data-driven based similarity-based approach was proposed by Li et al. [22] to predict the RUL of the electromagnetic relay. In addition, the similarity-based approach which was based on the framework of CBR was used for the fight trajectory prediction [23], pan-Arctic and regional sea ice area and volume anomalies prediction [24], and so on.
Although STM can effectively use the trajectory of historical data to predict the life of the equipment, the original monitoring data were usually smoothed to reduce the impact of random fluctuations on the similarity measurement [25]. However, for multiple operating conditions, the monitoring data cannot be smoothed effectively to extract the degradation trend due to the influence of operating conditions (the detailed description was employed in Section 4.3).
Aiming at the abovementioned problem that the degradation trend cannot be extracted effectively under multiple operating conditions, this paper proposes a novel prediction scheme for the life prediction of equipment under multiple operating conditions based on morphological pattern and symbolic aggregate approximation-based similarity measurement method (MP-SAX) and STM. According to the characteristics that the equipment performance degradation is reflected in the trend change of monitoring data, while the changes of operating conditions and environment are reflected in the detailed change of monitoring data, the MP-SAX is first used to measure the similarity between the monitoring data under multiple operating conditions. Then, the similar life candidate set, and corresponding weight are obtained according to the MP-SAX. Finally, the life prediction results of equipment under multiple operating conditions can be calculated by aggregating the similar life candidate set.
The rest of this paper is organized as follows. The background knowledge of the similarity measurement method based on morphological pattern and symbolic aggregate approximation (MP-SAX) is described in Section 2. In Section 3, the proposed method is described in detail. The dataset and problem in life prediction under multiple operating conditions are illustrated in Section 4. In Section 5, the results and discussion of the proposed method are explained to verify the effectiveness of the proposed method. Finally, the conclusion of this paper is drawn in Section 6. The meaning of all acronyms are listed in Table A1 in Appendix A.
2. Background of MP-SAX
For the whole life cycle of equipment, the performance degradation of equipment often leads to the change of trend component of monitoring signal, while the change of operating condition or environment often causes the change of detail component of monitoring signal. The similarity measurement method based on the morphological pattern and symbolic aggregate approximation (MP-SAX), which measured the similarity of time series by measuring the similarity of trend component and detail component respectively, can effectively measure the similarity of the time series with the changes both in trend and detail [26]. Therefore, the MP-SAX can be used to measure the similarity of monitoring signal during equipment degradation under multiple operating conditions. For two time series and , the MP-SAX of the two-time series can be obtained as follows:
Step 1: According to empirical mode decomposition (EMD) [27,28], the time series and are decomposed to IMFs and .
Step 2: According to multi-scale permutation entropy (MPE) [29], the MPEs and of each IMFs can be calculated. Then, the IMFs and are reconstructed into trend component ( and ) and detail component ( and ) according to the MPEs as follows:
where , , , .
Step 3: The trend component ( and ) are converted into morphological pattern (MP) symbol sequences and as follows (take as an example):
where is the time interval between two consecutive sample points.
Step 4: The detail component ( and ) are converted into symbolic aggregate approximation (SAX) symbol sequences and as follows (take as an example):
Step 4.1: The detail component is first normalized as follows:
where is the normalized series of , is the mean value of , and is its standard deviation.
Step 4.2: The normalized series is divided into equal-sized segments, then the normalized series can be represented by the average of each segment as follows:
where is the average of the segment of normalized series .
Step 4.3: The distribution space of on the amplitude is divided into equiprobable regions, the breakpoints refers to the lookup table in [30,31].
Step 4.4: The SAX symbol sequences can be obtained by assigning symbols to each region which is determined by breakpoints.
Step 5: The symbol sequences similarity of trend component and detail component are measured by the longest common subsequence (LCS) [32] respectively.
Step 6: The similarity between the two-time series and can be obtained as follows:
where and are the weight of trend component and detail component of time series respectively, the determination of weight refers to [26].
3. The Background and Proposed Method
3.1. The Description of Background
The similarity trajectory method (STM), as a life prediction method without fitting historical curves or constructing a specific prediction model, was widely used in the life prediction of equipment [16,20,21,25]. However, the traditional STM usually used Euclidean distance to measure the similarity between the test sample and historical samples. Although Euclidean distance was the simplest similarity measurement method, there are many limitations in the measurement process [33]. In addition, taking a set of turbofan engine simulation data from NASA Ames Prognostics Data Repository (Details of the simulation data are described in Section 4) as an example, the influence of operating conditions or equipment operating environment on monitoring data is illustrated as shown in Figure 1.
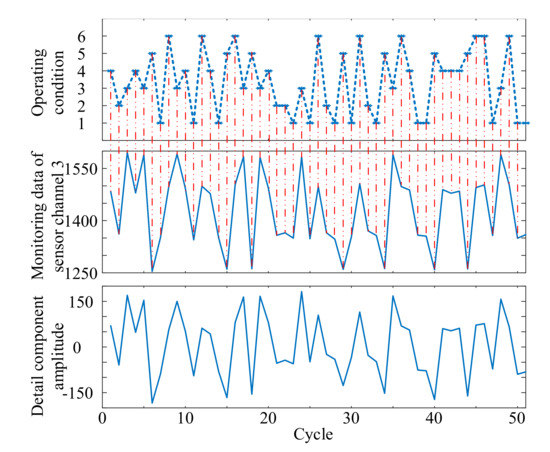
Figure 1.
The influence of multiple operating conditions on the detail component of monitoring data.
According to Section 2, the detail component of monitoring data of Sensor Channel 3 is extracted as shown in Figure 1. As shown in Figure 1, the detail component of monitoring data is basically consistent with the original monitoring data. Besides, although there are some differences in the shape between the original monitoring data and the operating condition, the change points of the operating condition are basically the turning points of the original monitoring data amplitude. Thus, it can be seen that the change of operating conditions will affect the shape of the detail components of monitoring data under multiple operating conditions.
3.2. The Proposed Method
Therefore, in order to solve the life prediction problem of equipment under multiple operating conditions, this paper proposes a novel similarity trajectory method based on morphological pattern and symbolic aggregate approximation (MP-SAX-STM) by using morphological pattern and symbolic aggregate approximation similarity measurement method. The diagrammatic sketch of the proposed method is shown in Figure 2. For the test sample , historical samples , where the historical sample is and the number of historical samples is , the process of the proposed method can be described as follows:
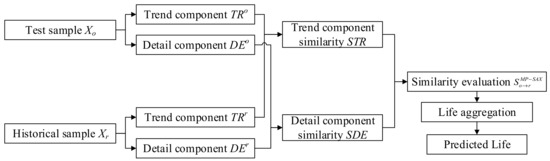
Figure 2.
The diagrammatic sketch of the proposed method.
Step 1: According to Step 1 and Step 2 in Section 2, the test sample and historical sample are divided into trend component ( and ) and detail component ( and ).
Step 2: According to Step 3 to Step 5 in Section 2, the similarity of the trend component and the detail component can be obtained, then the similarity between and can be calculated by Equation (8).
Step 3: Determine the similar life candidate set and corresponding weight. The life of the historical sample is regarded as a similar life candidate set as follows:
where is the time corresponding to the last set of data of the historical sample. And the weight corresponding to the candidate set is as follows:
where
and . Therefore, the RUL of the test sample can be obtained as follows:
Step 4: Aggregate life to obtain predicted life. According to the similar life candidate set and corresponding weight, the predicted life of test sample can be obtained as follows:
4. The Description of Dataset and Problem in Life Prediction under Multiple Operating Conditions
4.1. The Description and Analysis of the Dataset
The dataset used in this part to verify the effectiveness of the proposed method was the simulation data of turbofan engine from NASA Ames Prognostics Data Repository which was built by Saxena et al. based on the Commercial Modular Aero-Propulsion System Simulation (CMAPSS) [34]. As the simulation model accurately reflected the degradation law of the turbofan engine, the simulation data can effectively reflect the degradation of the turbofan engine under different failure modes. There were four sets of life cycle data in the simulation data, the information of operating condition and failure mode simulated by each set of data were shown in Table 1. Further, each set of data contained two subsets, namely the train set, and test set, the train set contained the complete life cycle of turbofan engines. In this part, only the train set of Set #2 and #4 was used to verify the proposed method. According to [25], the meaning of each column of data of each life cycle data in Set #2 and #4 was shown in Table 2. In addition, only the monitoring data of Sensor Channels 2, 3, 4, 7, 11, 12, 15, 20, and 21 were sensitive to the fault of the turbofan engine and had an obvious degradation trend [16,25]. However, there may be information redundancy among the monitoring data of each sensor channel. Therefore, cross calculate the correlation between the monitoring data of Sensor Channels 2, 3, 4, 7, 11, 12, 15, 20, and 21, and the results were shown in Figure 3.

Table 1.
The information of operating condition and failure mode simulated by each set of data.

Table 2.
Brief description of one life cycle data of simulation data.
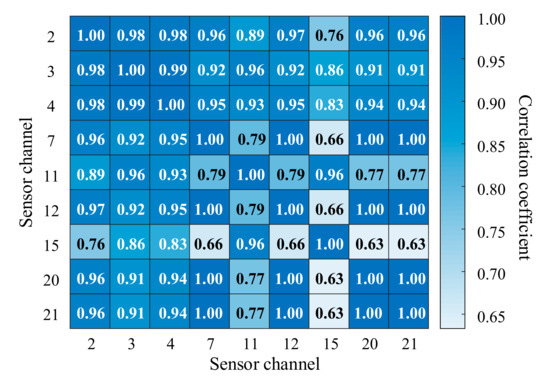
Figure 3.
Correlation coefficient between the monitoring data of each sensor.
As shown in Figure 3, there was a high correlation between the monitoring data of each sensor channel. And the correlation between the monitoring data of Sensor Channels 3, 4, and other sensor channel was the highest. Therefore, only the monitoring data of Sensor Channel 3 in Set #2 and #4 was taken as an example to verify the effectiveness of the proposed method.
4.2. Evaluation Indicators of Prediction Results
In order to more intuitively evaluate the performance of the proposed method from the quantitative perspective, we used mean absolute error (MAE), root mean square error (RMSE), mean absolute percentage error (MAPE), and mean absolute scaled error (MASE) to evaluate the prediction accuracy under each prediction experiment. MAE, RMSE, MAPE, and MASE have been proved to still have good performance in measuring prediction accuracy in some scenarios [35]. The MAE, RMSE, MAPE, and MASE can be obtained as following [35]:
where is the number of sample points, is the actual life, is the predicted life.
4.3. The Description of Problems in Life Prediction under Multiple Operating Conditions
The traditional STM usually extracted the degradation model (degradation trend) of the monitoring signal to eliminate the influence of noise and other random fluctuations on the overall degradation trend of equipment. However, as shown in Figure 4a, for some monitoring signals, when the equipment was operating under multiple operating conditions, the monitoring signals were affected by different operating conditions. Further, the obvious degradation trend cannot be seen from the monitoring signal. Therefore, according to [25], the influence of operating conditions on the degradation trend of monitoring signal was eliminated by normalization of operating conditions as follows:
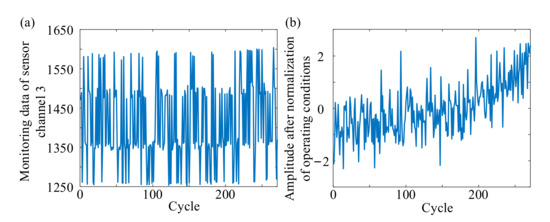
Figure 4.
The simulation data of turbofan engine. (a) Monitoring data of Sensor Channel 3. (b) Data after normalization of operating conditions.
It was assumed that each life cycle point can be divided into one of the operating regions , that was , where was the operating condition corresponding to each point . After dividing the operating conditions, the mean and variance of each operating condition were as follows:
Then the normalization of operating conditions can be obtained as follows:
Finally, according to the time position of each point in the original life cycle, the normalized monitoring signal of the operating condition can be obtained, as shown in Figure 4b.
Through the operating condition normalization, although the normalized monitoring signal of the operating condition can show an obvious degradation trend, the mean and variance of each operating condition needed to be known in the process of operating condition normalization. Therefore, this brought a problem, for the equipment in service, how to determine the mean and variance of each operating condition. Generally, there were two solutions: (1) the mean and variance were from each operating condition of service equipment in-service stage; (2) the mean and variance were from each operating condition of historical life cycle data. However, the mean and variance obtained by the two solutions were different from those of each operating condition after the complete failure of service equipment. As shown in Figure 5, the degradation model of the first half of Life Cycle 1 was obtained by the mean and variance obtained from the abovementioned two solutions respectively. As shown in Figure 5b,c, the degradation model of the first half of Life Cycle 1 obtained by the mean and variance which came from the abovementioned two solutions was obviously different from that of Life Cycle 1 obtained by the mean and variance of each operating condition of the whole life. This difference existed not only in shape but also in amplitude. Therefore, for the service equipment, the degradation model of monitoring data in-service stage cannot be accurately obtained under multiple operating conditions, which was an important problem encountered in using STM for life prediction under multiple operating conditions.
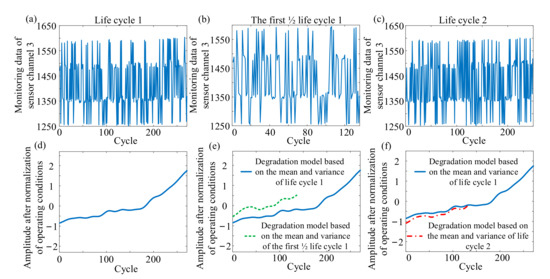
Figure 5.
Degradation model comparison based on different mean and variance. (a) Life cycle monitoring Data 1 of Sensor Channel 3. (b) The first half monitoring Data 1 of Sensor Channel 3. (c) Life cycle monitoring Data 2 of Sensor Channel 3. (d) Degradation model based on the mean and variance of life cycle monitoring data. (e) Degradation model comparison based on the mean and variance of the first half of monitoring Data 1. (f) degradation model comparison based on the mean and variance of life cycle monitoring data 2.
5. Results and Discussions
In order to further explain the influence of the degradation model which cannot be accurately obtained in-service stage on the prediction results, we randomly selected 30 sets of life cycle data from Set #2 and Set #4 respectively, then the first 1/2, 2/3, 3/4, and 4/5 of the selected life cycle data were used as the test samples. Since there was not one similar life candidate set selected in the process of life prediction by STM, the degradation model was calculated only according to the mean and variance which were from each operating condition of service equipment in-service stage. Finally, STM was used to predict the life based on the degradation model and original monitoring data respectively, and the MAE, RMSE, MAPE, and MASE were calculated as shown in Figure 6 and Figure 7.
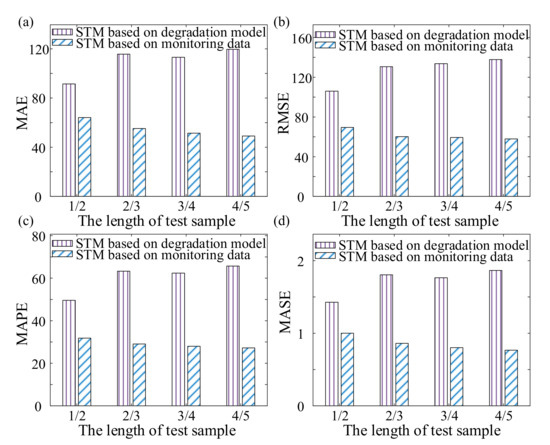
Figure 6.
MAE, RMSE, MAPE, and MASE results of Set #2 based on the different test dataset. (a) MAE. (b) RMSE. (c) MAPE. (d) MASE.
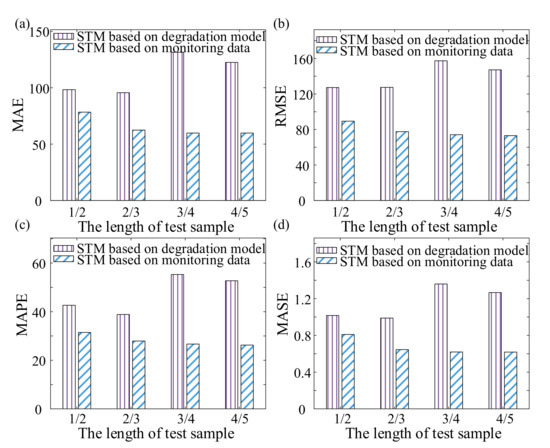
Figure 7.
MAE, RMSE, MAPE, and MASE results of Set #4 based on the different test dataset. (a) MAE. (b) RMSE. (c) MAPE. (d) MASE.
As shown in Figure 6 and Figure 7, in the same scenario that the life was predicted by STM, the evaluation indicators of prediction results based on the degradation model were significantly larger than those based on original monitoring data. Moreover, the evaluation indicators of prediction results based on the degradation model were not regular under the different lengths of test samples, while those based on original monitoring data shown a downward trend with the increase of test sample length. Therefore, in the scenario of multiple operating conditions, the degradation model obtained only based on part of the monitoring data of the service equipment cannot be completely equivalent to that obtained by whole life, and the accurate life prediction results cannot be obtained in the process of life prediction.
Consequently, the proposed method improved the life prediction results under multiple operating conditions by improving the accuracy of direct measurement of monitoring data similarity. Likewise, 30 sets of life cycle data from Set #2 and Set #4 were selected randomly respectively, then the first 1/2, 2/3, 3/4, and 4/5 of the selected life cycle data were used as the test samples. Finally, MP-SAX-STM was used for life prediction and compared with the prediction results of STM which was based on original monitoring data, and the MAE, RMSE, MAPE, and MASE were calculated as shown in Figure 8 and Figure 9. Where the subjective weight determination method was selected when calculating the similarity by MP-SAX, in which the weight of trend component is 0.75 and the weight of detail component is 0.25.
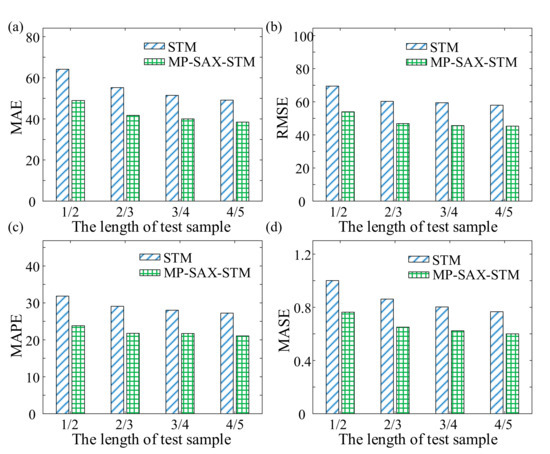
Figure 8.
MAE, RMSE, MAPE, and MASE results of Set #2. (a) MAE. (b) RMSE. (c) MAPE. (d) MASE.
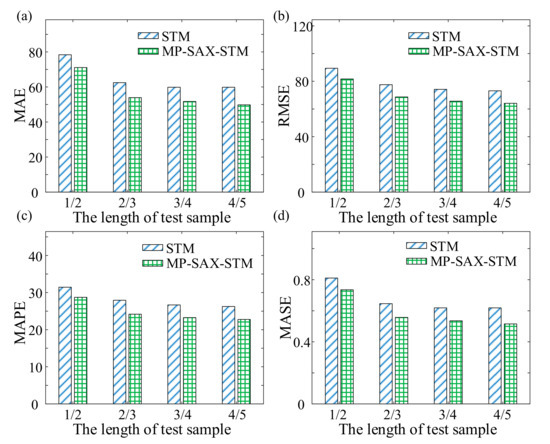
Figure 9.
MAE, RMSE, MAPE, and MASE results of Set #4. (a) MAE. (b) RMSE. (c) MAPE. (d) MASE.
As shown in Figure 8 and Figure 9, when only monitoring data were used for life prediction under multiple operating conditions, the evaluation indicators of MP-SAX-STM were lower than those of STM. Furthermore, with the increase of the length of the test sample, the evaluation indicators of MP-SAX-STM and STM showed a downward trend. Furthermore, for Set #2 and Set #4, the relative reduction of each indicator of MP-SAX-STM compared with STM was shown in Table 3 and Table 4, respectively.

Table 3.
Relative reduction of each indicator of MP-SAX-STM compared with STM of Set #2.

Table 4.
Relative reduction of each indicator of MP-SAX-STM compared with STM of Set #4.
As shown in Table 3 and Table 4, there was little difference among the relative change of each indicator under the same length. For Set #2, there was little difference in the change of the same indicator under different lengths, while, for Set #4, the variation under same indicator and different lengths increased approximately with the increase of length. Therefore, the prediction results of STM can be effectively improved by improving the accuracy of the similarity measurement of traditional STM. Moreover, in the case of only using monitoring data, MP-SAX-STM can also achieve life prediction, and the prediction results were better than the traditional STM. Besides, for Set #4, the improvement effect of MP-SAX-STM was also approximately enhanced with the increase of the know data length. To further illustrate the life prediction results of the MP-SAX-STM and STM, one set was randomly selected from the 30 sets of life cycle data from Set #2 and Set #4 to predict the remaining useful life (RUL) under different lengths as shown in Figure 10 respectively. And the RUL error was shown in Figure 11.
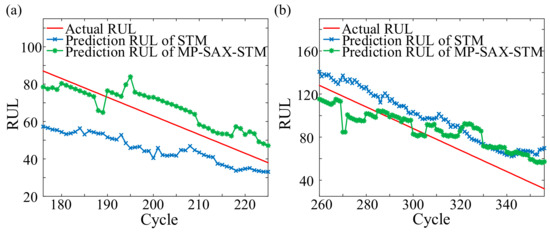
Figure 10.
RUL result of the single tested sample. (a) Set #2. (b) Set #4.
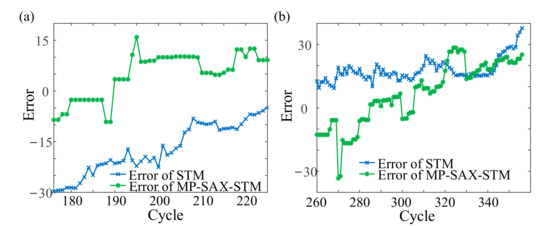
Figure 11.
RUL error of the single tested sample. (a) Set #2. (b) Set #4.
Compared with STM, as shown in Figure 10, both the MP-SAX-STM RUL prediction results of Set #2 and Set #4 were closer to the actual RUL. Therefore, under multiple operating conditions, the life prediction can be effectively realized by MP-SAX-STM even if the degradation model was not extracted and only the monitoring data which was sensitive to the operating condition was used. In addition, as shown in Figure 11, for Set #2, the RUL error of MP-SAX-STM fluctuated around 0, while the error of STM was much less than 0 and gradually approached 0. For Set #4, although the overall trend of the error of MP-SAX-STM passed through 0, the error of STM was always greater than 0. Therefore, for the life prediction problem under multiple operating conditions, MP-SAX-STM can improve the prediction accuracy compared with STM.
Altogether, the prediction result of STM can be effectively improved by improving the similarity measurement accuracy of STM. In addition, in the scenario of multiple operating conditions, MP-SAX-STM can effectively solve the life prediction problem that the degradation model of monitoring data cannot be accurately obtained, and effectively realized the life prediction.
6. Conclusions
This paper proposes an improved STM based on the morphological pattern and symbolic aggregate approximation-based similarity measurement method, which can directly and effectively use the original monitoring data for life prediction without extracting the degradation trend of the monitoring data. According to the characteristics that the equipment performance degradation is reflected in the trend change of monitoring data, while the changes of operating conditions and environment are reflected in the detail change of monitoring data, the MP-SAX is first used to measure the similarity between the monitoring data under multiple operating conditions. Then, the similar life candidate set and corresponding weight are obtained according to the MP-SAX. Finally, the life prediction results of equipment under multiple operating conditions can be calculated by aggregating the similar life candidate set. Through the analysis and verification of public datasets of the turbofan engine from the NASA Ames Prognostics Data Repository, it is proved that the proposed method can achieve life prediction only using original monitoring data without extracting degradation trend of monitoring data. In addition, the prediction result of STM can be effectively improved by improving the similarity measurement accuracy of STM.
Although some important techniques associated with the proposed method have been investigated in this paper, the STM can only obtain the prediction point of life and do not consider the uncertainty in the prediction.
Author Contributions
Conceptualization, J.Y.; formal analysis, J.Y.; investigation, J.Y.; methodology, J.Y.; project administration, M.X.; software, J.Y. and R.W.; supervision, M.X.; validation, Y.L.; writing—original draft, J.Y.; writing—review and editing, J.Y., Y.L., R.W. and M.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: [https://ti.arc.nasa.gov/m/project/prognostic-repository/CMAPSSData.zip].
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Meaning of acronyms.
Table A1.
Meaning of acronyms.
| Acronyms | Meaning | Acronyms | Meaning |
|---|---|---|---|
| AI | Artificial intelligence | MP-SAX | Morphological pattern and symbolic aggregate approximation-based similarity measurement method |
| CBM | Condition based maintenance | MP-SAX-STM | Similarity trajectory method based on morphological pattern and symbolic aggregate approximation |
| CBR | Case-based reasoning | OP | Operating parameters |
| CMAPSS | Commercial modular aero-propulsion system simulation | RMSE | Root mean square error |
| DE | Detail component | RUL | Remaining useful life |
| EMD | Empirical mode decomposition | S | Sensor |
| IMF | Intrinsic mode function | SAX | Symbolic aggregate approximation |
| LCS | Longest common subsequence | SC | Symbolic aggregate approximation symbol sequences |
| MAE | Mean absolute error | SDE | Similarity of detail component |
| MAPE | Mean absolute percentage error | STM | Similarity trajectory method |
| MASE | Mean absolute scaled error | STR | Similarity of trend component |
| MC | Morphological pattern symbol sequences | TR | Trend component |
| MP | Morphological pattern | - | - |
References
- Lei, Y.; Li, N.; Guo, L.; Li, N.; Yan, T.; Lin, J. Machinery health prognostics: A systematic review from data acquisition to RUL prediction. Mech. Syst. Signal Process. 2018, 104, 799–834. [Google Scholar] [CrossRef]
- Jardine, A.K.; Lin, D.; Banjevic, D. A review on machinery diagnostics and prognostics implementing condition-based maintenance. Mech. Syst. Signal Process. 2006, 20, 1483–1510. [Google Scholar] [CrossRef]
- Rezamand, M.; Kordestani, M.; Carriveau, R.; Ting, D.S.-K.; Orchard, M.E.; Saif, M. Critical Wind Turbine Components Prognostics: A Comprehensive Review. IEEE Trans. Instrum. Meas. 2020, 69, 9306–9328. [Google Scholar] [CrossRef]
- Bhargava, C.; Sharma, P.K.; Senthilkumar, M.; Padmanaban, S.; Ramachandaramurthy, V.K.; Leonowicz, Z.; Blaabjerg, F.; Mitolo, M. Review of Health Prognostics and Condition Monitoring of Electronic Components. IEEE Access 2020, 8, 75163–75183. [Google Scholar] [CrossRef]
- Nath, A.G.; Udmale, S.S.; Singh, S.K. Role of artificial intelligence in rotor fault diagnosis: A comprehensive review. Artif. Intell. Rev. 2020, 54, 2609–2668. [Google Scholar] [CrossRef]
- Lin, S.-L. Intelligent Fault Diagnosis and Forecast of Time-Varying Bearing Based on Deep Learning VMD-DenseNet. Sensors 2021, 21, 7467. [Google Scholar] [CrossRef]
- Tsai, C.-M.; Wang, C.-S.; Chung, Y.-J.; Sun, Y.-D.; Perng, J.-W. Multi-Sensor Fault Diagnosis of Underwater Thruster Propeller Based on Deep Learning. Sensors 2021, 21, 7187. [Google Scholar] [CrossRef]
- Cui, L.; Tian, X.; Shi, X.; Wang, X.; Cui, Y. A Semi-Supervised Fault Diagnosis Method Based on Improved Bidirectional Generative Adversarial Network. Appl. Sci. 2021, 11, 9401. [Google Scholar] [CrossRef]
- She, D.; Jia, M. A BiGRU method for remaining useful life prediction of machinery. Measurement 2021, 167, 108277. [Google Scholar] [CrossRef]
- Wang, B.; Lei, Y.; Yan, T.; Li, N.; Guo, L. Recurrent convolutional neural network: A new framework for remaining useful life prediction of machinery. Neurocomputing 2020, 379, 117–129. [Google Scholar] [CrossRef]
- Chen, Y.; Li, F.; Wang, J.; Tang, B.; Zhou, X. Quantum recurrent encoder–decoder neural network for performance trend prediction of rotating machinery. Knowl. Based Syst. 2020, 197, 105863. [Google Scholar] [CrossRef]
- Barraza, J.F.; Droguett, E.L.; Martins, M.R. Towards Interpretable Deep Learning: A Feature Selection Framework for Prognostics and Health Management Using Deep Neural Networks. Sensors 2021, 21, 5888. [Google Scholar] [CrossRef] [PubMed]
- Muneer, A.; Taib, S.M.; Naseer, S.; Ali, R.F.; Aziz, I.A. Data-Driven Deep Learning-Based Attention Mechanism for Remaining Useful Life Prediction: Case Study Application to Turbofan Engine Analysis. Electronics 2021, 10, 2453. [Google Scholar] [CrossRef]
- Muneer, A.; Taib, S.M.; Fati, S.M.; Alhussian, H. Deep-Learning Based Prognosis Approach for Remaining Useful Life Prediction of Turbofan Engine. Symmetry 2021, 13, 1861. [Google Scholar] [CrossRef]
- Aamodt, A.; Plaza, E. Case-Based Reasoning: Foundational Issues, Methodological Variations, and System Approaches. AI Commun. 1994, 7, 39–59. [Google Scholar] [CrossRef]
- Wang, T.; Yu, J.; Siegel, D.; Lee, J. A similarity-based prognostics approach for Remaining Useful Life estimation of engineered systems. Proceedings of 2008 International Conference on Prognostics and Health Management, Denver, CO, USA, 6–9 October 2008; pp. 1–6. [Google Scholar] [CrossRef]
- You, M.-Y.; Meng, G. A generalized similarity measure for similarity-based residual life prediction. J. Process. Mech. Eng. 2011, 225, 151–160. [Google Scholar] [CrossRef]
- Zeming, L.; Jianmin, G.; Hongquan, J.; Xu, G.; Zhiyong, G.; Rongxi, W. A similarity-based method for remaining useful life prediction based on operational reliability. Appl. Intell. 2018, 48, 2983–2995. [Google Scholar] [CrossRef]
- Liang, Z.; Gao, J.; Jiang, H.; Gao, X.; Gao, Z.; Wang, R. A Degradation Degree Considered Method for Remaining Useful Life Prediction Based on Similarity. Comput. Sci. Eng. 2018, 21, 50–64. [Google Scholar] [CrossRef]
- Cannarile, F.; Baraldi, P.; Zio, E. An evidential similarity-based regression method for the prediction of equipment remaining useful life in presence of incomplete degradation trajectories. Fuzzy Sets Syst. 2019, 367, 36–50. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Guo, Y.; Huang, Z.; Chen, N.; Li, L.; Jiang, Y.; He, N. Research on the milling tool wear and life prediction by establishing an integrated predictive model. Measurement 2019, 145, 178–189. [Google Scholar] [CrossRef]
- Li, L.L.; Ma, D.J.; Li, Z.G. Residual Useful Life Estimation by a Data-Driven Similarity-Based Approach. Qual. Reliab. Eng. Int. 2017, 33, 231–239. [Google Scholar] [CrossRef]
- Lin, Y.; Yang, B.; Zhang, J.; Liu, H. Approach for 4-D Trajectory Management Based on HMM and Trajectory Similarity. J. Mar. Sci. Technol. 2019, 27, 246–256. [Google Scholar] [CrossRef]
- Comeau, D.; Giannakis, D.; Zhao, Z.; Majda, A.J. Predicting regional and pan-Arctic sea ice anomalies with kernel analog forecasting. Clim. Dyn. 2019, 52, 5507–5525. [Google Scholar] [CrossRef] [Green Version]
- Wang, T. Trajectory Similarity Based Prediction for Remaining Useful Life Estimation; ProQuest Dissertations Publishing: Cincinnati, OH, USA, 2010; pp. 41–70. [Google Scholar]
- Yin, J.; Wang, R.; Zheng, H.; Yang, Y.; Li, Y.; Xu, M. A New Time Series Similarity Measurement Method Based on the Morphological Pattern and Symbolic Aggregate Approximation. IEEE Access 2019, 7, 109751–109762. [Google Scholar] [CrossRef]
- Yu, D.; Cheng, J.; Yang, Y. Application of EMD method and Hilbert spectrum to the fault diagnosis of roller bearings. Mech. Syst. Signal Process. 2005, 19, 259–270. [Google Scholar] [CrossRef]
- Li, Y.; Xu, M.; Wei, Y.; Huang, W. An improvement EMD method based on the optimized rational Hermite interpolation approach and its application to gear fault diagnosis. Measurement 2015, 63, 330–345. [Google Scholar] [CrossRef]
- Li, Y.; Xu, M.; Wei, Y.; Huang, W. A new rolling bearing fault diagnosis method based on multiscale permutation entropy and improved support vector machine based binary tree. Measurement 2016, 77, 80–94. [Google Scholar] [CrossRef]
- He, X.; Shao, C.; Xiong, Y. A non-parametric symbolic approximate representation for long time series. Pattern Anal. Appl. 2016, 19, 111–127. [Google Scholar] [CrossRef]
- Sun, Y.; Li, J.; Liu, J.; Sun, B.; Chow, C. An improvement of symbolic aggregate approximation distance measure for time series. Neurocomputing 2014, 138, 189–198. [Google Scholar] [CrossRef]
- Hsu, W.J.; Du, M.W. Computing a longest common subsequence for a set of strings. BIT Numer. Math. 1984, 24, 45–59. [Google Scholar] [CrossRef]
- Batista, G.E.; Keogh, E.J.; Tataw, O.M.; De Souza, V.M. CID: An efficient complexity-invariant distance for time series. Data Min. Knowl. Discov. 2014, 28, 634–669. [Google Scholar] [CrossRef]
- Saxena, A.; Kai, G.; Simon, D.; Eklund, N. Damage propagation modeling for aircraft engine run-to-failure simulation. In Proceedings of the International Conference on Prognostics and Health Management, Denver, CO, USA, 6–9 October 2008; pp. 1–9. [Google Scholar] [CrossRef]
- Hyndman, R.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).