A Convenient Way to Determine the Optimum Angle of Incidence of Fizeau Interferometer
Abstract
1. Introduction
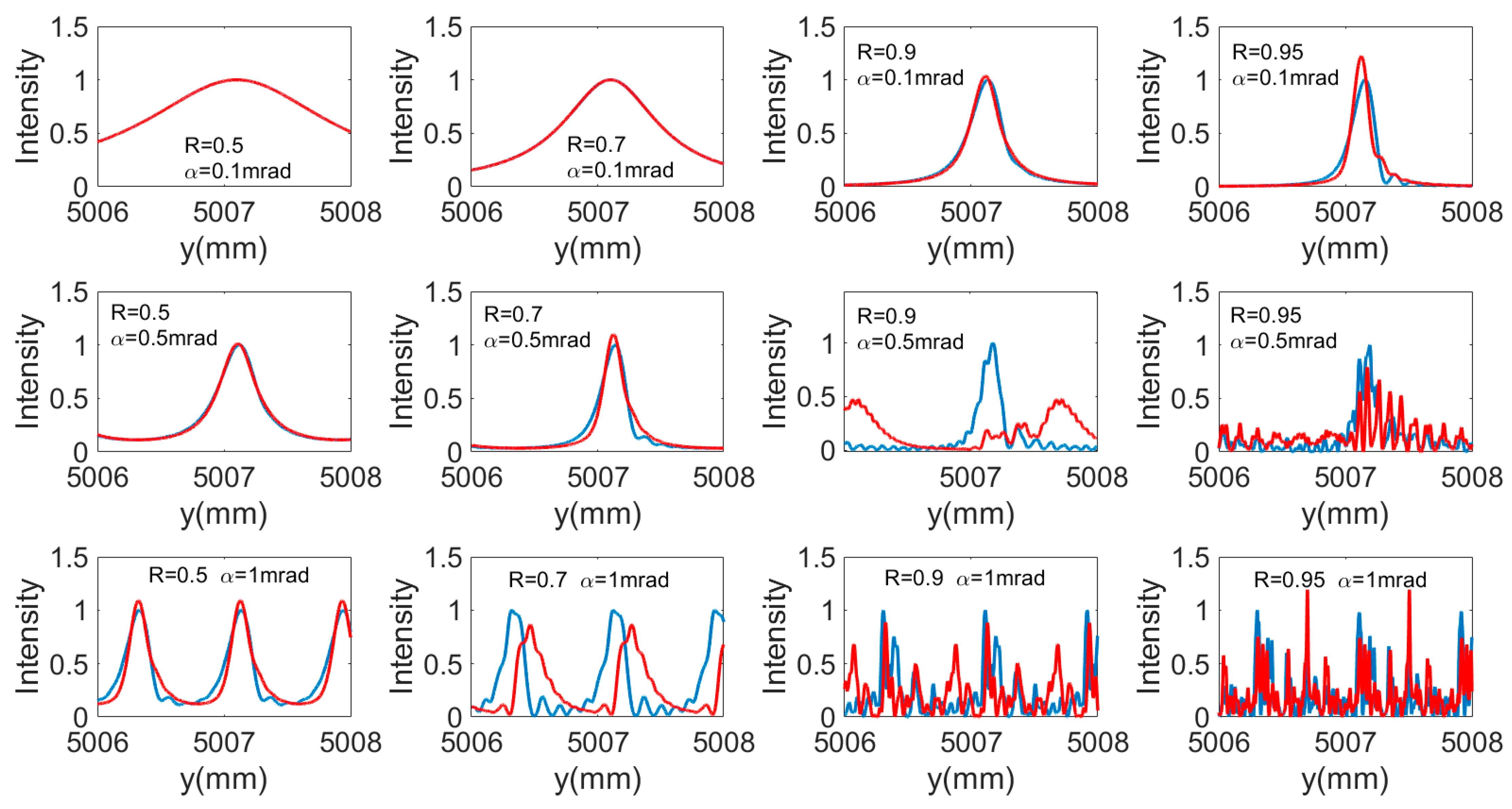
2. Analysis of Spatial Light Intensity Distribution
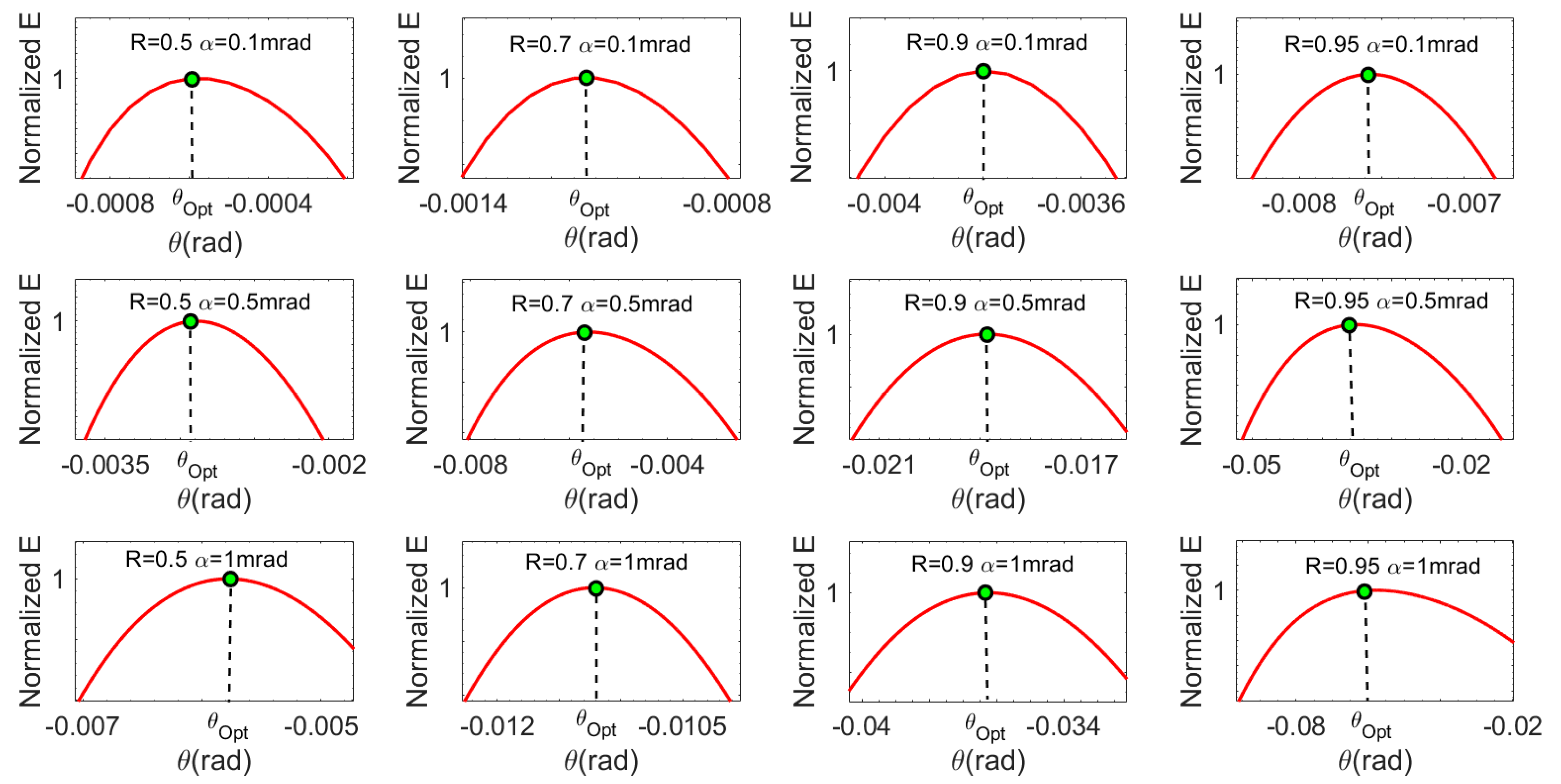
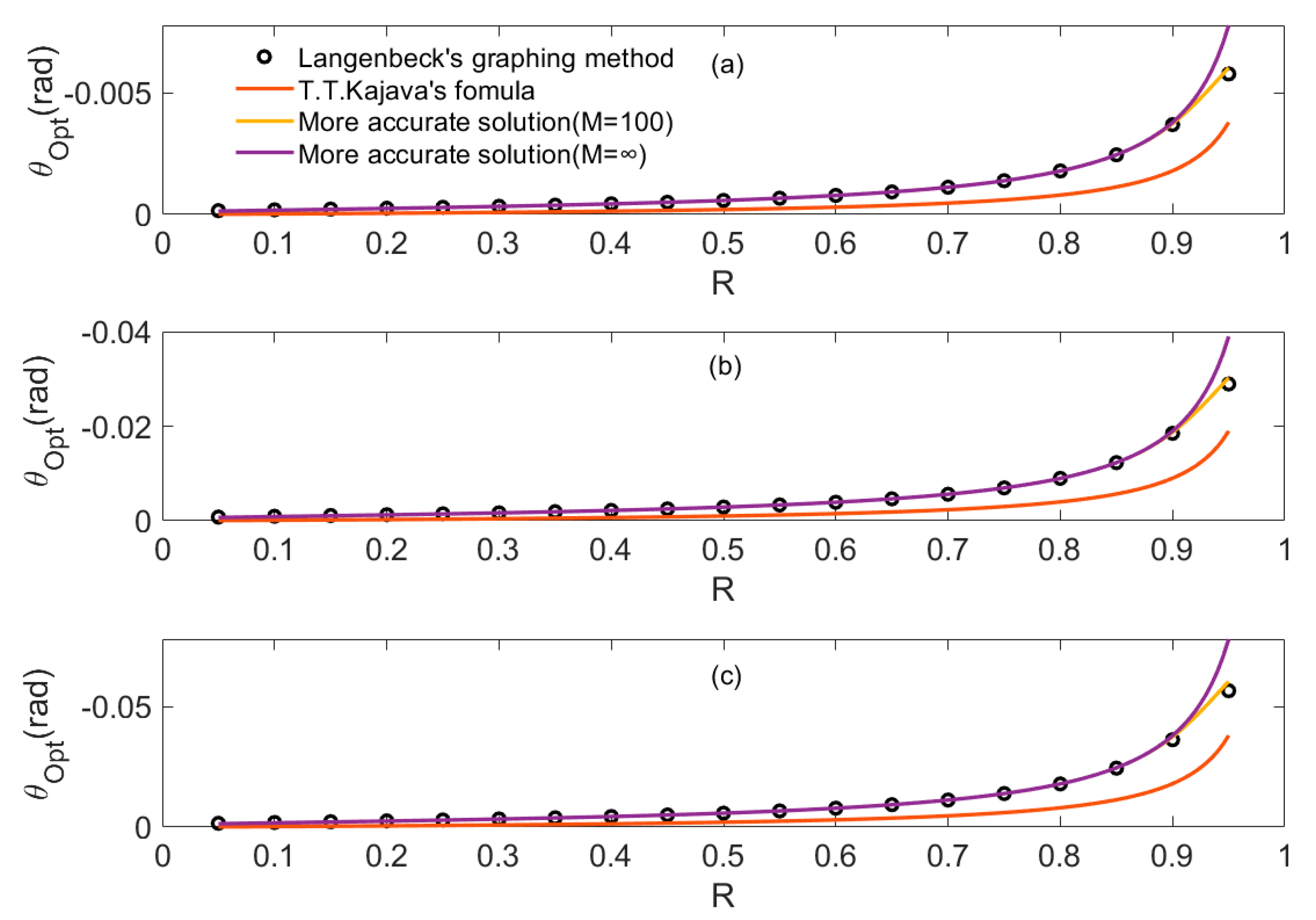
3. Determination of the Optimum Incident Angle
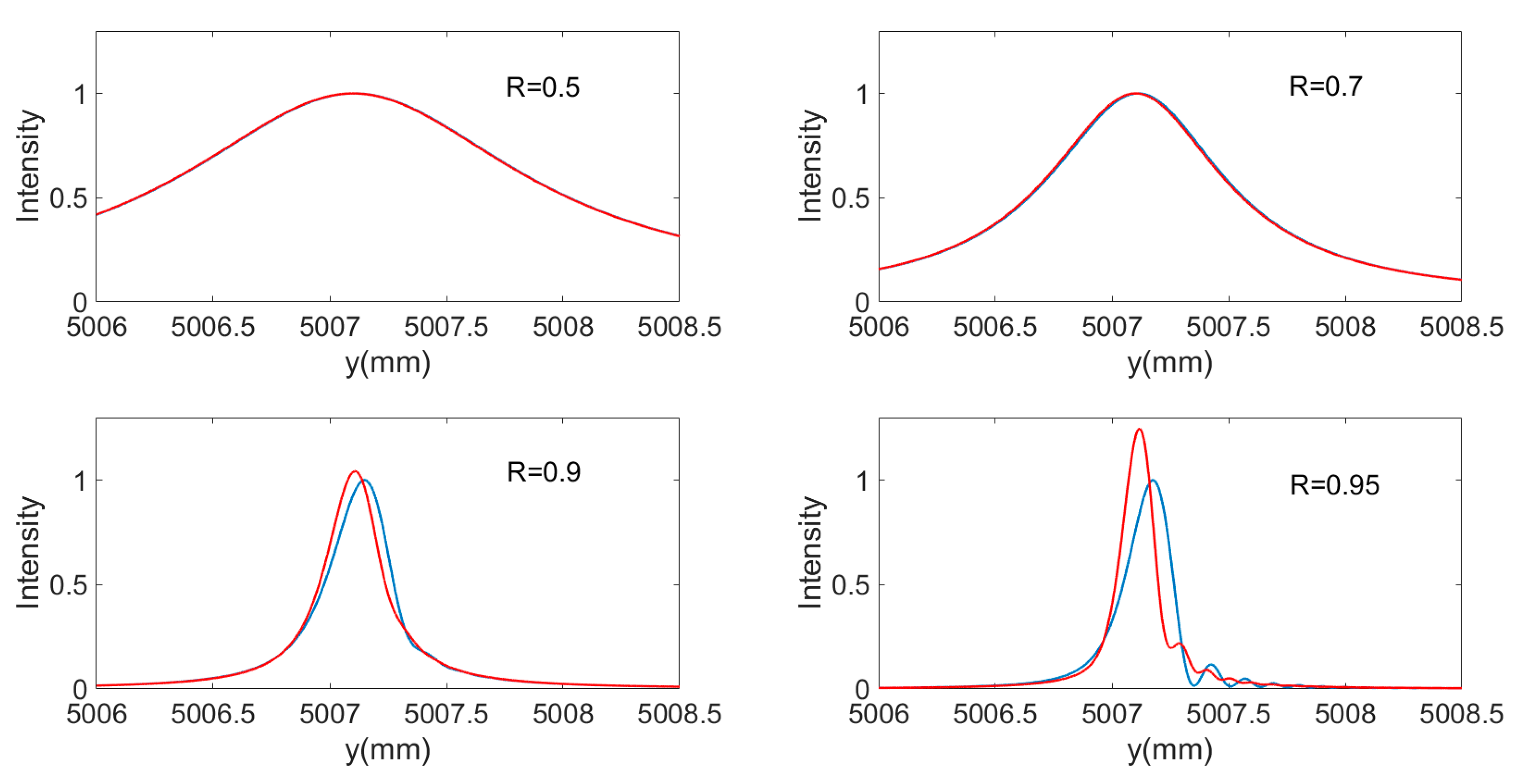
4. Intensity Optimization
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gillard, F.; Ferrec, Y.; Guérineau, N.; Rommeluère, S.; Taboury, J.; Chavel, P. Angular acceptance analysis of an infrared focal plane array with a built-in stationary Fourier transform spectrometer. JOSA A 2012, 29, 936–944. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Guerineau, N.; Rommeluere, S.; Deschamps, J.; De Borniol, E.; Million, A.; Chamonal, J.P.; Destefanis, G. Infrared focal plane array with a built-in stationary fourier-transform spectrometer: First experimental results. In Proceedings of the Fourier Transform Spectroscopy, Alexandria, VA, USA, 31 January–3 February 2005. [Google Scholar]
- Guerineau, N.; Suffis, S.; Cymbalista, P.; Primot, J. Conception of a stationary Fourier transform infrared spectroradiometer for field measurements of radiance and emissivity. In Proceedings of the Optical Design and Engineering, St. Etienne, France, 18 February 2004; Volume 5249, pp. 441–448. [Google Scholar]
- Gillard, F.; Rommeluère, S.; de la Barrière, F.; Druart, G.; Guérineau, N.; Ferrec, Y.; Lefebvre, S.; Fendler, M.; Taboury, J. Towards a handheld cryogenic FTIR spectrometer. In Proceedings of the Fourier Transform Spectroscopy, Toronto, ON, Canada, 10–14 July 2011. [Google Scholar]
- Ferrec, Y.; Rommeluère, S.; Lefebvre, S.; Benoît, C.; Gillard, F.; Guérineau, N. Infrared focal plane array with a built-in stationary Fourier-transform spectrometer (MICROSPOC): Physical limitations and numerical solutions. In Proceedings of the Fourier Transform Spectroscopy, Toronto, ON, Canada, 10–14 July 2011. [Google Scholar]
- Ferrec, Y.; de la Barrière, F.; le Coarer, E.; Diard, T.; Guérineau, N.; Martin, G.; Rommeluère, S.; Schmitt, B.; Thomas, F. Current status and perspectives for Microspoc, the miniature Fourier transform spectrometer. In Proceedings of the Fourier Transform Spectroscopy, Lake Arrowhead, CA, USA, 1–4 March 2015. [Google Scholar]
- Rommeluère, S.; Haïdar, R.; Guérineau, N.; Deschamps, J.; De Borniol, E.; Million, A.; Chamonal, J.P.; Destefanis, G. Single-scan extraction of two-dimensional parameters of infrared focal plane arrays utilizing a Fourier-transform spectrometer. Appl. Opt. 2007, 46, 1379–1384. [Google Scholar] [CrossRef] [PubMed]
- Novák, O.; Falconer, I.S.; Sanginés, R.; Lattemann, M.; Tarrant, R.N.; McKenzie, D.R.; Bilek, M.M.M. Fizeau interferometer system for fast high-resolution studies of spectral line shapes. Rev. Sci. Instrum. 2011, 82, 023105. [Google Scholar] [CrossRef] [PubMed]
- Bae, W.; Kim, Y. Phase extraction formula for glass thickness measurement using Fizeau interferometer. J. Mech. Sci. Technol. 2021, 35, 1623–1632. [Google Scholar] [CrossRef]
- Kim, Y.; Hibino, K.; Sugita, N.; Mitsuishi, M. Error-compensating phase-shifting algorithm for surface shape measurement of transparent plate using wavelength-tuning Fizeau interferometer. Opt. Lasers Eng. 2016, 86, 309–316. [Google Scholar] [CrossRef]
- Emadi, A.; Wu, H.; de Graaf, G.; Wolffenbuttel, R. Design and implementation of a sub-nm resolution microspectrometer based on a Linear-Variable Optical Filter. Opt. Express 2012, 20, 489–507. [Google Scholar] [CrossRef] [PubMed]
- DeCorby, R.G.; Ponnampalam, N.; Epp, E.; Allen, T.; McMullin, J.N. Chip-scale spectrometry based on tapered hollow Bragg waveguides. Opt. Express 2009, 17, 16632–16645. [Google Scholar] [CrossRef] [PubMed]
- Langenbeck, P. Fizeau interferometer–fringe sharpening. Appl. Opt. 1970, 9, 2053–2058. [Google Scholar] [CrossRef] [PubMed]
- Kajava, T.T.; Lauranto, H.M.; Friberg, A.T. Interference pattern of the Fizeau interferometer. JOSA A 1994, 11, 2045–2054. [Google Scholar] [CrossRef]
- Vasil’ev, K.K.; Dement’ev, V.E.; Andriyanov, N.A. Doubly stochastic models of images. Pattern Recognit. Image Anal. 2015, 25, 105–110. [Google Scholar] [CrossRef]
- Shirokanev, A.S.; Kibitkina, A.S.; Ilyasova NY, E.; Degtyaryov, A.A. Methods of mathematical modeling of fundus laser exposure for therapeutic effect evaluation. Comput. Opt. 2020, 44, 809–820. [Google Scholar] [CrossRef]
- Shirokanev, A.S.; Andriyanov, N.A.; Ilyasova, N.Y. Development of vector algorithm using CUDA technology for three-dimensional retinal laser coagulation process modeling. Comput. Opt. 2021, 45, 427–437. [Google Scholar] [CrossRef]
- Brossel, J. Multiple-beam localized fringes: Part I.-Intensity distribution and localization. Proc. Phys. Soc. 1947, 59, 224. [Google Scholar] [CrossRef]
- Brossel, J. Multiple-beam localized fringes: Part II.-Conditions of observation and formation of ghosts. Proc. Phys. Soc. 1947, 59, 234. [Google Scholar] [CrossRef]
- Meyer, Y.H. Fringe shape with an interferential wedge. JOSA 1981, 71, 1255–1263. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, B.; Zheng, Y.; Lin, C.; Zhang, H. A Convenient Way to Determine the Optimum Angle of Incidence of Fizeau Interferometer. Appl. Sci. 2021, 11, 10678. https://doi.org/10.3390/app112210678
Du B, Zheng Y, Lin C, Zhang H. A Convenient Way to Determine the Optimum Angle of Incidence of Fizeau Interferometer. Applied Sciences. 2021; 11(22):10678. https://doi.org/10.3390/app112210678
Chicago/Turabian StyleDu, Bowen, Yuquan Zheng, Chao Lin, and Hang Zhang. 2021. "A Convenient Way to Determine the Optimum Angle of Incidence of Fizeau Interferometer" Applied Sciences 11, no. 22: 10678. https://doi.org/10.3390/app112210678
APA StyleDu, B., Zheng, Y., Lin, C., & Zhang, H. (2021). A Convenient Way to Determine the Optimum Angle of Incidence of Fizeau Interferometer. Applied Sciences, 11(22), 10678. https://doi.org/10.3390/app112210678





