Topology Optimization of Deformable Bodies with Linear Dynamic Impact and Frictionless Contact Condition
Abstract
1. Introduction
2. Linear Dynamic Analysis with Condensed Localized Mortar Method
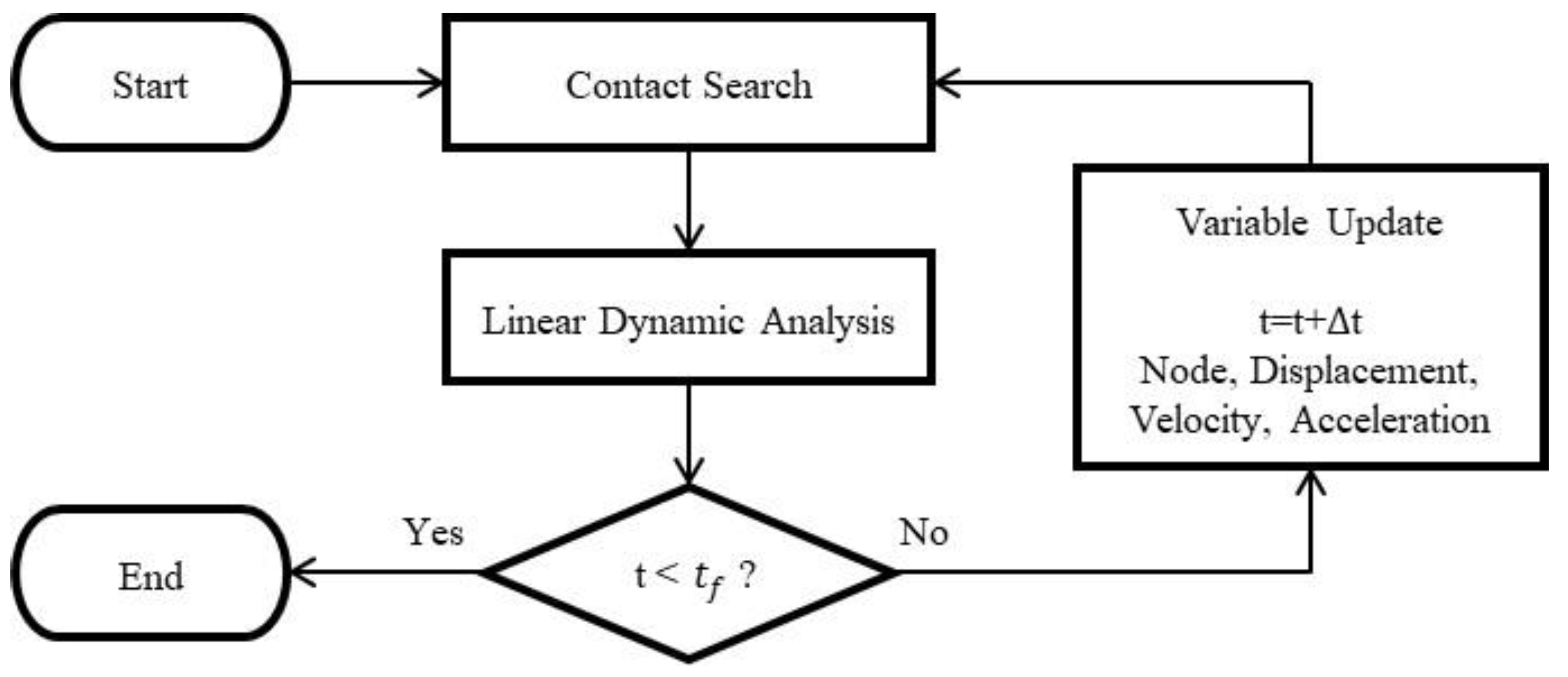
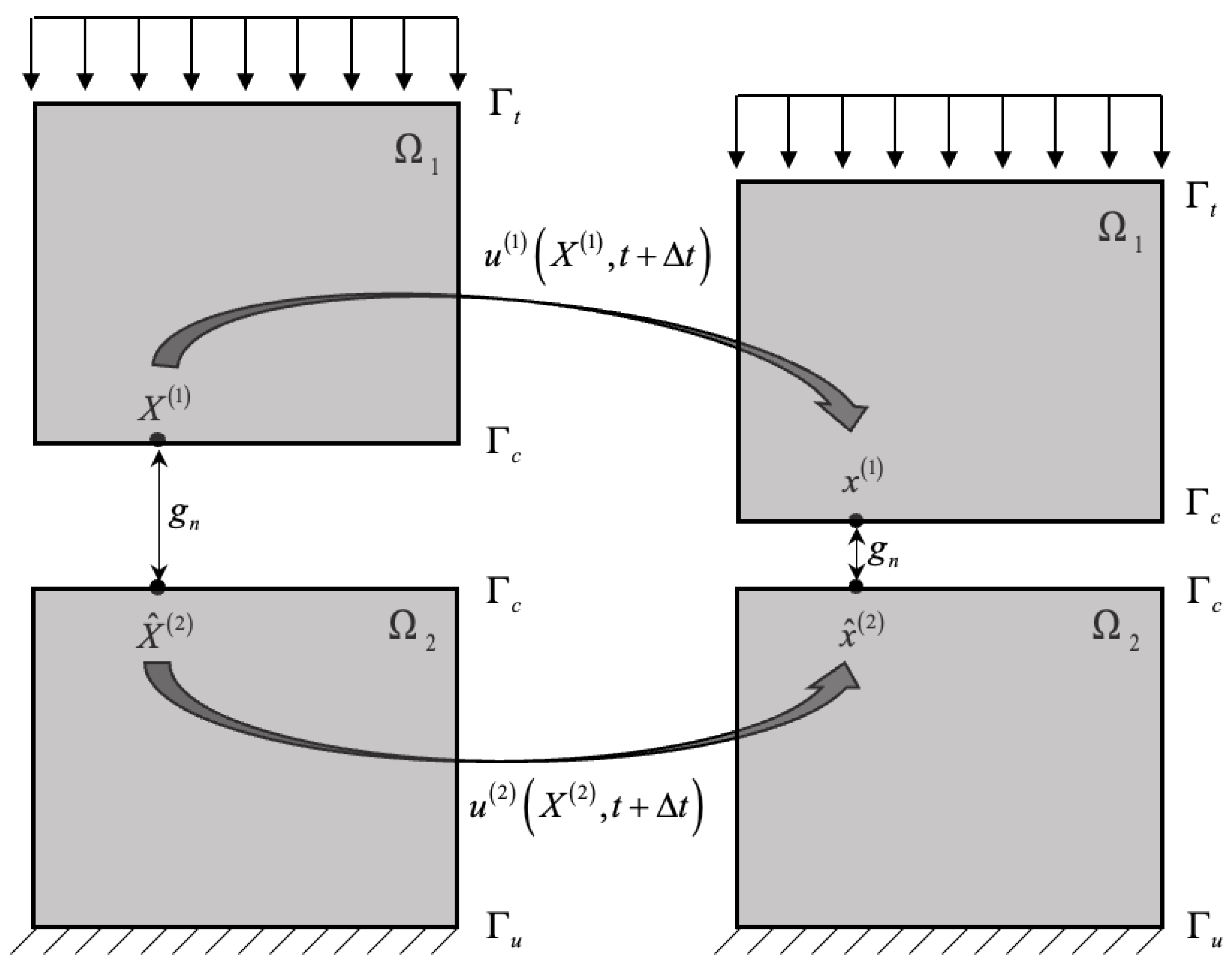
2.1. Linear Dynamic Finite Element Analysis Considering Contact Condition
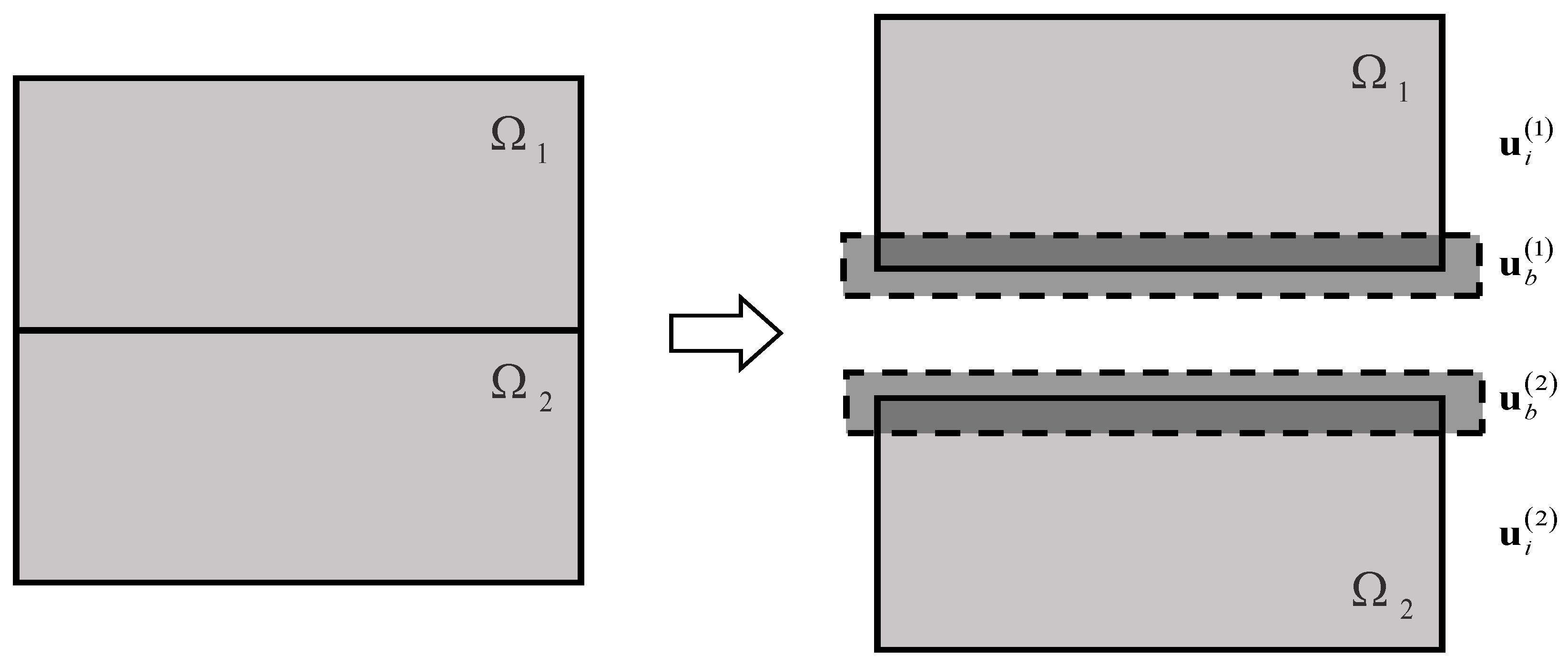
2.2. Application of Condensed Localized Mortar Method in Linear Dynamic Analysis
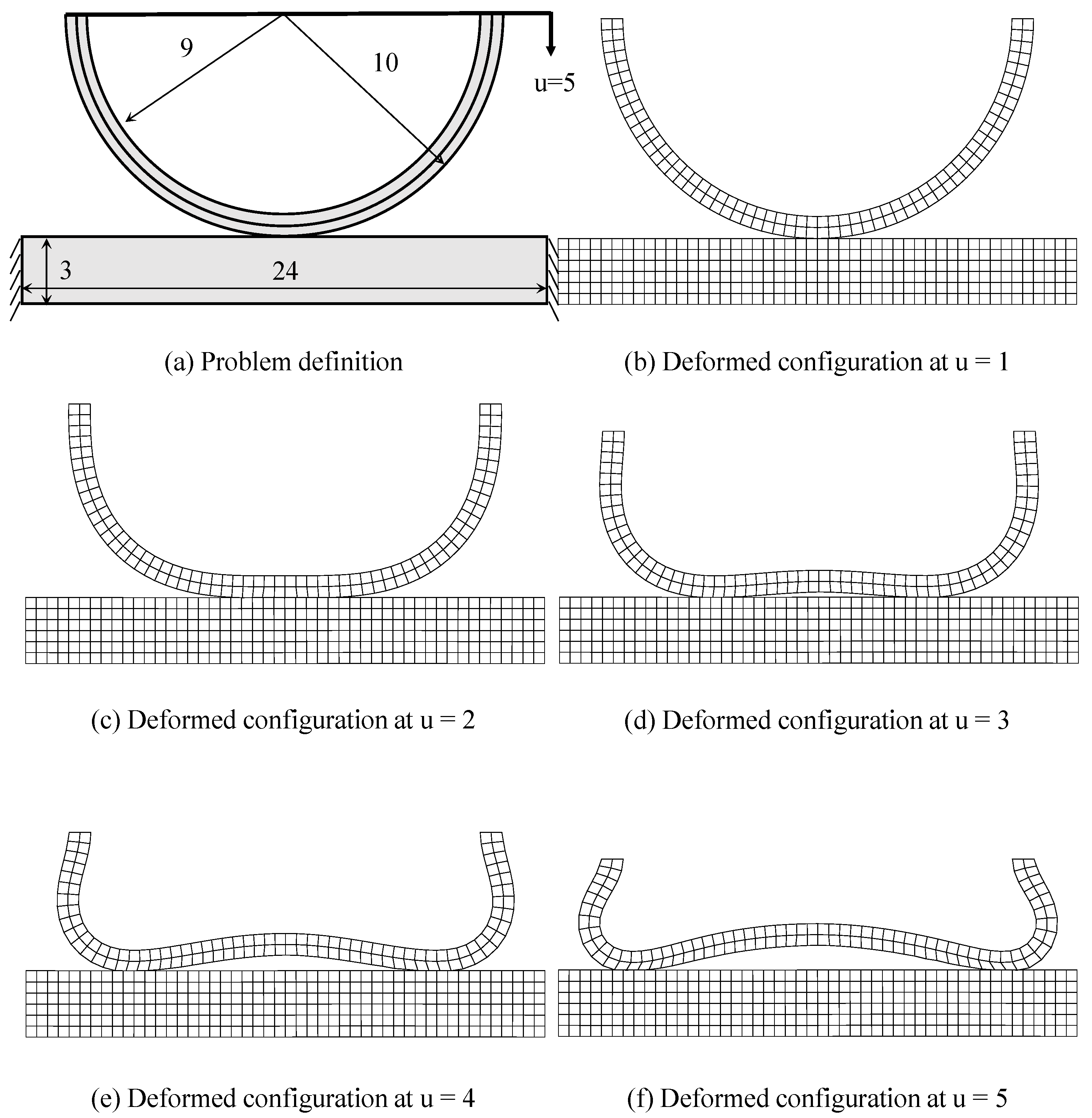
2.3. Verification Example for Linear Dynamic Impact and Frictionless Contact Problem
3. Dynamic Response Topology Optimization with Condensed Localized Mortar Method
3.1. Optimization Formulation with Condensed Localized Mortar Method
3.2. Verification Example for Dynamic Response Topology Optimization
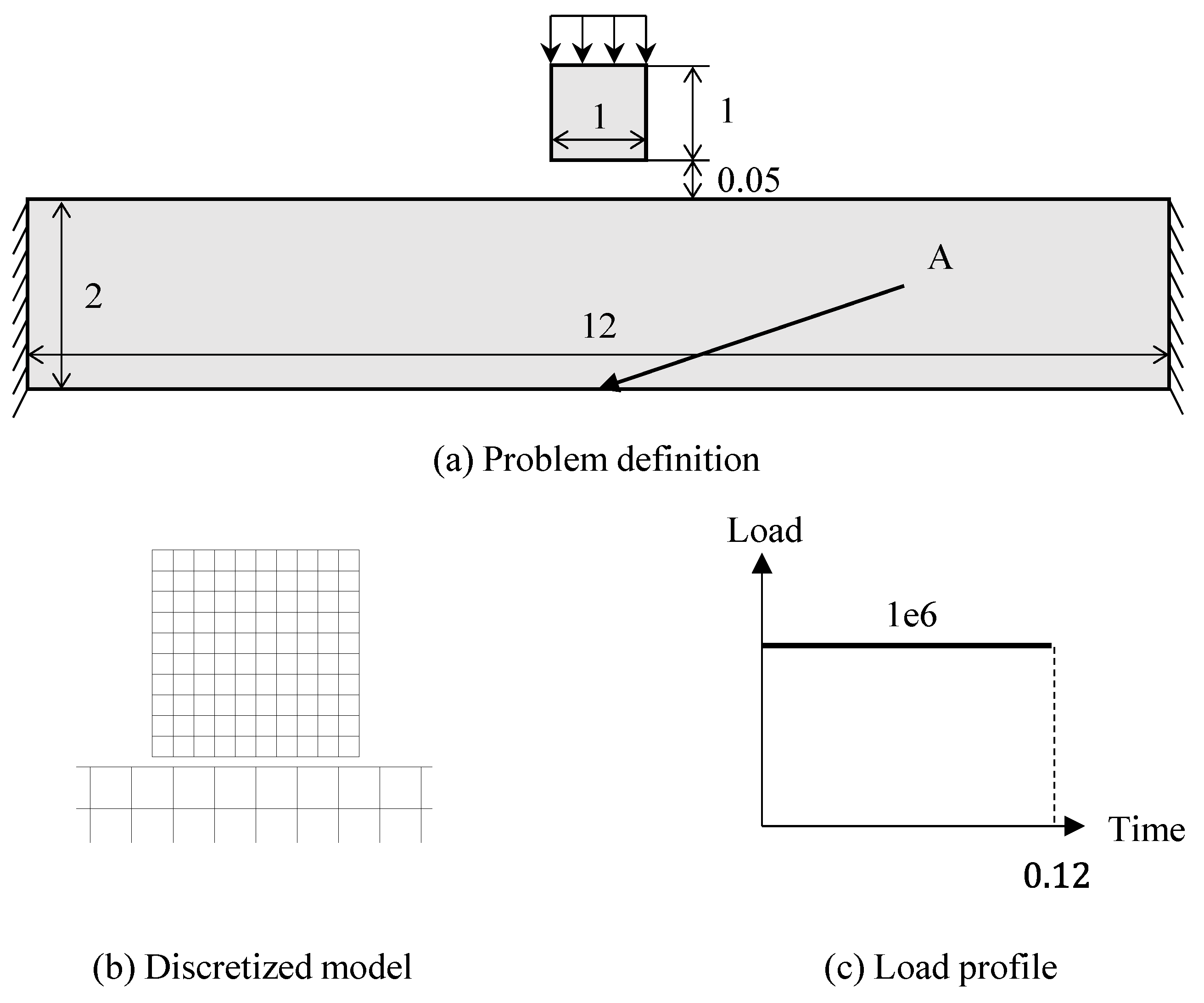
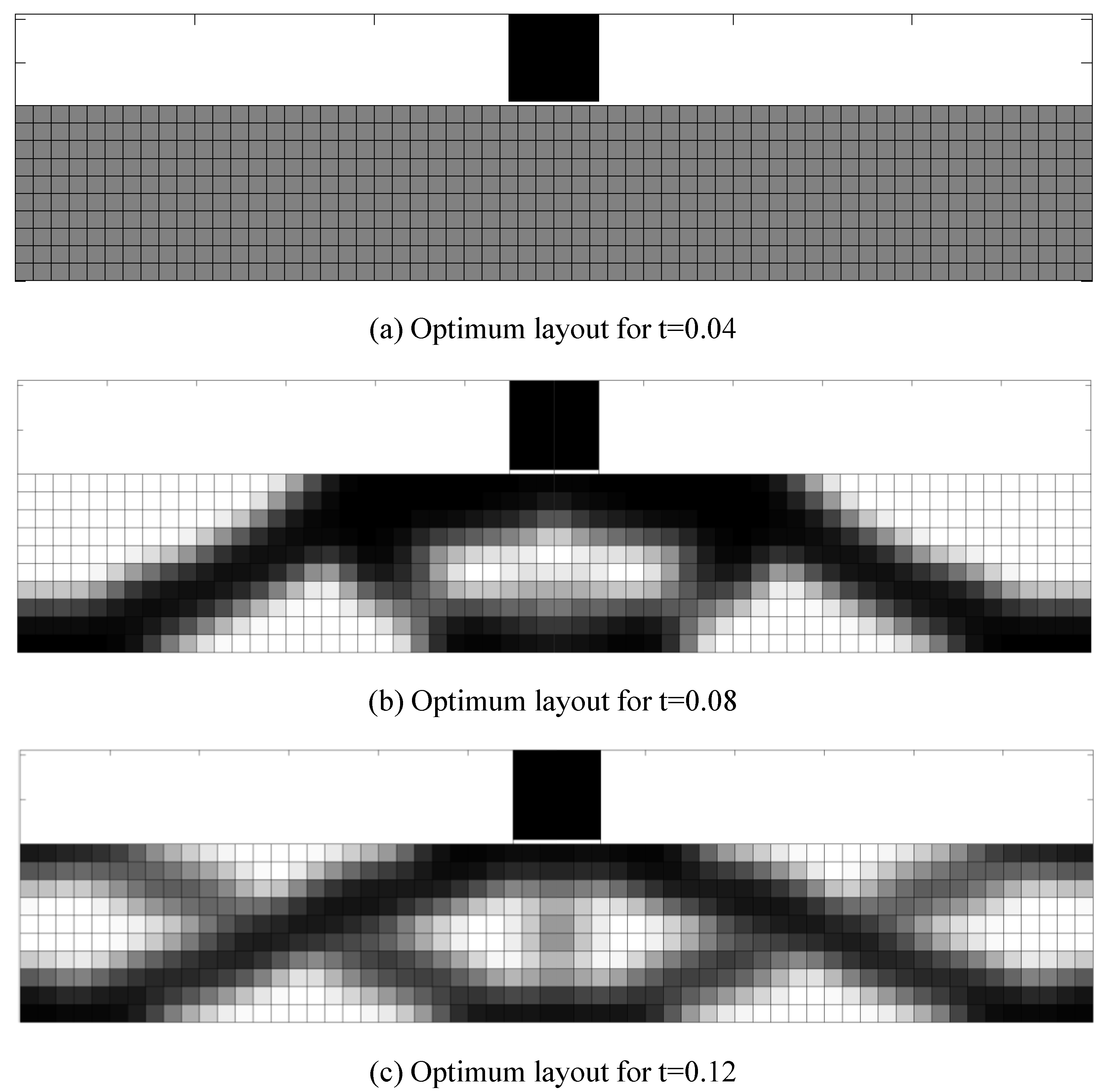
4. Numerical Example: Impact between Fixed Beam and Flying Block
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations/Nomenclature
| Domain for domain “i” | |
| Boundary (Subscript, u: Dirichlet, t: Neumann, c: Contact) | |
| Position for un-deformed domain “i” | |
| Position for deformed domain “i” | |
| Density | |
| Young’s modulus | |
| First Piola-Kirchhoff stress tensor | |
| External body force | |
| Displacement for domain “i” | |
| Gap function in normal direction | |
| Contact traction in normal direction | |
| Algorithmic parameter for Newmark method | |
| Lagrange multiplier | |
| Internal force vector | |
| Contact force vector | |
| External force vector | |
| Design variable for topology optimization | |
| Objective function for topology optimization | |
| Volume constraint for topology optimization | |
| Adjoint variable for topology optimization | |
| Transformed adjoint variable |
References
- Vaneker, T.; Bernard, A.; Moroni, G.; Gibson, I.; Zhang, Y. Design for Additive Manufacturing: Framework and Methodology. CIRP Ann. Manuf. Technol. 2020, 69, 578–599. [Google Scholar] [CrossRef]
- Kathryn, M.; Moroni, G.; Vaneker, T.; Fadel, G.; Campbell, I.; Gibson, I.; Bernard, A.; Schulz, J.; Graf, P.; Ahuja, B.; et al. Design for Additive Manufacturing: Trends, Opportunities, Considerations, and Constraints. CIRP Ann. Manuf. Technol. 2016, 65, 737–760. [Google Scholar] [CrossRef]
- Meng, L.; Zhang, W.; Quan, D.; Shi, G.; Tang, L.; Hou, Y.; Breitkopf, P.; Zhu, J.; Gao, T. From Topology Optimization Design to Additive Manufacturing: Today’s Success and Tomorrow’s Roadmap. Arch. Comput. Methods Eng. 2020, 27, 805–830. [Google Scholar] [CrossRef]
- Liu, J.; Gaynor, A.T.; Chen, S.; Kang, Z.; Suresh, K.; Takezawa, A.; Li, L.; Kato, J.; Tang, J.; Wang, C.C.L.; et al. Current and Future Trends in Topology Optimization for Additive Manufacturing. Struct. Multidiscip. Optim. 2018, 57, 2457–2483. [Google Scholar] [CrossRef]
- Guo, X.; Zhou, J.; Zhang, W.; Du, Z.; Liu, C.; Liu, Y. Self-Supporting Structure Design in Additive Manufacturing Through Explicit Topology Optimization. Comput. Methods Appl. Mech. Eng. 2017, 323, 27–63. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Sigmund, O. Topology Optimization-Theory, Methods and Applications; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Sigmund, O.; Maute, K. Topology Optimization Approaches. Struct. Multidiscip. Optim. 2013, 48, 1031–1055. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Kikuchi, N. Generating Optimal Topologies in Structural Design Using a Homogenization Method. Comput. Methods Appl. Mech. Eng. 1988, 71, 197–224. [Google Scholar] [CrossRef]
- Andreassen, E.; Clausen, A.; Schevenels, M.; Lazarov, B.S.; Sigmund, O. Efficient Topology Optimization in MATLAB Using 88 Lines of Code. Struct. Multidiscip. Optim. 2011, 43, 811–825. [Google Scholar] [CrossRef]
- Sigmund, O. A 99 Line Topology Optimization Code Written in MATLAB. Struct. Multidiscip. Optim. 2001, 21, 120–127. [Google Scholar] [CrossRef]
- Deaton, J.D.; Grandhi, R.V. A Survey of Structural and Multidisciplinary Continuum Topology Optimization: Post 2000. Struct. Multidiscip. Optim. 2014, 49, 1–38. [Google Scholar] [CrossRef]
- Sigmund, O. Morphology-Based Black and White Filters for Topology Optimization. Struct. Multidiscip. Optim. 2007, 33, 401–424. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, C. Dynamic Response Topology Optimization in the Time Domain Using Model Reduction Method. Struct. Multidiscip. Optim. 2016, 53, 101–114. [Google Scholar] [CrossRef]
- Mankame, N.D.; Ananthasuresh, G.K. Topology Optimization for Synthesis of Contact-Aided Compliant Mechanisms Using Regularized Contact Modeling. Comput. Struct. 2004, 82, 1267–1290. [Google Scholar] [CrossRef]
- Hilding, D.; Klarbring, A. Optimization of Structures in Frictional Contact. Comput. Methods Appl. Mech. Eng. 2012, 205–208, 83–90. [Google Scholar] [CrossRef][Green Version]
- Luo, Y.; Li, M.; Kang, Z. Topology Optimization of Hyperelastic Structures with Frictionless Contact Supports. Int. J. Solids Struct. 2016, 81, 373–382. [Google Scholar] [CrossRef]
- Strömberg, N.; Klarbring, A. Topology Optimization of Structures in Unilateral Contact. Struct. Multidiscip. Optim. 2010, 41, 57–64. [Google Scholar] [CrossRef]
- Strömberg, N. Topology Optimization of Two Linear Elastic Bodies in Unilateral Contact. In Proceedings of the 2nd International Conference Engenharia Optimisation, Lisbon, Portugal, 6–9 September 2010; pp. 1–8. [Google Scholar]
- Jeong, G.E.; Youn, S.K.; Park, K.C. Topology Optimization of Deformable Bodies with Dissimilar Interfaces. Comput. Struct. 2018, 198, 1–11. [Google Scholar] [CrossRef]
- Fernandez, F.; Puso, M.A.; Solberg, J.; Tortorelli, D.A. Topology Optimization of Multiple Deformable Bodies in Contact with Large Deformations. Comput. Methods Appl. Mech. Eng. 2020, 371, 113288. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method. J. Solid Mech. 2000. [Google Scholar]
- Fujun, W.; Jiangang, C.; Zhenhan, Y. A Contact Searching Algorithm for Contact-Impact Problems. Acta Mech. Sin. 2000, 16, 374–382. [Google Scholar] [CrossRef]
- Newmark, N.M. A Method of Computation for Structural Dynamics. J. Eng. Mech. Div. 1959, 85, 67–94. [Google Scholar] [CrossRef]
- Fischer, K.A.; Wriggers, P. Frictionless 2D Contact Formulations for Finite Deformations Based on the Mortar Method. Comput. Mech. 2005, 36, 226–244. [Google Scholar] [CrossRef]
- Hesch, C.; Betsch, P. A Mortar Method for Energy-Momentum Conserving Schemes in Frictionless Dynamic Contact Problems. Int. J. Numer. Methods Eng. 2009, 77, 1468–1500. [Google Scholar] [CrossRef]
- Flemisch, B.; Puso, M.A.; Wohlmuth, B.I. A New Dual Mortar Method for Curved Interfaces: 2D Elasticity. Int. J. Numer. Methods Eng. 2005, 63, 813–832. [Google Scholar] [CrossRef]
- Puso, M.A. A 3D Mortar Method for Solid Mechanics. Int. J. Numer. Meth. Eng. 2004, 59, 315–336. [Google Scholar] [CrossRef]
- Park, K.C.; Felippa, C.A. A Variational Principle for the Formulation of Partitioned Structural Systems. Int. J. Numer. Meth. Eng. 2000, 47, 395–418. [Google Scholar] [CrossRef]
- Park, K.C.; Felippa, C.A.; Gumaste, U.A. A Localized Version of the Method of Lagrange Multipliers and Its Applications. Comput. Mech. 2000, 24, 476–490. [Google Scholar] [CrossRef]
- Park, K.C.; Felippa, C.A.; Rebel, G. A Simple Algorithm for Localized Construction of Non-Matching Structural Interfaces. Int. J. Numer. Meth. Eng. 2002, 53, 2117–2142. [Google Scholar] [CrossRef]
- Jeong, G.E.; Song, Y.U.; Youn, S.K.; Park, K.C. A New Approach for Nonmatching Interface Construction by the Method of Localized Lagrange Multipliers. Comput. Methods Appl. Mech. Eng. 2020, 361, 112728. [Google Scholar] [CrossRef]
- Song, Y.; Jeong, G.; Youn, S.; Park, K.C. Virtual Tetrahedral Gap Element to Connect Three-Dimensional Non-Coincident Interfaces. Finite Elem. Anal. Des. 2018, 152, 18–26. [Google Scholar] [CrossRef]
- Wriggers, P. Computational Contact Mechanics, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Min, S.; Kikuchi, N.; Park, Y.C.; Kim, S.; Chang, S. Optimal Topology Design of Structures Under Dynamic Loads. Struct. Optim. 1999, 17, 208–218. [Google Scholar] [CrossRef]
- Rong, J.H.; Xie, Y.M.; Yang, X.Y.; Liang, Q.Q. Topology Optimization of Structures Under Dynamic Response Constraints. J. Sound Vib. 2000, 234, 177–189. [Google Scholar] [CrossRef]

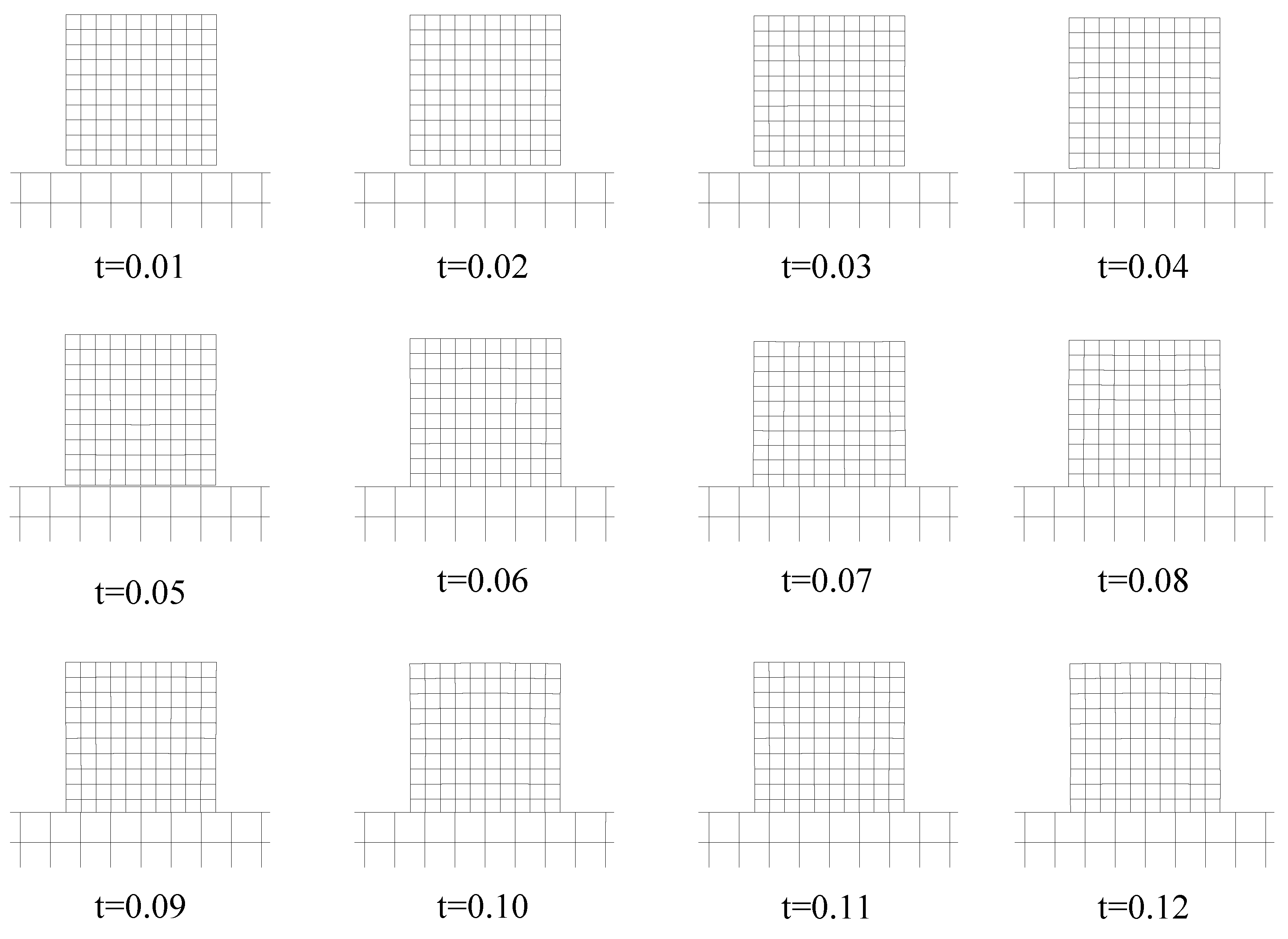
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeong, G.-E. Topology Optimization of Deformable Bodies with Linear Dynamic Impact and Frictionless Contact Condition. Appl. Sci. 2021, 11, 10518. https://doi.org/10.3390/app112210518
Jeong G-E. Topology Optimization of Deformable Bodies with Linear Dynamic Impact and Frictionless Contact Condition. Applied Sciences. 2021; 11(22):10518. https://doi.org/10.3390/app112210518
Chicago/Turabian StyleJeong, Gil-Eon. 2021. "Topology Optimization of Deformable Bodies with Linear Dynamic Impact and Frictionless Contact Condition" Applied Sciences 11, no. 22: 10518. https://doi.org/10.3390/app112210518
APA StyleJeong, G.-E. (2021). Topology Optimization of Deformable Bodies with Linear Dynamic Impact and Frictionless Contact Condition. Applied Sciences, 11(22), 10518. https://doi.org/10.3390/app112210518





