Unraveling Dissipation-Related Features in Magnetic Imaging by Bimodal Magnetic Force Microscopy
Abstract
:1. Introduction
2. Materials and Methods
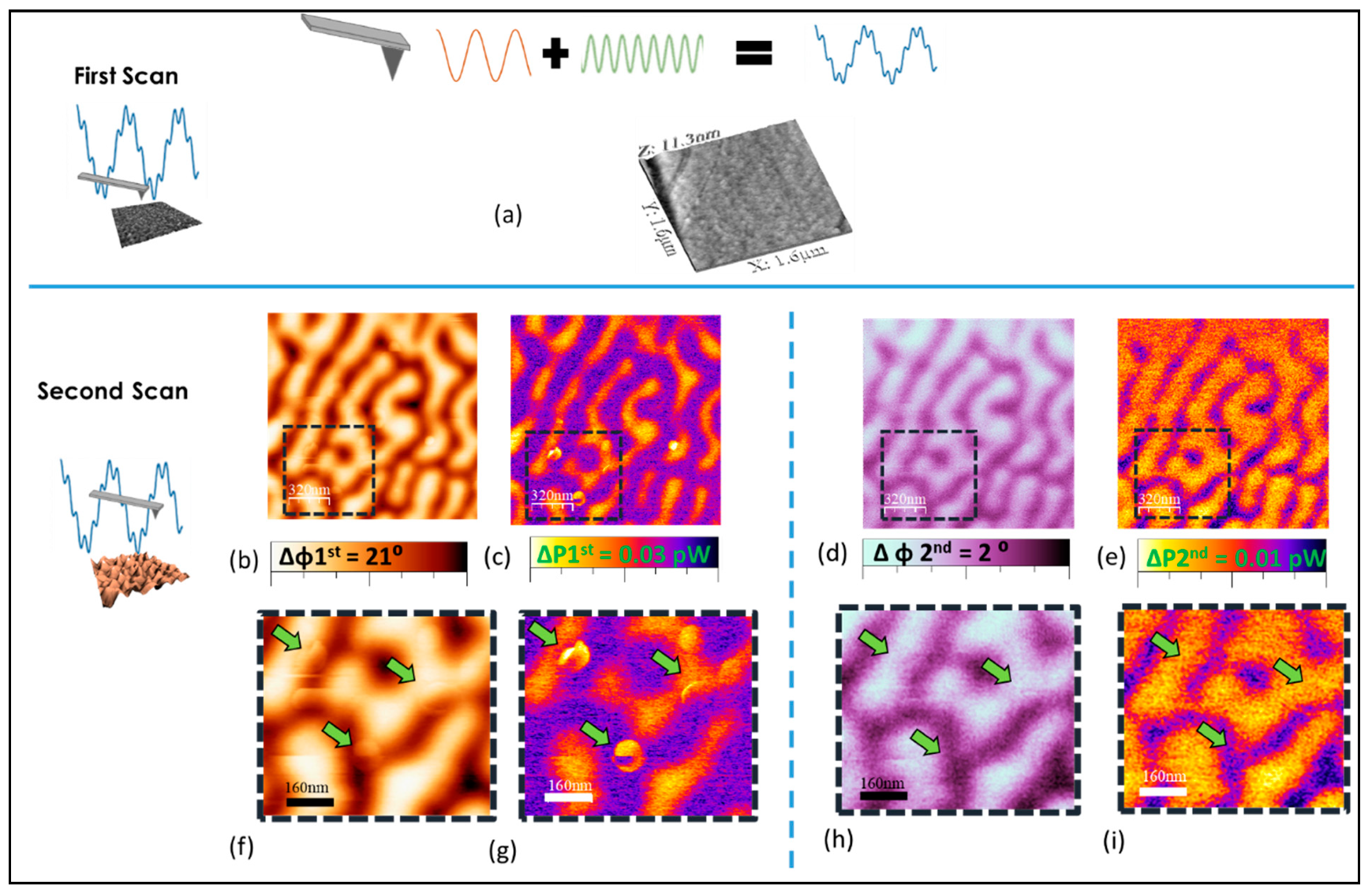
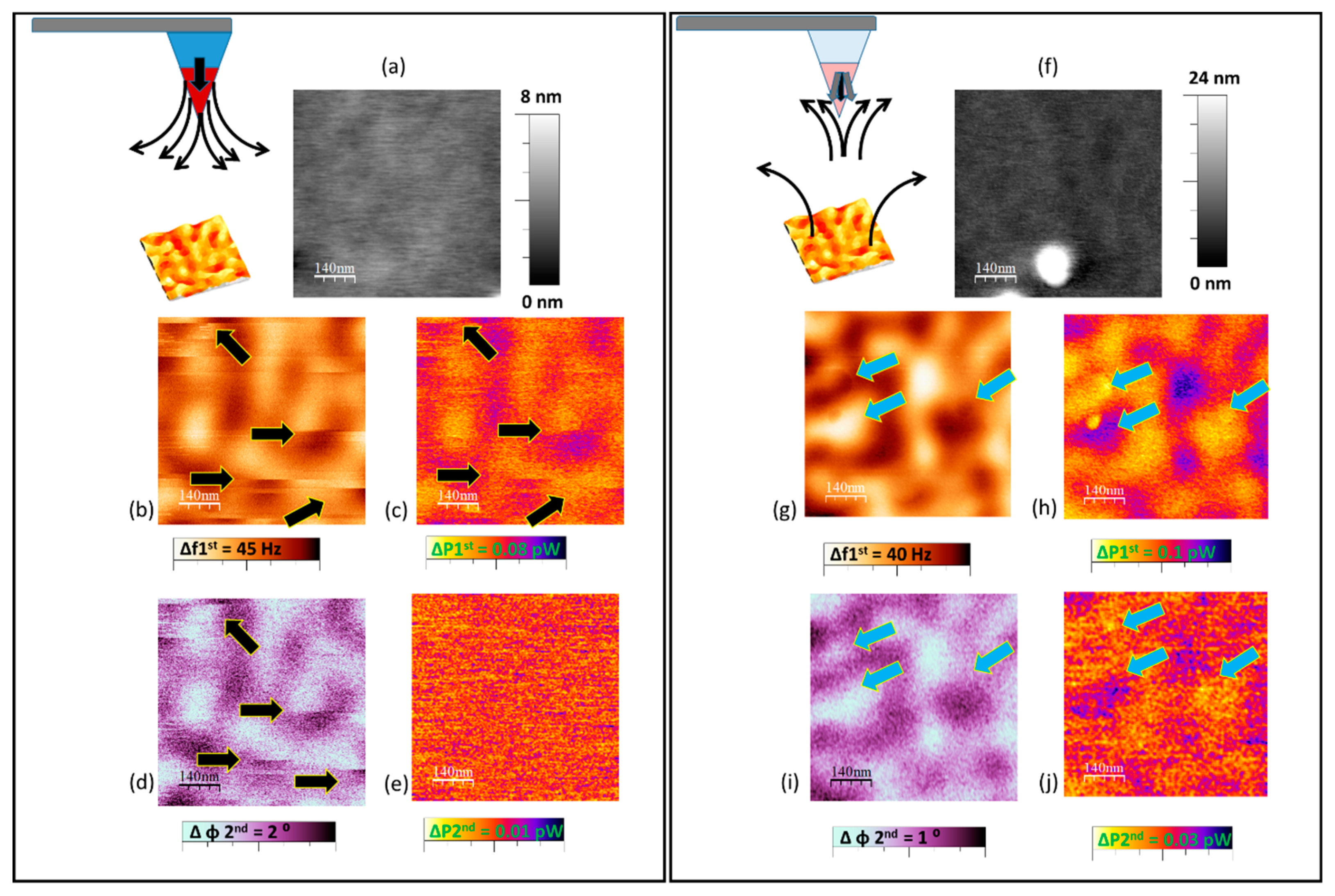
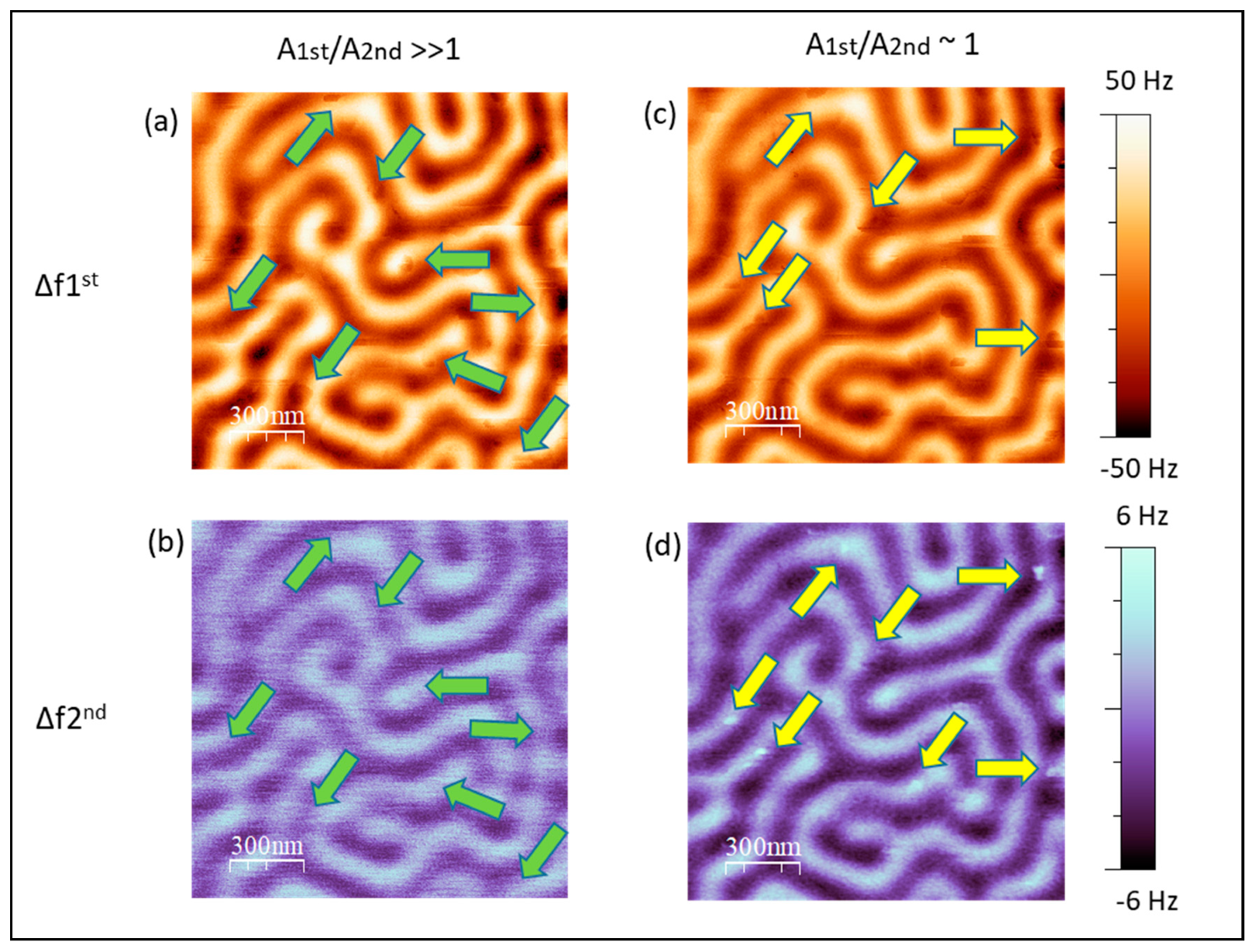
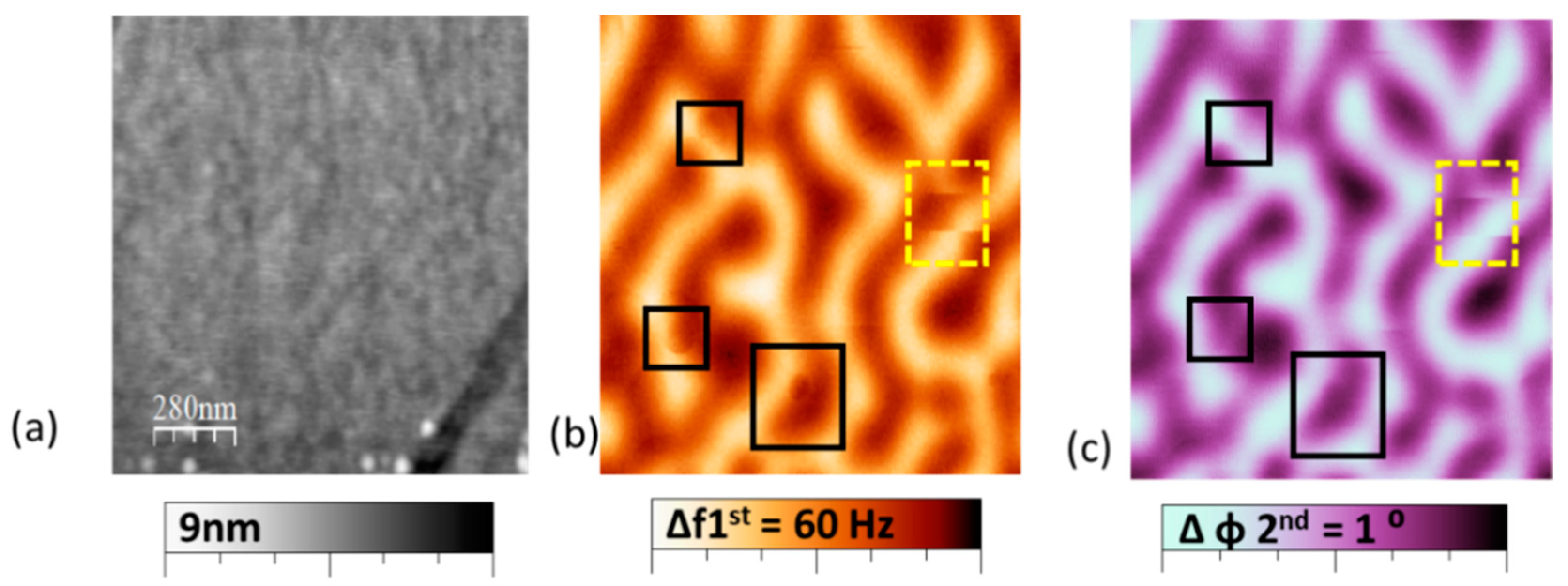
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Binnig, G.; Rohrer, H. Scanning tunneling microscopy. Surf. Sci. 1983, 126, 236–244. [Google Scholar] [CrossRef]
- Binnig, G.; Quate, C.F.; Gerber, C. Atomic Force Microscope. Phys. Rev. Lett. 1986, 56, 930. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sáenz, J.J.; García, N.; Grütter, P.; Meyer, E.; Heinzelmann, H.; Wiesendanger, R.; Rosenthaler, L.; Hidber, H.R.; Güntherodt, H.-J. Observation of magnetic forces by the atomic force microscope. J. Appl. Phys. 1998, 62, 4293. [Google Scholar] [CrossRef]
- Martin, Y.; Wickramasinghe, H.K. Magnetic imaging by “force microscopy” with 1000 Å resolution. Appl. Phys. Lett. 1998, 50, 1455. [Google Scholar] [CrossRef]
- Kazakova, O.; Puttock, R.; Barton, C.; Corte-León, H.; Jaafar, M.; Neu, V.; Asenjo, A. Frontiers of magnetic force microscopy. J. Appl. Phys. 2019, 125, 060901. [Google Scholar] [CrossRef]
- Rastei, M.V.; Meckenstock, R.; Bucher, J.P. Nanoscale hysteresis loop of individual Co dots by field-dependent magnetic force microscopy. Appl. Phys. Lett. 2005, 87, 222505. [Google Scholar] [CrossRef]
- Schwarz, A.; Wiesendanger, R. Magnetic sensitive force microscopy. Nano Today 2008, 3, 28–39. [Google Scholar] [CrossRef]
- Jaafar, M.; Gómez-Herrero, J.; Gil, A.; Ares, P.; Vázquez, M.; Asenjo, A. Variable-field magnetic force microscopy. Ultramicroscopy 2009, 109, 693–699. [Google Scholar] [CrossRef]
- Coïsson, M.; Barrera, G.; Celegato, F.; Manzin, A.; Vinai, F.; Tiberto, P. Magnetic vortex chirality determination via local hysteresis loops measurements with magnetic force microscopy. Sci. Rep. 2016, 6, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Ares, P.; Jaafar, M.; Gil, A.; Gõmez-Herrero, J.; Asenjo, A. Magnetic Force Microscopy in Liquids. Small 2015, 11, 4731–4736. [Google Scholar] [CrossRef] [Green Version]
- Grütter, P.; Liu, Y.; LeBlanc, P.; Dürig, U. Magnetic dissipation force microscopy. Appl. Phys. Lett. 1998, 71, 279. [Google Scholar] [CrossRef] [Green Version]
- Torre, B.; Bertoni, G.; Fragouli, D.; Falqui, A.; Salerno, M.; Diaspro, A.; Cingolani, R.; Athanassiou, A. Magnetic Force Microscopy and Energy Loss Imaging of Superparamagnetic Iron Oxide Nanoparticles. Sci. Rep. 2011, 1, 1–8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Iglesias-Freire, Ó.; Bates, J.R.; Miyahara, Y.; Asenjo, A.; Grütter, P.H. Tip-induced artifacts in magnetic force microscopy images. Appl. Phys. Lett. 2013, 102, 022417. [Google Scholar] [CrossRef] [Green Version]
- Lohau, J.; Kirsch, S.; Carl, A.; Dumpich, G.; Wassermann, E.F. Quantitative determination of effective dipole and monopole moments of magnetic force microscopy tips. J. Appl. Phys. 1999, 86, 3410. [Google Scholar] [CrossRef]
- Hug, H.J.; Stiefel, B.; van Schendel, P.J.A.; Moser, A.; Hofer, R.; Martin, S.; Güntherodt, H.-J.; Porthun, S.; Abelmann, L.; Lodder, J.C.; et al. Quantitative magnetic force microscopy on perpendicularly magnetized samples. J. Appl. Phys. 1998, 83, 5609. [Google Scholar] [CrossRef] [Green Version]
- Vock, Z.S.S.; Alexei, L.S.; Bogdanov, N. Quantitative Magnetic Force Microscopy Study of the Diameter Evolution of Bubble Domains in a Co/Pd Multilayer. IEEE Trans. Magn. 2011, 47, 2352. Available online: https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=6028183 (accessed on 30 September 2021). [CrossRef]
- Benassi, A.; Marioni, A.M.; Passerone, D.; Hug, H.J. Role of interface coupling inhomogeneity in domain evolution in exchange bias ETH Library. Sci. Rep. 2014, 4, 4508. [Google Scholar] [CrossRef] [Green Version]
- Gisbert, V.G.; Amo, C.A.; Jaafar, M.; Asenjo, A.; Garcia, R. Quantitative mapping of magnetic properties at the nanoscale with bimodal AFM. Nanoscale 2021, 13, 2026–2033. [Google Scholar] [CrossRef]
- Garcia, R.; Herruzo, E.T. The emergence of multifrequency force microscopy. Nat. Nanotechnol. 2012, 7, 217–226. [Google Scholar] [CrossRef] [Green Version]
- Benaglia, S.; Gisbert, V.G.; Perrino, A.P.; Amo, C.A.; Garcia, R. Fast and high-resolution mapping of elastic properties of biomolecules and polymers with bimodal AFM. Nat. Protoc. 2018, 13, 2890–2907. [Google Scholar] [CrossRef]
- Thompson, H.T.; Barroso-Bujans, F.; Herrero, J.G.; Reifenberger, R.; Raman, A. Subsurface imaging of carbon nanotube networks in polymers with DC-biased multifrequency dynamic atomic force microscopy. Nanotechnology 2013, 24, 135701. [Google Scholar] [CrossRef] [PubMed]
- Li, J.W.; Cleveland, J.P.; Proksch, R. Bimodal magnetic force microscopy: Separation of short and long range forces. Appl. Phys. Lett. 2009, 94, 163118. [Google Scholar] [CrossRef]
- Dietz, C.; Herruzo, E.T.; Lozano, J.R.; Garcia, R. Nanomechanical coupling enables detection and imaging of 5 nm superparamagnetic particles in liquid. Nanotechnology 2011, 22, 125708. [Google Scholar] [CrossRef] [PubMed]
- Schwenk, J.; Marioni, M.; Romer, S.; Joshi, N.R.; Hug, H.J. Non-contact bimodal magnetic force microscopy. Appl. Phys. Lett. 2014, 104, 112412. [Google Scholar] [CrossRef] [Green Version]
- Iglesias-Freire, Ó.; Jaafar, M.; Berganza, E.; Asenjo, A. Customized MFM probes with high lateral resolution. Beilstein J. Nanotechnol. 2016, 7, 1068–1074. [Google Scholar] [CrossRef] [Green Version]
- Neu, V.; Vock, S.; Sturm, T.; Schultz, L. Epitaxial hard magnetic SmCo5 MFM tips—A new approach to advanced magnetic force microscopy imaging. Nanoscale 2018, 10, 16881–16886. [Google Scholar] [CrossRef]
- Jaafar, M.; Iglesias-Freire, Ó.; García-Mochales, P.; Sáenz, J.J.; Asenjo, A. Negative dissipation gradients in hysteretic materials. Nanoscale 2016, 8, 16989–16994. [Google Scholar] [CrossRef]
- Krivcov, A.; Junkers, T.; Möbius, H. Understanding electrostatic and magnetic forces in magnetic force microscopy: Towards single superparamagnetic nanoparticle resolution. J. Phys. Commun. 2018, 2, 075019. [Google Scholar] [CrossRef]
- Ciuta, G.; Dumas-Bouchiat, F.; Dempsey, N.M.; Fruchart, O. Some aspects of magnetic force microscopy of hard magnetic films. IEEE Trans. Magn. 2016, 52, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Cinar, I.; Lacour, D.; Montaigne, F.; Puliafito, V.; Watelot, S.P.; Hehn, M.; Finocchio, G.; Ozatay, O.; Hauet, T. Artifacts in magnetic force microscopy under in-plane applied magnetic field: Magnetic bubble as a case study. J. Magn. Magn. Mater. 2020, 500, 166296. [Google Scholar] [CrossRef]
- Jaafar, M.; Iglesias-Freire, O.; Serrano-Ramón, L.; Ibarra, M.R.; de Teresa, J.M.; Asenjo, A. Distinguishing magnetic and electrostatic interactions by a Kelvin probe force microscopy- magnetic force microscopy combination. Beilstein J. Nanotechnol. 2011, 2, 552–560. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Neves, C.S.; Quaresma, P.; Baptista, P.V.; Carvalho, P.A.; Araújo, J.P.; Pereira, E.; Eaton, P. New insights into the use of magnetic force microscopy to discriminate between magnetic and nonmagnetic nanoparticles. Nanotechnology 2010, 21, 305706. [Google Scholar] [CrossRef] [PubMed]
- Horcas, I.; Fernández, R.; Gómez-Rodríguez, J.M.; Colchero, J.; Gómez-Herrero, J.; Baro, A.M. WSXM: A software for scanning probe microscopy and a tool for nanotechnology. Rev. Sci. Instrum. 2007, 78, 013705. [Google Scholar] [CrossRef] [PubMed]
- Cleveland, J.P.; Anczykowski, B.; Schmid, A.E.; Elings, V.B. Energy dissipation in tapping-mode atomic force microscopy. Appl. Phys. Lett. 1998, 72, 2613. [Google Scholar] [CrossRef] [Green Version]
- Diaz, A.J.; Eslami, B.; López-Guerra, E.A.; Solares, S.D. Selection of higher eigenmode amplitude based on dissipated power and virial contrast in bimodal atomic force microscopy. J. Appl. Phys. 2014, 116, 104901. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jaafar, M.; Asenjo, A. Unraveling Dissipation-Related Features in Magnetic Imaging by Bimodal Magnetic Force Microscopy. Appl. Sci. 2021, 11, 10507. https://doi.org/10.3390/app112210507
Jaafar M, Asenjo A. Unraveling Dissipation-Related Features in Magnetic Imaging by Bimodal Magnetic Force Microscopy. Applied Sciences. 2021; 11(22):10507. https://doi.org/10.3390/app112210507
Chicago/Turabian StyleJaafar, Miriam, and Agustina Asenjo. 2021. "Unraveling Dissipation-Related Features in Magnetic Imaging by Bimodal Magnetic Force Microscopy" Applied Sciences 11, no. 22: 10507. https://doi.org/10.3390/app112210507
APA StyleJaafar, M., & Asenjo, A. (2021). Unraveling Dissipation-Related Features in Magnetic Imaging by Bimodal Magnetic Force Microscopy. Applied Sciences, 11(22), 10507. https://doi.org/10.3390/app112210507






