Research on the High Reliable Electromagnetic Stirring Power Supply
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Structure and Principle of High-Reliability Electromagnetic Stirring Power Supply
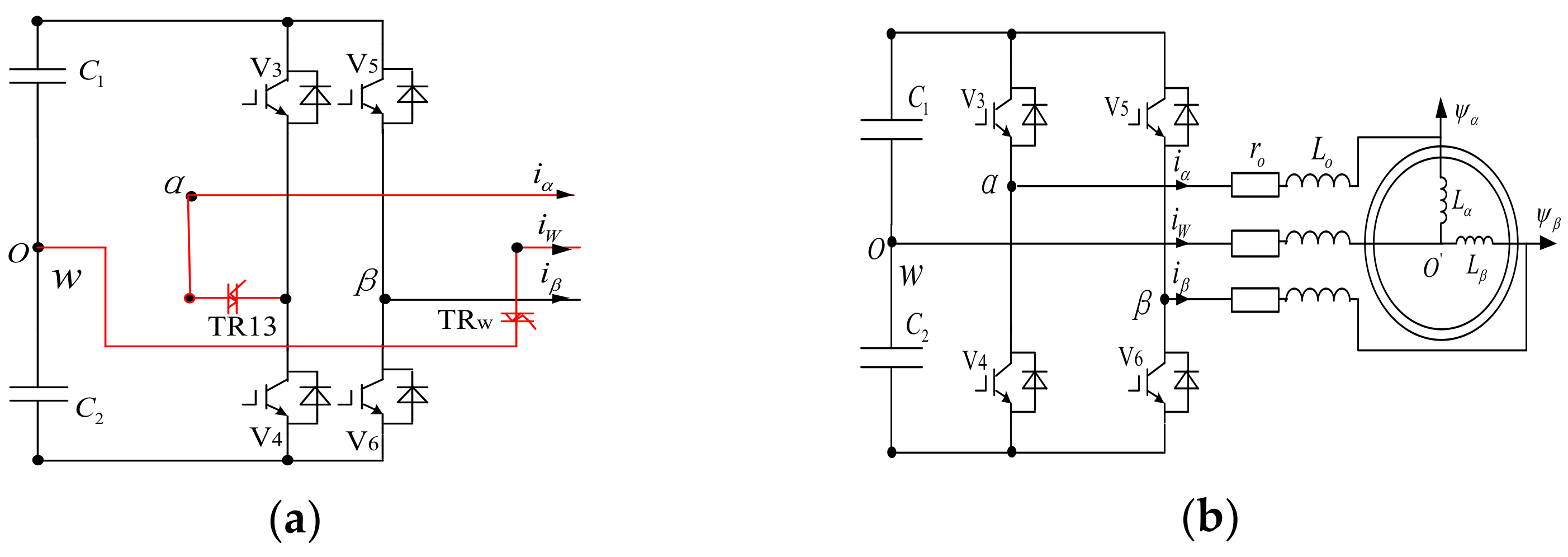
2.2. Fault Diagnosis and Reconstruction of the Back-Stage Two-Phase Quadrature Inverter
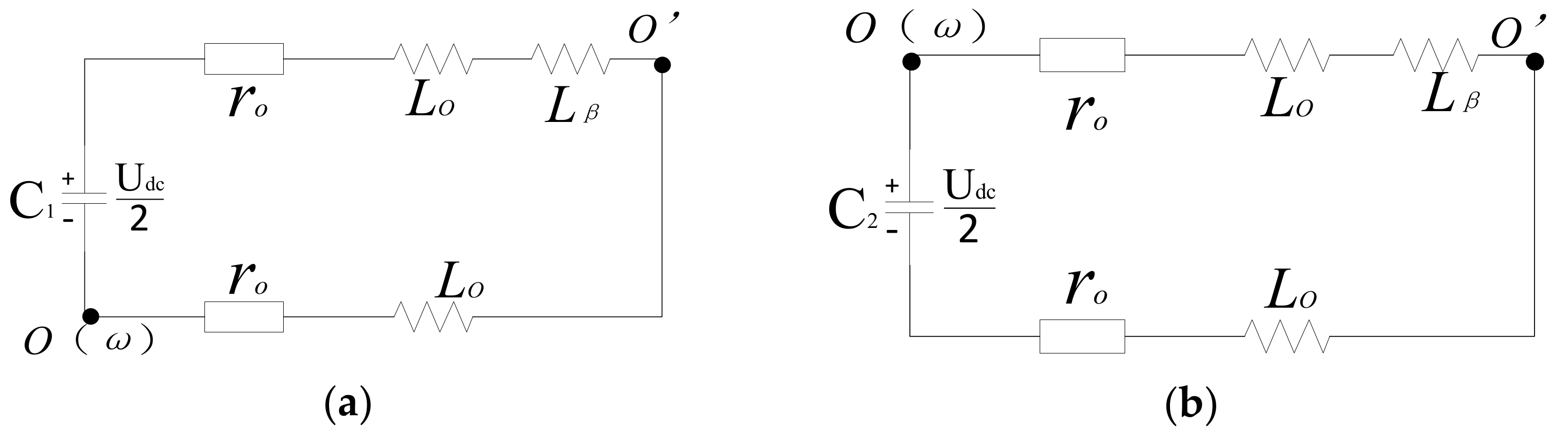
2.2.1. The Fault Diagnosis Algorithm and Reconstruction Strategy of the Back-Stage Two-Phase Quadrature Inverter after Primary Failure
2.2.2. The Fault Diagnosis Algorithm and Reconstruction Strategy after the Secondary Fault of the Back-Stage Two-Phase Quadrature Inverter
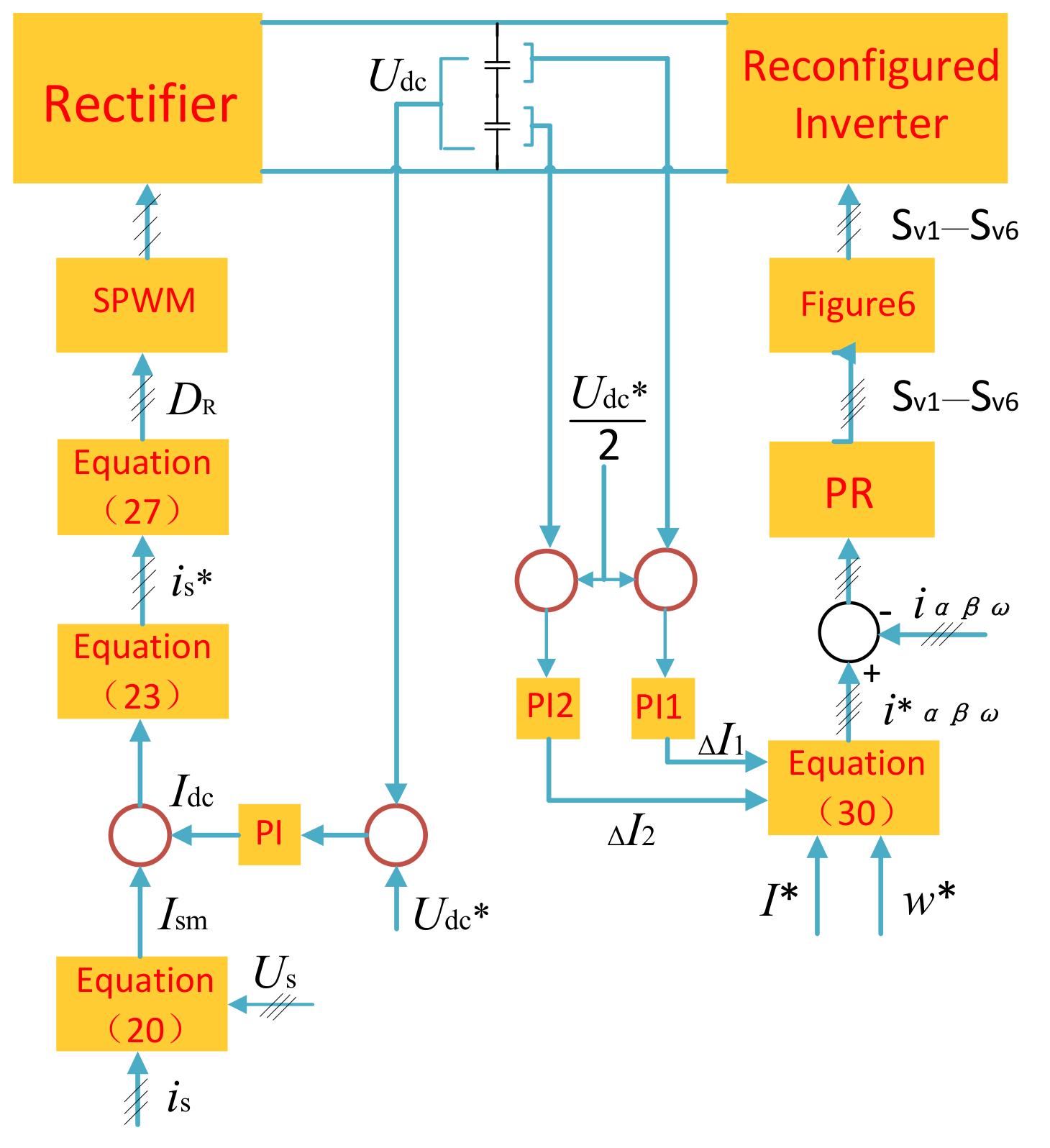
2.3. Fault-Tolerant Control Strategy
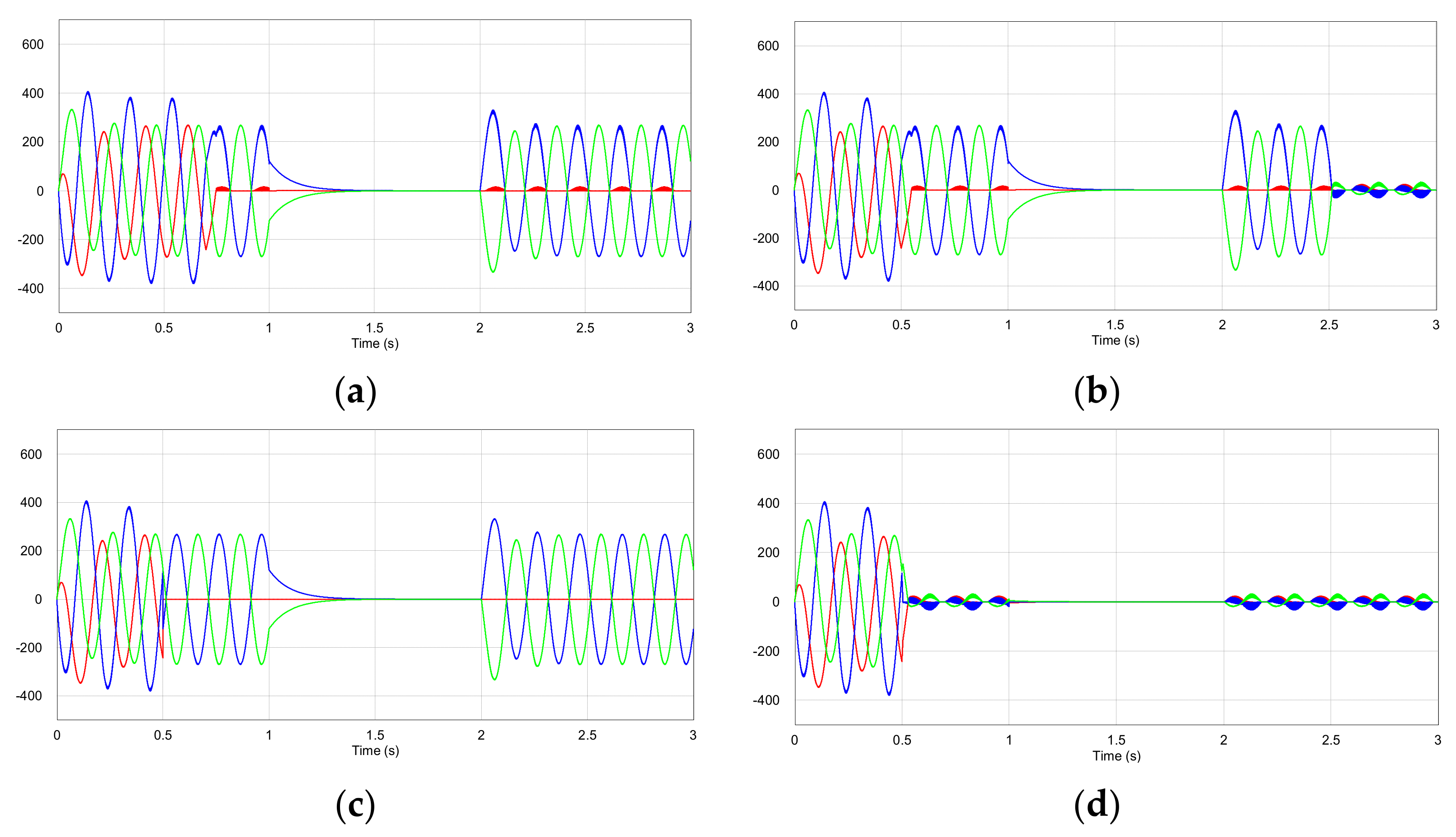
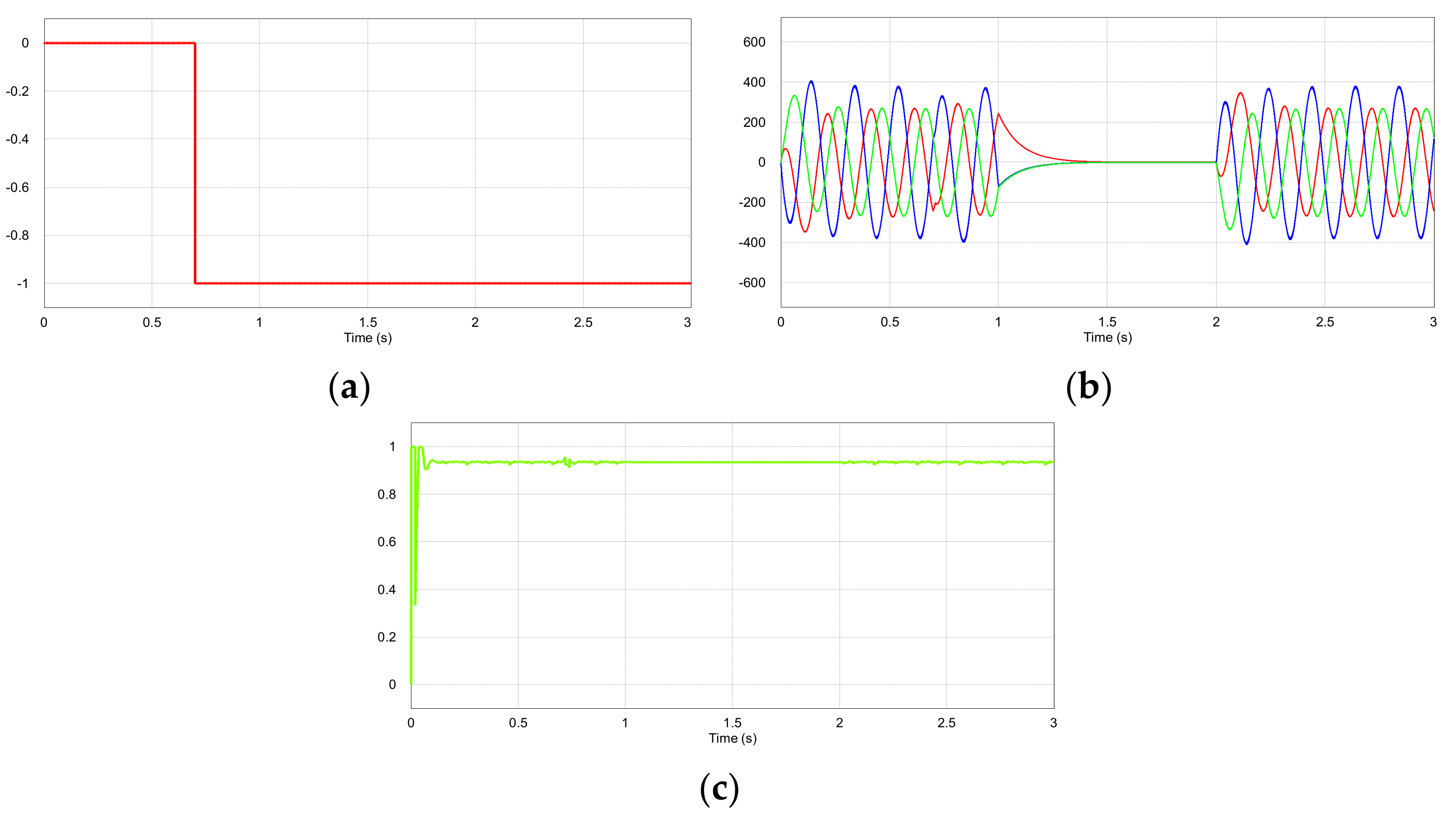
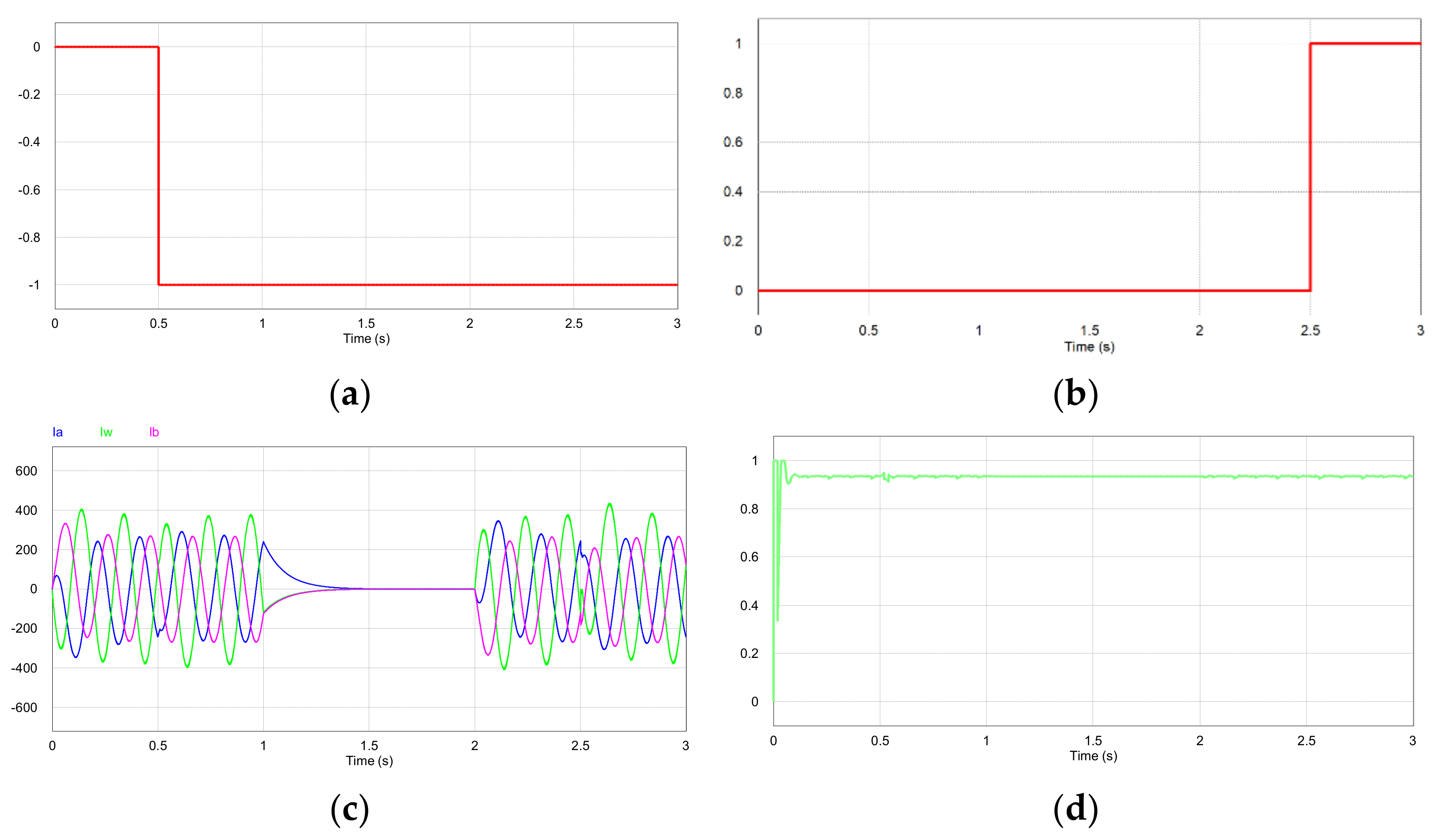
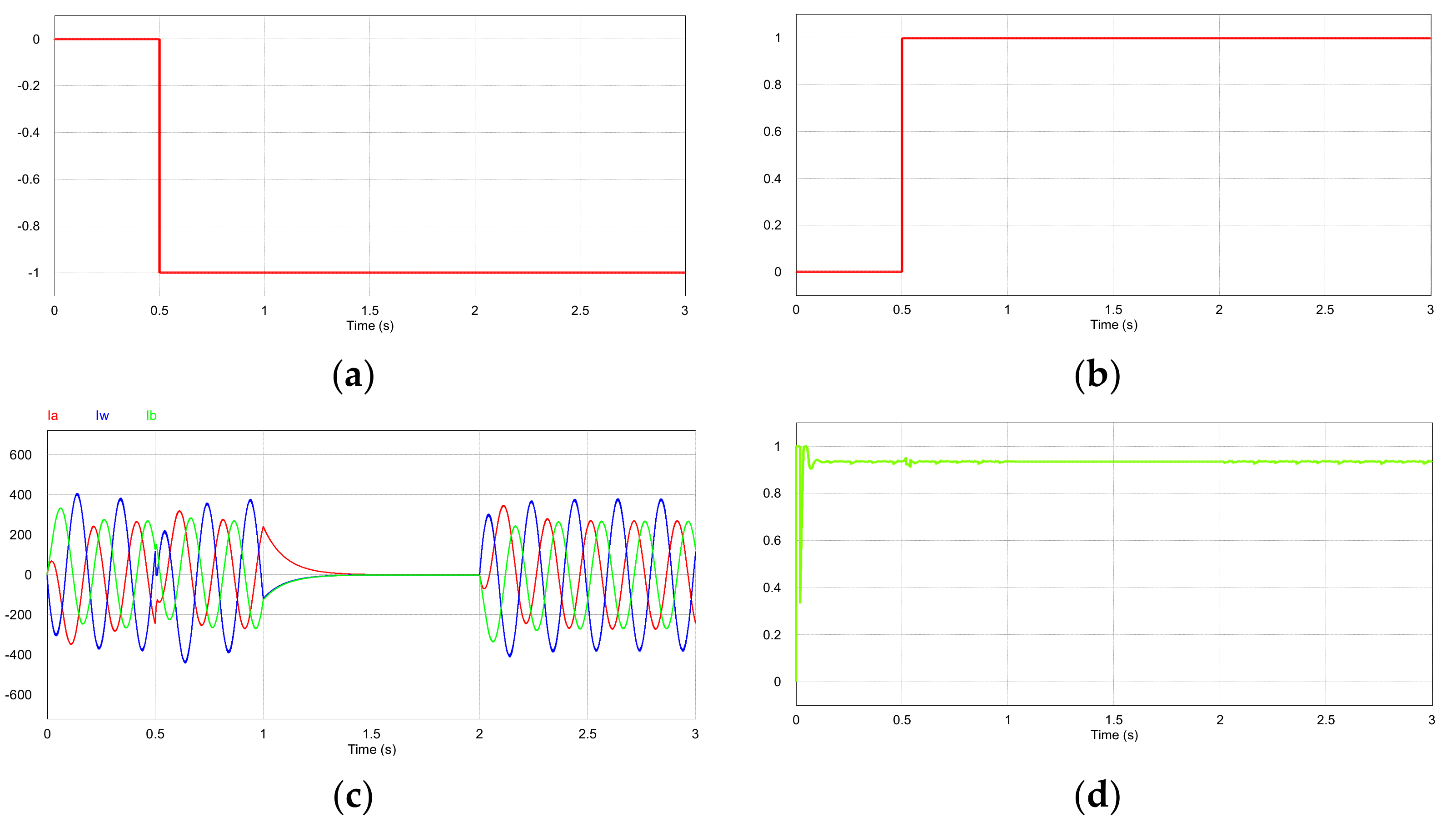
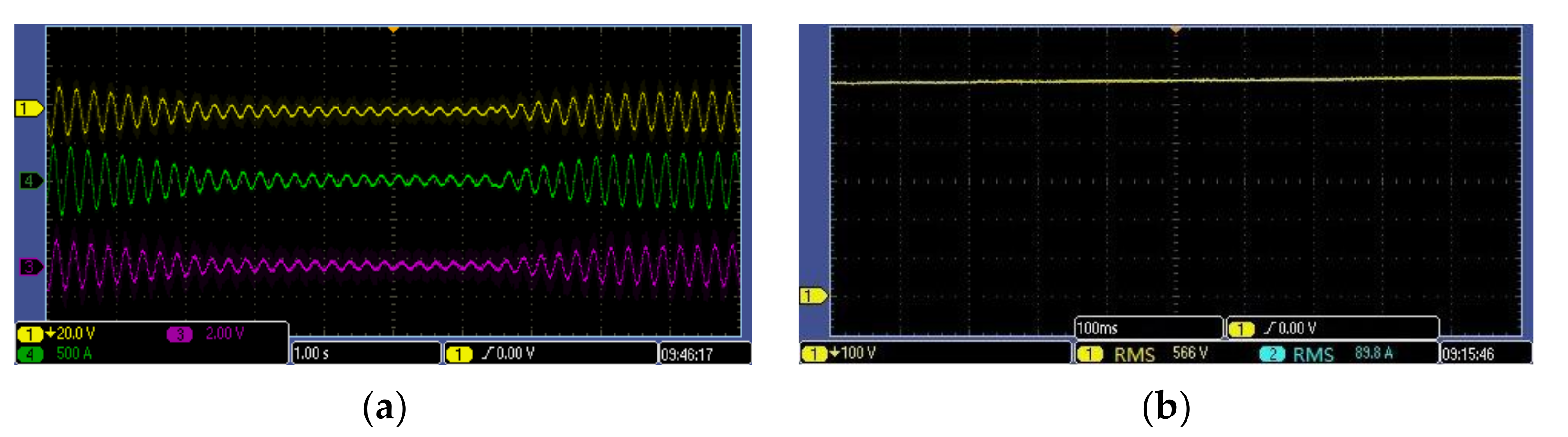
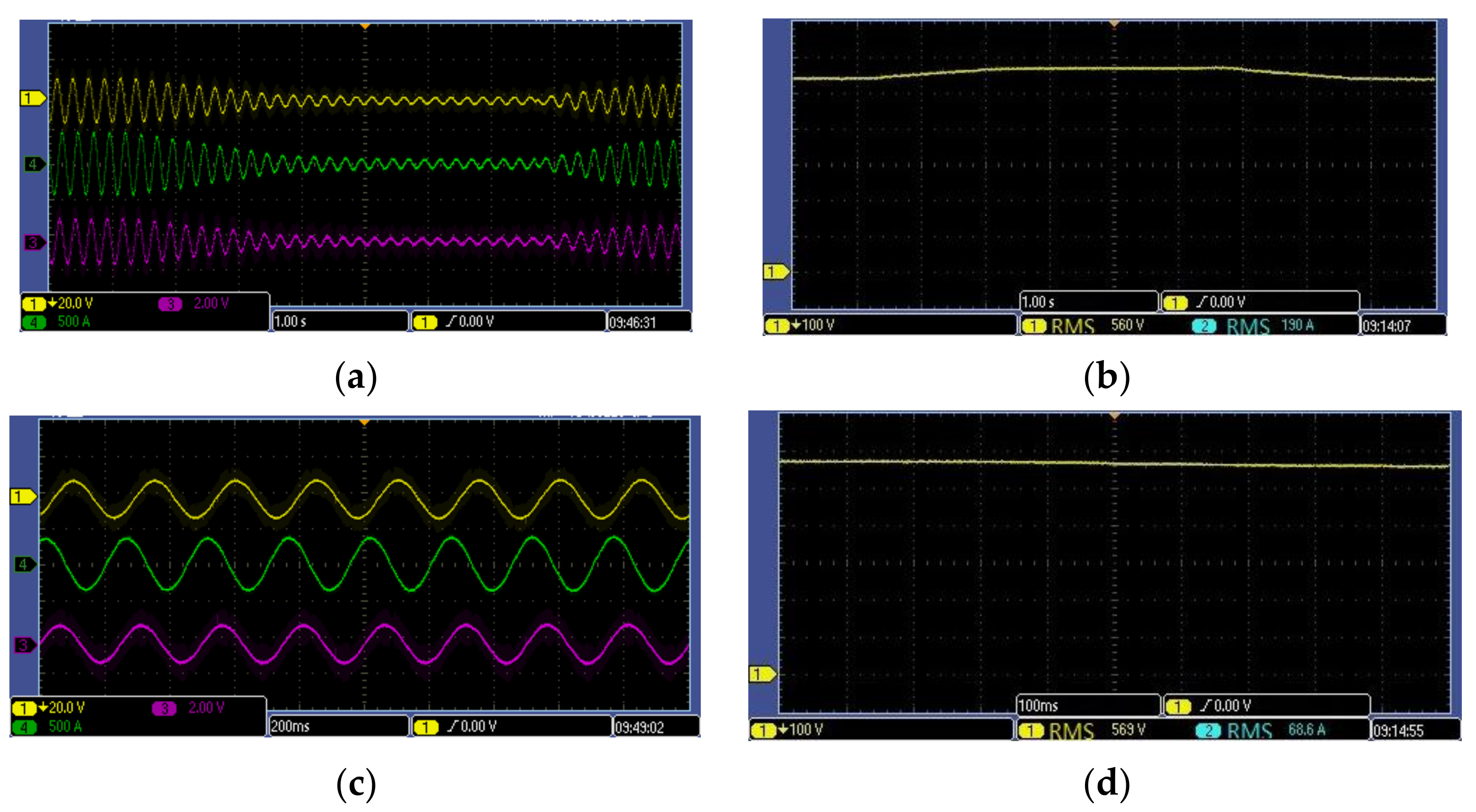
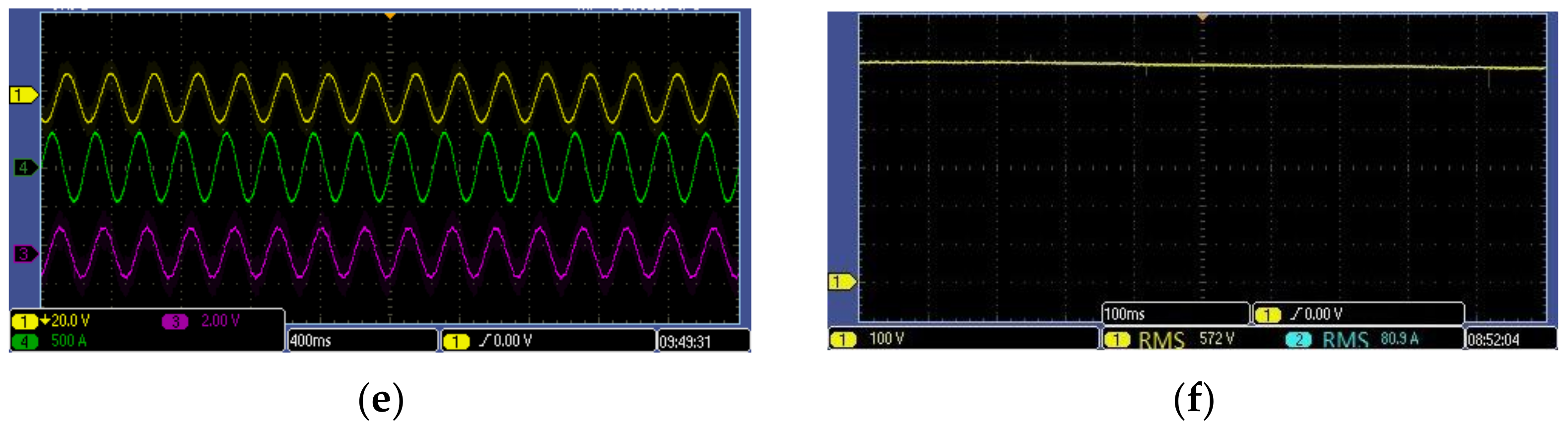
3. Results and Discussion
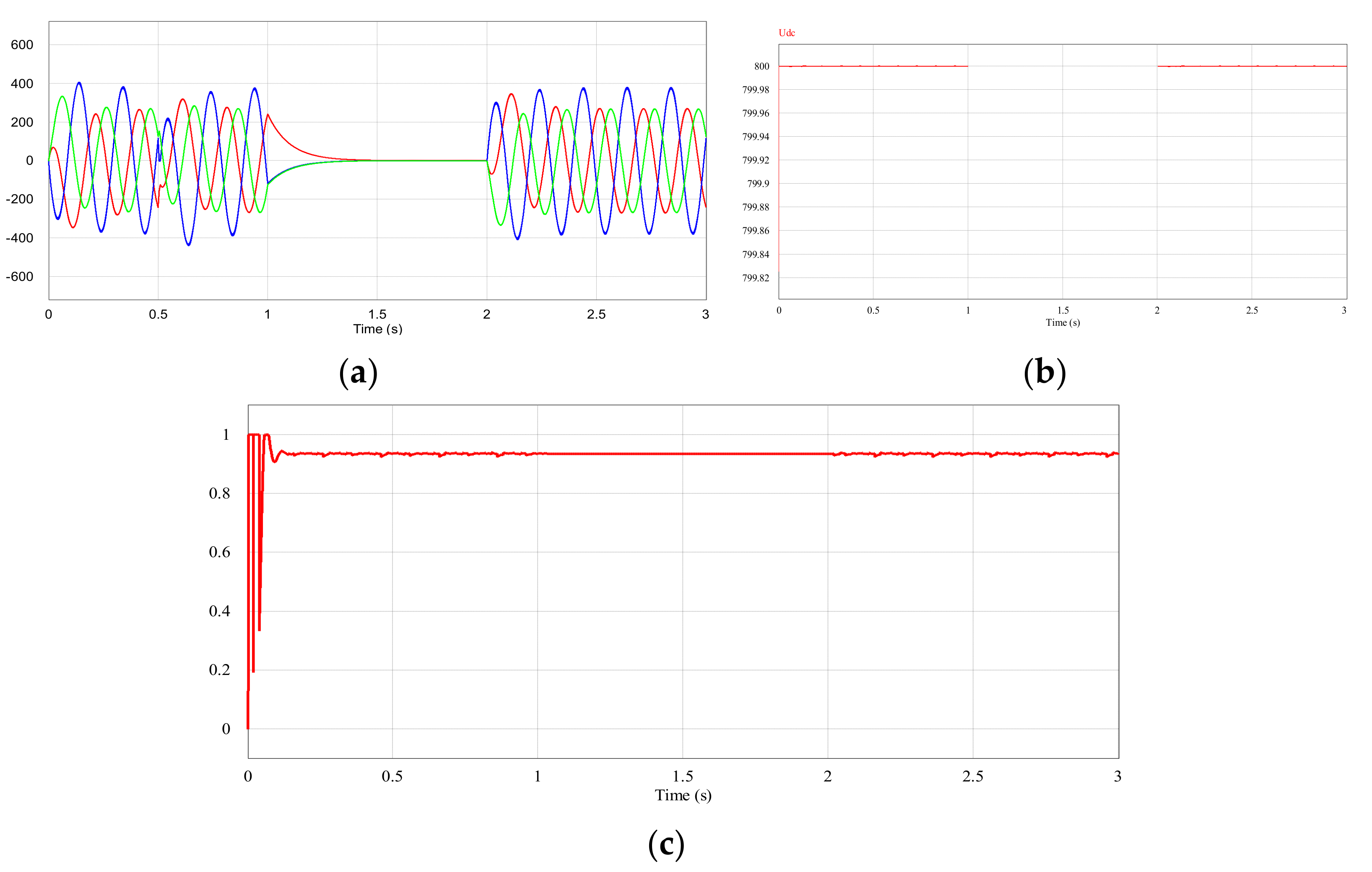
3.1. Simulation and Analysis
3.2. Experiment and Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Otake, R.; Yamada, T. Effects of Double-Axis Electromagnetic Stirring in Continuous Casting. IEEE Trans. Magn. 2008, 44, 4517–4520. [Google Scholar] [CrossRef]
- Liu, C.-T. Refined Model Development and Performance Assessment of a Linear Induction-Type Electromagnetic Stirrer. IEEE Trans. Magn. 2010, 46, 3724–3730. [Google Scholar] [CrossRef]
- Ege, Y.; Kalender, O. Electromagnetic Stirrer Operating in Double Axis. IRE Trans. Ind. Electron. 2010, 57, 2444–2453. [Google Scholar]
- Liu, C.-T.; Lin, C.-D.; Lee, W.-J.; Chen, J.-H. Electromagnetic stirring systems. IEEE Ind. Appl. Mag. 2011, 46, 38–43. [Google Scholar]
- Mao, B.; Zhang, G.; Li, A. Theory and Technology of Electromagnetic Stirring for Continuous Casting Steel. Metallurgical Industry Press: Beijing, China, 2012. [Google Scholar]
- Luo, A.; Xiao, H.; Ouyang, H.; Wu, C.; Ma, F.; Shuai, Z. Development and Application of the Two-Phase Orthogonal Power Supply for Electromagnetic Stirring. IEEE Trans. Power Electron. 2013, 28, 3438–3446. [Google Scholar] [CrossRef]
- Li, Y. Electromagnetic stirring power supply system with bidirectional energy flow and its control strategy. In Proceedings of the Power Electronics and Applications (EPE’17 ECCE Europe), Warsaw, Poland, 11–14 September 2017. [Google Scholar]
- Rojat, G.; Mertz, J.; Foggia, A. Theoretical and Experimental Analysis of a Two-Phase Inverter-Fed Induction Motor. IEEE Trans. Ind. Appl. 1969, 15, 601–605. [Google Scholar]
- Collins, E.R.; Puttgen, H.B.; Sayle, W.E. Single-phase induction motor adjustable speed drive: Direct phase angle control of the auxiliary winding supply. In Proceedings of the 1988 IEEE Industry Applications Society Annual Meeting, Pittsburgh, PA, USA, 2–7 October 1988. [Google Scholar]
- Young, C.M.; Liu, C.C.; Liu, C.H. New inverter-driven design and control method for two-phase induction motor drives. Proc. Electr. Power Appl. 1996, 143, 458–466. [Google Scholar] [CrossRef]
- Jang, D.H.; Yoon, D.Y. Space-vector PWM technique for two-phase inverterfed two-phase induction motors. In Proceedings of the 1999 IEEE Industry Applications Conference, Phoenix, AZ, USA, 3–7 October 1988. [Google Scholar]
- Jabbar, M.A.; Khambadkone, A.M.; Zhang, Y. Space-vector Modulation in a two-phase induction motor drive for constant-power operation. IRE Trans. Ind. Electron. 2004, 51, 1081–1088. [Google Scholar] [CrossRef]
- Rajaei, A.H.; Mohamadian, M. Single-phase induction motor drive system using z-source inverter. IET Electr. Power Appl. 2010, 4, 17–25. [Google Scholar] [CrossRef]
- Bartholet, M.T.; Nussbaumer, T.; Kolar, J.W. Comparison of Voltage-Source Inverter Topologies for Two-Phase Bearingless Slice Motors. IRE Trans. Ind. Electron. 2011, 58, 1921–1925. [Google Scholar]
- Wang, L.; Gao, H.; Zou, G. Modeling methodology and fault simulation of distribution networks integrated with inverter-based DG. Prot. Control. Mod. Power Syst. 2017, 2, 370–378. [Google Scholar]
- Noureldeen, O.; Hamdan, I. A novel controllable crowbar based on fault type protection technique for DFIG wind energy conversion system using adaptive neuro-fuzzy inference system. Prot. Control. Mod. Power Syst. 2018, 3, 328–339. [Google Scholar]
- Huang, K.; Liu, J.; Huang, S. Converters open-circuit fault diagnosis methods research for direct—driven permanent magnet wind power system. Trans. China Electrotech. Soc. 2015, 30, 129–136. [Google Scholar]
- dos Santos, E.C., Jr.; Jacobina, C.B.; Dias, A.A.; Rocha, N. Fault tolerant ac-dc-ac single-phase to three-phase converter. IET Power Electron. 2011, 4, 1023–1031. [Google Scholar]
- Zhang, F.; Mu, L. New protection scheme for internal fault of multi-microgrid. Prot. Control. Mod. Power Syst. 2019, 4, 159–170. [Google Scholar] [CrossRef]
- Nair, D.V.; Murty, M. Reconfigurable control as actuator fault-tolerant control design for power oscillation damping. Prot. Control. Mod. Power Syst. 2020, 5, 70–81. [Google Scholar] [CrossRef]
- Errabelli, R.R.; Mutschler, P. Fault-tolerant voltage source inverter for permanent magnet drives. IEEE Trans. Power Electron. 2012, 27, 500–508. [Google Scholar] [CrossRef]
- Munim, W.N.W.A.; Duran, M.J.; Che, H.S.; Bermudez, M.; GonzalezPrieto, I.; Rahim, N.A. A unified analysis of the fault tolerance capability in six-phase induction motor drives. IEEE Trans. Power Electron. 2017, 32, 7834–7836. [Google Scholar] [CrossRef]
- Abdel-Khalik, A.S.; Hamad, M.S.; Massoud, A.M.; Ahmed, S. Postfault operation of a nine-phase six-terminal induction machine under single open-line fault. IEEE Trans. Ind. Electron. 2018, 65, 1084–1096. [Google Scholar]
- Xia, Y.; Gou, B.; Xu, Y. A new ensemble-based classifier for IGBT open-circuit fault diagnosis in three-phase PWM converter. Prot. Control. Mod. Power Syst. 2018, 3, 364–372. [Google Scholar]
- Dhople, S.V.; Davoudi, A.; Domínguez-García, A.D.; Chapman, P.L. A unified approach to reliability assessment of multiphase DC–DC converters in photovoltaic energy conversion systems. IEEE Trans. Power Electron. 2012, 27, 739–751. [Google Scholar] [CrossRef]
- Pradeep Kumar, V.V.S.P.; Fernandes, B.G. A Fault-Tolerant Single-Phase Grid-Connected Inverter Topology With Enhanced Reliability for Solar PV Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1254–1263. [Google Scholar]





| Case | Primary Fault | Jαo | Jwo | Jβo |
| 1 | / | Z | Z | Z |
| 2 | V1 | N | Z | Z |
| 3 | V2 | P | Z | Z |
| 4 | V3 | Z | N | Z |
| 5 | V4 | Z | P | Z |
| 6 | V5 | Z | Z | N |
| 7 | V6 | Z | Z | P |
| 8 | V1 & V2 | N/P | Z | Z |
| 9 | V1 & V3 | N | N | Z |
| 10 | V1 & V4 | N | P | Z |
| 11 | V1 & V5 | N | Z | N |
| 12 | V1 & V6 | N | Z | P |
| 13 | V2 & V3 | P | N | Z |
| 14 | V2 & V4 | P | P | Z |
| 15 | V2 & V5 | P | Z | N |
| 16 | V2 & V6 | P | Z | P |
| 17 | V3 & V4 | Z | N/P | Z |
| 18 | V3 & V5 | Z | N | N |
| 19 | V3 & V6 | Z | N | P |
| 20 | V4 & V5 | Z | P | N |
| 21 | V4 & V6 | Z | P | P |
| 22 | V5 & V6 | Z | Z | N/P |
| No. | Primary Fault | Connection | First Reconstruction |
| 0 | / | TRb | / |
| 1 | V1 | TRw & TR13 | Sα (V3, V4) Sw (C1, C2) |
| 2 | V2 | TRw & TR13 | Sα (V3, V4) Sw (C1, C2) |
| 3 | V3 | TRw | Sw (C1, C2) |
| 4 | V4 | TRw | Sw (C1, C2) |
| 5 | V5 | TRw & TR35 | Sβ (V3, V4) Sw (C1, C2) |
| 6 | V6 | TRw & TR35 | Sβ (V3, V4) Sw (C1, C2) |
| 7 | V1 & V2 | TRw & TR13 | Sα (V3, V4) Sw (C1, C2) |
| 8 | V3 & V4 | TRw | Sw (C1, C2) |
| 9 | V5 & V6 | TRw & TR35 | Sβ (V3, V4) Sw (C1, C2) |
| 18 | V1 & V4 | TRw & TR13 | Sα(V3, V2) Sw (C1, C2) |
| 19 | V2 & V3 | TRw & TR13 | Sα(V1, V4) Sw (C1, C2) |
| 20 | V3 & V6 | TRw & TR35 | Sβ(V5, V4) Sw (C1, C2) |
| 21 | V4 & V5 | TRw & TR35 | Sβ(V3, V6) Sw (C1, C2) |
| Case | Primary Fault | Secondary Fault | Jαo | Jβo |
|---|---|---|---|---|
| 1 | V1 | V4 | P | Z |
| 2 | V1 | V6 | Z | P |
| 3 | V2 | V3 | N | Z |
| 4 | V2 | V5 | Z | N |
| 5 | V3 | V2 | P | Z |
| 6 | V3 | V6 | Z | P |
| 7 | V4 | V1 | N | Z |
| 8 | V4 | V5 | Z | N |
| 9 | V5 | V2 | P | P |
| 10 | V5 | V4 | P | Z |
| 11 | V6 | V1 | N | Z |
| 12 | V6 | V3 | N | Z |
| Case | Primary Fault | Connection | Secondary Fault | Secondary Construction |
|---|---|---|---|---|
| 1 | V1 | TRw & TR13 | V4 | Sα (V3, V2) |
| 2 | V2 | TRw & TR13 | V3 | Sα (V1, V4) |
| 3 | V3 | TRw & TR13 | V2 | Sα (V1, V4) |
| 4 | V3 | TRw & TR35 | V6 | Sβ (V5, V4) |
| 5 | V4 | TRw & TR13 | V1 | Sα (V3, V2) |
| 6 | V4 | TRw & TR35 | V5 | Sβ (V3, V6) |
| 7 | V5 | TRw & TR35 | V4 | Sβ (V3, V6) |
| 8 | V6 | TRw & TR35 | V3 | Sβ (V5, V4) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, X.; Luo, A.; Li, Y.; Chen, Y.; Li, A.; Peng, P. Research on the High Reliable Electromagnetic Stirring Power Supply. Appl. Sci. 2021, 11, 9874. https://doi.org/10.3390/app11219874
Xiang X, Luo A, Li Y, Chen Y, Li A, Peng P. Research on the High Reliable Electromagnetic Stirring Power Supply. Applied Sciences. 2021; 11(21):9874. https://doi.org/10.3390/app11219874
Chicago/Turabian StyleXiang, Xinxing, An Luo, Yan Li, Yandong Chen, Aiwu Li, and Peng Peng. 2021. "Research on the High Reliable Electromagnetic Stirring Power Supply" Applied Sciences 11, no. 21: 9874. https://doi.org/10.3390/app11219874
APA StyleXiang, X., Luo, A., Li, Y., Chen, Y., Li, A., & Peng, P. (2021). Research on the High Reliable Electromagnetic Stirring Power Supply. Applied Sciences, 11(21), 9874. https://doi.org/10.3390/app11219874







