Evaluating the Motor Imagery Classification Performance of a Double-Layered Feature Selection on Two Different-Sized Datasets

Abstract

Numerous investigations have been conducted to enhance the motor imagery-based brain–computer interface (BCI) classification performance on various aspects. However, there are limited studies comparing their proposed feature selection framework performance on both objective and subjective datasets. Therefore, this study aims to provide a novel framework that combines spatial filters at various frequency bands with double-layered feature selection and evaluates it on published and self-acquired datasets. Electroencephalography (EEG) data are preprocessed and decomposed into multiple frequency sub-bands, whose features are then extracted, calculated, and ranked based on Fisher’s ratio and minimum-redundancy-maximum-relevance (mRmR) algorithm. Informative filter banks are chosen for optimal classification by linear discriminative analysis (LDA). The results of the study, firstly, show that the proposed method is comparable to other conventional methods through accuracy and F1-score. The study also found that hand vs. feet classification is more discriminable than left vs. right hand (4–10% difference). Lastly, the performance of the filter banks common spatial pattern (FBCSP, without feature selection) algorithm is found to be significantly lower (p = 0.0029, p = 0.0015, and p = 0.0008) compared to that of the proposed method when applied to small-sized data.

1. Introduction

To help patients with functional motor disabilities, such as amyotrophic lateral sclerosis (ALS) or spinal cord injury (SCI), Brain-Computer Interface (BCI) has been researched for over decades. BCI is a system that establishes an artificial communication pathway between the central nervous system and external devices, acting as a peripheral motor, when a biological neuron path is weak, or no longer works properly [1]. Various applications applying BCI to real-world problems have been carried out: brain-actuated speller where a patient could type words on a computer screen with their thought [2,3]; controlling computer cursor by gazing [4]; controlling incoming calls [5]; computer control interface [6]. Owing to the emerging advances in novel signal processing and computational algorithms, BCI has an important role in facilitating the recovery of neural functions, restoring functional corticospinal, and corticomuscular connections and neurorehabilitation.

The non-invasive electroencephalography (EEG) technique has been widely used in BCI research because of its clinical simplicity, cost efficiency, and safety [7]. Event-related desynchronization/synchronization (ERD/ERS), in which the amplitude of mu and beta rhythms is suppressed or increased depending on the event [8,9,10], is one of the main types of non-invasive BCI. Specifically, motor imagery (MI) elicits mu and beta ERD/ERS patterns in both healthy subjects as well as patients with severe motor disabilities [11,12]. MI has the advantage over other methods as it only requires mental simulation of movements without actual actions or external stimuli.

In recent years, many studies put their focus on investigating and reinforcing feature extraction and classification algorithms for MI-based BCI, thus enhancing BCI performance. Traditional feature extractors have been widely used and claimed to be effective up to now, however, they still have drawbacks. For example, the temporal resolution and spectral resolution of the short-time Fourier transform (STFT) algorithm are determined by the width of the time window [13]. That is to say, there is a trade-off between temporal and spectral resolution: the better the frequency resolution as the window gets wider, the worse the time resolution and vice versa. Another example is wavelet transform, which can perform multi-scale time-frequency analysis. The main disadvantage of this algorithm is that it requires manual screening for statistical features such as maximum, minimum, mean, and standard deviation of wavelet coefficients, whereas EEG pattern, motor imagery to be specific, is not stationary and it varies among subjects [14]. Meanwhile, common spatial pattern (CSP) is one of the promising candidates for the shortcoming of EEG low spatial resolution characteristic [15]. Moreover, the CSP algorithm, one of the most effective filters optimizing spatial information in motor tasks discrimination [16,17], has not been fully investigated.

Since CSP needs to identify discriminative frequency bands for effective classification, there is a substantial amount of studies on finding optimal frequency bands. The first approach is a combination of CSP and time-frequency analysis [18,19]. The simultaneous optimization of the spatial spectrum filter is used in the second type [20,21]. The third type of approach involves filtering the original EEG signals into multiple frequency sub-bands, then CSP is applied to extract features from these sub-bands, and classification is performed based on the optimum frequency bands [22,23,24,25]. The intelligent optimization method is the fourth kind of technique utilized to determine the optimum frequency bands. This approach is capable of selecting informative frequency bands of any length and is independent of subjective experience [26,27,28]. In the first method, because frequency information is obtained via a time-frequency analysis, the EEG signals of each channel must be decomposed, which involves numerous calculations and takes considerable computation time. The second method is challenging to implement and effortlessly leads to local solutions [29]. The drawback of the fourth method is the requirement of a lengthy training phase of models, which is insufficient for practical BCI. Although sub-band filtering in the third method requires high computation cost, it seems to have surpassed the other methods in terms of performance and robustness.

With regard to feature selection, there are three main present methods: filter, wrapper, and embedded [30]. Filter method initiates with all of the features and these features are chosen based on criteria such as information gain, consistency, dependency, correlation, and distance measures [31,32]. The wrapper method evaluates feature selection by comparing it to the classifier’s performance [33,34,35]. However, when assessing each applicant feature subset, the wrapper method must train and test the classifier, and that is prone to overfitting and computationally costly. The embedded technique incorporates feature selection into the classifier’s training phase, performing both tasks concurrently [36,37]. Although proven to be efficient in most studies, the embedded technique has the highest computational cost in all three feature selection methods. In contrast, Fisher was used in a unified framework for feature extraction, selection, and classification [38]. Fisher’s ratio was also used in [39] as a channel selector along with the correlation coefficient. In [40], the author performed manual screening for optimal frequency bands and suggested building a more sophisticated algorithm for auto selection. Yet his following study [26] implemented temporal filter parameter optimization combined with optimization algorithms (particle swarm optimization, artificial bee colony, and genetic algorithm) and the drawback was long training time as the framework was so sophisticated. Hence, Fisher’s ratio is the right tool for a simpler, lower computational cost and more effective method. Furthermore, in [41], the author also suggested using mutual information-based feature selection (i.e., mRmR) as it is well-known for selecting the most significant features. Consequently, filter methods, Fisher’s ratio, and mRmR, are utilized in this study due to their low computational cost.

With regard to classifiers, the three most popular algorithms because of their robustness are linear discriminant analysis (LDA), support vector machine (SVM), and Bayesian [42,43,44]. Deep learning has emerged and is combined with traditional algorithms to create reliable and powerful techniques in MI tasks recognition problems in many studies [14,45,46,47,48]. However, deep learning not only poses a high computational cost but also extracts incomprehensible features [49]. Furthermore, deep learning has no clear advantages over conventional machine learning methods [50]. Hence, in this study, LDA is utilized for classification as it has been successfully implemented in various applications [51,52,53].

Lastly, most of the previous studies evaluated only on BCI competition datasets with the absence of comparing with their own data. Li et al. [38] established their own datasets of 16 subjects to evaluate the study’s proposed framework, which used Fisher’s objective function for feature extraction and feature selection. The study’s dataset size was small as it only contained 80 trials per class per subject and was not compared to other published datasets, such as BCI competition. Peterson et al. [18] also established a dataset of 7 subjects, 80 trials per class per subject, to evaluate his proposed combined CSP and time-frequency analysis framework. The study’s proposed framework was also evaluated on other BCI competition datasets. Consequently, carrying out both subjective and objective datasets would be more reliable.

To this end, the aim of this paper is to: (i) propose a novel framework for motor imagery tasks based on spatial filters, automatic feature selection, and traditional classifier; (ii) evaluate the proposed methods on both a self-acquired dataset and a BCI Competition dataset in terms of accuracy, F1-score, and ROC. The proposed framework (called Fisher—mRmR discriminative filter bank common spatial pattern, DFBCSP—FmRmR) would use filter bank for sub-band filtering of EEG signal, common spatial pattern as feature extractor, Fisher’s ratio and mutual information-based mRmR for automatic feature selection, and LDA as the classifier.

The content of this paper is organized as follows:

• Data acquisition, signal processing, conventional feature extraction, and feature selection algorithms as well as the proposed method are introduced in Section 2.
• The data visualizations and results are shown in Section 3.
• Discussion and further explanation are in Section 4.
• The conclusion is provided in Section 5.

2. Materials and Methods

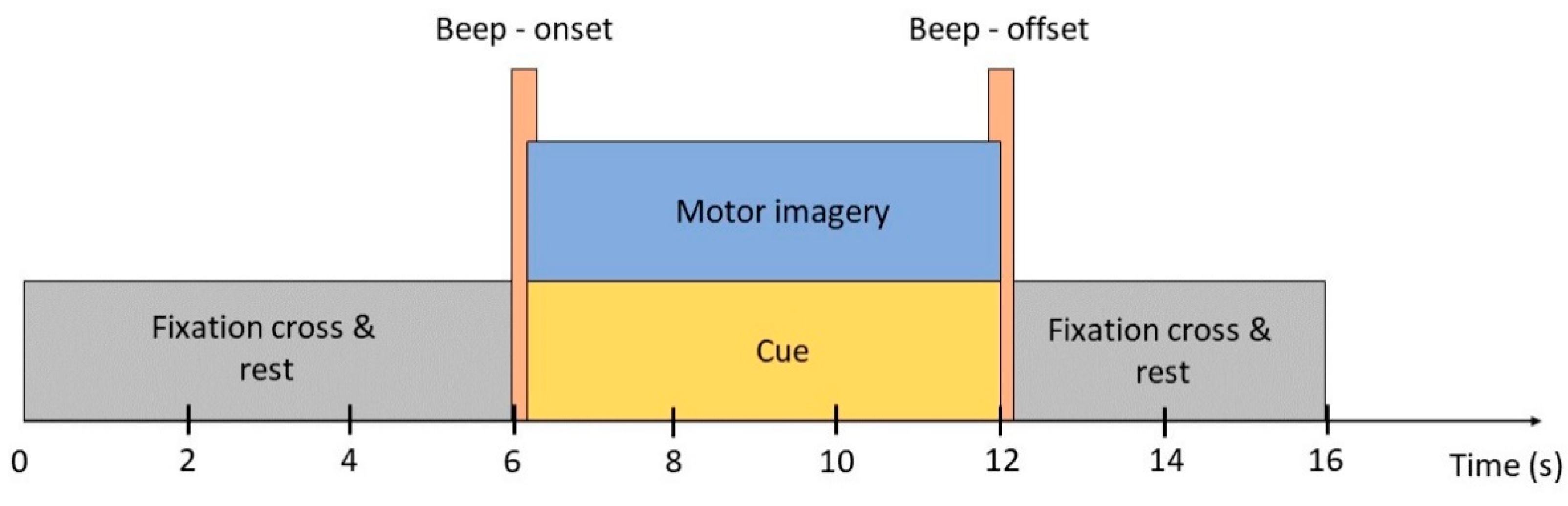
2.1. Data Acquisition of Self-Acquired Dataset (Dataset 1)

Subjects were 16 healthy, both undergraduate and graduate students (6 women, 10 men; age range 20–23 years, mean 21 ± 0.89). Surveys were given to subjects and reported that no subjects had disorders relating to neurology. None of them had any prior experience with BCI. Two to three preparatory runs were provided to all subjects before data acquisition and were paid USD 2 per measurement for taking part in. Before and after each session, subjects were asked to fill out some information relating to their conditions to ensure the consistency of awareness during the experiment. Throughout the whole procedure, subjects had to comply with some regulations: (i) no caffeine or any stimulants consumption a few hours before experiments; (ii) restrict negative feelings; (iii) avoid sleep deprivation. During the experiment, participants were asked to sit on a chair in a Faraday-shielded room that blocks electromagnetic radiation and observe a computer screen. Minimizing eye movements, body adjustments, and avoiding any undesired movements during a cue onset. Subjects were allowed to give signs to pause or stop the experiment should any unexpected conditions show up (cough, scratch, sleepy, tired, etc.).

Data were recorded by NicoletOne V32 (Natus Medical Inc., Pleasanton, CA, USA) with monopolar montage with electrodes C3, Cz, C4, P3, Pz, and P4 according to the International 10–20 electrode placement system [54] (Figure 1). A reference and a ground electrode were attached to the left and right earlobes accordingly. All electrodes’ impedance was kept below 5 kΩ and the sampling frequency was 500 Hz. Nuprep was used to clean the scalp to reduce skin impedance, and conductive gel Ten20 was used for electrode attachment (Figure 1). Six electrode positions were chosen based on the fact that the most noticeable mu and beta ERD/ERS can be recognized when performing imagery tasks [55,56].

There were five measurements that occurred on five different days for each participant. There were five 8 min sessions in each measurement and a 10 min break was provided between each session. In each session, subjects were asked to pay attention to a MATLAB simulation program for 30 segments. Each segment lasted for 16 s (Figure 2): the first 6 s, the fixation cross appeared on the screen denoted relaxation state (no physical movements or mental activities); the next 6 s were for kinesthetic motor imagery tasks accompanied with cue denoted by a red arrow pointing left, right, and downward (for left hand, right hand and feet respectively); the last 4 s were for cue offset and subjects returned to relaxation. A cue onset and offset were indicated by a beep sound. In total, each subject has around 220–250 trials for each class. However, some were unable to complete the full experiment due to an inappropriate schedule. Subjects “ID03”, “ID06”, “ID10”, “ID12” have exceptionally fewer trials, approximately 180, 195, 140, and 134 trials for each class, respectively.

Most MI-BCI research conducted worldwide follows the same measuring procedure: when the subject is at resting state and observing the screen, the arrow appears in a random order after a cue, and the subject performs the imagining; lastly, the subject rests for random durations. The time required for arrows to appear, the duration required to complete the task, and the resting period are the variations between the measured procedures in these studies. The procedure for measuring in [57] began with the subject observing a cross in the center of the screen, and then the subject observed an arrow from the 2nd to the 6th second. This was followed by a two-second blank screen and a random rest period between 0.5 and 1.5 s. The measuring method described in [56] begins with a cue at the 2nd second and the arrow at the 3rd to 5th seconds, followed by a blank screen for the next second and a random interval of 0–1 s. The research by [58] used a similar paradigm as [56], except that the arrow only showed up for 1.25 s instead of 2 s. Study [59] had an inter-trial transitional period between 0.5 and 2 s. The interval between time points is not significant and is altered to suit the data analysis procedure. As a result, the research will follow the procedure outlined above, with minor modifications to the timeline to accommodate the measuring object, the data analysis, and processing.

2.2. BCI Competition Datasset (Dataset 2)

Dataset IIa of BCI competition IV (2008) [60]. This dataset contains 22 channels at a 250 Hz sampling rate. Nine participants (A01–A09) performed left hand, right hand, foot, and tongue motor imagery. This dataset has two sessions recorded on two different days, each with six runs of 48 trials (12 trials per class), yielding 288 trials per session (72 trials per class). The first session was used as the training set and the second as the test set. In this study, only the first session of each subject is used to train and evaluate for the number of trials as close to that of one measurement of the self-acquired dataset as possible, hence it would be easier for comparison between datasets. Furthermore, only three tasks (left hand, right hand, and feet) are performed in this study. Consequently, each subject in this dataset has 216 trials in total, before any artifacts removal, equally divided into three classes. Please visit the following website for further information: http://www.bbci.de/competition/IV/ (accessed on 10 June 2021).

There are a few key differences between the author’s self-acquired and BCI Competition datasets:

• Firstly, the data acquisition paradigms are slightly different in terms of timing.
• Secondly, the number of measurements of the self-acquired dataset are more and occurred on different days while there is only one measurement for each subject in BCI Competition. That results in a different number of trials for each subject and possibly affects the outcomes.

2.3. Signal Pre-Processing

For the self-acquired dataset: Firstly, artifact removal is done to raw EEG data by eliminating any trial if its amplitude exceeds 100 µV. A 50 Hz notch filter is then applied to remove electrical interference. Thirdly, a 6th order Butterworth filter is applied to the EEG data for 4–40 Hz band-pass filtering with a time window of 6 s, starting from the beginning of the MI cue until the end.

For the BCI Competition IV dataset IIa: Firstly, trials affected by artifacts were marked previously by experts and removed subsequently in this study. Next, a 50 Hz notch filter is then applied to remove electrical interference. Lastly, clean trials with a time window of 3 s, from the beginning of the MI cue until the end, traverse through a 6th order Butterworth filter for 4–40 Hz band-pass filtering.

2.4. Common Spatial Pattern

The common spatial pattern (CSP) [21,61] method is increasingly used for feature extraction and classification in two-class MI-BCI, by linearly mapping the feature into a more discriminative space. It maximizes the variance of the filtered data in one class while reducing the variance of the filtered data in the other. As a function, the resulting feature vectors enhance discriminating between the two classes by lowering intra-class variance and increasing class difference. The CSP attempts to convert the multi-channel EEG data into a low-dimensional area via linear transformation by using a projection matrix.

$$Z=WE,$$

(1)

where E is an N × T matrix containing the raw EEG measurement data from a single trial, N is the number of channels, T is the number of samples, and W is the CSP projection matrix. This is accomplished by designing the rows of W or spatial filters so that the variances of the first and last rows of Z provide the greatest discrimination between two classes of MI tasks. As a result, the feature vector Fp is generated by (2), where Zp is the first and last m rows of Z, p ∈ {1 … 2m}.

$$F_p=\log [\left(var\left(Z_p\right)\right)/\left({\sum }_{i=1}^{2m}var\left(Z_i\right)\right)]$$

(2)

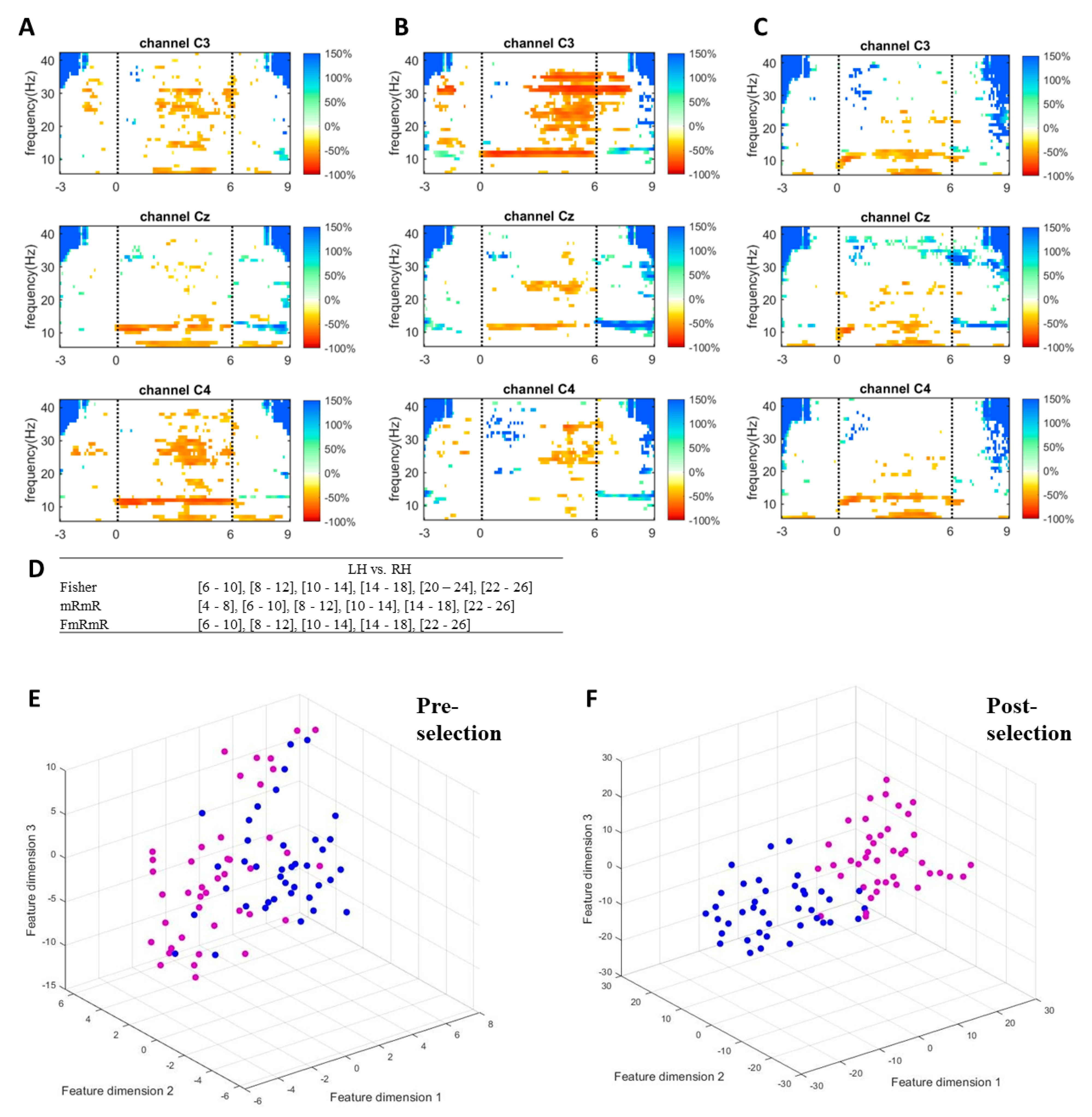
2.5. Fisher’s Ratio

The DFBCSP method uses a series of filters called parent FB in the sequel [23] to ex-tract subject-specific discriminative frequency bands. The band selection block leverages the parent FB filters EEG and the Fisher’s ratio of the filtered EEG to identify subject-specific discriminative frequency bands. The parent filter bank analyzes signals and for the purposes of acquiring subject-specific DFB, the equation below is utilized to compute an approximation of spectral power associated with each sub-band:

$$P\left(f_i,t\right)=\frac{1}{T}{\sum }_{n=1}^T{x}_{t,f}{\left(n\right)}^2,$$

(3)

for each t trial, $P\left(f_i,t\right)$ is the spectral power estimated in the ith band output, and the sample count in the filtered EEG signal $x_f\left(n\right)$ is denoted by T. N_f is the total number of bands, and N_t is the total number of trials, thus an N_f × N_t matrix matching to spectral power is produced. Across all frequency bands, each trial is paired with an estimated p-value calculated.

For the purpose of selecting the most useful filter banks, the Fisher’s ratio, or F_R, is computed from all filter outputs from the parent filter bank. The following equation is used to get the Fisher’s ratio at each band output:

$$F_R\left(f\right)=\frac{S_B}{S_W},$$

(4)

where S_W and S_B are the within-class variance and between-class variance, respectively. S_W and S_B are computers in Equations (5) and (6):

$$S_W={\sum }_{k=1}^C{\sum }_{t=1}^{n_k}{(P_t-m_k)}^2,$$

(5)

$$S_B={\sum }_{t=1}^C{n}_k{\left(m-m_k\right)}^2,$$

(6)

where m is the average power across classes, $m_k$ is the average power within class $k, \left(k=1, 2\right)$, $C$ denotes the number of classes, and n_k denotes the number of trials for class $k$. A filter bank with a higher F_R index permits for better classification and after selecting out the subject-specific frequency bands, these discriminative bands are used to filter in the range of all data channels.

2.6. Minimum-Redundancy-Maximum-Relevance (mRmR)

Minimum-redundancy-maximum-relevance (mRmR) [62,63] function selection works by means of selecting features that have an excessive correlation with the class and low correlation with different features. After CSP, mRmR is adopted in automatic feature selection by substituting the correlation between variables with the statistical dependence, which is defined through mutual information. It is possible to assess non-linear relationships between two random variables by measuring their mutual information with each other. Furthermore, it reveals how much information can be gleaned from a random variable by monitoring another random variable.

$$I_{\left(x;y\right)}={\sum }_{i,j}\log \frac{p_{\left(x_i,y_j\right)}}{p_{\left(x_i\right)}{p}_{\left(y_j\right)}}$$

(7)

The variables x and y are feature vectors in Equation (7), $p\left(x,y\right)$ is the joint probability function, and $p\left(x\right)$, $p\left(y\right)$ are the marginal probability functions of x and y, respectively. Assume that S is a predefined set of features and h is a variable belonging to a specific class. The redundancy of S is quantified as follows:

$$W_I=\frac{1}{{\left|S\right|}^2}{\sum }_{i,j\in S}I\left(i,j\right)$$

(8)

The relevance of S is determined by the following criteria:

$$V_I=\frac{1}{\left|S\right|}{\sum }_{i\in S}I\left(h,j\right)$$

(9)

Two methods are used to evaluate S:

$$MID:V_I-W_I$$

(10)

$$MIQ:V_I/W_I$$

(11)

In the vast majority of cases, MIQ is proven to be superior to MID. Due to the fact that we cannot test all possible subsets of features S for a given dataset, the mRMR algorithm employs a forward search approach in its implementation.

2.7. Proposed Framework

After the preprocessing block: notch filter is for electrical grid interference elimination, low-pass and high-pass filters are for cut-off frequency from 4–40 Hz; peak removal for each trial has voltage exceeding 100 µV, the preprocessed data is then split into 3 pairs, namely: Left hand vs. right hand (pair 1), Right hand vs. feet (pair 2) and feet vs. left hand (pair 3), for binary classification. Train and test data are created based on 10-fold cross-validation (Figure 3).

In the training phase, a filter bank is applied to each EEG trial with a frequency range of 4–40 Hz, a bandwidth of 4 Hz, and 2 Hz overlapping; thus creating 17 filter banks in total. The proposed frequency configuration is based on study [18,23,64]. Next, the Fisher’s ratio and mRmR algorithms are applied to data in each filter bank to select the most discriminative filter banks. By calculating the power of data samples, Fisher’s ratio of each channel can be calculated through the criterion “maximize between-class variance and minimize within-class variance” and sorted in descending order. In this study, the most discriminative filter bank in each channel that has the highest Fisher’s ratio is selected for further selection. The maximum filter banks we can have in this case are 6 as dataset 1 has 6 channels. For dataset 2, the maximum filter banks would be 17 filter banks as it has a number of channels exceeding the number of filter banks.

Meanwhile, prior to using the mRmR feature selection algorithm, features of data of each filter bank have to be extracted by CSP. mRmR works on the two independent variables, which are “features” and “labels” in this study. mRmR finds the relationship, or how much information, the two independent variables have in common. As a result, the features in dataset 1, which are 6 channels multiplied by 17 filter banks, are sorted in descending order based on the amount of mutual information the algorithm found. For dataset 2, the number of features would be 22 channels multiplied by 17 filter banks. The top 6 filter banks are selected for further selection, regardless of which channel they are generated from. The maximum number of filter banks we can have in this case is 6 to match with Fisher’s case.

The selection criteria of this study are as follows: we take the intersection of the two cases, which means the common filter banks are selected as the final selection. If the intersection is not possible, the filter banks selected in the mRmR case will be chosen as it is claimed to be more effective than Fisher’s [40,65,66]. In the testing phase, the test data goes through the filter bank which was previously chosen in the training phase and the features are extracted with the corresponding W_CSP. In the last step, LDA is utilized to perform binary classification.

To visualize how informative features are extracted and selected by the proposed method, ERD/ERS responses, discriminative frequency bands, and features dimensions of a single measurement of a random subject of the self-acquired dataset are plotted in Figure 4. Figure 4A–C shows the responses in the time-frequency map of a random subject when performing left hand, right hand, and feet imagery respectively. Only C3, Cz, and C4 were plotted to represent the sides of the cortex. The imagination of limb movement causes ERD in mu and beta waves on the contralateral hemisphere [8,9,10,11,12]. The more dominant mu (10–14 Hz) and beta (22–26 Hz) suppressions of left-hand imagery can be seen on channel C4, while those of right-hand imagery are on channel C3. As feet imagery involves imagination of moving both feet and its somatosensory area is close to the mid-central of the cortex, the feet imagery causes mu suppression in C3, Cz, and C4. These features (frequency bands and channels) are informative for discriminating the tasks from one another. The proposed method successfully selected the most informative features (Figure 4D) for left hand vs. right hand. By simultaneously performing Fisher’s ratio and mRmR algorithms, the proposed method selected features by choosing the common bands between the two algorithms. Comparison between pre-selection of features (Figure 4E) and post-selection of features (Figure 4F) is performed by mapping the feature vectors on a 3D plane using t-distributed stochastic neighbor embedding (t-SNE) [67]. t-SNE is a non-linear dimensionality reduction algorithm that visualizes high dimensional data in two or three dimensions but preserves relative distances between objects. The features in Figure 4F are more discriminable than those in Figure 4E after the bands were selected by the proposed method.

2.8. Evaluation

The proposed framework is compared with three other conventional algorithms:

• FBCSP (without feature selection): this method has 17 filter banks, ranging from 4–40 Hz, a 4 Hz bandwidth, 2 Hz overlapping, and the number of spatial filters m is three.
• DFBCSP—Fisher: This method has 17 filter banks, ranging from 4–40 Hz, a 4 Hz bandwidth, 2 Hz overlapping and the number of spatial filters m is three Fisher’s ratio is used for band selection.
• DFBCSP—mRmR: This method has 17 filter banks, ranging from 4–40 Hz, a 4 Hz bandwidth, 2 Hz overlapping, and the number of spatial filters m is three. mRmR is used for band selection, which could have a maximum of six filter banks.
• Proposed method (DFBCSP—FmRmR): t\This method has 17 filter banks, ranging from 4–40 Hz, a 4 Hz bandwidth, 2 Hz overlapping, and the number of spatial filters m is three. Both Fisher’s ratio and mRmR are used for band selection, which can be carried out without manual screening. The selected bands are varied after each loop and can be up to six filter banks.

The results are compared in terms of accuracy and F1-score. While accuracy is a metric indicating the proportion of properly recognized instances, F1-score is primarily concerned with the disagreement between the true positive rate and the positive predictive value. Consequently, this study employs both metrics for a more objective evaluation. The models are evaluated on both the self-acquired dataset and the public BCI competition dataset. The results are visualized through bar charts, confusion matrixes, tables, and ROC curves.

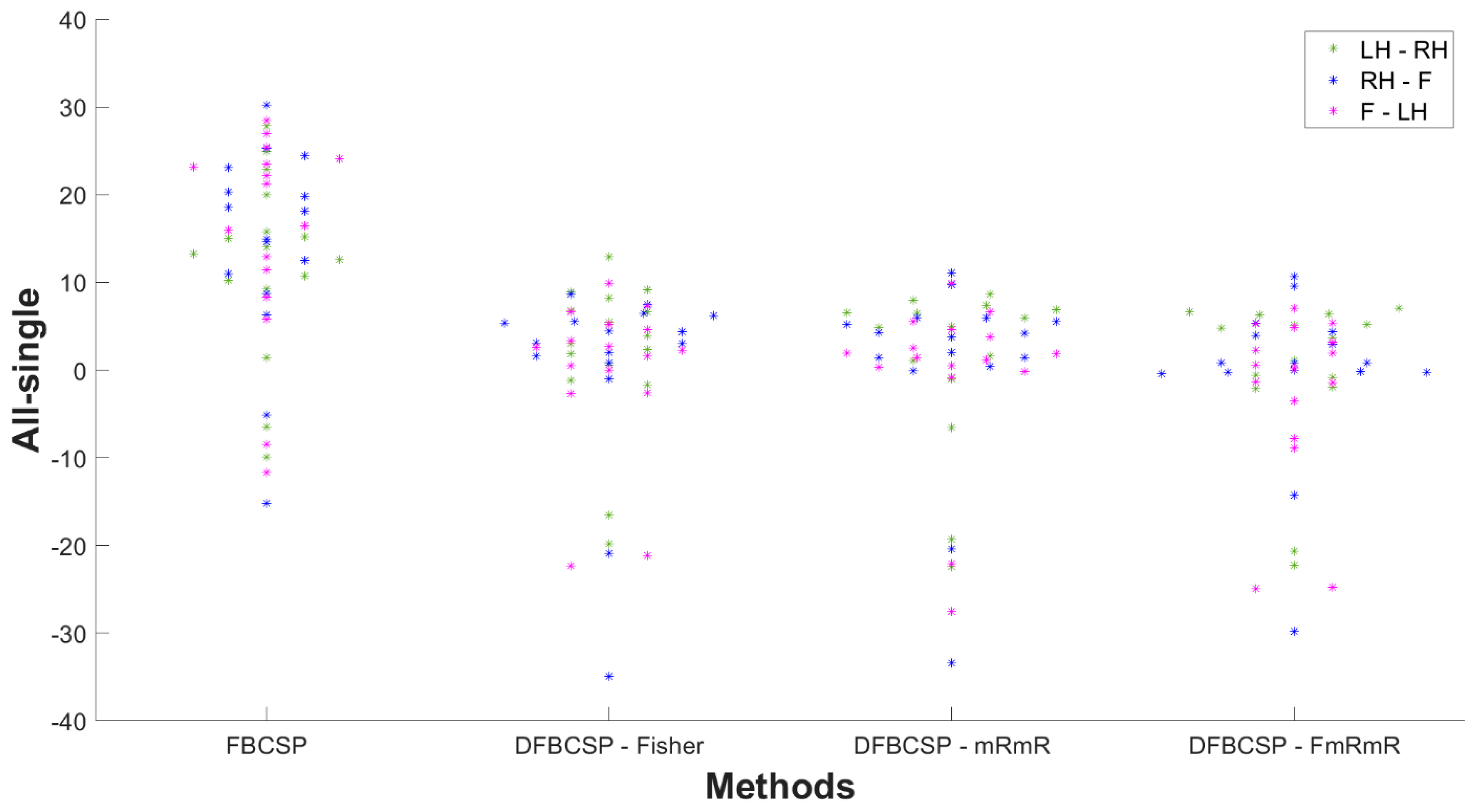
3. Results

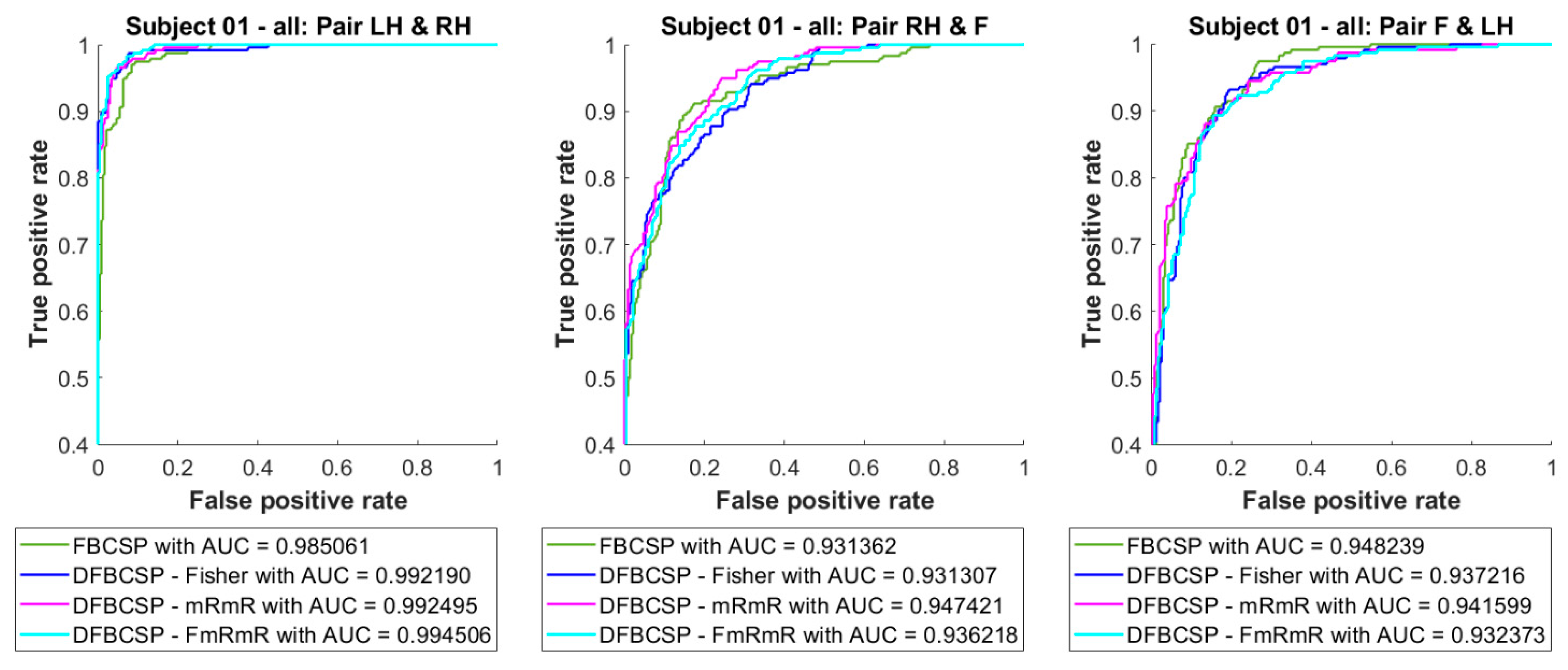
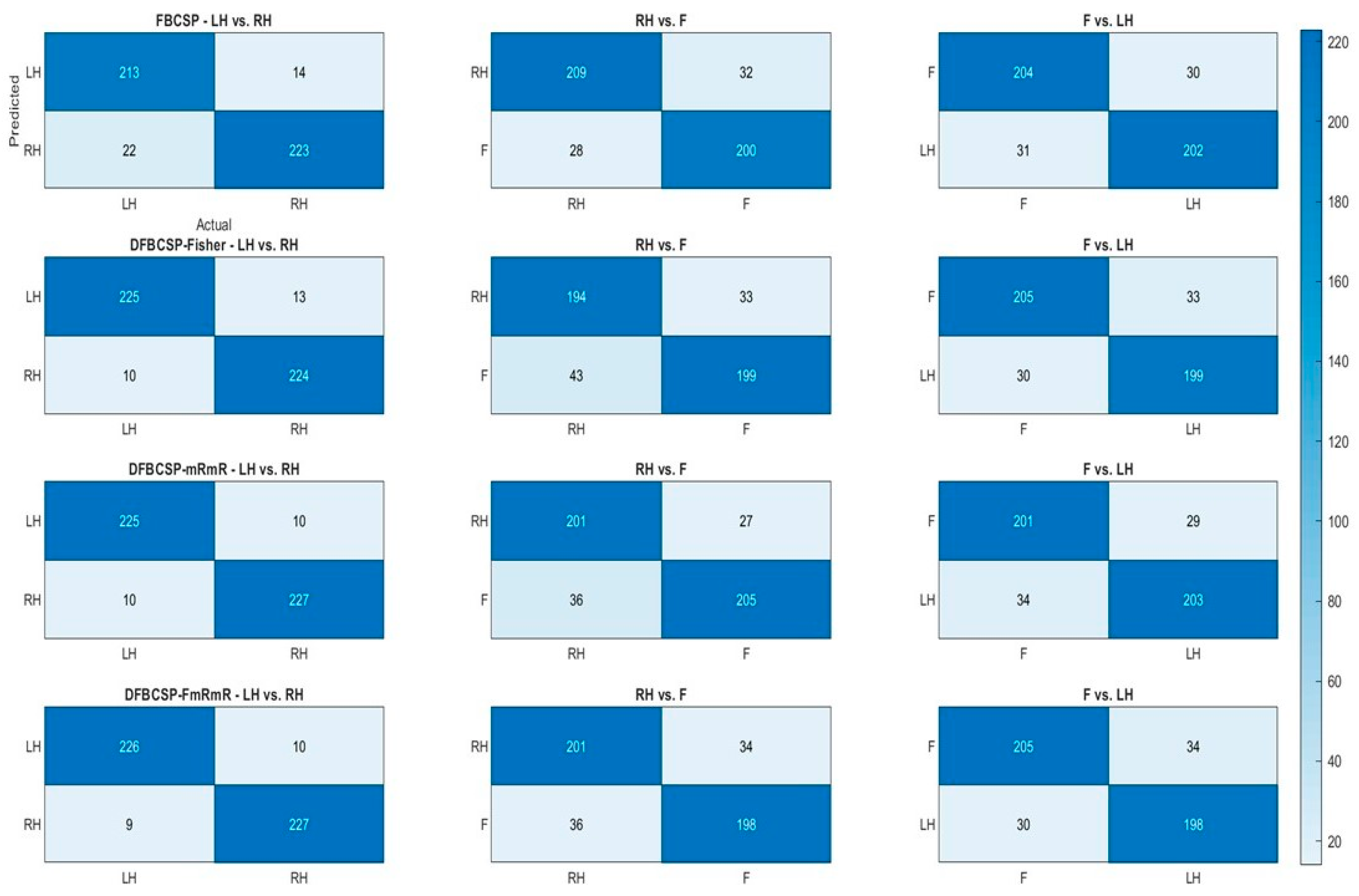
3.1. ROC and AUC

To examine how well LDA adapts to the self-acquired dataset and evaluate its performance, we compare three binary classifiers (pair 1—“Left hand vs. Right hand”, pair 2—“Right hand vs. Feet”, and pair 3 “Feet vs. Left hand”) of four methods. Receiver operator character (ROC) curves and area under the curve (AUC) of three LDA models combined with four feature extraction are shown in Figure 5. It is found that the ROC curves of all three classifiers are close to the top left corner and the AUC values are over 0.93. Noticeably, the proposed method follows a similar pattern compared to other methods, and even surpasses the FBCSP (0.99 compared to 0.98 in pair 1), although it is not significant. Additionally, the “Left hand vs. Right hand” pair performance is surprisingly higher than the other two (0.99 and 0.98 compared to 0.93 and 0.94). Besides ROC curves and AUC values, the confusion matrix is also an indication of the suitability of the models.

To further examine the performance of the four frameworks, heat maps are generated based on a confusion matrix (Figure 6). Actual labels are compared with predicted labels generated by 4 methods with a heat bar indicating the number of trials. We find that the performance of the proposed method surpasses conventional FBCSP in the “Left hand vs. Right hand” pair. Furthermore, the 1st pair classifications (left column) of the four methods are better than those of the 2nd and 3rd pair (middle and right column), around 20–30 trials. The accuracy of each pair for each method is computed by dividing the number of correctly classified samples (the darker blue diagonal) by the total within one confusion matrix. The result above is well supported by the ROC curve and AUC in Figure 5. Taken together, we can conclude that these methods are highly effective for the subject. The accuracy and F1-score of both datasets are compiled in the following subsections for a more transparent verification.

The averaged ROC curves and AUC values are depicted in Figure 7. There are no significant discrepancies between curves as well as the AUC values between methods. However, pair 2 and pair 3 have higher AUC values than pair 1.

3.2. Accuracy and F1-Score of BCI Competition’s Dataset

To evaluate the classification capacity of conventional and proposed frameworks on a reliable published dataset, both parameters for evaluation are composed in

Table 1. Accuracy and F1-score of four methods on BCI Competition’s dataset for three pairs.

Subject	LH-RH
	FBCSP		DFBCSP—Fisher		DFBCSP—mRmR		DFBCSP—FmRmR
	Acc	F1	Acc	F1	Acc	F1	Acc	F1
01	71.01	0.7	76.09	0.76	77.54	0.78	73.91	0.74
02	56.62	0.54	61.76	0.62	54.41	0.49	61.03	0.57
03	72.26	0.74	92.7	0.93	88.32	0.89	90.51	0.91
04	50.59	0.45	51.76	0.44	63.53	0.61	62.35	0.57
05	57.36	0.57	52.71	0.51	61.24	0.58	51.94	0.5
06	59.29	0.57	53.98	0.5	50.44	0.49	60.18	0.59
07	62.41	0.63	69.92	0.71	76.69	0.77	68.42	0.69
08	71.97	0.73	88.64	0.89	85.61	0.85	87.88	0.88
09	39.66	0.39	62.93	0.57	70.69	0.69	65.52	0.61
Mean ± SD	60.13 ± 10.85	0.59 ± 0.12	67.83 ± 15.26	0.66 ± 0.17	69.83 ± 13.35	0.68 ± 0.15	69.08 ± 12.9	0.67 ± 0.14
Subject	RH-F
	FBCSP		DFBCSP—Fisher		DFBCSP—mRmR		DFBCSP—FmRmR
	Acc	F1	Acc	F1	Acc	F1	Acc	F1
01	83.21	0.84	97.08	0.97	97.81	0.98	97.08	0.97
02	69.63	0.69	83.7	0.84	81.48	0.83	80	0.81
03	85.07	0.86	94.78	0.95	96.27	0.96	97.01	0.97
04	55.17	0.54	56.32	0.59	57.47	0.55	55.17	0.57
05	44.7	0.47	53.03	0.54	50.76	0.51	63.64	0.64
06	55.66	0.58	61.32	0.64	62.26	0.67	65.09	0.69
07	74.44	0.74	87.97	0.88	87.97	0.87	89.47	0.89
08	58.46	0.58	86.92	0.88	83.85	0.84	90.77	0.91
09	58.87	0.58	72.58	0.73	77.42	0.77	69.35	0.72
Mean ± SD	65.02 ± 13.79	0.65 ± 0.14	77.08 ± 16.77	0.78 ± 0.16	77.25 ± 16.88	0.78 ± 0.17	78.62 ± 15.77	0.8 ± 0.15
Subject	F-LH
	FBCSP		DFBCSP—Fisher		DFBCSP—mRmR		DFBCSP—FmRmR
	Acc	F1	Acc	F1	Acc	F1	Acc	F1
01	75.18	0.76	96.35	0.96	94.89	0.95	94.16	0.94
02	72.18	0.71	83.46	0.84	89.47	0.89	88.72	0.89
03	78.52	0.79	95.56	0.96	94.81	0.95	93.33	0.93
04	57.14	0.6	67.86	0.7	63.1	0.62	76.19	0.76
05	55.04	0.51	55.81	0.56	51.94	0.47	51.94	0.48
06	57.14	0.58	57.14	0.59	62.86	0.65	54.29	0.57
07	76.12	0.77	93.28	0.93	88.06	0.88	93.28	0.93
08	63.08	0.64	82.31	0.82	82.31	0.84	83.08	0.84
09	48.25	0.44	72.81	0.7	72.81	0.68	76.32	0.73
Mean ± SD	64.74 ± 11	0.64 ± 0.12	78.29 ± 15.75	0.78 ± 0.15	77.81 ± 15.72	0.77 ± 0.17	79.03 ± 16.23	0.79 ± 0.17

, for pair 1, pair 2, and pair 3, accordingly. The variation between F1-score and accuracy in Table 1 is not considerable, mostly under 4%, except for the pair 1 discrimination by DFBCSP—Fisher in subject 4, which is nearly 7%. Furthermore, the mean values of the two metrics are not different from each other, indicating the stability of the method as well as the data. A noteworthy point here is that DFBCSP frameworks achieve higher performance than the FBCSP framework in nine subjects. The mean values show that DFBCSP is 7–15% better than FBCSP in terms of accuracy and F1-score. This result is consistent with previous studies [40,65]. Subjects “01”, “02”, “03”, “07”, and “08” have good performance based on DFBCSP frameworks in general. Moreover, the proposed DFBCSP outweighs other methods in subjects “03” and “06 for pair 1, subjects “03”, “05”, “06”, “07”, and “08” for pair 2, and subject “04”, “07”, “08”, and “09” for pair 3 (bolded values). It can be concluded that DFBCSP—FmRmR is comparable to other methods.

Another key point is that the classification of pair 2 and pair 3 is better than that of pair 1 in most subjects, and the mean values also reassure that. In the FBCSP approach, approximately 60% from pair 1 compared to 65% from pair 2 and 64% from pair 3. In DFBCSP (3 approaches) around 68% from pair 1 compared to 78% from both pair 2 and pair 3. Only subject “08” shows an opposite trend. It can be concluded that MI patterns between hands and feet are easier to be recognized than those between the left and right hand.

However, the variations in performance between subjects are considerable as they elicit high standard deviation, which indicates the methods are not suitable for every participant. Further discussion will be given to the matter in the next section.

3.3. Accuracy and F1-Score of Self-Acquired Dataset

To both evaluate the performance of the proposed framework and validity of the self-acquired dataset, accuracy, and F1-score are compiled in

Table 2. Accuracy and F1-score of four methods on the author’s dataset for “Left hand vs. Right hand” pair.

Subject	LH-RH
	FBCSP		DFBCSP—Fisher		DFBCSP—mRmR		DFBCSP—FmRmR
	Acc	F1	Acc	F1	Acc	F1	Acc	F1
01	92.37	0.92	95.13	0.95	95.76	0.96	95.97	0.96
02	80.86	0.81	79.23	0.79	81.06	0.81	81.06	0.81
03	49.3	0.49	52.96	0.55	54.93	0.58	53.52	0.56
04	78.36	0.78	78.99	0.79	77.31	0.77	76.26	0.77
05	71.56	0.69	73.89	0.71	76.92	0.75	73.19	0.69
06	67.19	0.66	65.63	0.66	70.31	0.7	64.58	0.65
07	69.3	0.69	73.81	0.75	74.72	0.76	76.3	0.77
08	70.7	0.71	71.34	0.71	72.19	0.72	64.97	0.65
09	44.94	0.44	49.58	0.51	45.78	0.45	47.26	0.45
10	69.23	0.69	69.23	0.7	61.92	0.61	68.85	0.7
11	96.99	0.97	97.19	0.97	96.99	0.97	96.79	0.97
12	68.01	0.68	68.75	0.69	68.01	0.69	70.59	0.7
13	89.46	0.89	89.89	0.9	90.75	0.91	90.54	0.91
14	72.71	0.73	75.05	0.75	74.63	0.75	70.58	0.71
15	61.01	0.61	53.96	0.54	58.37	0.59	54.19	0.55
16	81.69	0.82	84.98	0.85	84.16	0.84	81.48	0.81
Mean ± SD	72.73 ± 14.08	0.72 ± 0.14	73.73 ± 14.09	0.74 ± 0.14	73.99 ± 14.28	0.74 ± 0.14	72.88 ± 14.42	0.73 ± 0.14

,

Table 3. Accuracy and F1-score of four methods on the author’s dataset for “Right hand vs. Feet” pair.

Subject	RH-F
	FBCSP		DFBCSP—Fisher		DFBCSP—mRmR		DFBCSP—FmRmR
	Acc	F1	Acc	F1	Acc	F1	Acc	F1
01	87.21	0.87	83.8	0.84	86.57	0.86	85.07	0.85
02	85.43	0.86	80.36	0.81	87.45	0.88	83.4	0.84
03	49.72	0.49	49.72	0.46	50.28	0.46	49.44	0.47
04	69.83	0.7	71.28	0.72	72.52	0.72	70.66	0.71
05	76.36	0.76	73.85	0.73	78.45	0.78	77.2	0.77
06	82.64	0.82	87.05	0.87	86.79	0.87	85.49	0.86
07	67.82	0.68	67.82	0.68	67.59	0.67	67.59	0.69
08	93.51	0.93	91.42	0.92	93.51	0.94	88.91	0.89
09	51.27	0.5	45.99	0.47	48.95	0.49	47.89	0.47
10	67.18	0.67	66.41	0.64	69.5	0.7	64.86	0.64
11	92.38	0.92	89.78	0.9	88.78	0.89	86.97	0.87
12	74.16	0.74	81.65	0.82	80.52	0.81	78.28	0.78
13	99.79	1	98.94	0.99	98.72	0.99	99.79	1
14	72.86	0.73	75.85	0.76	71.58	0.71	70.94	0.71
15	65.39	0.66	65.17	0.66	62.47	0.64	59.78	0.62
16	89.53	0.9	91.79	0.92	90.76	0.91	84.19	0.85
Mean ± SD	76.57 ± 14.58	0.76 ± 0.15	76.31 ± 14.9	0.76 ± 0.15	77.15 ± 14.81	0.77 ± 0.15	75.03 ± 14.48	0.75 ± 0.15

and

Table 4. Accuracy and F1-score of four methods on the author’s dataset for “Feet vs. Left hand” pair.

Subject	F-LH
	FBCSP		DFBCSP—Fisher		DFBCSP—mRmR		DFBCSP—FmRmR
	Acc	F1	Acc	F1	Acc	F1	Acc	F1
01	86.94	0.87	86.51	0.87	86.51	0.86	86.3	0.86
02	89.61	0.9	89.21	0.89	88.19	0.88	87.58	0.88
03	54.29	0.54	55.68	0.55	53.46	0.53	53.19	0.51
04	77.62	0.77	79.71	0.79	79.08	0.79	78.45	0.78
05	75.62	0.73	75.62	0.72	76.3	0.72	76.52	0.73
06	86.79	0.86	87.31	0.87	87.31	0.87	88.6	0.88
07	63.82	0.64	61.29	0.63	62.44	0.64	63.82	0.65
08	93.53	0.93	92.9	0.93	93.11	0.93	91.65	0.92
09	49.58	0.49	46.85	0.48	46.64	0.48	47.27	0.48
10	63.71	0.64	59.85	0.6	67.95	0.69	54.44	0.54
11	94.18	0.94	94.98	0.95	93.78	0.94	91.97	0.92
12	72.32	0.73	74.17	0.74	75.65	0.77	69	0.7
13	98.92	0.99	99.35	0.99	99.57	1	98.28	0.98
14	84.71	0.85	81.53	0.82	82.38	0.82	72.82	0.73
15	65.1	0.65	63.53	0.65	66.22	0.68	60.85	0.63
16	84.8	0.85	80.08	0.8	82.55	0.83	71.66	0.72
Mean ± SD	77.6 ± 14.83	0.77 ± 0.15	76.79 ± 15.39	0.77 ± 0.15	77.57 ± 14.88	0.78 ± 0.15	74.53 ± 15.56	0.74 ± 0.15

for pair 1, pair 2, and pair 3 accordingly. Similar to Table 1, the variation between F1-score and accuracy in Table 2, Table 3 and Table 4 is not considerable, mostly under 4%. Moreover, the mean values of the two metrics are not different from each other, indicating the stability of the method as well as the data. It can be observed that there are subjects (“ID01”, “ID02”, “ID06”, “ID08”, “ID11”, “ID13” and “ID16”) achieving high classification rates, except for pair 1 of subjects “ID06” and “ID08”, approximately 85 to over 90%. The DFBCSP—FmRmR has an equal efficiency to its variants. Although it does outperform other methods, we can conclude that the proposed framework is effective in both datasets. Furthermore, the aforementioned subjects in this dataset have the potential to use a practical BCI system, while others are affected by the “BCI illiteracy” phenomenon.

Likewise, subjects in the self-acquired dataset, except for subjects “ID 01”, “ID 04”, “ID 07”, and “ID 10”, elicit a similar pattern of having discrimination for pair 2 and pair 3 better than pair 1. For the four methods, the difference in the mean values is from 2–5%, and it is not as significant as in dataset IIa. Surprisingly, the mean and SD values of this dataset (Table 2, Table 3 and Table 4) are almost equivalent to those of dataset IIa (Table 1), which ranges from 70–80% (mean) ± 10–15% (SD). The results above further verify the validity and similarity between the two datasets as well as the consistency of the proposed framework.

However, it is of great importance to notice that FBCSP has an equal efficiency to the other three models in most subjects, unlike in dataset 2. This outcome is inconsistent with studies [40,65], in which only BCI Competition was used. We hypothesize that this inconsistency might be due to the differences between the two datasets. As mentioned in the previous section, the number of trials in the BCI competition dataset is only 72 per class while that of the self-acquired dataset is over 200 trials per class for each subject. Therefore, we decided to analyze models in each measurement for each subject for a more balanced comparison (72 trials compared to 50 trials). That is also why we chose only one session in the BCI competition dataset (Figure 8).

To test our hypothesis of FBCSP performance affected by the amount of data, the evaluation on one subject is broken down to each measurement (Figure 8). Three pairs and four models are also evaluated and the maximum number of measurements for each subject is five. The last column is the data for all measurements. The most obvious recognition is that FBCSP in each measurement (or each day) is outweighed by other algorithms, approximately 20–30%. The DFBCSP frameworks still perform well compared to each other. However, all algorithms, including FBCSP, have almost equal efficiency when all measurements of one subject are computed. This can be inferred that FBCSP works better when the number of data is large enough, while DFBCSP algorithms only require a lower amount to be sufficient. Consequently, BCI utilizing DFBCSP would require less data and time for both training and testing. This also implies that DFBCSP algorithms are more suitable for a robust and practical BCI system.

To further reassure our hypothesis, the difference in the accuracy of “all measurement” and “single measurement” of every subject is shown in Figure 9. “All” is defined as data of all recordings taken into account, and “single” is defined as data of each day taken into account and then accuracy is averaged across each measurement. A positive value indicates the accuracy of “all measurement” is better than that of “single measurement”, and vice versa. Most subjects have an accuracy difference between “all measurement” and “single measurement” to be positive. This indicates that a larger data size improves classification performance. The differences in all three DFBCSP frameworks are mainly below 8%, which is not remarkable as there were variations in performance among measurements of each subject. However, there is a great fall of the FBCSP framework in three pairs in most subjects when the evaluation is performed in each measurement (smaller data size). The difference ranges from 10–30%, which means the performance of FBCSP in “single measurement” is significantly lower than in “all measurement” (p = 0.0029, p = 0.0015 and p = 0.0008 for pair 1, pair 2 and pair 3 accordingly). The mean values of the difference of three DFBCSP frameworks are no more than 3% for three pairs, while that of FBCSP is 12.30%, 14.22%, and 15.37% for pair 1, pair 2, and pair 3, respectively (

Table 5. Mean difference in accuracy of “all measurement” and “single measurement” of self-acquired dataset.

LH-RH				RH-F				F-LH
FBCSP	DFBCSP—Fisher	DFBCSP—mRmR	DFBCSP—FmRmR	FBCSP	DFBCSP—Fisher	DFBCSP—mRmR	DFBCSP—FmRmR	FBCSP	DFBCSP—Fisher	DFBCSP—mRmR	DFBCSP—FmRmR
12.30	1.91	1.45	0.12	14.22	0.14	0.45	−0.37	15.37	−0.14	−0.65	−2.62

). Taken together, FBCSP performance is negatively affected by limited data size while that of the proposed DFBCSP is not. There are no differences between pairs.

4. Discussion

Intelligent optimization methods [26] along with deep learning networks [14,45,46,47,48] have widely been investigated in recent years. Although their performances are slightly superior to traditional machine learning, the burdens in terms of computational complexity and massive data requirement are far from trading off. Secondly, traditional algorithms such as CSP have been proved in countless studies to be effective for practical BCI, yet its potential needs further exploration. Finally, most studies evaluated their proposed framework on the BCI competition dataset but in the absence of actual data of local population, which is one of the criteria both to evaluate the validity of the proposed method and examine the suitability of various populations. Consequently, the novel approach of this study make contributions as follows:

• Propose a novel and reliable framework for motor imagery tasks based on spatial filters, automatic feature selection, and traditional classifier
• Evaluate the proposed methods on both self-acquired dataset and a BCI Competition dataset in terms of accuracy, F1-score, and ROC

From the results, there are numerous key points that have to be taken into account. Firstly, the validity of the self-acquired dataset has been proven through similarities with BCI Competition dataset IIa. The pattern of better classification of hands vs. feet over that of left vs. right hand is seen in both datasets, Table 1, Table 2, Table 3 and Table 4, and also consistent with previous studies [68]. Moreover, DFBCSP methods outweigh the FBCSP method in both datasets (single measurement cases for self-acquired data) and it has been clearly proven in several studies [18,39,40,65,69,70]. This can be explained because FBCSP (without feature selection) generates an enormous amount of features, i.e., 22 × 17 features in BCI competition datasets IIa, and obviously also contains redundant information that would degrade the performance. Molla et al. [70] also stated that the mean accuracy of a framework without feature selection is far worse than that of a framework integrated with feature selection as it does not use irrelevant features. That is why several algorithms have been built to select informative features to mainly improve the performance and reduce computational costs. The third similarity between the two datasets is in the mean values and their standard deviation. Both datasets imply that the BCI performance varied among users (moderate mean value and high standard deviation) and not every subject is suitable for a certain framework, or decoder, or even type of BCI. The phenomenon is known as “BCI illiteracy” which will be explained later.

Secondly, the robustness and reliability of the proposed method are clearly demonstrated by the results. ROC curve, accuracy, and F1-score of the proposed method are consistent throughout the study and they are comparative to other methods. Although the framework might not be better than other conventional ones, there are some cases that have proven its superiority. Likewise, other methods are superior to one another depending on subjects and pairs. It can be inferred that the subjects from both datasets suffer from “BCI illiteracy”. BCI illiteracy is caused by a variety of factors that may be classified into two categories [71]: physiological and non-physiological causes. Regarding physiological reasons, variations in the brain’s anatomy, such as the dispersion of neurons in the brain folds, may make recording brain signals through the electrodes problematic. Additionally, transitory variables should be considered. These could include changes in attention level, exhaustion, or impediment, as well as social aspects such as emotional reactions, interactions, and social cues encountered during BCI training, which should be taken into consideration. Non-physiological reasons include a lack of proficiency in operating the system or inadequate training procedures, which lead the participant to misunderstand the instructions and execute the experiment erroneously [71]. That is why it leads to high standard deviation values in both datasets. Consequently, the proposed method could only handle a few cases in “BCI illiteracy” and further research is required to tackle the phenomenon.

Thirdly, the classification of feet vs. hand imagery is more discriminative than left vs. right-hand imagery as shown in both datasets, although it is more noticeable in BCI competition dataset IIa (4–10% difference) than in self-acquired dataset (2–5% difference). This might be due to more discriminable EEG patterns generated by feet MI than those induced by the left or right hand. Pfurtscheller et al. [68] explained that feet MI would elicit both mu and/or beta ERD in the mid-central cortex and mu ERS on two hemispheres, specifically in the hand presentation area [72]. The so-called “focal ERD/surround ERS” phenomenon was found in [8]. Hence, the authors in the aforementioned studies reported a more significant variation in 10–12 Hz band power when comparing different limbs (hand vs. feet) than homologous ones.

Finally, the FBCSP (without feature selection) could only work with data that is large enough, while DFBCSP could be effectively functional with small-sized data. It can clearly be seen that FBCSP efficiency is comparative to other methods (Table 2, Table 3 and Table 4) when it is applied to the self-acquired dataset, whose number of trials ranges from 220–250 per class, but downgrades to 10–30% if applied to a BCI competition IIa (72 trials per class) or single measurement of the self-acquired dataset (50 trials per class) (Figure 9). To the best of the author’s knowledge, the bottom line of this outcome lies in the number of features and physiological differences between days of data recording. In a single measurement, FBCSP extracts all possible features, including redundant ones, while DFBCSP selectively chooses them; thus, it has a better performance than FBCSP. However, due to daily physiological changes of human nature, the EEG patterns when performing MI tasks may have changed as well leading to changes in required features for task discrimination. When including all data of each subject into one evaluation, redundant features may become informative ones, resulting in better FBCSP performance. Further research is needed to confirm this hypothesis. Yet, the FBCSP is obviously unable to have an optimal computation cost as DFBCSP. Hence, DFBCSP is more suitable as a practical BCI system in terms of performance and computation cost.

5. Conclusions

Brain–computer interface has attracted a lot of interest in the hope of improving human life. Motor imagery-based BCI is expected to have potential in the medical field, especially in neurorehabilitation. However, this type of system has been encountered several challenges in terms of the limited number of commands, insufficient performance and training time, robust online analysis, and so forth. Various algorithms and approaches have been proposed to deal with the challenges, and CSP is one of the candidates for a practical BCI. Hence, numerous researchers put their effort in harnessing the full potential of CSP and its variants through methods such as the combination of CSP and time-frequency analysis, simultaneous optimization of the spatial spectrum filter, filtering the EEG signals into several frequency bands, and intelligent optimization. In addition, filter, wrapper, and embedded methods have also been established to further improve the performance. Yet, there are still limitations requiring further investigations to shed light on. To this end, the authors hope to make contributions to this crusade. The study successfully proposed a novel DFBCSP framework in combination with Fisher’s ratio and the mRmR algorithm. The framework was evaluated on both datasets and produced noteworthy findings mentioned in the previous section. The proposed method could be applied in any classification problems, mainly in electrophysiological signal processing but not limited to other researches requiring pattern recognition, biometrics identification, and machine learning-related problems. Furthermore, the proposed method could be utilized in small-sized data, which is essential in real-world applications. Lastly, the reassurance of the discrimination between hand vs. feet better than left vs. right hand provides more proof about responses on motor cortex when performing motor imagery in the field of neuroscience.

Nevertheless, there are some drawbacks to the study. Firstly, the performance of the proposed method is yet satisfactory for practical BCI, especially in a medical context. One way to address this issue is utilizing SVM and tuning its parameters to obtain optimal results. In addition, trial selection could be performed in the pre-processing step to eliminate undesired trials. Secondly, other metrics such as information transfer rate (ITR) and computational time, which are critical for practical BCI, are not considered in the paper. Thirdly, the study is carried out only in offline analysis. The authors hope to conduct further investigations into these matters. Segmenting the time window into 1 s makes it suitable to establish a model to perform online analysis. Hence the authors hope to establish a robust decoder for real-time motor imagery training with feedbacks. In future investigations, comparison with other feature selection methods or combination with optimization methods [26,27,29] while minimizing computation cost should be carried out.