Performance Comparison for Single-User and Multi-User Network MIMO Cellular Systems with Power Management

Abstract

Cellular mobile systems aim at aggressive spectrum reuse to achieve high spectral efficiency. Unfortunately, this leads to unacceptable interference near cell borders. To control this, network multi-input multiple-output (MIMO) can be adopted to improve coverage and cell-edge throughput through multi-cell cooperation. With network MIMO, multiple geographically separated base stations (BSs) cooperatively serve their cell-edge users (CEUs) using their antennas, acting together as a network of distributed antenna array. It can be single-user (SU) or multi-user (MU) network MIMO by coordinating channel allocation in adjacent cells. In this paper, we make a capacity comparison of SU- and MU-network MIMO. In network MIMO, a collaborative BS simultaneously serves its own cell-center users (CCUs) and CEUs, and the CEUs of other partner BSs under a power constraint. As a result, power management among three types of users (intra-cell CCUs/CEUs, inter-cell CEUs) becomes necessary. Accordingly, we propose power management methods to help raise the signal strength of inter-cell CEUs and in the meantime gratify the performance of intra-cell users. Simulation results show that MU-network MIMO with superposition coding offers much better CEU capacity than SU-network MIMO. As for the CCU capacity, MU-network MIMO is generally better than SU-network MIMO.

1. Introduction

Cellular systems are targeting aggressive spectrum reuse via universal frequency reuse to achieve high spectral efficiency and simplify frequency planning [1,2,3,4,5]. However, universal frequency reuse leads to unacceptable interference level at cell borders, i.e., the quality of service (QoS) remarkably depends on user location. To control this, cellular systems adopt several interference mitigation techniques to achieve uniform levels of QoS. Among these, network multiple-input multiple-output (MIMO) is used to mitigate the serious co-channel interference (CCI) and improve cell-edge performance. With network MIMO, multiple geographically separated base stations (BSs) collectively serve their cell-edge users (CEUs) using their antennas. These collaborative BSs can together serve either each individual CEU or a group of their CEUs during cooperative network MIMO transmission, which are called the single-user (SU) and multi-user (MU)-network MIMO, respectively. Network MIMO is referred to as coordinated multi-point (CoMP) in the Long-Term Evolution-Advanced (LTE-A) [6].

Another key technique to combat the serious interference is inter-cell interference coordination (ICIC) [7,8]. Among a variety of ICIC strategies, the soft frequency reuse (SFR) and fractional frequency reuse (FFR) are widely adopted [9,10,11]. Both schemes assign a frequency reuse factor of one for cell-center users (CCUs) and a larger frequency reuse factor for CEUs. In LTE-A cellular systems, FFR has been used to keep the inter-cell interference at cell edges as low as possible.

Combining both network MIMO and FFR-based ICIC can have the advantages of complexity reduction and throughput enhancement [12]. In addition, the studies of network MIMO on top of the FFR-based cellular system have drawn increasing interest [11,12,13,14,15]. It has been shown that using a 3-cell coordinated network MIMO with tri-sector frequency partition can outperform the 7-cell one with omni-directional antennas [12]. The 3-cell coordinated network MIMO architectures have been particularly adopted by the IEEE802.16m WiMAX standard body, which has specified that the default number of neighboring cells in the collaborative network MIMO transmission is three. The FFR-related research was generally associated with the orthogonal frequency-division multiple access (OFDMA) systems [11,13].

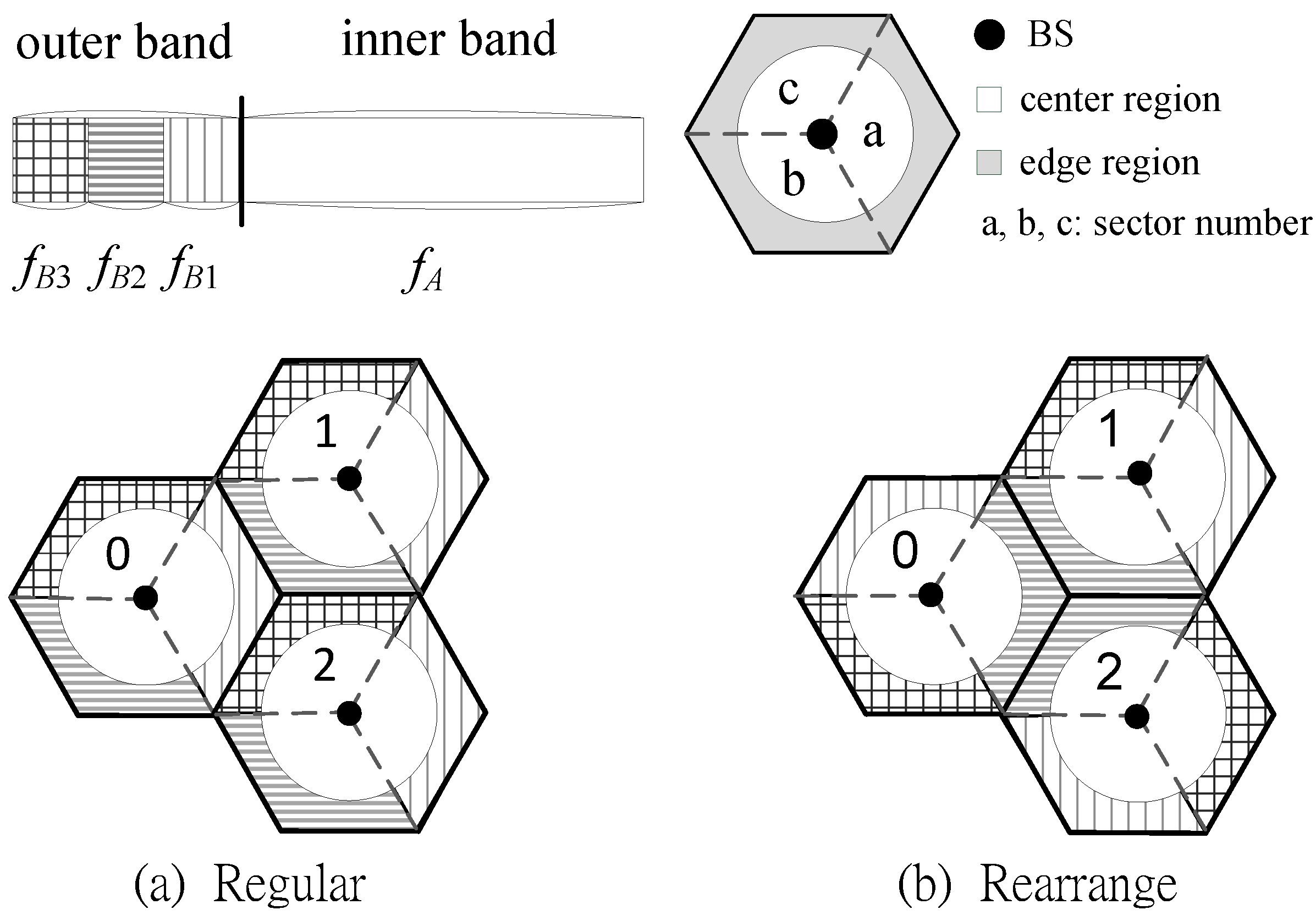
In this paper, we consider two FFR-based frequency reuse methods for 3-cell network MIMO with tri-sector cells in OFDMA-based downlink cellular systems. They are regular and rearranged frequency partitions as shown in Figure 1. In the conventional regular one, the adjacent sectors of neighboring cells are with different frequency bands [13,14,16]. On the contrary, the rearranged frequency partition has the adjacent sectors of neighboring cells use the same frequency band. Thus, the rearranged frequency partition would yield serious CCI for network MIMO transmission. Regular and rearranged frequency partitions are associated with SU- and MU-network MIMO, respectively, to realize multi-cell cooperation. In this paper, we investigate the performance comparison between SU- and MU-network MIMO. In OFDMA systems, a collaborative BS can together serve its own users and the CEUs of other partner BSs under a transmitter power constraint. As a result, power management among three types of users (i.e., intra-cell CCUs, intra-cell CEUs, and inter-cell CEUs) becomes necessary. To the best of our knowledge, however, there has been no related literature dealing with this issue. Accordingly, we will develop methods of managing power to help raise the signal strength of inter-cell CEUs and in the meantime gratify the performance of intra-cell users. The rest of the paper is organized as follows. Tri-sector FFR-based frequency partitions (regular and rearrange) are introduced in Section 2. In Section 3, we present the signal model. Joint preprocessing techniques to eliminate serious CCI for MU-network MIMO are discussed in Section 4. Methods of managing transmitter power are given in Section 5. Simulation results are presented in Section 6 and finally the conclusions are given in Section 7.

2. Tri-Sector FFR-Based Frequency Partition

ICIC technique aims at minimizing CCI by efficiently coordinating channel allocation in adjacent cells. On top of network MIMO, this section introduces two FFR-based ICIC frequency reuse schemes as shown in Figure 1. The spectrum is divided into the inner frequency band $f_A$ and outer frequency band $f_B$, where $f_B$ is further partitioned into three equal sub-bands ($f_{B1}$, $f_{B2}$ and $f_{B3}$) [12,15]. The inner and outer frequency bands are for CCUs’ and CEUs’ exclusive use, respectively. The differentiation between CEU and CCU can be made based on the received signal-to-interference-plus-noise ratio (SINR) at the user equipment [17]. All the CCUs within a cell share the sub-channels in inner frequency band $f_A$. However, we serve a CEU either on a specific sub-channel of a sub-band $f_{Bi}$ or on an entire sub-band $f_{Bi}$ for SU- and MU-network MIMO, respectively. Specifically, the inner band $f_A$ adopts universal reuse factor with omni-directional antenna for CCUs; the outer bands $f_B$ uses frequency reuse factor of three for CEUs in each sector.

As mentioned in the previous section, we consider two frequency partitions (regular and rearranged) in Figure 1 [12]. Traditionally, the regular frequency planning in Figure 1a is the FFR-based frequency partition for a tri-sector cellular system, where the sectors of different cells with the same outer sub-band have the same main-beam direction. Accordingly, with regular frequency planning, the contiguous cell-edge areas of neighboring cells are assigned to different orthogonal outer sub-bands $\left\{f_{B1},f_{B2},f_{B3}\right\}$ to avoid CCI as shown in Figure 1a. On the contrary, with rearranged frequency planning, the sectors of different cells with the same outer sub-band have different main-beam direction as shown in Figure 1b, where contiguous cell-edge areas of neighboring cells are with the same outer sub-bands.

In both SU- and MU-network MIMO, each CEU is served by a group of collaborative BSs. These BSs form a cooperative cell set (CCS) associated with that CEU. For convenience, let a BS sector $n\left(q\right)$ denote the sector $q$ of cell $n$. For example, consider a certain CEU $u$ located in the cell-edge area of sector $0\left(a\right)$ for regular frequency planning in Figure 1a. For this CEU $u$, we have the corresponding CCS $C_u=\left\{0\left(a\right),1\left(b\right),2\left(c\right)\right\}$, which use a particular sub-channel selected from outer sub-band $f_{B1}$ to collectively serve the CEU $u$. This is SU-network MIMO transmission. As in frequency-division multiple access (FDMA), SU-network MIMO allocates each CEU a unique sub-channel from an outer sub-band and thus the cooperative BSs in a CCS result in no multi-user interference. As for the rearranged one in Figure 1b, the collaborative BSs in CCS $\left\{0\left(a\right),1\left(b\right),2\left(c\right)\right\}$ turn to together serve a group of their CEUs using the sub-band $f_{B2}$ (i.e., MU-network MIMO), i.e., all CEUs in this group share the entire sub-band $f_{B2}$. As a result, the serious multi-user interference is inevitable. To control this, joint preprocessing among cooperative BSs is necessary in MU-network MIMO with rearranged frequency planning.

3. Signal Model

In this section, we present OFDMA-based signal models for CCU point-to-point transmission and 3-cell coordinated transmission, including MU- and SU-network MIMO. Consider a CCS $\left\{0\left(a\right),1\left(b\right),2\left(c\right)\right\}$ as shown in Figure 1, where each cell employs 120° sectoring and is divided into cell-center and cell-edge regions. Users located in cell-center and cell-edge regions are referred to as CCUs and CEUs, respectively. We apply the traditional point-to-point and 3-cell coordinated transmission to CCUs and CEUs, respectively. Assume that each sector and each user are equipped with $N_T$ sector antennas and $N_R$ receiver antennas, respectively. The antenna pattern for each sector antenna in decibel is specified by [18]

$$A{\left(\theta \right)}_{\mathrm{dB}}=-\min \left[12{\left(\theta /{\theta }_{3\mathrm{dB}}\right)}^2,A_m\right],-{180}^{\circ }\le \theta \le {180}^{\circ },$$

(1)

where $\theta$ is the angle between the direction of interest and the main-beam of the antenna, ${\theta }_{3\mathrm{dB}}={70}^{\circ }$ is the 3-dB beamwidth in degree and $A_m=20 \mathrm{dB}$ is the maximum attenuation for the sidelobe.

The overall radio channel model at subcarrier $k$ of user $u$ with respect to BS $b$ is represented by

$${\lambda }_k^{\left(b,u\right)}=H_k^{\left(b,u\right)}\sqrt{A\left({\theta }^{\left(b,u\right)}\right)K^{\left(b,u\right)}{L}^{\left(b,u\right)}},$$

(2)

where $H_k^{\left(b,u\right)}$ denotes the small-scale Rayleigh fading, $K^{\left(b,u\right)}$ represents the shadowing effect and $L^{\left(b,u\right)}$ is the path loss. The cross-correlation model for the shadowing effect is given by

$$\rho =\{\begin{array}{c}0.8-\left|\theta \right|/150 \mathrm{if} \left|\theta \right|\le {60}^{°}\\ 0.4 \mathrm{if} \left|\theta \right|>{60}^{°}\end{array},$$

(3)

where $\theta$ is the difference of angle-of-arrival between two radio links observed at the receiver. The propagation loss model between a user $u$ and a BS $b$ is given by [19]

$$L^{\left(b,u\right)}={\beta }_0\times {\left(d^{\left(b,u\right)}\right)}^{-\gamma },$$

(4)

where ${\beta }_0$ represents the propagation constant, $d^{\left(b,u\right)}$ is the propagation distance in kilometer and $\gamma$ denotes the path loss exponent. According to Shannon theorem, the achievable channel capacity is given by

$$W\times {\log }_2\left(1+\Gamma /\eta \right) \mathrm{bits}/\sec ,$$

(5)

where $W$ denotes bandwidth of the channel, $\Gamma$ represents the SINR. The parameter $\eta \equiv -\ln \left(5\times P_e\right)/1.5$ is the SINR gap with the target bit error rate (BER) $p_e$ [20]. In this paper, the target BER is given by ${10}^{-4}$.

3.1. MU-Network MIMO Signal Model

Consider a 3-cell coordinated MU-network MIMO as shown in Figure 1b, where 3 cooperative BSs together serve a group of their $N_{CEU}$ CEUs using the whole outer sub-band $f_{B2}$. Assume a proper cyclic-prefix length is appended to the inverse discrete Fourier transform (IDFT) sequence such that the inter-symbol interference can be ignored. After DFT, the signal reception at subcarrier $k$ by receiver antenna $v$ of CEU $u$ is:

$$Y_k^{\left(u,v\right)}={{\displaystyle \sum }}_{b=0}^2{{\displaystyle \sum }}_{q=0}^{N_T-1}{\lambda }_k^{\left(b,u,q,v\right)}\left(X_k^{\left(b,u,q\right)}+\underset{\mathrm{multi}-\mathrm{user}\mathrm{interference}}{\underbrace{{{\displaystyle \sum }}_{\begin{array}{c}{u}^{\prime }=0\\ \left(u\prime \ne u\right)\end{array}}^{N_{CEU}-1}{X}_k^{\left(b,u\prime ,q\right)}}}\right)+W_k^{\left(u,v\right)}, k\in {\Im }^{\left(u\right)},$$

(6)

where ${\lambda }_k^{\left(b,u,q,v\right)}$ denotes the overall channel gain at subcarrier $k$ from transmitter antenna $q$ of BS $b$ to receiver antenna $v$ of CEU $u$. Similarly, $X_k^{\left(b,u,q\right)}$ represents the pre-coded symbol transmitted from antenna $q$ of BS $b$ to CEU $u$. The notation ${\Im }^{\left(u\right)}$ denotes the index set of subcarriers of the outer sub-band $f_{B2}$. $W_k^{\left(u,v\right)}$ is the received noise with single-sided power spectral density $N_0$.

Let $I_k^{\left(u\right)}$ denote the index of the $k$th subcarrier in ${\Im }^{\left(u\right)}$ for $k=0,1,\dots ,\left|{\Im }^{\left(u\right)}\right|-1$, where $\left|{\Im }^{\left(u\right)}\right|$ represents the cardinality of the set ${\Im }^{\left(u\right)}$. We further represent the DFT sequence of (6) as a $\left|{\Im }^{\left(u\right)}\right|\times 1$ vector $Y^{\left(u,v\right)}\equiv {\left[Y_{I_0^{\left(u\right)}}^{\left(u,v\right)},Y_{I_1^{\left(u\right)}}^{\left(u,v\right)},\dots ,Y_{I_{\left|{\Im }^{\left(u\right)}\right|-1}^{\left(u\right)}}^{\left(u,v\right)}\right]}^T$, which is given by the following matrix-vector form

$$Y^{\left(u,v\right)}={{\displaystyle \sum }}_{b=0}^2{{\displaystyle \sum }}_{q=0}^{N_T-1}{\Lambda }^{\left(b,u,q,v\right)}\left(X^{\left(b,u,q\right)}+\underset{\mathrm{multi}-\mathrm{user}\mathrm{interference}}{\underbrace{{{\displaystyle \sum }}_{\begin{array}{c}{u}^{\prime }=0\\ \left(u\prime \ne u\right)\end{array}}^{N_{CEU}-1}{\mathit{X}}^{\left(b,u\prime ,q\right)}}}\right)+W^{\left(u,v\right)}, v=0,1,\dots ,N_R-1,$$

(7)

where ${\Lambda }^{\left(b,u,q,v\right)}$ is a $\left|{\Im }^{\left(u\right)}\right|\times \left|{\Im }^{\left(u\right)}\right|$ diagonal channel matrix with ${\lambda }_{I_k^{\left(u\right)}}^{\left(b,u,q,v\right)}$ as its $k$th diagonal element. Both $X^{\left(b,u,q\right)}$ and $W^{\left(u,v\right)}$ are $\left|{\Im }^{\left(u\right)}\right|\times 1$ vectors, whose $k$th entry are $X_{I_k^{\left(u\right)}}^{\left(b,u,q\right)}$ and $W_{I_k^{\left(u\right)}}^{\left(u,v\right)}$, respectively.

For later use, we define ${\Lambda }^{\left(b,u,v\right)}\equiv \left[{\Lambda }^{\left(b,u,0,v\right)},{\Lambda }^{\left(b,u,1,v\right)},\dots ,{\Lambda }^{\left(b,u,N_T-1,v\right)}\right]$, which denotes the $\left|{\Im }^{\left(u\right)}\right|\times \left|{\Im }^{\left(u\right)}\right|N_T$ aggregate channel matrix observed at the receiver antenna $v$ of CEU $u$ from $N_T$ transmit antennas of BS $b$. Similarly, the aggregate channel matrix observed at the antenna $v$ of CEU $u$ from all three cooperative BSs is given by

$${\Lambda }^{\left(u,v\right)}\equiv \left[{\Lambda }^{\left(0,u,v\right)},{\Lambda }^{\left(1,u,v\right)},{\Lambda }^{\left(2,u,v\right)}\right]\in {ℂ}^{\left|{\Im }^{\left(u\right)}\right|\times 3\left|{\Im }^{\left(u\right)}\right|N_T},$$

(8)

where $ℂ$ represents the complex space. The aggregate signal vector sent to CEU $u$ from $N_T$ transmit antennas of BS $b$ can be represented as

$$X^{\left(b,u\right)}\equiv {\left[X^{\left(b,u,0\right)}{}^T,X^{\left(b,u,1\right)}{}^T,\dots ,X^{\left(b,u,N_T-1\right)}{}^T\right]}^T\in {ℂ}^{\left|{\Im }^{\left(u\right)}\right|N_T\times 1},$$

(9)

To gain insight into how joint preprocessing works, we cascade all the $\left|{\Im }^{\left(u\right)}\right|\times 1$ received vectors of (7) to form a $\left|{\Im }^{\left(u\right)}\right|N_R\times 1$ received vector, as shown below:

$$Y^{\left(u\right)}\equiv {\left[Y^{\left(u,0\right)}{}^T,Y^{\left(u,1\right)}{}^T,\dots ,Y^{\left(u,N_R-1\right)}{}^T\right]}^T={\Lambda }^{\left(u\right)}\left(X^{\left(u\right)}+\underset{\begin{array}{c}\mathrm{m}\mathrm{u}\mathrm{l}\mathrm{t}\mathrm{i}-\mathrm{u}\mathrm{s}\mathrm{e}\mathrm{r} \\ \mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{f}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e}\end{array}}{\underbrace{{{\displaystyle \sum }}_{\begin{array}{c}{u}^{\prime }=0\\ \left(u\prime \ne u\right)\end{array}}^{N_{CEU}-1}{X}^{\left(u\prime \right)}}}\right)+W^{\left(u\right)},$$

(10)

where ${\Lambda }^{\left(u\right)}\equiv {\left[{\Lambda }^{\left(u,0\right)}{}^T,{\Lambda }^{\left(u,1\right)}{}^T,\dots ,{\Lambda }^{\left(u,N_R-1\right)}{}^T\right]}^T$ is the $\left|{\Im }^{\left(u\right)}\right|N_R\times 3\left|{\Im }^{\left(u\right)}\right|N_T$ aggregate channel matrix of user $u$, $X^{\left(u\right)}\equiv {\left[X^{\left(0,u\right)}{}^T,X^{\left(1,u\right)}{}^T,X^{\left(2,u\right)}{}^T\right]}^T$ is the $3\left|{\Im }^{\left(u\right)}\right|N_t\times 1$ aggregate signal vector sent for CEU $u$ from all 3 coordinated BSs, and $W^{\left(u\right)}\equiv {\left[W^{\left(u,0\right)}{}^T,W^{\left(u,1\right)}{}^T,\dots ,W^{\left(u,N_R-1\right)}{}^T\right]}^T$ is the aggregate received noise vector.

The aggregate signal vector $X^{\left(u\right)}$ associated with CEU $u$ results from jointly processing a $K^{\left(u\right)}\times 1$ data vector $d^{\left(u\right)}\equiv \left[d_0^{\left(u\right)},d_1^{\left(u\right)},\dots ,d_{K^{\left(u\right)}-1}^{\left(u\right)}\right]$ by all cooperative BSs, where $K^{\left(u\right)}$ is the number of data symbols sent to CEU $u$ in a network MIMO transmission. Specifically, the cooperative BSs jointly design a $3\left|{\Im }^{\left(u\right)}\right|N_T\times K^{\left(u\right)}$ preprocessing matrix $F^{\left(u\right)}$ for the $K^{\left(u\right)}\times 1$ data vector $d^{\left(u\right)}$, by which the $3\left|{\Im }^{\left(u\right)}\right|N_T\times 1$ signal vector $X^{\left(u\right)}$ is produced in the sense of mitigating the multi-user interference from other $N_{CEU}-1$ co-channel CEUs. In summary, the aggregate signal vector $X^{\left(u\right)}$ is produced according to

$$X^{\left(u\right)}=F^{\left(u\right)}{d}^{\left(u\right)}, u=0,1,\dots ,N_{CEU}-1.$$

(11)

Define $K\equiv {\displaystyle \sum }_{u=0}^{N_{CEU}-1}{K}^{\left(u\right)}$, which is the total number of CEU data symbols sent in a network MIMO transmission. Substituting (11) into (10), we have a more concise expression for the aggregate received DFT vector of (10) as follows:

$$Y^{\left(u\right)}={\Lambda }^{\left(u\right)}Fd+W^{\left(u\right)}, u=0,1,\dots ,N_{CEU}-1,$$

(12)

where the $K\times 1$ aggregate data vector is

$$d\equiv {\left[d^{\left(0\right)}{}^T,d^{\left(1\right)}{}^T,\dots ,d^{\left(N_{CEU}-1\right)}{}^T\right]}^T\in {ℂ}^{K\times 1},$$

(13)

and $F$ is the $3\left|{\Im }^{\left(u\right)}\right|N_t\times K$ completely aggregate preprocessing matrix given by

$$F\equiv \left[F^{\left(0\right)},F^{\left(1\right)},\dots ,F^{\left(N_{CEU}-1\right)}\right]\in {ℂ}^{3\left|{\Im }^{\left(u\right)}\right|N_T\times K}.$$

(14)

3.2. CCU Point-to-Point and SU-Network MIMO Signal Models

We have presented the signal model for CEUs in MU-network MIMO. In this sub-section, we first present the CCU point-to-point signal model. For CCU $u$, the DFT signal at subcarrier $k$ received from the serving BS $b$ by its receiver antenna $v$ is

$$Y_k^{\left(u,v\right)}={{\displaystyle \sum }}_{q=0}^{N_T-1}{\lambda }_k^{\left(b,u,q,v\right)}{X}_k^{\left(b,u,q\right)}+W_k^{\left(u,v\right)}, k\in {\Im }_A^{\left(u\right)}.$$

(15)

There is no intra-cell interference because each CCU is assigned a different sub-channel from the inner band $f_A$. Here, the index set ${\Im }_A^{\left(u\right)}$ of subcarriers is associated with a particular sub-channel selected from the inner band $f_A$.

As for the CEUs in SU-network MIMO, consider a 3-cell coordinated network MIMO as shown in Figure 1a, where each CEU is together served by 3 cooperative BSs using a different sub-channel from an outer sub-band. For instance, a CEU located at cell-edge region of sector 0(a) would be collectively served by the 3 cooperative BSs using a sub-channel selected from outer sub-band $f_{B1}$. Thus, after DFT, the signal reception at subcarrier $k$ by receiver antenna $v$ of CEU $u$ can be expressed as

$$Y_k^{\left(u,v\right)}={{\displaystyle \sum }}_{b=0}^2{{\displaystyle \sum }}_{q=0}^{N_T-1}{\lambda }_k^{\left(b,u,q,v\right)}{X}_k^{\left(b,u,q\right)}+W_k^{\left(u,v\right)}, k\in {\Im }_{Bi}^{\left(u\right)},$$

(16)

where the index set ${\Im }_{Bi}^{\left(u\right)}$ of subcarriers is associated with a particular sub-channel selected from an outer band f_Bi.

4. Joint Preprocessing Techniques for MU-Network MIMO

As mentioned previously, the serious multi-user interference is inevitable in MU-network MIMO. To control this, joint preprocessing among cooperative BSs is necessary. With per-sector antenna power constraint, we derive various joint preprocessing schemes for OFDMA-based MU-network MIMO. They include MU joint time-division multiple access (MU-JTDMA), MU joint zero-forcing (MU-JZF), and MU joint minimum mean-square error (MU-JMMSE). Both MU-JZF and MU-JMMSE are superposition-coding schemes and MU-JTDMA is an orthogonal one.

Recall that the signal vector sent to CEU $u$ from all 3 coordinated BSs is the $3\left|{\Im }^{\left(u\right)}\right|N_t\times 1$ aggregate signal vector $X^{\left(u\right)}\equiv {\left[X^{\left(0,u\right)}{}^T,X^{\left(1,u\right)}{}^T,X^{\left(2,u\right)}{}^T\right]}^T$. Accordingly, the preprocessing matrix $F^{\left(u\right)}$ in (11) can be decomposed as

$$F^{\left(u\right)}\equiv {\left[F^{\left(0,u\right)}{}^T,F^{\left(1,u\right)}{}^T,F^{\left(2,u\right)}{}^T\right]}^T\in {ℂ}^{3\left|{\Im }^{\left(u\right)}\right|N_T\times K^{\left(u\right)}},$$

(17)

where BS $b$ uses sub-matrix $F^{\left(b,u\right)}\in {ℂ}^{\left|{\Im }^{\left(u\right)}\right|N_T\times K^{\left(u\right)}}$ to pre-code data vector $d^{\left(u\right)}$, i.e., $X^{\left(b,u\right)}=F^{\left(b,u\right)}{d}^{\left(u\right)}$. Then the total power required by BS $b$ to serve all the $N_{CEU}$ CEUs is given by

$$T^{\left(b\right)}=\mathrm{E}\left\{{{\displaystyle \sum }}_{u=0}^{N_{CEU}-1}\mathrm{tr}\left[X^{\left(b,u\right)}{X}^{\left(b,u\right)}{}^H\right]\right\}={{\displaystyle \sum }}_{u=0}^{N_{CEU}-1}\mathrm{tr}\left[F^{\left(b,u\right)}{R}^{\left(u\right)}{F}^{\left(b,u\right)}{}^H\right],$$

(18)

where $\mathrm{E}[·]$ is the statistical expectation operator, $\mathrm{tr}[·]$ denotes the trace of a square matrix, the superscript $H$ denotes Hermitian transpose and $R^{\left(u\right)}\equiv \mathrm{E}\left[d^{\left(u\right)}{d}^{\left(u\right)}{}^H\right]$ is the covariance matrix of $d^{\left(u\right)}$ with zero-mean uncorrelated data symbols.

4.1. MU-JTDMA

In MU-JTDMA, the collaborative BSs together serve each of their CEUs at a different time slot. Thus, it is free from multi-user interference at the cost of spectral efficiency. In [21], it was shown that the receiver side (say CEU $u$) equivalently observes a $K^{\left(u\right)}$ equivalent parallel channels:

$$Y_k^{\left(u\right)}={\sigma }_k^{\left(u\right)}{d}_k^{\left(u\right)}+W_k^{\left(u\right)}, k=0,1,\dots ,K^{\left(u\right)}-1,$$

(19)

where ${\sigma }_k^{\left(u\right)}$ is the $k$th non-zero singular value of aggregate channel matrix ${\Lambda }^{\left(u\right)}$ and $W_k^{\left(u\right)}$ denotes the received noise.

4.2. MU-JZF

The MU-JZF scheme enables complete suppression of interference, but it demands higher transmitter power for the jointly pre-coding process. To derive the preprocessing matrix, we stack up the $N_{CEU}$ received vector in (12) to form

$$Y\equiv {\left[Y^{\left(0\right)}{}^T,Y^{\left(1\right)}{}^T,\dots ,Y^{\left(N_{CEU}-1\right)}{}^T\right]}^T=\Lambda Fd+W,$$

(20)

where $\Lambda \equiv {\left[{\Lambda }^{\left(0\right)}{}^T,{\Lambda }^{\left(1\right)}{}^T,\dots ,{\Lambda }^{\left(N_{CEU}-1\right)}{}^T\right]}^T$, $F\equiv \left[F^{\left(0\right)},F^{\left(1\right)},\dots ,F^{\left(N_{CEU}-1\right)}\right]$ and $W\equiv {\left[W^{\left(0\right)}{}^T,W^{\left(1\right)}{}^T,\dots ,W^{\left(N_{CEU}-1\right)}{}^T\right]}^T$ are the $N_{CEU}\left|{\Im }^{\left(u\right)}\right|N_R\times 3\left|{\Im }^{\left(u\right)}\right|N_T$ aggregate channel matrix, aggregate preprocessing matrix and $N_{CEU}\left|{\Im }^{\left(u\right)}\right|N_R\times 1$ aggregate noise vector for the entire network MIMO, respectively. Since the aggregate channel matrix $\Lambda$ is a random matrix, it has full rank with probability one. With ZF criterion, the square $\left(N_{CEU}\left|{\Im }^{\left(u\right)}\right|N_R\times N_{CEU}\left|{\Im }^{\left(u\right)}\right|N_R\right)$ matrix product $\Lambda F$ in (20) must be an identity matrix. This requires that the aggregate channel matrix $\Lambda$ have a full row rank of $N_{CEU}\left|{\Im }^{\left(u\right)}\right|N_R$ [22]. As a result, this leads to the inequality $N_{CEU}{N}_R\le 3N_T$, which is usage constraint of MU-JZF. To satisfy this constraint, each $\left|{\Im }^{\left(u\right)}\right|N_R\times 3\left|{\Im }^{\left(u\right)}\right|N_T$ per-CEU channel matrix ${\Lambda }^{\left(u\right)}$ of $\Lambda$ must be full row rank of $\left|{\Im }^{\left(u\right)}\right|N_R$ and $K^{\left(u\right)}$ (the number of data symbols sent to CEU $u$) will be equal to $\left|{\Im }^{\left(u\right)}\right|N_R$.

Then the $3\left|{\Im }^{\left(u\right)}\right|N_t\times K$ aggregate preprocessing matrix $F$ in (20) is the following pseudo-inverse of aggregate channel matrix $\Lambda$:

$$F={\Lambda }^H{\left(\Lambda {\Lambda }^H\right)}^{-1}.$$

(21)

Applying (21) to (20), the received signal vector of (12) becomes the $K^{\left(u\right)}$ equivalent parallel channels:

$$Y_k^{\left(u\right)}=d_k^{\left(u\right)}+W_k^{\left(u\right)}, k=0,1,\dots ,K^{\left(u\right)}-1.$$

(22)

4.3. MU-JMMSE

The MU-JZF completely eliminates the multi-user interference at the cost of demanding higher transmitter power. The MU-JMMSE makes an acceptable compromise between interference suppression and transmitter power efficiency. Based on the MMSE criterion [21,23], the aggregate preprocessing matrix $F$ is

$$F={\Lambda }^H{\left(\Lambda {\Lambda }^H+\left(N_0/P_d\right)I\right)}^{-1}.$$

(23)

where $P_d$ is the transmission power for each data symbol.

5. Transmission Power Management

As mentioned earlier, each of BSs in a CCS together serves its own users and the CEUs of other collaborative BSs under a power constraint. Therefore, it is necessary to develop a method of distributing transmitter power among intra-cell CCUs, intra-cell CEUs, and inter-cell CEUs. To the best of our knowledge, however, there has been no literature dealing with this issue. The purpose of power management is to achieve a uniform capacity regardless of user position. Because of the cooperation with the neighboring BSs, the design of power management may involve the information exchange among the cooperative-based stations. Due to the time-variant characteristics of channel, this continuing need for information exchange will consume a lot of radio resources. In the absence of information exchange, our method of power management for MU-network MIMO cellular systems only needs the number of different types of users to realize an independent power adjustment among BSs.

Let $P_C$, $P_E$ and $P_E^{\prime }$ denote the sub-channel power allocated for an intra-cell CCU, intra-cell CEU, and inter-cell CEU, respectively. Let $P_b$ denote a sub-channel baseline power and $P_{\max }$represent the maximum transmission power constraint in a sector antenna. In our method, a CCU and a CEU are respectively allotted the initial power $P_b$ and $\alpha P_b$, where the power coefficient $\alpha >0$, i.e., we initially set $P_C=P_b$ and $P_E=P_E^{\prime }=\alpha P_b$.

The power management is conducted in a per-sector basis. Let $x$, $y$ and $z$ denote the number of intra-cell CCUs, intra-cell CEUs, and the inter-cell CEUs served by a particular sector antenna, respectively. Thus, the total power requirement is $P_T=x{P}_C+y{P}_E+z{P}_E^{\prime }$, where the power required to serve other cells’ CEUs is $z{P}_E^{\prime }$. In the subsequent sub-sections, we present transmission power management for SU- and MU-network MIMO, respectively.

5.1. Power Management for SU-Network MIMO

For a specific CCS, define $K_{\max }$ to be the power ratio consumed by inter-cells’ CEUs, i.e., we partition the total transmitter power $P_{\max }$ into two parts: power for intra-cell users $\left(\left(1-K_{\max }\right)P_{\max }\right)$ and power for inter-cells’ CEUs ($K_{\max }{P}_{\max }$). Accordingly, we can use the power ratio $K_{\max }$ to limit the maximum power dispensed to inter-cells CEUs. Therefore, the power consumption $z{P}_E^{\prime }$ is limited within $K_{\max }{P}_{\max }$. In a per-sector antenna basis, the procedure of power management is presented as follows.

(a)

Initialize the power allocation to each of CCUs and CEUs by $P_C=P_b$ and $P_E=P_E^{\prime }=\alpha P_b$, respectively.

(b)

Calculate the amount of power consumed by the other cells’ CEUs (i.e., $z{P}_E^{\prime }$). If $z{P}_E^{\prime }>K_{\max }{P}_{\max }$, then reduce the power allocation for each inter-cell CEU by a factor of ${\rho }_1$ such that the amount of power consumption by the other cells’ CEUs equals the power constraint $K_{\max }{P}_{\max }$, where ${\rho }_1=K_{\max }{P}_{\max }/z{P}_E^{\prime }$; elsewise ${\rho }_1=1$.

(c)

Next calculate the total transmission power for intra-cell users (i.e., $x{P}_C+y{P}_E$). If $x{P}_C+y{P}_E>\left(1-K_{\max }\right)P_{\max }$, then reduce the initial power by a factor of ${\rho }_2$ such that $x{P}_C+y{P}_E$ equals the upper bound power $\left(1-K_{\max }\right)P_{\max }$, where ${\rho }_2=\left(1-K_{\max }\right)P_{\max }/\left(x{P}_C+y{P}_E\right)$; elsewise ${\rho }_2=1$.

(d)

Finally, we achieve $P_C={\rho }_2{P}_b$, $P_E=\alpha \left({\rho }_2{P}_b\right)$ and $P_E^{\prime }={\rho }_1\left(\alpha P_b\right)$.

In summary, the method consists of a CEU power coefficient $\alpha$ and two power reduction factors (${\rho }_1$ and ${\rho }_2$). The coefficient $\alpha$ is used to determine the power proportion between a CCU and a CEU. The power allotted to other cells’ CEUs can be restricted by power reduction factor ${\rho }_1$ together with the power ratio $K_{\max }$. As for the power reduction factor ${\rho }_2$, it prohibits a power requirement from exceeding the corresponding power constraint $\left(1-K_{\max }\right)P_{\max }$. To best use the transmitter power, we initially assume that the baseline power $P_b$ is equal to $P_{\max }$. Thus, the two power portions $\left(1-K_{\max }\right)P_{\max }$ and $K_{\max }{P}_{\max }$ can be fully used.

5.2. Power Management for MU-Network MIMO

Unlike SU-network MIMO, each of CEUs in MU-network MIMO shares the entire sub-band $f_{B2}$ instead, as shown in Figure 1b. This yields serious multi-user interference and thus joint preprocessing among cooperative BSs becomes necessary, as discussed in Section 4. Since the preprocessing matrices are jointly designed for all the CEUs, there is no distinction between intra-cell and inter-cell CEUs $\left(\mathrm{i}.\mathrm{e}., P_E=P_E^{\prime }\right)$. Thus, there is no need for $K_{\max }$ for power management in MU-network MIMO. Initially the power $P_C$ for each intra-cell CCU is $P_C=P_b$. The total power requirement for cooperative BS $b$ to serve the $N_{CEU}$ CEUs is $T^{\left(b\right)}$ as shown in (18). We define the average preprocessing power for a CEU as ${\overline{T}}^{\left(b\right)}=T^{\left(b\right)}/N_{CEU}$. As in SU-network MIMO, the CEU power is $P_E=\alpha P_C$. However, the CEU power depends on the average preprocessing power ${\overline{T}}^{\left(b\right)}$, which is variable because of the time-variant channel. Thus, we further let the CEU power be $P_E=\beta {\overline{T}}^{\left(b\right)}$, where $\beta$ is determined such that $P_E=\alpha P_C$. Therefore, we achieve $\beta =\alpha P_C/{\overline{T}}^{\left(b\right)}$.

For each sector antenna, the procedure of power management is as follows.

(a)

Initialize the power allocation to each of CCUs by $P_C=P_b$.

(b)

Calculate the average preprocessing power ${\overline{T}}^{\left(b\right)}=T^{\left(b\right)}/N_{CEU}$ according to (18). Then set the CEU power $P_E=\beta {\overline{T}}^{\left(b\right)}$, where $\beta =\alpha P_C/{\overline{T}}^{\left(b\right)}$.

(c)

Next, calculate the total power requirement $P_T=x{P}_C+N_{CEU}{P}_E$. If $P_T>P_{\max }$, then reduce the baseline power $P_b$ by a factor of ${\rho }_2$ such that the value of $P_T$ equals the power constraint $P_{\max }$, where ${\rho }_2=P_{\max }/P_T$; elsewise ${\rho }_2=1$.

(d)

Finally, we achieve $P_C={\rho }_2{P}_b$ and $P_E={\rho }_2\beta {\overline{T}}^{\left(b\right)}$.

In summary, the method consists of a CEU power coefficient $\alpha$ and a power reduction factor ${\rho }_2$. We adaptively adjust the value of $\beta$ such that $P_E=\alpha P_C$. The power reduction factor ${\rho }_2$ is used to make sure that the total power requirement does not exceed the power constraint $P_{\max }$.

6. Simulation Results

This section presents performance comparison between SU and MU-network MIMO with the power management methods. Unless otherwise stated, the cell radius $R$ and cell-center radius $D$ are 1000 m and 787.55 m, respectively. Accordingly, within a sector, the ratio of cell-center area to cell-edge area is 3 to 1. Assume users are uniformly distributed in each cell. Thus, we set the ratio of sub-channel number between inner band $f_A$ and outer band $f_B$ to be 3 to 1 as well. To this end, we assume the total number of OFDMA sub-channels is 60 such that the numbers of sub-channels in $f_A$ and $f_B$ are integers 45 and 15, respectively. Therefore, each outer sub-band $f_{Bi}$ consists of 5 OFDMA sub-channels. As a result, for SU-network MIMO, there are at most five active CEUs in each sector (hard CEU capacity). As for MU-network MIMO, joint preprocessing makes it possible that more than five CEUs in each sector can be served at the same time (soft CEU capacity). Assume there are 12 subcarriers in a sub-channel and the sub-channel bandwidth $W$ is 138.8 KHz. The maximum power constraint $P_{\max }$ is 46.523 dBm [2]. The propagation constant ${\beta }_0$ and path loss exponent $\gamma$ are $1.35\times {10}^7$ and 3, respectively [20]. The standard deviation of log-normal shadowing is 12 dB. Unless otherwise stated, there are 15 CCUs $\left(x=15\right)$ and 5 CEUs $\left(y=5\right)$ uniformly distributed in each sector, each sector is equipped with five transmission antennas $\left(N_T=5\right)$ and the power coefficient is one $\left(\alpha =1\right)$. As for users, each of them is equipped with a single receiver antenna $\left(N_R=1\right)$. 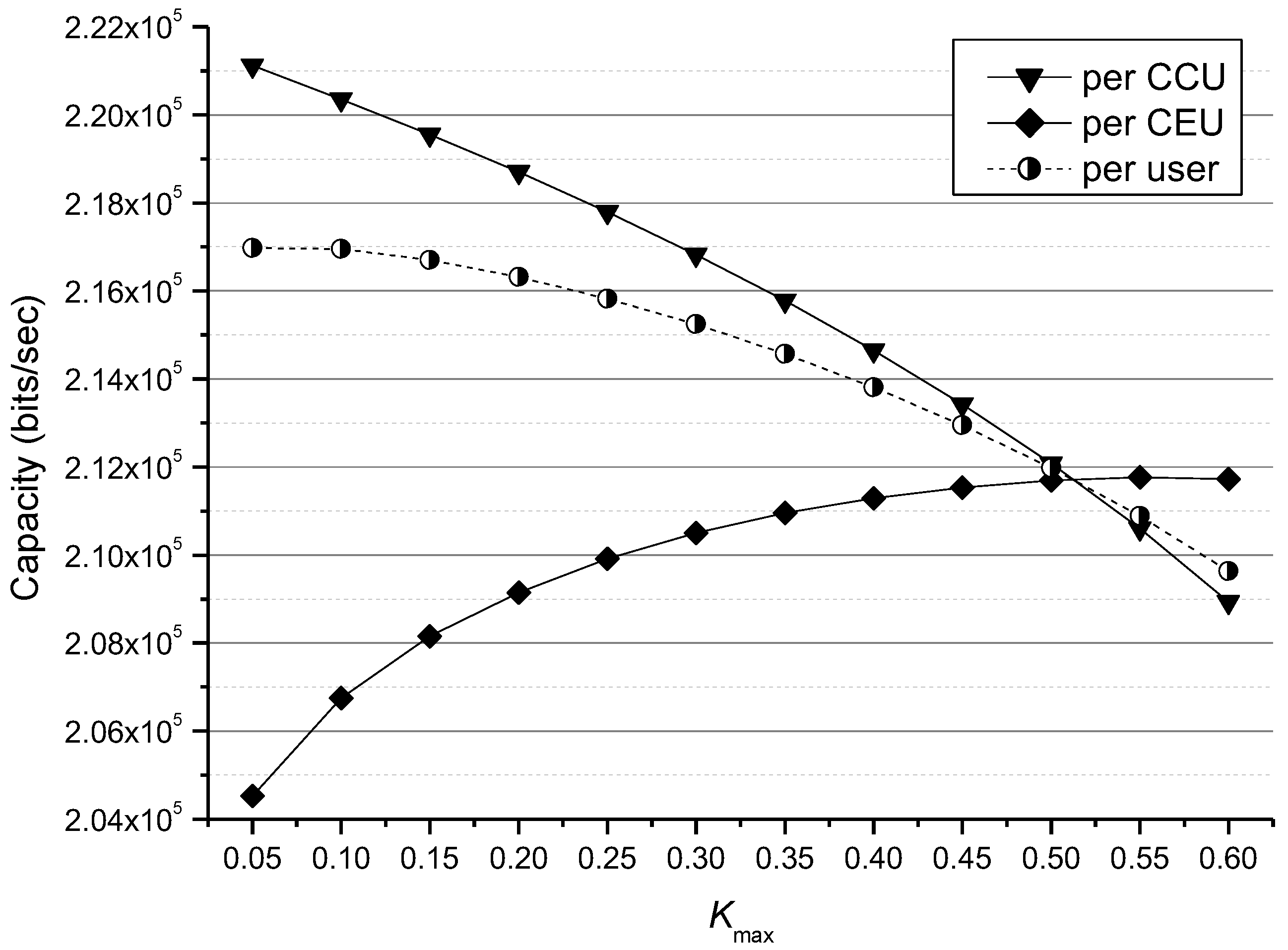In terms of different values of $K_{\max }$, Figure 2 shows the capacity comparison for SU-network MIMO and Figure 3 presents its corresponding curves of power reduction factors. In Figure 2, we find that smaller $K_{\max }$ yields better per-user (average) capacity than larger $K_{\max }$. However, smaller $K_{\max }$ results in bigger capacity gap between CCU and CEU than larger $K_{\max }$. Thus, through continuing enlarging the value of $K_{\max }$, the capacity gap can be reduced, but it is at the cost of decreasing the average capacity. For example, in Figure 2, an equal CCU and CEU capacity (zero capacity gap) occurs at about $K_{\max }=0.513$, i.e., a uniform capacity is achieved regardless of user position; however, it obviously reduces the average capacity. Figure 3 shows that while the value of $K_{\max }$ is increasing, the power factor ${\rho }_1$ is increasing as well. This is because a larger value the $K_{\max }$ means that more transmitter power is allocated to the inter-cell CEUs. Accordingly, the power factor ${\rho }_2$ associated with intra-cell users is decreasing while the value of $K_{\max }$ is increasing.

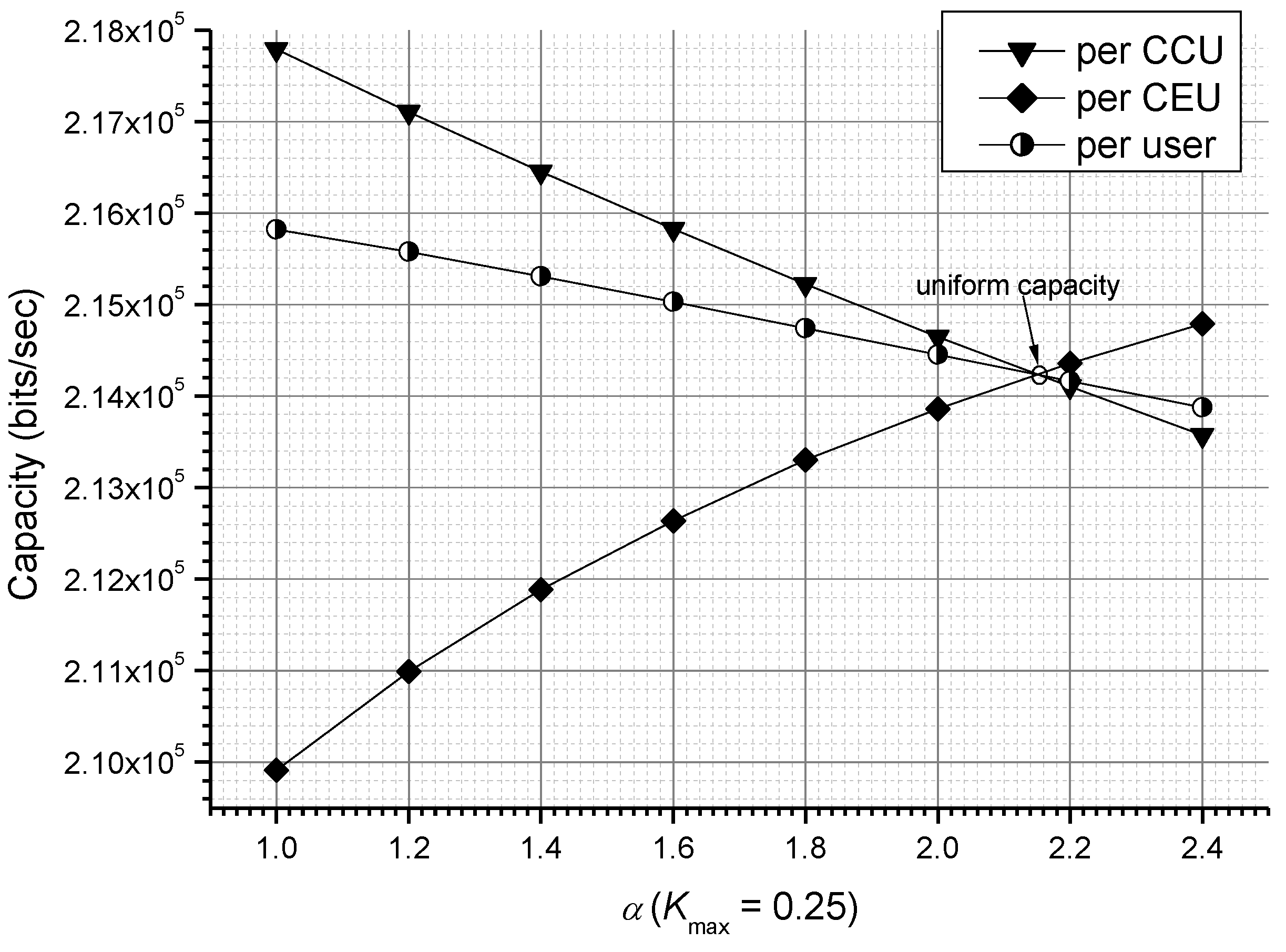
As a function of power coefficient $\alpha$, Figure 4 shows the capacity comparison for SU-network MIMO with a small $K_{\max }$ (say $K_{\max }=0.25$). Please note that the CEU power is given by $P_E=P_E^{\prime }=\alpha P_C$. Thus, we can raise the CEU power by increasing the value of $\alpha$. It is found that increasing the value of $\alpha$ can actually diminish the capacity gap between CCU and CEU, and a uniform capacity is achieved at $\alpha =2.75$. However, the average (per-user) capacity is also slowly decreasing at the same time, while the capacity gap is decreasing. 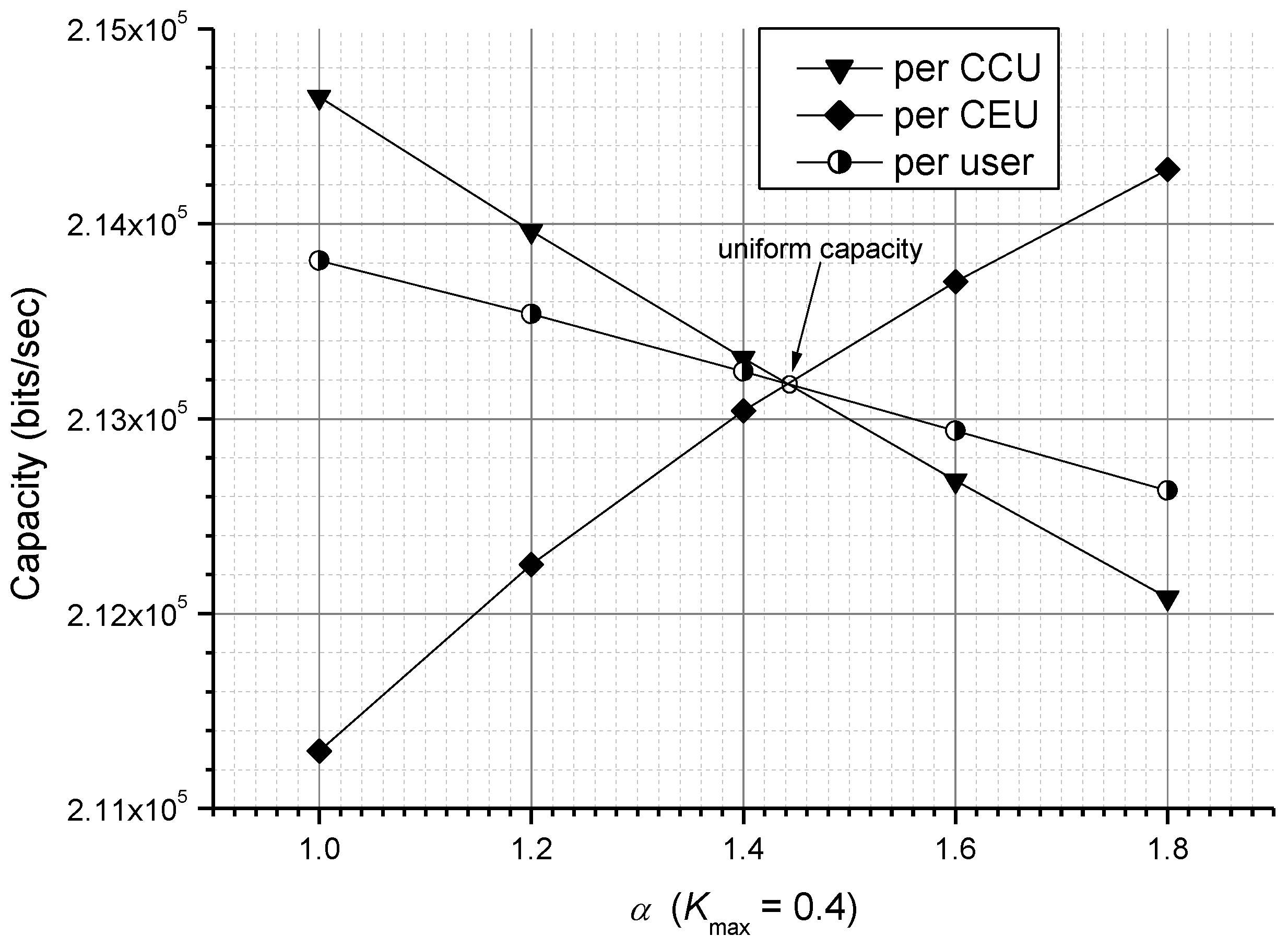In Figure 5, we present the capacity comparison as a function of $\alpha$ for a large $K_{\max }$ (say $K_{\max }=0.4$). It is shown that the uniform capacity occurs at a smaller $\alpha$, $\left(\alpha =1.42\right)$, as compared with $\alpha =2.15$ associated with the smaller $K_{\max }$ in Figure 4. By making a comparison between Figure 4 and Figure 5, it is found that the per-user (average) capacity with smaller $K_{\max }$ is always better than that with larger $K_{\max }$, although it yields larger capacity gap than that of larger $K_{\max }$. Nevertheless, while achieving uniform capacity (zero capacity gap), the smaller $K_{\max }$ still yields better average capacity (about $2.143\times {10}^5$ bits/sec) than that with the larger $K_{\max }$ (about $2.132\times {10}^5$ bits/sec). Therefore, with $K_{\max }=0.25$, SU-network MIMO offers $1.1\times {10}^3$ more bits per second than that with $K_{\max }=0.4$. In conclusion, with uniform capacity, smaller $K_{\max }$ can generally provide the SU-network MIMO with larger average capacity.

Uniform capacity makes sure that users have uniform data rate regardless of their position. According to the previous results, we found that uniform data rate comes at the price of reducing the average capacity. Studies on wireless usage show that more than 50% of all voice calls and more than 70% of data traffic originate from indoors (i.e., immobile conditions) [24]. As a result, the uniform capacity is only important for the small part of truly mobile users. For example, as a mobile user with SU-network MIMO moves from cell center to cell border, the cell-edge capacity will drop a small percentage as compared with cell-center capacity, and thus the user may be deficient in capacity. Thus, uniform data rate is essential for this scenario.

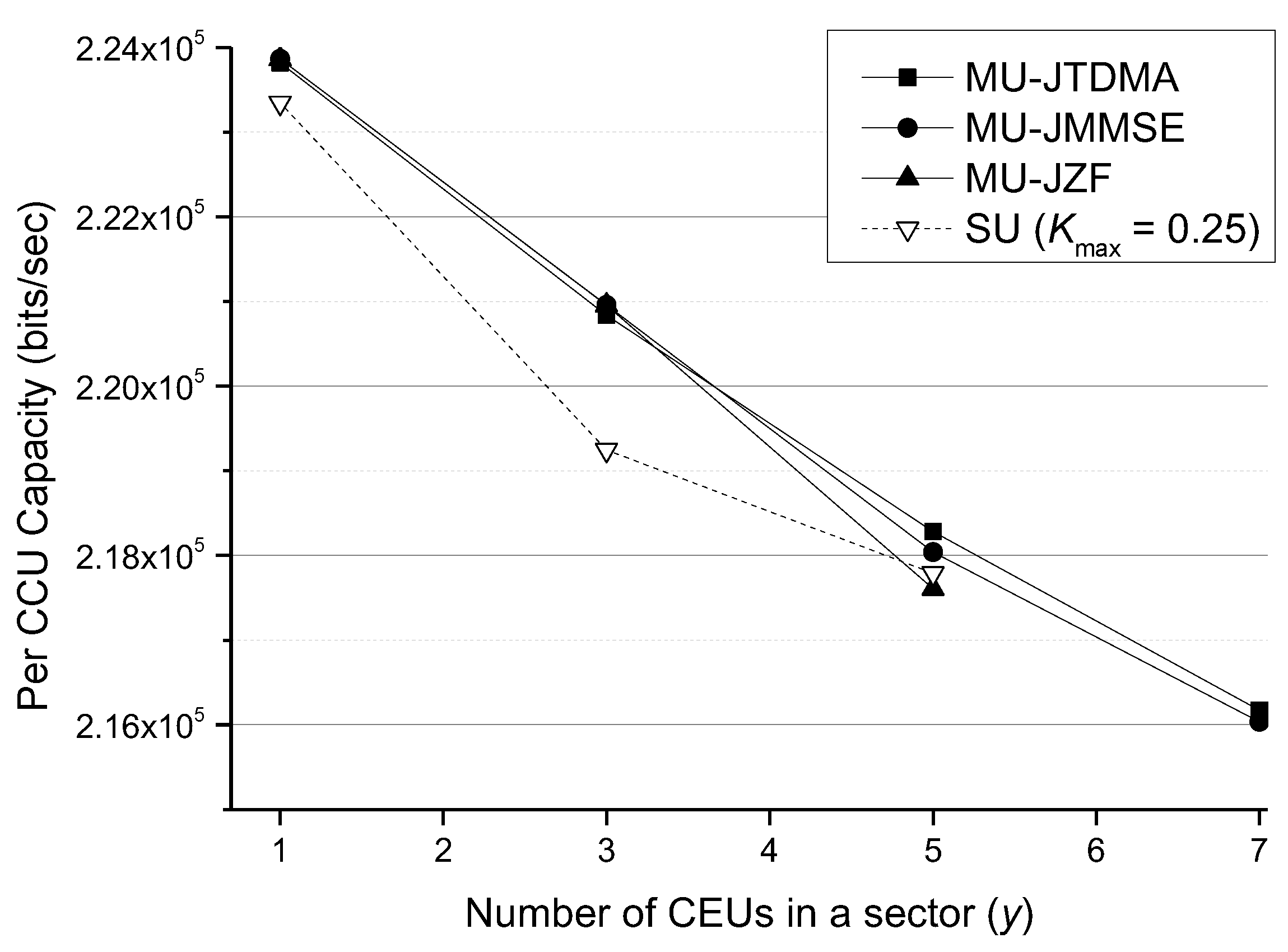
Now we turn our attention to the MU-network MIMO and in the meantime, make comparison with SU-network MIMO. In terms of the number of per-sector CEUs ($y$), Figure 6 presents the per-CCU capacity comparison for three MU-network MIMO schemes and the SU-network MIMO. Recall that three cooperative BSs in a CCS collectively serve a group of $N_{CEU}$ CEUs using a whole out sub-band. Thus, we have $N_{CEU}=3y$ for MU-network MIMO. In MU-network MIMO, both MU-JMMSE, and MU-JTDMA have soft CEU capacity, but MU-JZF does not, because it is subject to the usage constraint $N_{CEU}{N}_R\le 3N_T$ as shown in Section 4.2. In general, it is found that MU-network MIMO is better than SU-network MIMO in CCU capacity, except for MU-JZF at $y=5$, whose CCU capacity is slightly less than SU-network MIMO. 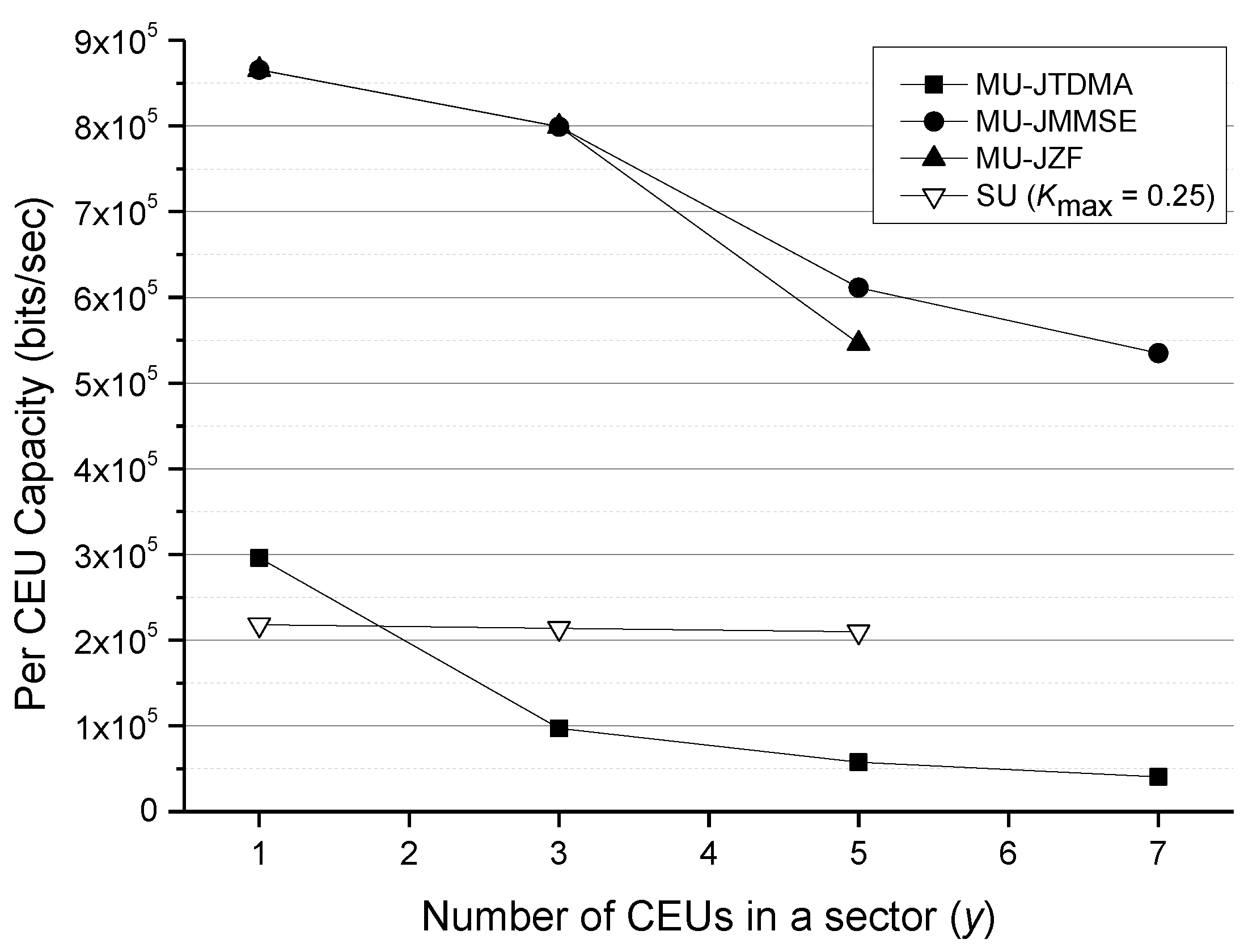Figure 7 gives the per-CEU capacity comparison. Except for the orthogonal scheme (MU-JTDMA), it is found that the superposition-coding schemes (MU-JMMSE and MU-JZF) have obvious CEU capacity improvement over the SU-network MIMO [25]. In addition, since there are just 5 sub-channels in an outer frequency sub-band, the SU-network MIMO only can serve up to 5 CEUs per sector. By contrast, the MU-network MIMO has a soft capacity for CEUs, except for MU-JZF because it is subject to the usage constraint $N_{CEU}{N}_R\le 3N_T$. For example, as increasing two additional CEUs from 5 CEUs to 7 CEUs in each sector, we calculate that the MU-JMMSE only drop about 0.9% and 15.2% for per-CCU and per-CEU capacity, as shown in Figure 6 and Figure 7, respectively.

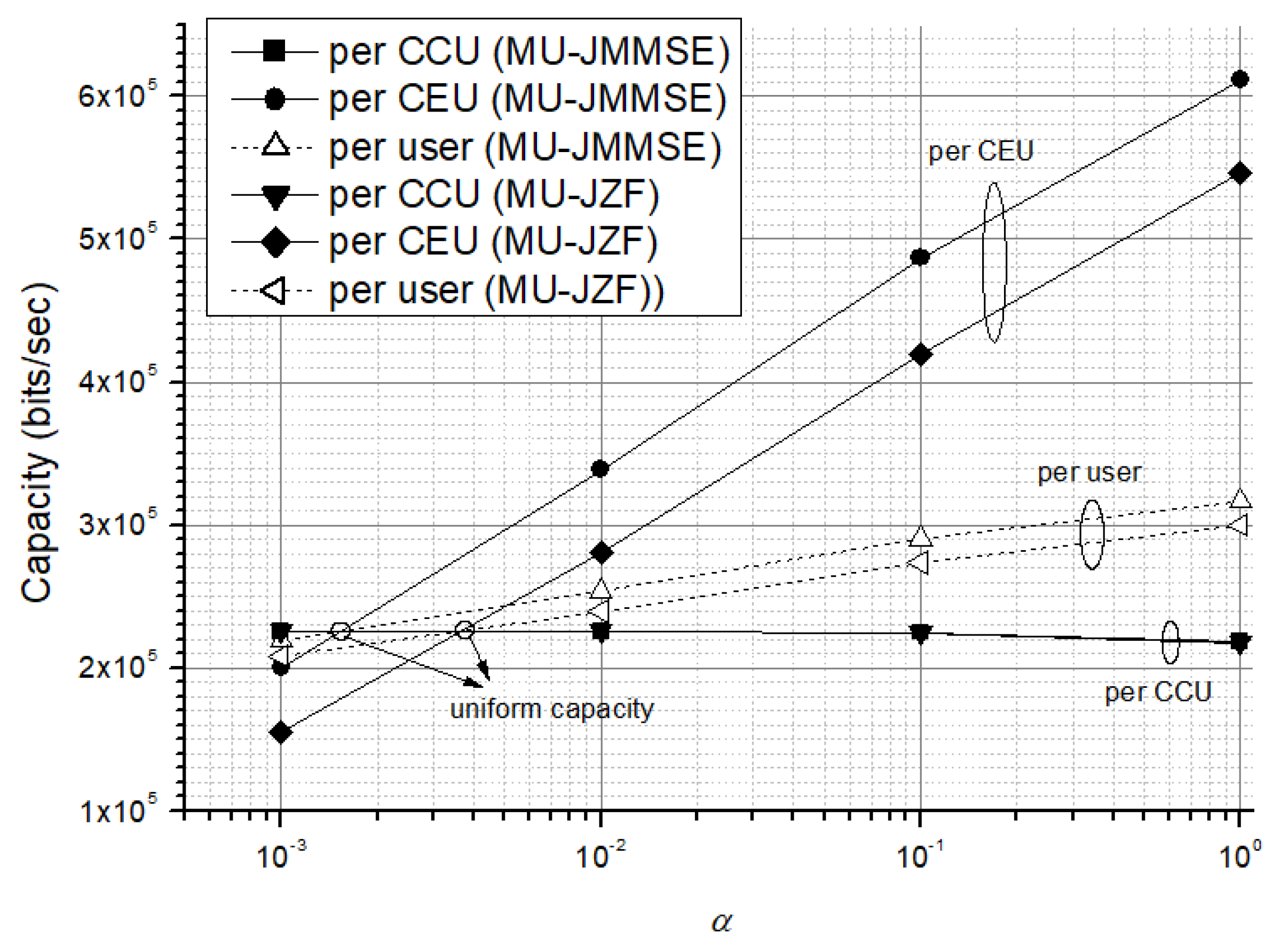
Figure 8 shows the capacity comparison for both superposition-coding schemes (MU-JMMSE and MU-JZF) as a function of $\alpha$. It is found that the per-CEU capacity is much better than the per-CCU capacity (at $\alpha =1$) because of joint preprocessing. By contrast, for SU-network MIMO with $\alpha =1$, its per-CEU capacity is still distinctly worse than the per-CCU capacity, as shown previously in Figure 4 and Figure 5. This means that the joint preprocessing (superposition coding) offers great preprocessing gain that benefits per-CEU and per-user (average) capacities. Recall that $P_E=\alpha P_C$, where $P_C$ is the CCU power. Due to the excellent preprocessing gain, the MU-network MIMO can use extremely small value of $\alpha$ (i.e., very small CEU power) to achieve uniform data rate, say $\alpha \cong 1.5\times {10}^{-3}$ and $\alpha \cong 4\times {10}^{-3}$ for MU-JMMSE and MU-JZF, respectively. This is opposite to SU-network MIMO. Moreover, it is found that MU-JMMSE is better than MU-JZF. This is because MU-JZF completely eliminates the CCI at the cost of demanding higher transmitter power. However, MU-JMMSE makes an acceptable compromise between interference suppression and transmitter power efficiency.

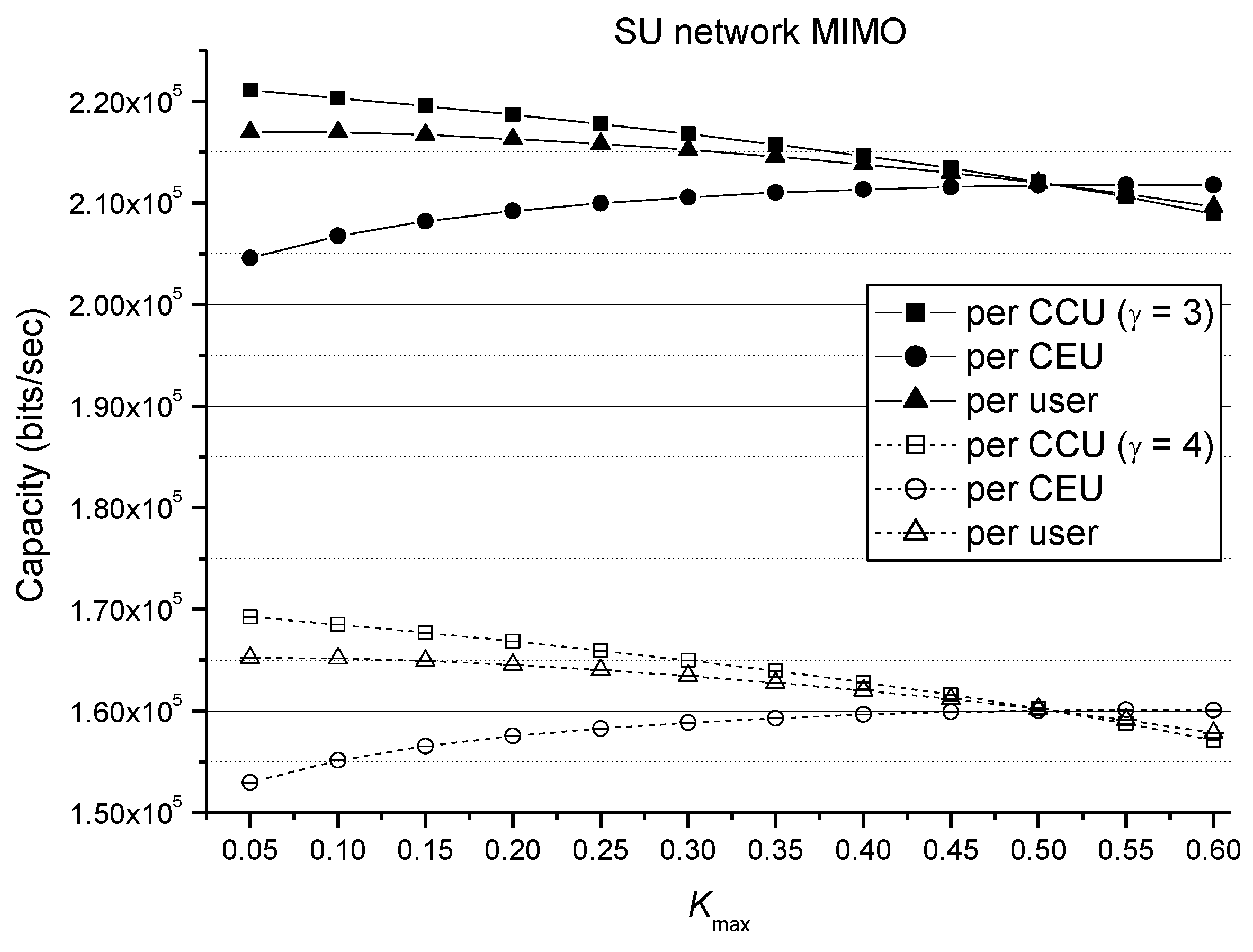
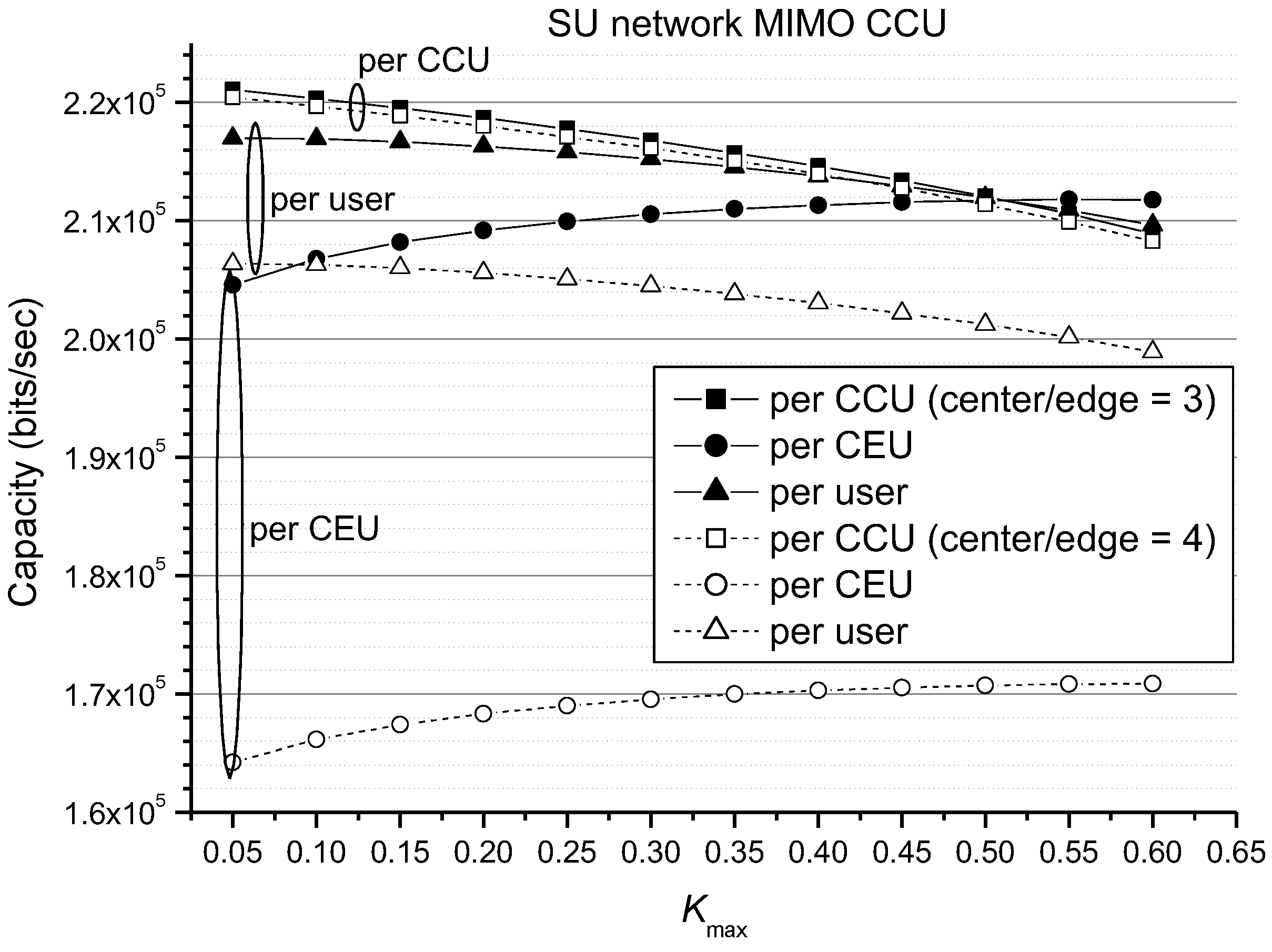
The numerical results above are obtained under the path loss exponent $\gamma$ of 3. Changing the value of $\gamma$ to a typical value of 4 does not influence the previous numerical results. For example, Figure 9 shows the same observations in SU-network MIMO for both path loss exponents ($\gamma =3,4$), i.e., smaller $K_{\max }$yields better per-user (average) capacity than larger $K_{\max }$. However, smaller $K_{\max }$ produces bigger capacity gap between CCU and CEU than larger $K_{\max }$. Likewise, in MU-network MIMO, the observed phenomena are also the same for different values of path loss exponent. 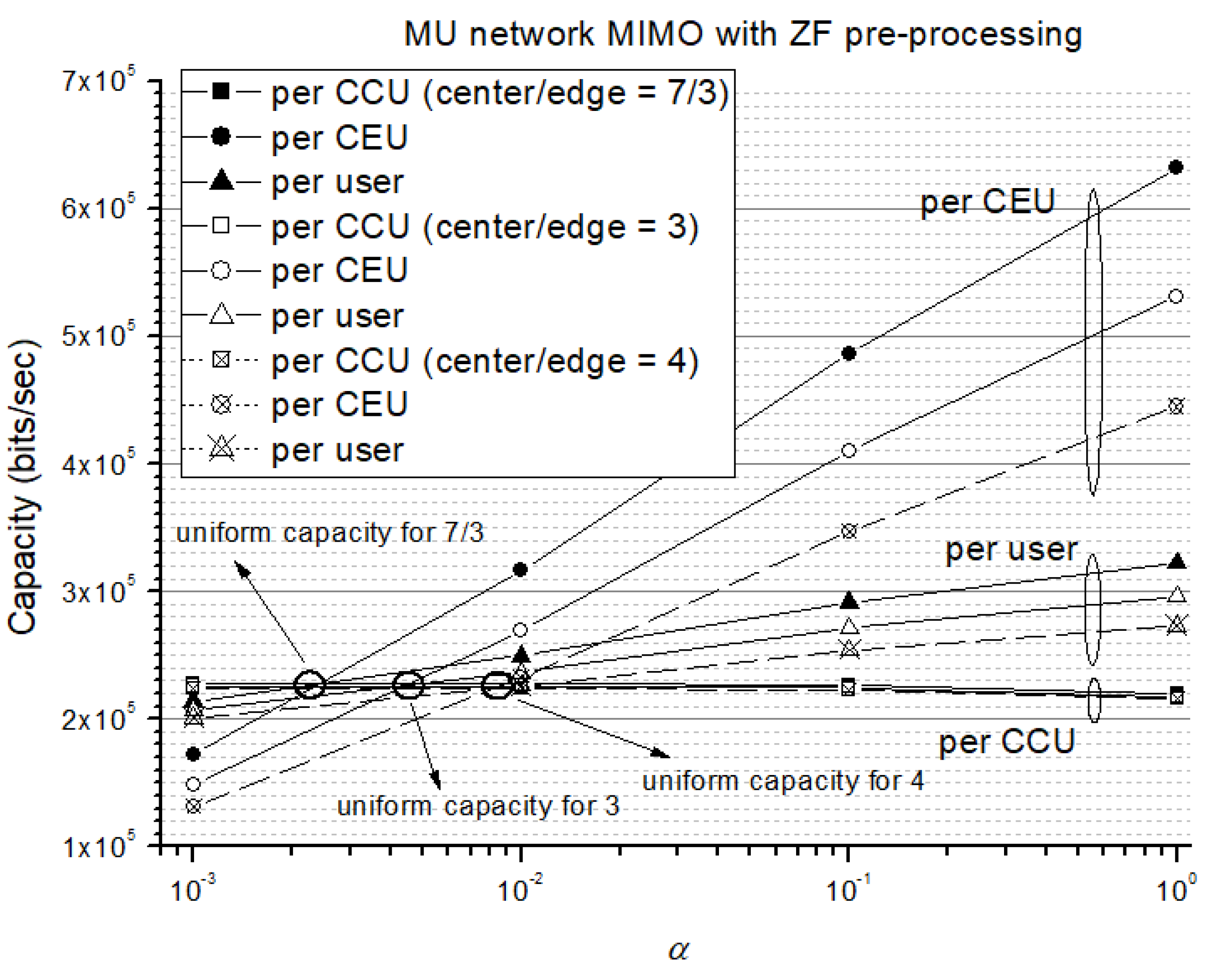Figure 10 and Figure 11 show the capacity comparison between different values of path loss exponent $\gamma$ with MMSE and ZF joint preprocessing, respectively. It is found that the per-CEU capacity is much better than the per-CCU capacity at $\alpha =1$ because of taking advantage of joint preprocessing. It is worth mentioning that, however, although the path loss increases with a larger path loss exponent $\gamma$, we need to allocate more power to CEUs by increasing the value of $\alpha$ to achieve a uniform capacity as shown in Figure 10 and Figure 11.

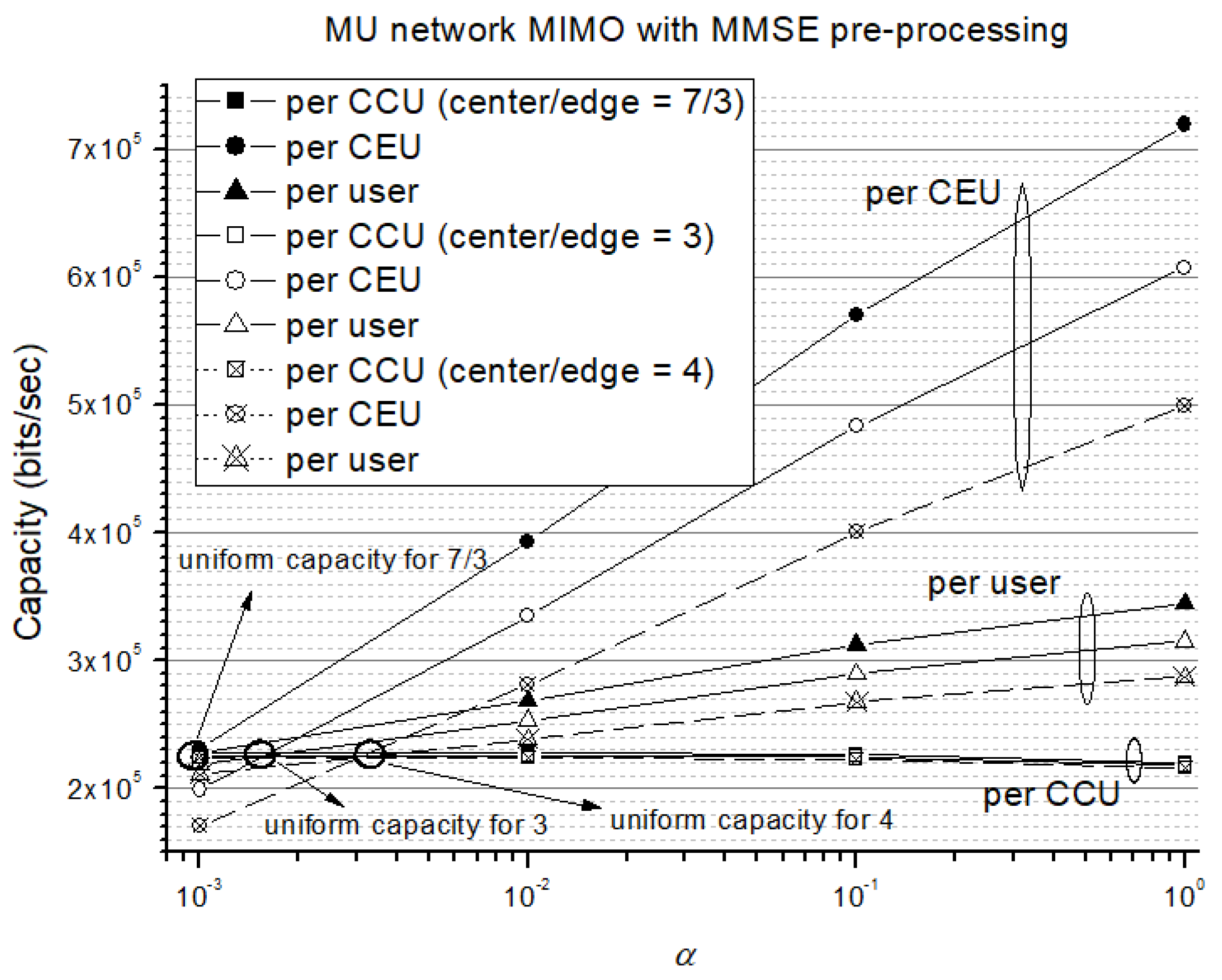
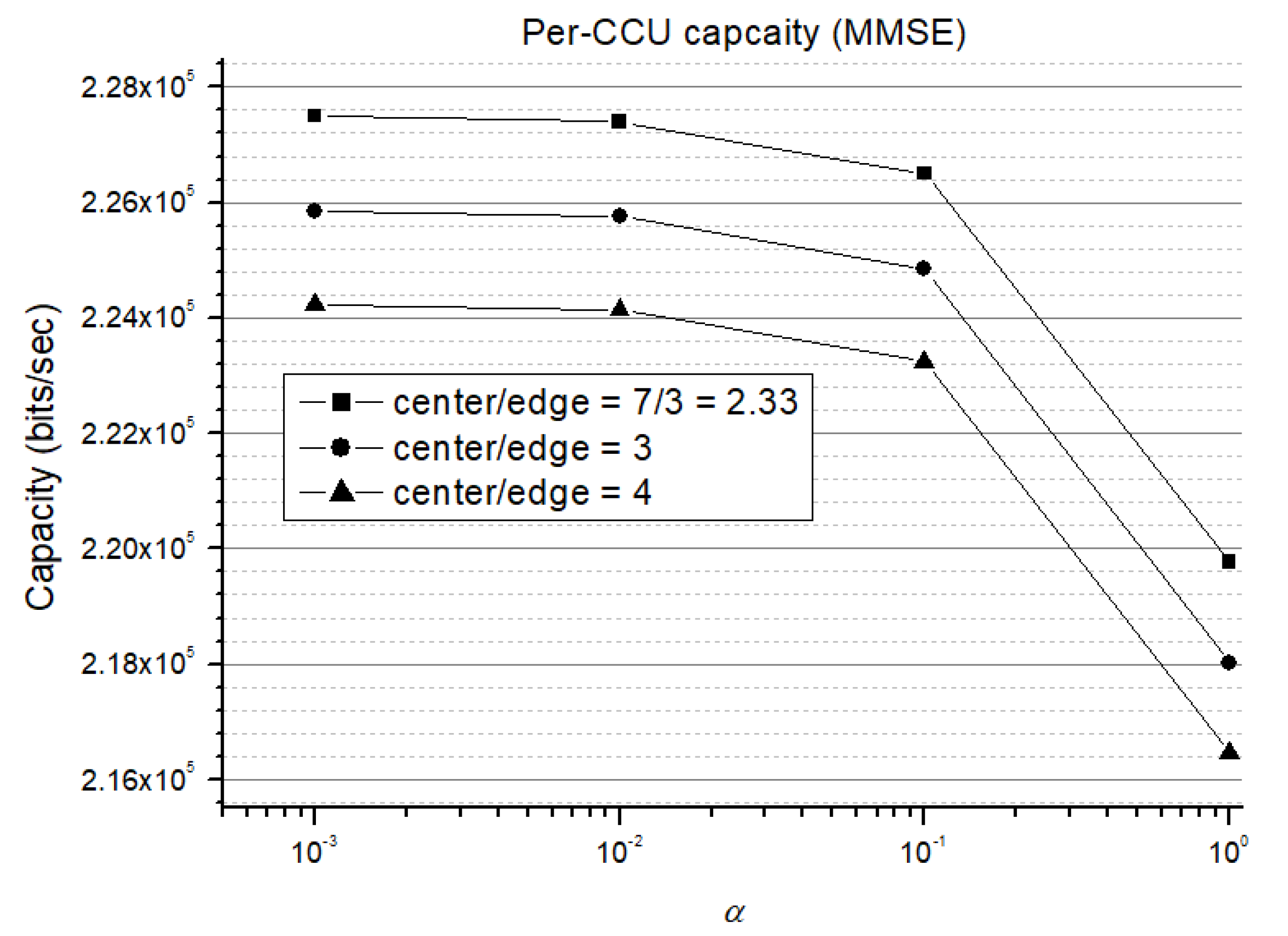
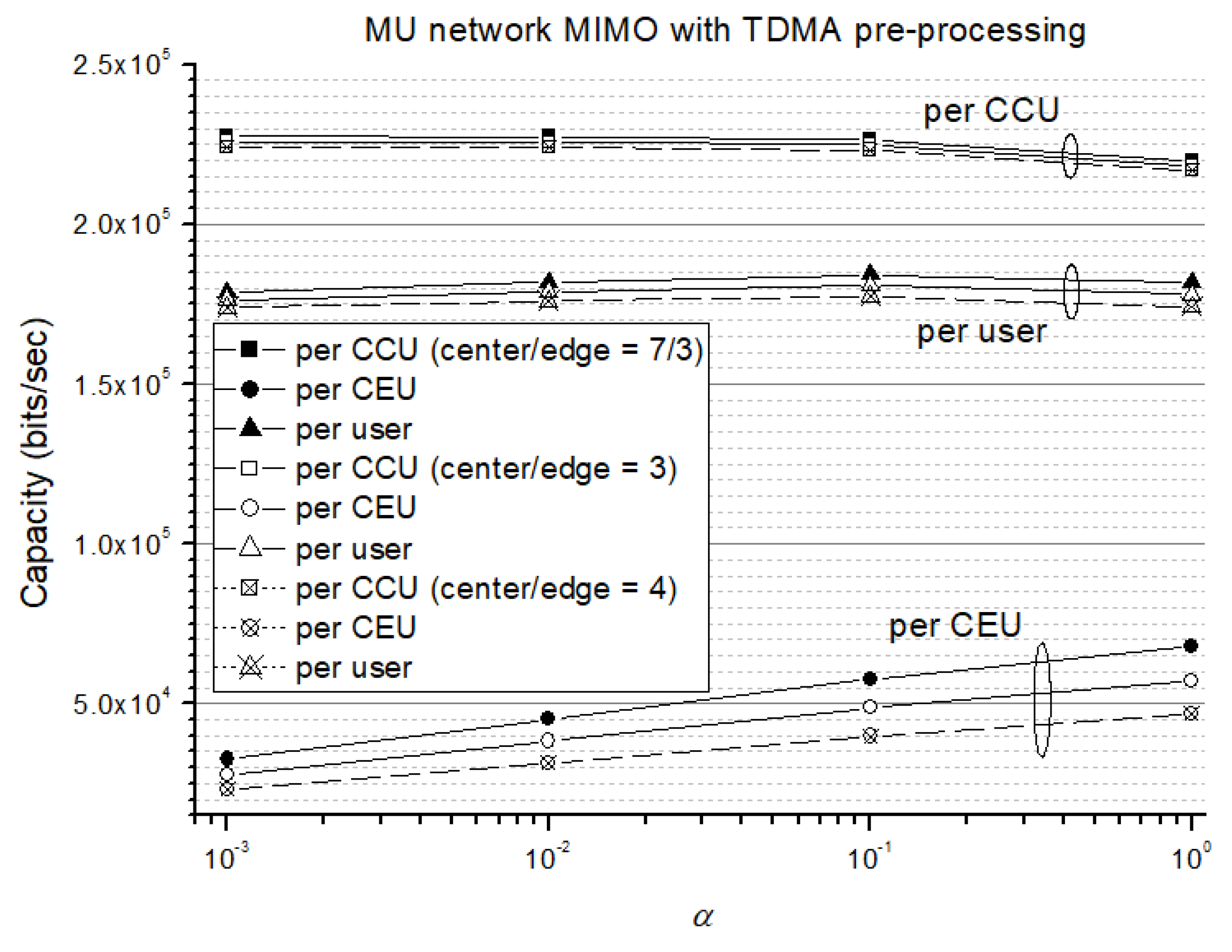
Next, we show how the different ratios between cell-center and cell-edge area influence the result. Figure 12 and Figure 13 are numerical results for the superposition-coding MU-MMSE and MU-ZF joint preprocessing schemes, respectively. Because the variation of CCU capacity is much less obvious than that of CEU capacity, we give a separate illustration for CEU capacity in Figure 14, where only the MMSE CCU capacity is shown because both MMSE and ZF are similar. The result of the orthogonal MU-TDMA joint preprocessing scheme is given in Figure 15. Finally, Figure 16 shows the result for the SU-network MIMO. With superposition-coding MU-MMSE and MU-ZF schemes, Figure 12 and Figure 13 indicate that reducing the ratio (i.e., increasing the edge area, but decreasing the center area) significantly benefits the CEU capacity. For example, this can be found from the decrease in the value of α to achieve uniform data rate as shown in

Table 1. The distribution of the value of $\alpha$.

	Ratio between Cell-Center and Cell-Edge Area
	7/3	3	4
MMSE	$9\times {10}^{-2}$	$1.52\times {10}^{-3}$	$3.5\times {10}^{-3}$
ZF	$2.3\times {10}^{-3}$	$4.5\times {10}^{-3}$	$9\times {10}^{-3}$

. As for the CCU, while cell-center area is reduced, the interference from neighboring cells is decreased and thus there is also a slight increase in CCU capacity as shown in Figure 14. In Figure 15, the result of the orthogonal MU-TDMA joint preprocessing scheme is similar to the superposition-coding schemes, i.e., increasing the cell-edge area benefits the capacity for either CEU or CCU capacity. The same observations are also true for SU-network MIMO in Figure 16, where we just show two different area ratios for clarity of illustration. It also shows that decreasing the center area significantly benefits the CEU capacity and improves the CCU capacity slightly. Overall, the system capacity increases due to enlarging the cell-edge area, which directly increases the proportion of downlink multi-cell cooperation (network MIMO) transmission. With network MIMO, multiple geographically separated base stations cooperatively serve their CEUs using their antennas, acting together as a network of distributed antenna array. In fact, this network architecture not only can effectively mitigate the serious co-channel interference but also provide diversity transmission. However, it is worth mentioning that the disadvantages of cooperative transmission require additional overhead for information exchange among cooperative BSs.

7. Conclusions

In this paper, we have investigated both the SU and MU-network MIMO based on FFR-based ICIC, together with their power management methods. Two considered FFR-based ICIC are regular and rearranged frequency partitions, which are associated with SU and MU-network MIMO, respectively. With regular partition, the SU-network MIMO can avoid the multi-user interference, but it just has a hard CEU capacity. As for rearrange partition, MU-network MIMO needs joint preprocessing among cooperative BSs to deal with the serious multi-user interference. However, it can provide soft capacity for CEUs. To this end, we have derived three joint preprocessing schemes, including two superposition-coding schemes (MU-JZF and MU_JMMSE) and an orthogonal one (MU-JTDMA).

Uniform capacity makes sure that users can acquire uniform data rate regardless of their position. To achieve uniform data rate for SU-network MIMO, we can adjust either the power coefficient $\alpha$ or power ratio K_max. For MU-network MIMO with unit power coefficient, because of the excellent preprocessing gain, the superposition-coding schemes yield much better CEU capacity and slightly better CCU capacity as compared with the SU-network MIMO. As a result, the MU-network MIMO can allocate very small power to CEUs by greatly reducing the value of power coefficient to achieve a uniform data rate.