Parameter Estimation and Application of Anisotropic Yield Criteria for Cylindrical Aluminum Extrusions: Theoretical Developments and StereoDIC Measurements
Abstract
:1. Introduction
2. Background Theory for Yield Functions and Plastic Strain
3. Experimental Investigations and Parameters Determination
3.1. Material Properties and Microstructure
3.2. Anisotropic Yield Function and Hardening Parameters
4. Theoretical Prediction and Experiments for Simple Torsion Case
5. Discussion of Results
6. Summary and Conclusions
- Uniaxial tension and simple torsion experiments were performed on a series of specially machined tubular and dog-boned rectangular specimens extracted from two longitudinally extruded Al6061-T6 cylindrical bars to obtain the required material parameters for anisotropic yield criteria. Here, the yield function Yld91 developed by Barlat et al., with six measured material parameters, is used to model the anisotropic response of the extruded aluminum material and an isotropic yield criterion using the Von Mises criteria is employed to predict an isotropic response.
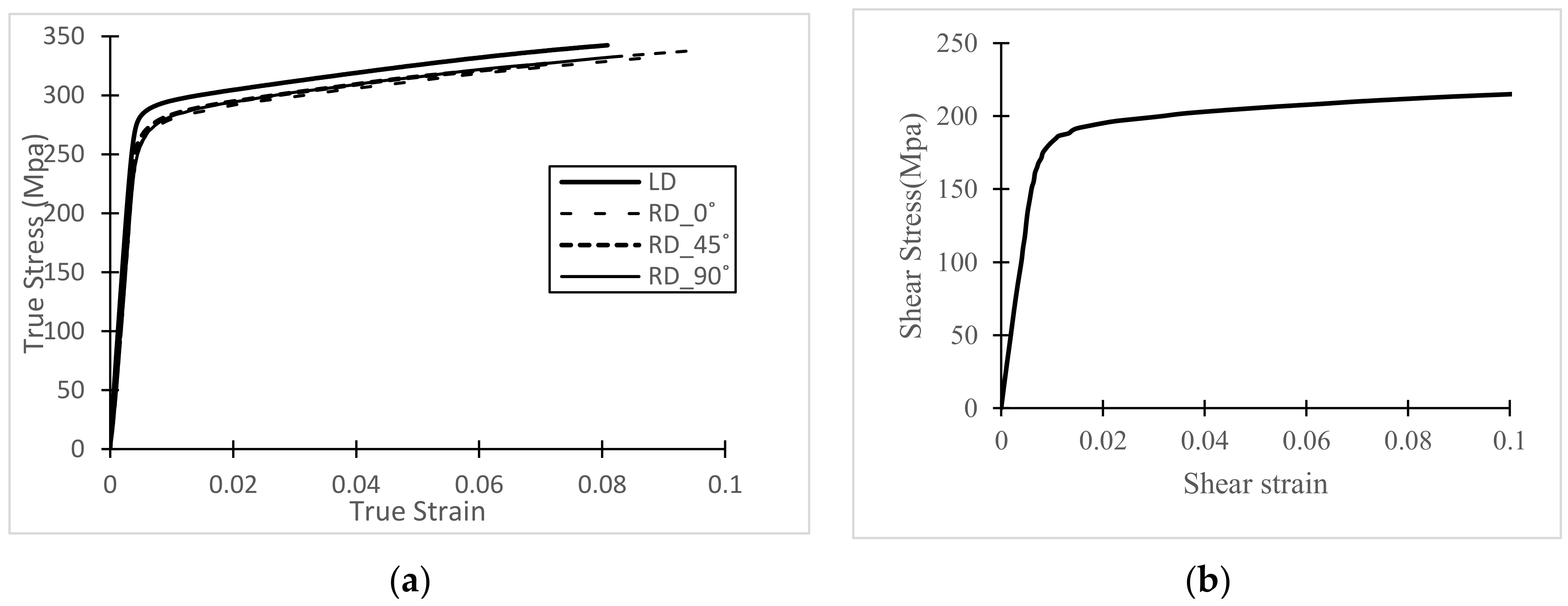
- Since the extrusion process is circumferentially symmetric for our longitudinal extrusions, yield stresses in all radial directions are expected to be similar, a condition that was confirmed from a series of radially oriented specimen experiments.
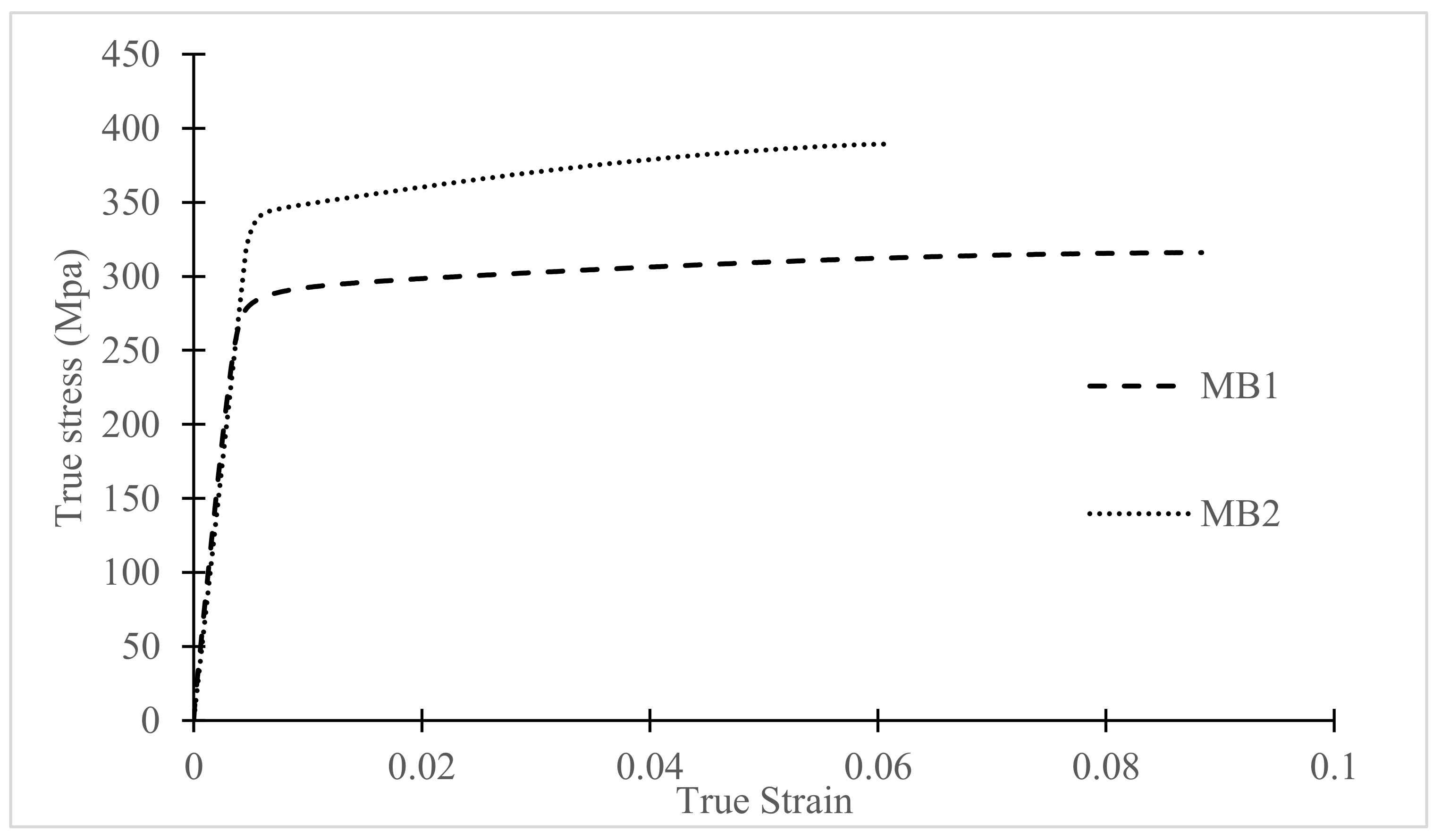
- Assuming isotropic strain hardening beyond yielding, the Von Mises isotropic and Barlat Yld91 parameters yield functions with power-law hardening and incremental theory of plasticity are used to develop and then implement a constitutive model for elastic-plastic material behavior and predict the response of the extruded MB1 and MB2 material. These constitutive models are implemented in a relatively simple numerical analysis platform to predict the stress-strain response for both materials undergoing torsional loading.
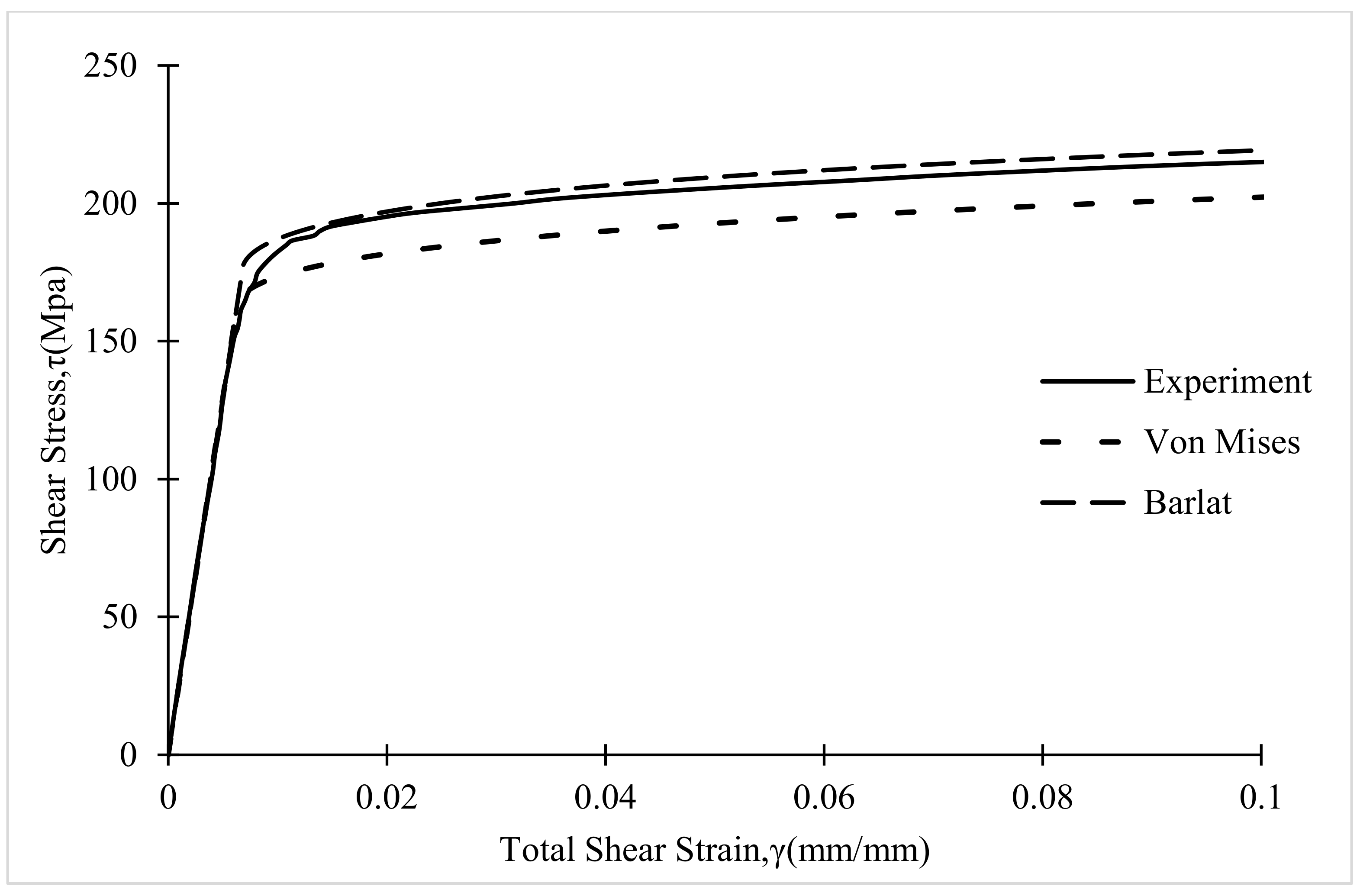
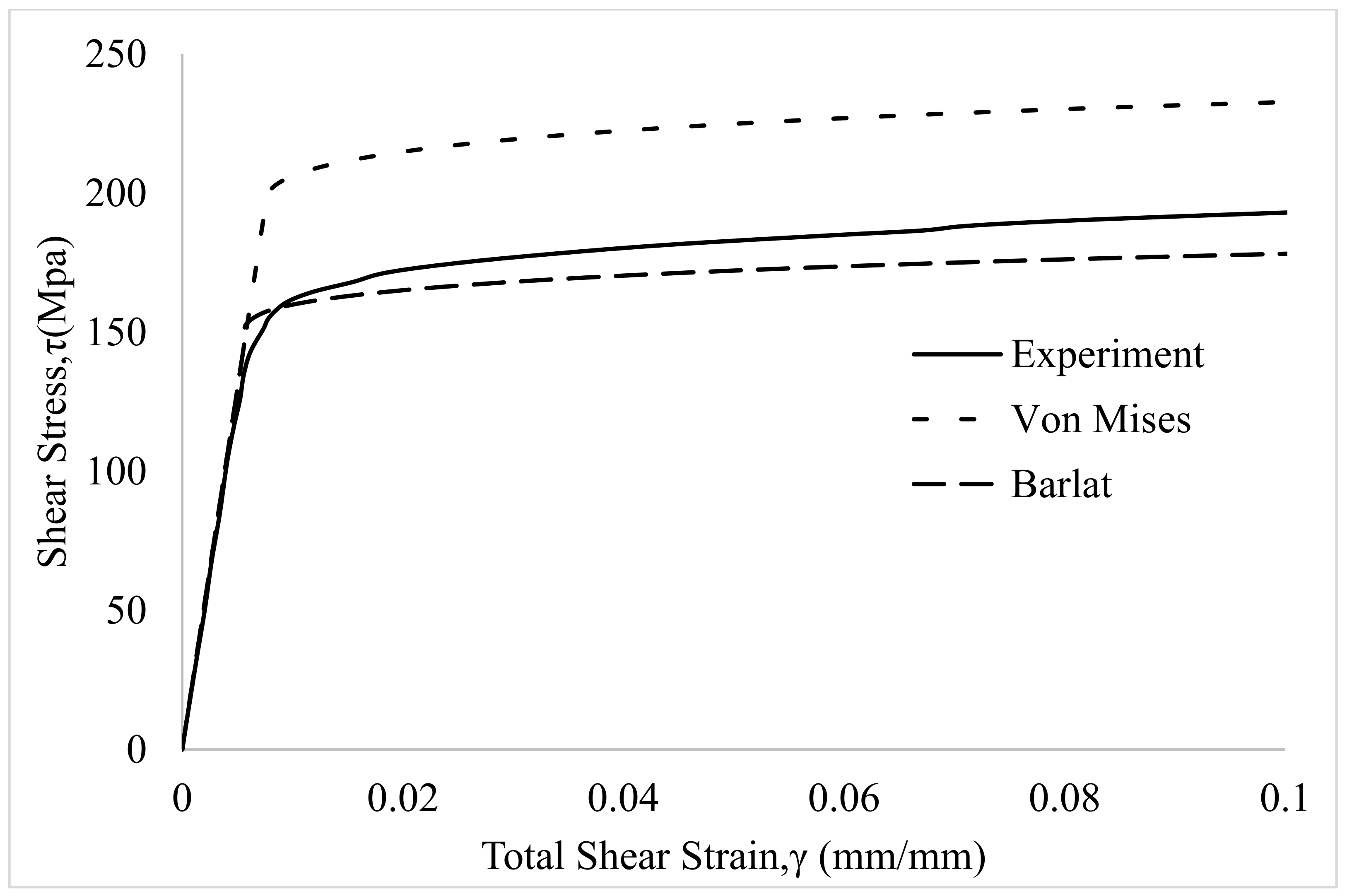
- Theoretical results indicate that results obtained using the anisotropic yield function are in excellent agreement with simple torsion experiments for both materials. Conversely, results obtained using an isotropic yield function underestimate, and then over-estimate, the stress-strain response of the MB1 and MB2 specimens, respectively.
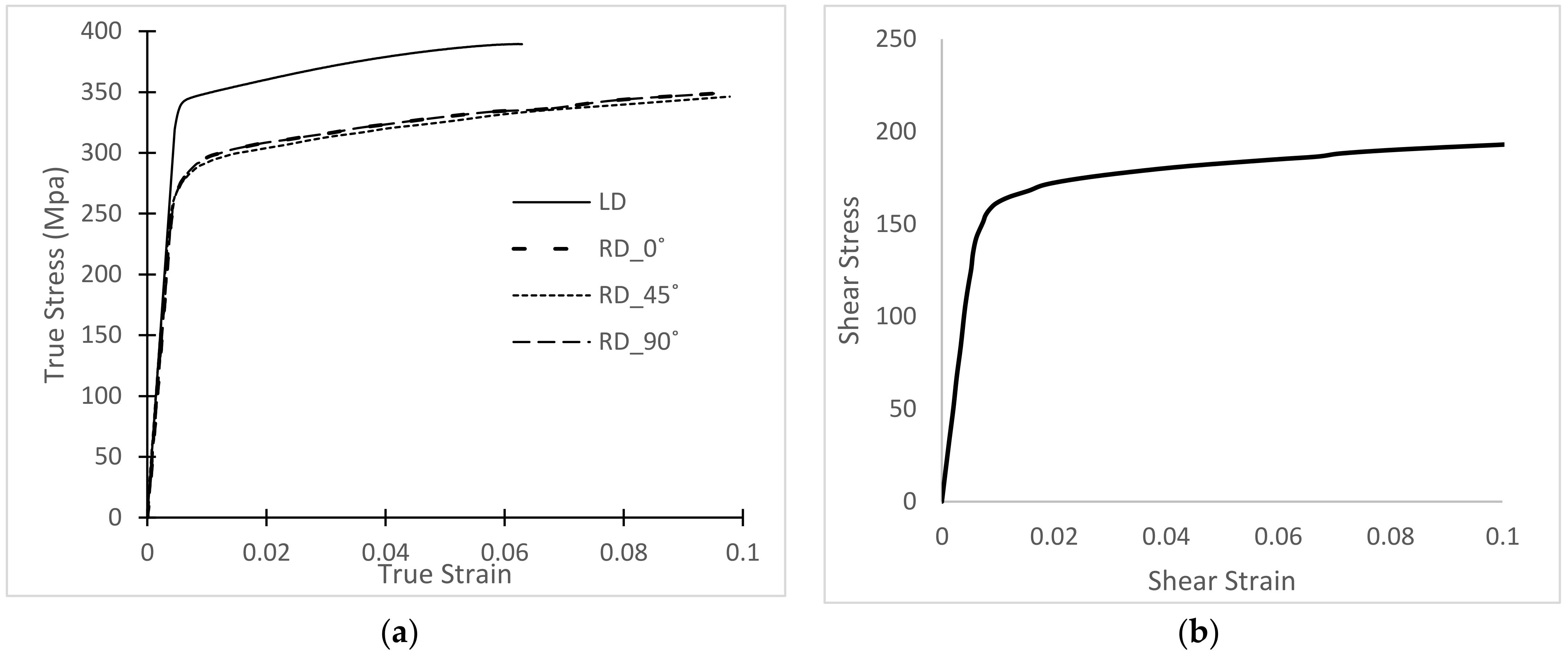
- Direct comparison of the experimental and theoretical results indicates that both extruded Al6061-T6 materials are significantly anisotropic, with the longitudinal yield stress deviating from the radial yield behavior in the extruded materials by over 20%. Furthermore, for biaxial loading cases, the Barlat yield criteria provides improved accuracy in the prediction of yielding for those applications where isotropic yielding is not adequate.
- Predictions of the stress-strain response for the MB1 and MB2 tubular specimens using the Barlat Yld91 anisotropic yield criterion are in excellent agreement with experimental measurements, with differences less than 5% for both specimens, clearly demonstrating the importance of yielding anisotropy for accurate prediction of material response when undergoing complex manufacturing processes, including longitudinal extrusion.
- Results also show that the nominally similar extrusion processes for mother bars MB1 and MB2 are not the same, with substantial differences in the stress-strain behavior for the two materials being consistent with microstructural features that indicate the MB2 extrusion process was more severe.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Sample Design and Preparation
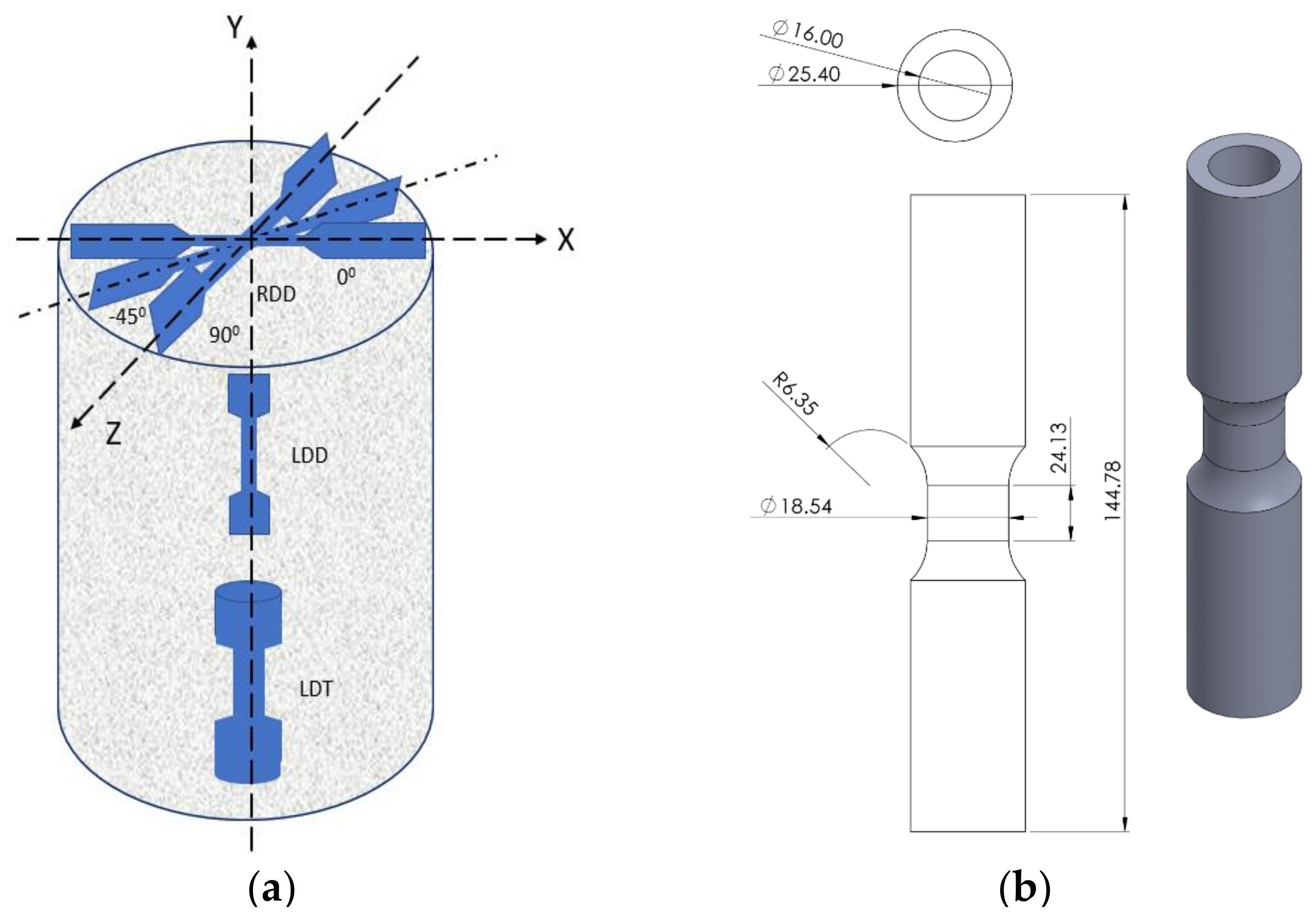
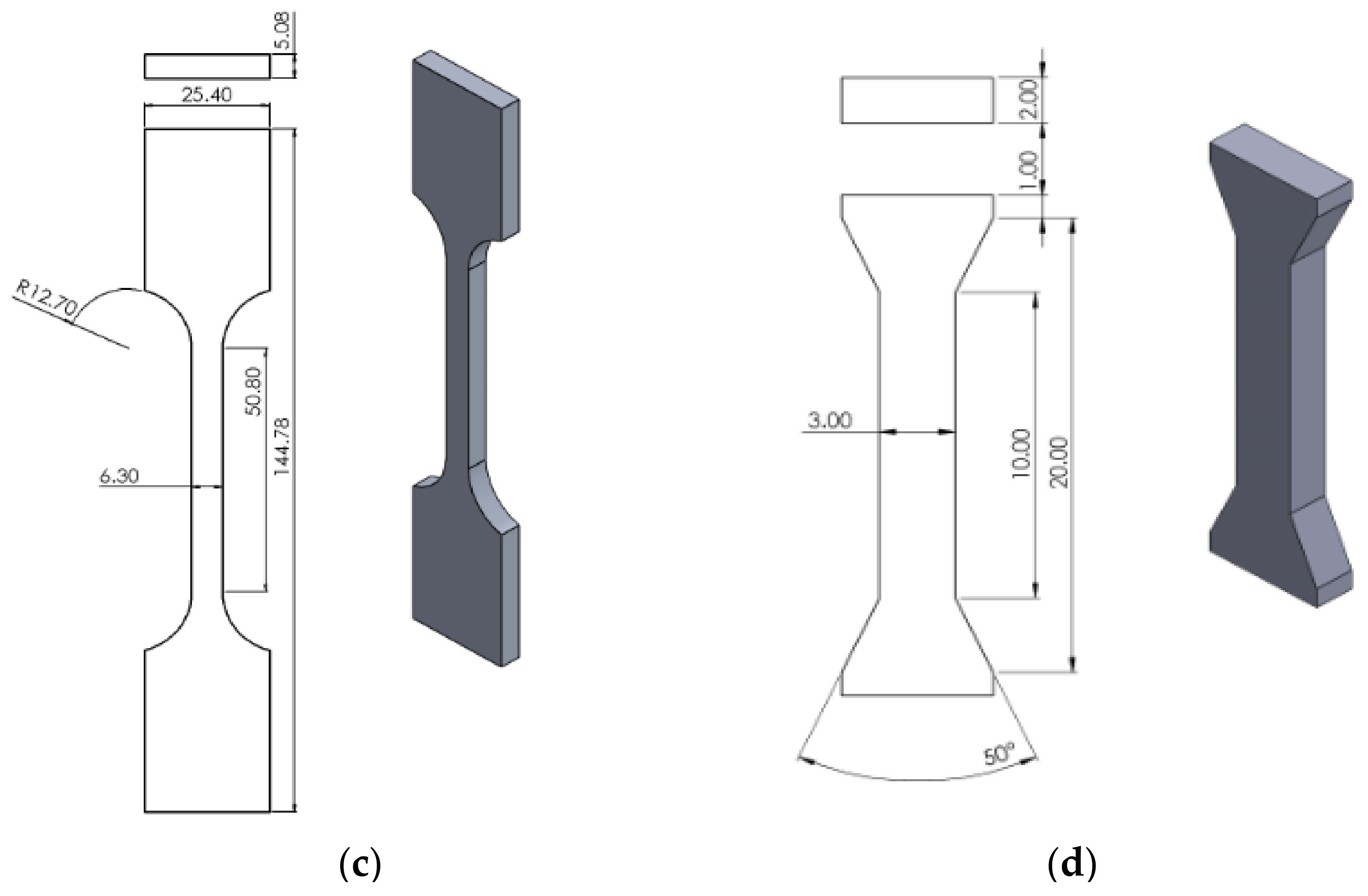
Appendix A.2. Experimental Setup


| Parameter # | Vic-3D | Vic-3D Stereo-Microscope |
|---|---|---|
| Cameras and Lenses | Grasshopper3 GS3-U3-91S6M (8 bits, 3376 × 2704) Schneider XENOPLAN 1.9/35-0511 | 5 MP CMOS PointGrey camera (2448 × 2048) |
| Lighting | White LED Lighting | LEO with a linear polarizing film |
| Calibration | 14 × 10 dot grid, 5 mm dot size (H95-00-03), 70 stereo calibration image pairs | 15 × 15 dot grid, 0.28 mm dot size, 70 stereo calibration image pairs |
| Lens distortion | 1st order radial distortion correction | 10 stereo distortion image pairs |
| Subset size | 29 × 29 pixels2 | 35 × 35 pixels2 |
| Step size | 9 pixels | 11 pixels |
| Filter type | Center-weighted Gaussian filter | |
| Shape function | Affine | |
| Strain filter size | 5 × 5 | |
| Strain measurement | Lagrangian large strain tensor definition for all strain components | |
| Average speckle size | 0.25 mm | 0.013 mm |
Appendix A.3. Elastic Modulus, Poisson’s Ratio and Hardening Parameter for Extruded Rods
References
- Zhou, W.; Shao, Z.; Yu, J.; Lin, J. Advances and Trends in Forming Curved Extrusion Profiles. Materials 2021, 14, 1603. [Google Scholar] [CrossRef]
- Hirsch, J. Aluminium Alloys for Automotive Application. Mater. Sci. Forum 1997, 242, 33–50. [Google Scholar] [CrossRef]
- Tisza, M.; Czinege, I. Comparative study of the application of steels and aluminium in lightweight production of automotive parts. Int. J. Light. Mater. Manuf. 2018, 1, 229–238. [Google Scholar] [CrossRef]
- Zhou, W.; Yu, J.; Lu, X.; Lin, J.; Dean, T.A. A comparative study on deformation mechanisms, microstructures and mechanical properties of wide thin-ribbed sections formed by sideways and forward extrusion. Int. J. Mach. Tools Manuf. 2021, 168, 103771. [Google Scholar] [CrossRef]
- Becker, D.; Schikorra, M.; Tekkaya, A.E. Manufacture of 3D Curved Profiles for Structure Components. Adv. Mater. Res. 2008, 43, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Staupendahl, D.; Becker, C.; Weinrich, A.; Hermes, M.; Tekkaya, A.E. Innovative forming processes for tubes, profiles and sheets made of modern steel grades [Innovative umformverfahren für rohre, profile und bleche aus modernen stahlwerkstof-fen]. Stahl Eisen 2012, 132, 47–54. [Google Scholar]
- Tresca, H. Memoire sur l’écoulement des solides à de forte pressions. Acad. Sci. Paris 1864, 2, 59. [Google Scholar]
- Mises, R.V. Mechanik der festen Körper im plastisch-deformablen Zustand. Nachr. Ges. Wiss. Göttingen Math.-Phys. Kl. 1913, 1913, 582–592. [Google Scholar]
- Hill, R. A theory of the yielding and plastic flow of anisotropic metals. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1948, 193, 281–297. [Google Scholar] [CrossRef] [Green Version]
- Hill, R. Theoretical Plasticity of Textured Aggregates. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1979; Volume 85, pp. 179–191. [Google Scholar]
- Hill, R. Constitutive modelling of orthotropic plasticity in sheet metals. J. Mech. Phys. Solids 1990, 38, 405–417. [Google Scholar] [CrossRef]
- Hill, R. A user-friendly theory of orthotropic plasticity in sheet metals. Int. J. Mech. Sci. 1993, 35, 19–25. [Google Scholar] [CrossRef]
- Hosford, W.F. A generalized isotropic yield criterion. J. Appl. Mech. 1972, 39, 1172. [Google Scholar] [CrossRef]
- Gotoh, M. A theory of plastic anisotropy based on a yield function of fourth order (plane stress state)—I. Int. J. Mech. Sci. 1977, 19, 505–512. [Google Scholar] [CrossRef]
- Logan, R.W.; Hosford, W.F. Upper-bound anisotropic yield locus calculations assuming <111>-pencil glide. Int. J. Mech. Sci. 1980, 22, 419–430. [Google Scholar] [CrossRef] [Green Version]
- Barlat, F.; Lian, K. Plastic behavior and stretchability of sheet metals. Part I: A yield function for orthotropic sheets under plane stress conditions. Int. J. Plast. 1989, 5, 51–66. [Google Scholar] [CrossRef]
- Barlat, F.; Lege, D.J.; Brem, J.C. A six-component yield function for anisotropic materials. Int. J. Plast. 1991, 7, 693–712. [Google Scholar] [CrossRef]
- Barlat, F.; Maeda, Y.; Chung, K.; Yanagawa, M.; Brem, J.C.; Hayashida, Y.; Lege, D.J.; Matsui, K.; Murtha, S.J.; Hattori, S.; et al. Yield function develop-ment for aluminum alloy sheets. J. Mech. Phys. Solids 1997, 45, 1727–1763. [Google Scholar] [CrossRef]
- Barlat, F.; Becker, R.; Hayashida, Y.; Maeda, Y.; Yanagawa, M.; Chung, K.; Brem, J.; Lege, D.; Matsui, K.; Murtha, S.; et al. Yielding description for solution strengthened aluminum alloys. Int. J. Plast. 1997, 13, 385–401. [Google Scholar] [CrossRef]
- Barlat, F.; Brem, J.; Yoon, J.W.; Chung, K.; Dick, R.; Lege, D.; Pourboghrat, F.; Choi, S.-H.; Chu, E. Plane stress yield function for aluminum alloy sheets—part 1: Theory. Int. J. Plast. 2003, 19, 1297–1319. [Google Scholar] [CrossRef]
- Barlat, F.; Aretz, H.; Yoon, J.W.; Karabin, M.; Brem, J.; Dick, R. Linear transfomation-based anisotropic yield functions. Int. J. Plast. 2005, 21, 1009–1039. [Google Scholar] [CrossRef]
- Karafillis, A.; Boyce, M. A general anisotropic yield criterion using bounds and a transformation weighting tensor. J. Mech. Phys. Solids 1993, 41, 1859–1886. [Google Scholar] [CrossRef]
- Bron, F.; Besson, J. A yield function for anisotropic materials Application to aluminum alloys. Int. J. Plast. 2004, 20, 937–963. [Google Scholar] [CrossRef]
- Cazacu, O.; Plunkett, B.; Barlat, F. Orthotropic yield criterion for hexagonal closed packed metals. Int. J. Plast. 2006, 22, 1171–1194. [Google Scholar] [CrossRef]
- Plunkett, B.; Cazacu, O.; Barlat, F. Orthotropic yield criteria for description of the anisotropy in tension and com-pression of sheet metals. Int. J. Plast. 2008, 24, 847–866. [Google Scholar] [CrossRef]
- Bai, Y.; Wierzbicki, T. A new model of metal plasticity and fracture with pressure and Lode dependence. Int. J. Plast. 2008, 24, 1071–1096. [Google Scholar] [CrossRef]
- Fourmeau, M.; Børvik, T.; Benallal, A.; Lademo, O.G.; Hopperstad, O.S. On the plastic anisotropy of an aluminium alloy and its influence on constrained multi-axial flow. Int. J. Plast. 2011, 27, 2005–2025. [Google Scholar] [CrossRef]
- Tardif, N.; Kyriakides, S. Determination of anisotropy and material hardening for aluminum sheet metal. Int. J. Solids Struct. 2012, 49, 3496–3506. [Google Scholar] [CrossRef] [Green Version]
- Korkolis, Y.; Kyriakides, S. Inflation and burst of anisotropic aluminum tubes for hydroforming applications. Int. J. Plast. 2008, 24, 509–543. [Google Scholar] [CrossRef]
- Korkolis, Y.P.; Kyriakides, S. Inflation and burst of aluminum tubes. Part II: An advanced yield function including deformation-induced anisotropy. Int. J. Plast. 2008, 24, 1625–1637. [Google Scholar] [CrossRef]
- Korkolis, Y.P.; Kyriakides, S. Hydroforming of anisotropic aluminum tubes: Part II analysis. Int. J. Mech. Sci. 2011, 53, 83–90. [Google Scholar] [CrossRef]
- Korkolis, Y.P.; Kyriakides, S. Path-dependent failure of inflated aluminum tubes. Int. J. Plast. 2009, 25, 2059–2080. [Google Scholar] [CrossRef]
- Korkolis, Y.P.; Kyriakides, S.; Giagmouris, T.; Lee, L.-H. Constitutive Modeling and Rupture Predictions of Al-6061-T6 Tubes Under Biaxial Loading Paths. J. Appl. Mech. 2010, 77, 064501. [Google Scholar] [CrossRef]
- Giagmouris, T.; Kyriakides, S.; Korkolis, Y.; Lee, L.-H. On the localization and failure in aluminum shells due to crushing induced bending and tension. Int. J. Solids Struct. 2010, 47, 2680–2692. [Google Scholar] [CrossRef] [Green Version]
- Seidt, J.; Gilat, A. Plastic deformation of 2024-T351 aluminum plate over a wide range of loading conditions. Int. J. Solids Struct. 2013, 50, 1781–1790. [Google Scholar] [CrossRef]
- Zhang, K.; Holmedal, B.; Hopperstad, O.; Dumoulin, S.; Gawad, J.; Van Bael, A.; Van Houtte, P. Multi-level modelling of mechanical anisotropy of commercial pure aluminium plate: Crystal plasticity models, advanced yield functions and parameter identification. Int. J. Plast. 2014, 66, 3–30. [Google Scholar] [CrossRef]
- Kuwabara, T.; Mori, T.; Asano, M.; Hakoyama, T.; Barlat, F. Material modeling of 6016-O and 6016-T4 aluminum alloy sheets and application to hole expansion forming simulation. Int. J. Plast. 2016, 93, 164–186. [Google Scholar] [CrossRef]
- Esmaeilpour, R.; Kim, H.; Park, T.; Pourboghrat, F.; Mohammed, B. Comparison of 3D yield functions for finite element simulation of single point incremental forming (SPIF) of aluminum 7075. Int. J. Mech. Sci. 2017, 133, 544–554. [Google Scholar] [CrossRef]
- Esmaeilpour, R.; Kim, H.; Park, T.; Pourboghrat, F.; Xu, Z.; Mohammed, B.; Abu-Farha, F. Calibration of Barlat Yld2004-18P yield function using CPFEM and 3D RVE for the simulation of single point incremental forming (SPIF) of 7075-O aluminum sheet. Int. J. Mech. Sci. 2018, 145, 24–41. [Google Scholar] [CrossRef]
- Pahlevanpour, A.; Behravesh, S.; Adibnazari, S.; Jahed, H. Characterization of anisotropic behaviour of ZK60 extrusion under stress-control condition and notes on fatigue modeling. Int. J. Fatigue 2019, 127, 101–109. [Google Scholar] [CrossRef]
- Mooney, B.; Kourousis, K.I.; Raghavendra, R.; Agius, D. Process phenomena influencing the tensile and anisotropic characteristics of additively manufactured maraging steel. Mater. Sci. Eng. A 2018, 745, 115–125. [Google Scholar] [CrossRef]
- Kondori, B.; Madi, Y.; Besson, J.; Benzerga, A. Evolution of the 3D plastic anisotropy of HCP metals: Experiments and modeling. Int. J. Plast. 2019, 117, 71–92. [Google Scholar] [CrossRef]
- Rahmaan, T.; Noder, J.; Abedini, A.; Zhou, P.; Butcher, C.; Worswick, M.J. Anisotropic plasticity characterization of 6000- and 7000-series aluminum sheet alloys at various strain rates. Int. J. Impact Eng. 2019, 135, 103390. [Google Scholar] [CrossRef]
- Sutton, M.A.; Deng, X.; Liu, J.; Yang, L. Determination of elastic-plastic stresses and strains from measured surface strain data. Exp. Mech. 1996, 36, 99–112. [Google Scholar] [CrossRef]
- Kim, J.H.; Serpantié, A.; Barlat, F.; Pierron, F.; Lee, M.G. Characterization of the post-necking strain hardening be-havior using the virtual fields method. Int. J. Solids Struct. 2013, 50, 3829–3842. [Google Scholar] [CrossRef] [Green Version]
- Pannier, Y.; Avril, S.; Rotinat, R.; Pierron, F. Identification of Elasto-Plastic Constitutive Parameters from Statically Undetermined Tests Using the Virtual Fields Method. Exp. Mech. 2006, 46, 735–755. [Google Scholar] [CrossRef] [Green Version]
- Avril, S.; Pierron, F.; Pannier, Y.; Rotinat, R. Stress Reconstruction and Constitutive Parameter Identification in Plane-Stress Elasto-plastic Problems Using Surface Measurements of Deformation Fields. Exp. Mech. 2007, 48, 403–419. [Google Scholar] [CrossRef]
- Coppieters, S.; Cooreman, S.; Sol, H.; Van Houtte, P.; Debruyne, D. Identification of the post-necking hardening behaviour of sheet metal by comparison of the internal and external work in the necking zone. J. Mater. Process. Technol. 2011, 211, 545–552. [Google Scholar] [CrossRef]
- Coppieters, S.; Kuwabara, T. Identification of Post-Necking Hardening Phenomena in Ductile Sheet Metal. Exp. Mech. 2014, 54, 1355–1371. [Google Scholar] [CrossRef] [Green Version]
- Ludwik, P. Elemente der Technologischen Mechanik; Springer: Berlin/Heidelberg, Germany, 1909. [Google Scholar] [CrossRef]
- Hollomon, J.H. Tensile deformation. Aime Trans. 1945, 12, 1–22. [Google Scholar]
- Voce, E. The relationship between stress and strain for homogeneous deformation. J. Inst. Met. 1948, 74, 537–562. [Google Scholar]
- Swift, H. Plastic instability under plane stress. J. Mech. Phys. Solids 1952, 1, 1–18. [Google Scholar] [CrossRef]
- Ludwigsen, D.C. Modified stress-strain relation for FCC metals and alloys. Metall. Trans. 1971, 2, 2825–2828. [Google Scholar] [CrossRef]
- Stoughton, T.B.; Yoon, J.W. Anisotropic hardening and non-associated flow in proportional loading of sheet metals. Int. J. Plast. 2009, 25, 1777–1817. [Google Scholar] [CrossRef]
- Rousselier, G.; Barlat, F.; Yoon, J.W. A novel approach for anisotropic hardening modeling. Part II: Anisotropic hardening in proportional and non-proportional loadings, application to initially isotropic material. Int. J. Plast. 2010, 26, 1029–1049. [Google Scholar] [CrossRef]
- Feng, X.; Cui, B.; Liu, Y.; Li, L.; Shi, X.; Zhang, X. Curved-layered material extrusion modeling for thin-walled parts by a 5-axis machine. Rapid Prototyp. J. 2021, 27, 1378–1387. [Google Scholar] [CrossRef]
- Vyavahare, S.; Teraiya, S.; Kumar, S. Auxetic structures fabricated by material extrusion: An experimental investigation of gradient parameters. Rapid Prototyp. J. 2021, 27, 1041–1058. [Google Scholar] [CrossRef]
- Jiang, S.; Sun, M.; Zhan, Y.; Li, H.; Sun, W. A dynamic model of laminated material extrusion additive manufacturing plate with the property of orthogonal anisotropy. Rapid Prototyp. J. 2021, 27, 785–796. [Google Scholar] [CrossRef]
- Parpala, R.C.; Popescu, D.; Pupaza, C. Infill parameters influence over the natural frequencies of ABS specimens obtained by extrusion-based 3D printing. Rapid Prototyp. J. 2021, 27, 1273–1285. [Google Scholar] [CrossRef]
- Kaill, N.; Campbell, R.; Pradel, P. Porosity in multi-axis material extrusion of short-fibre composites. Rapid Prototyp. J. 2021, 27, 362–370. [Google Scholar] [CrossRef]
- Meguid, S.A.; Malvern, L.E. An Experimental Investigation into the Plastic Flow and Strain Hardening of Mild Steel Under Proportional and Abruptly Changing Deformation Paths at a Controlled Rate. J. Eng. Mater. Technol. 1983, 105, 147–154. [Google Scholar] [CrossRef]
- Correlated Solutions, Inc. Available online: https://www.correlatedsolutions.com/ (accessed on 1 July 2020).
- Kahn-Jetter, Z.L.; Chu, T. Three-dimensional displacement measurements using digital image correlation and photogrammic analysis. Exp. Mech. 1990, 30, 10–16. [Google Scholar] [CrossRef]
- Luo, P.F.; Chao, Y.J.; Sutton, M.A.; Peters, W.H. Accurate measurement of three-dimensional deformations in deformable and rigid bodies using computer vision. Exp. Mech. 1993, 33, 123–132. [Google Scholar] [CrossRef]
- Sutton, M.A.; Orteu, J.J.; Schreier, H. Image Correlation for Shape, Motion and Deformation Measurements: Basic Concepts, Theory and Applications; Springer Science & Business Media: Boston, MA, USA, 2009. [Google Scholar]
- Sutton, M.A.; Yan, J.H.; Tiwari, V.; Schreier, H.W.; Orteu, J.J. The effect of out-of-plane motion on 2D and 3D digital image correlation measurements. Opt. Lasers Eng. 2008, 46, 746–757. [Google Scholar] [CrossRef] [Green Version]
- Yasmeen, F.; Rajan, S.; Sutton, M.A.; Schreier, H.W. Experimental Study of Measurement Errors in 3D-DIC Due to Out-of-Plane Specimen Rotation. In International Digital Imaging Correlation Society; Springer: Cham, Switzerland, 2017; pp. 211–215. [Google Scholar] [CrossRef]
- Yasmeen, F.; Balcaen, R.; Sutton, M.A.; Debruyne, D.; Rajan, S.; Schreier, H.W. Sensitivity of in-plane strain measurement to calibration parameter for out-of-plane specimen rotations. Exp. Mech. 2018, 58, 1115–1132. [Google Scholar] [CrossRef]
- Yasmeen, F.; Sutton, M.A.; Rajan, S.; Schreier, H.; Campbell, A. Effect of surface normal variability on local surface strain measurements in StereoDIC. Opt. Lasers Eng. 2020, 138, 106373. [Google Scholar] [CrossRef]
- Psylotech Incorporated. 2006. Available online: https://www.psylotech.com/μs/ (accessed on 1 July 2020).




| Rod Stock | Mechanical Properties | Chemical Composition | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Alloy | Dia (mm) | Ultimate Strength (MPa) | Yield Strength (MPa) | Elongation (%) | Si | Fe | Cu | Mn | Mg | Cr | Zn | Ti | |||
| Min | Max | Min | Max | Min | Max | ||||||||||
| 6061-T6 MB1 | 28.575 | 317.2 | 327.5 | 286.1 | 299.4 | 16.5 | 18 | 0.71 | 0.28 | 0.33 | 0.05 | 0.89 | 0.05 | 0.02 | 0.02 |
| 6061-T6 MB2 | 28.575 | 341.3 | 375.8 | 319.3 | 355.8 | 15.8 | 19.5 | 0.76 | 0.37 | 0.33 | 0.11 | 0.90 | 0.11 | 0.06 | 0.03 |
| Trial No | Mode | Load Cell | Strain Measurement Approach | Specimen | Material Al 6061-T6 | Number of Experiments |
|---|---|---|---|---|---|---|
| 1 | Tension | MTS | Extensometer | LDD | MB1 | 2 |
| MB2 | 2 | |||||
| 2 | Tension | Psylotech micro- tensile tester | VIC 3D with stereo microscope | RDD0 | MB1 | 2 |
| MB2 | 2 | |||||
| RDD45 | MB1 | 2 | ||||
| MB2 | 2 | |||||
| RDD90 | MB1 | 2 | ||||
| MB2 | 2 | |||||
| 3 | Torsion | Electromechanical TestResources frame with torsion load cells | VIC 3D software with standard cameras | LDT | MB1 | 2 |
| MB2 | 2 |
| 6061-T6 Al Tube | m | a | b | c | f | g | h |
|---|---|---|---|---|---|---|---|
| MB1 | 8 | 1.0000 | 1.1516 | 1.000 | 0.8750 | 1.0835 | 0.8750 |
| MB2 | 8 | 1.0000 | 1.4452 | 1.000 | 1.2069 | 1.3059 | 1.2069 |
| Material Properties | 6061-T6 Al Tube (MB1) | 6061-T6 Al Tube (MB2) |
|---|---|---|
| Modulus of Elasticity | 69 Gpa | 69 Gpa |
| Poisson’s ratio | 0.33 | 0.33 |
| Hardening Parameter, n | 13.51 | 16.47 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yasmeen, F.; Sutton, M.A.; Deng, X.; Ryan, M.; Reynolds, A.P. Parameter Estimation and Application of Anisotropic Yield Criteria for Cylindrical Aluminum Extrusions: Theoretical Developments and StereoDIC Measurements. Appl. Sci. 2021, 11, 9701. https://doi.org/10.3390/app11209701
Yasmeen F, Sutton MA, Deng X, Ryan M, Reynolds AP. Parameter Estimation and Application of Anisotropic Yield Criteria for Cylindrical Aluminum Extrusions: Theoretical Developments and StereoDIC Measurements. Applied Sciences. 2021; 11(20):9701. https://doi.org/10.3390/app11209701
Chicago/Turabian StyleYasmeen, Farzana, Michael A. Sutton, Xiaomin Deng, Megan Ryan, and Anthony P. Reynolds. 2021. "Parameter Estimation and Application of Anisotropic Yield Criteria for Cylindrical Aluminum Extrusions: Theoretical Developments and StereoDIC Measurements" Applied Sciences 11, no. 20: 9701. https://doi.org/10.3390/app11209701
APA StyleYasmeen, F., Sutton, M. A., Deng, X., Ryan, M., & Reynolds, A. P. (2021). Parameter Estimation and Application of Anisotropic Yield Criteria for Cylindrical Aluminum Extrusions: Theoretical Developments and StereoDIC Measurements. Applied Sciences, 11(20), 9701. https://doi.org/10.3390/app11209701





