A Simple Water Retention Model Based on Grain Size Distribution
Abstract
1. Introduction
2. Key Phenomena for Water Retention Curve Models
2.1. Pore Dimension and Pore Filling
2.2. Contact Angle between Water and Soil Surface
3. Proposed Model
- Achieve reasonably accurate predictions without requiring calibration to WRC data;
- Preferably use input parameters that are relatively easy to measure;
- Consider pore filling;
- Be capable of considering variation in contact angle with respect to particle size.
- The GSD of a material is used to calculate its clay, silt, and sand and larger fractions.
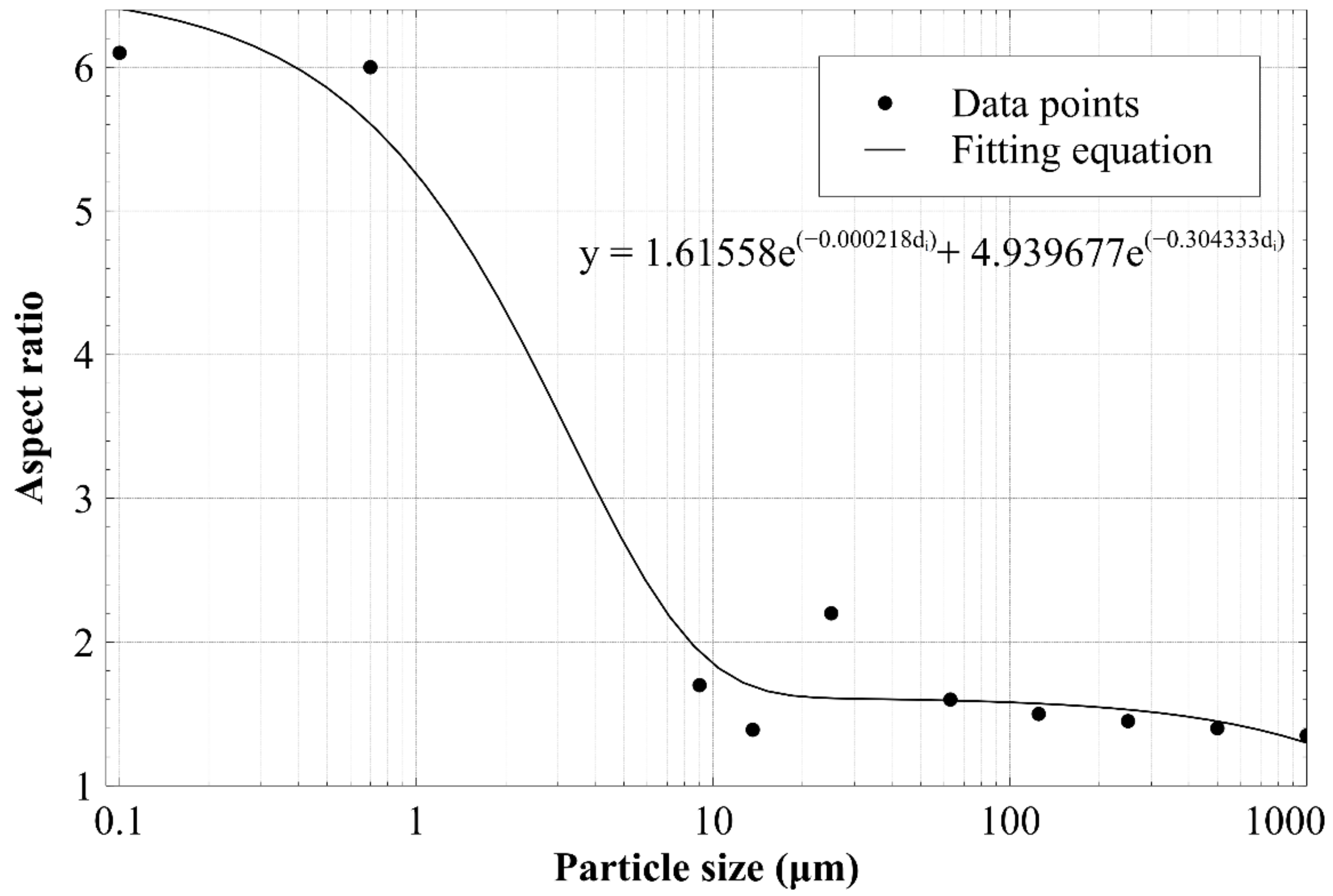
- The sizes in the GSD are then adjusted using an aspect ratio, such that smaller particles (e.g., clay or silt) are reduced in size to a greater extent than larger particles.
- A series of primary pore sizes are then created, by assuming the particles in each particle size bin of the adjusted GSD pack together to create a total volume of pores of a proportional size.
- The volume of primary pores associated with each pore size is estimated by assuming the pore volume fraction is proportional to the mass fraction of the associated particle size bin. That is, for a particle size bin accounting for 10% of a soil’s mass, the volume of pores associated with this bin account for 10% of its total pore volume, as determined from its adopted saturated volumetric water content.
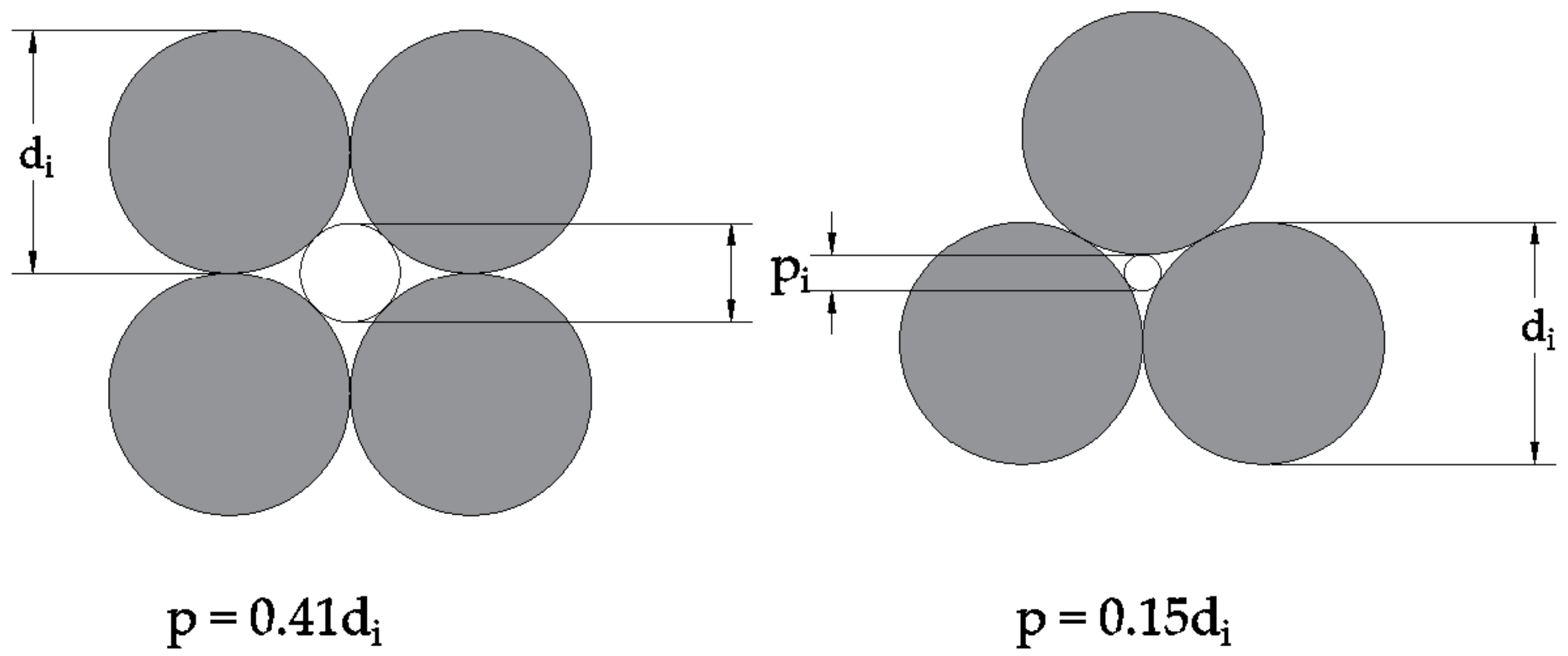
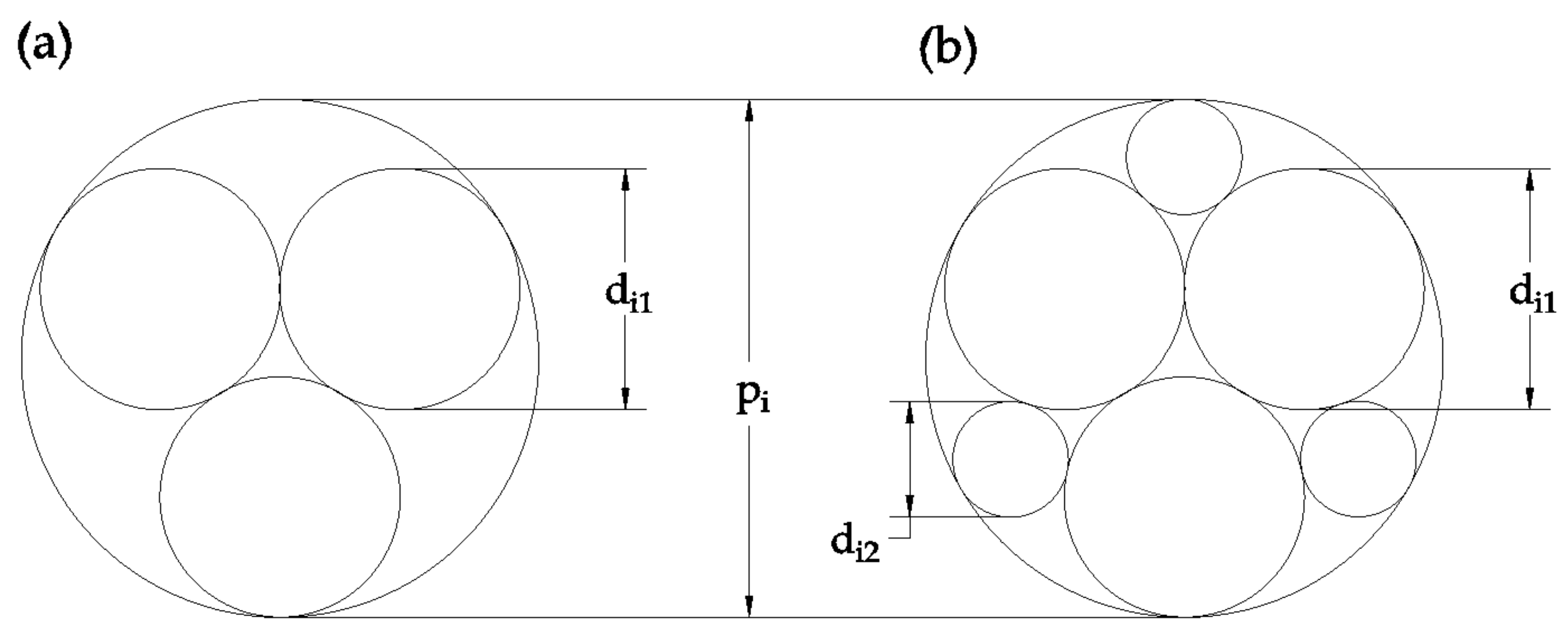
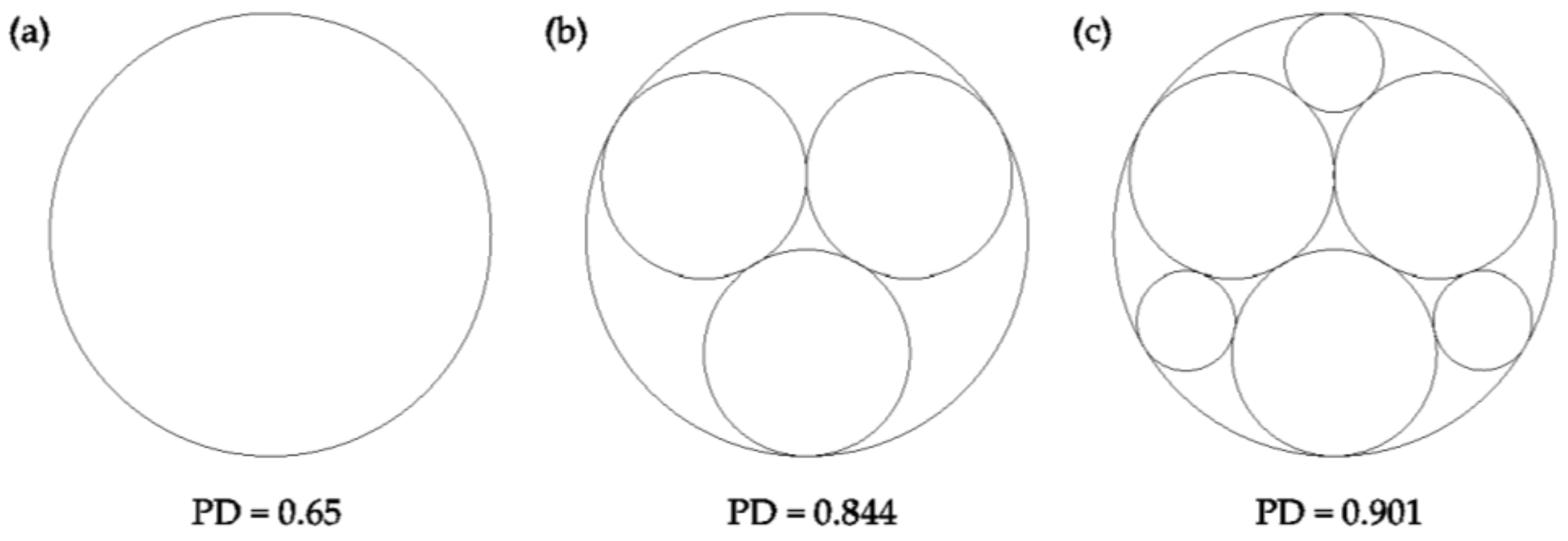
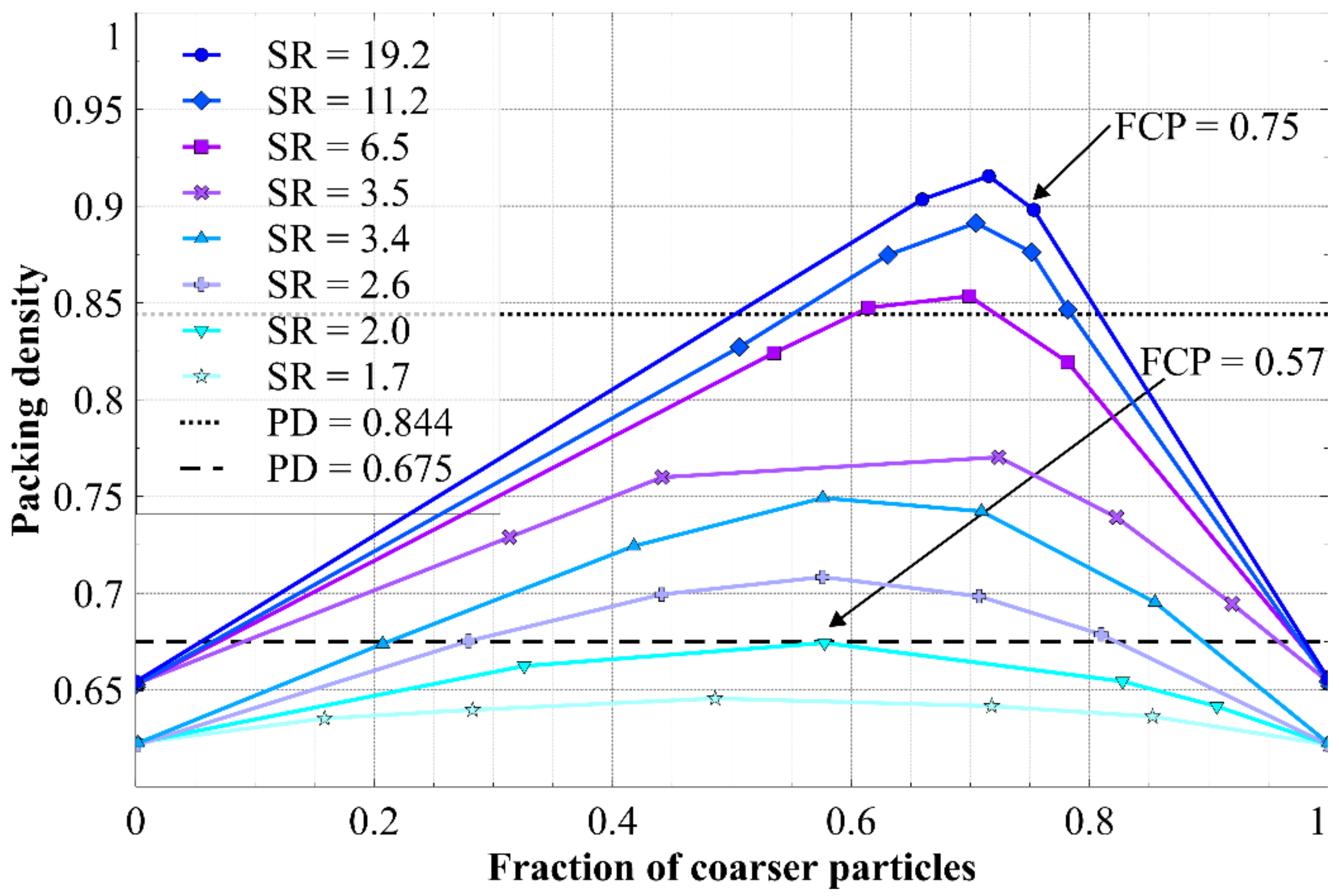
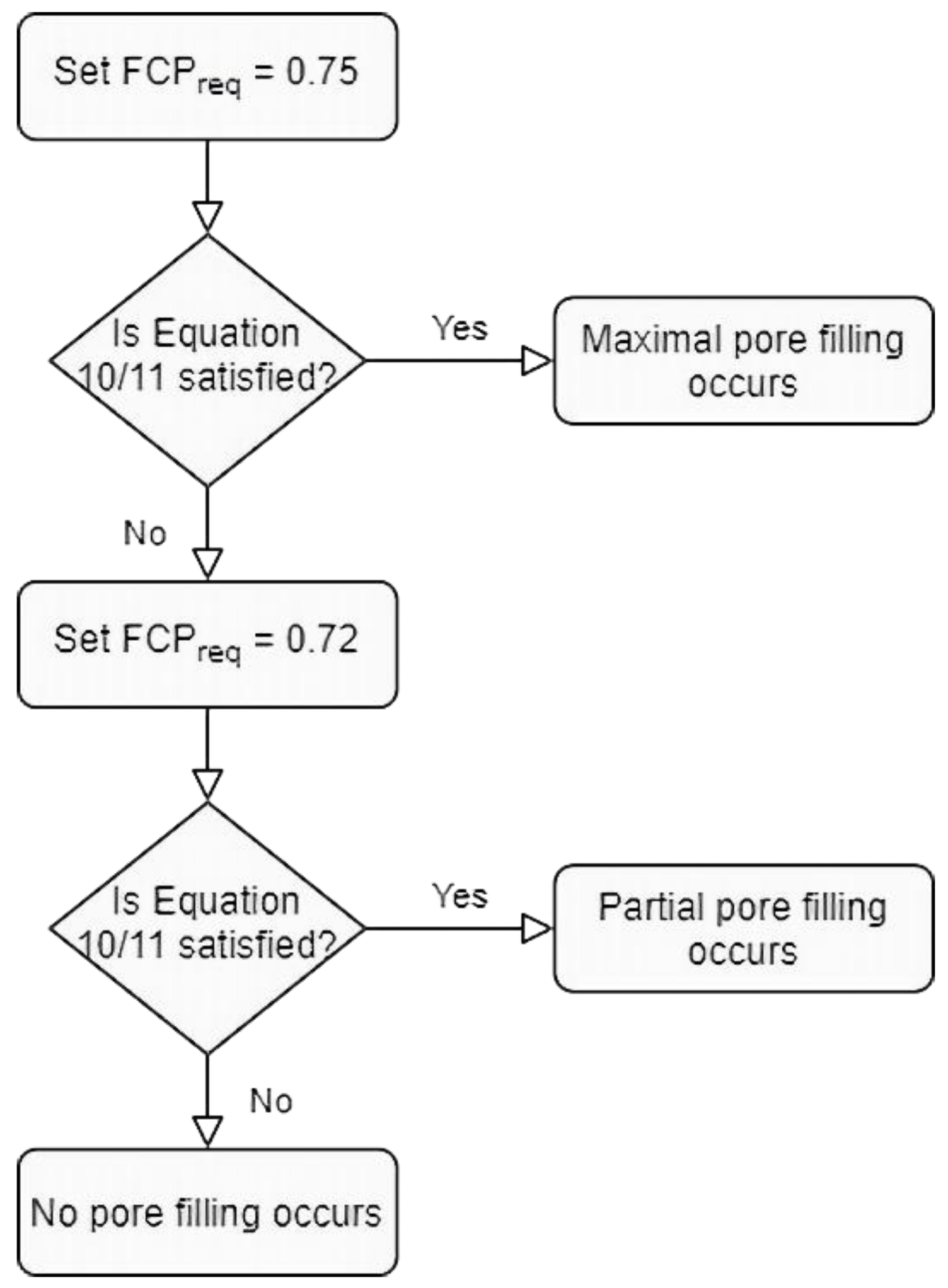
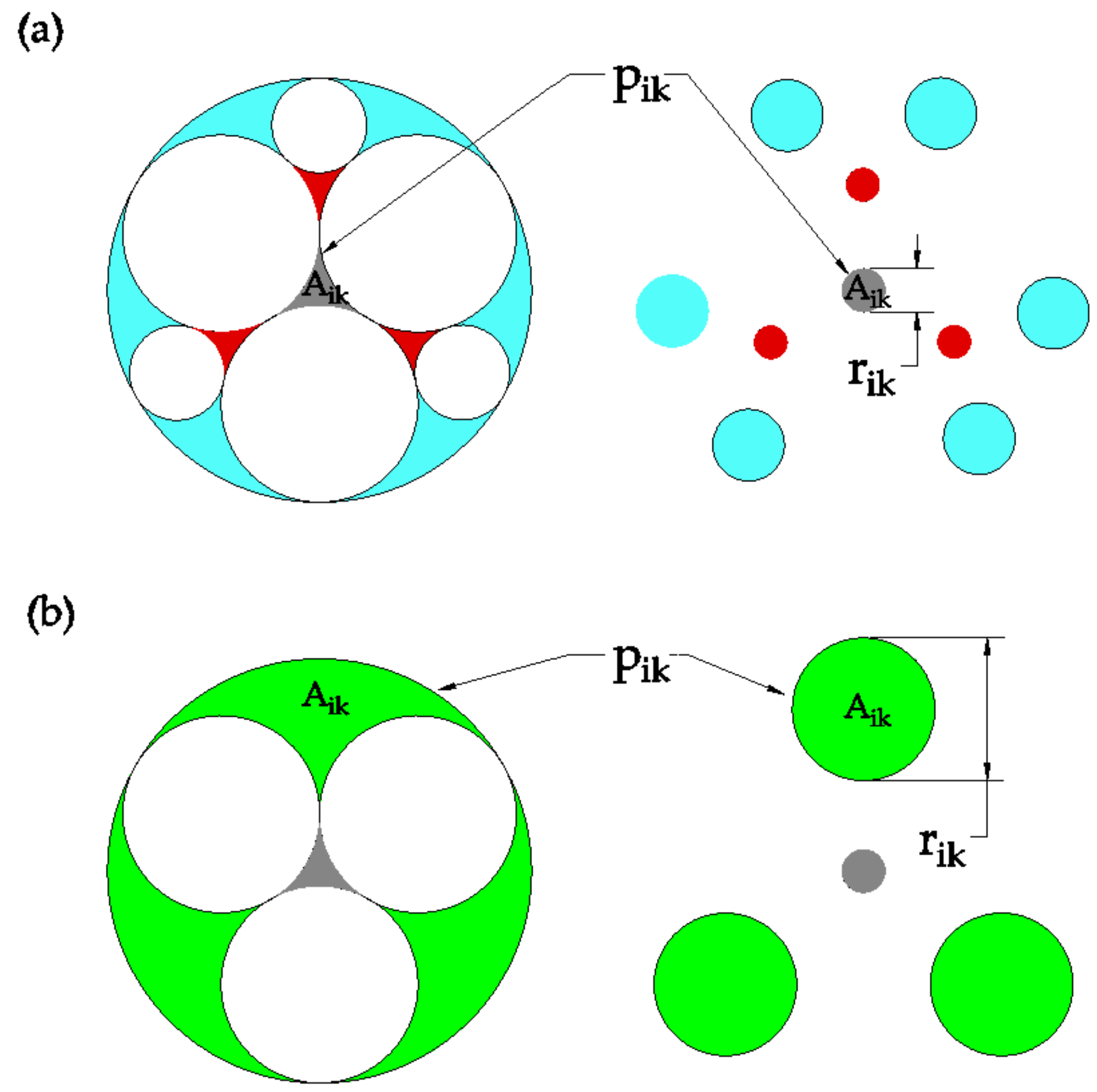
- A set of criteria are applied to each primary pore size to determine what degree of pore filling should occur within each pore size. Any required pore filling is done so to achieve the packing densities at different levels of Apollonian packing.
- Whether pores are unfilled, partially filled, or filled is determined by considering whether there is a sufficient volume of smaller particle fractions that could fill each set of primary pores in a binary mixture to achieve the packing density corresponding to Apollonian packing.
- Having determined the degree of filling for each set of primary pores, they are then redistributed (as required) into a larger number of smaller pores, according to the appropriate Apollonian geometry, and combined to give a final pore size distribution.
- Each pore size in the final distribution is transformed to an equivalent area circular pore, with a drainage suction, creating the final pore size distribution.
- The predicted WRC is the theoretical WRC of the pore size distribution, which is estimated by assuming a number of arbitrary suctions, and calculating the volumetric water content of the water filled or undrained pores.
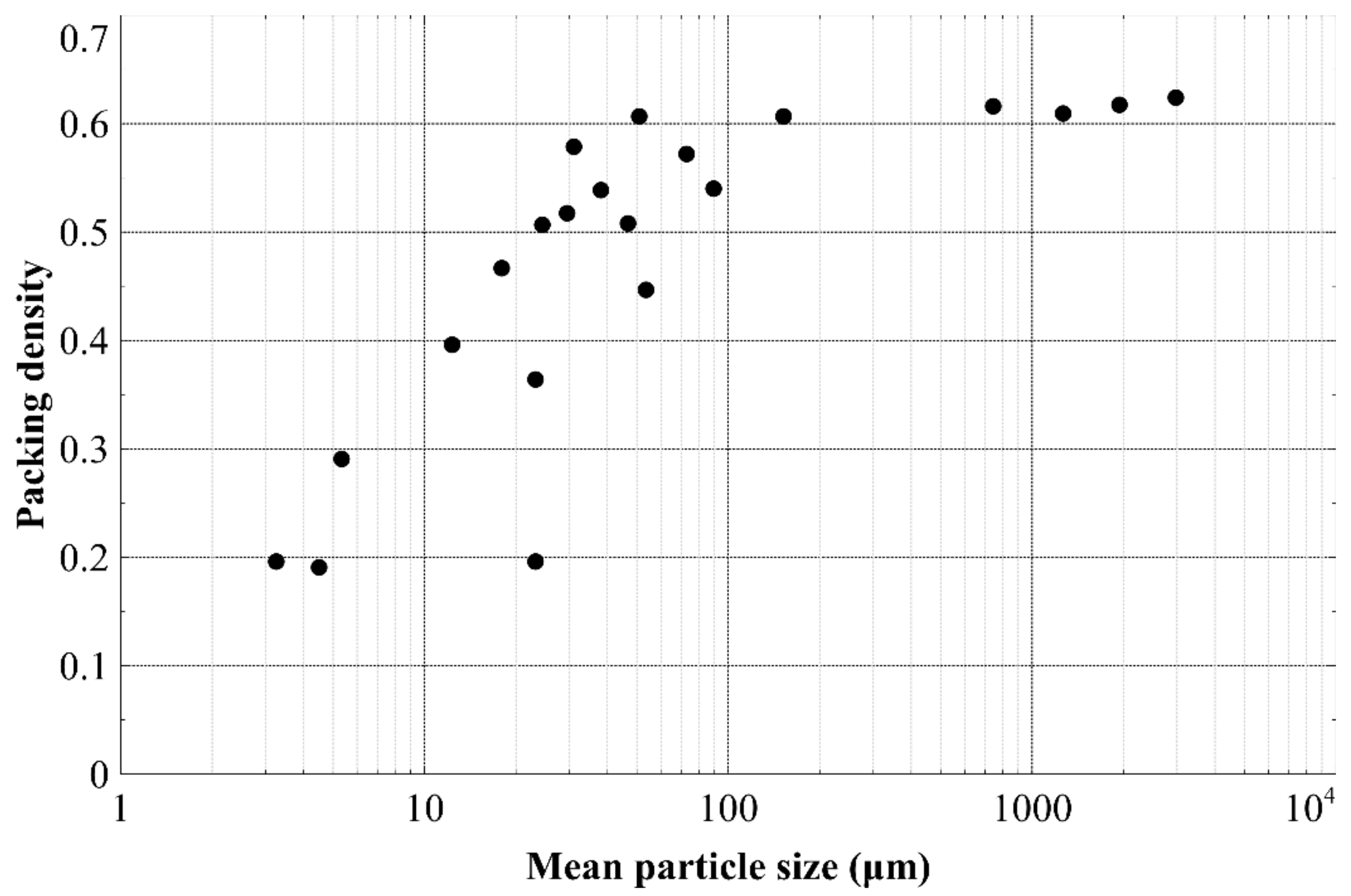
3.1. Inferring a Primary Pore Size Distribution from Grain Size Distribution (GSD)
3.2. Primary Pore Filling
3.2.1. Smallest Particle Criterion
3.2.2. Filling of Pores Associated with Clay Sized Particles
3.2.3. Filling of Pores Associated with Silt Sized Particles
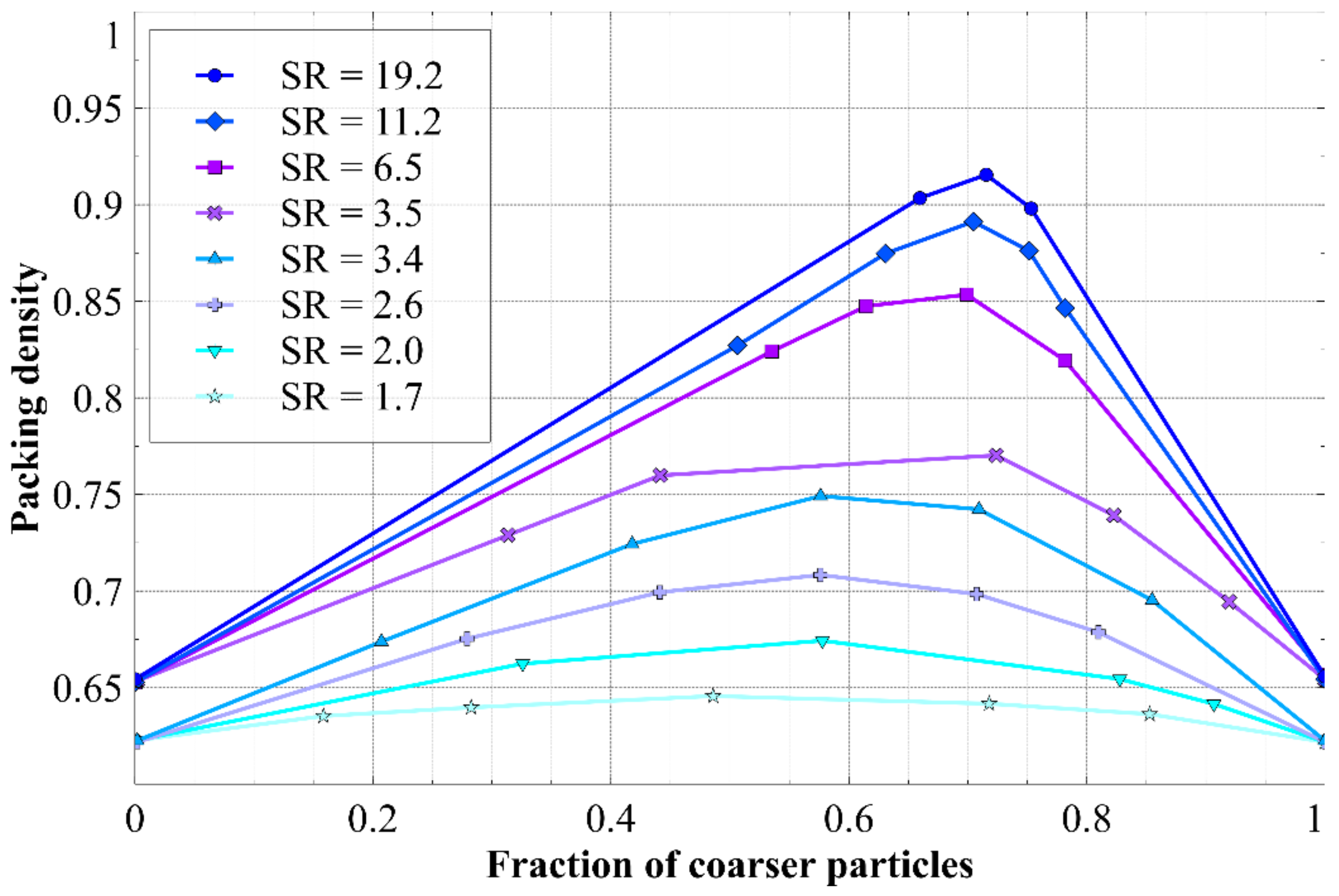
- What is the size ratio that defines a suitably smaller particle, to form a binary mixture with a particular degree of filling (packing density)? That is, what size particles (dss,i) are small enough to effectively fill the pores between the larger particles di,adjusted?
- What is the maximum fraction xi of larger particles di,adjusted that still ensures that there are enough smaller particles (dss,i) to achieve the assumed packing density in the coarser particle fraction? That is, how to decide when there are too few smaller particles to effectively fill the pores between larger particles?
3.2.4. Filling of Pores Associated with Sand and Larger Sized Particles
3.3. Pore Size Distribution to Water Retention Curve
3.4. Summary of Model Inputs and Outputs
- Sand fraction;
- Silt fraction;
- Clay fraction;
- Saturated volumetric water content;
- Receding contact angle;
- Particle size bins from the grain size distribution (GSD).
4. Materials and Methods
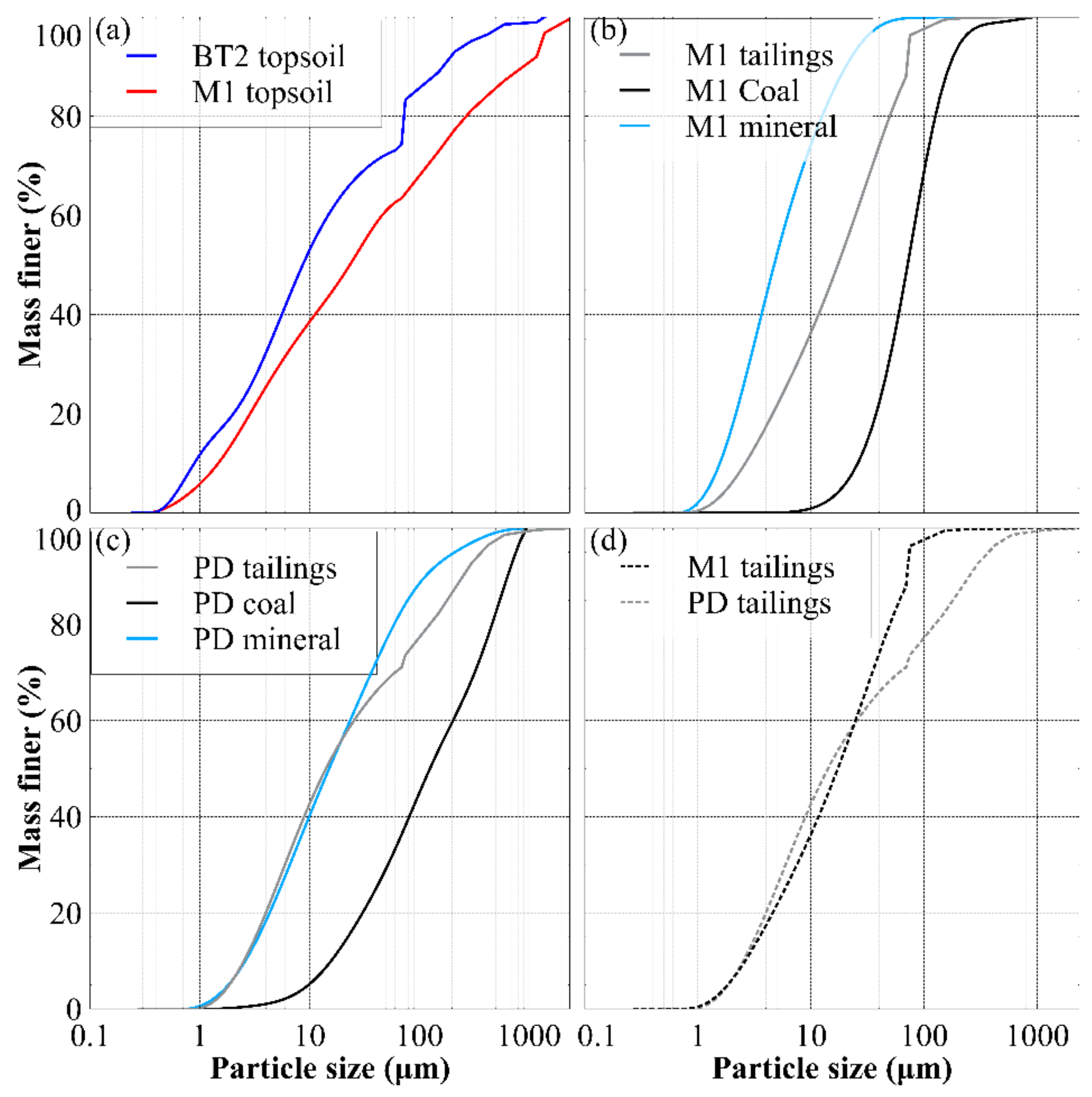
4.1. Materials
4.2. Methods
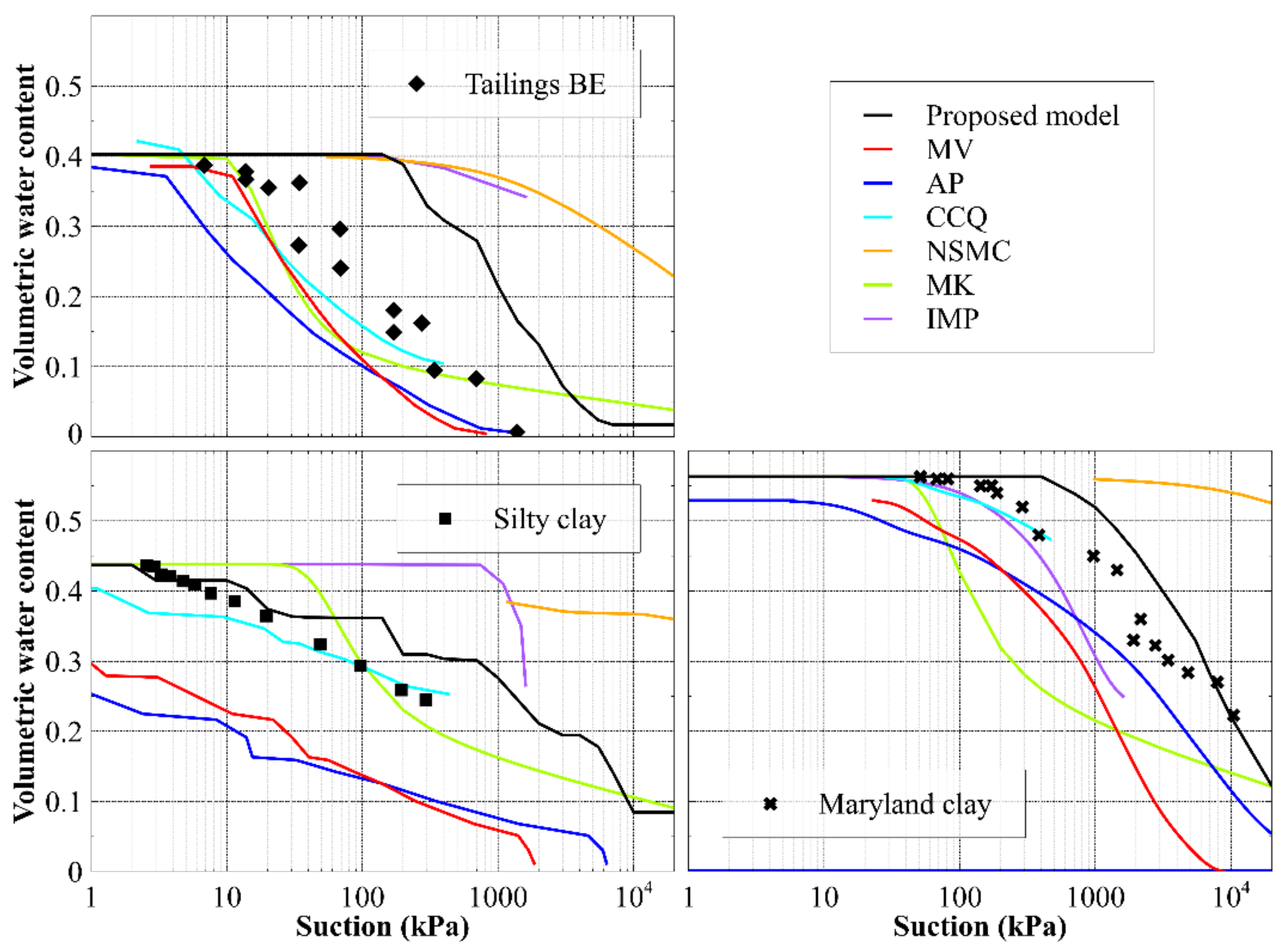
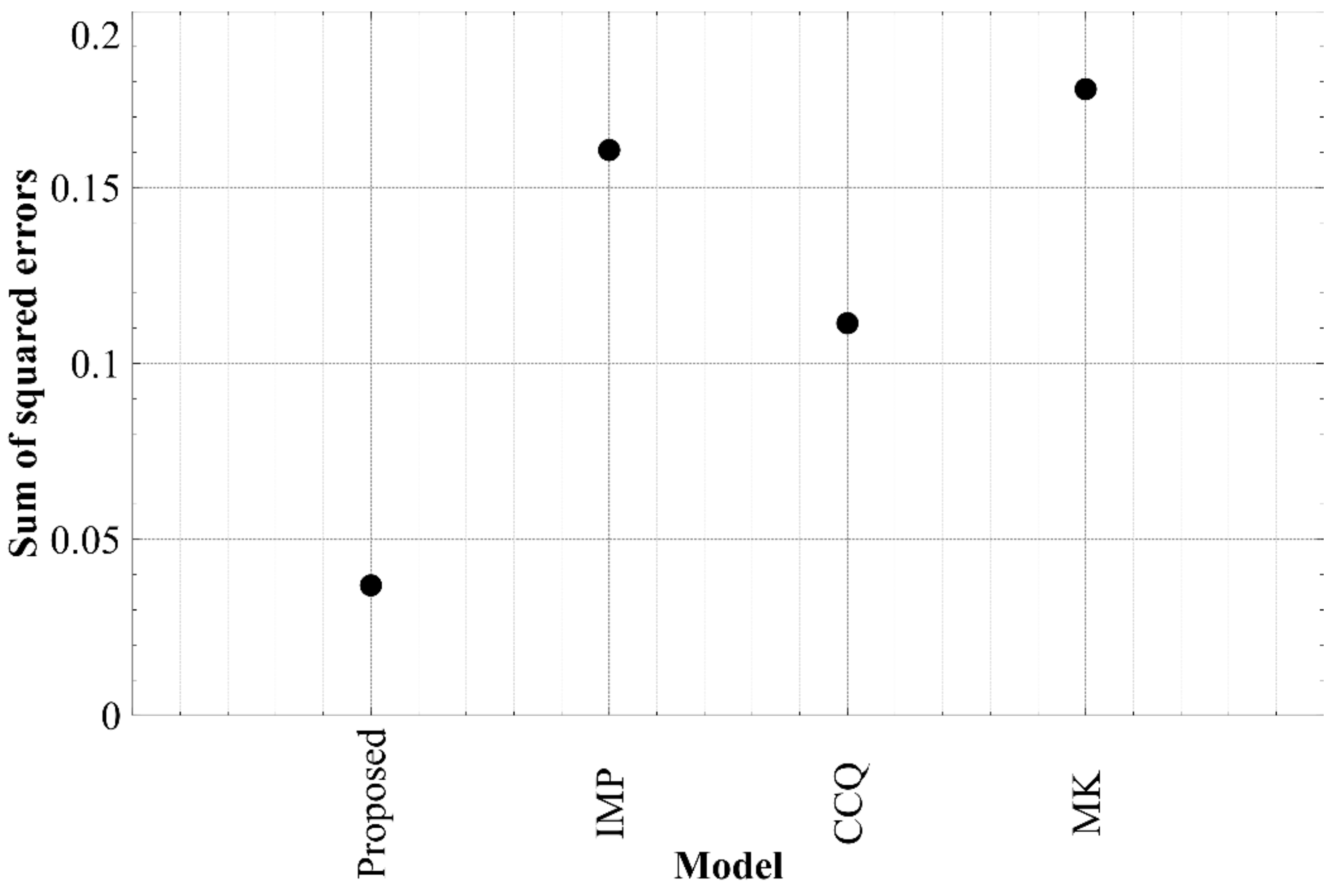
4.3. Validation of the Proposed WRC Prediction Model
5. Results and Discussion
Retention Curves of the Mine Materials
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Material | Gs | Liquid Limit | Plastic Limit | Receding CA (°) | Initial Porosity | Source |
|---|---|---|---|---|---|---|
| Tailings BE | 2.65 2 | 0.17 | - 1 | 0 2 | 0.403 | [58,59] |
| Silty clay | 2.65 2 | 0.404 | 0.248 | 0 2 | 0.438 | [60] |
| Silt Loam 10861 | 2.65 2 | - 1 | - 1 | 0 2 | 0.402 | [61] |
| Loam 1260 | 2.77 | - 1 | - 1 | 0 2 | 0.4 | UNSODA [62] |
| Maryland clay | 2.65 | 0.7 | 0.24 | 0 2 | 0.563 | [63] 3 |
| Loamy sand 10741 | 2.65 2 | N/A | N/A | 0 2 | 0.355 | [61] |
| Grenoble sand | 2.65 2 | N/A | N/A | 0 2 | 0.385 | [13] |
Appendix B
| Material | Sand Fraction | Silt Fraction | Clay Fraction | Receding CA (°) | Saturated Volumetric Water Content, θs |
|---|---|---|---|---|---|
| BT2 topsoil | 0.28 | 0.54 | 0.18 | 3 | 0.52 |
| M1 tailings | 0.12 | 0.82 | 0.06 | Varied 1 | 0.441 |
| M1 topsoil | 0.38 | 0.48 | 0.14 | 6 | 0.39 |
| PD tailings | 0.3 | 0.64 | 0.06 | Varied 1 | 0.45 |
| Tailings BE | 0.3 | 0.65 | 0.05 | 0 2 | 0.403 |
| Silty clay | 0.31 | 0.35 | 0.34 | 0 2 | 0.438 |
| Silt Loam 10861 | 0.06 | 0.78 | 0.16 | 0 2 | 0.402 |
| Loam 1260 | 0.36 | 0.52 | 0.12 | 0 2 | 0.4 |
| Maryland clay | 0 | 0.29 | 0.71 | 0 2 | 0.563 |
| Loamy sand 10741 | 0.78 | 0.15 | 0.7 | 0 2 | 0.355 |
| Grenoble sand | 1 | 0 | 0 | 0 2 | 0.385 |
| Material | Initial Void Ratio, e | Saturated Volumetric Water Content, θs | Receding CA (°) |
|---|---|---|---|
| BT2 topsoil | 1.083 | 0.52 | 3 |
| M1 tailings | 0.789 | 0.441 | Varied 1 |
| M1 topsoil | 0.652 | 0.39 | 6 |
| PD tailings | 0.82 | 0.45 | Varied 1 |
| Tailings BE | 0.674 | 0.403 | 0 2 |
| Silty clay | 0.78 | 0.438 | 0 2 |
| Silt Loam 10861 | 0.67 | 0.402 | 0 2 |
| Loam 1260 | 0.665 | 0.4 | 0 2 |
| Maryland clay | 1.29 | 0.563 | 0 2 |
| Loamy sand 10741 | 0.55 | 0.355 | 0 2 |
| Grenoble sand | 0.625 | 0.385 | 0 2 |
| Material | Initial Void Ratio, e | Specific Gravity, Gs | α | Receding CA (°) |
|---|---|---|---|---|
| BT2 topsoil | 1.083 | 2.63 | 1.35 | 3 |
| M1 tailings | 0.789 | 1.96 | 1.35 | Varied 1 |
| M1 topsoil | 0.652 | 2.66 | 1.35 | 6 |
| PD tailings | 0.82 | 2.22 | 1.35 | Varied 1 |
| Tailings BE | 0.674 | 2.65 2 | 1.35 | 0 2 |
| Silty clay | 0.78 | 2.65 2 | 1.35 | 0 2 |
| Silt Loam 10861 | 0.67 | 2.65 2 | 1.35 | 0 2 |
| Loam 1260 | 0.665 | 2.77 | 1.35 | 0 2 |
| Maryland clay | 1.29 | 2.65 | 1.35 | 0 2 |
| Loamy sand 10741 | 0.55 | 2.65 2 | 1.5 | 0 2 |
| Grenoble sand | 0.625 | 2.65 2 | 1.5 | 0 2 |
| Material | Clay Fraction | β | Saturated Volumetric Water Content, θs | Receding CA (°) |
|---|---|---|---|---|
| BT2 topsoil | 0.18 | 0.516 | 0.52 | 3 |
| M1 tailings | 0.06 | 0.516 | 0.441 | 0 1 |
| M1 topsoil | 0.14 | 0.516 | 0.39 | 6 |
| PD tailings | 0.06 | 0.516 | 0.45 | 0 1 |
| Tailings BE | 0.05 | 0.516 | 0.403 | 0 2 |
| Silty clay | 0.34 | 0.516 | 0.438 | 0 2 |
| Silt Loam 10861 | 0.16 | 0.516 | 0.402 | 0 2 |
| Loam 1260 | 0.12 | 0.516 | 0.4 | 0 2 |
| Maryland clay | 0.71 | 0.516 | 0.563 | 0 2 |
| Loamy sand 10741 | 0.7 | 0.516 | 0.355 | 0 2 |
| Grenoble sand | 0 | 0.516 | 0.385 | 0 2 |
| Material | Initial Void Ratio, e | Specific Gravity, Gs | Saturated Volumetric Water Content, θs | Receding CA (°) |
|---|---|---|---|---|
| BT2 topsoil | 1.083 | 2.63 | 0.52 | 3 |
| M1 tailings | 0.789 | 1.96 | 0.441 | Varied 1 |
| M1 topsoil | 0.652 | 2.66 | 0.39 | 6 |
| PD tailings | 0.82 | 2.22 | 0.45 | Varied 1 |
| Tailings BE | 0.674 | 2.65 2 | 0.403 | 0 2 |
| Silty clay | 0.78 | 2.65 2 | 0.438 | 0 2 |
| Silt Loam 10861 | 0.67 | 2.65 2 | 0.402 | 0 2 |
| Loam 1260 | 0.665 | 2.77 | 0.4 | 0 2 |
| Maryland clay | 1.29 | 2.65 | 0.563 | 0 2 |
| Loamy sand 10741 | 0.55 | 2.65 2 | 0.355 | 0 2 |
| Grenoble sand | 0.625 | 2.65 2 | 0.385 | 0 2 |
| Material | D10 (μm) | D60 (μm) | ac | Liquid Limit | Specific Gravity, Gs | m | Initial Void Ratio, e | λ (m2/kg) | Receding CA (°) |
|---|---|---|---|---|---|---|---|---|---|
| BT2 topsoil | N/A | N/A | 0.0007 | 0.462 | 2.63 | 0.00003 | 1.083 | 200 | 3 |
| M1 tailings | N/A | N/A | 0.0007 | 0.497 | 1.96 | 0.00003 | 0.789 | 200 | Varied 1 |
| M1 topsoil | N/A | N/A | 0.0007 | 0.274 | 2.66 | 0.00003 | 0.652 | 200 | 6 |
| PD tailings | N/A | N/A | 0.0007 | 0.482 | 2.22 | 0.00003 | 0.82 | 200 | Varied 1 |
| Tailings BE | N/A | N/A | 0.0007 | 0.17 | 2.652 | 0.00003 | 0.674 | 200 | 0 2 |
| Silty clay | N/A | N/A | 0.0007 | 0.404 | 2.652 | 0.00003 | 0.78 | 200 | 0 2 |
| Silt Loam 10861 | - 4 | - 4 | - 4 | - 3,4 | - 4 | - 4 | - 4 | - 4 | - 4 |
| Loam 1260 | 1 | 50 | 0.01 | N/A | 2.77 | N/A | 0.665 | 200 | 0 2 |
| Maryland clay | N/A | N/A | 0.0007 | 0.7 | 2.65 | 0.00003 | 1.29 | 200 | 0 2 |
| Loamy sand 10741 | 7.4 | 265 | 0.01 | N/A | 2.652 | N/A | 0.55 | 200 | 0 2 |
| Grenoble sand | 140 | 310 | 0.01 | N/A | 2.652 | N/A | 0.625 | 200 | 0 2 |
| Material | Saturated Volumetric Water Content, θs | ξ1 | p | β1 | β2 | ψmax (kPa) | θr_max | α1 | α2 | λ | Receding CA (°) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| BT2 topsoil | 0.52 | 11.07 | 2 | 0.09 | 0.95 | 1600 | 0.25 | 16.02 | 2.01 | 2 | 3 |
| M1 tailings | 0.441 | 11.07 | 2 | 0.09 | 0.95 | 1600 | 0.25 | 16.02 | 2.01 | 2 | Varied 1 |
| M1 topsoil | 0.39 | 11.07 | 2 | 0.09 | 0.95 | 1600 | 0.25 | 16.02 | 2.01 | 2 | 6 |
| PD tailings | 0.45 | 11.07 | 2 | 0.09 | 0.95 | 1600 | 0.25 | 16.02 | 2.01 | 2 | Varied 1 |
| Tailings BE | 0.403 | 11.07 | 2 | 0.09 | 0.95 | 1600 | 0.25 | 16.02 | 2.01 | 2 | 0 2 |
| Silty clay | 0.438 | 11.07 | 2 | 0.09 | 0.95 | 1600 | 0.25 | 16.02 | 2.01 | 2 | 0 2 |
| Silt Loam 10861 | 0.402 | 11.07 | 2 | 0.09 | 0.95 | 1600 | 0.25 | 16.02 | 2.01 | 2 | 0 2 |
| Loam 1260 | 0.4 | 11.07 | 2 | 0.09 | 0.95 | 1600 | 0.25 | 16.02 | 2.01 | 2 | 0 2 |
| Maryland clay | 0.563 | 11.07 | 2 | 0.09 | 0.95 | 1600 | 0.25 | 16.02 | 2.01 | 2 | 0 2 |
| Loamy sand 10741 | - 3 | - 3 | - 3 | - 3 | - 3 | - 3 | - 3 | - 3 | - 3 | - 3 | - 3 |
| Grenoble sand | - 3 | - 3 | - 3 | - 3 | - 3 | - 3 | - 3 | - 3 | - 3 | - 3 | - 3 |

References
- Brown, G.M.C.; Grant, C.D. Nutrient status of pasture ecosystems established on rehabilitated overburden and topsoil sites in the Hunter Valley, New South Wales. Soil Res. 2000, 38, 479–492. [Google Scholar] [CrossRef]
- Dragovich, D.; Patterson, J. Condition of rehabilitated coal mines in the Hunter Valley, Australia. Land Degrad. Dev. 1995, 6, 29–39. [Google Scholar] [CrossRef]
- Kundu, N.; Ghose, M. Shelf life of stock-piled topsoil of an opencast coal mine. Environ. Conserv. 1997, 24, 24–30. [Google Scholar] [CrossRef]
- Ghose, M.K.; Kundu, N.K. Deterioration of soil quality due to stockpiling in coal mining areas. Int. J. Environ. Stud. 2004, 61, 327–335. [Google Scholar] [CrossRef]
- Sheoran, V.; Sheoran, A.; Poonia, P. Soil Reclamation of Abandoned Mine Land by Revegetation: A Review. Int. J. Soil Sediment Water 2010, 3, 13. [Google Scholar]
- Mushia, N.M.; Ramoelo, A.; Ayisi, K.K. The Impact of the Quality of Coal Mine Stockpile Soils on Sustainable Vegetation Growth and Productivity. Sustainability 2016, 8, 546. [Google Scholar] [CrossRef]
- Mercuri, A.; Duggin, J.; Grant, C. The use of saline mine water and municipal wastes to establish plantations on rehabilitated open-cut coal mines, Upper Hunter Valley NSW, Australia. For. Ecol. Manag. 2005, 204, 195–207. [Google Scholar] [CrossRef]
- Çiçek, T.; Cöcen, İ.; Engin, V.T.; Cengizler, H. An Efficient Process for Recovery of Fine Coal from Tailings of Coal Washing Plants. Energy Sources Part A Recover. Util. Environ. Eff. 2008, 30, 1716–1728. [Google Scholar] [CrossRef]
- Ryu, C.; Finney, K.; Sharifi, V.N.; Swithenbank, J. Pelletised fuel production from coal tailings and spent mushroom compost—Part I: Identification of pelletisation parameters. Fuel Process. Technol. 2008, 89, 269–275. [Google Scholar] [CrossRef]
- Kirkham, M. Field Capacity, Wilting Point, Available Water, and the Nonlimiting Water Range. In Principles of Soil and Plant Water Relations; Elsevier: Amsterdam, The Netherlands, 2014; pp. 153–170. [Google Scholar]
- Arya, L.M.; Paris, J.F. A Physicoempirical Model to Predict the Soil Moisture Characteristic from Particle-Size Distribution and Bulk Density Data. Soil Sci. Soc. Am. J. 1981, 45, 1023–1030. [Google Scholar] [CrossRef]
- Chang, C.-C.; Cheng, D.-H.; Qiao, X.-Y. Improving estimation of pore size distribution to predict the soil water retention curve from its particle size distribution. Geoderma 2019, 340, 206–212. [Google Scholar] [CrossRef]
- Haverkamp, R.; Parlange, J.-Y. Predicting the water-retention curve from particle-size distribution. Soil Sci. 1986, 142, 325–339. [Google Scholar] [CrossRef]
- Meskini-Vishkaee, F.; Mohammadi, M.H.; Vanclooster, M. Predicting the soil moisture retention curve, from soil particle size distribution and bulk density data using a packing density scaling factor. Hydrol. Earth Syst. Sci. 2014, 18, 4053–4063. [Google Scholar] [CrossRef][Green Version]
- Mohammadi, M.; Meskini-Vishkaee, F. Predicting Soil Moisture Characteristic Curves from Continuous Particle-Size Distribution Data. Pedosphere 2013, 23, 70–80. [Google Scholar] [CrossRef]
- Mohammadi, M.H.; Vanclooster, M. Predicting the Soil Moisture Characteristic Curve from Particle Size Distribution with a Simple Conceptual Model. Vadose Zone J. 2011, 10, 594–602. [Google Scholar] [CrossRef]
- Chang, C.-C.; Cheng, D.-H. Predicting the soil water retention curve from the particle size distribution based on a pore space geometry containing slit-shaped spaces. Hydrol. Earth Syst. Sci. 2018, 22, 4621–4632. [Google Scholar] [CrossRef]
- Romero, E.; Della Vecchia, G.; Jommi, C. An insight into the water retention properties of compacted clayey soils. Géotechnique 2011, 61, 313–328. [Google Scholar] [CrossRef]
- Romero, E.; Simms, P.H. Microstructure Investigation in Unsaturated Soils: A Review with Special Attention to Contribution of Mercury Intrusion Porosimetry and Environmental Scanning Electron Microscopy. Geotech. Geol. Eng. 2008, 26, 705–727. [Google Scholar] [CrossRef]
- Zhuang, J.; Jin, Y.; Miyazaki, T. Estimating water retention characteristic from soil particle-size distribution using a non-similar media concept. Soil Sci. 2001, 166, 308–321. [Google Scholar] [CrossRef]
- Fredlund, M.; Wilson, G.W.; Fredlund, D.G. Use of the grain-size distribution for estimation of the soil-water characteristic curve. Can. Geotech. J. 2002, 39, 1103–1117. [Google Scholar] [CrossRef]
- Hamamoto, S.; Moldrup, P.; Kawamoto, K.; De Jonge, L.W.; Schjønning, P.; Komatsu, T. Two-Region Extended Archie’s Law Model for Soil Air Permeability and Gas Diffusivity. Soil Sci. Soc. Am. J. 2011, 75, 795–806. [Google Scholar] [CrossRef]
- Sakaki, T.; Komatsu, M.; Takahashi, M. Rules-of-Thumb for Predicting Air-Entry Value of Disturbed Sands from Particle Size. Soil Sci. Soc. Am. J. 2014, 78, 454–464. [Google Scholar] [CrossRef]
- Dinger, D.R.; Funk, J.E. Particle-Packing Phenomena and Their Application in Materials Processing. MRS Bull. 1997, 22, 19–23. [Google Scholar] [CrossRef]
- Yu, A.; Standish, N. An analytical—Parametric theory of the random packing of particles. Powder Technol. 1988, 55, 171–186. [Google Scholar] [CrossRef]
- Liu, Z.-R.; Ye, W.-M.; Zhang, Z.; Wang, Q.; Chen, Y.-G.; Cui, Y.-J. A nonlinear particle packing model for multi-sized granular soils. Constr. Build. Mater. 2019, 221, 274–282. [Google Scholar] [CrossRef]
- Schmidt, J.; Parteli, E.J.; Uhlmann, N.; Wörlein, N.; Wirth, K.-E.; Pöschel, T.; Peukert, W. Packings of micron-sized spherical particles—Insights from bulk density determination, X-ray microtomography and discrete element simulations. Adv. Powder Technol. 2020, 31, 2293–2304. [Google Scholar] [CrossRef]
- Prior, J.M.; Almeida, I.; Loureiro, J.M. Prediction of the packing porosity of mixtures of spherical and non-spherical particles with a geometric model. Powder Technol. 2013, 249, 482–496. [Google Scholar] [CrossRef]
- Li, G.-Y.; Zhan, L.-T.; Hu, Z.; Chen, Y.-M. Effects of particle gradation and geometry on the pore characteristics and water retention curves of granular soils: A combined DEM and PNM investigation. Granul. Matter 2021, 23, 1–16. [Google Scholar] [CrossRef]
- Zhou, Z.-Y.; Zou, R.-P.; Pinson, D.; Yu, A.-B. Dynamic Simulation of the Packing of Ellipsoidal Particles. Ind. Eng. Chem. Res. 2011, 50, 9787–9798. [Google Scholar] [CrossRef]
- Rodriguez, J.M. Importance of the Particle Shape on Mechanical Properties of Soil Materials; Luleå University of Technology: Luleå, Sweden, 2013. [Google Scholar]
- Dodds, J. Particle Shape and Stiffness—Effects on Soil Behavior; Georgia Institute of Technology: Atlanta, GA, USA, 2003; Available online: https://smartech.gatech.edu/bitstream/handle/1853/8063/Dodds_Jake_S_200405.pdf (accessed on 6 July 2021).
- Veghte, D.P.; Freedman, M.A. Facile Method for Determining the Aspect Ratios of Mineral Dust Aerosol by Electron Microscopy. Aerosol Sci. Technol. 2014, 48, 715–724. [Google Scholar] [CrossRef]
- Anishchik, S.; Medvedev, N.N. Three-Dimensional Apollonian Packing as a Model for Dense Granular Systems. Phys. Rev. Lett. 1995, 75, 4314–4317. [Google Scholar] [CrossRef]
- Jańczuk, B.; Zdziennicka, A. A study on the components of surface free energy of quartz from contact angle measurements. J. Mater. Sci. 1994, 29, 3559–3564. [Google Scholar] [CrossRef]
- Mazurek, A.K.; Pogorzelski, S.J.; Boniewicz-Szmyt, K. Adsorption of natural surfactants present in sea waters at surfaces of minerals: Contact angle measurements. Oceanologia 2009, 51, 377–403. [Google Scholar] [CrossRef]
- Vidler, A.; Buzzi, O.; Fityus, S. The Significance of Hydrophobicity for the Water Retention Properties of Sand and Coal. Appl. Sci. 2021, 11, 5966. [Google Scholar] [CrossRef]
- Gutierrez-Rodriguez, J.; Purcell, R.; Aplan, F. Estimating the hydrophobicity of coal. Colloids Surf. 1984, 12, 1–25. [Google Scholar] [CrossRef]
- Kaji, R.; Muranaka, Y.; Miyadera, H.; Hishinuma, Y. Effect of electrolyte on the rheological properties of coal-water mixtures. AIChE J. 1987, 33, 11–18. [Google Scholar] [CrossRef]
- Wang, N.; Sasaki, M.; Yoshida, T.; Kotanigawa, T. Estimation of coal hydrophilicity by flow microcalorimetry. Colloids Surf. A Physicochem. Eng. Asp. 1998, 135, 11–18. [Google Scholar] [CrossRef]
- Arnold, B.; Aplan, F. The hydrophobicity of coal macerals. Fuel 1989, 68, 651–658. [Google Scholar] [CrossRef]
- Parekh, B.K.; Aplan, F.F. The critical surface tension of wetting of coal. In Recent Developments in Separation Science: Volume 4; CRC Press: West Palm Beach, FL, USA, 1978; pp. 107–113. [Google Scholar]
- Zhou, A.-N. A contact angle-dependent hysteresis model for soil–water retention behaviour. Comput. Geotech. 2013, 49, 36–42. [Google Scholar] [CrossRef]
- Rafraf, S.; Guellouz, L.; Guiras, H.; Bouhlila, R. A New Model Using Dynamic Contact Angle to Predict Hysteretic Soil Water Retention Curve. Soil Sci. Soc. Am. J. 2016, 80, 1433–1442. [Google Scholar] [CrossRef]
- Azizi, A.; Jommi, C.; Musso, G. A water retention model accounting for the hysteresis induced by hydraulic and mechanical wetting-drying cycles. Comput. Geotech. 2017, 87, 86–98. [Google Scholar] [CrossRef]
- Vidler, A.; Buzzi, O.; Fityus, S. Effect of coal on mine tailings’ water permeability and water retention. E3S Web Conf. 2020, 195, 03004. [Google Scholar] [CrossRef]
- Zbik, M. Nanomorphology of Kaolinites: Comparative SEM and AFM Studies. Clays Clay Miner. 1998, 46, 153–160. [Google Scholar] [CrossRef]
- Nadeau, P.H. Relationships between the mean area, volume and thickness for dispersed particles of kaolinites and micaceous clays and their application to surface area and ion exchange properties. Clay Miner. 1987, 22, 351–356. [Google Scholar] [CrossRef]
- Negri, S.; Raimondo, E.; D’Amico, M.E.; Stanchi, S.; Basile, A.; Bonifacio, E. Loess-derived polygenetic soils of North-Western Italy: A deep characterization of particle size, shape and color to draw insights about the past. Catena 2021, 196, 104892. [Google Scholar] [CrossRef]
- Wei, T.; Fan, W.; Yu, N.; Wei, Y.-N. Three-dimensional microstructure characterization of loess based on a serial sectioning technique. Eng. Geol. 2019, 261, 105265. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, F.; Ma, F.; Wang, M.; Bai, X.; Zheng, Y.; Yin, H.; Zhang, G. Collapsibility, composition, and microstructure of loess in China. Can. Geotech. J. 2016, 53, 673–686. [Google Scholar] [CrossRef]
- Lagarias, J.C.; Mallows, C.L.; Wilks, A.R. Beyond the Descartes Circle Theorem. Am. Math. Mon. 2002, 109, 338–361. [Google Scholar] [CrossRef][Green Version]
- Kasner, E.; Supnick, F. The Apollonian Packing of Circles. Proc. Natl. Acad. Sci. USA 1943, 29, 378–384. [Google Scholar] [CrossRef]
- Graham, R.L.; Lagarias, J.C.; Mallows, C.L.; Wilks, A.R.; Yan, C.H. Apollonian Circle Packings: Geometry and Group Theory I. The Apollonian Group. Discret. Comput. Geom. 2005, 34, 547–585. [Google Scholar] [CrossRef]
- Bourke, P. An introduction to the Apollonian fractal. Comput. Graph. 2006, 30, 134–136. [Google Scholar] [CrossRef]
- Scott, G.D.; Kilgour, D.M. The density of random close packing of spheres. J. Phys. D Appl. Phys. 1969, 2, 863–866. [Google Scholar] [CrossRef]
- Shen, C.; Liu, S.; Xu, S.; Wang, L. Rapid estimation of maximum and minimum void ratios of granular soils. Acta Geotech. 2019, 14, 991–1001. [Google Scholar] [CrossRef]
- Aubertin, M.; Ricard, J.-F.; Chapuis, R.P. A predictive model for the water retention curve: Application to tailings from hard-rock mines. Can. Geotech. J. 1998, 35, 55–69. [Google Scholar] [CrossRef]
- Aubertin, M. Évaluation en Laboratoire de Barrières Sèches Construites à Partir de Résidus Miniers; MEND: Ottawa, ON, Canada, 1995. [Google Scholar]
- Li, J.; Lu, Z.; Guo, L.; Zhang, L. Experimental study on soil-water characteristic curve for silty clay with desiccation cracks. Eng. Geol. 2017, 218, 70–76. [Google Scholar] [CrossRef]
- Fredlund, M.D.; Fredlund, D.; Wilson, G. Prediction of the Soil-Water Characteristic Curve from Grain-Size Distribution and Volume-Mass Properties. In Proceedings of the 3rd Brazilian Symposium on Unsaturated Soils, Rio de Janeiro, Brazil, 22–25 April 1997. [Google Scholar]
- Nemes, A.; Schaap, M.; Leij, F.; Wösten, J. Description of the unsaturated soil hydraulic database UNSODA version 2.0. J. Hydrol. 2001, 251, 151–162. [Google Scholar] [CrossRef]
- Liu, X.; Buzzi, O.; Yuan, S.; Mendes, J.; Fityus, S. Multi-scale characterization of retention and shrinkage behaviour of four Australian clayey soils. Can. Geotech. J. 2016, 53, 854–870. [Google Scholar] [CrossRef]
- Karas, J.; Pugmire, R.J.; Woolfenden, W.R.; Grant, D.M.; Blair, S. Comparison of physical and chemical properties of maceral groups separated by density dradient centrifugation. Int. J. Coal Geol. 1985, 5, 315–338. [Google Scholar] [CrossRef]
- Drelich, J. Guidelines to measurements of reproducible contact angles using a sessile-drop technique. Surf. Innov. 2013, 1, 248–254. [Google Scholar] [CrossRef]
- Bachmann, J.; Horton, R.; van der Ploeg, R.R.; Woche, S. Modified sessile drop method for assessing initial soil-water contact angle of sandy soil. Soil Sci. Soc. Am. J. 2000, 64, 564–567. [Google Scholar] [CrossRef]
- Das, B.M. 8.5 Standard one-dimensional consolidation test and interpretation. In Advanced Soil Mechanics, 4th ed.; CRC Press: Boca Raton, FL, USA, 2013; pp. 338–346. [Google Scholar]
- Mendes, J.; Buzzi, O. Performance of the University of Newcastle high capacity tensiometers. In Proceedings of the 6th International Conference on Unsaturated Soils, Sydney, Australia, 2–5 July 2014; Volume 2, pp. 1611–1616. [Google Scholar]
- Liu, X.; Buzzi, O. Use of Hand-Spray Plaster as a Coating for Soil Bulk Volume Measurement. Geotech. Test. J. 2014, 37. [Google Scholar] [CrossRef]
- Aubertin, M.; Mbonimpa, M.; Bussière, B.; Chapuis, R.P. A model to predict the water retention curve from basic geotechnical properties. Can. Geotech. J. 2003, 40, 1104–1122. [Google Scholar] [CrossRef]
- Pollacco, J.; Fernández-Gálvez, J.; Carrick, S. Improved prediction of water retention curves for fine texture soils using an intergranular mixing particle size distribution model. J. Hydrol. 2020, 584, 124597. [Google Scholar] [CrossRef]





| Material | Gs | Liquid Limit | Plastic Limit | Receding CA (°) |
|---|---|---|---|---|
| BT2 topsoil | 2.63 | 0.462 | 0.372 | 3 |
| M1 tailings | 1.96 | 0.497 | 0.353 | 25 |
| M1 topsoil | 2.66 | 0.274 | 0.191 | 6 |
| PD tailings | 2.22 | 0.482 | 0.208 | 21 |
| M1 coal particles | - * | - * | - * | 47 |
| M1 mineral particles | - * | - * | - * | 4 |
| PD coal particles | - * | - * | - * | 44 |
| PD mineral particles | - * | - * | - * | 15 |
| Model | Input Parameters | Equation Related to Volumetric Water Content | Equation for Suction or Suction Head | Outputs | Source |
|---|---|---|---|---|---|
| Proposed | Sand, silt and clay fraction, θs, GSD | A PSD and its theoretical WRC | N/A | ||
| MV | e, θs, GSD | Volumetric water content and suction head for each GSD bin | [16] | ||
| AP | e, Gs, α, GSD | Volumetric water content and suction head for each GSD bin | [11] | ||
| CCQ | Clay fraction, β, θs, GSD | Volumetric water content and suction head for a range of GSD bins | [12] | ||
| NSMC | e, Gs, θs, GSD | Volumetric water content and suction head for pores between an arbitrary particle size are water filled | [20] | ||
| MK | D10, D60, ac, LL, Gs, m, e, λ | N/A | Saturation degree at an arbitrary suction | [70] | |
| IMP | θs, ξ1, p, β1, β2, ψmax, θr_max, α1, α2, λ, GSD | Volumetric water content and suction for each GSD bin | [71] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vidler, A.; Buzzi, O.; Fityus, S. A Simple Water Retention Model Based on Grain Size Distribution. Appl. Sci. 2021, 11, 9452. https://doi.org/10.3390/app11209452
Vidler A, Buzzi O, Fityus S. A Simple Water Retention Model Based on Grain Size Distribution. Applied Sciences. 2021; 11(20):9452. https://doi.org/10.3390/app11209452
Chicago/Turabian StyleVidler, Andrew, Olivier Buzzi, and Stephen Fityus. 2021. "A Simple Water Retention Model Based on Grain Size Distribution" Applied Sciences 11, no. 20: 9452. https://doi.org/10.3390/app11209452
APA StyleVidler, A., Buzzi, O., & Fityus, S. (2021). A Simple Water Retention Model Based on Grain Size Distribution. Applied Sciences, 11(20), 9452. https://doi.org/10.3390/app11209452







