Abstract
The thin wobble motors that are required to hold rating shafts employ an electropermanent magnet. This turns the holding force on and off by applying a momentary electrical pulse. To design the magnet devices without the need for finite element analyses, a theoretical force model is necessary for predicting the attractive force. In this paper, first, a force model is derived by estimating the permeance around the air gap. A magnetic circuit is constructed, employing a relatively simple method to build the model in clouding leakage flux. Thus, the basic structure and driving principle are also presented. Next, an analytical force model is constructed on the basis of distribution parameter analysis between the stator and the rotating shaft. The design of the electromagnet core and the control method are presented. Finally, a prototype model of the motor that is 30 mm in diameter and 7 mm in thick is fabricated. The two models are verified by comparing the results of FEM with the results of the experiments. They can properly predict the attractive force, so the thin wobble motor with holding force can be applied in portable electric equipment.
1. Introduction
Electromagnetic actuators, which have many advantages, including their small size, light weight, high precision, high accuracy, and high efficiency, have been widely used as rotary driving motors in various fields such as industrial machinery, medicine, human care device, electronic parts assembly, military equipment and mobile robots. These motors are manufactured depending on the target application in various ways. For example, new motors shapes have been developed using physical and chemical phenomena such as electromagnetic force, smart polymers, shape-memory alloy (SMA), electrostatic force, etc. Some of the materials used to drive these motors are difficult to control, and, therefore, there are limitations to their use. For this reason, we chose electromagnetically driven motors that are easy to manufacture and control and can easily calculate the generated force. However, these motors require a reduction gear device to increase their driving torque. The added reduction gear equipment increases the total volume of the driving motor, making it difficult to drive or install. In addition, it may cause mechanical backlash, added friction, or assembly errors, which may further occur to malfunctions when motor is operated. To solve these problems, there have been a number of research and development efforts aiming to increase torque through the application of various types of reduction gear device [1,2]. Several new types of stepping motors have been developed, such as a wobble motor [3,4,5,6]. In this research, we selected a wobble motor because it is simple structure, with an eccentric structure, and the torque generated per unit volume is very high due to the gear ratio while it also has the advantage of a precise control [7,8,9]. However, existing wobble motors have the main disadvantage that they cannot fix a rotating shaft while the shaft is halted. To fix the shaft, we introduce a new type of wobble actuator with an electropermanent magnet (EPM). It comprises semi-hard (Alnico 5) and neodymium (NdFeB) magnets, and it can be used to fix the rotating shaft.
In this paper, we introduce the two theoretical force models for application with portable electric devices and fabricate a thin electromagnetic wobble motor that is 50 mm in diameter and 7 mm thick including the EPM device. First, it is necessary to predict the magnetic force generated by the magnets of the EPM device. The most accurate method predicting force is used by commercial finite element method software. FEM is one of the ways to solve problems using numerical approximation for problems that are difficult to obtain an accurate theoretical interpretation. In addition, FEM has the advantage of being compatible with Auto CAD or other design programs, and accuracy of the model analysis and user convenience are very high, and high-quality analysis is possible even if there is a lack of professional knowledge about FEM. On the other hand, it will take several hours to obtain the precise analysis of the complex model and variables in the model. However, this comes with the problem of having to perform numerous iterations in the initial design step. On the other hand, a more systematic method is magnetic circuit analysis. An EPM device with two magnets is expressed as a model in which a magnetic flux source and an internal reluctance are connected in parallel. The magnetic flux paths, including the reluctance of the core of the magnetic material and the reluctance in the air gap, are shown as an electric circuit. The method for calculating the magnetic force in a magnetic circuit is similar to calculate the current in an electric circuit and is very simple. Since the fringing effect and the leakage flux around the air gap are not considered, the results of magnetic circuit analysis led to a considerably large degree of error. This is because it is difficult to accurately include them in magnetic circuits. Therefore, we introduce a theoretical force method into the initial design for use in the magnetic circuit. In addition, we design an EPM device including magnets with a flat plate and a constant air gap, and propose a simple 3D model for the leakage flux and fringing effect around the gap. The paths of magnetic flux are modeled using a simplified method consisting of several arcs, straight lines, and a mean flux line. Additionally, we introduce the schematic of the EPM device to validate the proposed theoretical force model, and the basic principle and structure, are presented in a straightforward manner. Its effectiveness is confirmed on the basis of a comparison with the results of FEM analysis, and experiments carried out using a prototype. Second, in order to analyze the characteristics existing between the electromagnet core and the rotating shaft, it is necessary to predict the magnetic flux density and magnetic force when changing the air gap. To this end, we introduce a distribution parameter method in order to propose a theoretical force model. This method was used to calculate the gap by mapping the air gap, which does not have a constant structure, onto the Cartesian coordinates. We also present a schematic of a thin wobble motor in order to validate the proposed force model, as well as the optimization of core shape, basic driving principle, basic structure and control method of the motor. Finally, the experimental results are presented for the EPM device and a thin wobble motor.
2. Driving Principle and Structure
2.1. Driving Principle and Structure of the Wobble Motor
Figure 1 shows the basic working principle and structure of the wobble motor, which comprises of cylindrical stator A and columnar rotating shaft rotor B. The rolling point of Figure 1a is in contact with the stator A and the rotor B. , , and denote in the radius of stator A, the radius of a rotor B, the central point of rotor B, and central point of stator A, respectively. The primary feature of the wobble motor is that rotor B rolls along stator A’s inner surface as shown in Figure 1b. If the input current is supplied in a clockwise direction in a continuous manner, the force will be generated from the input current. The attractive force pulls the rotor, and the rotor rolls along the inner of the stator via the generated attractive force. The driving direction of stator A is in the opposite direction of rolling direction of rotor B [10,11,12,13,14,15].
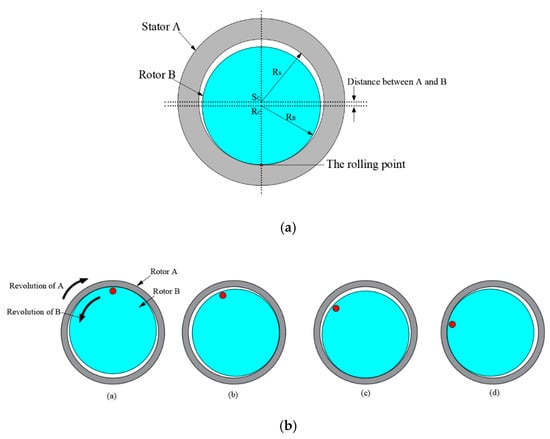
Figure 1.
Driving principle of a wobble motor: (a) Schematic of a wobble motor; (b) Driving principle.
2.2. Driving Principle and Structure of the EPM
The EPM composes of two magnetic materials, NdFeB magnet and another Alnico5 magnet; a coil is wrapped around these, as shown in Figure 2. The basic principle driving of the EPM was showed using the MagNet 7.0 electromagnetic analysis software from Mentor. If the magnetization directions of the two magnets are oppositely combined, the magnetic flux only circulates inside connected iron as shown in Figure 2a. After a switching current pulse of the opposite polarity applied to Alinico5, the magnetization directions of the two magnets were the same, and the EPM generated an external magnetic flux as shown in Figure 2b. The magnetization direction of the NdFeB material is unchanged because it has high coercivity. In ferromagnetic materials, the phenomenon of magnetic hysteresis occurs. J.A. Ewing coined the term “hysteresis” to describe his observation that the magnetic induction in a metal behind the applied current, and he also demonstrated that the molecules of a ferromagnetic material acted as reversible permanent magnets [16]. The normal coercivity of Alnico 5 is approximately 50 kA/m, and the remnant flux density is approximately 1.2 T. The normal coercivity of NdFeB is approximately 1000 kA/m, and the remnant flux density is approximately 1.2~1.3 T [17].
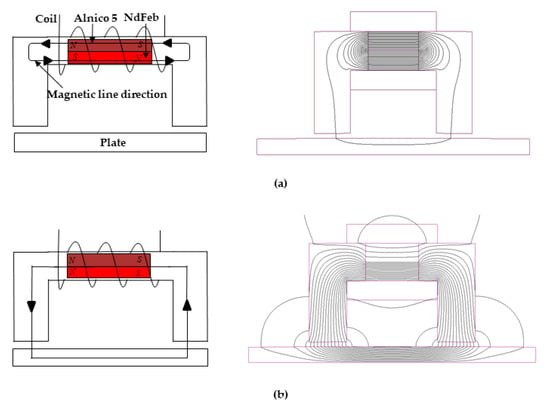
Figure 2.
Basic principle driving an electropermanent magnet: (a) In the no current state, the two magnets are oppositely polarized; (b) In the switching current state, the two magnetic magnets are polarized in the same direction.
When a switching current is applied to the coil wound, the magnetization direction of the Alnico 5 magnet changes, and the external magnetic force generates attractive force.
3. Derivation of Theoretical Force Model
3.1. Theoretical Force Analysis of the EPM
Figure 3 shows a full schematic of the EPM device for holding the rotating shaft of the wobble motor. Alnico 5 and NdFeB magnets are described as square magnets in the schematic, but the two magnets used in the theoretical analysis and the experiment were replaced with cylindrical magnets. To predict the attractive force, first, the structure is assumed to be a simple structure with a constant gap, and a core that contains two permanent magnets. Additionally, we assume that the rotating shaft is replaced with the plate. Second, in order to simplify the calculations for magnetic flux density, including the leakage flux, we simplified the path through which the leakage flux flows. Additionally, the fringing flux was assumed to be the leakage flux, and the path of flux was consisted as a combination of arcs and straight line, as shown in Figure 4a [18]. The fringing fluxes were considered a kind of leakage flux. It was also assumed that the paths detouring on the top outside of the surrounding air gap were connected in the quadrant with a straight line and the length of the air gap [19]. Figure 4b shows a consideration of the mean leakage flux line. The specifications of the electromagnetic elements in use and their parameters are summarized in Table 1.
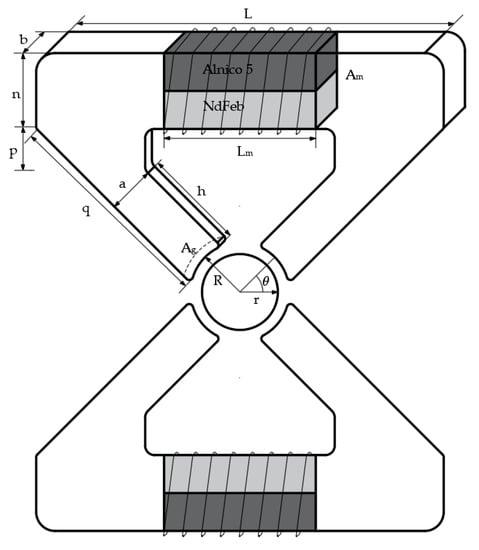
Figure 3.
Schematic of the switchable eletropermanent magnet construction.
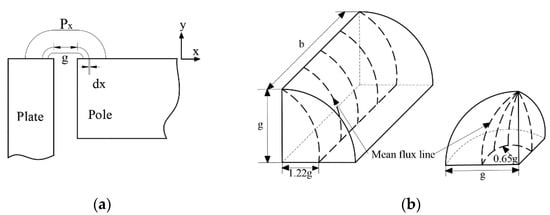
Figure 4.
Paths model for leakage flux: (a) Paths for the leaked flux; (b) Mean length of flux path.

Table 1.
Parameters of the electropermanent magnet device.
For the leakage flux paths of , as shown in Figure 4a, the length of the magnetic flux path is equal to , which is the sum of the lengths of two quadrant arcs of radius and the length of the gap. The permeance in the path is as follows:
The permeance of the total leakage flux can be obtained by integrating Equation (1).
If the core and the plate have a constant air gap, as shown in Figure 5a, it is assumed that the leakage flux paths diverting to the outside of the gap are connected to two quadrants of the same magnetic flux in a straight line along the length of the air gap. Each leakage flux path indicated by a line has a reluctance, and all of them in the magnetic circuit are connected in parallel, expressing it as shown in Figure 5b. Therefore, it is possible to use a permeance that has an inverse relationship with a reluctance.
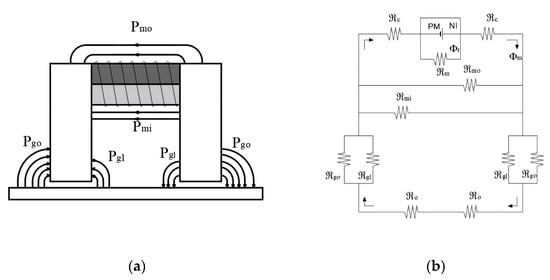
Figure 5.
Analysis model consisting of an electropermanent magnet: (a) Flux leakage of the electropermanent magnet; (b) Magnetic circuit.
In Figure 5b, the reluctance and in the iron are ignored. Therefore, when the permeances of the leakage flux path are and , respectively, they can be expressed as reciprocal reluctances and , , and are the source of the magnet, the magnetic flux of the magnetic flux passing through the air gap. To more accurately consider the leakage flux generated in the gap, it is regarded as a geometry as shown in Figure 6. The permeance of each of the flux paths through the gap can be expressed as permeance and . Permeance is . The mean length of the flux path of permeance can be considered to be equal to the length of a line drawn midway between the radius and a quarter of circumference as shown in Figure 6b. Permeance and with a quadrant of the cylindrical volume are and , respectively.
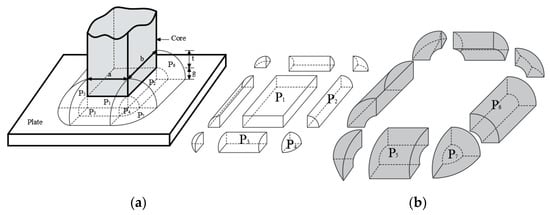
Figure 6.
Permeance of flux paths through the air gap: (a) Permeance of parallel to end of the core; (b) Simple-shaped volumes of permeance.
The mean length of the flux path for permeance with one eighth of the spherical volume can be approximated by considering the mean flux line to be situated 0.65 of the way between the center of the sphere and the circumference, as shown in Figure 5b. Therefore, with one-eighth of the spherical volume is . and with one-half of the half annulus are and , respectively. with one-half of the quadrant of the spherical shell is . Permeance and detouring into the air without going through the plate are and , respectively. The reciprocal of permeance is defined as reluctance. is the total reluctance; thus, all reluctance in the magnetic circuit can be calculated. To calculate the magnetic field in consideration of the leakage flux, we used Gauss’ law and a magnetic force circuit, which can be expressed as follows
where is the axial magnetic field intensity when combining two magnets, is the magnetic field density in the air gap, and is the pole-to-pole leakage flux. The axial magnetic flux densities of the Alnico 5 and NdFeb magnets are and , respectively. Finally, the generated attractive force can be obtained using the Maxwell stress tensor, which can be written as
3.2. Theoretical Force Analysis of Motor
The side view used for theoretical analysis is showed in Figure 7. An idealized model was assumed in which the end effects were neglected. The idealized model is thus similar to an idealized rotating machine. A distribution equation of the electromagnetic system can be expressed using Maxwell’s equation and Ohm’s law. The magnetic vector potential is defined as . Their solutions have previously been studied in related research areas [20,21,22,23]. Therefore, we briefly describe the theoretical analysis of the flux density of the air gap. To establish analytical solutions as a function of the air gap, variations in the r-direction are ignored, and can also be assumed, and six terms of g, h, t, p, and are air gap, the pole width, thickness of the stator, pole pitch, the permeability of air gap and the permeability of the material, respectively.
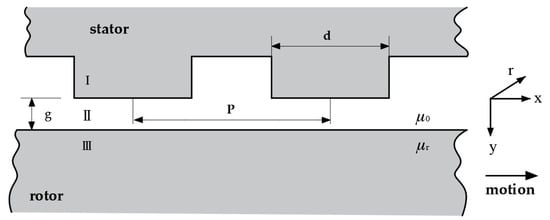
Figure 7.
Geometric model for theoretical analysis.
The governing equation of the electromagnetic phenomena in the wobble motor can be calculated as
where is the permeability of the free space, is the speed of the moving rotor (m/s), and is electrical conductivity (). is expressed from the Fourier series as
where and . and are the wave number and angular velocity, respectively.
The y-direction flux density in the air gap can be calculated using the following equation:
where and indicate x-and y-axis unit vectors, respectively, and represents the layer of the air gap.
where , and and indicate slip and a synchronous speed, respectively.
The boundary conditions are as follows:
The coefficients in Equation (8) form boundary conditions that can be solved, and the coefficients is as follows:
where .
Finally, in order to calculate the Equation (7) on the basis of the change in the air gap [24], the air gap of the wobble motor can be simplified by representing it as a rectangular coordinate system as shown in Figure 8.
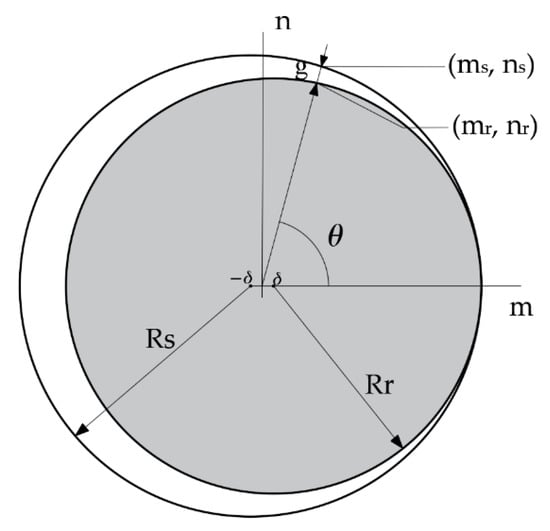
Figure 8.
Simplified geometry.
The air gap, g, between the rotor and stator as a function of is expressed and simplified. and are the radius of stator and rotor, respectively. In addition, the distance of the air gap, g, between these points on the stator and the rotor was then calculated.
where .
The magnetic flux density can be calculated by substituting the valid gap obtained from Equation (10) into Equation (9). The final magnetic force can be determined using Maxwell’s stress tensor, which can be written as
4. Validation of Theoretical Force Model
4.1. Modeling and Structure of Motor with EPM
To validate the proposed two force models, we developed a prototype based on a thin wobble motor with EPM 30 mm in diameter and 7 mm in thickness, the schematic of which is as shown in Figure 9. It was composed of a stator with an electromagnet core and coil, rotating shaft, and an EPM device. First, we decided to consider the shape of the core, as this was important for increasing the generated force, and then the core was simply optimized. The parameters of the core were , as shown in Figure 10a. To increase the magnetic force and to decrease the leak of magnetic flux, we also carried out electromagnetic field analysis, and the original material of the core was pure iron. In this FEM analysis, the magnetic flux density was obtained by exciting two cores when the rotor was momentarily in contact with the end of the stator. The optimal shape for the core in order to increase attractive force and the magnetic flux density distribution of the core were determined through FEM, as shown in Figure 10b.
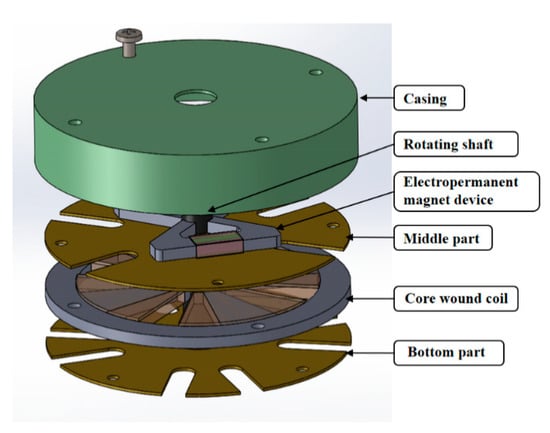
Figure 9.
Schematic of the thin wobble motor with an Electropermanent magnet.
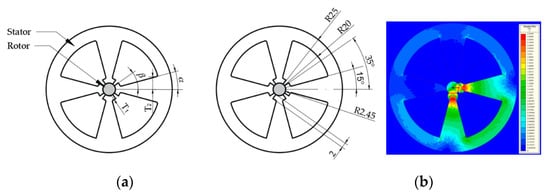
Figure 10.
Shape of the core: (a) Parameters for optimization of the core; (b) optimized core and the magnetic flux density distribution.
Second, we propose a wobble with EPM device so that the rotating shaft can be fixed without the continuous use of a power supply. Therefore, it is to be used to solve the difficulties presented by existing wobble motors, and the schematic is represented in Figure 11. 3D FEM simulation was conducted to estimate the flow of the magnetic flux of EPM, but the results of FEM was expressed in 2D as shown in Figure 11 to confirm the change of magnetic flux. The diameter and length of the two magnets used in FEM were 2 mm and 8 mm, respectively.
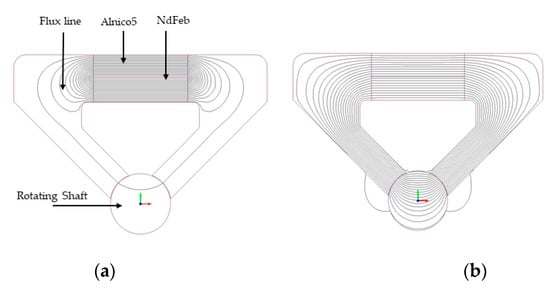
Figure 11.
Basic principle driving a proposed electropermanent manent magnet: (a) Flux path when the magnetization direction of magnets is in the opposite direction; (b) Flux path through air gap between iron and shaft.
When the magnetization directions of the two magnets are opposite, the magnetic flux flows only toward the inside as shown Figure 11a. It means that the rotating shaft in unaffected. When the current for changing the magnetization direction of the Alnico 5 magnet is applied, the magnetization direction is changed. However, when a current is applied to the coil wound, the magnetization direction of NdFeb does not change. Therefore, the magnetization direction of the two magnets is the same, and an external magnetic flux is generated as shown in Figure 11b.
4.2. Experimental System and Driving Principle
The driving method of the motor and the experimental system of driving motor are as shown in Figure 12. Current is applied to two electromagnets simultaneously, and the rotational speed of the wobble motor is controlled by the frequency of the controller. The U, V, W, and Z at four-phase from the signal controller matches with coil A, coil B, coil C, and coil D wrapped around the four-pole core. The coil is operated as follows: (coil A and coil B), (coil B and coil C), (coil C and coil D), and (coil D and coil A).
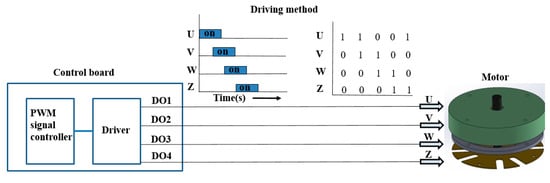
Figure 12.
The driving method of the motor and total system of driving motor.
4.3. Experiment for Theoretical Model Validation
To experimentally validate the proposed theoretical model, a prototype of a thin wobble motor with an EPM device was fabricated. Pictures of the prototype are shown in Figure 13. It has the same dimensions as the one used for FEM. The magnets used for the EPM were 2 mm in diameter, 8 mm in length, and around them was wrapped a coil with a diameter of 0.18mm for 120 turns, as shown in Figure 13b. Four electromagnetic arms of core were arranged around the wobble shaft and wrapped with a coil as shown in Figure 13c. In the experiment, a core with a thickness of 1 mm, around which a coil with a diameter of 0.16 mm was wound for 150 turns, was used to create an attractive rotating shaft. To maximize the force and minimize the iron losses, the material was changed from pure iron to electrical steel. The material selected for the electrical steel was 50PN350, characterized by Bsat = 1.62 T and an iron loss of 3.50 Watts per kilogram from Pohang Iron and Steel Company (POSCO), and the core shape was then manufacturing by Electro Discharge Machining (EDM). Additionally, pure iron (SS400) was used as the material for the rotating shaft. This had the highest electrical conductivity, high permeability, low coercive intensity, and was also easy to purchase. We fabricated a prototype of the EPM device using a Computer Numerical Control (CNC) machine. From the FEM results, it was confirmed that a change occurs when the magnetization direction of the Alnico 5 momentarily larger than 5A. To change the magnetization direction of the Alnico 5 magnet in EPM device, we used the controller of an NI cRio-9022 from NATIONAL INSTRUMENTS and a high-performance capacitor-type driver capable of momentarily applying a current of larger than 5A. The signal controller was a TMS320F28335, and the driver was expressly made for use with four-pole cores.

Figure 13.
Pictures of a thin wobble motor with EPM. (a) Parts a thin wobble motor; (b) Fabricated EPM device; (c) Core with the coil wound.
4.4. Validation Results
Figure 14 shows the predictions of the magnetic circuit model in three cases, as well as the experimental results with respect to variation in the air gap of the EPM device. The black curve shows the neglecting leakage permeance; the red curve shows the 2D leakage permeance in consideration of and , as shown Figure 6; the blue curve shows the 3D leakage permeance; and the green curve shows the 3D FEM results. When the air gap was set at 0, 0.1 mm and 0.2mm, the measured forces were 5.853 N, 1.762 N and 0.926 N, respectively. When the air gap was set at 0.1 mm, the results without considering magnetic flux and the FEM results showed considerable error. However, the error between the results in which the magnetic leakage flux was 3D and the FEM results was the 20 percent. Based on the plot, it can be seen that pole-to-pole leakage did not change the holding force when the air gap was, but the slope of the force vs. the distance curve changed significantly with the zero air gap. This is an important effect to consider when designing EPM devices, even those which operate over relatively small air gaps.
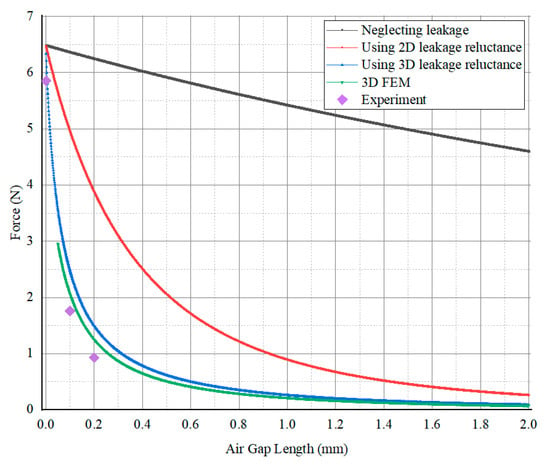
Figure 14.
Experiment results, and comparisons of the force vs. air, calculated using the mantic circuit with and without leakage flux.
Table 2 summarizes the results of FEM, the experimental results, and the theoretical model results according to the applied current. An experimental test was conducted using the method shown in Figure 12. The theoretically calculated stall torque and the stall torque generated from FEM comprise the moment when the rotating shaft moves. It was confirmed that the error between the theoretical method and the FEM analysis results was 26 percent on average, and between the experiment and the FEM analysis results was 12 percent average. As the input current to the electromagnet core was increased, the stall torque of the wobble motor also increased.

Table 2.
Comparison of stall torque according to current variation.
5. Conclusions
This paper proposed the two force models in order to theoretically calculate the generated force in a thin wobble motor with the EPM device. First, the EPM can change the holding force on and off by applying a momentary electrical pulse, and the structure and driving principle are presented. It is difficult to establish an analysis model that accurately presents the magnetic leakage fluxes, but by assuming their paths to consists of straight lines and arcs, the mean length of the flux path could be obtained. Therefore, in order to increase the accuracy of the theoretical force model of the EPM device, a method considering the leakage fluxes was proposed. Comparing the FEM results and the force calculated using the proposed method, it was confirmed that there was a reduction in the error of the force generated when considering leakage fluxes were considered. However, there were differences between the theoretical and the experimental results, because the loss of friction and assembly error of the magnets and the iron influenced the experimental measurements. Despite the assembly error, it successfully generated holding force at the rotating shaft. These results can not only be used in selecting the initial design parameters necessary for FEM analysis for the design of EPM devices, but also indicate that the proposed magnetic circuit analysis results can be used as the basis for its design. Secondly, we simply presented the optimal design of the electromagnets with respect to various parameters, as well as a partial differential equation on the basis of the distribution parameters as a function of the variation of the air gap between the stator and the rotating shaft. The theoretical force model for the generated force of the electromagnetic field using the distribution parameters was calculated by approximating the model using a linear coordinate system. We conducted experiments using a prototype motor with respect to the changing current. As shown in Table 2, it was confirmed that the theoretical method results and the FEM results were similar. Differences were observed in the experimental results owing to the loss of friction and error occurring when manufacturing the rotating shaft. However, our study shows advantages in that this method is less time consuming and systematic, because a large number of iterative analyses are not required during the initial design step. As a result, the proposed a thin motor with EPM device has great potential for commercialization as a driving part of small robots, in the medical industry, and especially in thin portable equipment in the future.
Author Contributions
FEM analysis, designed and manufactured of the motor, controller, and wrote the paper, S.Y.P.; edited and revision, analyzed the date, B.S.; investigation and validation S.Y.P. and B.S.; supervision, Y.S.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
This paper is no data.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviation
| EPM | Electropermanent Magnet |
References
- Viviani, A. Experimental and Theoretical Study of Hypocycloidal Motors with Two-Harmonic Field Windings. IEEE Trans. Power Appar. Syst. 1980, 1, 292–300. [Google Scholar]
- Hayashi, I.; Iwatsuki, N.; Shibata, J.; Matsunaga, H.; Wada, S. An Electromagnetic Cycloid Motor. J. Jpn. Soc. Precis. Eng. 1995, 61, 95–99. [Google Scholar] [CrossRef]
- Nagata, T.; Suzumori, K.; Kanda, T.; Uzuka, K.; Enomoto, I. Electro Direct-Drive Stepping Motor for Robots. In Proceedings of the IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 26 April–1 May 2004; pp. 4493–4498. [Google Scholar]
- Kimura, H.; Hirose, S.; Nakaya, K. Development of the Crown Motor. In Proceedings of the 2001 ICRA, IEEE International Conference on Robotics and Automation, Seoul, Korea, 21–26 May 2001; pp. 2442–2447. [Google Scholar]
- Okamoto, K.; Suzumori, K.; Kanda, T.; Yamada, Y. Development of Three-Chamber Micro Pneumatic Wobble Motor. Proc. Mach. Des. Tribol. Div. 2006, 295–297. [Google Scholar] [CrossRef]
- De Cristofaro, S.; Stefanini, C.; Ng Pak, N.; Susilo, E.; Carrozza, M.C.; Dario, P. Electromagnetic wobble micromotor for microrobots actuation. Sens. Actuators A Phys. 2010, 161, 234–244. [Google Scholar] [CrossRef]
- Jacobsen, S.C.; Price, R.H.; Wood, J.E.; Rytting, T.H.; Rafaelof, M. The Wobble Motor: Design, Fabrication and Testing of an Eccentric-Motion Electrostatic Microactuator. In Proceedings of the IEEE International Conference on Robotics and Automation, Scottsdale, AZ, USA, 14–19 May 1989; pp. 1536–1546. [Google Scholar]
- Suzumori, K.; Hori, K. Micro Electrostatic Wobble Motor with Toothed Electrodes. In Proceedings of the IEEE Tenth Annual International Workshop, Nagoya, Japan, 26–30 January 1997; pp. 227–232. [Google Scholar]
- Miyake, M.; Suzumori, K.; Uzuka, K. Development of a Thin Electromagnetic Wobble Motor. In Proceedings of the 2011 IEEE International Conference on Robotics and Biomimetics, Karon Beach, Phuket, Thailand, 7–11 December 2011; pp. 2523–2528. [Google Scholar]
- Jacobsen, S.C.; Price, R.H.; Wood, J.E.; Rytting, T.H.; Rafaelof, M. The Wobble Motor: An Electrostatic, Planetary-Armature, Microactuator. In Proceedings of the IEEE Micro Electro Mechanical Systems, An Investigation of Micro Structures, Sensors, Actuators, Machines and Robots, Salt Lake City, UT, USA, 20–22 February 1989. [Google Scholar]
- Jungreis, A.M.; Kelley, A.W. The axial air gap wobble motor—An appropriate topology for magnetic micromotors. In Proceedings of the Conference Record of the 1995 IEEE Industry Applications Conference Thirtieth IAS Annual Meeting, Orlando, FL, USA, 8–12 October 1995. [Google Scholar]
- Mehergancy, M.; Nagarkar, P.; Senturia, S.D.; Lang, J.H. Operation of Microfabricated Harmonic and Ordinary Side-Drive Motors. In Proceedings of the IEEE Proceedings on Micro Electro Mechanical Systems, An Investigation of Micro Structures, Sensors, Actuators, Machines and Robots, Napa Valley, CA, USA, 11–14 February 1990. [Google Scholar]
- Dhuler, V.R.; Mehregany, M.; Phillips, S.M. An experimental technique and a model for studying the operation of harmonic side-drive micromotors. IEEE Trans. Electron Devices 1993, 40, 1977–1984. [Google Scholar] [CrossRef]
- Deng, K.; Meheregany, M. Outer-Rotor Polysilicon Wobble Micromotors. In Proceedings of the IEEE Workshop on Micro Electromechanical Systems, Oiso, Japan, 25–28 January 1994. [Google Scholar]
- Furuhata, T.; Hirano, T.; Lane, L.H.; Fontana, R.E.; Fan, L.S.; Fujita, H. Outer Rotor Surface-Micromachined Wobble Micromotor. In Proceedings of the IEEE Micro Electro Mechanical Systems, Fort Lauderdale, FL, USA, 10 February 1993. [Google Scholar]
- Ewing, J.A.; Klaassen, H.G. Magnetic qualities of Iron. Philos. Trans. R. Soc. A 1893, 184, 985–1039. [Google Scholar]
- Campbell, P.; Al-Murshid, S. A model of anisotropic Alnico magnets for field Computation Magnetics. IEEE Trans. Magn. 1982, 18, 898–904. [Google Scholar] [CrossRef]
- Hanselman, D.C. Brushless Permanent Magnet Motor Design; McGraw-Hill: Cranston, RI, USA, 1994. [Google Scholar]
- Roters, H.C. Electromagnetic Devices, 1st ed.; John Wiley & Sons: New York, NY, USA, 1941. [Google Scholar]
- Yamamura, S. Theory of Linear Induction Motors, 2nd ed.; Wiley: New York, NY, USA, 1979. [Google Scholar]
- Wangsness, R.K. Electromagnetic Fields, 2nd ed.; Wiley: New York, NY, USA, 1986. [Google Scholar]
- Griffiths, D.J. Introduction to Electrodynamics, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1989. [Google Scholar]
- Nasar, S.A. Linear Motion Electric Machines; John Wiley & Sons: New York, NY, USA, 1976. [Google Scholar]
- Trimmer, W.; Jebens, R. An Operational Harmonic Electrostatic Motor. In Proceedings of the IEEE Micro Electro Mechanical Systems, An Investigation of Micro Structures, Sensors, Actuators, Machines and Robots, Salt Lake City, UT, USA, 20–22 February 1989; pp. 13–16. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).