Self-Evaporation Dynamics of Quantum Droplets in a 41K-87Rb Mixture
Abstract
1. Introduction
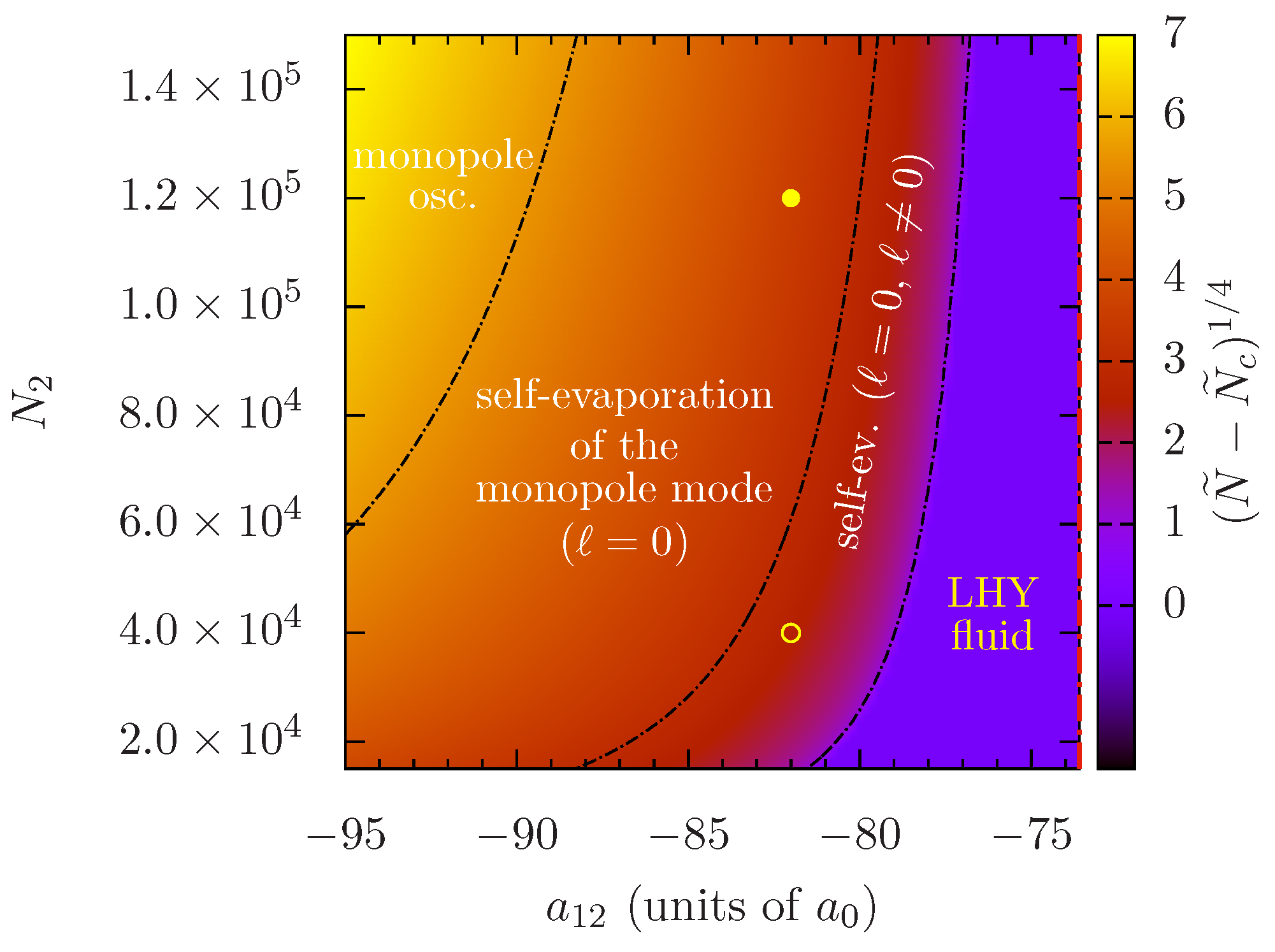
2. Self-Bound Droplets
3. Preparation of the Initial State
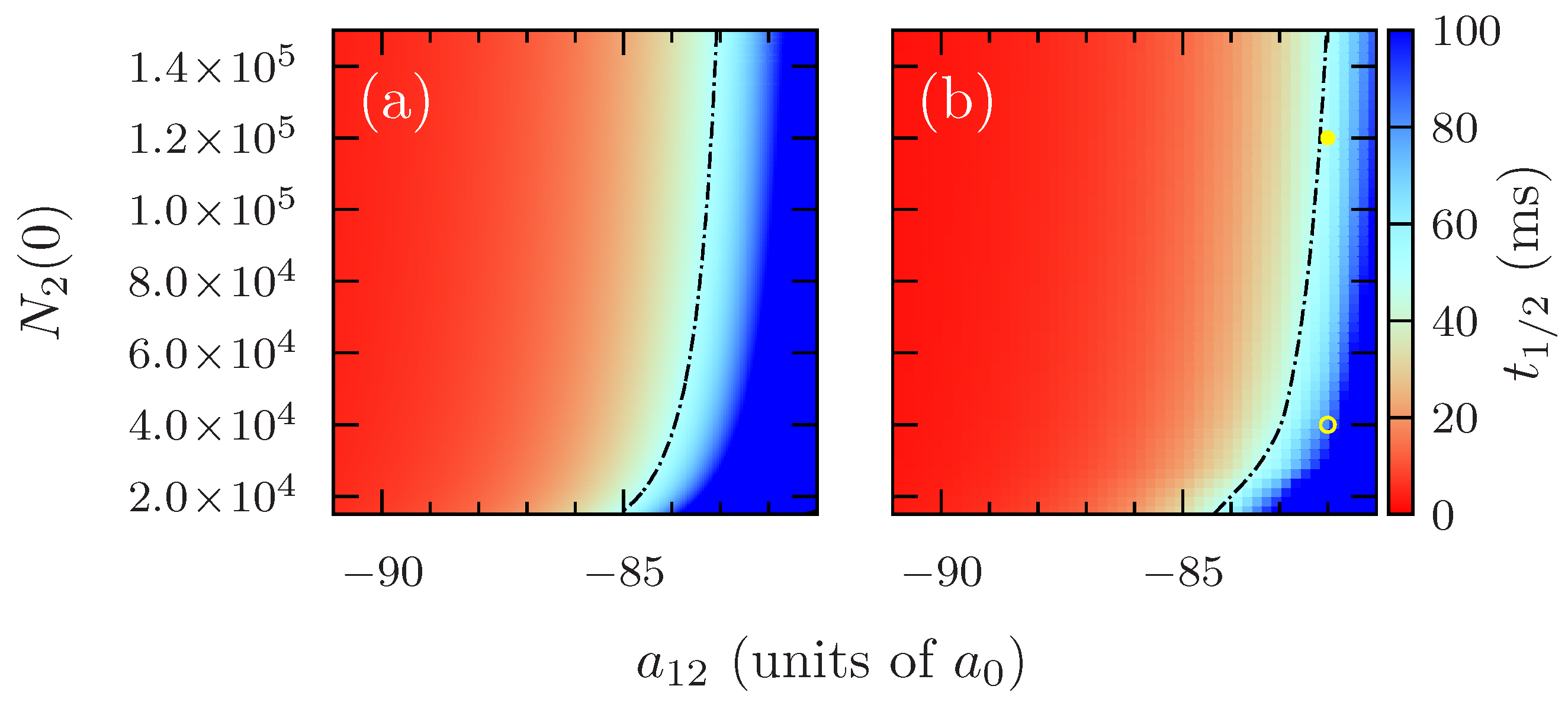
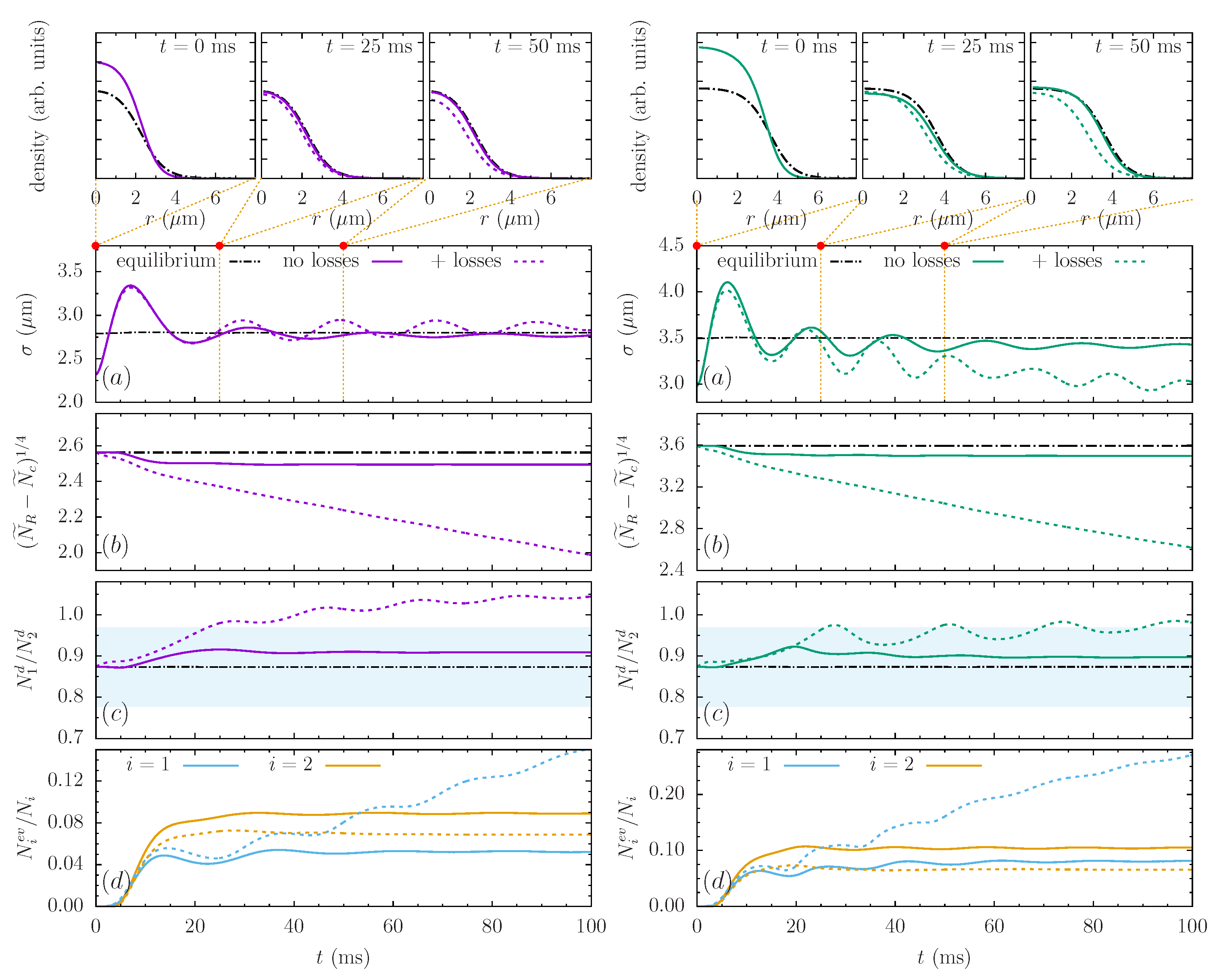
4. Dynamics
4.1. Estimate of the Droplet Lifetime
4.2. Damped Monopole Oscillations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A. Numerical Methods
References
- Petrov, D.S. Quantum Mechanical Stabilization of a Collapsing Bose-Bose Mixture. Phys. Rev. Lett. 2015, 115, 155302. [Google Scholar] [CrossRef]
- Petrov, D.S. Liquid beyond the van der Waals paradigm. Nat. Phys. 2018, 14, 211–212. [Google Scholar] [CrossRef]
- Ferrier-Barbut, I.; Pfau, T. Quantum liquids get thin. Science 2018, 359, 274–275. [Google Scholar] [CrossRef] [PubMed]
- Ferrier-Barbut, I. Ultradilute Quantum Droplets. Phys. Today 2019, 72, 46–52. [Google Scholar] [CrossRef]
- Ferrier-Barbut, I.; Kadau, H.; Schmitt, M.; Wenzel, M.; Pfau, T. Observation of Quantum Droplets in a Strongly Dipolar Bose Gas. Phys. Rev. Lett. 2016, 116, 215301. [Google Scholar] [CrossRef] [PubMed]
- Ferrier-Barbut, I.; Schmitt, M.; Wenzel, M.; Kadau, H.; Pfau, T. Liquid quantum droplets of ultracold magnetic atoms. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 214004. [Google Scholar] [CrossRef]
- Schmitt, M.; Wenzel, M.; Böttcher, F.; Ferrier-Barbut, I.; Pfau, T. Self-bound droplets of a dilute magnetic quantum liquid. Nature 2016, 539, 259. [Google Scholar] [CrossRef]
- Chomaz, L.; Baier, S.; Petter, D.; Mark, M.J.; Wächtler, F.; Santos, L.; Ferlaino, F. Quantum-Fluctuation-Driven Crossover from a Dilute Bose-Einstein Condensate to a Macrodroplet in a Dipolar Quantum Fluid. Phys. Rev. X 2016, 6, 041039. [Google Scholar] [CrossRef]
- Tanzi, L.; Lucioni, E.; Famà, F.; Catani, J.; Fioretti, A.; Gabbanini, C.; Bisset, R.N.; Santos, L.; Modugno, G. Observation of a Dipolar Quantum Gas with Metastable Supersolid Properties. Phys. Rev. Lett. 2019, 122, 130405. [Google Scholar] [CrossRef]
- Cabrera, C.R.; Tanzi, L.; Sanz, J.; Naylor, B.; Thomas, P.; Cheiney, P.; Tarruell, L. Quantum liquid droplets in a mixture of Bose-Einstein condensates. Science 2018, 359, 301–304. [Google Scholar] [CrossRef]
- Semeghini, G.; Ferioli, G.; Masi, L.; Mazzinghi, C.; Wolswijk, L.; Minardi, F.; Modugno, M.; Modugno, G.; Inguscio, M.; Fattori, M. Self-Bound Quantum Droplets of Atomic Mixtures in Free Space. Phys. Rev. Lett. 2018, 120, 235301. [Google Scholar] [CrossRef] [PubMed]
- Cheiney, P.; Cabrera, C.R.; Sanz, J.; Naylor, B.; Tanzi, L.; Tarruell, L. Bright Soliton to Quantum Droplet Transition in a Mixture of Bose-Einstein Condensates. Phys. Rev. Lett. 2018, 120, 135301. [Google Scholar] [CrossRef] [PubMed]
- Ferioli, G.; Semeghini, G.; Masi, L.; Giusti, G.; Modugno, G.; Inguscio, M.; Gallemí, A.; Recati, A.; Fattori, M. Collisions of Self-Bound Quantum Droplets. Phys. Rev. Lett. 2019, 122, 090401. [Google Scholar] [CrossRef] [PubMed]
- D’Errico, C.; Burchianti, A.; Prevedelli, M.; Salasnich, L.; Ancilotto, F.; Modugno, M.; Minardi, F.; Fort, C. Observation of quantum droplets in a heteronuclear bosonic mixture. Phys. Rev. Res. 2019, 1, 033155. [Google Scholar] [CrossRef]
- Burchianti, A.; D’Errico, C.; Prevedelli, M.; Salasnich, L.; Ancilotto, F.; Modugno, M.; Minardi, F.; Fort, C. A Dual-Species Bose-Einstein Condensate with Attractive Interspecies Interactions. Condens. Matter 2020, 5, 21. [Google Scholar] [CrossRef]
- Böttcher, F.; Schmidt, J.N.; Hertkorn, J.; Ng, K.S.H.; Graham, S.D.; Guo, M.; Langen, T.; Pfau, T. New states of matter with fine-tuned interactions: Quantum droplets and dipolar supersolids. Rep Prog Phys. 2020. [Google Scholar] [CrossRef]
- Luo, Z.; Pang, W.; Liu, B.; Li, Y.; Malomed, B.A. A new form of liquid matter: Quantum droplets. Front. Phys. 2020. [Google Scholar] [CrossRef]
- Jørgensen, N.B.; Bruun, G.M.; Arlt, J.J. Dilute Fluid Governed by Quantum Fluctuations. Phys. Rev. Lett. 2018, 121, 173403. [Google Scholar] [CrossRef]
- Minardi, F.; Ancilotto, F.; Burchianti, A.; D’Errico, C.; Fort, C.; Modugno, M. Effective expression of the Lee-Huang-Yang energy functional for heteronuclear mixtures. Phys. Rev. A 2019, 100, 063636. [Google Scholar] [CrossRef]
- Skov, T.G.; Skou, M.G.; Jørgensen, N.B.; Arlt, J.J. Observation of a Lee-Huang-Yang Fluid. arXiv 2020, arXiv:2011.02745. [Google Scholar]
- Morera, I.; Astrakharchik, G.E.; Polls, A.; Juliá-Díaz, B. Quantum droplets of bosonic mixtures in a one-dimensional optical lattice. Phys. Rev. Res. 2020, 2, 022008. [Google Scholar] [CrossRef]
- Lavoine, L.; Bourdel, T. 1D to 3D beyond-mean-field dimensional crossover in mixture quantum droplets. arXiv 2020, arXiv:2011.12394. [Google Scholar]
- Hu, H.; Wang, J.; Liu, X.J. Microscopic pairing theory of a binary Bose mixture with interspecies attractions: Bosonic BEC-BCS crossover and ultradilute low-dimensional quantum droplets. Phys. Rev. A 2020, 102, 043301. [Google Scholar] [CrossRef]
- Hu, H.; Liu, X.J. Microscopic derivation of the extended Gross-Pitaevskii equation for quantum droplets in binary Bose mixtures. Phys. Rev. A 2020, 102, 043302. [Google Scholar] [CrossRef]
- Hu, H.; Liu, X.J. Collective excitations of a spherical ultradilute quantum droplet. Phys. Rev. A 2020, 102, 053303. [Google Scholar] [CrossRef]
- Zin, P.; Pylak, M.; Gajda, M. Zero-energy modes of two-component Bose-Bose droplets. arXiv 2020, arXiv:2011.05135. [Google Scholar]
- Ota, M.; Astrakharchik, G. Beyond Lee-Huang-Yang description of self-bound Bose mixtures. SciPost Phys. 2020, 9, 020. [Google Scholar] [CrossRef]
- Ferioli, G.; Semeghini, G.; Terradas-Briansó, S.; Masi, L.; Fattori, M.; Modugno, M. Dynamical formation of quantum droplets in a 39K mixture. Phys. Rev. Res. 2020, 2, 013269. [Google Scholar] [CrossRef]
- Ancilotto, F.; Barranco, M.; Guilleumas, M.; Pi, M. Self-bound ultradilute Bose mixtures within local density approximation. Phys. Rev. A 2018, 98, 053623. [Google Scholar] [CrossRef]
- Riboli, F.; Modugno, M. Topology of the ground state of two interacting Bose-Einstein condensates. Phys. Rev. A 2002, 65, 063614. [Google Scholar] [CrossRef]
- Astrakharchik, G.E.; Malomed, B.A. Dynamics of one-dimensional quantum droplets. Phys. Rev. A 2018, 98, 013631. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Dalfovo, F.; Giorgini, S.; Pitaevskii, L.P.; Stringari, S. Theory of Bose-Einstein condensation in trapped gases. Rev. Mod. Phys. 1999, 71, 463–512. [Google Scholar] [CrossRef]
- Wächtler, F.; Santos, L. Ground-state properties and elementary excitations of quantum droplets in dipolar Bose-Einstein condensates. Phys. Rev. A 2016, 94, 043618. [Google Scholar] [CrossRef]
- Wächtler, F.; Santos, L. Quantum filaments in dipolar Bose-Einstein condensates. Phys. Rev. A 2016, 93, 061603. [Google Scholar] [CrossRef]
- Altin, P.A.; Dennis, G.R.; McDonald, G.D.; Döring, D.; Debs, J.E.; Close, J.D.; Savage, C.M.; Robins, N.P. Collapse and three-body loss in a 85Rb Bose-Einstein condensate. Phys. Rev. A 2011, 84, 033632. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; ninth dover printing, tenth gpo printing ed.; Dover: New York, NY, USA, 1964. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fort, C.; Modugno, M. Self-Evaporation Dynamics of Quantum Droplets in a 41K-87Rb Mixture. Appl. Sci. 2021, 11, 866. https://doi.org/10.3390/app11020866
Fort C, Modugno M. Self-Evaporation Dynamics of Quantum Droplets in a 41K-87Rb Mixture. Applied Sciences. 2021; 11(2):866. https://doi.org/10.3390/app11020866
Chicago/Turabian StyleFort, Chiara, and Michele Modugno. 2021. "Self-Evaporation Dynamics of Quantum Droplets in a 41K-87Rb Mixture" Applied Sciences 11, no. 2: 866. https://doi.org/10.3390/app11020866
APA StyleFort, C., & Modugno, M. (2021). Self-Evaporation Dynamics of Quantum Droplets in a 41K-87Rb Mixture. Applied Sciences, 11(2), 866. https://doi.org/10.3390/app11020866




