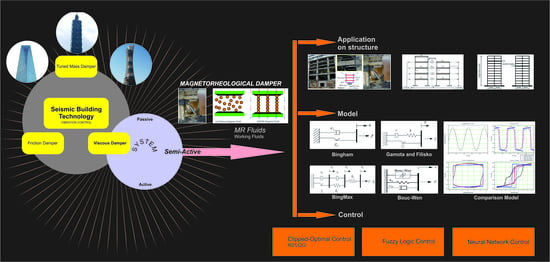
Review of Magnetorheological Damping Systems on a Seismic Building
Abstract
Featured Application
Abstract
1. Introduction
2. Types of Dampers on Structural Buildings
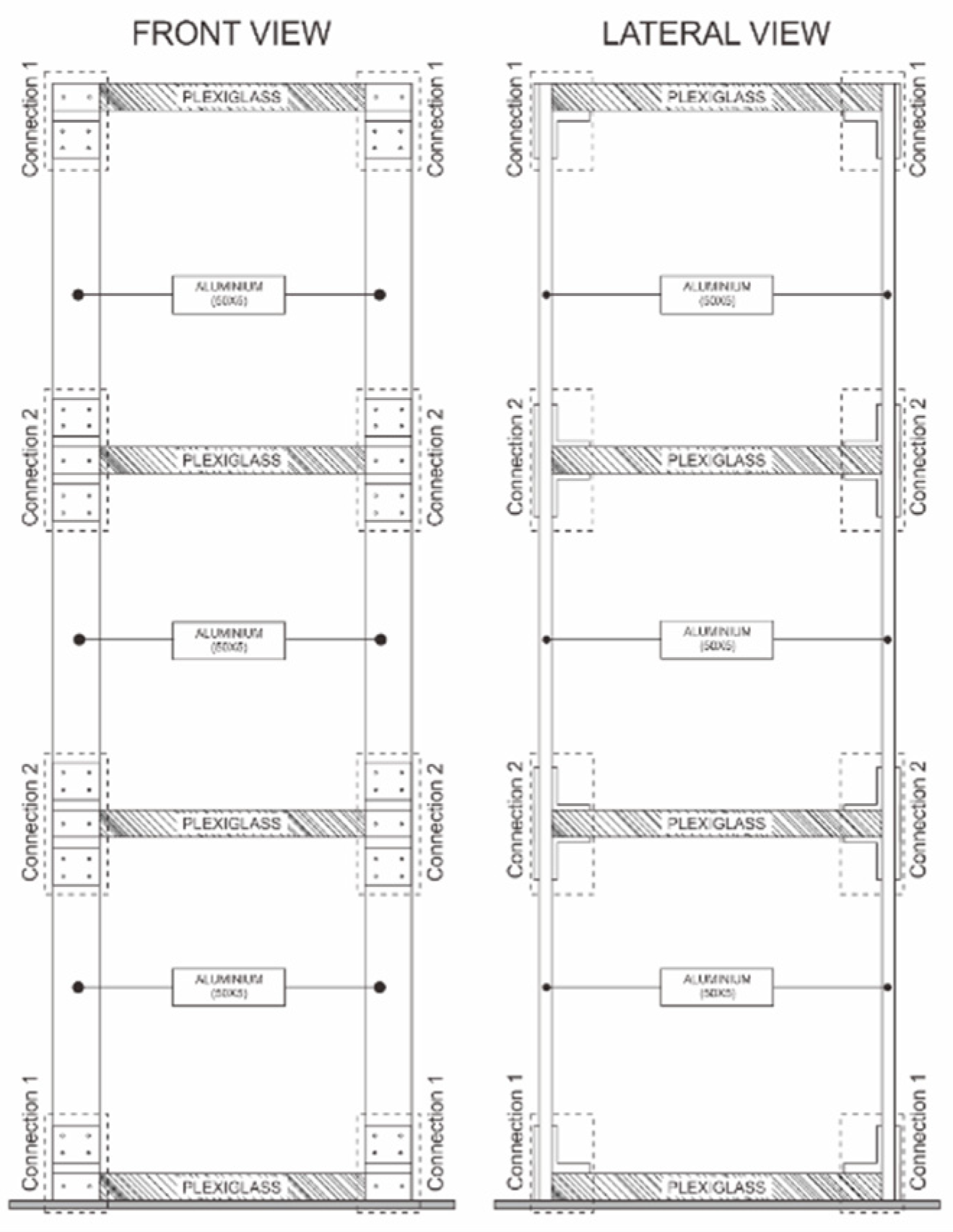
2.1. Friction Dampers
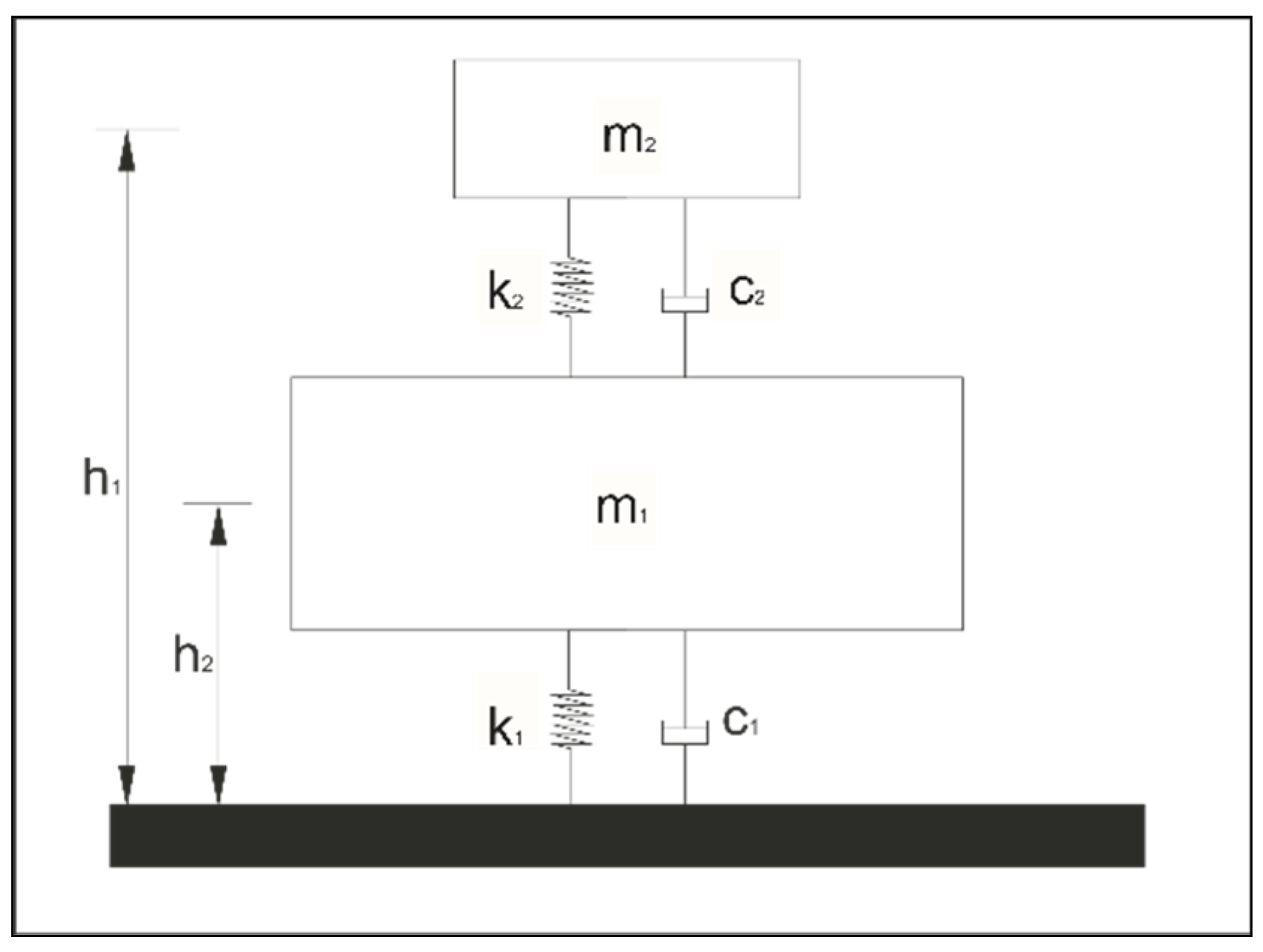
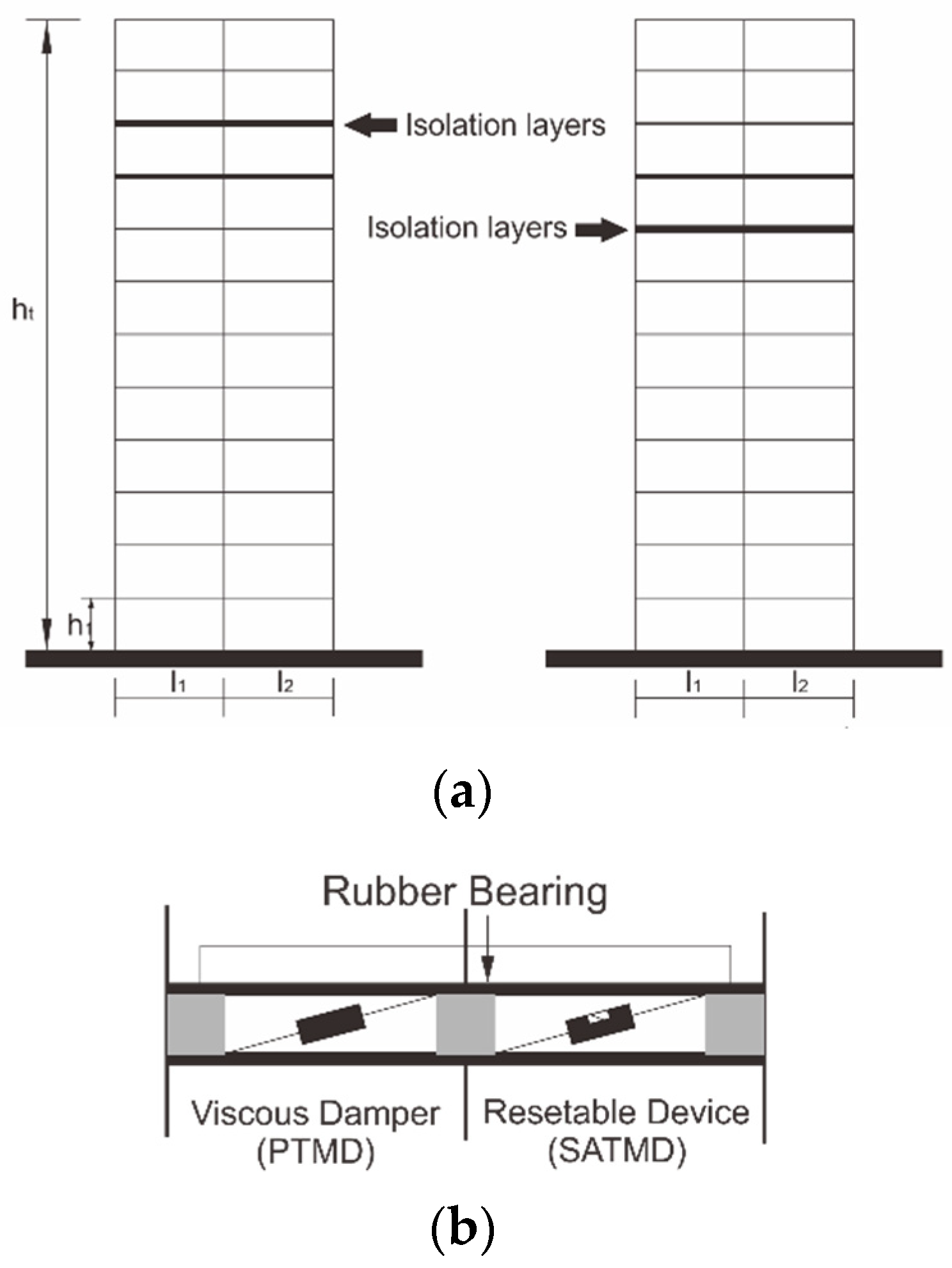
2.2. Tuned Mass Dampers
2.3. Viscous Dampers
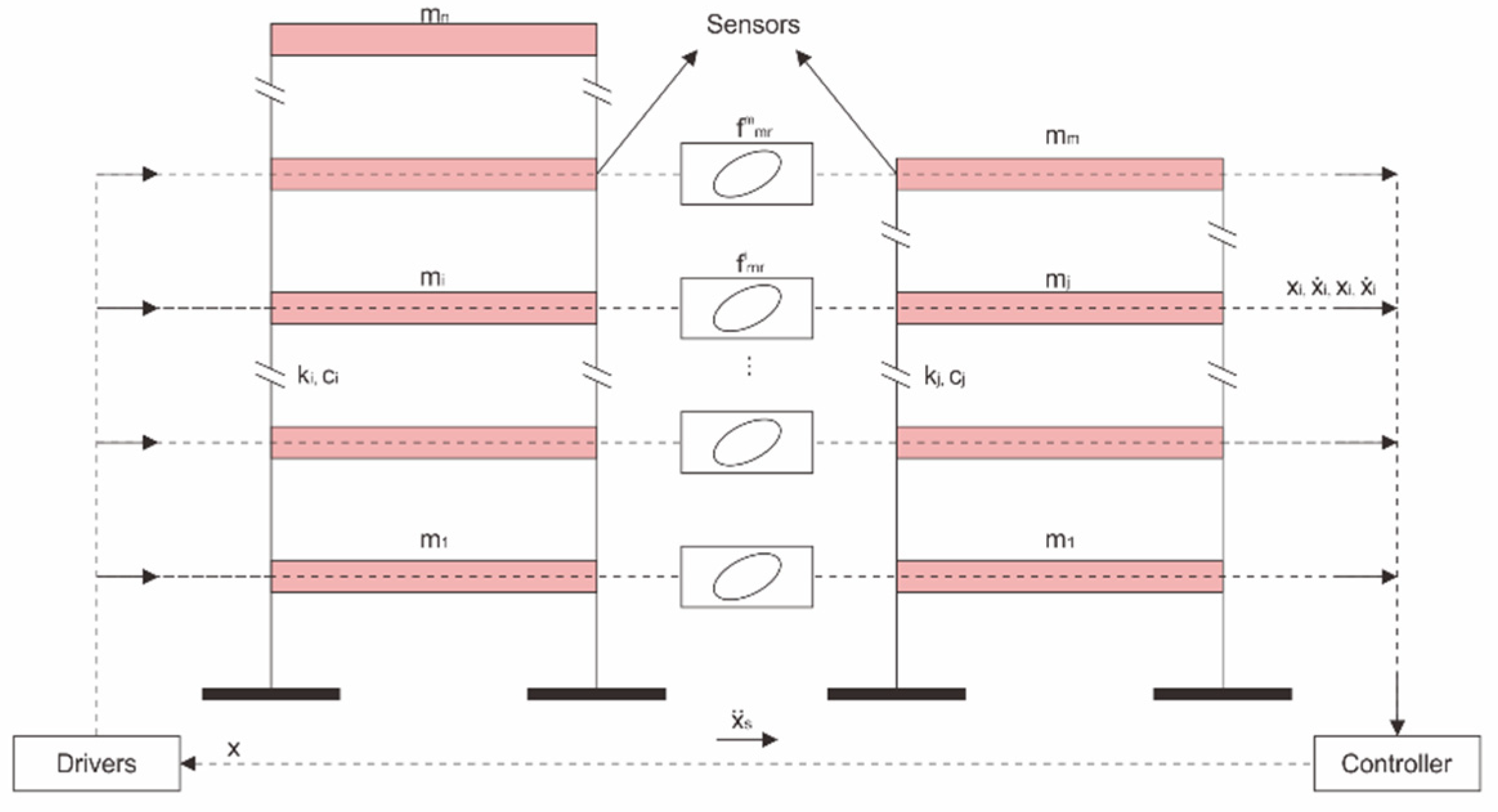
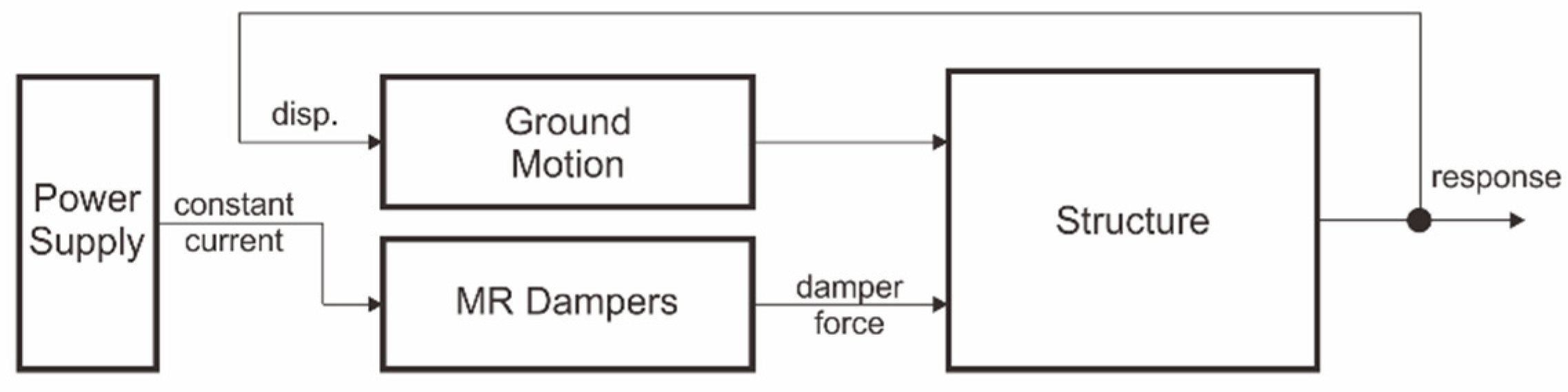
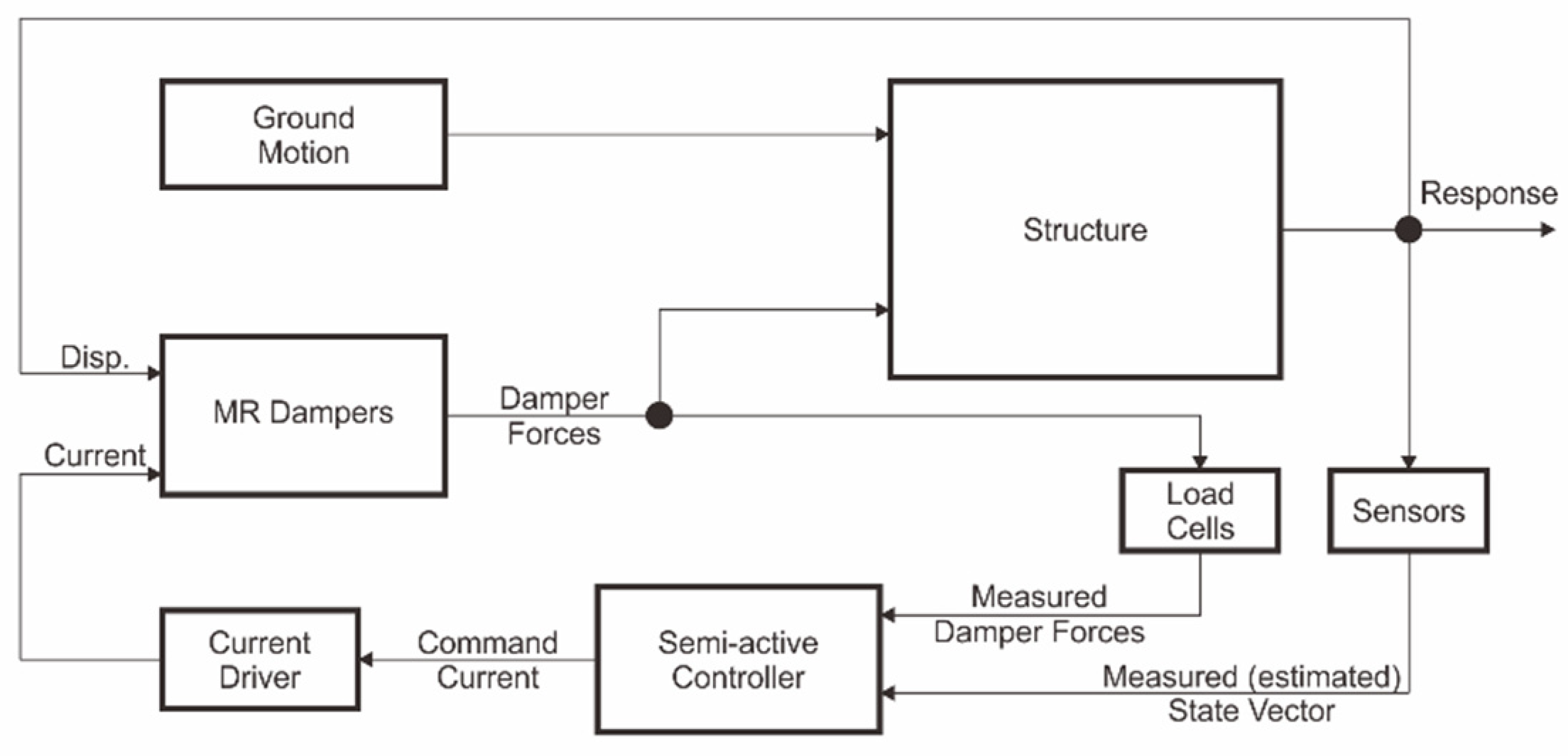
3. Magnetorheological Dampers for Structural Buildings
3.1. Magnetorheological Fluids
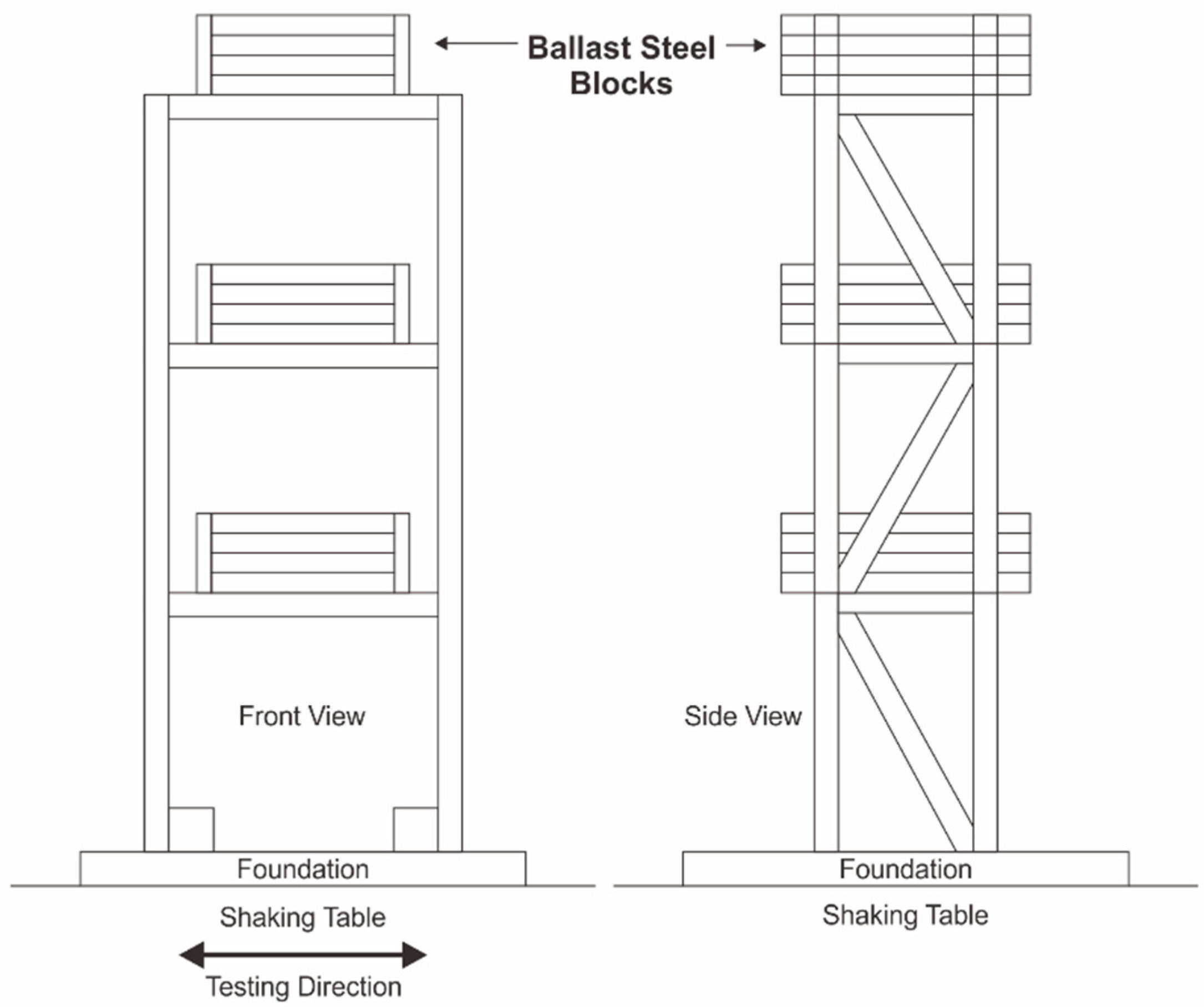
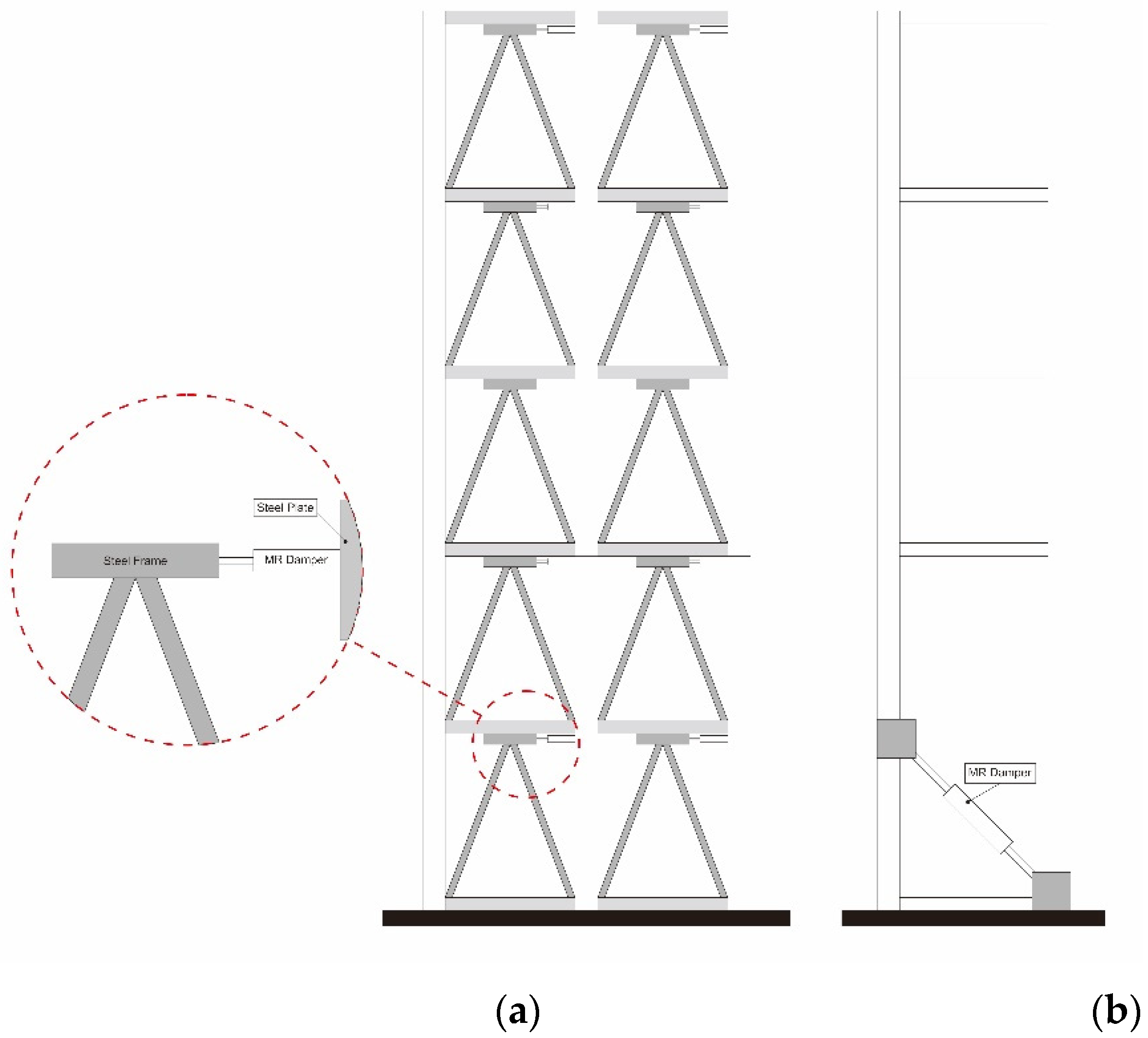
3.2. Application of MR Dampers in Building Structures
4. Modeling and Control of MR Dampers for Structural Buildings
4.1. Modeling of MR Dampers
4.2. Semi-Active Controllers for MR Dampers
5. Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ozbulut, O.E.; Hurlebaus, S.; Desroches, R. Seismic Response Control Using Shape Memory Alloys: A Review. J. Intell. Mater. Syst. Struct. 2011, 22, 1531–1549. [Google Scholar] [CrossRef]
- Takagi, J.; Wada, A. Recent earthquakes and the need for a new philosophy for earthquake-resistant design. Soil Dyn. Earthq. Eng. 2019, 119, 499–507. [Google Scholar] [CrossRef]
- Tehseen, R.; Farooq, M.S.; Abid, A. Earthquake Prediction Using Expert Systems: A Systematic Mapping Study. Sustainability 2020, 12, 2420. [Google Scholar] [CrossRef]
- Ahumada, A.; Altunkaynak, A.; Ayoub, A. Fuzzy logic-based attenuation relationships of strong motion earthquake records. Expert Syst. Appl. 2015, 42, 1287–1297. [Google Scholar] [CrossRef]
- Bahrami, B.; Shafiee, M. Fuzzy Descriptor Models for Earthquake Time Prediction Using Seismic Time Series. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2015, 23, 505–519. [Google Scholar] [CrossRef]
- Nasrollahnejad, A. Prediction of Peak ground acceleration for earthquakes by using intelligent methods. In Proceedings of the 2017 5th Iranian Joint Congress on Fuzzy and Intelligent Systems, Tehran, Iran, 7–9 March 2017. [Google Scholar] [CrossRef]
- Lamsal, M.R. Siesmic Activity and its Periphery. Himal. Phys. 2017, 6, 86–91. [Google Scholar] [CrossRef][Green Version]
- Komura, K.; Aiyama, K.; Nagata, T.; Sato, H.P.; Yamada, A.; Aoyagi, Y. Surface rupture and characteristics of a fault associated with the 2011 and 2016 earthquakes in the southern Abukuma Mountains, northeastern Japan, triggered by the Tohoku-Oki earthquake. Earth Planets Space 2019, 71, 1–23. [Google Scholar] [CrossRef]
- Grünthal, G.; Wahlström, R.; Stromeyer, D. The unified catalogue of earthquakes in central, northern, and northwestern Europe (CENEC)—Updated and expanded to the last millennium. J. Seism. 2009, 13, 517–541. [Google Scholar] [CrossRef]
- Dziewonski, A.M.; Chou, T.-A.; Woodhouse, J.H. Determination of earthquake source parameters from waveform data for studies of global and regional seismicity. J. Geophys. Res. Space Phys. 1981, 86, 2825–2852. [Google Scholar] [CrossRef]
- Allen, T.I.; Wald, D.J.; Worden, C.B. Intensity attenuation for active crustal regions. J. Seism. 2012, 16, 409–433. [Google Scholar] [CrossRef]
- Nievas, C.I.; Bommer, J.J.; Crowley, H.; Van Elk, J. Global Occurrence and Impact of Small-to-Medium Magnitude Earthquakes: A Statistical Analysis; Springer: Amsterdam, The Netherlands, 2020; Volume 18, pp. 1–35. [Google Scholar] [CrossRef]
- Musson, R. Intensity and Intensity Scales, New Man. Seismol. Obs. Pract. 2012, 2, 1–41. [Google Scholar] [CrossRef]
- Doglioni, C.; Barba, S.; Carminati, E.; Riguzzi, F. Fault on-off versus strain rate and earthquakes energy. Geosci. Front. 2015, 6, 265–276. [Google Scholar] [CrossRef]
- Chung, T.-W. Attenuation of High-Frequency P and S Waves in the Crust of Southeastern South Korea. Bull. Seism. Soc. Am. 2001, 91, 1867–1874. [Google Scholar] [CrossRef]
- Hamzehloo, H.; Doloei, G.J. Attenuation of high frequency Pand Swaves in the crust of the East-Central Iran. Geophys. J. Int. 2009, 179, 1669–1678. [Google Scholar] [CrossRef]
- Kennett, B.; Furumura, T. Significant P wave conversions from upgoing S waves generated by very deep earthquakes around Japan. Prog. Earth Planet. Sci. 2019, 6, 49. [Google Scholar] [CrossRef]
- Stern, T.; Lamb, S.; Moore, J.D.P.; Okaya, D.; Hochmuth, K. High mantle seismic P-wave speeds as a signature for gravitational spreading of superplumes. Sci. Adv. 2020, 6, eaba7118. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Sharma, R.; Rizzo, A.N.; Siegler, J.H.; Garcia, J.G.N.; Jacobson, J.R. Role of Claudin-5 in the Attenuation of Murine Acute Lung Injury by Simvastatin. Am. J. Respir. Cell Mol. Biol. 2013, 50, 1–33. [Google Scholar] [CrossRef]
- Kern, H. Measuring and Modeling of P- and S-Wave Velocities on Crustal Rocks: A Key for the Interpretation of Seismic Reflection and Refraction Data. Int. J. Geophys. 2011, 2011, 1–9. [Google Scholar] [CrossRef]
- Takemura, S.; Yoshimoto, K.; Tonegawa, T. Scattering of trapped P and S waves in the hydrated subducting crust of the Philippine Sea plate at shallow depths beneath the Kanto region, Japan. Geophys. J. Int. 2015, 203, 2261–2276. [Google Scholar] [CrossRef]
- Ma, X.; Huang, Z. Attenuation of High-Frequency P and S Waves in the Crust of Central and Western Tien Shan. Pure Appl. Geophys. 2020, 177, 4127–4142. [Google Scholar] [CrossRef]
- Asudeh, I. Seismic structure of Iran from surface and body wave data. Geophys. J. Int. 1982, 71, 715–730. [Google Scholar] [CrossRef]
- Wu, X.; Lu, H.; Huang, K.; Wu, S.; Qiao, W. Frequency Spectrum Method-Based Stress Analysis for Oil Pipelines in Earthquake Disaster Areas. PLoS ONE 2015, 10, e0115299. [Google Scholar] [CrossRef] [PubMed]
- Maiti, B.B. Ajayswarup Fan Footing Soil Foundation to Safeguard High and Low Rise Buildings from Seismic Waves. Int. J. Adv. Eng. Res. Sci. 2018, 5, 11–21. [Google Scholar] [CrossRef]
- Heyburn, R.; Selby, N.D.; Fox, B. Estimating earthquake source depths by combining surface wave amplitude spectra and teleseismic depth phase observations. Geophys. J. Int. 2013, 194, 1000–1010. [Google Scholar] [CrossRef][Green Version]
- Maupin, V. Encyclopedia of Earthquake Engineering. Encycl. Earthq. Eng. 2014, 1–15. [Google Scholar] [CrossRef]
- Trifunac, M.D.; Brady, A.G. Correlations of peak acceleration, velocity and displacement with earthquake magnitude, distance and site conditions. Earthq. Eng. Struct. Dyn. 1976, 4, 455–471. [Google Scholar] [CrossRef]
- Society, S. A study on the duration of strong earthquake ground motion. 14F, 1T, Refs. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1976, 13, 28. [Google Scholar] [CrossRef]
- Elhout, E.A. The correlation between the ground motion intensity measure parameters of earthquakes. Asian J. Civ. Eng. 2020, 21, 829–840. [Google Scholar] [CrossRef]
- Pejovic, J.; Jankovic, S. Selection of Ground Motion Intensity Measure for Reinforced Concrete Structure. Procedia Eng. 2015, 117, 588–595. [Google Scholar] [CrossRef]
- Ye, L.; Ma, Q.; Miao, Z.; Guan, H.; Zhuge, Y. Numerical and comparative study of earthquake intensity indices in seismic analysis. Struct. Des. Tall Spéc. Build. 2013, 22, 362–381. [Google Scholar] [CrossRef]
- Atkinson, G.M.; Kaka, S.I. Relationships between Felt Intensity and Instrumental Ground Motion in the Central United States and California. Bull. Seism. Soc. Am. 2007, 97, 497–510. [Google Scholar] [CrossRef]
- Kaka, S.I.; Atkinson, G.M. Relationships between Instrumental Ground-Motion Parameters and Modified Mercalli Intensity in Eastern North America. Bull. Seism. Soc. Am. 2004, 94, 1728–1736. [Google Scholar] [CrossRef]
- Pailoplee, S. Relationship between Modified Mercalli Intensity and peak ground acceleration in Myanmar. Nat. Sci. 2012, 04, 624–630. [Google Scholar] [CrossRef]
- Nemati, M. Relationships between Modified Mercalli Intensity and Engineering Ground-Motion of the Earthquakes in Persia. J. Earthq. Eng. 2016, 20, 795–808. [Google Scholar] [CrossRef]
- Atkinson, G.M.; Kaka, S.I. Relationships Between Felt Intensity and Instrumental Ground Motion for New Madrid Shake Maps. Dep. Earth Sci. Carlet. Univ. 2006, 1–27. [Google Scholar]
- Wu, Y.-M.; Chang, C.-H.; Hsiao, N.-C.; Wu, F.T. Relocation of the 1998 Rueyli, Taiwan, earthquake sequence using three-dimensions velocity structure with stations corrections. Terr. Atmos. Ocean. Sci. 2003, 14, 421. [Google Scholar] [CrossRef][Green Version]
- Wald, D.; Quitoriano, V.; Heaton, T.H.; Kanamori, H.; Scrivner, C.W.; Worden, C.B. TriNet “ShakeMaps”: Rapid Generation of Peak Ground Motion and Intensity Maps for Earthquakes in Southern California. Earthq. Spectra 1999, 15, 537–555. [Google Scholar] [CrossRef]
- Gerstenberger, M.C.; Wiemer, S.; Jones, L.M.; Reasenberg, P.A. Real-time forecasts of tomorrow’s earthquakes in California. Nat. Cell Biol. 2005, 435, 328–331. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.Y.; Tung, D.P.; Li, Y. Equivalent Energy Design Procedure for Earthquake Resilient Fused Structures. Earthq. Spectra 2018, 34, 795–815. [Google Scholar] [CrossRef]
- Sahin, C. Seismic Retrofitting of Existing Structures. Int. Assoc. Erathquake Eng. 2014, 111, 1–111. Available online: http://pdxscholar.library.pdx.edu/cengin_gradprojects%0Ahttp://pdxscholar.library.pdx.edu/cengin_gradprojects?utm_source=pdxscholar.library.pdx.edu/cengin_gradprojects/7&utm_medium=PDF&utm_campaign=PDFCoverPages (accessed on 28 August 2021).
- Balendra, T. Earthquake-resistant Design of Buildings. Vib. Build. Wind Earthq. Loads 1993, 115–144. [Google Scholar] [CrossRef]
- Meheta, V.V.; Murty, C.V.R.; Goswami, R.; Vijayanarayanan, A.R. Earthquake Behaviour of Buildings; Gujarat State Disaster Management Authority: Gujarat, India, 2012; p. 268. [Google Scholar]
- Thilakarathna, S.N.; Anwar, N.; Norachan, P.; Naja, F.A. The Effect of Wind Loads on the Seismic Performance of Tall Buildings. Athens J. Τechnol. Eng. 2018, 5, 251–276. [Google Scholar] [CrossRef]
- Heiza, K.M.; Tayel, M.A. Comparative Study of The Effects of Wind and Earthquake Loads on High-rise Buildings. Concr. Res. Lett. 2012, 3, 386–405. [Google Scholar]
- Cherry, S.; Ward, H.S.; Dalgliesh, W.A. Earthquake and Wind Loads in Building Design; National Research Canada: Ottawa, ON, Canada, 1963. [Google Scholar]
- Shashidhar, K.; Balaji, K.V.G.D.; Poleswararao, K.; Malavika, P.G. Chakravarthy, Comparison of influence of wind and earthquake forces on low-rise and high-rise multi storey structures. Int. J. Appl. Eng. Res. 2015, 10, 35810–35816. [Google Scholar]
- Tao, D.; Lin, J.; Lu, Z. Time-Frequency Energy Distribution of Ground Motion and Its Effect on the Dynamic Response of Nonlinear Structures. Sustainability 2019, 11, 702. [Google Scholar] [CrossRef]
- Fajfar, P. Analysis in seismic provisions for buildings: Past, present and future. The fifth Prof. Nicholas Ambraseys lecture. Bull. Earthq. Eng. 2018, 16, 2567–2608. [Google Scholar] [CrossRef]
- Kagawa, T.; Irikura, K.; Somerville, P.G. Differences in ground motion and fault rupture process between the surface and buried rupture earthquakes. Earth Planets Space 2004, 56, 3–14. [Google Scholar] [CrossRef]
- Mavroeidis, G.P.; Papageorgiou, A.S. Effect of Fault Rupture Characteristics on Near-Fault Strong Ground Motions. Bull. Seism. Soc. Am. 2010, 100, 37–58. [Google Scholar] [CrossRef]
- Yang, D.; Chen, G. Recent advances in engineering characteristics of near-fault ground motions and seismic effects of building structures. In Proceedings of the Second International Conference on Performance-based and Life-cycle Structural Engineering (PLSE 2015), Brisbane, QLD, Australia, 9–11 December 2015; pp. 1296–1305. [Google Scholar]
- Zhao, Z.; Zhao, Z.; Xu, J.; Kubota, R.; Liu, L. Strong ground motion simulation for seismic hazard assessment in an urban area. J. Geophys. Eng. 2007, 4, 308–316. [Google Scholar] [CrossRef][Green Version]
- Athamnia, B.; Ounis, A.; Abdeddaim, M. Effect of a Near Fault on the Seismic Response of a Base-Isolated Structure with a Soft Storey. Slovak J. Civ. Eng. 2017, 25, 34–46. [Google Scholar] [CrossRef]
- Rai, D.C. Future trends in earthquake-resistant design of structures. Curr. Sci. 2000, 79, 1291–1300. [Google Scholar]
- Sarwar, W.; Sarwar, R. Vibration Control Devices for Building Structures and Installation Approach: A Review. Civ. Environ. Eng. Rep. 2019, 29, 74–100. [Google Scholar] [CrossRef]
- Shekhar, S.; Shukla, S.P.; Zafar, S. Seismic Isolation Devices. J. Civ. Eng. Environ. Technol. 2017, 4, 336–340. [Google Scholar]
- Gao, H.; Wang, C.; Huang, C.; Shi, W.; Huo, L. Development of a Frequency-Adjustable Tuned Mass Damper (FATMD) for Structural Vibration Control. Shock. Vib. 2020, 2020, 1–16. [Google Scholar] [CrossRef]
- Alam, M.; Youssef, M.; Nehdi, M. Analytical prediction of the seismic behaviour of superelastic shape memory alloy reinforced concrete elements. Eng. Struct. 2008, 30, 3399–3411. [Google Scholar] [CrossRef]
- El-Sinawi, A.H.; Alhamaydeh, M.H.; Jhemi, A.A. Optimal Control of Magnetorheological Fluid Dampers for Seismic Isolation of Structures. Math. Probl. Eng. 2013, 2013, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Frahm, H. Device for damping vibration of bodies. U.S. Patent US989958A, 18 April 1911. [Google Scholar]
- Ontiveros-Pérez, S.P.; Miguel, L.F.F.; Miguel, L.F. Optimization of location and forces of friction dampers. REM Int. Eng. J. 2017, 70, 273–279. [Google Scholar] [CrossRef][Green Version]
- Ontiveros-Pérez, S.P.; Miguel, L.F.F.; Miguel, L.F.F. A New Assessment in the Simultaneous Optimization of Friction Dampers in Plane and Spatial Civil Structures. Math. Probl. Eng. 2017, 2017, 1–18. [Google Scholar] [CrossRef]
- Constantinou, M.C.; Soong, T.T.; Dargush, G.F. Passive Energy Dissipation Systems for Structural Design and Retrofit; National Science Foundation: Arlington, VA, USA, 1998. [Google Scholar]
- Pall, A.S.; Marsh, C.; Fazio, P. Friction Joints for Seismic Control of Large Panel Structures. PCI J. 1980, 25, 38–61. [Google Scholar] [CrossRef]
- Desjardins, C.; Avtar, S.P.; Cedric, M.; T.S.N.C. Group. Response of friction damped braced frames. ASCE J. Struct. Div. 1982, 108, 1313–1323. [Google Scholar]
- Aiken, I.D.; Kelly, J.M. Earthquake Simulator Testing and Analytical Studies of Two Energy-Absorbing Systems for Multi-Story Structures; Earthquake Engineering Research Center, National Technical Information Service: Berkeley, CA, USA, 1990; p. 276. [Google Scholar]
- Ray, S.S.; Sahoo, S.; Das, S. Formulation and solutions of fractional continuously variable order mass-spring-damper systems controlled by viscoelastic and viscous-viscoelastic. Adv. Mater. Eng. 2016, 8, 1687814016646505. [Google Scholar] [CrossRef]
- Raut, B.R.; Jangid, R.S. Seismic behavior of benchmark building with semi active variable friction damper. Asian J. Civ. Eng. 2015, 16, 417–436. [Google Scholar]
- Pengyun, L.; Jiedong, L.; Ming, N.; Wanli, Z.; Anguo, H. Vibration Energy of Earthquake Excited Building Structures Based on Computer Simulation. Energy Procedia 2012, 17, 1116–1123. [Google Scholar] [CrossRef][Green Version]
- Armali, M.; Damerji, H.; Hallal, J.; Fakih, M. Effectiveness of friction dampers on the seismic behavior of high rise building vs. shear wall system. Eng. Rep. 2019, 1, 1–14. [Google Scholar] [CrossRef]
- Apostolakis, G. Optimal Evolutionary Seismic Design of Three-Dimensional Multistory Structures with Damping Devices. J. Struct. Eng. 2020, 146, 04020205. [Google Scholar] [CrossRef]
- Pall, A.S.; Pall, R.T. Performance-Based Design Using Pall Friction Dampers—An Economical Design Solution. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Park, J.-H.; Kim, J.; Min, K.-W. Optimal design of added viscoelastic dampers and supporting braces. Earthq. Eng. Struct. Dyn. 2004, 33, 465–484. [Google Scholar] [CrossRef]
- Levy, R.; LaVan, O. Fully stressed design of passive controllers in framed structures for seismic loadings. Struct. Multidiscip. Optim. 2006, 32, 485–498. [Google Scholar] [CrossRef]
- Whittle, J.K.; Williams, M.S.; Karavasilis, T.; Blakeborough, A. A Comparison of Viscous Damper Placement Methods for Improving Seismic Building Design. J. Earthq. Eng. 2012, 16, 540–560. [Google Scholar] [CrossRef]
- Filiatrault, B.A.; Member, A.; Cherry, S. Seismic design spectra for friction. Damped Struct. 1990, 116, 1334–1355. [Google Scholar]
- Moreschi, L.M.; Singh, M.P. Design of yielding metallic and friction dampers for optimal seismic performance. Earthq. Eng. Struct. Dyn. 2003, 32, 1291–1311. [Google Scholar] [CrossRef]
- Fallah, N.; Honarparast, S. NSGA-II based multi-objective optimization in design of Pall friction dampers. J. Constr. Steel Res. 2013, 89, 75–85. [Google Scholar] [CrossRef]
- De Matteis, G.; Brando, G.; Caldoso, F.; D’Agostino, F. Seismic performance of dual steel frames with dissipative metal shear panels. Ing. Sismica 2018, 35, 124–141. [Google Scholar]
- Zahrai, S.M.; Moradi, A.; Moradi, M. Using friction dampers in retrofitting a steel structure with masonry infill panels. Steel Compos. Struct. 2015, 19, 309–325. [Google Scholar] [CrossRef]
- Mualla, I.H.; Belev, B. Performance of steel frames with a new friction damper device under earthquake excitation. Eng. Struct. 2002, 24, 365–371. [Google Scholar] [CrossRef]
- Barati, F.; Esfandiari, A. Exploring the Efficiency of Dampers for Repair and Strengthening of Existing Buildings. J. Struct. Eng. Geo-Tech. 2012, 2, 67–73. [Google Scholar]
- Chandra, R.; Masand, M.; Nandi, S.K.; Tripathi, C.P.; Pall, R.; Pall, A. Friction-Dampers for Seismic Control of La Gardenia Towers South City, Gurgaon, India. Engineering 2008, 1–8. [Google Scholar]
- Saeedi, F.; Shabakhty, N.; Mousavi, S.R. Seismic assessment of steel frames with triangular-plate added damping and stiffness devices. J. Constr. Steel Res. 2016, 125, 15–25. [Google Scholar] [CrossRef]
- Mahmoudi, M.; Abdi, M.G. Evaluating response modification factors of TADAS frames. J. Constr. Steel Res. 2012, 71, 162–170. [Google Scholar] [CrossRef]
- De Matteis, G.; Sarracco, G.; Brando, G. Experimental tests and optimization rules for steel perforated shear panels. J. Constr. Steel Res. 2016, 123, 41–52. [Google Scholar] [CrossRef]
- Vian, D.; Bruneau, M.; Purba, R. Special Perforated Steel Plate Shear Walls with Reduced Beam Section Anchor Beams. II: Analysis and Design Recommendations. J. Struct. Eng. 2009, 135, 221–228. [Google Scholar] [CrossRef]
- Valizadeh, H.; Sheidaii, M.; Showkati, H. Experimental investigation on cyclic behavior of perforated steel plate shear walls. J. Constr. Steel Res. 2012, 70, 308–316. [Google Scholar] [CrossRef]
- Chan, R.; Albermani, F.; Kitipornchai, S. Experimental study of perforated yielding shear panel device for passive energy dissipation. J. Constr. Steel Res. 2013, 91, 14–25. [Google Scholar] [CrossRef]
- Egorova, N.; Eatherton, M.R.; Maurya, A. Experimental study of ring-shaped steel plate shear walls. J. Constr. Steel Res. 2014, 103, 179–189. [Google Scholar] [CrossRef]
- Brando, G.; De Matteis, G. Design of low strength-high hardening metal multi-stiffened shear plates. Eng. Struct. 2014, 60, 2–10. [Google Scholar] [CrossRef]
- Brando, G.; De Matteis, G. Experimental and numerical analysis of a multi-stiffened pure aluminium shear panel. Thin-Walled Struct. 2011, 49, 1277–1287. [Google Scholar] [CrossRef]
- De Matteis, G.; Brando, G.; Panico, S.; Mazzolani, F.M. Bracing type pure aluminium stiffened shear panels: An experimental study. Adv. Steel Constr. 2009, 5, 106–119. [Google Scholar]
- Hamed, A.A.; Mofid, M. On the equivalent simple models of braced steel shear panels. Proc. Inst. Civ. Eng. Struct. Build. 2015, 168, 570–577. [Google Scholar] [CrossRef]
- Hamed, A.A.; Mofid, M. On the experimental and numerical study of braced steel shear panels. Struct. Des. Tall Spéc. Build. 2015, 24, 853–872. [Google Scholar] [CrossRef]
- Zhang, C.; Zhu, J.; Wu, M.; Yu, J.; Zhao, J. The Lightweight Design of a Seismic Low-Yield-Strength Steel Shear Panel Damper. Materials 2016, 9, 424. [Google Scholar] [CrossRef]
- Kang, T.H.-K.; Martin, R.D.; Park, H.-G.; Wilkerson, R.; Youssef, N. Tall building with steel plate shear walls subject to load reversal. Struct. Design Tall Spec. Build. 2013, 22, 500–520. [Google Scholar] [CrossRef]
- Jain, S.; Rai, D.C.; Sahoo, D.R. Postyield Cyclic Buckling Criteria for Aluminum Shear Panels. J. Appl. Mech. 2008, 75, 021015. [Google Scholar] [CrossRef]
- Deng, K.; Pan, P.; Li, W.; Xue, Y. Development of a buckling restrained shear panel damper. J. Constr. Steel Res. 2015, 106, 311–321. [Google Scholar] [CrossRef]
- De Matteis, G.; D’Agostino, F.; Brando, G. Experimental tests on steel buckling inhibited shear panels. Open Constr. Build. Technol. J. 2014, 8, 279–288. [Google Scholar]
- De Matteis, G.; Brando, G.; Mazzolani, F.M. Pure aluminium: An innovative material for structural applications in seismic engineering. Constr. Build. Mater. 2012, 26, 677–686. [Google Scholar] [CrossRef]
- Liu, L.; Tan, P.; Ma, H.; Yan, W.; Zhou, F. A Novel Energy Dissipation Outrigger System with Rotational Inertia Damper. Adv. Struct. Eng. 2018, 21, 1865–1878. [Google Scholar] [CrossRef]
- Housner, G.W.; Bergman, L.A.; Caughey, T.K.; Chassiakos, A.G.; Claus, R.O.; Masri, S.F.; Skelton, R.E.; Soong, T.T.; Spencer, B.F.; Yao, J.T.P. Structural Control: Past, Present, and Future. J. Eng. Mech. 1997, 123, 897–971. [Google Scholar] [CrossRef]
- Soong, T.; Spencer, B. Supplemental energy dissipation: State-of-the-art and state-of-the-practice. Eng. Struct. 2002, 24, 243–259. [Google Scholar] [CrossRef]
- Chakraborty, S.; Roy, B.K. Reliability based optimum design of Tuned Mass Damper in seismic vibration control of structures with bounded uncertain parameters. Probabilistic Eng. Mech. 2011, 26, 215–221. [Google Scholar] [CrossRef]
- Zuo, L.; Nayfeh, S.A. The Two-Degree-of-Freedom Tuned-Mass Damper for Suppression of Single-Mode Vibration Under Random and Harmonic Excitation. J. Vib. Acoust. 2005, 128, 56–65. [Google Scholar] [CrossRef]
- James, K.R.; Haritos, N.; Ades, P.K. Mechanical stability of trees under dynamic loads. Am. J. Bot. 2006, 93, 1522–1530. [Google Scholar] [CrossRef]
- Marano, G.C.; Greco, R.; Trentadue, F.; Chiaia, B. Constrained reliability-based optimization of linear tuned mass dampers for seismic control. Int. J. Solids Struct. 2007, 44, 7370–7388. [Google Scholar] [CrossRef]
- Pinkaew, T.; Lukkunaprasit, P.; Chatupote, P. Seismic effectiveness of tuned mass dampers for damage reduction of structures. Eng. Struct. 2003, 25, 39–46. [Google Scholar] [CrossRef]
- Matta, E. Lifecycle cost optimization of tuned mass dampers for the seismic improvement of inelastic structures. Earthq. Eng. Struct. Dyn. 2018, 47, 714–737. [Google Scholar] [CrossRef]
- Huang, M.F.; Tse, K.T.; Chan, C.M.; Lou, W. Integrated Structural Optimization and Vibration Control for Improving Wind-Induced Dynamic Performance Of Tall Buildings. Int. J. Struct. Stab. Dyn. 2011, 11, 1139–1161. [Google Scholar] [CrossRef]
- Wang, D.; Tse, T.K.; Zhou, Y.; Li, Q. Structural performance and cost analysis of wind-induced vibration control schemes for a real super-tall building. Struct. Infrastruct. Eng. 2014, 11, 990–1011. [Google Scholar] [CrossRef]
- Ronagh, M. Plastic Hinge Length of RC Columns Subjected to Both Far-Fault and Near-Fault Ground Motions Having Forward Directivity. Struct. Des. Tall Spec. Build. 2011, 24, 421–439. [Google Scholar] [CrossRef]
- Tse, K.T.; Kwok, K.; Tamura, Y. Performance and Cost Evaluation of a Smart Tuned Mass Damper for Suppressing Wind-Induced Lateral-Torsional Motion of Tall Structures. J. Struct. Eng. 2012, 138, 514–525. [Google Scholar] [CrossRef]
- Bhattacharjee, E.; Halder, L.; Sharma, R.P. An experimental study on tuned liquid damper for mitigation of structural response. Int. J. Adv. Struct. Eng. 2013, 5, 3. [Google Scholar] [CrossRef]
- Min, L. Studies on Tuned Liquid Damper (Tld) By Free-Oscillation. Struct. Eng. 1988, 5, 381–391. [Google Scholar]
- Park, E.; Heo, J.S.; Lee, S.K.; Lee, S.H.; Kim, H.J.; Jo, J.S.; Cho, B.C.; Joo, S.J.; Min, K.W. Performance Test of a Tuned Liquid Mass Damper installed in a Real-Scaled Structure. J. Comput. Struct. Eng. Inst. Korea 2017, 21, 6. [Google Scholar]
- Gur, S.; Roy, K.; Mishra, S.K. Tuned liquid column ball damper for seismic vibration control. Struct. Control. Health Monit. 2015, 22, 1325–1342. [Google Scholar] [CrossRef]
- Fei, Z.; Jinting, W.; Feng, J.; Liqiao, L. Control performance comparison between tuned liquid damper and tuned liquid column damper using real-time hybrid simulation. Earthq. Eng. Eng. Vib. 2019, 18, 695–701. [Google Scholar] [CrossRef]
- Karavasilis, T.L.; Kerawala, S.; Hale, E. Hysteretic model for steel energy dissipation devices and evaluation of a min-imal-damage seismic design approach for steel buildings. J. Constr. Steel Res. 2012, 70, 358–367. [Google Scholar] [CrossRef]
- Brando, G.; D’Agostino, F.; De Matteis, G. Seismic performance of MR frames protected by viscous or hysteretic dampers. Struct. Des. Tall Spéc. Build. 2015, 24, 653–671. [Google Scholar] [CrossRef]
- Ribakov, Y.; Gluck, J. Active viscous damping system for control of MDOF structures. In Proceedings of the 25th International Conference Noise Vibration Enginering ISMA, Leuven, Belgium, 13–15 September 2000; pp. 147–154. [Google Scholar]
- Franklin, G.F.; Powell, J.D.; Emami-Naeini, A. Feedback Control of Dynamic Systems; Prentice Hall: Upper Saddle River, NJ, USA, 1995. [Google Scholar]
- Oliveira, F.; Morais, P. Semi-active control of a fluid viscous damper for vibration mitigation. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012. [Google Scholar]
- Waghmare, M.V.; Madhekar, S.N.; Matsagar, V.A. Semi-Active Fluid Viscous Dampers for Seismic Mitigation of RC Elevated Liquid Storage Tanks. Int. J. Struct. Stab. Dyn. 2019, 19. [Google Scholar] [CrossRef]
- Bogdan, P.; Stefania, P.; Muresan, I. Active, Semi-active and Hibrid Control Systems Properties and Applications. Acta Tech. Napoc. Civ. Eng. Archit. 2011, 54, 153–161. [Google Scholar]
- Ashour, O.; Rogers, C.A.; Kordonsky, W. Ashour. Magnetorheological Fluids: Materials, Characterization, and Devices. J. Intell. Mater. Syst. Struct. 1996, 7, 123–130. [Google Scholar] [CrossRef]
- Carlson, J.D.; Weiss, K.D. Magnetorheological Materials Based on Alloy Particles. U.S. Patent No. 5,382,373, 17 January 1995. [Google Scholar]
- Özsoy, K.; Usal, M.R. A mathematical model for the magnetorheological materials and magneto reheological devices. Eng. Sci. Technol. Int. J. 2018, 21, 1143–1151. [Google Scholar] [CrossRef]
- Kordonski, W.; Gorodkin, S. The behavior of a magnetorheological (MR) fluid under compressive deformation. J. Rheol. 2016, 60, 129–139. [Google Scholar] [CrossRef]
- Spaggiari, A. Properties and applications of Magnetorheological fluids. Frat. Integrità Strutt. 2012, 7, 48–61. [Google Scholar] [CrossRef]
- Morillas, J.R.; De Vicente, J. Magnetorheology: A review. Soft Matter 2020, 16, 9614–9642. [Google Scholar] [CrossRef]
- Ashtiani, M.; Hashemabadi, S.; Ghaffari, A. A review on the magnetorheological fluid preparation and stabilization. J. Magn. Magn. Mater. 2015, 374, 716–730. [Google Scholar] [CrossRef]
- Wang, D.H.; Liao, W.-H. Magnetorheological fluid dampers: A review of parametric modelling. Smart Mater. Struct. 2011, 20. [Google Scholar] [CrossRef]
- Robinson, J.; Xi, K.; Kumar, R.V.; Ferrari, A.C.; Au, H.; Titirici, M.-M.; Parra Puerto, A.; Kucernak, A.; Fitch, S.D.S.; Garcia-Araez, N. 2021 roadmap on lithium sulfur batteries. J. Phys. Energy 2020, 2, 1–31. [Google Scholar]
- Kumar, J.S.; Paul, P.S.; Raghunathan, G.; Alex, D.G. A review of challenges and solutions in the preparation and use of magnetorheological fluids. Int. J. Mech. Mater. Eng. 2019, 14, 13. [Google Scholar] [CrossRef]
- Bombard, A.J.F.; Antunes, L.S.; Gouvêa, D. Redispersibility in magnetorheological fluids: Surface interactions between iron powder and wetting additives. J. Phys. Conf. Ser. 2009, 149, 012038. [Google Scholar] [CrossRef]
- Premalatha, S.E.; Chokkalingam, R.; Mahendran, M. Magneto Mechanical Properties of Iron Based MR Fluids. Am. J. Polym. Sci. 2012, 2, 50–55. [Google Scholar] [CrossRef]
- Zhang, J.Q.; Jing, Q. Effect of seven different additives on the properties of MR fluids. J. Physics: Conf. Ser. 2009, 149, 012086. [Google Scholar] [CrossRef]
- Carlson, J.D. What Makes a Good MR Fluid? J. Intell. Mater. Syst. Struct. 2002, 13, 431–435. [Google Scholar] [CrossRef]
- Balbás, L.; Borstel, G.; Alonso, J.A. Nonlocal density functional calculation of the electron affinity of atoms. Phys. Lett. A 1986, 114, 236–240. [Google Scholar] [CrossRef]
- Aly, A.M. Vibration Control of Buildings Using Magnetorheological Damper: A New Control Algorithm. J. Eng. 2013, 2013, 1–10. [Google Scholar] [CrossRef]
- Khan, S.A.; Suresh, A.; Seetha, R.N. Principles, Characteristics and Applications of Magneto Rheological Fluid Damper in Flow and Shear Mode. Procedia Mater. Sci. 2014, 6, 1547–1556. [Google Scholar] [CrossRef]
- Dobre, A.; Andreescu, C.N.; Stan, C. The influence of the current intensity on the damping characteristics for a magneto-rheological damper of passenger car. IOP Conf. Ser. Mater. Sci. Eng. 2016, 147, 012110. [Google Scholar] [CrossRef]
- Paciello, V.; Pietrosanto, A. Magnetorheological Dampers: A New Approach of Characterization. IEEE Trans. Instrum. Meas. 2011, 60, 1718–1723. [Google Scholar] [CrossRef]
- Gordaninejad, F.; Wang, X.; Hitchcock, G.; Bangrakulur, K.; Ruan, S.; Siino, M. Modular High-Force Seismic Magne-to-Rheological. J. Struct. Eng. 2010, 136, 135–143. [Google Scholar] [CrossRef]
- Jung, H.; Spencer, B.J.; Ni, Y.; Lee, I. State-of-the-art of semiactive control systems using MR fluid dampers in civil engineering applications. Struct. Eng. Mech. 2004, 17, 493–526. [Google Scholar] [CrossRef]
- Roesset, J.M.; Yao, J.T.P. State of the Art of Structural Engineering. J. Struct. Eng. 2002, 128, 965–975. [Google Scholar] [CrossRef]
- Lenggana, B.W.; Ubaidillah, U.; Imaduddin, F.; Widyarso, W.; Purnomo, E.D.; Utami, D.; Mazlan, S.A. Performance prediction of a novel modular magnetorheological damper for seismic building. J. Adv. Res. Fluid Mech. Therm. Sci. 2019, 58, 275–286. [Google Scholar]
- Kim, H.-C.; Shin, Y.-J.; You, W.; Jung, K.C.; Oh, J.-S.; Choi, S.-B. A ride quality evaluation of a semi-active railway vehicle suspension system with MR damper: Railway field tests. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2016, 231, 306–316. [Google Scholar] [CrossRef]
- Lau, Y.K.; Liao, W.-H. Design and Analysis of Magnetorheological Dampers for Train Suspension. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2005, 219, 261–276. [Google Scholar] [CrossRef]
- Wang, D.H.; Liao, W.-H. Semi-active suspension systems for railway vehicles using magnetorheological dampers. Part I: System integration and modelling. Veh. Syst. Dyn. 2009, 47, 1305–1325. [Google Scholar] [CrossRef]
- Carlson, J.; Matthis, W. Structures and, undefined 2001, Smart prosthetics based on magnetorheological fluids, Spied-igitallibrary.Org. In Proceedings of the SPIE’s 8th Annual International Symposium on Smart Structures and Materials, Newport Beach, CA, USA, 4–8 March 2001; 2001; Volume 4332, pp. 308–316. Available online: https://www.spiedigitallibrary.org/conference-proceedings-of-spie/4332/0000/Smart-prosthetics-based-on-magnetorheological-fluids/10.1117/12.429670.short (accessed on 28 August 2021).
- Spelta, C.; Previdi, F.; Savaresi, S.M.; Fraternale, G.; Gaudiano, N. Control of magnetorheological dampers for vibration reduction in a washing machine. Mechatronics 2009, 19, 410–421. [Google Scholar] [CrossRef]
- Lee, D.Y.; Nam, Y.J.; Yamane, R.; Park, M.K. Performance evaluation on vibration control of MR landing gear. J. Phys. Conf. Ser. 2009, 149, 012068. [Google Scholar] [CrossRef]
- Ubaidillah, U.; Lenggana, B.W.; Son, L.; Imaduddin, F.; Widodo, P.J.; Harjana, H.; Doewes, R.I. A New Magnetorheological Fluids Damper for Unmanned Aerial Vehicles. J. Adv. Res. Fluid Mech. Therm. Sci. 2020, 73, 35–45. [Google Scholar] [CrossRef]
- Choi, S.-B.; Nam, M.-H.; Lee, B.-K. Vibration Control of a MR Seat Damper for Commercial Vehicles. J. Intell. Mater. Syst. Struct. 2000, 11, 936–944. [Google Scholar] [CrossRef]
- Milecki, A.; Hauke, M. Application of magnetorheological fluid in industrial shock absorbers. Mech. Syst. Signal Process. 2012, 28, 528–541. [Google Scholar] [CrossRef]
- Wereley, N.M.; Hu, W.; Kothera, C.S.; Chen, P.C.; Ngatu, G.T. Magnetorheological Fluid Elastic Lag Damper for Helicopter Rotors. U.S. Patent No. 8,413,772, 9 April 2013. [Google Scholar]
- Guo, C.; Gong, X.; Zong, L.; Peng, C.; Xuan, S. Twin-tube- and bypass-containing magneto-rheological damper for use in railway vehicles. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2015, 229, 48–57. [Google Scholar] [CrossRef]
- Braz-César, M.T.; Barros, R.C. Semi-active control of an experimental frame using mr dampers: Numerical results and experimental validation. In Proceedings of the 3rd International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Corfu, Greece, 26–28 May 2011; pp. 25–28. [Google Scholar]
- Barros, R.C. Experimental Behaviour and Numerical Analysis of MR Dampers dampers. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012. [Google Scholar]
- Chey, M.-H.; Chase, J.G.; Mander, J.B.; Carr, A.J. Semi-active tuned mass damper building systems: Design. Earthq. Eng. Struct. Dyn. 2009, 39, 119–139. [Google Scholar] [CrossRef]
- Uz, M.E. Seismic Design of Magnetorheological Dampers Between Different Sizes Buildings Under Optimum Parameters. Celal Bayar Üniversitesi Fen Bilimleri Derg. 2017, 13, 1–13. [Google Scholar] [CrossRef][Green Version]
- Makris, N.; Constantinou, M. Viscous Dampers: Testing Modeling and Application in Vibration and Seismic Isolation; National Center for Earthquake Engenering Research, State University of New York Buffalo: Buffalo, NY, USA, 1990. [Google Scholar] [CrossRef]
- Constantinou, M.C.; Symans, M.D. Experimental study of seismic response of buildings with supplemental fluid dampers. Struct. Des. Tall Build. 1993, 2, 93–132. [Google Scholar] [CrossRef]
- Guo, T.; Xu, J.; Xu, W.; Di, Z. Seismic Upgrade of Existing Buildings with Fluid Viscous Dampers: Design Methodologies and Case Study. J. Perform. Constr. Facil. 2015, 29, 04014175. [Google Scholar] [CrossRef]
- Wang, S.; Mahin, S.A. Seismic Upgrade of an Existing Tall Building Using Different Supplemental Energy Dissipation Devices. J. Struct. Eng. 2018, 144, 04018091. [Google Scholar] [CrossRef]
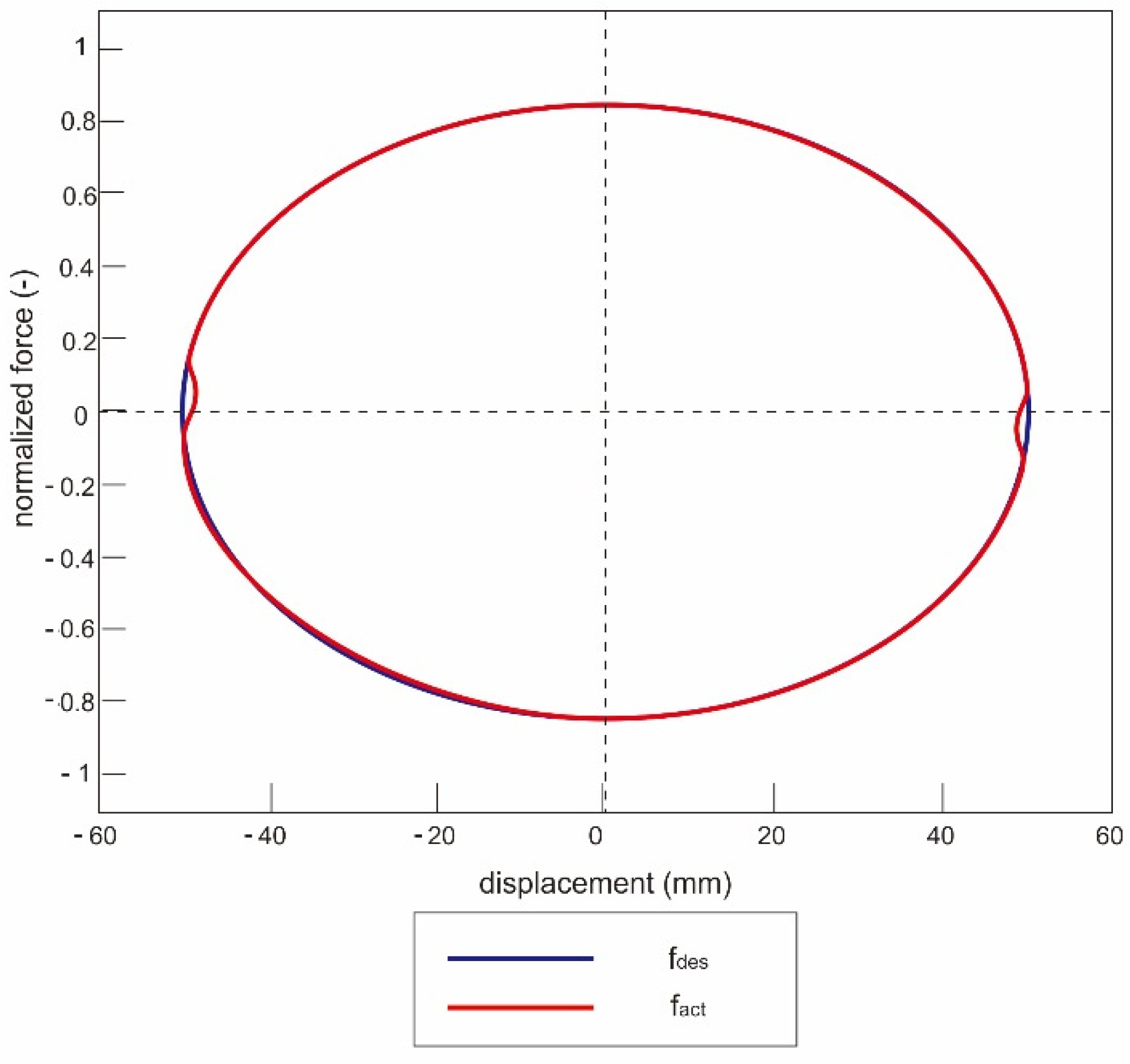
- Weber, F. Robust force tracking control scheme for MR dampers. Struct. Control. Health Monit. 2015, 22, 1373–1395. [Google Scholar] [CrossRef]
- Guo, S.; Yang, S.; Pan, C. Dynamic Modeling of Magnetorheological Damper Behaviors. J. Intell. Mater. Syst. Struct. 2006, 17, 3–14. [Google Scholar] [CrossRef]
- Singru, P.; Raizada, A.; Krishnakumar, V.; Garg, A.; Tai, K.; Raj, V. Modeling of a magneto-rheological (MR) damper using genetic programming. J. Vibroengineering 2017, 19, 3169–3177. [Google Scholar] [CrossRef][Green Version]
- Guan, X.; Guo, P.; Ou, J. Modeling and Analyzing of Hysteresis Behavior of Magneto Rheological Dampers. Procedia Eng. 2011, 14, 2756–2764. [Google Scholar] [CrossRef]
- Rossi, A.; Orsini, F.; Scorza, A.; Botta, F.; Belfiore, N.P.; Sciuto, S.A. A Review on Parametric Dynamic Models of Magnetorheological Dampers and Their Characterization Methods. Actuators 2018, 7, 16. [Google Scholar] [CrossRef]
- Zapateiro, M.; Luo, N.; Rodellar, J. Modeling and Identification of Hysteretic Dynamics of Mr Dampers and Application to Semiactive Vibration. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Ahn, K.K.; Truong, D.Q.; Islam, M.A. Modeling of a magneto-rheological (MR) fluid damper using a self tuning fuzzy mechanism. J. Mech. Sci. Technol. 2009, 23, 1485–1499. [Google Scholar] [CrossRef]
- Weber, F. Bouc–Wen model-based real-time force tracking scheme for MR dampers. Smart Mater. Struct. 2013, 22, 045012. [Google Scholar] [CrossRef]
- Soltane, S.; Montassar, S.; Ben Mekki, O.; El Fatmi, R. A hysteretic Bingham model for MR dampers to control cable vibrations. J. Mech. Mater. Struct. 2015, 10, 195–206. [Google Scholar] [CrossRef]
- Spencer, B.F., Jr.; Dyke, S.; Sain, M.K.; Carlson, J.D. Phenomenological Model for Magnetorheological Dampers. J. Eng. Mech. 1997, 123, 230–238. [Google Scholar] [CrossRef]
- Chae, Y. Seismic Hazard Mitigation of Building Structures Using Magneto-Rheological Dampers. PhD Thesis, Lehigh University, Bethlehem, PA, USA, 2011; p. 449. [Google Scholar]
- Jansen, L.M.; Dyke, S.J. Semiactive Control Strategies for MR Dampers: Comparative Study. J. Eng. Mech. 2000, 126, 795–803. [Google Scholar] [CrossRef]
- Rodriguez, R.; Stathis, J.H.; Linder, B.P. Modeling and Experimental Verification of the Effect of Gate Oxide Breakdown on CMOS Inverters. In Proceedings of the 2003 IEEE International Reliability Physics Symposium Proceedings, Dallas, TX, USA, 30 March–4 April 2003; pp. 11–16. [Google Scholar]
- Wei, S.; Wang, J.; Ou, J. Method for improving the neural network model of the magnetorheological damper. Mech. Syst. Signal Process. 2021, 149, 107316. [Google Scholar] [CrossRef]
- Ndemanou, B.P.; Nbendjo, B.R.N. Fuzzy magnetorheological device vibration control of the two Timoshenko cantilever beams interconnected under earthquake excitation. Struct. Des. Tall Spéc. Build. 2018, 27, e1541. [Google Scholar] [CrossRef]
- Mehrkian, B.; Bahar, A.; Chaibakhsh, A. Semiactive conceptual fuzzy control of magnetorheological dampers in an irregular base-isolated benchmark building optimized by multi-objective genetic algorithm. Struct. Control. Health Monit. 2019, 26, e2302. [Google Scholar] [CrossRef]
- Iemura, H.; Igarashi, A.; Pradono, M.H.; Kalantari, A. Negative stiffness friction damping for seismically isolated structures. Struct. Control. Health Monit. 2006, 13, 775–791. [Google Scholar] [CrossRef]
- Iemura, H.; Pradono, M.H. Application of pseudo-negative stiffness control to the benchmark cable-stayed bridge. J. Struct. Control. 2003, 10, 187–203. [Google Scholar] [CrossRef]
- Weber, F.; Distl, J.; Meier, L.; Braun, C. Curved surface sliders with friction damping, linear viscous damping, bow tie friction damping, and semiactively controlled properties. Struct. Control. Health Monit. 2018, 25, e2257. [Google Scholar] [CrossRef]
- Zafarani, M.M.; Halabian, A.M. A new supervisory adaptive strategy for the control of hysteretic multi-story irregular buildings equipped with MR-dampers. Eng. Struct. 2020, 217, 110786. [Google Scholar] [CrossRef]
- Mohebbi, M.; Dadkhah, H.; Dabbagh, H.R. A genetic algorithm–based design approach for smart base isolation systems. J. Intell. Mater. Syst. Struct. 2017, 29, 1315–1332. [Google Scholar] [CrossRef]
- Zizouni, K.; Fali, L.; Sadek, Y.; Bousserhane, I.K. Neural network control for earthquake structural vibration reduction using MRD. Front. Struct. Civ. Eng. 2019, 13, 1171–1182. [Google Scholar] [CrossRef]
- Bozorgvar, M.; Zahrai, S.M. Semi-active seismic control of buildings using MR damper and adaptive neural-fuzzy intelligent controller optimized with genetic algorithm. J. Vib. Control. 2018, 25, 273–285. [Google Scholar] [CrossRef]
- Li, L.; Liang, H. Semiactive Control of Structural Nonlinear Vibration Considering the MR Damper Model. J. Aerosp. Eng. 2018, 31, 04018095. [Google Scholar] [CrossRef]
- Braz-César, M.; Barros, R. Optimization of a Fuzzy Logic Controller for MR Dampers Using an Adaptive Neuro-Fuzzy Procedure. Int. J. Struct. Stab. Dyn. 2016, 17, 1740007. [Google Scholar] [CrossRef]
- Al-Fahdawi, O.A.; Barroso, L.R. Adaptive neuro-fuzzy and simple adaptive control methods for full three-dimensional coupled buildings subjected to bi-directional seismic excitations. Eng. Struct. 2021, 232, 111798. [Google Scholar] [CrossRef]
- Mousavi, S.H. Modeling and controlling a semi-active nonlinear single-stage vibration isolator using intelligent inverse model of an MR damper. J. Mech. Sci. Technol. 2020, 34, 1–8. [Google Scholar] [CrossRef]

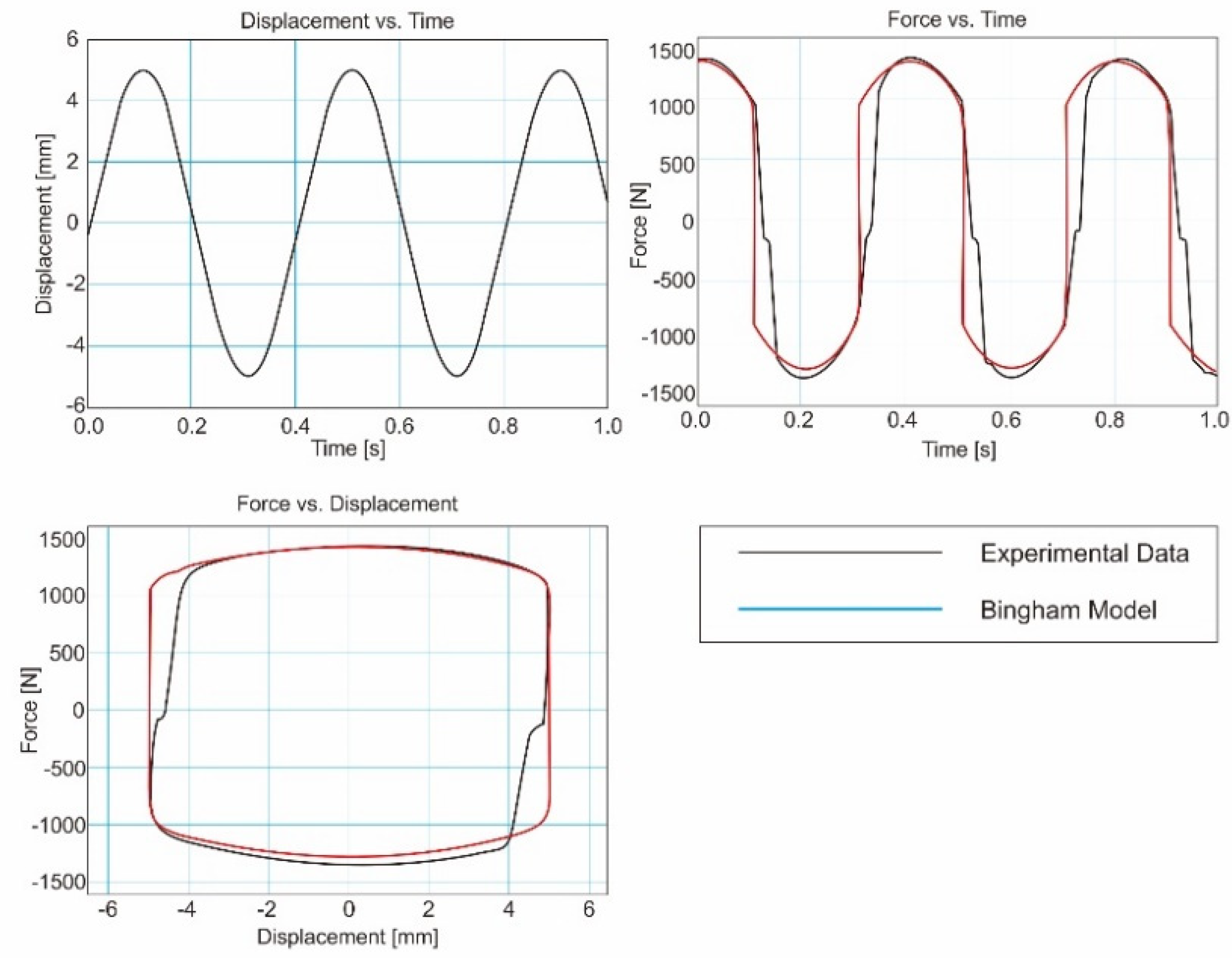
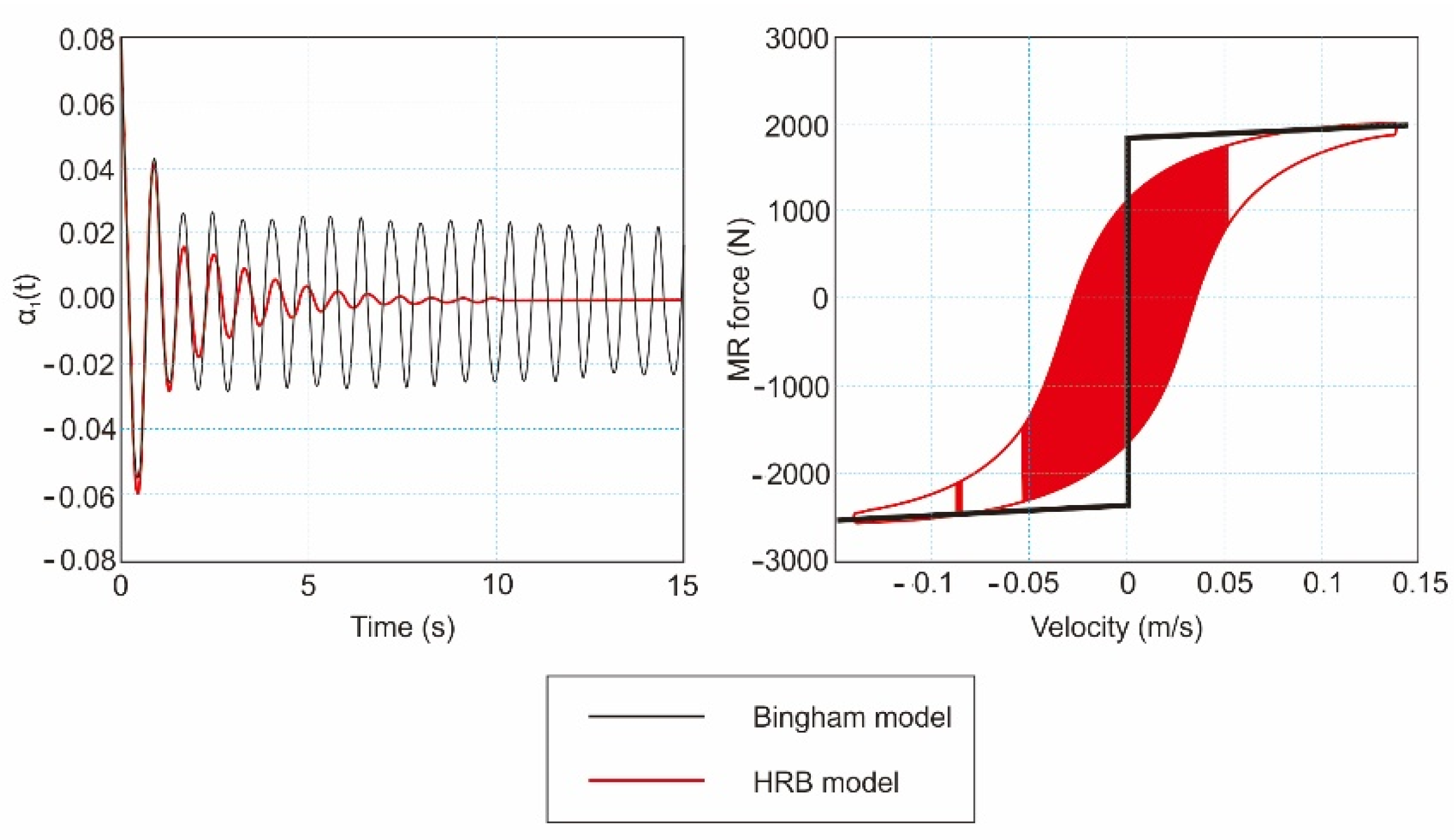
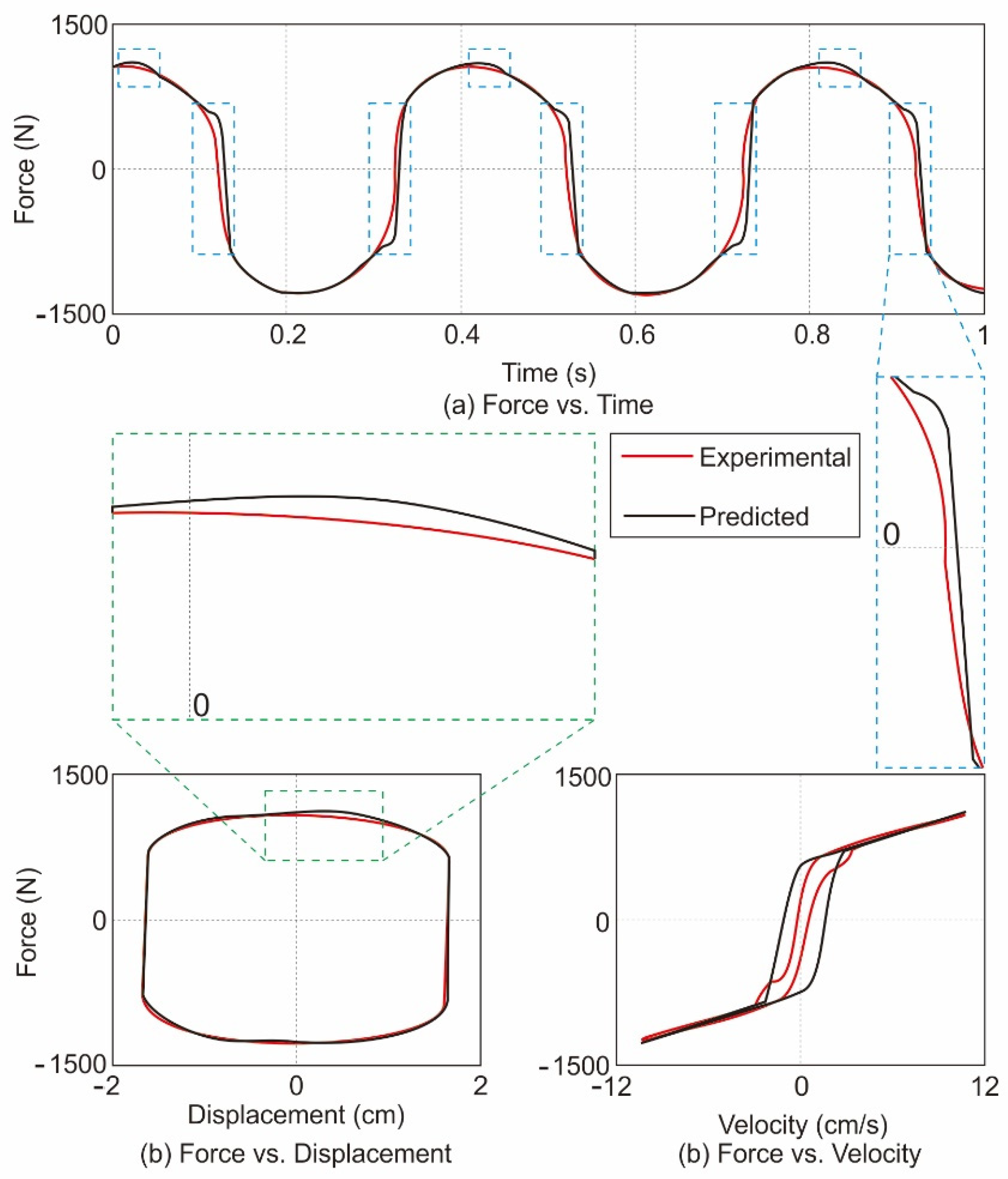
| Model | Equation | Figure |
|---|---|---|
| Bingham Model | where c1 and f0 are equal to the damping coefficient and the shear friction force, respectively; and sgn () is a function of the signum. The damping force is linearly dependent on the damper speed, while the friction force depends on the velocity [177,179]. | 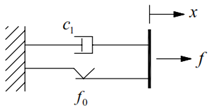 |
| Gamota and Filisko Model | where c0 is the damping coefficient of the Bingham model, and k1, k2, and c1 are the coefficients of stiffness and viscous damping, respectively, in relation to the linear solid material [179,180]. | 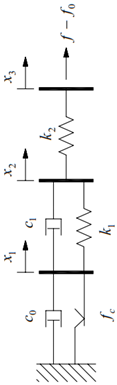 |
| Bouc-Wen Model | k1 represents the damper stiffness of the accumulator and c0 is the dashpot coefficient associated with viscous damping at higher velocities. A dashpot c1 was included in the model to produce the roll-off observed in the experimental data at a low velocity. k0 is the stiffness control at a higher velocity, and x0 is the initial displacement of the spring k1 in relation to the nominal damper force due to the battery [180]. | 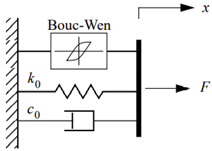 |
| BingMax Model | where a = c/k is the quotient of the dashpot c and the spring k, and fy is the friction force on the slider [180]. | 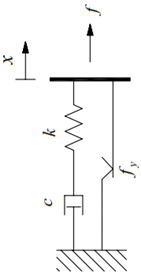 |
| LuGre Model | where g(v) is the Coulomb friction and the Stribeck effect, and f(v) represents viscous friction. | 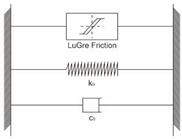 |
| No. | Author and Year | Controller | Finding |
|---|---|---|---|
| 1 | Zafarani and Halabian (2020) [190] | Clipped optimal with LQG control | Control of the seismic inelastic torque response of multi-story buildings. |
| 2 | Mohebbi et. al. (2018) [191] | H2/LQG control | Modification of H2/LQG control to optimize the control system’s performance |
| 3 | Zizouni et. al. (2019) [192] | Neural network control | Efficacy of neural network control on a three-story small-scale structure using the Tōhoku 2011 and Boumerdès 2003 earthquake data. |
| 4 | Bozorgvar and Zahrai (2019) [193] | Adaptive Neuro-Fuzzy inference system | Neuro-fuzzy optimization adapted to genetic algorithms. |
| 5 | Li and Liang (2018) [194] | Sliding mode control Fuzzy system | Developed a sliding mode control method based on a fuzzy system. Fuzzy logic control mitigates the chattering phenomenon. |
| 6 | Cesar and Barros (2017) [195] | Adaptive Neuro-Fuzzy inference system | Verified the efficacy of neuro-fuzzy controllers in reducing the responses of building structures equipped with MR dampers. |
| 7 | Al-Fahdawi and Barroso (2021) [196] | Adaptive Neuro-Fuzzy inference system and Simple adaptive control | Reduction of the seismic response of three-dimensional combined buildings under two-way seismic excitation with adaptive neuro-fuzzy inference system control and simple adaptive control. |
| 8 | Mousavi (2020) [197] | Fuzzy logic controller | Use of wavelet networks and fuzzy logic controllers to copy the inverse dynamics of MR dampers and nonlinear isolators. |
| 9 | Ndemanou and Nbendjo (2018) [185] | Fuzzy logic controller | Fuzzy logic controls are better than traditional controls and algorithmic controls and are critical when optimizing the response of a structure to seismic loads. |
| 10 | Mehrkian et. al. (2017) [186] | Fuzzy logic controller | Improving a fuzzy control system with a smart multi-objective fuzzy–genetic controller produced controls that were more effective than others. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lenggana, B.W.; Ubaidillah, U.; Imaduddin, F.; Choi, S.-B.; Purwana, Y.M.; Harjana, H. Review of Magnetorheological Damping Systems on a Seismic Building. Appl. Sci. 2021, 11, 9339. https://doi.org/10.3390/app11199339
Lenggana BW, Ubaidillah U, Imaduddin F, Choi S-B, Purwana YM, Harjana H. Review of Magnetorheological Damping Systems on a Seismic Building. Applied Sciences. 2021; 11(19):9339. https://doi.org/10.3390/app11199339
Chicago/Turabian StyleLenggana, Bhre Wangsa, Ubaidillah Ubaidillah, Fitrian Imaduddin, Seung-Bok Choi, Yusep Muslih Purwana, and Harjana Harjana. 2021. "Review of Magnetorheological Damping Systems on a Seismic Building" Applied Sciences 11, no. 19: 9339. https://doi.org/10.3390/app11199339
APA StyleLenggana, B. W., Ubaidillah, U., Imaduddin, F., Choi, S.-B., Purwana, Y. M., & Harjana, H. (2021). Review of Magnetorheological Damping Systems on a Seismic Building. Applied Sciences, 11(19), 9339. https://doi.org/10.3390/app11199339