Dermoscopy Images Enhancement via Multi-Scale Morphological Operations
Abstract
1. Introduction
- (a)
- Propose a new MTH based strategy which incorporates the geodesic reconstruction concept in combination with a mathematical morphological approach;
- (b)
- Design a novel contrast enhancement algorithm based on the proposed MTH approach.
2. Mathematical Morphology
2.1. Dilation and Erosion
2.2. Opening and Closing
2.3. Classical Top-Hat Transform
2.4. Geodesic Transformation and Reconstruction
2.5. Top-Hat by Reconstruction
3. Proposed Algorithm
- First stage:
- the bright structures at level i are extracted by as follows:where is the mask obtained by Equation (3), is the marker obtained by Equation (7). Each represents the m-level of bright structures of the original image I controlled by which is the size of the structuring element, and the dark structures at level m are extracted by as follows:where is the mask obtained by Equation (3), is the marker obtained by Equation (7). Each represents the m-level of dark structures of the original I controlled by the size of the structuring element.
- Second stage:
- the light residues are extracted from the dark structures at levels m and and the dark residues are extracted from the light structures at levels m and as follows:
- Third stage:
- The maximum bright scaled details are computed from the bright structures extracted at the first stage by , and the maximum dark scaled details are computed from the dark structures extracted at the first stage by as follows:
- Fourth stage:
- The maximum light residues are computed from the light residues extracted at the second stage by , and the maximum dark residues are computed from the dark residues extracted at the second stage by as follows [13]:
- Final stage:
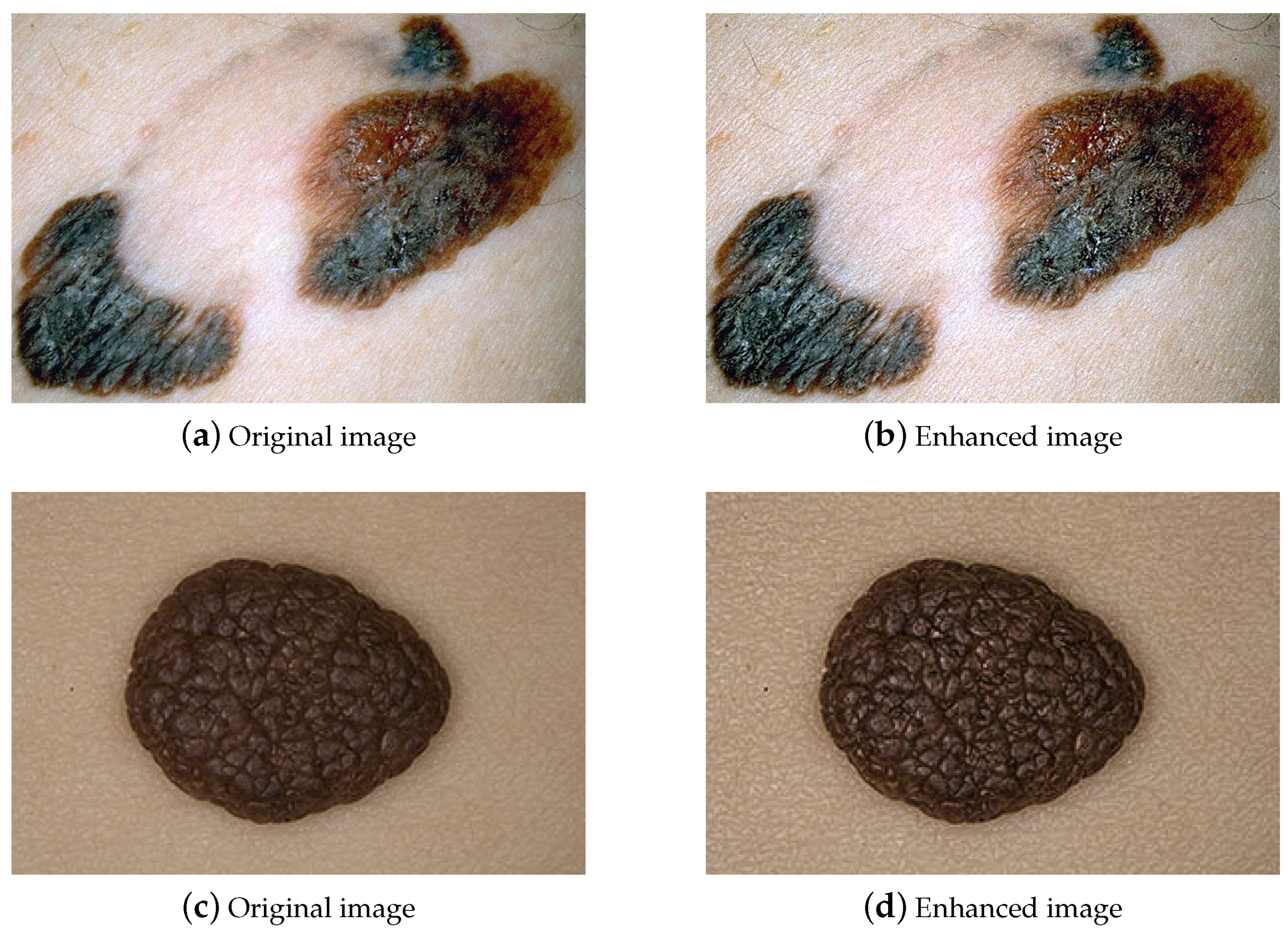
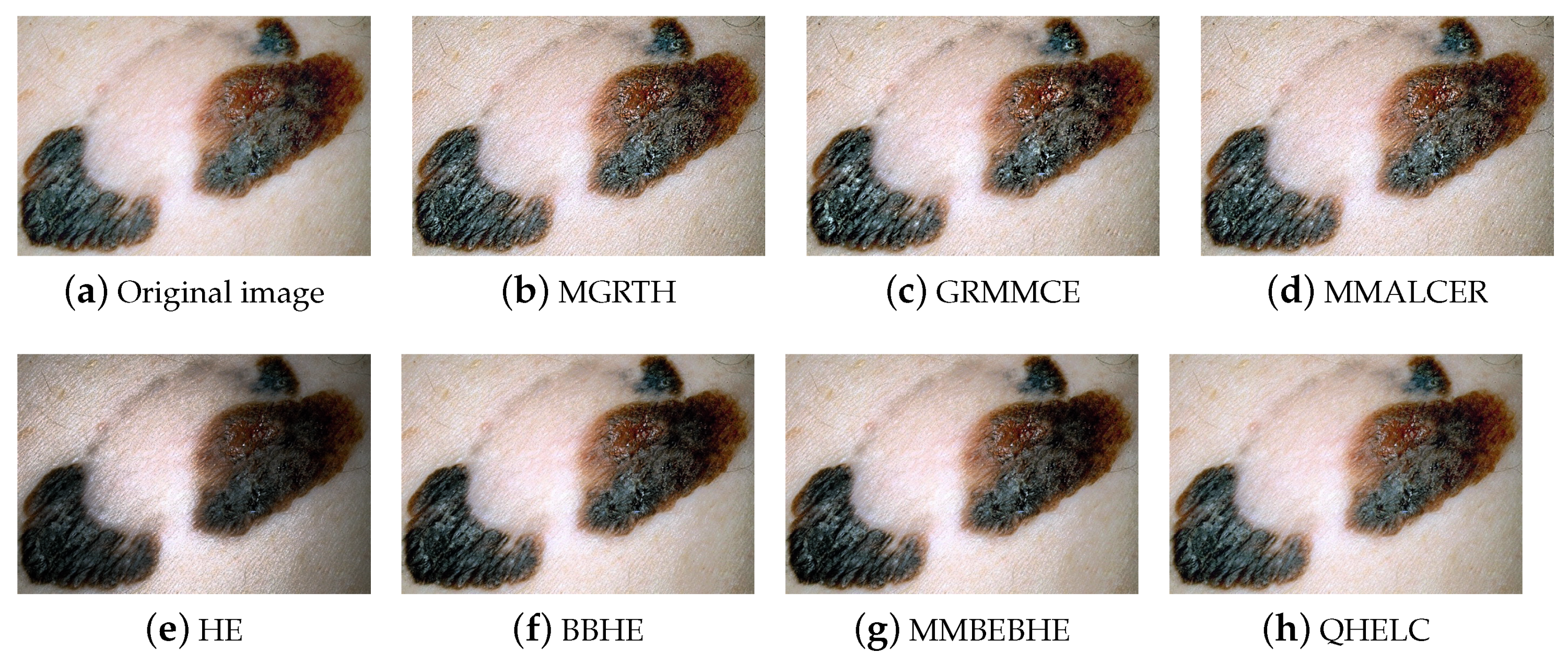
- the enhanced image is performed per pixel as follows:where is a factor used to adjust the level of brightness or darkness added to the image.Figure 1 shows the original melanoma images on the left (a,c) and the MGRTH-enhanced images on the right (b,d).
4. Results and Discussions
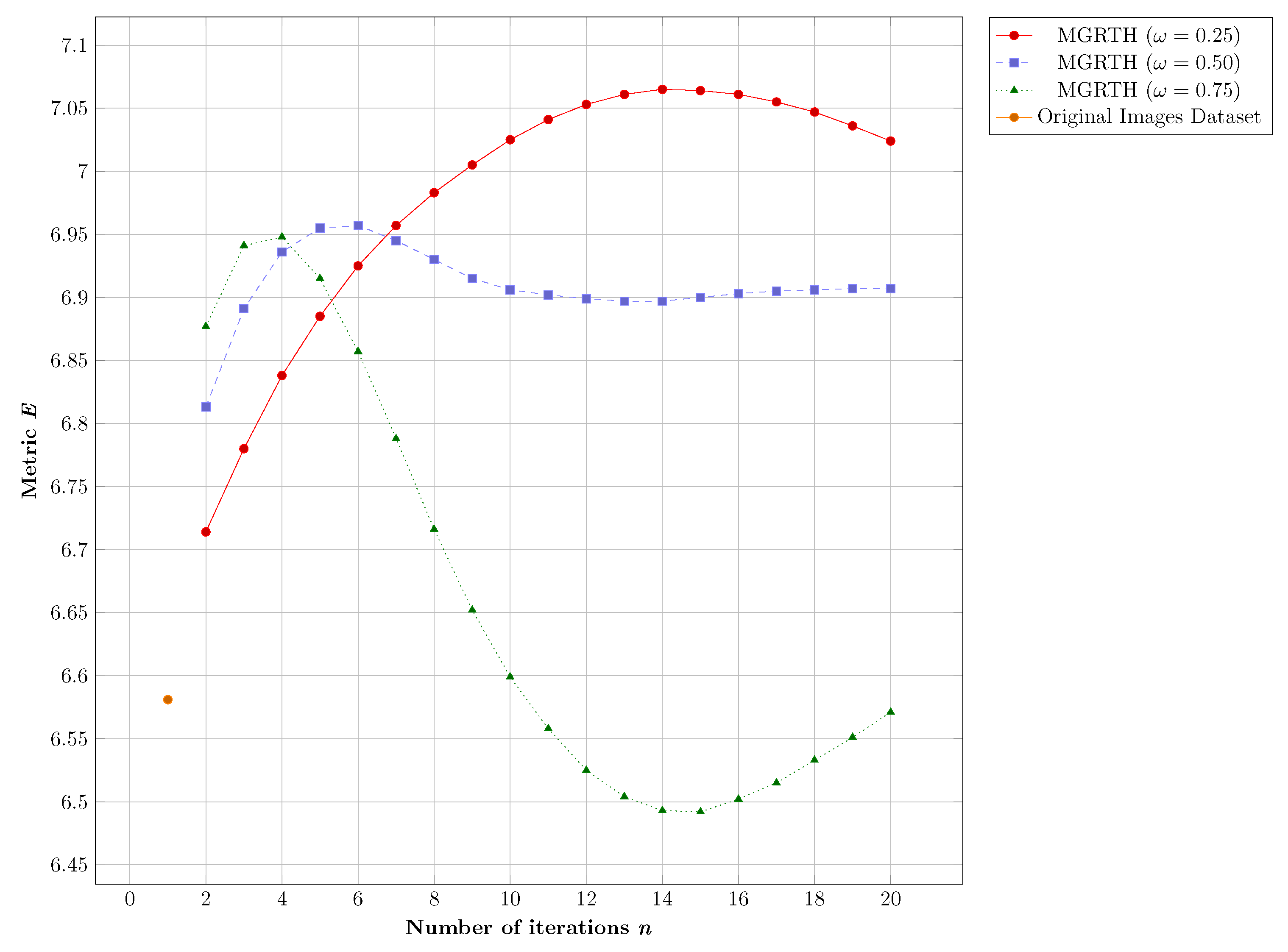
- Entropy (E) [13,21,36]: E is used to measure the details in the image. E is defined as,where I is melanoma image, k is intensity of the pixel in the image, is probability of occurrence of the k-value in the image. If b is number of bits of the image then L is equal to ( for grayscale images). An image is considered to have good detail when its entropy value is high;
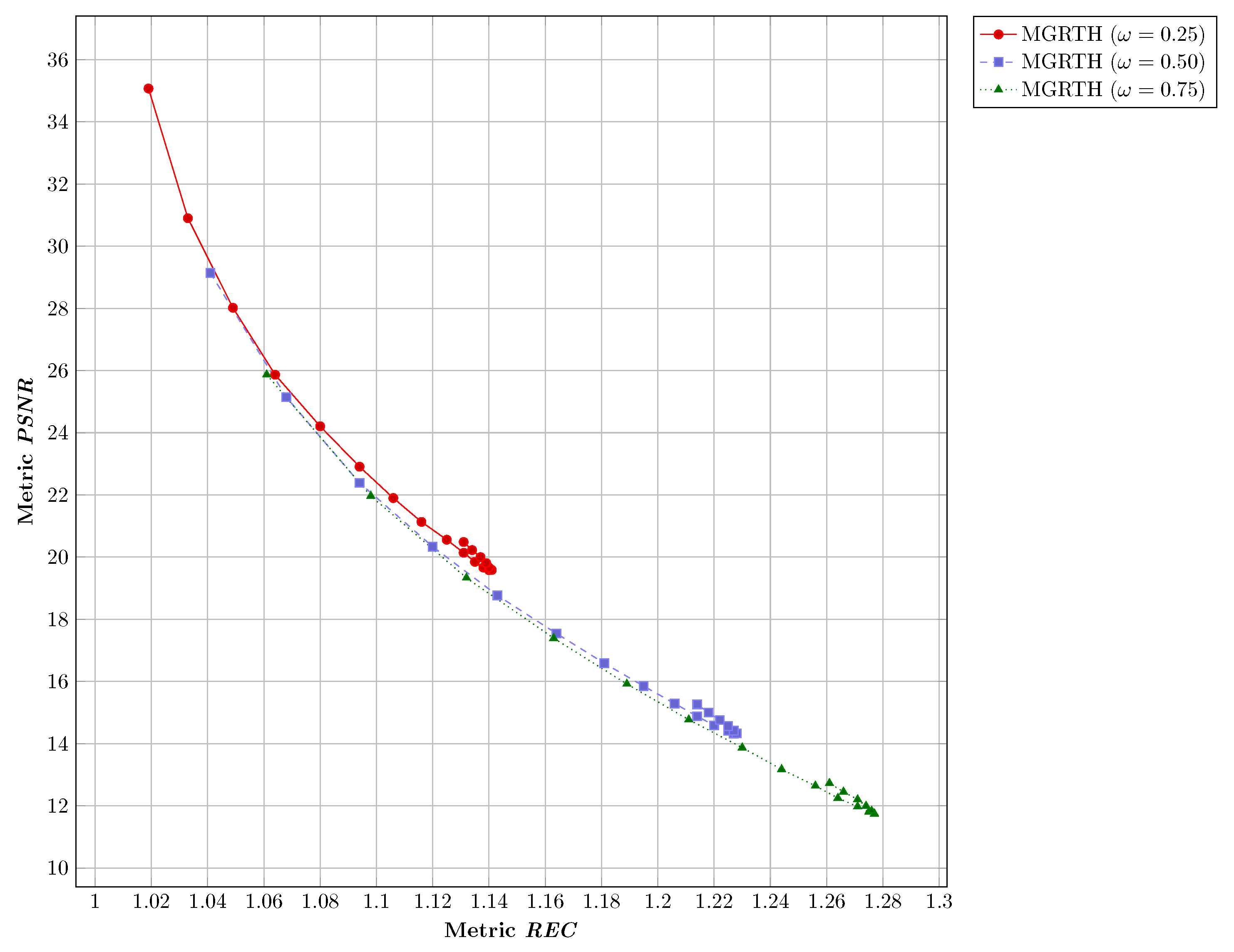
- Peak Signal-to-Noise Ratio (PSNR) [10,21,37]: PSNR measures how much distortion is added to the image in the contrast enhancement process. PSNR is defined as,where Mean Squared Error (MSE) is defined as,After the enhancement process, an image is considered to have low distortion if it has a high PSNR value;
- Relative Enhancement in Contrast (REC) [36,38]: REC measures the contrast of the enhanced melanoma image. REC is defined as,where I is the melanoma image, is the melanoma image with contrast enhancement, C is the image contrast and C is calculated as follows,where are the dimensions of the melanoma image and () are the spatial coordinates and is calculated as follows,After image processing, if the REC value is higher than 1, the enhanced image is considered to have enhanced contrast.
- In the first part (Section 4.1), we performed parameter tuning to find good parameter values and n of the proposed algorithm. For this purpose, a comparison of the results obtained with respect to the number of iterations and the contrast adjustment weight was performed. The objective of this experiment was to observe the performance of the proposal with respect to the E, PSNR, and REC metrics;
- Then, in the second part (Section 4.2) the proposed algorithm was compared with algorithms based on the multiscale top-hat transform and algorithms based on histogram equalization.
4.1. Parameters Tuning
4.1.1. Numerical Results
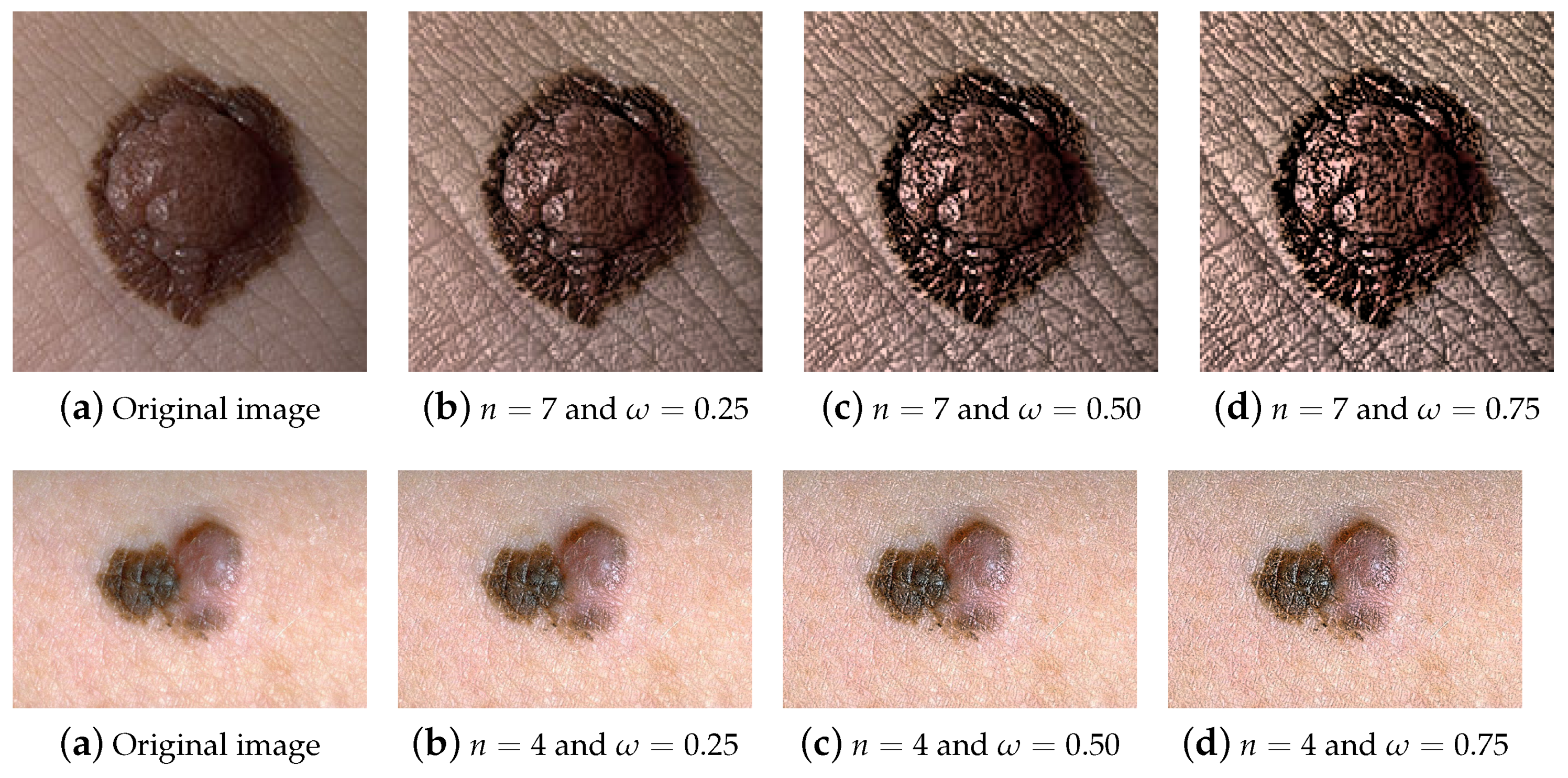
4.1.2. Visual Assessment by the Dermatologist
4.2. Comparison of the Proposed Algorithm with State-of-the-Art Algorithms
4.2.1. Numerical Results
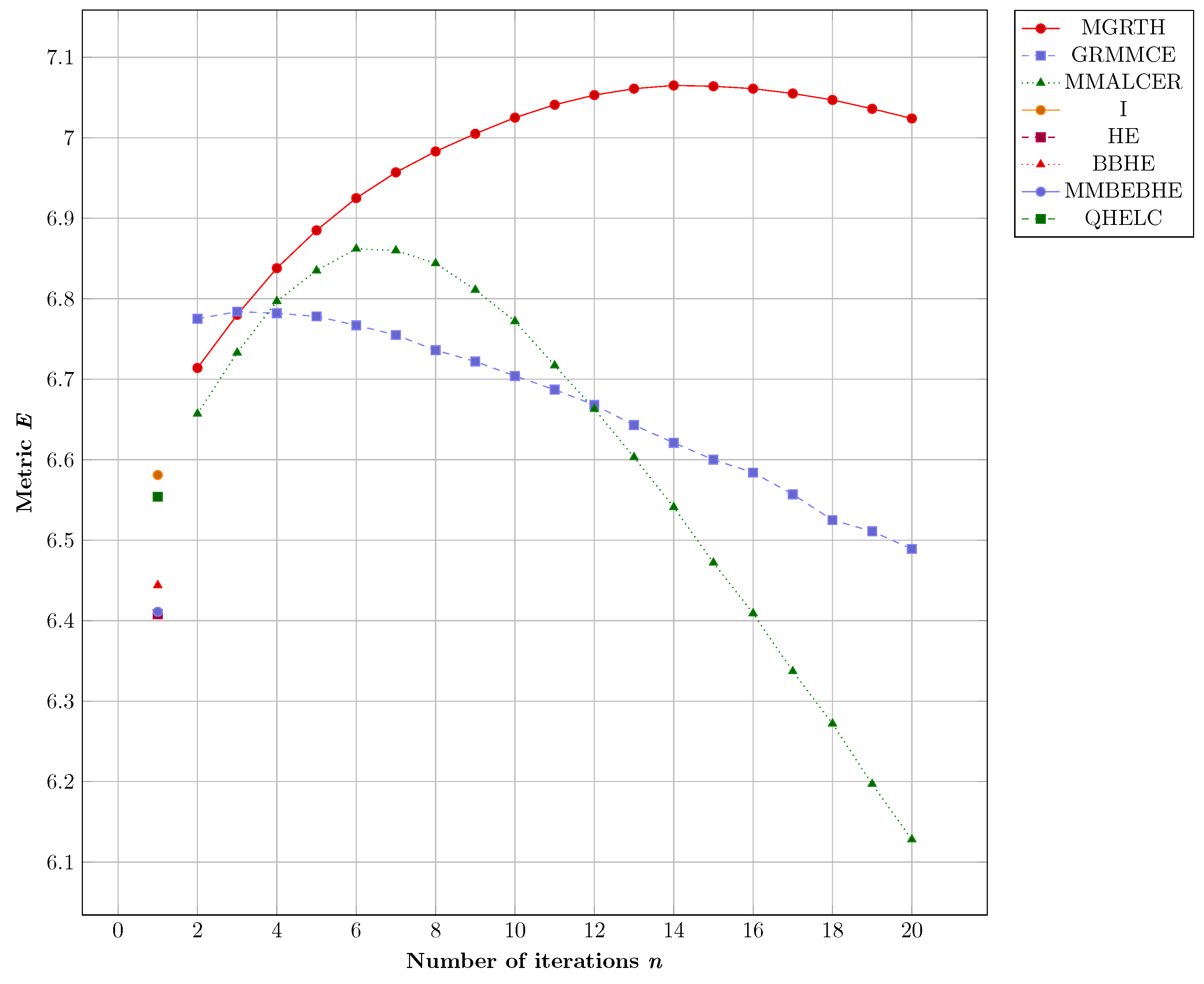
- MGRTH has better average performance according to the E metric, indicating that the approach enhances the details of melanoma images;
- Among the algorithms based on the multiscale top-hat transform, MGRTH is the second best performer for PSNR. This means that it introduces low distortion to the images;
- According to the REC metric, all compared algorithms enhance images on average.
- The proposed algorithm has obtained higher values in the E metric than the other evaluated algorithms;
- For the REC metric, the proposed algorithm has obtained lower values than the HE, BBHE and MMBEBHE algorithms, and higher values than those obtained by QHELC and MMALCER;
- For the PSNR metric, the proposed algorithm has obtained lower values than the GRMMCE, MMALCER, and QHELC algorithms, and higher values than those obtained by HE, BBHE, and MMBEBHE.
4.2.2. Visual Assessment by the Dermatologist
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, H.; Wang, Z. Perceptual Quality Assessment of Medical Images. In Encyclopedia of Biomedical Engineering; Elsevier: Amsterdam, The Netherlands, 2019; pp. 588–596. [Google Scholar]
- Sequeira, A.; Joao, A.; Tiago, J.; Gambaruto, A. Computational advances applied to medical image processing: An update. Open Access Bioinform. 2016, 8, 1–15. [Google Scholar] [CrossRef][Green Version]
- Gonzalez, R.; Woods, R. Digital Image Processing, 2nd ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 2002; Volume 793. [Google Scholar]
- Zhang, G.; Yan, P.; Zhao, H.; Zhang, X. A Contrast Enhancement Algorithm for Low-Dose CT Images Based on Local Histogram Equalization. In Proceedings of the 2008 2nd International Conference on Bioinformatics and Biomedical Engineering, Shanghai, China, 16–18 May 2008. [Google Scholar]
- Veluchamy, M.; Subramani, B. Image contrast and color enhancement using adaptive gamma correction and histogram equalization. Optik 2019, 183, 329–337. [Google Scholar] [CrossRef]
- Kim, Y.T. Contrast enhancement using brightness preserving bi-histogram equalization. IEEE Trans. Consum. Electron. 1997, 43, 1–8. [Google Scholar]
- Wang, Y.; Chen, Q.; Zhang, B. Image enhancement based on equal area dualistic sub-image histogram equalization method. IEEE Trans. Consum. Electron. 1999, 45, 68–75. [Google Scholar] [CrossRef]
- Chen, S.D.; Ramli, A. Minimum mean brightness error bi-histogram equalization in contrast enhancement. IEEE Trans. Consum. Electron. 2003, 49, 1310–1319. [Google Scholar] [CrossRef]
- Pineda, I.A.B.; Caballero, R.D.M.; Silva, J.J.C.; Román, J.C.M.; Noguera, J.L.V. Quadri-histogram equalization using cutoff limits based on the size of each histogram with preservation of average brightness. Signal Image Video Process. 2019, 13, 843–851. [Google Scholar] [CrossRef]
- Bai, X.; Zhou, F.; Xue, B. Image enhancement using multi scale image features extracted by top-hat transform. Opt. Laser Technol. 2012, 44, 328–336. [Google Scholar] [CrossRef]
- Hassanpour, H.; Samadiani, N.; Salehi, S.M. Using morphological transforms to enhance the contrast of medical images. Egypt. J. Radiol. Nucl. Med. 2015, 46, 481–489. [Google Scholar] [CrossRef]
- Arya, A.; Bhateja, V.; Nigam, M.; Bhadauria, A.S. Enhancement of Brain MR-T1/T2 Images Using Mathematical Morphology. In Information and Communication Technology for Sustainable Development; Springer: Singapore, 2019; pp. 833–840. [Google Scholar]
- Román, J.C.M.; Noguera, J.L.V.; Legal-Ayala, H.; Pinto-Roa, D.; Gomez-Guerrero, S.; García-Torres, M. Entropy and Contrast Enhancement of Infrared Thermal Images Using the Multiscale Top-Hat Transform. Entropy 2019, 21, 244. [Google Scholar] [CrossRef]
- Soille, P. Morphological Image Analysis; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Damian, F.A.; Moldovanu, S.; Dey, N.; Ashour, A.S.; Moraru, L. Feature Selection of Non-Dermoscopic Skin Lesion Images for Nevus and Melanoma Classification. Computation 2020, 8, 41. [Google Scholar] [CrossRef]
- Aswini, S.; Suresh, A.; Priya, S.; Krishna, B.V.S. Retinal Vessel Segmentation Using Morphological Top Hat Approach On Diabetic Retinopathy Images. In Proceedings of the 2018 Fourth International Conference on Advances in Electrical, Electronics, Information, Communication and Bio-Informatics (AEEICB), Chennai, India, 27–28 February 2018. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Chanda, B. A multiscale morphological approach to local contrast enhancement. Signal Process. 2000, 80, 685–696. [Google Scholar] [CrossRef]
- Peng, B.; Wang, Y.; Yang, X. A Multiscale Morphological Approach to Local Contrast Enhancement for Ultrasound Images. In Proceedings of the 2010 International Conference on Computational and Information Sciences, Chengdu, China, 17–19 December 2010. [Google Scholar]
- Kamra, A.; Jain, V.K. Enhancement of subtle signs in mammograms using multiscale morphological approach. In Proceedings of the 2013 IEEE Point-of-Care Healthcare Technologies (PHT), Bangalore, India, 16–18 January 2013. [Google Scholar]
- Bai, X. Morphological feature extraction for detail maintained image enhancement by using two types of alternating filters and threshold constrained strategy. Optik 2015, 126, 5038–5043. [Google Scholar] [CrossRef]
- Wang, G.; Wang, J.; Li, M.; Zheng, Y.; Wang, K. Hand Vein Image Enhancement Based on Multi-Scale Top-Hat Transform. Cybern. Inf. Technol. 2016, 16, 125–134. [Google Scholar] [CrossRef]
- Landini, G.; Galton, A.; Randell, D.; Fouad, S. Novel applications of discrete mereotopology to mathematical morphology. Signal Process. Image Commun. 2019, 76, 109–117. [Google Scholar] [CrossRef]
- Román, J.C.M.; Escobar, R.; Martínez, F.; Noguera, J.L.V.; Legal-Ayala, H.; Pinto-Roa, D.P. Medical Image Enhancement With Brightness and Detail Preserving Using Multiscale Top-hat Transform by Reconstruction. Electron. Notes Theor. Comput. Sci. 2020, 349, 69–80. [Google Scholar] [CrossRef]
- Román, J.C.M.; Fretes, V.R.; Adorno, C.G.; Silva, R.G.; Noguera, J.L.V.; Legal-Ayala, H.; Mello-Román, J.D.; Torres, R.D.E.; Facon, J. Panoramic Dental Radiography Image Enhancement Using Multiscale Mathematical Morphology. Sensors 2021, 21, 3110. [Google Scholar] [CrossRef]
- Nasr-Esfahani, E.; Samavi, S.; Karimi, N.; Soroushmehr, S.; Ward, K.; Jafari, M.; Felfeliyan, B.; Nallamothu, B.; Najarian, K. Vessel extraction in X-ray angiograms using deep learning. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016. [Google Scholar] [CrossRef]
- Wang, Y.L.; Mu, S.S. Edge Detection Algorithm Based on the Top-hat Operator. In DEStech Transactions on Computer Science and Engineering; DEStech Publications: Lancaster, PA, USA, 2017. [Google Scholar] [CrossRef][Green Version]
- Bai, X. Morphological image fusion using the extracted image regions and details based on multi-scale top-hat transform and toggle contrast operator. Digit. Signal Process. 2013, 23, 542–554. [Google Scholar] [CrossRef]
- Fazlali, H.R.; Karimi, N.; Soroushmehr, S.M.R.; Shirani, S.; Nallamothu, B.K.; Ward, K.R.; Samavi, S.; Najarian, K. Vessel segmentation and catheter detection in X-ray angiograms using superpixels. Med. Biol. Eng. Comput. 2018, 56, 1515–1530. [Google Scholar] [CrossRef]
- Sengar, N.; Dutta, M.K. Automated method for hierarchal detection and grading of diabetic retinopathy. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2017, 1163, 1–11. [Google Scholar] [CrossRef]
- Atli, İ.; Gedik, O.S. Sine-Net: A fully convolutional deep learning architecture for retinal blood vessel segmentation. Eng. Sci. Technol. Int. J. 2021, 24, 271–283. [Google Scholar] [CrossRef]
- Zuiderveld, K. Contrast Limited Adaptive Histogram Equalization. In Graphic Gems IV; Elsevier: Amsterdam, The Netherlands, 1994; pp. 474–485. [Google Scholar] [CrossRef]
- Lantuejoul, C.; Maisonneuve, F. Geodesic methods in quantitative image analysis. Pattern Recognit. 1984, 17, 177–187. [Google Scholar] [CrossRef]
- Beuren, A.T.; Janasieivicz, R.; Pinheiro, G.; Grando, N.; Facon, J. Skin melanoma segmentation by morphological approach. In Proceedings of the International Conference on Advances in Computing, Communications and Informatics—ICACCI ’12, Chennai, India, 3–5 August 2012; ACM Press: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef] [PubMed]
- Legland, D.; Arganda-Carreras, I.; Andrey, P. MorphoLibJ: Integrated library and plugins for mathematical morphology with ImageJ. Bioinformatics 2016, 32, 3532–3534. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Wang, Z.; Li, H.; Wu, X.; Qiao, S.; Sun, J. A new approach for medical image enhancement based on luminance-level modulation and gradient modulation. Biomed. Signal Process. Control 2019, 48, 189–196. [Google Scholar] [CrossRef]
- Salem, N.; Malik, H.; Shams, A. Medical image enhancement based on histogram algorithms. Procedia Comput. Sci. 2019, 163, 300–311. [Google Scholar] [CrossRef]
- Joseph, J.; Periyasamy, R. A fully customized enhancement scheme for controlling brightness error and contrast in magnetic resonance images. Biomed. Signal Process. Control 2018, 39, 271–283. [Google Scholar] [CrossRef]
- Bai, X. Image enhancement through contrast enlargement using the image regions extracted by multiscale top-hat by reconstruction. Optik 2013, 124, 4421–4424. [Google Scholar] [CrossRef]
- Walpole, R.E.; Myers, R.H.; Myers, S.L.; Cruz, R. Probabilidad y Estadística; McGraw-Hill: Mexico City, Mexico, 1992; Volume 624. [Google Scholar]



| Algorithm | Initial Structuring Element (Disk) | Number of Iterations | Contrast Setting Weight |
|---|---|---|---|
| H | n | ||
| MGRTH | 1 | [2–20] | [0.25,0.50,0.75] |
| Algorithms | Initial Structuring Element (Disk) | Number of Iterations | Contrast Setting Weight | |
|---|---|---|---|---|
| H | H′ | n | ||
| MGRTH | 1 | - | [2–20] | 0.25 |
| GRMMCE [23] | 1 | - | [2–20] | 1 |
| MMALCER [39] | 1 | - | [2–20] | 0.5 |
| Algorithms | E | REC | PSNR |
|---|---|---|---|
| I | 6.581 | - | - |
| MGRTH | 6.838 | 1.049 | 28.018 |
| GRMMCE | 6.782 | 1.054 | 28.109 |
| MMALCER | 6.797 | 1.044 | 29.032 |
| HE | 6.408 | 1.249 | 12.420 |
| BBHE | 6.444 | 1.241 | 17.191 |
| MMBEBHE | 6.411 | 1.186 | 20.223 |
| QHELC | 6.554 | 1.024 | 38.342 |
| Algorithms | Metrics | |||
|---|---|---|---|---|
| E | REC | PSNR | ||
| MGRTH-I | Negative ranks | 33 | - | - |
| Positive ranks | 203 | - | - | |
| Z | −11.55 | - | - | |
| Sig. asymptotic (bilateral) | ≈0 | - | - | |
| MGRTH-GRMMCE | Negative ranks | 40 | 160 | 133 |
| Positive ranks | 196 | 76 | 103 | |
| Z | −10.871 | −6.987 | −1.63 | |
| Sig. asymptotic (bilateral) | ≈0 | ≈0 | 0.103 | |
| MGRTH-MMALCER | Negative ranks | 32 | 29 | 232 |
| Positive ranks | 204 | 207 | 4 | |
| Z | −10.188 | −11.524 | −13.267 | |
| Sig. asymptotic (bilateral) | ≈0 | ≈0 | ≈0 | |
| MGRTH-HE | Negative ranks | 6 | 218 | 4 |
| Positive ranks | 230 | 18 | 232 | |
| Z | −13.228 | −12.981 | −13.287 | |
| Sig. asymptotic (bilateral) | ≈0 | ≈0 | ≈0 | |
| MGRTH-BBHE | Negative ranks | 8 | 214 | 15 |
| Positive ranks | 228 | 22 | 221 | |
| Z | −13.156 | −12.789 | −12.698 | |
| Sig. asymptotic (bilateral) | ≈0 | ≈0 | ≈0 | |
| MGRTH-MMBEBHE | Negative ranks | 9 | 212 | 30 |
| Positive ranks | 227 | 24 | 206 | |
| Z | −13.167 | −12.547 | −11.935 | |
| Sig. asymptotic (bilateral) | ≈0 | ≈0 | ≈0 | |
| MGRTH-QHELC | Negative ranks | 24 | 48 | 232 |
| Positive ranks | 212 | 188 | 4 | |
| Z | −12.182 | −10.467 | −13.303 | |
| Sig. asymptotic (bilateral) | ≈0 | ≈0 | ≈0 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mello-Román, J.C.; Vázquez Noguera, J.L.; Legal-Ayala, H.; García-Torres, M.; Facon, J.; Pinto-Roa, D.P.; Grillo, S.A.; Salgueiro Romero, L.; Salgueiro Toledo, L.A.; Bareiro Paniagua, L.R.; et al. Dermoscopy Images Enhancement via Multi-Scale Morphological Operations. Appl. Sci. 2021, 11, 9302. https://doi.org/10.3390/app11199302
Mello-Román JC, Vázquez Noguera JL, Legal-Ayala H, García-Torres M, Facon J, Pinto-Roa DP, Grillo SA, Salgueiro Romero L, Salgueiro Toledo LA, Bareiro Paniagua LR, et al. Dermoscopy Images Enhancement via Multi-Scale Morphological Operations. Applied Sciences. 2021; 11(19):9302. https://doi.org/10.3390/app11199302
Chicago/Turabian StyleMello-Román, Julio César, José Luis Vázquez Noguera, Horacio Legal-Ayala, Miguel García-Torres, Jacques Facon, Diego P. Pinto-Roa, Sebastian A. Grillo, Luis Salgueiro Romero, Lizza A. Salgueiro Toledo, Laura Raquel Bareiro Paniagua, and et al. 2021. "Dermoscopy Images Enhancement via Multi-Scale Morphological Operations" Applied Sciences 11, no. 19: 9302. https://doi.org/10.3390/app11199302
APA StyleMello-Román, J. C., Vázquez Noguera, J. L., Legal-Ayala, H., García-Torres, M., Facon, J., Pinto-Roa, D. P., Grillo, S. A., Salgueiro Romero, L., Salgueiro Toledo, L. A., Bareiro Paniagua, L. R., Leguizamon Correa, D. N., & Mello-Román, J. D. (2021). Dermoscopy Images Enhancement via Multi-Scale Morphological Operations. Applied Sciences, 11(19), 9302. https://doi.org/10.3390/app11199302









