Abstract
Lack of education is a major concern in underdeveloped countries because it leads to poor human and economic development. The level of education in public institutions varies across all regions around the globe. Current disparities in access to education worldwide are mostly due to systemic regional differences and the distribution of resources. Previous research focused on evaluating students’ academic performance, but less has been done to measure the performance of educational institutions. Key performance indicators for the evaluation of institutional performance differ from student performance indicators. There is a dire need to evaluate educational institutions’ performance based on their disparities and academic results on a large scale. This study proposes a model to measure institutional performance based on key performance indicators through data mining techniques. Various feature selection methods were used to extract the key performance indicators. Several machine learning models, namely, J48 decision tree, support vector machines, random forest, rotation forest, and artificial neural networks were employed to build an efficient model. The results of the study were based on different factors, i.e., the number of schools in a specific region, teachers, school locations, enrolment, and availability of necessary facilities that contribute to school performance. It was also observed that urban regions performed well compared to rural regions due to the improved availability of educational facilities and resources. The results showed that artificial neural networks outperformed other models and achieved an accuracy of 82.9% when the relief-F based feature selection method was used. This study will help support efforts in governance for performance monitoring, policy formulation, target-setting, evaluation, and reform to address the issues and challenges in education worldwide.
1. Introduction
The education system enhances nation-building, reduces poverty, and promotes learning opportunities [1]. Children’s education is essential for economic development. Past research revealed that initial schooling and the living environment significantly impact an individual’s personality and education [2]. Human capital is a fundamental resource for a country’s economic growth. Massive public investment in education facilitates human capital formation, which returns rewards in the form of higher productivity, higher wages, and financial growth [3,4]. Students’ academic performance plays a vital role in the generation of a qualified professional workforce, which is responsible for the country’s social and economic development. Student academic performance has attracted substantial attention in past research [5]. Student performance is based on personal, social, economic, psychological, and environmental factors. Most researchers used student results or grade point averages (GPA) to evaluate the individual performance. Various studies also considered teachers’ education, family background, gender, class environment, class size, lesson plans, reading materials, innovation in class, examination frameworks, family, work, and extracurricular activities [6]. The distribution of resources strongly affects the performance of rural and urban students, and mostly rural students appear to be deprived. This implies differences in student academic performance and other social outcomes such as intelligence, aspirations, grooming, motivation, and aptitude. Rural–urban inequality in academic performance remains challenging and unresolved and has become a global issue [2]. School performance varies among different regions and groups due to differences in educational opportunities. These variations in opportunities and achievement have become a global concern, especially for developing countries [1,4], and such problems have also been recorded in emerging regions for female students [1]. The quality of education has been declining across Pakistan, including Punjab. Conditions in public schools are not satisfactory, especially since the academic outcomes of students in rural areas are poor compared to those in the country’s urban regions [7]. The insufficient allocation of resources for education and a large budget deficit, especially in developing countries such as Pakistan, decrease school performance and present a challenge for policymakers. Limited studies on educational inputs and output in Pakistan mostly focused on specific regions [3,7]. One study conducted in Khyber Pakhtunkhwa revealed that essentials of educational infrastructure such as teaching quality, drinking water, gas, electricity, and school building conditions positively impact educational outcomes [3].
Researchers have recognised the impact of the surrounding environment on the performance of academic institutions [1,4,8]. Mostly, their focus remained on student academic performance [8,9], but some researchers targeted a particular region on a small scale [3,7]. Some research focused on early predictors of student success rates in higher education institutions (HEIs) [10]. Some studies considered basic facility parameters (i.e., electricity, gas, libraries, and teaching quality) and showed their impact on schools in some districts of Khyber Pakhtunkhwa province, in Pakistan [3]. Educational opportunities reflect the local school environment and socio-economic factors [1] because the performance of educational institutions in urban areas is different from that in rural areas [1,2,4]. The disparities in school education are due to regional differences and gender inequalities across Turkey [11]. The association of different parameters in different country regions was analysed. In some regions, the number of females in the local population is higher because males tend to migrate earlier for employment.
Moreover, institutional facilities and learning environments directly affect the performance of school institutions. Punjab’s school education department conducts quarterly district rankings to track school performance and timely highlight those schools that are lagging. This ranking is based on various indicators such as student attendance, teacher presence, and the availability of boundary walls, toilets, drinking water, and furniture. The ranking statistics still show the need to uplift educational levels in different districts of Punjab [12]. Discovering new information from a massive amount of data is challenging and sometimes too expensive [8]. The most commonly adopted process used to extract hidden information from a large amount of data is data mining (DM). The approach used to extract meaningful knowledge from educational data is known as education data mining (EDM). Different machine learning-based models are used for performance measurement, including random forest, decision tree, K-nearest neighbour, and naïve Bayes [13]. This study proposes a framework to measure the institutional performance based on key performance indicators through data mining techniques.
Contributions: This study offers several contributions in the education domain to measure the performance of educational institutions.
- A state-of-the-art dataset has been collected regarding the different indicators to measure the performance of educational institutions. The collected dataset was prone to noise, biases, and missing and outlier values.
- Much work has been done to evaluate individual schools or measure student performance rather than institutional performance. To the best of our knowledge, no work has been done to measure institutional performance. However, a novel method for performance measurement of public institutions through machine learning models has been proposed in this study.
- Regarding institutional performance, a regional perspective has been applied. This indicator has not been explored in the literature to investigate the performance of institutions.
- Significant feature selection techniques were combined with machine learning models to develop the proposed framework for the performance measurement of public schools. It has also been observed that differences in demographics and provided facilities emerged due to regional differences.
- This study will help support governance for performance monitoring, policy formulation, target-setting, evaluation, and reforms. The achieved results will help to address the issues and challenges in education worldwide.
The rest of the paper is organised as follows: Section 2 provides the related work. Section 3 describes the proposed methodology of our implementation methods. Section 4 presents the implementation results, while Section 5 analyses the results and implications of our study. Finally, we state our conclusions in Section 6.
2. Literature Review
Jamil et al. [3] explained the effect of institutional factors on student educational performance. The research was carried out on a large dataset consisting of 1642 schools in Khyber Pakhtunkhwa province, Pakistan. A positive relationship was found between student performance and institutional factors such as the availability of electricity, gas, and library facilities. In rural areas, electricity and gas had a positive impact, and well-constructed schools improved students’ outcomes in these areas. However, factors such as infrastructure and teaching quality were not considered in their study. Tesema and Braeken [1] investigated students’ educational achievement in terms of regional and gender differences. The regional differences were based on socio-economic and school environment-related factors. The analysis examined 2 years of grade 12 results. The results in developed regions were found to be better compared to those in emerging regions.
The results also revealed that those regions where the gender gap was minimal had a higher education rate than those with a high gender gap. But their study only considered one district, which may not be generalised. Eduardo Fernandes et al. [8] presented a predictive analysis of students in public schools in terms of their academic performance. A data mining classification model, gradient boosting machine (GBM), was implemented to predict student academic outcomes at the end of the year. The results showed the most significant attributes for prediction were students’ grades and their class absence rates. Moreover, other important attributes such as the school medium, school segregation by gender, and the number of teachers were also crucial.
Gumus and Chudgar [11] concluded that unschooled children were a consequence of regional differences and gender inequalities. The analytical approach of binary logistic regression was applied to the dataset. The results indicated that student demographic characteristics such as gender, age, and home factors such as parent education and family financial status were significantly associated with students’ school participation. Their study was limited in the perspective of the impact of regional dimensions on student performance. It concluded that disparities among regions must be considered in terms of socio-economic, demographic, and geographic factors that affect school participation. Nurliana and Sudaryana [14] investigated the factors that improve the student learning process and increase student knowledge. The experiment was performed on the dataset of students and teachers at one school for 1 year. Some students were taught using the old, traditional methods while other students were taught with the latest methods and proper equipment and facilities. The behaviour and interest of students revealed that better instructional tools and facilities increase the interest of students toward learning. However, they could not be considered key factors like number of students, number of classrooms, or availability of classrooms.
Hameen et al. [15] considered school facilities factors and determined their impact on student attendance, academic performance, and health. Their research covered schools in the United States. The analysis showed that schools with good classroom heating facilities and air conditioning for the summer season had a high attendance rate compared to schools that lacked these facilities. It was concluded that investments in school mechanical and plumbing systems improve student health and lead to better academic outcomes. Their study did not consider the availability of playgrounds in the schools. Belmonte et al. [16] explored the impact of investments in school infrastructure on student outcomes. The research was conducted with data on high schools that received extra funds following the 2012 earthquake in Italy. Their approach utilized a quasi-experimental design and an instrumental variable strategy. Variations in the distribution of funds were noted. The results revealed that spending more on school infrastructure improves student outcomes. A better learning environment boosts motivation to study, in turn increasing student achievement. Gul and Farooq [17] highlighted the World Health Organization (WHO) guidelines for developing countries such as Pakistan to improve access to the physical environment of schools. The analysis was performed on schools in one region, Multan. A questionnaire approach was adopted for analysis purposes and to obtain feedback from school teaching staff. The questionnaire consisted of 10 core indicators. The 10 indicators were water facilities, water quantity, water quality, hygiene promotion practices, control of vector-borne diseases, toilet and handwashing facilities, cleaning and waste disposal systems, school safety, school building conditions, and supportive classroom conditions. Based on the analysis results, it was concluded that schools did not meet these 10 core indicators due to a district score (1.01) that was below the WHO’s recommended score (1.5). These deficiencies were causes of poor student performance outcomes and had a negative impact on student health. However, the researchers only considered one district in their study. An overview of existing research techniques is presented in Table 1.

Table 1.
Overview of existing techniques.
3. Methodology
The traditional cross-industry standard process for data mining (CRISP-DM) was utilised to predict the performance of schools, as shown in Figure 1. The methodology consists of dataset collection, data preparation, modelling, and validation of results. Firstly, Punjab annual census data were obtained from the official website. Secondly, data preparation techniques were applied, i.e., data cleaning, data transformation, data normalisation, and discretisation. Thirdly, various feature selection techniques were utilised to extract significant features. Fourthly, various machine learning classifiers were employed to train the model. Lastly, different performance measures were utilised to check the performance of classifiers. Microsoft Azure Machine Learning Studio and WEKA were utilised for data analysis, preparation, and modelling.
Figure 1.
Proposed methodology.
3.1. Dataset
In Pakistan, students are awarded a secondary school certificate (SSC) after completing 10 years of schooling, also known as Matric. So, the study was delimited to 10th grade students in public schools. The dataset contained 108 attributes related to student enrolment, employee availability, location, the status of school basic facilities, and student outcomes (Matric results). The raw file is available at http://dx.doi.org/10.17632/637d4s7vjh.1. A few attributes in the raw data, e.g., school gender, library presence, school shift, school medium, and building condition were categorical attributes that contained various categories. Furthermore, many attributes, e.g., total schools, total urban schools, total computer labs, and total available classrooms, students without furniture, open-air class sections, students with furniture, total rural schools, total students, total playgrounds, total science labs, school with electricity facility, deficiency of classrooms, and total teachers were continuous attributes. These attributes contained numerical values after data pre-processing (data discretisation); continuous attributes have were converted into categorical (specified range) attributes. The target attribute was categorised into three classes based on institution-wise Matric marks: below 50% for low, between 51 and 70% for medium, and more than 70% for high. The Matric result or class attribute contained three values, i.e., high, medium, and low.
3.2. Data Preparation
This covers the steps related to the preparation of the dataset from raw data. Data preparation tasks are often performed repeatedly and not in any predefined order. These tasks include data cleaning, data normalisation, outlier detection, data reduction, and data transformation. Data preparation aids in generating a good model that may help to obtain effective results.
3.2.1. Data Cleaning
In data cleaning, redundant instances are detected and removed from the data. Data cleaning includes outlier detection and missing values imputation. Certain attributes observed to contain missing values, such as open-air class sections, total functional classrooms, are replaced with median values by using Equations (1) and (2):
Outliers are those extreme values that show extreme deviation from mean values of the data, which can cause an error. Some negative values were observed in the “students without furniture” attribute, and was replaced with 0 after comparing and analysing the other instances.
3.2.2. Data Transformation
Data transformation has a meaningful effect on data mining since it helps fix the missing values in the data and brings information to the surface by creating new features to represent trends and other ratios. Some features, such as total playground, schools with electricity facilities, total computer labs, and total science labs, held values in Yes and No, which were converted to 0, 1. The attribute “deficiency of classrooms” was calculated based on available classrooms and by considering the general formula of one room for 40 students as stated in Equation (3):
The attribute “Students without furniture” was calculated based on the “Students with furniture” and “Total Enrolment” as described in Equation (4):
The attribute “school location” was further split into two attributes (rural, urban) based on type of area. The data was converted into tehsil wise by aggregating values (by applying sum, count, average functions) to prepare the attributes such as total school, total teachers, total students, total rural schools, total urban schools, open-air class sections, total computer labs, total science labs, total playgrounds, total available classrooms, deficiency of classrooms, students with furniture, students without furniture, schools with electricity facilities, and Matric result.
3.2.3. Data Normalization
When multiple attributes have different scales, results may be affected. Normalisation brings all attributes to the same scale. All attributes were scaled into smaller ranges between 0 and 1. All integer attributes such as total computer labs, total science labs, and playgrounds were scaled between 0–1. The most common normalisation method is the Min-Max normalisation, used in this study. Furthermore, the Min-Max technique is efficient because results may be enhanced when data have outliers or missing values, as in our dataset [18]. This technique scaled all the numerical values of a numerical feature to a specified range and computed them through Equation (5).
3.2.4. Data Discretisation
In data discretisation, numeric data are transformed by mapping values to interval or concept labels. This could be achieved using various techniques such as binning, correlation, cluster, and decision tree analysis. The binning method was utilised for data discretisation in this study. Additionally, the equal-frequency interval-based discretisation method was employed. In this method, the minimum and maximum values of all discretised attributes are determined. Then, these values are sorted in ascending order. The sorted values are further divided into k intervals, as each interval contains data instances. There may occur continuous value, which can cause the occurrence to be assigned into different bins. The limitation of equal width interval discretisation is overcome by adopting the domain’s approach according to the same distribution of data points. This method also tries to overcome the limitation of equal-width interval discretisation. In this research, all attributes of the dataset were discretised by this method.
3.3. Feature Selection
Feature selection was used to combat the curse of dimensionality and accelerate the training phase of machine learning algorithms. This was done by selecting only the most important or relevant features according to certain measures. Two significant classifications for feature selection are the wrapper and filter methods. Wrapper methods utilise the machine learning algorithm to test each feature subset. The result is typically better than filter methods but at the cost of further computational complexity. Filter methods are independent of the machine learning method to be applied but perform much faster. Data features were reduced in this process, but data integrity was also preserved to make it suitable for further analysis. Irrelevant and useless features were also eliminated for the quality preparation of data to obtain good results.
3.3.1. Information Gain
The concept behind information gain (also known as entropy) measures the bits of information available for class prediction. Given a single attribute, each value will be evaluated through Equation (6):
where denotes the probability of class 2 occurring with the attribute value, indicates the probability of class 1 occurrence, and indicates the probability of class 0 occurrence. Given these values, the expected new entropy can be calculated through Equation (7):
where denotes the probability of the value occurring, and indicates the entropy for this value. Then, the information gain using Equation (8) will be:
Original entropy is simply the entropy using the probability of each target class occurrence. Given that the original entropy of the data remains static, the smaller the expected entropy value, the larger the information gain. In the context of feature selection, a feature with the lowest expected entropy will be seen as the most valuable by this measure.
3.3.2. Relief-F Algorithm
The Relief algorithm [19] is a generic method initially developed for classification problems with binary classes. It attempts to estimate the quality of predictors and of how well their values distinguish between instances near each other. For a randomly selected training instant , the Relief algorithm finds its two nearest neighbours: one from the same class called the nearest hit , and the other from the different class, called the nearest miss . It updates the quality estimation for all predictors depending on their values for , , and . If instances and have different values of the predictor , then the predictor separates two instances with the same class, which is not desirable, so the quality estimation is decreased. On the other hand, if instances and have different values of the predictor , then the predictor separates two instances with different class values, which is desirable, so the quality estimation is increased. The whole process was repeated times. The Relief-F algorithm [20] is an improved version of the Relief algorithm used for classification problems with more than two classes. It employs more than a single nearest neighbour and can handle missing predictor values. The Relief-F algorithm is another extension to handle regression problems. In contrast to the majority of heuristic methods for estimating the quality of predictors, which assume the conditional independence of the predictors, relief algorithms can determine the quality of the predictors with high dependencies between themselves.
3.3.3. Wrapper Method
In the Wrapper method, a predictor (or classifier) is used to evaluate the feature subset. This method takes classifier performance, i.e., error rate, accuracy, etc., as a measure to determine the relative usefulness of a subset. Before the selection process is performed, we need to define the search space of all possible variable subsets and which classifier is used, and assess classifier performance and stopping criteria [21]. The subset search can be performed sequentially or heuristically, and the proposed subset is evaluated until maximum performance is gained with the minimum number of features. Since the Wrapper method uses particular classifiers as the main component for evaluation, the whole process highly relies on a specific classifier being used. The most popular classification algorithms used for the Wrapper method are SVM, RF, and ANN. Defining how to search the subset space is an important step in the Wrapper method. Generally, a subset search algorithm can be classified into two types: sequential selection algorithm (SSA) and heuristic search algorithm (HSA) [22].
The SSA technique can be performed in two ways: forward selection (SFS) and backward selection (BFS). Forward selection starts from an empty set of feature subsets, then adds a feature that maximises objective function one by one until there is no more improvement in objective function score. The subset that provides the best objective function score is chosen and validated. A backward selection has the same idea, but it starts from the full-feature set and removes the most features that reduced the objective function score. One drawback of SSA is that it is prone to “nesting effects”, which means the already selected or removed feature cannot be removed or selected in later stages. Some variations of SSA are developed to avoid the nesting effect, such as “plus-L-minus-R” selection (LRS), sequential backward floating selection (SBFS), and sequential forward floating selection (SFFS). The HSA approach is based on heuristic optimisation using an evolutionary algorithm to find the optimal solution of the objective function. Genetic algorithm (GA) is often used for HSA. Individual features and output variables are represented as a gene. An individual represents a single solution containing possible feature combinations (in GA terms, also called chromosome). HSA tries to find an optimal solution by selecting the best individual in the population (collection of random solutions) and producing a possibly better set of solutions through mating, reproduction, and induced mutation [23].
The wrapper method can produce the best feature subset that suits a particular classifier and scores high in performance evaluation, typically better than the filter method. However, its reliance on particular classifiers and overtraining might lead to overfitting or poor generalisation. The wrapper method requires a training classifier model for each subset evaluation. An exhaustive search could result in the best accuracy but would be too expensive to perform, especially when the number of features or samples is enormous. Nevertheless, even with more advanced search algorithms, the computation required to achieve the desired criteria could still be too much.
3.3.4. Lasso
The famous least absolute shrinkage and selection operator (Lasso), proposed by Tibshirani [24], is very popular because of its variable selection property and has been used in many fields of statistics. This method shrinks values of some coefficients to zero by a constraint on the sum of absolute values of regression coefficients so that Lasso can serve as a tool for variable selection. The substantial difference between Lasso and the subset selection procedures or the information criteria is that Lasso selects variables, estimates the coefficients simultaneously, and retains good subset selection and ridge regression features. Lasso is a regularisation and variable selection algorithm that performs mostly better than other methods. Suppose we have a selected subset of features with size k, denoted by is the vector of selected features for individual, and is the intercept, and is the parameter vector. The simple logistic regression of the selected features is explained through Equation (9):
We can estimate by minimising the negative log-likelihood via Equation (10):
We add L1 Lasso (Least absolute shrinkage and selection operator) penalty for obtaining sparse solutions and enhancing predictive performance. The Lasso estimator is obtained from the penalised minus log-likelihood using Equation (11):
where, is the total number of dummy variables of selected features, and is the tuning parameter. Note that the intercept is not included in the penalty term. Lasso penalty corresponds to a Laplace before Bayesian inference. Hence, it will obtain a subset of important features with non-zero coefficients and shrink the reset to zero. Increasing will shrink more coefficients to zero by adding a heavier penalty. Because this optimisation problem is convex, it can be solved efficiently for large data. There are several algorithms for calculating the Lasso estimator, among which coordinate descent performs the best. Coordinate descent optimises each parameter separately while holding all others fixed. Feature selection reduced the data dimensions by reducing the number of features. Initially, there were 108 attributes in our data set. Fourteen most-contributing attributes were selected for school performance measurement through various feature selection methods, as shown in Table 2.

Table 2.
Significant feature selection through feature selection methods.
3.4. Modelling
In this study, the following models were utilised for the performance measurement of institutions. Machine learning models are also widely used in the domain of healthcare [25,26,27], robotics [28,29], and business [30,31].
3.4.1. J48 Classifier
C4.5, known as J48, is a classifier first developed by Ross Quinlan and an extension of the ID3 algorithm. Most of the machine learning classifiers adopt greedy and top-down approaches for making a decision tree. In J48, classification is based on existing observations and training datasets; new data is labelled. While formulating a decision tree, the training dataset is partitioned into smaller partitions by dividing and conquering at each node. The dataset consists of collections of objects and objects that can be either an activity or an event. Each tuple of the dataset contains a class label that defines which object belongs to which class. If the tuples belong to different classes, then further splitting can be performed. While partitioning a dataset, a heuristic approach is followed, which chooses an attribute for the best partition known as the selection measure. The type of branching formation at each node is the responsibility of this selection measure. Like information gain, the Gini index is an example of partitioning the node to multi-label and binary, respectively [32]. For a better working understanding, let us have dataset , where denotes the dependent variable n representing the number of independent variables, the value of i can be from 1, 2, : :: , K. K represents the classes of the dependent variable. At every partition, a new node is added to the decision tree. In S partition, X is chosen for further partitioning into different sets like . These new child nodes are then added into the main node S of the decision tree. The primary node S is labelled with text X and newly created partitions are partitioned again recursively. The partition will not be further split into sub-partitions if all records in a partition have identical class labels. Its corresponding leaf will be labelled as a dependent variable.
The following steps are followed to construct a decision tree using J48. In step 1, we calculate the Entropy of training set S through Equation (12).
where samples in the training set are represented with |S|. is identified as dependent variable, i = 1, 2, : : : , K. K represents classes belong to the dependent variable, and freq(, S) has total samples that class contains.
In step 2, for partition, Information Gain X(S) is calculated for the test attribute X as explained in Equation (13):
where is denoted as a subset of S for that particular ith output, and |Si| defines the dependent variables of a subset. L represents the test outputs, X. That subset will be selected as a threshold for a specific attribute partition to provide maximum information gain. S and S-Si partition will be the branch of the node. If the instance belongs to the same class, then the tree’s leaf will be labelled and returned as a dependent variable (class).
In step 3, partition information value Split Info(X) will be calculated by acquiring for S partitioned into L subsets through Equation (14):
In step 4, we calculate using Equation (15):
In step 5, based on the value of the gain ratio, the attribute having the highest value is declared root node, and the same computation is repeated from step 1 to step 4 for intermediate nodes till all the instances are exhausted and reach the leaf node as per step 2 [33].
3.4.2. Support Vector Machines
Support vector machines (SVMs) are primarily constructed for multiclass classification, although they can perform binary separation. The idea of SVMs is that a classification problem with number of input features can be solved by finding a hyperplane of dimension. The hyperplane separates the N-dimensional space in parts where the data points in the same subspace also belong to the same class. The equation for the separating hyperplane will have several solutions [34]. For the sake of simplicity, consider a linear SVM where, then the hyperplane is a line. The line can be moved sideways between its two closest points to separate and even be tilted in new angles and still separate training data points of the N-classes into their own spaces. A poorly chosen hyperplane out of the alternatives may make the performance on test data suffer, although the training performance is the same. A similar problem will be found in higher dimensions and non-linear settings as well. To obtain a good model, a good hyperplane must be found. One such hyperplane is the maximum margin hyperplane. The maximum margin hyperplane is the maximum distance to the data points closest to the hyperplane, thus a hyperplane with the maximal possible margin.
The data points on the margin to the hyperplane are called “support vectors” since they support the placement of the hyperplane. The maximal margin hyperplane is only dependent on the support vectors for its positioning. If the training set is changed by adding or removing data points, it will not affect the classifier unless the set of support vectors is altered. However, it is not satisfactory that the classifier can be fundamentally changed by adding just one training sample. Moreover, the scenario that there is no perfectly separating hyperplane needs a solution. A solution for both problems is to introduce a soft margin. The soft margin introduces an error tolerance of the model, which allows some of the training data points to be on the wrong side of the margin, or even the wrong side of the hyperplane. The constraint added is that the total errors may sum up to a specific constant but no more. Data points within the margin will also be considered as support vectors.
A linear separating hyperplane will follow Equation (16):
where are the parameters to find by training. The corresponding classification function is explained in Equation (17):
Here, are the features of the sample to classify. The class of a new data point is determined by whether has a value above or below zero. The linear classification function of the SVM utilises the inner products of the observations. Therefore, the classification function can be rewritten as described in Equation (18):
where are the parameters found by the training, and is the inner product between observations (Equation (19)):
SVM has primarily been constructed for multiclass classification. The idea of SVM is that a classification problem with number of input features can be solved by finding a hyperplane of dimension. SVM classification is an optimisation problem. Linear discriminant analysis (LDA) and kernel functions are two analytical solutions used for optimisation. We utilised kernel methods for SVM to transform a linear classifier into a non-linear classifier. In the linear classifier, the inner product is called the kernel function, or Kernel for short. The kernel of a classifier quantifies the similarity of two observations. To separate classes that have non-linear boundaries, the hyperplane must be described by a non-linear equation. If the non-linear equation is polynomial, the classifier function will use a polynomial kernel, where d is the degree presented in Equation (20):
Past researchers also utilised LDA, which uses the entire dataset to estimate covariance matrices and is also prone to outliers that are a significant limitation; hence, we utilised kernel functions instead of LDA. Our dataset also had diversity in values, performance or percentage of results that differed significantly between schools in big cities such as Lahore and the schools in Southern Punjab, which made the performance values of the schools in backward areas an outlier. As in our dataset, few attributes or features had outlier values, e.g., some negative values were observed in the “students without furniture” attribute, which was replaced with zero after comparing and analysing the rest of the instances. LDA does not work well if the dataset is imbalanced (i.e., the number of objects in various classes is different). Our dataset had three classes in the class label that were different because only a few cases were good and bad, whereas most cases were in the medium category. We implemented the LDA, but the results were not persuasive at all. We chose SVM for further experiments and analysis.
3.4.3. Random Forest
The random forest (RF) algorithm is based on the decision tree model and is straightforward, flexible, and fast. RF, including nominal, binary can handle different types of data and numerical, and has high predictive capability. RF works by building multiple trees and aggregating trees to generate efficient results [35]. The trees are generated based on seeds. Randomness in seeds generates random trees that are efficient and result in better prediction.
Similarly, a random and different subset of attributes gives more accurate results on large datasets. The classifications for the new input data are based on each contributed tree’s functions for one class. RF then performs prediction by checking the plurality of votes for the new instances. Every internal node tests an attribute, and the test result is represented by edge [36]. RF is based upon the concept of bagging and boosting. In bagging (bootstrapping), a model is constructed again and again, sampling from a large set of examples used for training, and then results are aggregated through a majority vote. So, to construct a good classifier from uncorrelated weak classifiers, boosting is an optimal solution. The tuning of hyperparameters controls the number of features in each tree [37].
RFs are ensemble learners, which means many weak “base learners” contribute their votes for prediction. Base learners are called decision trees in RF, consisting of a branching composite of binary decisions for separating the data into classes. At each node of the tree, the input is separated by choosing threshold t and a single feature d. The resulting split should have minimal impurity (by mean of class labels). Entropy H is presented for two-class learning as explained in Equation (21):
where c denotes the class and represents the proportion to the examples in c. Maximisation in information gain is equivalent to minimising entropy. In RF, the number of trees and selection of features are controlled by tuning hyperparameters. An importance matric can be assigned to the features based on their impact on node impurity, weighted by the importance and worth of the node in classification [38]. In a single tree t, this feature importance for feature d is formulated as presented in Equation (22):
, denotes the entropy before node splitting, and represents the entropy after the split of child node s. represents the set of all nodes split by feature d. For the given node n, denotes the proportion of samples at that node. The scores are overall averages of the built decision tree T for preparation of a resultant importance weighting: [39].
Combining the multiple decision trees to attain better variance reduction results is also important, but there is a potential downside. The RF algorithm selects a fixed number of predicators from the available features in the pool at each split to overcome this. The predicators of all individual decision trees are combined to prepare the final predicator by averaging the majority vote [40]. A few more reasons support the excellent prediction power of the RF algorithm and its wide adoption. One key feature of this algorithm is its stabilisation with fewer iterations than another state-of-the-art ensemble method such as boosting. Secondly, it is working, visualising, and tuning on different inputs that influence and attract users.
3.4.4. Rotation Forest
The main difference from other tree algorithms is that rotation forest does not require as many trees to be created to achieve impressive accuracy. Unlike the random forest, the rotation forest is used when the number of ensembles is small. Rotation forest is an ensemble-based method first proposed by Rodriguez et al. [41]. The rotation forest model requires some parameters that the user defines. Hence, it spares much time in creating trees, which is relatively time-consuming.
Interestingly, the authors of the algorithm claim that an underlying estimator can be not only a tree but anything else, as well, although what remains unchanged is that it still uses bagging as one of the basic techniques. The user should specify the number of trees. When that is done, the algorithm looks like this:
For each tree T, perform the following:
- Split the attributes in training set into K non-overlapping subsets of equal size.
- For each of the K datasets with k attributes, perform the next steps.
- Create a rotation matrix of size N × N, where N is the total number of attributes. In the matrix, each principal component should match the position of the feature in the original training dataset.
- Project the training dataset on the rotation matrix using matrix multiplication.
- Build a decision tree with the projected dataset.
- Store the tree and rotation matrix.
3.4.5. Artificial Neural Networks
An artificial neural network (ANN) consists of several interconnected processing units that process information. It contains three types of layers: the first is called the input layer, then the hidden layer, and the last output layer. The transformation is carried out through the centred layer (hidden layer) between the input and output layer through units to detect complex patterns and learns accordingly. The idea of ANN working has been perceived by the working mechanism of the human brain. The brain consists of billions of neurons, and a single neuron is known as a perceptron, and each neuron is connected to others by axons. The neurons are finally connected with the synapses, which allow neurons to pass the signal. The neural network is formed with a large number of simulated neurons.
Similarly, ANN contains multiple nodes in itself that are connected. The joining among units is denoted by weight. Inputs passed to the ANN consist of different values that are connected with weight vectors. The weight can be either positive or negative. For results generation, the function used to sum the weights and map to output is .
ANN has been used for both supervised and unsupervised learning. This study applied supervised learning because the input and output were known and provided to the model. The model was tuned with different values to adjust the weights to the best to obtain the expected efficient output [35]. In multiclass classification, classifiers are used to predict multiple outcomes. In this study, a multiclass neural network was used to build a classification framework. Let us have K classes and want to classify one instance from one class. Then, the best choice is to use a linear neural network with multiclass classification. It is an extension of the binary classification setup. The second layer node will generate output as 0, 1 … K-1. The basic working principle of a multiclass artificial neural network is shown in Figure 2.
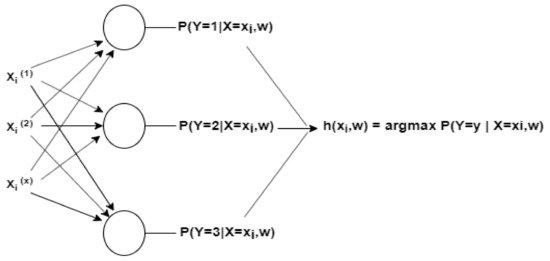
Figure 2.
The basic working mechanism of a multiclass artificial neural network.
We have |w| = MK, where M denotes the number of features and K represents classes. If K = 3 and M = 3, then the total weight will be formed as 9. To support the neural network view of multinomial logistic regression, we receive help from binary logistic regression (Equation (23)) as:
In the case of K number of classes, we will have Equation (24):
In the above equation, Y is the dependent variable representing a value we are trying to predict. The variables (Xi = 1 to n) are used to predict values for the dependent variable. W represents weight value, one for each data instance. It shows the strength and type of relationship with a particular data instance with Y. Larger values of weight represent a stronger relationship [42].
4. Results
In machine learning classification, the results are measured on the basis of accuracy, recall, precision, F-measure, ROC, and root mean square error (RMSE). Accuracy is the ratio of correct predictions of the sample over the total number of predictions. The results may vary among DM models due to internal changes in processing functionality. All of the evaluation metrics are built on four types of classifications: true positives (TP), true negatives (TN), false positives (FP), and false negatives (FN).
For binary classification, the accuracy is measured using Equation (25) or Equation (26):
TP represents true positive, TN is a true negative, FP is false positive, and FN represents false negative. AUC-ROC is also used to calculate the performance of multiclassification problems. ROC is a probability curve that stands for Receiver Operating Characteristics, and Area under the Curve (AUC) measures the degree of separability. It states the capability of the model to distinguish between classes, and the higher the AUC, the better the model distinguishes between classes. The ROC curve is plotted with TPR against FPR, where TPR is on the y-axis and FPR is on the x-axis. True positive rate (TPR) or recall value is calculated through Equation (27):
False positive rate (FPR) is calculated through Equation (28):
Precision is used to determine the number of predicted positive instances correctly classified by the algorithm as presented in Equation (29).
F-measure is used to represent the harmonic mean between two parameters, precision and recall, as shown in Equation (30). A high value of F-measure indicates that both precision and recall are reasonably high.
RMSE is a frequently used measure of the differences between values predicted by a model and observed values. The RMSE represents the sample standard deviation of the differences between predicted values and observed values. where is the predicted value and is the true value for subject . The RMSE values are calculated through Equation (31):
As ML models grow rapidly, they also need more tuning and configuration. This tuning often comes in the form of hyperparameters. The hyperparameter describes all parameters that have to be determined before the actual process of fitting a model to the data is started. These hyperparameters exist because data-based models are designed to work in different scenarios, requiring both algorithm and model modifications. In the past, these modifications were often performed by using domain knowledge or rules of thumb. However, hyperparameters are generally challenging to set. Hyperparameters in machine learning describe variables that modify how a particular model is derived from data. These parameters can modify the algorithm that performs this process, but they can also be a model parameter that the algorithm cannot reasonably determine. Most model parameters are determined through training by applying the machine learning algorithm to the data. Hyperparameters are usually not independent of each other. The number of possible combinations of hyperparameters increases exponentially with the number of hyperparameters. Because training machine learning models is computationally expensive, the main goal is to find good or optimal points with as few function evaluations as possible. A common hyperparameter in the neural network case is the learning rate. It changes the rate at which neuron weights are adjusted per learning step and is essential for the performance of a neural network. While the consensus is that low learning rates slow learning down, high learning rates might keep the network from converging. This study utilised J48, SVM, RF, rotation forest, and ANN for training with various hyperparameters. The ranges of the hyperparameters are presented in Table 3.

Table 3.
The ranges of the hyperparameters of the classifiers.
Usually, machine learning models split data sets into training and testing sets. Training is used to train the model while testing sets are used to test the model. Various approaches such as k-fold cross-validation and train test Split are used to validate results [8,35,43]. In the train test split, values are set for the model on how much data the model has to train and test. Mostly, it performs well for large datasets. In this research, the 10-fold cross-validation technique was utilised to obtain effective results on small datasets. The cross-validation approach works, as it splits the dataset into three portions to train, test, and validate the set. K sets the value to guide the model regarding how many equal folds of datasets to prepare after division. The first fold was used for testing purposes, the remaining k − 1 folds were used to train the model, and the whole process was repeated k times.
In this study, various machine learning models with feature selection methods were used. The stopping criteria for feature selection methods was set so that when the performance of the models decreased, the execution of feature selection methods stopped. The fourteen most significant features, as selected through feature selection methods, were used. The J48 algorithm derived results by using the approach of post-pruning. Post pruning is the process of evaluating decision tree error at each decision tree junction. The pruning of decision trees optimises the computational efficiency of the model. The pruning method reduces the size of the tree and unnecessary complexity. To test the effectiveness of post-pruning, the hyperparameter is often labelled as a confidence factor. If the value of the confidence factor is kept low, then the amount of post-pruning is decreased.
Moreover, the minimum instances per leaf node are set, which means to set the minimum amount of separation. It guarantees that at least two of the branches have the minimum number of instances at each split. For example, if one instance is separated from 100 instances, it does not give much information. The J48 decision tree model was combined with feature selection methods. The best results were obtained using the relief-F-based feature selection technique, which achieved maximum accuracy of 68.5% with an ROC value of 0.63 when the model has was with a confidence factor of 0.50. The minimum number of instances per leaf node was 6. The complete results for the J48 classifier with feature selection methods are presented in Table 4. After the J48 decision tree, SVM was utilised to obtain more effective results.

Table 4.
Performance of J48 classifier through various feature selection techniques.
In SVM, the kernel type was selected. Hence, the kernel type, i.e., PolyKernel, Normalized PolyKernel, and radial basis function (RBF) Kernel, were chosen for better performance. In this experiment, the model was initially tuned with PolyKernel, and the predicted results revealed an accuracy of 61.4% while employing an information gain-based feature selection method. The model was again tuned with different feature selection methods, and this process was repeated multiple times until the highest accuracy value was achieved. The highest accuracy of 68.5% with RBF Kernel was achieved while employing the Relief-F based feature selection method. Complete results for the SVM classifier with various feature selection methods are presented in Table 5. After the SVM model, the random forest was utilised to obtain more effective results. Several machine learning models such as random forest and ANN are non-deterministic, requiring a random seed argument for reproducible results. Random seed denotes the random initial value for the algorithms.

Table 5.
Performance of SVM classifier through various feature selection methods.
We used different seed values to perform the experiments. In random forest, multiple trees were built with seeds that made a forest because the similar nature of trees decreased model performance. So, to achieve better performance, individual trees were built differently. The randomness in the generation of trees could be achieved with the use of random seeds. In this experiment, the model was initially tuned with 50 trees with random seed =7, and the predicted results revealed an accuracy of 68.5%. In contrast, the information gain-based feature selection method was employed. The model was again tuned with different combinations of values, and this process was repeated multiple times until the highest accuracy value was achieved. The highest accuracy of 71.3% with an ROC of 0.65 was obtained when the number of trees was set to 100, and the random seed was set to 8 while using the relief-F-based feature selection method. Complete results for the RF classifier with various feature selection methods are presented in Table 6. After the random forest, the rotation forest was utilised to obtain more effective results. In the rotation forest, ensemble trees were built because the similar nature of trees decreased the model performance. So, to achieve better performance, individual trees were constructed differently. In this experiment, the model was initially tuned with an ensemble size of 5, and the predicted results revealed an accuracy of 65.2%.

Table 6.
Performance of random forest classifier through various feature selection techniques.
In contrast, the information gain-based feature selection method was employed. The model was again tuned with different combinations of values, and this process was repeated multiple times until the highest accuracy value was achieved. The highest accuracy of 73.2% was obtained when the ensemble size was set to 15 while using the relief-F based feature selection method. Complete results for the rotation forest classifier with various feature selection methods are presented in Table 7.

Table 7.
Performance of rotation forest through various feature selection techniques.
After J48, SVM, random forest, and rotation forest, artificial neural networks were used to achieve more efficient results. The model was used to create a neural network that predicted the target based on multiple input values. The model was tuned with different parameters to generate the best result. One of them is known as random number seed. It was used to ensure repeatability across runs of the same experiment. The model was initially tuned with 6 random seeds, and the predicted accuracy was recorded as 79.0% while using the information gain-based feature selection method. It was observed that the model predicted its best results with an accuracy of 82.9% when the number of random seeds was 10 while utilising the relief-F based feature selection method. Complete results for the artificial neural network classifier with different feature selection methods are presented in Table 8.

Table 8.
Performance of multiclass neural network through various feature selection techniques.
Among the five classifiers utilised in this study, the artificial neural network outperformed and obtained the highest accuracy of 82.9% while utilising the relief-F based feature selection technique, as shown in Figure 3. It was observed that ANN also performed efficiently while utilising other feature selection techniques. The performance of ANN was also good while evaluating other performance metrics.
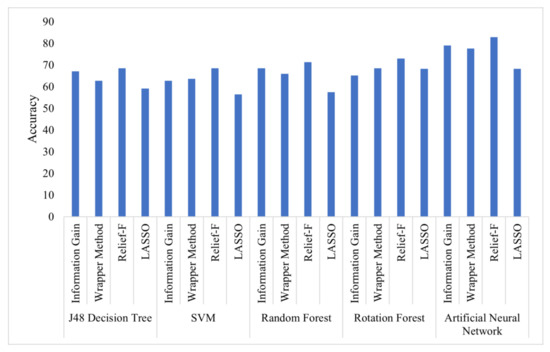
Figure 3.
Performance comparison of models based on accuracy with utilisation of various feature selection techniques.
5. Discussion
In the past, most educational research has been focused on and evaluated students’ academic performance in specific institutions or regions. Performance was calculated with consideration for various influences including socio-economic and demographic factors as well as students’ personal, family, and academic backgrounds. Apart from student academic results, other factors also have a substantial impact on the performance of any educational institution. The present study focused on the importance of other highly influential factors along with student academic results, such as the students per teacher ratio, the number of schools in a region, whether schools were located in rural or urban areas, the availability or lack of classrooms, electrical facilities in schools, availability or lack of furniture for students, open-air classes, computer lab facilities, science labs, and playgrounds in schools. Previous research [44,45,46,47,48] suggested that data pre-processing (normalisation, discretisation) techniques enhanced classifier performance, as these techniques reduce the biases among features. Furthermore, related studies showed that the min-max normalisation method performed better than other data normalisation methods [49,50,51]. It has also been observed in related studies that binning-based data discretisation techniques outperformed other techniques based on their results [52,53,54]. This study will help in the identification of underperforming regions based on institutional performance. It will also support governance in performance monitoring, policy formulation, target-setting, evaluation, and reforms to address the issues and challenges of education. In this research, various feature selection methods were combined with machine learning models to obtain efficient results. The fourteen most significant features were used, as selected through feature selection methods. The J48 decision tree model was combined with feature selection methods. The best results were obtained using the relief-F-based feature selection technique, which achieved maximum accuracy of 68.5% with an ROC value of 0.63. The highest accuracy of 68.5% was achieved with the SVM (RBF kernel) model while employing the relief-F based feature selection method. After the SVM model, the random forest was utilised to obtain more effective results. The highest accuracy of 71.3% with an ROC of 0.65 was obtained. After the random forest, the rotation forest was utilised to obtain more effective results. The highest accuracy of 73.2% was obtained. After J48, SVM, random forest, and rotation forest, artificial neural networks were used to achieve more efficient results. It has been observed that this model predicted the best results with an accuracy of 82.9% while utilising the relief-F based feature selection method. The artificial neural network outperformed and yielded the highest accuracy, of 82.9%, among the five classifiers employed in this study. The performance of ANN also proved efficient while evaluating other performance metrics. It was also observed that the target class (medium) results were better than other target classes (low and high). This is because the number of instances in the medium class were significantly higher than in the high and low classes. The performance of machine learning models is better when trained on large datasets. In our study, the performance of machine learning models on medium classes was also high due to the large amount of data as compared to other classes.
This study provides additional support for researchers to employ the ANN model and apply it to social science studies. Moreover, this study showed that there is value in including special education-related predictors to improve classification accuracy. The study demonstrated how geographical and demographic variables could all add to the classification accuracy of prediction models. Lastly, the study results offered strong evidence that school facilities are highly predictive for the performance measurement of public schools. Classification into high, medium, and low support levels could also help to illustrate the relationship between variables and classification levels. More importantly, it could highlight the importance of going beyond single-variable, single-threshold early warning systems (e.g., systems that focus on only one KPI), which overlook complex interactions among predictors. One variable is not sufficient to predict measurements of public school performance. The proposed model based on ANN produces more accurate prediction values than the other existing approaches because of its heuristic learning and correction technique. The proposed work was developed on the basis of a bio inspirational approach for increasing the performance of the prediction process. ANN assigns weights based on trial and error during the training phase. This proposed work utilised the knowledge of the genetic algorithm to assign the weights of the hidden nodes, and thus its expected outcome and the actual outcome were closely matched. Hence, the proposed model’s error rate is very low compared to other algorithms, while its prediction accuracy is also greatly improved.
On the map of the world, Pakistan is facing severe social, demographic, and educational disparities. It is ranked 143rd out of 144 countries on the Global Gender Gap (GGG) index with a score of 0.546, the worst in South Asia [55]. Among South Asian counties, Pakistan’s performance in education is not reasonably satisfactory. Moreover, its educational disparities are higher, and significant efforts towards alleviating them have not been observed. Pakistan consists of five provinces, of which Punjab is the most populous. Punjab accounts for more than 56 percent of Pakistan’s total population and 52 percent of its gross domestic product. Punjab consists of nine divisions and 36 districts. In Punjab, demographic disparities exist among the various districts [56]. Lahore (its developed district) ranks first and Muzaffargarh (underdeveloped district) last on the Human Development Index. In terms of educational disparities measured in average years of schooling, Muzaffargarh is more deprived, with 4.41 years for males and 1.95 for females, contrary to Lahore, with an average of 8.5 years of education for males and 7.34 years for females.
The same trend is found in all other provinces [57]. One of the probable reasons might be the strong family system in Pakistan, which places all economic responsibility on males, whereas females are not supposed to earn or spend within the family. Hence, education, whose primary purpose is to help secure jobs and livelihoods, might be male-focused. In addition, cultural values in Pakistan do not support the unrestricted mobility of females. They must be accompanied by male members of their families when travelling. Thus, the preferences for educating females are lower within a family. Such values are stronger in rural areas, where education appears to be considered a luxury for girls. Consequently, many females discontinue their education after exhausting the available resources in their hometowns, leading to educational disparities.
The Annual Status of Education Report: Pakistan (ASER-PAK) 2018 presented the current education status in Pakistan in all aspects. Even if we only consider the report for the most advanced province in Pakistan, Punjab, it cited 11% absenteeism among children and 13% among teachers still in public schools. Only 31% of teachers had graduated from an institution, while 59% had obtained professional qualifications or bachelors degrees in education. Regarding school facilities, 79% of public schools had computer labs, and 83% had a library facility. Furthermore, only 2% of primary schools lacked toilets, while 4% were without drinking water. Other factors such as a lack of grants to schools, insufficient classrooms, fewer playgrounds, etc., are also detailed in the report [58]. Such surveys have been performed in the past with attention to specific institutions or regions and considering a limited set of institutional parameters [7,8]. In this research, a maximal set of influencing institutional parameters were included with a broader scope covering the regional level to measure overall, region-wide institutional performance. The results proved that the efficient provision of resources yields better educational results. It was also observed that the urban areas performed well compared to their rural counterparts due to the maximum availability of facilities and resources. Better school infrastructure and physical facilities increased student attendance, strengthened staff motivation, and improved student academic results.
There is always a link between school users (students, teachers) and school architecture. Past studies have demonstrated that a clean and safe learning environment plays a valuable role in academic achievement. Moreover, overcrowding of classrooms, toilets, laboratories, and dormitories, and dilapidated school structures create an uncomfortable school environment. Unhealthy school environments lower the morale of students, teachers, and parents, leading to higher dropout rates and poorer academic achievement [59,60,61]. Taking the 2030 agenda into consideration, formulating reliable education measures, measuring education disparities among districts, and investigating factors behind education disparities at the household level will all be imperative to the task of recommending effective policy options and the tackling the targets of the Sustainable Development Goals in earnest. This study will help support governance for performance monitoring, policy formulation, target-setting, evaluations, and reforms aimed at addressing the issues and challenges in education worldwide. Gaps in school participation can be better understood in terms of regional socio-economic, demographic, and geographic disparities. There were a few limitations to our study. Firstly, it only covered data for high schools in one province of Pakistan, and the results for other provinces may differ. Secondly, our model utilised a structured dataset, but the results may vary when unstructured or semi-structured data are utilised.
6. Conclusions
Whenever the government introduces educational policies that are based on analyses of performance not of a single school but of schools on a massive scale, region-wide—rather than individual--school performance measurements are a practical approach. The level of education in public institutions varies across all regions of Pakistan. The current disparities in access to education in Pakistan are mostly due to systemic regional differences and the distribution of resources. This study, therefore, sought to fill the gaps and emphasise the importance of region-wide measurements of school performance. A machine learning-based method was developed to generate results. It was revealed that aside from student academic results, other factors substantially impact the performance of any school institution. The present study focused on the importance of these other highly influential factors along with student academic results, e.g., teacher–student ratios, the number of schools per region, school locations in rural or urban areas, and the availability of classrooms, electricity in schools, furniture for students, open-air classes, computer labs, science labs, and school playgrounds. Our finding was that in Pakistan, discrepancies in the performance of educational institutions in different regions of the country are due to inequality in the distribution of resources, differences in essential facilities, the number of schools by region, and the influence of school location on motivation, literacy rates, and awareness levels in the local population. This study will help support governance for performance monitoring, policy formulation, target-setting, evaluations, and reforms to address the issues and challenges for education. Moreover, changing socio-economic factors may lead to different results. This research could be conducted on all schools—primary, middle, high—and even institutions of higher learning or in different regions of the nation. In the future, a few advanced ensemble-based machine learning algorithms such as extreme gradient boosting could be utilised in this domain.
Author Contributions
Conceptualization, T.M.A., M.M. and K.S.; methodology, T.M.A.,M.M., K.S., I.A.H.; software, I.A.H., M.U.S. and S.L.; validation, M.U.S. and S.L.; formal analysis, T.M.A., M.M. and K.S.; investigation, M.U.S. and S.L.; resources, M.U.S. and S.L.; data curation, T.M.A., M.M., K.S. and I.A.H.; writing—original draft preparation, T.M.A., M.M. and K.S.; writing—review and editing, T.M.A., M.M. and K.S.; visualization, M.U.S. and S.L.; supervision, M.U.S. and S.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data associated with this article can be found in the online version at doi:10.17632/637d4s7vjh.1.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tesema, M.T.; Braeken, J. Regional inequalities and gender differences in academic achievement as a function of educational opportunities: Evidence from Ethiopia. Int. J. Educ. Dev. 2018, 60, 51–59. [Google Scholar] [CrossRef]
- Faisal, R.; Shinwari, L.; Mateen, H. Evaluation of the academic achievement of rural versus urban undergraduate medical students in pharmacology examinations. Asian Pac. J. Reprod. 2016, 5, 317–320. [Google Scholar] [CrossRef]
- Jamil, M.; Mustafa, G.; Ilyas, M. Impact of school infrastructure and pedagogical materials on its academic performance: Evidence from Khyber Pakhtunkhwa. FWU J. Soc. Sci. 2018, 12, 42–55. [Google Scholar]
- Ning, B.; Damme, J.V.; Noortgate, W.V.N.; Gielen, S.; Bellens, K.; Dupriez, V.; Dumay, X. Regional inequality in reading performance: An exploration in Belgium. Sch. Eff. Sch. Improv. 2016, 27, 642–668. [Google Scholar] [CrossRef]
- Gbollie, C.; Keamu, H.P. Student academic performance: The role of motivation, strategies, and perceived factors hindering Liberian junior and senior high school students learning. Educ. Res. Int. 2017, 2017, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Honicke, T.; Broadbent, J. The influence of academic self-efficacy on academic performance: A systematic review. Educ. Res. Rev. 2016, 17, 63–84. [Google Scholar] [CrossRef]
- Abdullah, N.A.; Bhatti, N. Failure in quality of academic performance of students in public sector schools of Sheikhupura. J. Educ. Educ. Dev. 2018, 5, 289–305. [Google Scholar] [CrossRef]
- Fernandes, E.; Holanda, M.; Victorino, M.; Borges, V.; Carvalho, R.; Van Erven, G. Educational data mining: Predictive analysis of academic performance of public school students in the capital of Brazil. J. Bus. Res. 2019, 94, 335–343. [Google Scholar] [CrossRef]
- Kassarnig, V.; Mones, E.; Bjerre-Nielsen, A.; Sapiezynski, P.; Dreyer Lassen, D.; Lehmann, S. Academic performance and behavioral patterns. EPJ Data Sci. 2018, 7, 1–16. [Google Scholar] [CrossRef]
- Natek, S.; Zwilling, M. Student data mining solution–knowledge management system related to higher education institutions. Expert Syst. Appl. 2014, 41, 6400–6407. [Google Scholar] [CrossRef]
- Gumus, S.; Chudgar, A. Factors affecting school participation in Turkey: An analysis of regional differences. Compare 2016, 46, 929–951. [Google Scholar] [CrossRef]
- Chaudhry, R.; Tajwar, A.W. The Punjab Schools Reform Roadmap: A Medium-Term Evaluation. In Implementing Deeper Learning and 21st Education Reforms; Springer: Cham, Switzerland, 2021; pp. 109–128. [Google Scholar]
- Aluko, R.O.; Daniel, E.I.; Oshodi, O.S.; Aigbavboa, C.O.; Abisuga, A.O. Towards reliable prediction of academic performance of architecture students using data mining techniques. J. Eng. Des. Technol. 2018, 16, 385–397. [Google Scholar] [CrossRef] [Green Version]
- Nurliana, M.; Sudaryana, B. The influence of competence, learning methods, infrastructure facilities on graduate quality (case study (vocational high school) smkn 5 bandung indonesia). Indones. J. Soc. Res. 2020, 2, 18–43. [Google Scholar] [CrossRef]
- Hameen, E.C.; Ken-Opurum, B.; Priyadarshini, S.; Lartigue, B.; Anath-Pisipati, S. Effects of school facilities’ mechanical and plumbing characteristics and conditions on student attendance, academic performance and health. Int. J. Civ. Environ. Eng. 2020, 14, 193–201. [Google Scholar]
- Belmonte, A.; Bove, V.; D’Inverno, G.; Modica, M. School infrastructure spending and educational outcomes: Evidence from the 2012 earthquake in Northern Italy. Econ. Educ. Rev. 2020, 75, 101951. [Google Scholar] [CrossRef]
- Gul, M.; Shah, A.F. Assessment of physical school environment of public sector high schools in Pakistan and World Health Organization’s Guidelines. Glob. Reg. Rev. 2019, 4, 238–249. [Google Scholar] [CrossRef]
- Alasadi, S.A.; Bhaya, W.S. Review of data preprocessing techniques in data mining. J. Eng. Appl. Sci. 2017, 12, 4102–4107. [Google Scholar]
- Kira, K.; Rendell, L.A. The feature selection problem: Traditional methods and a new algorithm. In Proceedings of the 10th National Conference on Artificial Intelligence, San Jose, CA, USA, 12–16 July 1992. [Google Scholar]
- Robnik-Šikonja, M.; Kononenko, I. Theoretical and empirical analysis of ReliefF and RReliefF. Mach. Learn. 2003, 53, 23–69. [Google Scholar] [CrossRef] [Green Version]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Chandrashekar, G.; Sahin, F. A survey on feature selection methods. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar] [CrossRef]
- Xue, B.; Zhang, M.; Browne, W.N.; Yao, X. A survey on evolutionary computation approaches to feature selection. IEEE Trans. Evol. Comput. 2015, 20, 606–626. [Google Scholar] [CrossRef] [Green Version]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Khushi, M.; Shaukat, K.; Alam, T.M.; Hameed, I.A.; Uddin, S.; Luo, S.; Yang, X.; Reyes, M.C. A comparative performance analysis of data resampling methods on imbalance medical data. IEEE Access 2021, 9, 109960–109975. [Google Scholar] [CrossRef]
- Alam, T.M.; Shaukat, K.; Mahboob, H.; Sarwar, M.U.; Iqbal, F.; Nasir, A.; Hameed, I.A.; Luo, S. A machine learning approach for identification of malignant mesothelioma etiological factors in an imbalanced dataset. Comput. J. 2021, 00, 1–12. [Google Scholar]
- Alam, T.M.; Shaukat, K.; Hameed, I.A.; Khan, W.A.; Sarwar, M.U.; Iqbal, F.; Luo, S. A novel framework for prognostic factors identification of malignant mesothelioma through association rule mining. Biomed. Signal Process. Control 2021, 68, 102726. [Google Scholar] [CrossRef]
- Shaukat, K.; Iqbal, F.; Alam, T.M.; Aujla, G.K.; Devnath, L.; Khan, A.G.; Iqbal, R.; Shahzadi, I.; Rubab, A. The impact of artificial intelligence and robotics on the future employment opportunities. Trends Comput. Sci. Inf. Technol. 2020, 5, 50–54. [Google Scholar]
- Shaukat, K.; Alam, T.M.; Luo, S.; Shabbir, S.; Hameed, I.A.; Li, J.; Abbas, S.K.; Javed, U. A Review of Time-Series Anomaly Detection Techniques: A Step to Future Perspectives. In Advances in Information and Communication, Proceedings of the Future of Information and Communication Conference (FICC 2021), Vancouver, BC, Canada, 29–30 April 2021; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Shaukat, K.; Luo, S.; Abbas, N.; Mahboob Alam, T.; Ehtesham Tahir, M.; Hameed, I.A. An analysis of blessed Friday sale at a retail store using classification models. In Proceedings of the 4th International Conference on Software Engineering and Information Management (ICSIM 2021), Yokohama, Japan, 16–18 January 2021. [Google Scholar]
- Shaukat, K.; Alam, T.M.; Ahmed, M.; Luo, S.; Hameed, I.A.; Iqbal, M.S.; Li, J.; Iqbal, M.A. A model to enhance governance issues through opinion extraction. In Proceedings of the 11th IEEE Annual Information Technology, Electronics and Mobile Communication Conference (IEMCON), Vancouver, BC, Canada, 4–7 November 2020. [Google Scholar]
- Bashir, U.; Chachoo, M. Performance evaluation of j48 and bayes algorithms for intrusion detection system. Int. J. Netw. Secur. Its Appl. 2017, 9, 1–11. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Singh, D.; Pandey, A.S.; Maini, T. A novel feature selection and short-term price forecasting based on a decision tree (J48) model. Energies 2019, 12, 3665. [Google Scholar] [CrossRef] [Green Version]
- Guenther, N.; Schonlau, M. Support vector machines. Stata J. 2016, 16, 917–937. [Google Scholar] [CrossRef] [Green Version]
- Alam, T.M.; Iqbal, M.A.; Ali, Y.; Wahab, A.; Ijaz, S.; Baig, T.I.; Hussain, A.; Malik, M.A.; Raza, M.M.; Ibrar, S.; et al. A model for early prediction of diabetes. Inform. Med. Unlocked 2019, 16, 100204. [Google Scholar] [CrossRef]
- Qi, Y. Random forest for bioinformatics. In Ensemble Machine Learning; Springer: Berlin/Heidelberg, Germany, 2012; pp. 307–323. [Google Scholar]
- Boulesteix, A.L.; Janitza, S.; Kruppa, J.; König, I.R. Overview of random forest methodology and practical guidance with emphasis on computational biology and bioinformatics. Wiley Interdiscip. Rev. 2012, 2, 493–507. [Google Scholar] [CrossRef] [Green Version]
- Niehaus, K.E.; Uhlig, H.H.; Clifton, D.A. Phenotypic characterisation of Crohn’s disease severity. In Proceedings of the 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015. [Google Scholar]
- Louppe, G.; Wehenkel, L.; Sutera, A.; Geurts, P. Understanding variable importances in forests of randomized trees. Adv. Neural Inf. Process. Syst. 2013, 26, 431–439. [Google Scholar]
- Dawer, G.; Barbu, A. Relevant ensemble of trees. arXiv 2017, arXiv:1709.05545. [Google Scholar]
- Rodriguez, J.J.; Kuncheva, L.I.; Alonso, C.J. Rotation forest: A new classifier ensemble method. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1619–1630. [Google Scholar] [CrossRef]
- Fegade, K.G.; Gupta, R.; Namdeo, V. Predictive model for multiclass classification of e-commerce data: An azure machine learning approach. Int. J. Comput. Appl. 2017, 168, 37–42. [Google Scholar]
- Đurđević Babić, I. Machine learning methods in predicting the student academic motivation. Croat. Oper. Res. Rev. 2017, 8, 443–461. [Google Scholar] [CrossRef]
- Borkin, D.; Némethová, A.; Michaľčonok, G.; Maiorov, K. Impact of Data Normalization on Classification Model Accuracy. Res. Pap. Fac. Mater. Sci. Technol. Slovak Univ. Technol. 2019, 27, 79–84. [Google Scholar] [CrossRef] [Green Version]
- Alshdaifat, E.; Alshdaifat, D.; Alsarhan, A.; Hussein, F.; El-Salhi, S.M.D.F.S. The effect of preprocessing techniques, applied to numeric features, on classification algorithms’ performance. Data 2021, 6, 11. [Google Scholar] [CrossRef]
- Tsai, C.-F.; Chen, Y.C. The optimal combination of feature selection and data discretization: An empirical study. Inf. Sci. 2019, 505, 282–293. [Google Scholar] [CrossRef]
- Lavangnananda, K.; Chattanachot, S. Study of discretization methods in classification. In Proceedings of the 9th International Conference on Knowledge and Smart Technology (KST), Pattaya, Thailand, 1–4 February 2017. [Google Scholar]
- Alam, T.M.; Shaukat, K.; Hameed, I.A.; Luo, S.; Sarwar, M.U.; Shabbir, S.; Li, J.; Khushi, M. An investigation of credit card default prediction in the imbalanced datasets. IEEE Access 2020, 8, 201173–201198. [Google Scholar] [CrossRef]
- Singh, D.; Singh, B. Investigating the impact of data normalization on classification performance. Appl. Soft Comput. 2020, 97, 105524. [Google Scholar] [CrossRef]
- Weiss, S.; Xu, Z.Z.; Peddada, S.; Amir, A.; Bittinger, K.; Gonzalez, A.; Lozupone, C.; Zaneveld, J.R.; Vázquez-Baeza, Y.; Birmingham, A. Normalization and microbial differential abundance strategies depend upon data characteristics. Microbiome 2017, 5, 1–18. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alam, T.M.; Shaukat, K.; Mushtaq, M.; Ali, Y.; Khushi, M.; Luo, S.; Wahab, A. Corporate bankruptcy prediction: An approach towards better corporate world. Comput. J. 2020, 65, 1–16. [Google Scholar]
- Ramírez-Gallego, S.; García, S.; Mouriño-Talín, H. Data discretization: Taxonomy and big data challenge. Wiley Interdiscip. Rev. 2016, 6, 5–21. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Phan, N.Y.K.; Luong, H.H.; Le, T.P.; Tran, N.C. Efficient discretization approaches for machine learning techniques to improve disease classification on gut microbiome composition data. Adv. Sci. Technol. Eng. Syst. 2020, 5, 547–556. [Google Scholar] [CrossRef]
- Jishan, S.T.; Rashu, R.I.; Mahmood, A.; Billah, F.; Rahman, R.M. Application of optimum binning technique in data mining approaches to predict students’ final grade in a course. In Computational Intelligence in Information Systems; Springer: Berlin/Heidelberg, Germany, 2015; pp. 159–170. [Google Scholar]
- The Global Gender Gap Report; World Economic Forum: Cologne, Germany; Geneva, Switzerland, 2017.
- Yasmeen, G.; Begum, R.; Mujtaba, B. Human development challenges and opportunities in Pakistan: Defying income inequality and poverty. J. Bus. Stud. Q. 2011, 2, 1. [Google Scholar]
- Wang, Z.; Zhang, B.; Wang, B. Renewable energy consumption, economic growth and human development index in Pakistan: Evidence form simultaneous equation model. J. Clean. Prod. 2018, 184, 1081–1090. [Google Scholar] [CrossRef]
- Shaukat, K.; Nawaz, I.; Aslam, S.; Zaheer, S.; Shaukat, U. Student’s Performance: A Data Mining Perspective; LAP Lambert Academic Publishing: Saarbrücken, Germany, 2017. [Google Scholar]
- Shaukat, K.; Nawaz, I.; Aslam, S.; Zaheer, S.; Shaukat, U. Student’s performance in the context of data mining. In Proceedings of the 2016 19th International Multi-Topic Conference (INMIC), Islamabad, Pakistan, 5–6 December 2016; pp. 1–8. [Google Scholar]
- Lian, B.; Kristiawan, M.; Fitriya, R. Giving creativity room to students through the friendly school’s program. Int. J. Sci. Technol. Res. 2018, 7, 1–7. [Google Scholar]
- Matshipi, M.; Mulaudzi, N.; Mashau, T. Causes of overcrowded classes in rural primary schools. J. Soc. Sci. 2017, 51, 109–114. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).