Analytical Solutions for the Radial Consolidation of Unsaturated Foundation with Prefabricated Vertical Drain Based on Fourier Series Expansion Theory
Abstract
:1. Introduction
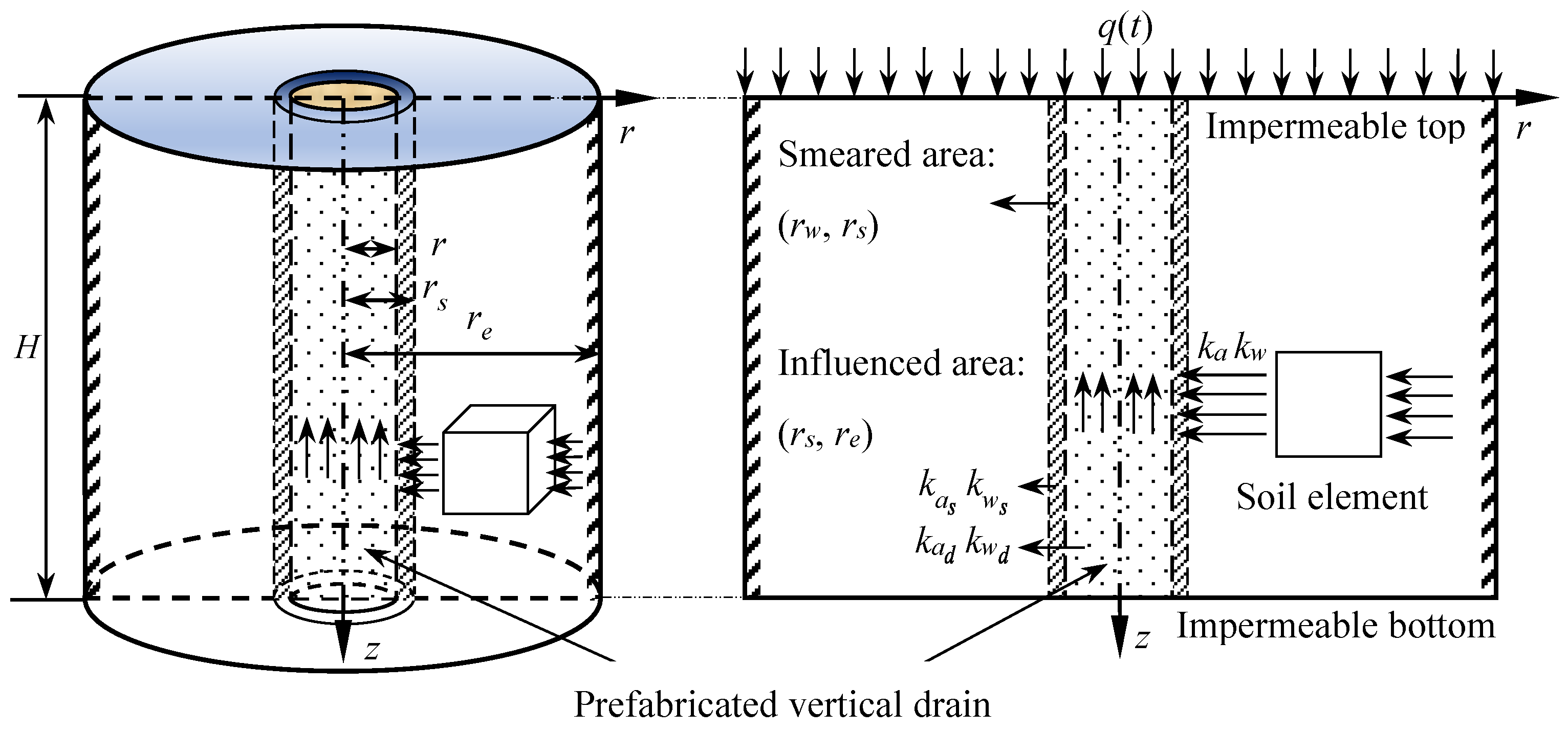
2. Mathematical Modeling
2.1. Basic Assumptions
- The soil layer is homogeneous.
- Solid particles and the water phase are incompressible.
- Air and water phases can only flow along the radial direction.
- The air and water phases are continuous and independent.
- Permeability coefficients related to air and water phases are constant.
2.2. Governing Equations
2.3. Initial and Boundary Conditions
2.3.1. Initial Conditions
2.3.2. Boundary Conditions
3. Analytical Solutions
4. Verification Work
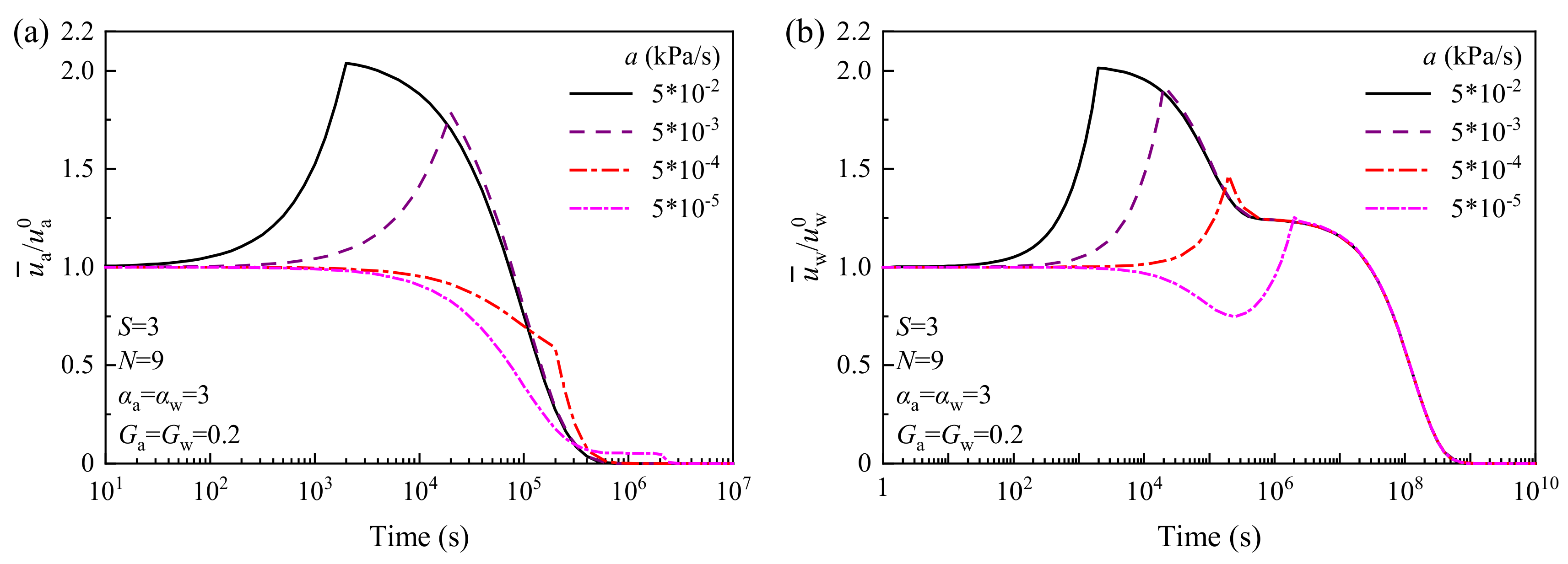
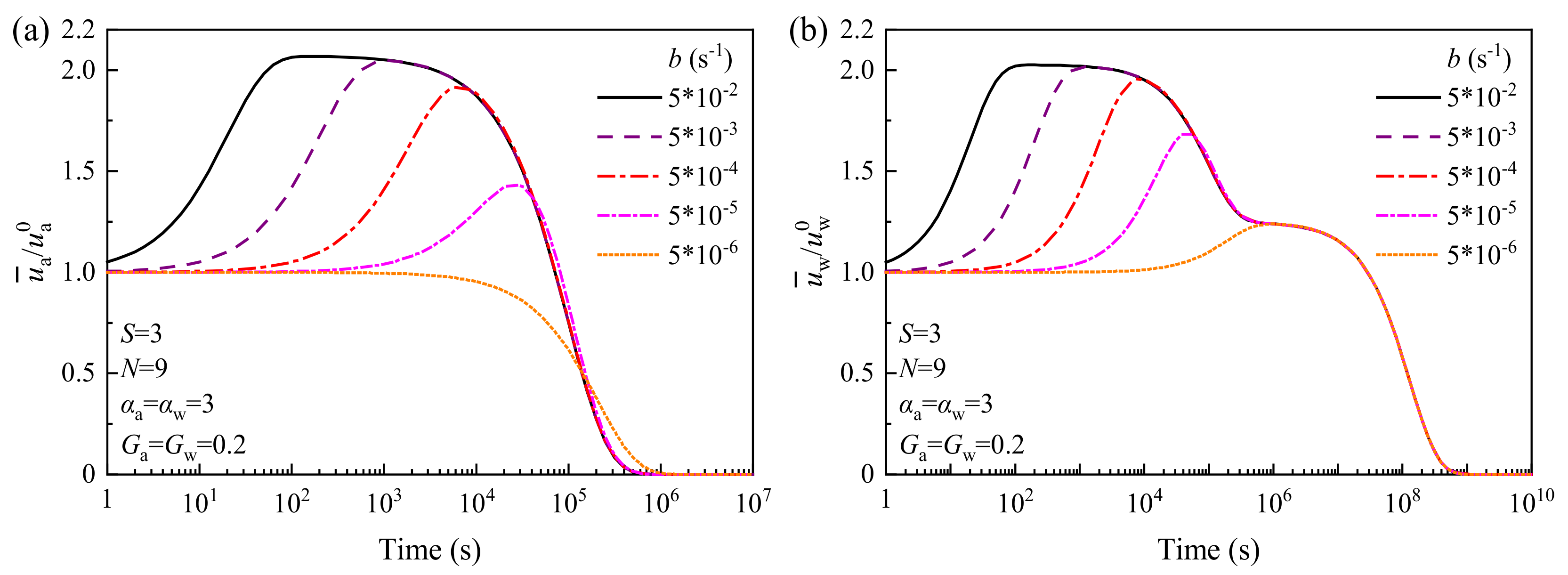
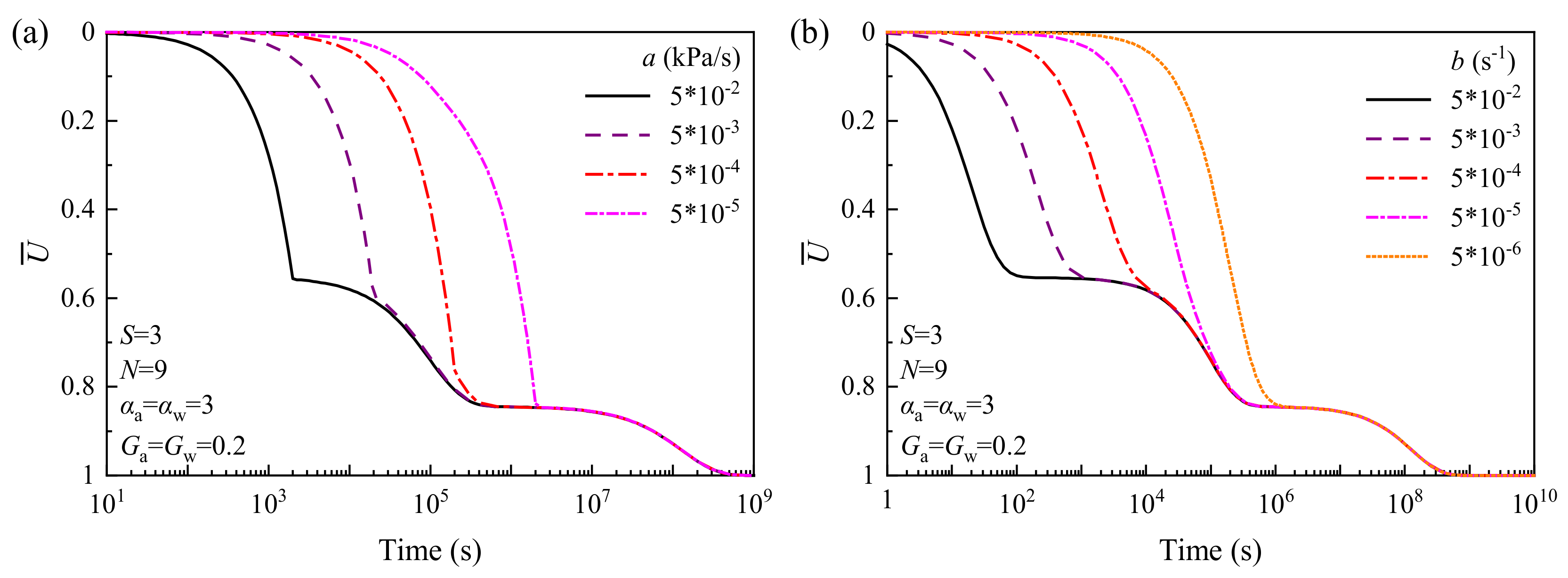
5. Case Study
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| the applied external loading at t = 0 | |
| the ramp loading parameter | |
| the exponential loading parameter | |
| the radius of the drain | |
| the largest radius of the smeared zone | |
| the largest radius of the influenced region | |
| the thickness of the foundation | |
| the excess pore-air pressure | |
| the excess pore-water pressure | |
| the excess pore-air pressure in the smeared zone | |
| the excess pore-water pressure in the smeared zone | |
| the initial excess pore-air pressure | |
| the initial excess pore-water pressure | |
| the average excess pore-air pressure | |
| the average excess pore-water pressure | |
| the air-related permeability coefficient of influenced area | |
| the water-related permeability coefficient of influenced area | |
| the air-related permeability coefficient of smeared zone | |
| the water-related permeability coefficient of smeared zone | |
| the air-related permeability coefficient in the drain | |
| the water-related permeability coefficient in the drain | |
| the air-related smear coefficient | |
| the water-related smear coefficient | |
| the air-related drain resistance factor | |
| the water-related drain resistance factor | |
| the water-related interaction constant related to air phase | |
| the water-related interaction constant related to water phase | |
| the air-related consolidation coefficient | |
| the water-related consolidation coefficient | |
| the air-related parameter of net normal stress, q0-ua | |
| the air-related parameter of the net normal stress, q0-ua | |
| the water-related parameter of the net normal stress, q0-ua, and suction, ua-uw | |
| the water-related parameter of the net normal stress, q0-ua, and suction, ua-uw | |
| the atmospheric pressure | |
| the air mass molecular | |
| the porosity | |
| the saturation | |
| the universal air constant | |
| the absolute temperature | |
| the gravitational acceleration | |
| the water unit weight |
References
- Leo, C.J. Consolidation of fine-grained compressible soils by vertical drains based on the free strain approach. Appl. Mech. 2002, 207–212. [Google Scholar] [CrossRef]
- Nogami, T.; Li, M.X. Consolidation of clay with a system of vertical and horizontal drains. J. Geotech. Geoenviron. Eng. 2003, 129, 838–848. [Google Scholar] [CrossRef] [Green Version]
- Leo, C.J. Equal strain consolidation by vertical drains. J. Geotech. Geoenviron. Eng. 2004, 130, 316–327. [Google Scholar] [CrossRef] [Green Version]
- García-Ros, G.; Alhama, I.; Cánovas, M. Powerful software to simulate soil consolidation problems with prefabricated vertical drains. Water 2018, 10, 242. [Google Scholar] [CrossRef] [Green Version]
- García-Ros, G.; Alhama, I.; Cánovas, M. Use of discriminated nondimensionalization in the search of universal solutions for 2-D rectangular and cylindrical consolidation problems. Open Geosci. 2018, 10, 209–221. [Google Scholar] [CrossRef]
- Chen, Z.; Ni, P.P.; Mei, G.X.; Chen, Y.F. Semi-Analytical Solution for Consolidation of Ground with Partially Penetrating PVDs under the Free-Strain Condition. J. Eng. Mech. 2021, 147, 04020148. [Google Scholar] [CrossRef]
- Deng, Y.B.; Xie, K.H.; Lu, M.M.; Tao, H.B.; Liu, G.B. Consolidation by prefabricated vertical drains considering the time dependent well resistance. Geotext. Geomembr. 2013, 36, 20–26. [Google Scholar] [CrossRef]
- Fu, C.W.; Lei, G.H. A general solution for vertical-drain consolidation with impeded drainage boundaries. J. Cent. South Univ. 2016, 23, 934–943. [Google Scholar] [CrossRef]
- Geng, X.Y. Non-linear consolidation of soil with vertical and horizontal drainage under time-dependent loading. In Proceedings of the 2008 International Conference on Advanced Computer Theory and Engineering, Phuket, Thailand, 20–22 December 2008; pp. 800–804. [Google Scholar]
- Indraratna, B.; Sathananthan, I.; Rujikiatkamjorn, C.; Balasubramaniam, A.S. Analytical and numerical modeling of soft soil stabilized by prefabricated vertical drains incorporating vacuum preloading. Int. J. Geomech. 2005, 5, 114–124. [Google Scholar] [CrossRef]
- Lei, G.H.; Zheng, Q.; Ng, C.W.W.; Chiu, A.C.F.; Xu, B. An analytical solution for consolidation with vertical drains under multi-ramp loading. Géotechnique 2015, 65, 531–547. [Google Scholar] [CrossRef]
- Zhou, W.H.; Lok, T.M.H.; Zhao, L.S.; Mei, G.X.; Li, X.B. Analytical solutions to the axisymmetric consolidation of a multi-layer soil system under surcharge combined with vacuum preloading. Geotext. Geomembr. 2017, 45, 487–498. [Google Scholar] [CrossRef]
- Zhou, W.H.; Zhao, L.S.; Lok, T.M.H.; Mei, G.X.; Li, X.B. Analytical Solutions to the Axisymmetrical Consolidation of Unsaturated Soils. J. Eng. Mech. 2018, 144, 04017152. [Google Scholar] [CrossRef]
- Zhu, G.F.; Yin, J.H. Consolidation analysis of soil with vertical and horizontal drainage under ramp loading considering smear effects. Geotext. Geomembr. 2004, 22, 63–74. [Google Scholar] [CrossRef]
- Huang, Y.C.; Li, T.Y.; Fu, X.L.; Chen, Z. Analytical solutions for the consolidation of unsaturated foundation with prefabricated vertical drain. Int. J. Numer. Anal. Methods Geomech. 2020, 44, 2263–2282. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Hasan, J.U. One-dimensional consolidation theory: Unsaturated soils. Can. Geotech. J. 1979, 16, 521–531. [Google Scholar] [CrossRef] [Green Version]
- Fredlund, D.G.; Morgenstern, N.R. Constitutive relations for volume change in unsaturated soils. Can. Geotech. J. 1976, 13, 261–276. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Rahardjo, H. Soil Mechanics for Unsaturated Soils; Wiley: Hoboken, NJ, USA, 1993. [Google Scholar]
- Qin, A.F.; Sun, D.A.; Tan, Y.W. Semi-analytical solution to one-dimensional consolidation in unsaturated soils. Appl. Math. Mech. 2010, 31, 215–226. [Google Scholar] [CrossRef]
- Li, L.Z.; Qin, A.F.; Jiang, L.H.; Mei, G.X. Semianalytical Solution for One-Dimensional Consolidation in a Multilayered Unsaturated Soil System with Exponentially Time-Growing Permeable Boundary. J. Eng. Mech. 2021, 147, 04021025. [Google Scholar] [CrossRef]
- Shan, Z.D.; Ling, D.S.; Ding, H.J. Exact solutions for one-dimensional consolidation of single-layer unsaturated soil. Int. J. Numer. Anal. Methods Geomech. 2012, 36, 708–722. [Google Scholar] [CrossRef]
- Shan, Z.D.; Ling, D.S.; Ding, H.J. Analytical solution for 1D consolidation of unsaturated soil with mixed boundary condition. J. Zhejiang Univ. -Sci. A 2013, 14, 61–70. [Google Scholar] [CrossRef] [Green Version]
- Shan, Z.D.; Ling, D.S.; Ding, H.J. Analytical solution for the 1D consolidation of unsaturated multi-layered soil. Comput. Geotech. 2014, 57, 17–23. [Google Scholar] [CrossRef]
- Zhou, W.H.; Zhao, L.S. One-dimensional consolidation of unsaturated soil subjected to time-dependent loading with various initial and boundary conditions. Int. J. Geomech. 2014, 14, 291–301. [Google Scholar] [CrossRef]
- Zhou, W.H.; Zhao, L.S.; Li, X.B. A simple analytical solution to one-dimensional consolidation for unsaturated soils. Int. J. Numer. Anal. Methods Geomech. 2014, 38, 794–810. [Google Scholar] [CrossRef]
- Zhou, W.H.; Zhao, L.S.; Garg, A.; Yuen, K.V. Generalized analytical solution for the consolidation of unsaturated soil under partially permeable boundary conditions. Int. J. Geomech. 2017, 17, 04017048. [Google Scholar] [CrossRef]
- Wang, L.; Sun, D.A.; Qin, A.F. General semi-analytical solutions to one-dimensional consolidation for unsaturated soils. Appl. Math. Mech. -Engl. 2017, 38, 831–850. [Google Scholar] [CrossRef]
- Wang, L.; Sun, D.A.; Qin, A.F.; Xu, Y.F. Semi-analytical solution to one-dimensional consolidation for unsaturated soils with semi-permeable drainage boundary under time-dependent loading. Int. J. Numer. Anal. Methods Geomech. 2017, 41, 1636–1655. [Google Scholar] [CrossRef]
- Ho, L.; Fatahi, B. Analytical solution for the two-dimensional plane strain consolidation of an unsaturated soil stratum subjected to time-dependent loading. Comput. Geotech. 2015, 67, 1–16. [Google Scholar] [CrossRef]
- Wang, L.; Xu, Y.F.; Xia, X.H.; He, Y.L. Semi-analytical solutions of two-dimensional plane strain consolidation in unsaturated soils subjected to the lateral semipermeable drainage boundary. Int. J. Numer. Anal. Methods Geomech. 2019, 43, 2628–2651. [Google Scholar] [CrossRef]
- Wang, L.; Xu, Y.F.; Xia, X.H.; He, Y.L.; Li, T.Y. Semi-analytical solutions to two-dimensional plane strain consolidation for unsaturated soils under time-dependent loading. Comput. Geotech. 2019, 109, 144–165. [Google Scholar] [CrossRef]
- Li, L.Z.; Qin, A.F.; Jiang, L.H. Semi-analytical solution for one-dimensional consolidation of a two-layered soil system with unsaturated and saturated conditions. Int. J. Numer. Anal. Methods Geomech. 2021, 45, 2284–2300. [Google Scholar] [CrossRef]
- Qin, A.F.; Sun, D.A.; Yang, L.P.; Weng, Y.F. A semi-analytical solution to consolidation of unsaturated soils with the free drainage well. Comput. Geotech. 2010, 37, 867–875. [Google Scholar] [CrossRef]
- Zhou, W.H.; Tu, S. Unsaturated consolidation in a sand drain foundation by differential quadrature method. Procedia Earth Planet. Sci. 2012, 5, 52–57. [Google Scholar]
- Ho, L.; Fatahi, B.; Khabbaz, H. Analytical solution to axisymmetric consolidation in unsaturated soils with linearly depth-dependent initial conditions. Comput. Geotech. 2016, 74, 102–121. [Google Scholar] [CrossRef]
- Ho, L.; Fatahi, B. Axisymmetric consolidation in unsaturated soil deposit subjected to time-dependent loadings. Int. J. Geomech. 2017, 17, 04016046. [Google Scholar] [CrossRef]
- Ho, L.; Fatahi, B. Analytical solution to axisymmetric consolidation of unsaturated soil stratum under equal strain condition incorporating smear effects. Int. J. Numer. Anal. Methods Geomech. 2018, 42, 1890–1913. [Google Scholar] [CrossRef]
- Huang, Y.C.; Li, T.Y.; Fu, X.L. Consolidation of Unsaturated Drainage Well Foundation with Smear Effect under Time-Dependent Loading. KSCE J. Civ. Eng. 2021, 25, 768–781. [Google Scholar] [CrossRef]
- Li, T.Y.; Qin, A.F.; Pei, Y.C.Q.; Sun, D.A.; Fu, X.L. Semianalytical solutions to the consolidation of drainage well foundations in unsaturated soils with radial semipermeable drainage boundary under time-dependent loading. Int. J. Geomech. 2020, 20, 04020150. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, Q.; Xu, Q.; Luo, X.; Chen, Y.; Li, T. Analytical Solutions for the Radial Consolidation of Unsaturated Foundation with Prefabricated Vertical Drain Based on Fourier Series Expansion Theory. Appl. Sci. 2021, 11, 9285. https://doi.org/10.3390/app11199285
Meng Q, Xu Q, Luo X, Chen Y, Li T. Analytical Solutions for the Radial Consolidation of Unsaturated Foundation with Prefabricated Vertical Drain Based on Fourier Series Expansion Theory. Applied Sciences. 2021; 11(19):9285. https://doi.org/10.3390/app11199285
Chicago/Turabian StyleMeng, Qiang, Qianwei Xu, Xianmin Luo, Yang Chen, and Tianyi Li. 2021. "Analytical Solutions for the Radial Consolidation of Unsaturated Foundation with Prefabricated Vertical Drain Based on Fourier Series Expansion Theory" Applied Sciences 11, no. 19: 9285. https://doi.org/10.3390/app11199285
APA StyleMeng, Q., Xu, Q., Luo, X., Chen, Y., & Li, T. (2021). Analytical Solutions for the Radial Consolidation of Unsaturated Foundation with Prefabricated Vertical Drain Based on Fourier Series Expansion Theory. Applied Sciences, 11(19), 9285. https://doi.org/10.3390/app11199285





