Practical Formation Control for Multiple Anonymous Robots System with Unknown Nonlinear Disturbances
Abstract
:1. Introduction
2. Preliminaries and Problem Formulation
2.1. Preliminaries
2.2. Problem Formulation
3. Distributed Hybrid Formation Control
3.1. Distributed Control Law Design
3.2. Stability Analysis
- (1)
- Example of
- (2)
- Example of and
4. Numerical Examples
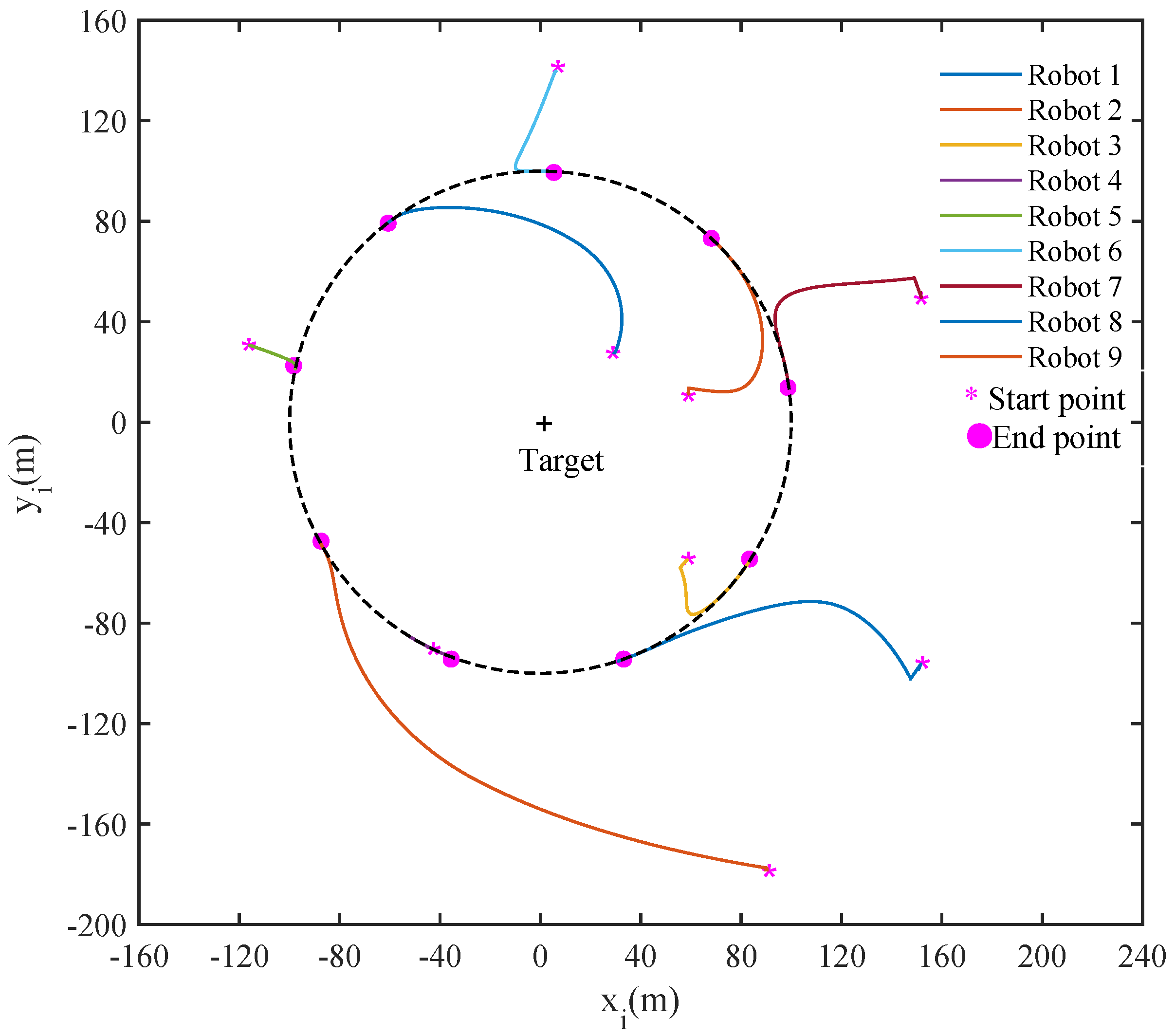
4.1. Uniform Circle Formation
4.2. Non-Uniform and Non-Circular Formation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Han, Q.; Liu, P.; Zhang, H.; Cai, Z. A wireless sensor network for monitoring environmental quality in the manufacturing industry. IEEE Access 2019, 7, 78108–78119. [Google Scholar] [CrossRef]
- Mas, I.; Kitts, C.A. Dynamic control of mobile multirobot systems: The cluster space formulation. IEEE Access 2014, 2, 558–570. [Google Scholar] [CrossRef]
- Napora, S.; Paley, D.A. Observer-based feedback control for stabilization of collective motion. IEEE Trans. Control Syst. Technol. 2013, 21, 1846–1857. [Google Scholar] [CrossRef] [Green Version]
- Chung, T.H.; Hollinger, G.A.; Isler, V. Search and pursuit-evasion in mobile robotics: A survey. Auton. Robots 2011, 31, 299–316. [Google Scholar] [CrossRef] [Green Version]
- Ren, W. Collective motion from consensus with cartesian coordinate coupling. IEEE Trans. Autom. Control 2009, 54, 1330–1335. [Google Scholar] [CrossRef]
- Ding, W.; Yan, G.; Lin, Z. Pursuit formations with dynamic control gains. Int. J. Robust Nonlin 2012, 22, 300–317. [Google Scholar] [CrossRef]
- Bullo, F.; Cortes, J.; Martinez, S. Distributed Control of Robotic Networks; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Pavone, M.; Arsie, A.; Frazzoli, E.; Bullo, F. Distributed algorithms for environment partitioning in mobile robotic networks. IEEE Trans. Autom. Control 2011, 56, 1834–1848. [Google Scholar] [CrossRef]
- Yu, W.W.; Zheng, W.Z.; Chen, G.R.; Lv, J.H. Distributed control gains design for consensus in multi-agent systems with second-order nonlinear dynamics. Automatica 2013, 49, 2107–2115. [Google Scholar] [CrossRef]
- Zhao, Y.; Duan, Z.S.; Wen, G.H.; Zhang, Y.J. Distributed finite-time tracking control for multi-agent systems: An observer-based approach. Syst. Control Lett. 2013, 62, 22–28. [Google Scholar] [CrossRef]
- Xu, P.; Zhao, H.F.; Xie, G.M.; Tao, J.; Xu, M.Y. Pull-based distributed event-triggered circle formation control for multi-agent systems with directed topologies. Appl. Sci. 2019, 9, 4995. [Google Scholar] [CrossRef] [Green Version]
- Marcolino, L.S.; Jiang, A.X.; Tambe, M. Multi-agent team formation: Diversity beats strength? In Proceedings of the 23th International Conference Artificial Intelligence (IJCAI ’13), Beijing, China, 3–9 August 2013; pp. 279–285. [Google Scholar]
- Pinto, T.; Morais, H.; Oliveira, P.; Vale, Z.; Praça, I.; Ramos, C. A new approach for multi-agent coalition formation and management in the scope of electricity markets. Energy 2011, 36, 5004–5015. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.L.P.; Yu, D.; Liu, L. Automatic leader-follower persistent formation control for autonomous surface vehicles. IEEE Access 2019, 7, 12146–12155. [Google Scholar] [CrossRef]
- Défago, X.; Souissi, S. Non-uniform circle formation algorithm for oblivious mobile robots with convergence toward uniformity. Theor. Comput. Sci. 2008, 396, 97–112. [Google Scholar] [CrossRef]
- Flocchini, P.; Prencipe, G.; Santoro, N. Self-deployment of mobile sensors on a ring. Theor. Comput. Sci. 2008, 402, 67–80. [Google Scholar] [CrossRef] [Green Version]
- Guo, J.; Yan, G.F.; Lin, Z.Y. Local control strategy for moving-target-enclosing under dynamically changing network topology. Syst. Control Lett. 2010, 59, 654–661. [Google Scholar] [CrossRef]
- Xiao, Y.; Liu, L. Distributed circular formation control of ring-networked nonholonomic vehicles. Automatica 2016, 68, 92–99. [Google Scholar]
- Défago, X.; Konagaya, A. Circle formation for oblivious anonymous mobile robots with no common sense of orientation. In Proceedings of the Second ACM International Workshop on Principles of Mobile Computing, Toulouse, France, 30–31 October 2002; pp. 97–104. [Google Scholar]
- Marshall, J.; Broucke, M.; Francis, B. Formations of vehicles in cyclic pursuit. IEEE Trans. Autom. Control 2004, 49, 1963–1974. [Google Scholar] [CrossRef]
- Cheng, S.; Liu, L.; Xu, S.Y. Circle formation control of mobile agents with limited interaction range. IEEE Trans. Autom. Control 2018, 64, 2115–2121. [Google Scholar]
- Chatzigiannakis, I.; Markou, M.; Nikoletseas, S. Distributed circle formation for anonymous oblivious robots. In Proceedings of the International Workshop on Experimental and Efficient Algorithms, Angra dos Reis, Brazil, 25–28 May 2004; pp. 159–174. [Google Scholar]
- Song, C.; Liu, L.; Feng, G. Coverage control for mobile sensor networks with input saturation. Unmanned Syst. 2016, 4, 15–21. [Google Scholar] [CrossRef]
- Shi, Y.; Li, R.; Teo, K. Cooperative enclosing control for multiple moving targets by a group of agents. Int. J. Control 2015, 88, 80–89. [Google Scholar] [CrossRef]
- Wang, C.; Xia, W.; Xie, G. Limit-cycle-based design of formation control for mobile agents. IEEE Trans. Autom. Control 2019, 65, 3530–3543. [Google Scholar] [CrossRef]
- Chen, H.; Sun, J.; Li, K.; Wang, M. Autonomous spacecraft swarm formation planning using artificial field based on nonlinear bifurcation dynamics. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, AIAA2017-1269, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar]
- Brinón-Arranz, L.; Seuret, A.; Canudas-de-Wit, C. Cooperative control design for time-varying formations of multi-agent systems. IEEE Trans. Autom. Control 2014, 59, 2283–2288. [Google Scholar] [CrossRef] [Green Version]
- Zheng, R.; Liu, Y.; Sun, D. Enclosing a target by nonholonomic mobile robots with bearing-only measurements. Automatica 2015, 53, 400–407. [Google Scholar] [CrossRef]
- Yu, X.; Liu, L. Cooperative control for moving-target circular formation of nonholonomic vehicles. IEEE Trans. Autom. Control 2016, 62, 3448–3454. [Google Scholar] [CrossRef]
- Wang, C.; Xie, G.; Cao, M. Controlling anonymous mobile agents with unidirectional locomotion to form formations on a circle. Automatica 2014, 50, 1100–1108. [Google Scholar] [CrossRef]
- Peng, L.; Ren, W.; Song, Y.D. Distributed multi-agent optimization subject to nonidentical constraints and communication delays. Automatica 2016, 65, 120–131. [Google Scholar]
- Leonard, N.E.; Paley, D.A.; Davis, R.E.; Fratantoni, D.M.; Lekien, F.; Zhang, F.M. Coordinated control of an underwater glider fleet in an adaptive ocean sampling field experiment in Monterey Bay. J. Field Robot. 2010, 27, 718–740. [Google Scholar] [CrossRef]
- Damasceno, B.C.; Xie, X. Deadlock-free scheduling of manufacturing systems using Petri nets and dynamic programming. IFAC Proc. Vol. 1999, 32, 4870–4875. [Google Scholar] [CrossRef]
- Sherif, F.; Balakrishnan, S.; ElMekkawy, T. Deadlock prevention and performance oriented supervision in flexible manufacturing cells: A hierarchical approach. Robot. Comput. Integr. Manuf. 2011, 27, 591–603. [Google Scholar]
- Mehdi, F.; Gunawan, I.; Smith-Miles, K. Resolution of deadlocks in a robotic cell scheduling problem with post-process inspection system: Avoidance and recovery scenarios. In Proceedings of the 2015 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Singapore, 6–9 December 2015. [Google Scholar]
- Wang, C.; Xie, G.; Cao, M. Forming circle formations of anonymous mobile agents with order preservation. IEEE Trans. Autom. Control 2013, 58, 3248–3254. [Google Scholar] [CrossRef]
- Liu, R.; Cao, X.; Liu, M. Finite-time synchronization control of spacecraft formation with network-induced communication delay. IEEE Access 2017, 5, 27242–27253. [Google Scholar] [CrossRef]
- Song, C.; Liu, L.; Feng, G.; Xu, S.Y. Coverage control for heterogeneous mobile sensor networks on a circle. Automatica 2016, 63, 349–358. [Google Scholar] [CrossRef]
- Wang, C.; Xie, G. Limit-cycle-based decoupled design of circle formation control with collision avoidance for anonymous agents in a plane. IEEE Trans. Autom. Control 2017, 62, 6560–6567. [Google Scholar] [CrossRef]
- Mao, X. Stochastic versions of the LaSalle theorem. J. Differ. Equ. 1999, 153, 175–195. [Google Scholar] [CrossRef] [Green Version]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, P.; Tao, J.; Xu, M.; Xie, G. Practical Formation Control for Multiple Anonymous Robots System with Unknown Nonlinear Disturbances. Appl. Sci. 2021, 11, 9170. https://doi.org/10.3390/app11199170
Xu P, Tao J, Xu M, Xie G. Practical Formation Control for Multiple Anonymous Robots System with Unknown Nonlinear Disturbances. Applied Sciences. 2021; 11(19):9170. https://doi.org/10.3390/app11199170
Chicago/Turabian StyleXu, Peng, Jin Tao, Minyi Xu, and Guangming Xie. 2021. "Practical Formation Control for Multiple Anonymous Robots System with Unknown Nonlinear Disturbances" Applied Sciences 11, no. 19: 9170. https://doi.org/10.3390/app11199170
APA StyleXu, P., Tao, J., Xu, M., & Xie, G. (2021). Practical Formation Control for Multiple Anonymous Robots System with Unknown Nonlinear Disturbances. Applied Sciences, 11(19), 9170. https://doi.org/10.3390/app11199170








