Ventilation Characteristics and Performance Evaluation of Different Window-Opening Forms in a Typical Office Room
Abstract
:1. Introduction
2. Evaluation Model of Ventilation Performance
3. Full-Scale Experiments
3.1. Experimental Site and Test Instruments
3.2. Data Acquisition
3.3. Experimental Conditions and Procedures
4. CFD Simulation
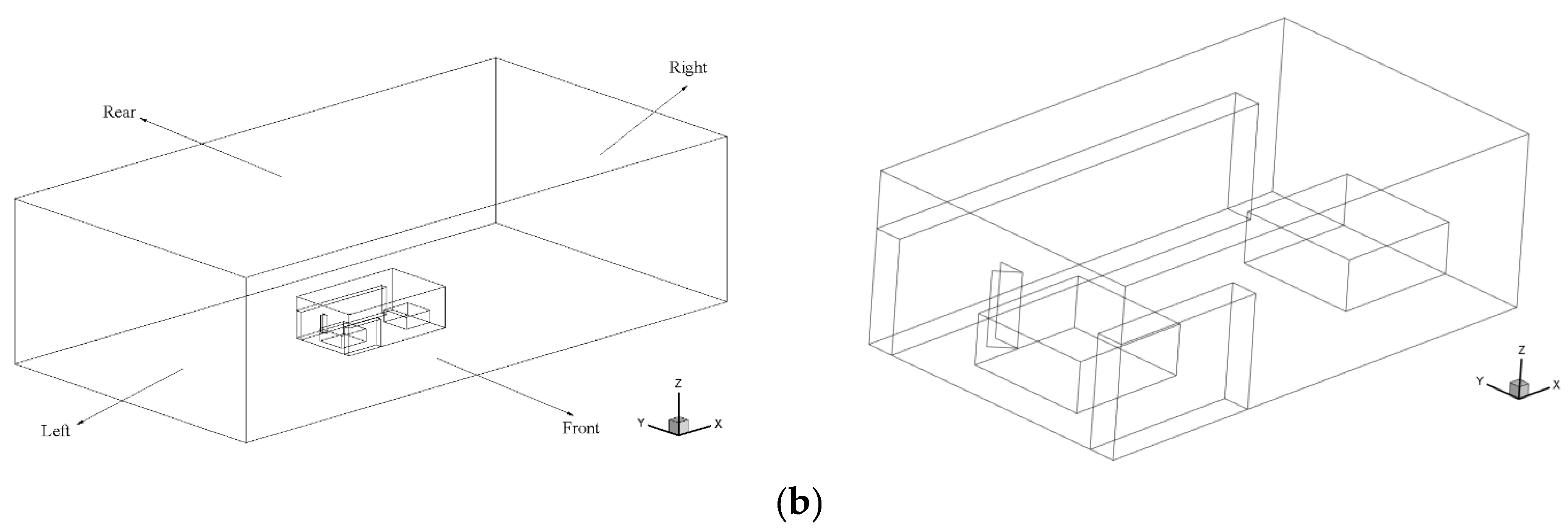
4.1. Geometrical Models and Numerical Methods
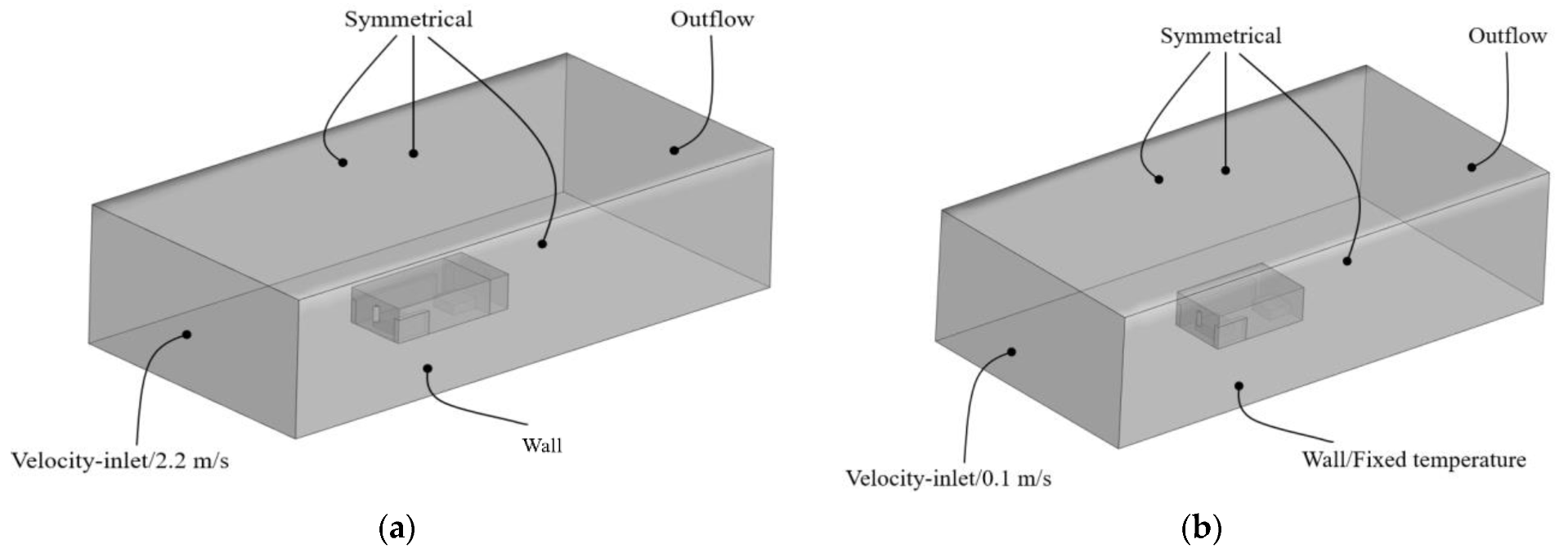
4.2. Numerical Grids and Boundary Conditions
4.3. CFD Validation
4.3.1. Validation of Wind Pressure Difference and Discharge Coefficient for CV Model
4.3.2. Validation of the Discharge Coefficient for SV Model
5. Results and Discussion
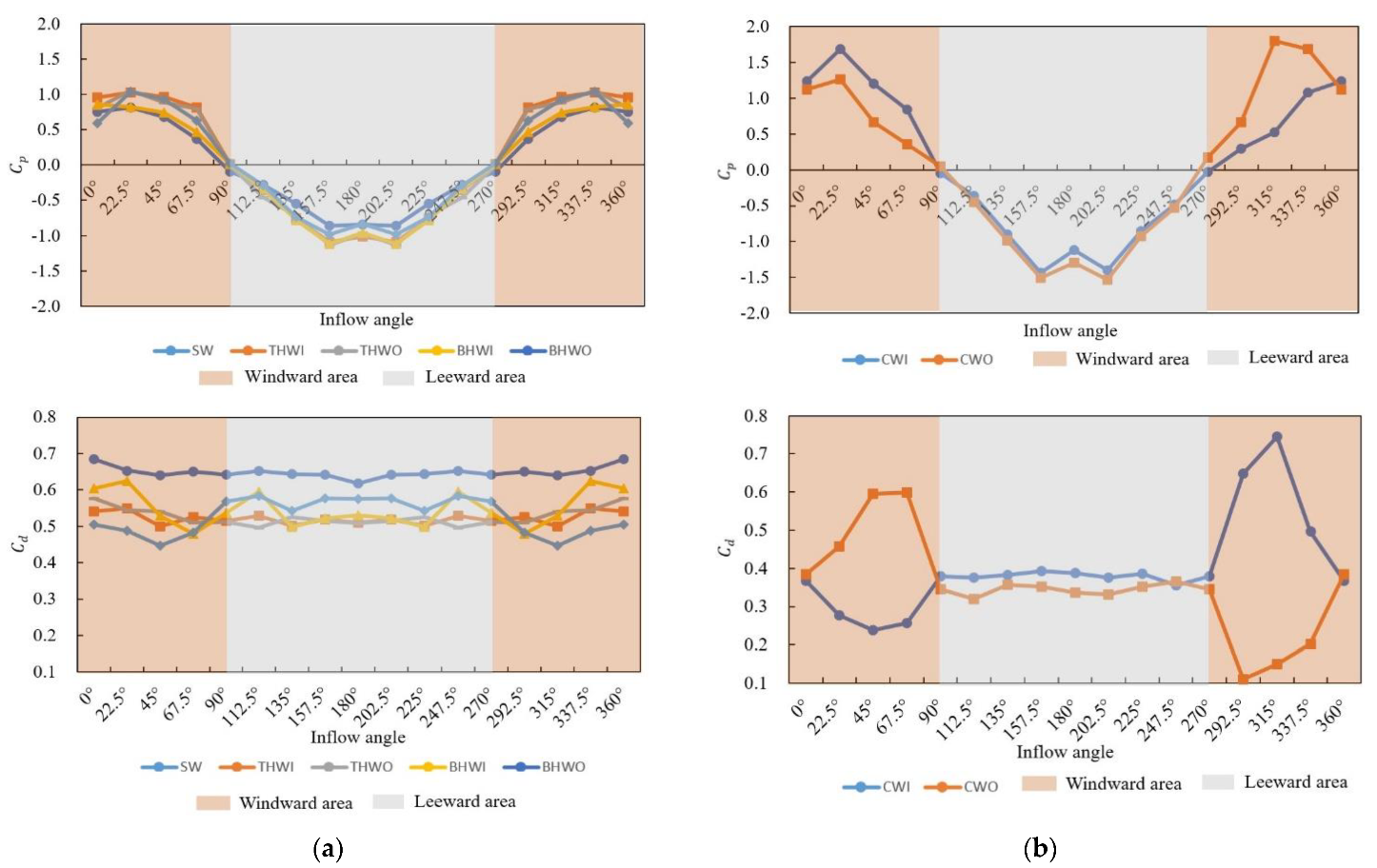
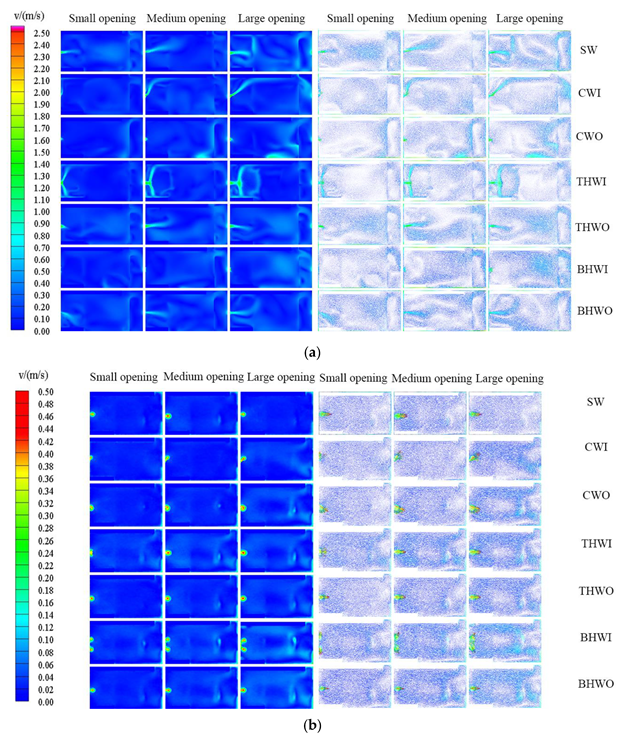
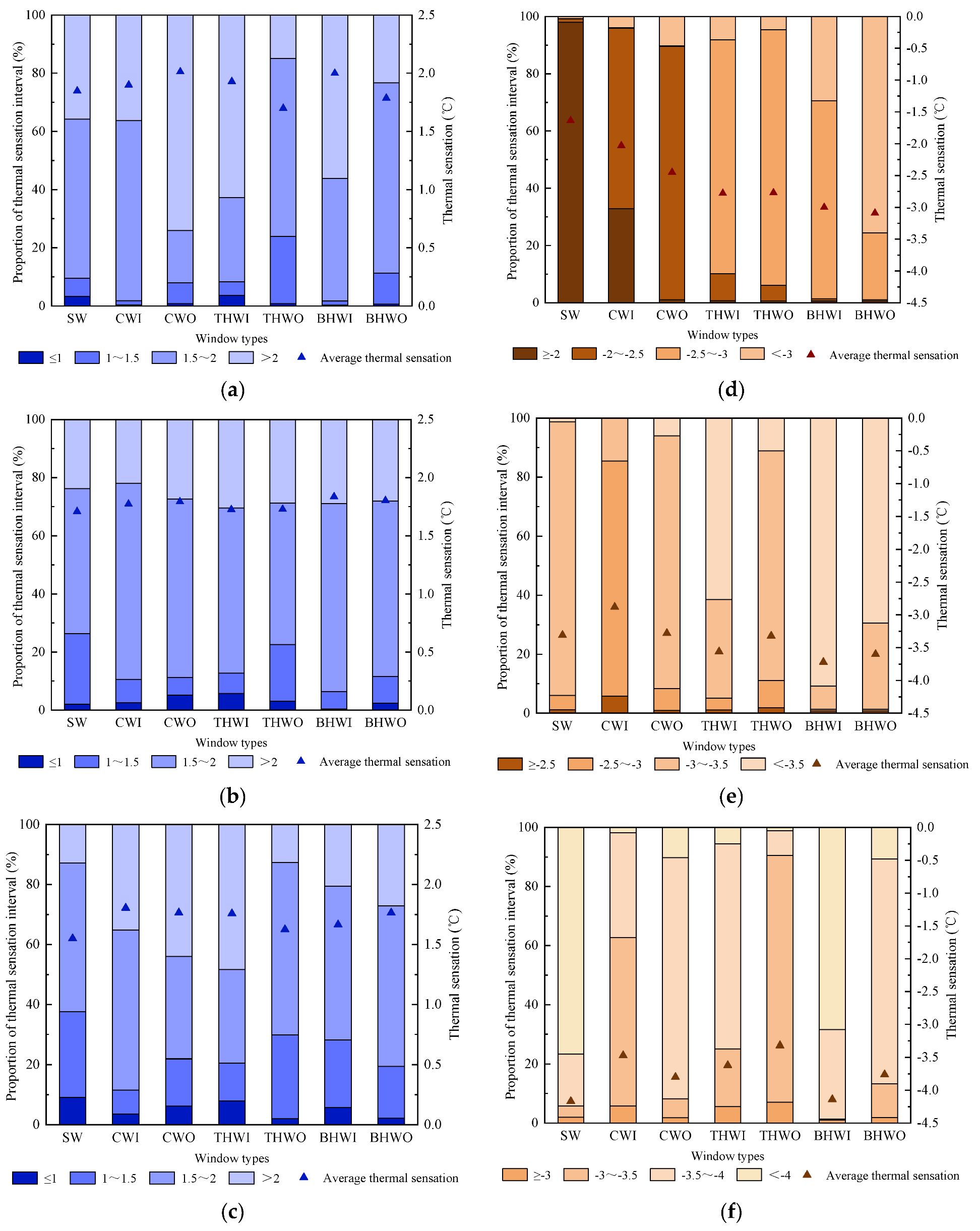
5.1. Comparison of Ventilation Characteristics of Seven Window Types with Different Wind Directions under CV
5.2. Comparison of Ventilation Characteristics of Seven Window Types with Three Opening Angles under CV and SV
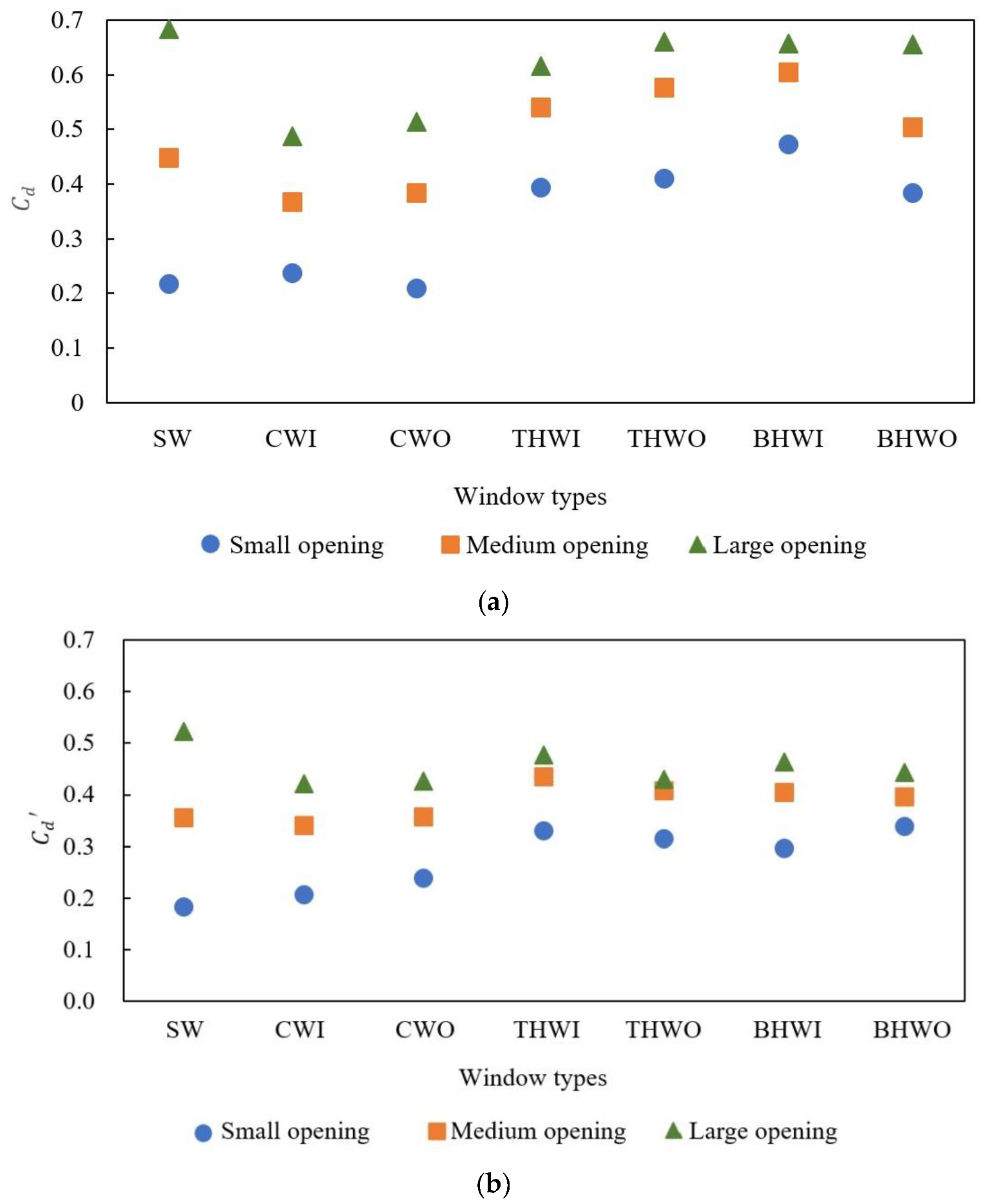
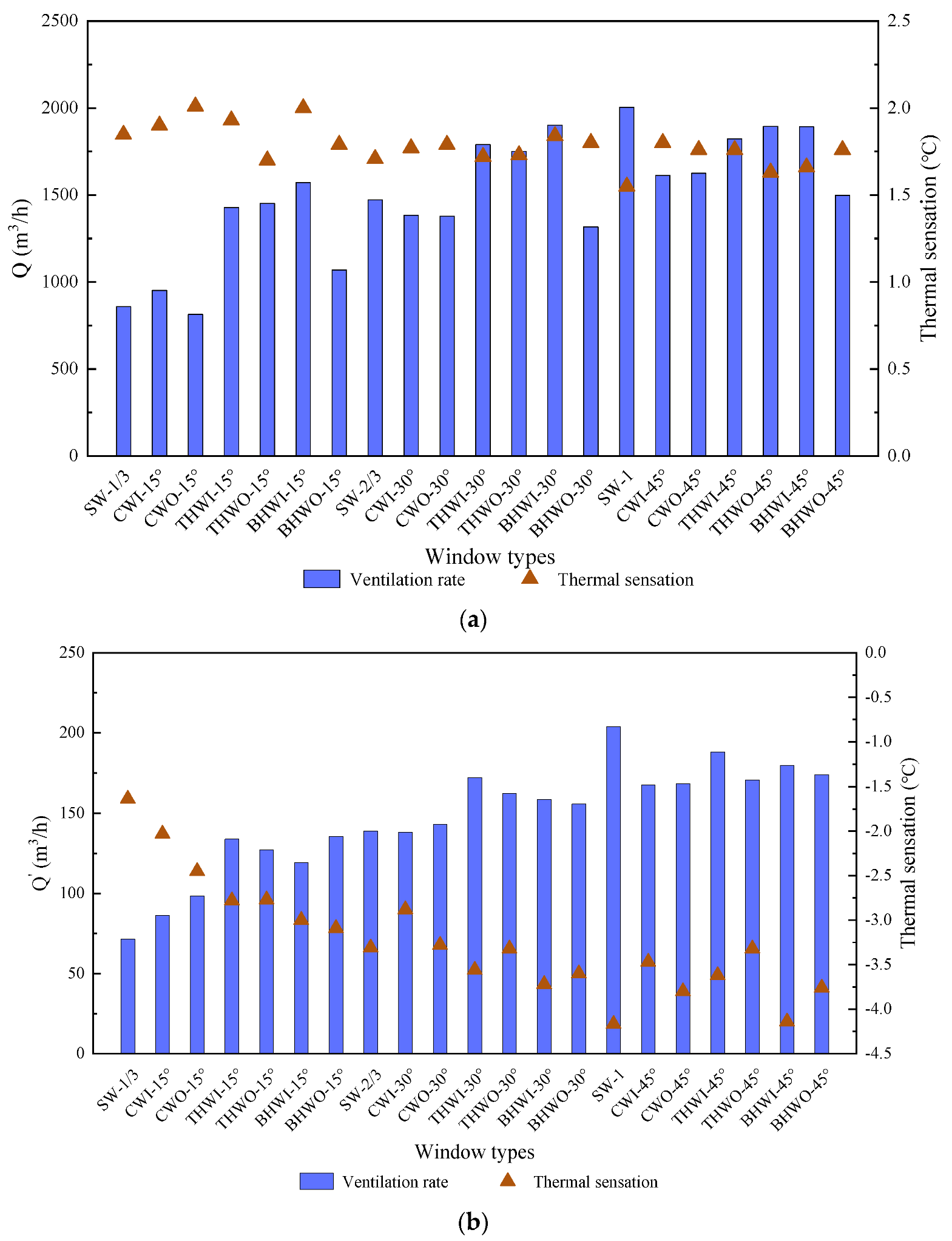
5.3. Comprehensive Evaluation of Ventilation Performance of Different Window Types
6. Conclusions
- (1)
- For CV, on the windward side, the maximum value of the wind pressure coefficient of different window types does not appear at 0° (360°), but under the symmetrical condition of 22.5° (337.5°); there is a similar situation on the leeward side, where the minimum value of the coefficient appears in the symmetrical conditions of 157.5° (202.5°).
- (2)
- For CV and SV, the discharge coefficient increases with the increase in window opening, and the full opening of the sliding window has the highest discharge coefficient, which is 0.68 and 0.52, respectively. For medium and small openings, the discharge coefficient of the bottom-hung window opening inwards is the highest under CV, whereas that of the top-hung window opening inwards is the highest under SV.
- (3)
- Based on the evaluation of the ventilation performance of different window-opening forms, it is concluded that the sliding window with a full opening has the best ventilation performance under CV, with a ratio of 1293.26, whereas the ventilation performance is the best under SV when the opening of the top-hung window opening inwards is 45°, with a ratio of 51.97. In general, the two types of top-hung windows have better ventilation performance under the two ventilation modes. The results of this study are useful for designers when selecting window types and designing windows with opening restrictors for office buildings.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| BHWI | Bottom-hung window opening inwards |
| BHWI-15° | Bottom-hung window opening inwards at 15° |
| BHWI-30° | Bottom-hung window opening inwards at 30° |
| BHWI-45° | Bottom-hung window opening inwards at 45° |
| BHWO | Bottom-hung window opening outwards |
| BHWI | Bottom-hung window opening inwards |
| BHWI-15° | Bottom-hung window opening inwards at 15° |
| BHWI-30° | Bottom-hung window opening inwards at 30° |
| BHWI-45° | Bottom-hung window opening inwards at 45° |
| BHWO | Bottom-hung window opening outwards |
| BHWO-15° | Bottom-hung window opening outwards at 15° |
| BHWO-30° | Bottom-hung window opening outwards at 30° |
| BHWO-45° | Bottom-hung window opening outwards at 45° |
| CFD | Computational fluid dynamics |
| CV | Wind-driven cross-ventilation |
| BHWI | Bottom-hung window opening inwards |
| BHWI-15° | Bottom-hung window opening inwards at 15° |
| BHWI-30° | Bottom-hung window opening inwards at 30° |
| BHWI-45° | Bottom-hung window opening inwards at 45° |
| CWO-30° | Casement window opening outwards at 30° |
| CWO-45° | Casement window opening outwards at 45° |
| Ventilation rate for wind-driven cross-ventilation () | |
| Ventilation rate for temperature-driven single-sided ventilation () | |
| SV | Temperature-driven single-sided ventilation |
| SW | Sliding window |
| SW-1/3 | Sliding window with 1/3 opening |
| SW-2/3 | Sliding window with 2/3 opening |
| SW-1 | Sliding window with full opening |
| Human thermal sensation neutral temperature | |
| THWI | Top-hung window opening inwards |
| THWI-15° | Top-hung window opening inwards at 15° |
| THWI-30° | Top-hung window opening inwards at 30° |
| THWI-45° | Top-hung window opening inwards at 45° |
| THWO | Top-hung window opening outwards |
| THWO-15° | Top-hung window opening outwards at 15° |
| THWO-30° | Top-hung window opening outwards at 30° |
| THWO-45° | Top-hung window opening outwards at 45° |
References
- Michael, A.; Demosthenous, D.; Philokyprou, M. Natural Ventilation for Cooling in Mediterranean Climate: A Case Study in Vernacular Architecture of Cyprus. Energy Build. 2017, 144, 333–345. [Google Scholar] [CrossRef]
- Yao, R.; Li, B.; Steemers, K.; Short, A. Assessing the natural ventilation cooling potential of office buildings in different climate zones in China. Renew. Energy 2009, 34, 2697–2705. [Google Scholar] [CrossRef]
- Moosavi, L.; Zandi, M.; Bidi, M. Experimental study on the cooling performance of solar-assisted natural ventilation in a large building in a warm and humid climate. J. Build. Eng. 2018, 19, 228–241. [Google Scholar] [CrossRef]
- Cheng, J.; Qi, D.H.; Katal, A.; Wang, L.Z.; Stathopoulos, T. Evaluating wind-driven natural ventilation potential for early building design. J. Wind Eng. Ind. Aerodyn. 2018, 182, 160–169. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, B.; You, S.; Ye, T.; Zheng, W.; Wei, S.; Yang, S.; Wang, Y.; Li, K. The effects of manual airing strategies and architectural factors on the indoor air quality in college classrooms: A case study. Air Qual. Atmos. Health 2021. [Google Scholar] [CrossRef]
- Dino, G.; Walter, M.; Günter, B.; Hrvoje, K. Wind-tunnel analysis of natural ventilation in a generic building in sheltered and unsheltered conditions: Impact of Reynolds number and wind direction. J. Wind Eng. Ind. Aerodyn. 2020, 207, 1–17. [Google Scholar]
- Oropeza-Perez, I.; Ostergaard, P.A. Energy saving potential of utilizing natural ventilation under warm conditions—A case study of Mexico. Appl. Energy 2014, 130, 20–32. [Google Scholar] [CrossRef]
- Tong, Z.; Chen, Y.; Malkawi, A.; Liu, Z.; Freeman, R.B. Energy saving potential of natural ventilation in China: The impact of ambient air pollution. Appl. Energy 2016, 179, 660–668. [Google Scholar] [CrossRef] [Green Version]
- Xiaofeng, L. Design and Application of Natural Ventilation in Buildings; China Architecture & Building Press: Beijing, China, 2018. [Google Scholar]
- David, E. Natural Ventilation of Buildings:Theory, Measurement and Design; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Allocca, C.; Chen, Q.; Glicksman, L.R. Design analysis of single-sided natural ventilation. Energy Build. 2003, 35, 785–795. [Google Scholar] [CrossRef]
- Abdullah, H.K.; Alibaba, H.Z. Window Design of Naturally Ventilated Offices in the Mediterranean Climate in Terms of CO2 and Thermal Comfort Performance. Sustainability 2020, 12, 473. [Google Scholar] [CrossRef] [Green Version]
- Sacht, H.; Lukiantchuki, M.A. Windows Size and the Performance of Natural Ventilation. Procedia Eng. 2017, 196, 972–979. [Google Scholar] [CrossRef]
- Du, L.; Lau, S.-K.; Lee, S.E.; Danzer, M.K. Experimental study on noise reduction and ventilation performances of sound-proofed ventilation window. Build. Environ. 2020, 181, 1–9. [Google Scholar] [CrossRef]
- Grabe, J.V.; Svoboda, P.; Baeumler, A. Window ventilation efficiency in the case of buoyancy ventilation. Energy Build. 2014, 72, 203–211. [Google Scholar] [CrossRef]
- Liang, W.; Jun, L.; Juan, Z.; Lei, H.; Xi, L.Y. Analysis of the influence of window opening modes on natural ventilation in living room. J. Chongqing Univ. 2011, 34, 75–79. [Google Scholar]
- Fan, S.; Davies Wykes, M.S.; Lin, W.E.; Jones, R.L.; Robins, A.G.; Linden, P.F. A full-scale field study for evaluation of simple analytical models of cross ventilation and single-sided ventilation. Build. Environ. 2021, 187, 1–11. [Google Scholar] [CrossRef]
- Chen, Z.; Bai, L.; Li, F. Effects of external window form on residential building energy consumption. In Proceedings of the 4th International Conference on Manufacturing Science and Engineering (ICMSE 2013), Dalian, China, 30–31 March 2013; pp. 1619–1624. [Google Scholar]
- Barlow, S.; Fiala, D. Occupant comfort in UK offices—How adaptive comfort theories might influence future low energy office refurbishment strategies. Energy Build. 2007, 39, 837–846. [Google Scholar] [CrossRef]
- Favarolo, P.A.; Manz, H. Temperature-driven single-sided ventilation through a large rectangular opening. Build. Environ. 2005, 40, 689–699. [Google Scholar] [CrossRef]
- Heiselberg, P.; Svidt, K.; Nielsen, P.V. Characteristics of airflow from open windows. Build. Environ. 2001, 36, 859–869. [Google Scholar] [CrossRef]
- Yang, C.; Shi, H.; Yang, X.; Zhao, B. Research on Flow Resistance Characteristics with Different Window/Door Opening Angles. HVACR Res. 2010, 16, 813–824. [Google Scholar] [CrossRef]
- Liu, T.Q.; Lee, W.L. Influence of window opening degree on natural ventilation performance of residential buildings in Hong Kong. Sci. Technol. Built Environ. 2020, 26, 28–41. [Google Scholar] [CrossRef]
- Jin, R.Q.; Hang, J.; Liu, S.S.; Wei, J.J.; Liu, Y.; Xie, J.L.; Sandberg, M. Numerical investigation of wind-driven natural ventilation performance in a multi-storey hospital by coupling indoor and outdoor airflow. Indoor Built Environ. 2016, 25, 1226–1247. [Google Scholar] [CrossRef]
- Deng, H.Y.; Feng, Z.B.; Cao, S.J. Influence of air change rates on indoor CO2 stratification in terms of Richardson number and vorticity. Build. Environ. 2018, 129, 74–84. [Google Scholar] [CrossRef]
- Buratti, C.; Mariani, R.; Moretti, E. Mean age of air in a naturally ventilated office: Experimental data and simulations. Energy Build. 2011, 43, 2021–2027. [Google Scholar] [CrossRef]
- Yang, R.Q.; Zhang, H.; You, S.J.; Zheng, W.D.; Zheng, X.J.; Ye, T.Z. Study on the thermal comfort index of solar radiation conditions in winter. Build. Environ. 2020, 167, 106456. [Google Scholar] [CrossRef]
- He, Y.D.; Chen, W.H.; Wang, Z.; Zhang, H. Review of fan-use rates in field studies and their effects on thermal comfort, energy conservation, and human productivity. Energy Build. 2019, 194, 140–162. [Google Scholar] [CrossRef] [Green Version]
- de Dear, R.J.; Brager, G.S. Thermal comfort in naturally ventilated buildings: Revisions to ASHRAE Standard 55. Energy Build. 2002, 34, 549–561. [Google Scholar] [CrossRef] [Green Version]
- Yu, Z.; Fu, Y.; Chen, M. Research on Thermal Comfort Models for Naturally Ventilated Buildings. Build. Sci. 2017, 33, 176–182. [Google Scholar]
- Su, X.; Zhang, X.; Gao, J. Evaluation method of natural ventilation system based on thermal comfort in China. Energy Build. 2009, 41, 67–70. [Google Scholar] [CrossRef]
- General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China. GB/T 18883-2002 Indoor Air Quality Standard; China Standards Press: Beijing, China, 2002. [Google Scholar]
- Li, Z. Analysis and Research on Resistance Characteristics of Building Windows. Master’s Thesis, Chang’an University, Xi’an, China, 2012. [Google Scholar]
- Qing, L. Study on the Influence of Door and Window Opening on Indoor Natural Ventilation Environment. Master’s Thesis, Chongqing University, Chongqing, China, 2014. [Google Scholar]
- Yao, M.; Zhao, B. Measurement of natural ventilation rate of residences in Beijing, China. Procedia Eng. 2017, 205, 3435–3440. [Google Scholar] [CrossRef]
- Zhangwu, X.; Qingyuan, Y.; Shiwei, H.; Yagang, Z. Influence of neighbouring tenants’ windowing conditions to the room ventilation. Shanxi Archit. 2015, 41, 121–122. [Google Scholar]
- Wen, L. Experimental and Simulation Study on Single-Sided Natural Ventilation Caused by Buoyancy. Master’s Thesis, Hunan University, Changsha, China, 2008. [Google Scholar]
- Fujun, W. Computational Fluid Dynamics Analysis; Tsinghua University Press: Beijing, China, 2004. [Google Scholar]
- Tominaga, Y.; Mochida, A.; Yoshie, R.; Kataoka, H.; Nozu, T.; Yoshikawa, M.; Shirasawa, T. AIJ guidelines for practical applications of CFD to pedestrian wind environment around buildings. J. Wind. Eng. Ind. Aerodyn. 2008, 96, 1749–1761. [Google Scholar] [CrossRef]
- Meng, F.Q.; He, B.J.; Zhu, J.; Zhao, D.X.; Darko, A.; Zhao, Z.Q. Sensitivity analysis of wind pressure coefficients on CAARC standard tall buildings in CFD simulations. J. Build. Eng. 2018, 16, 146–158. [Google Scholar] [CrossRef]
- Montazeri, H.; Blocken, B. CFD simulation of wind-induced pressure coefficients on buildings with and without balconies: Validation and sensitivity analysis. Build. Environ. 2013, 60, 137–149. [Google Scholar] [CrossRef]
- Nicol, J.F.; Humphreys, M.A. A stochastic approach to thermal comfort—Occupant behavior and energy use in buildings. Ashrae Trans. 2004, 110, 554–568. [Google Scholar]
- ASHRAE. ANSI/Standard 55-2013 Thermal Environment Conditions for Human Occupancy; ASHRAE: Atlanta, GA, USA, 2013. [Google Scholar]
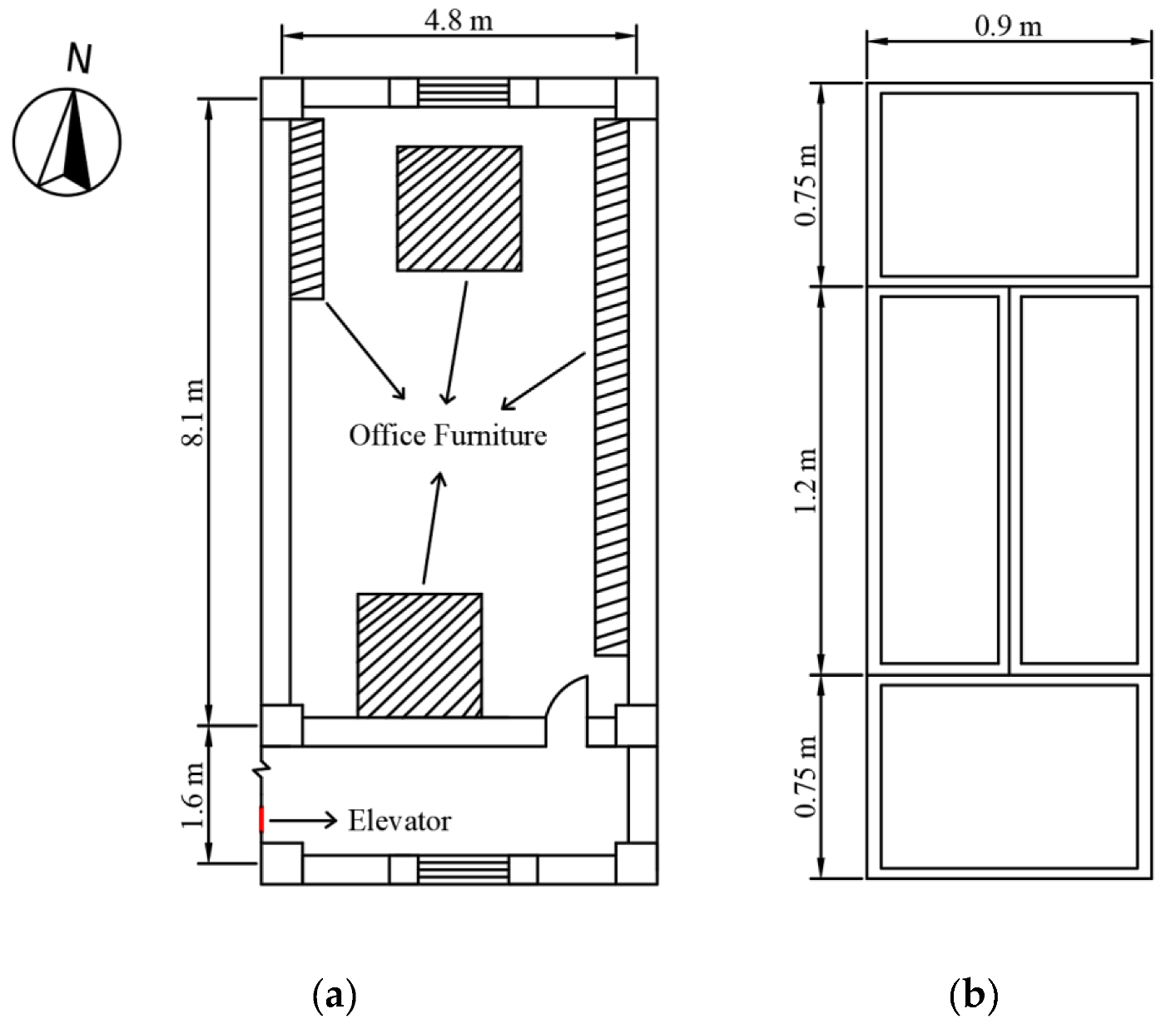

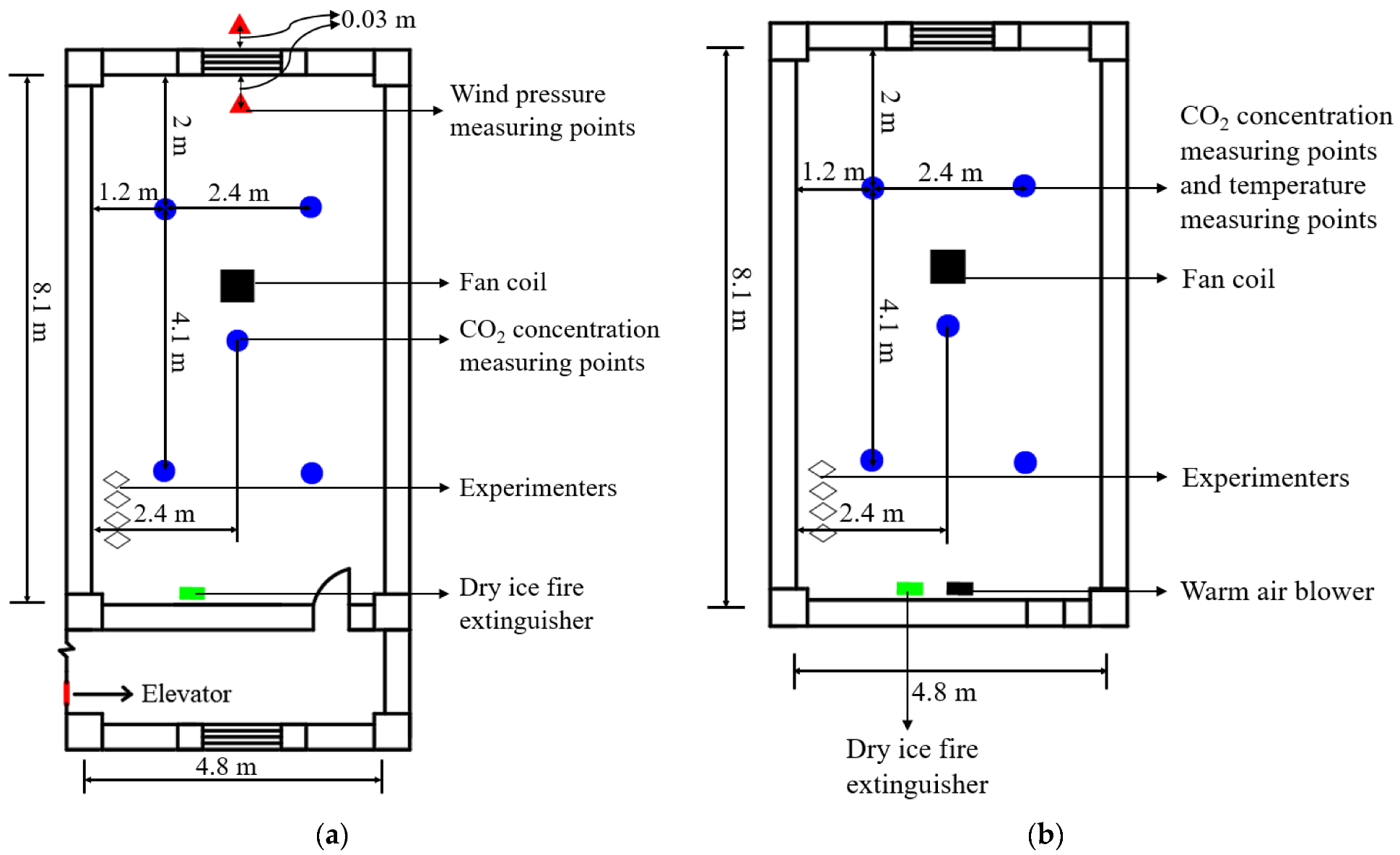
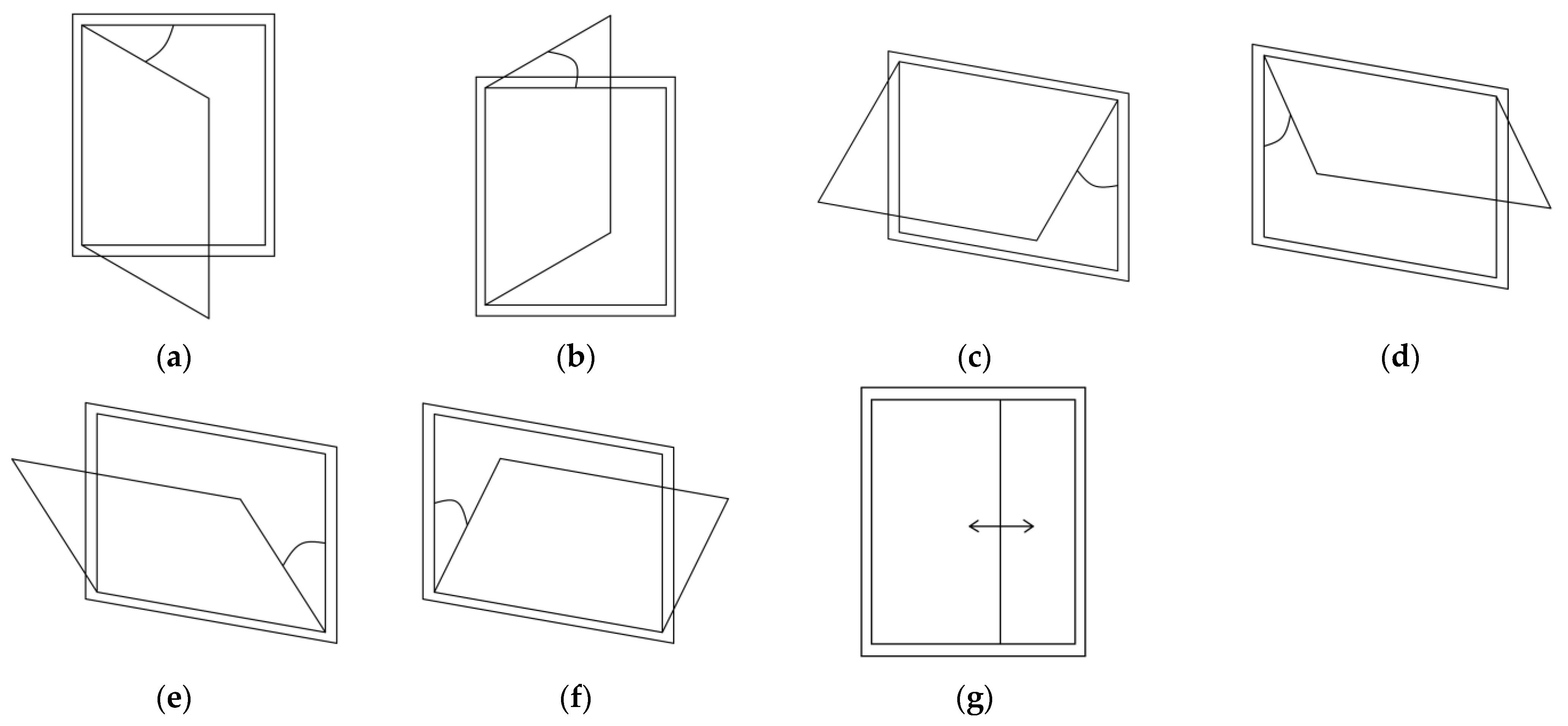
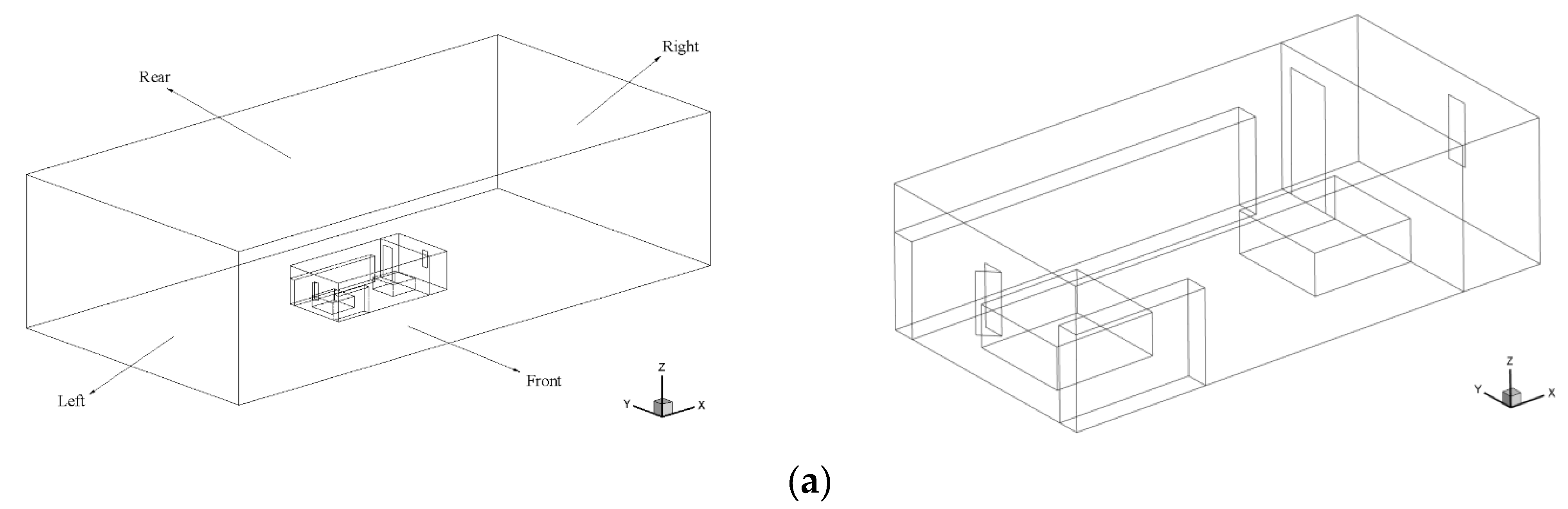
| Exterior Wall Area (m2) | Exterior Window Area (m2) | Sheet Area of the Exterior Window (m2) | Interior Wall Area (m2) | Door Area (m2) | Room Area (m2) |
|---|---|---|---|---|---|
| 5.67 | 2.43 | 1.08 | 52.48 | 2.11 | 38.88 |
| Total Volume (m3) | Furniture Volume (m3) | Net Volume (m3) |
|---|---|---|
| 104.98 | 16.64 | 88.34 |
| Instrument | Parameter Category | Measuring Range | Resolution | Precision | Model | Supplier |
|---|---|---|---|---|---|---|
| Small weather station | Wind speed | 1–68 m/s | 0.1 m/s | ±5% (1.5 m/s) | Vantage pro2 | DAVIS |
| Wind direction | 0°–360° | 1° | ±3° | |||
| Air temperature | −40–65 °C | 0.1 °C | ±0.5 °C | |||
| Relative humidity | 0–100% | 1% | ±3% | |||
| Temperature and humidity recorder | Air temperature | 20–70 °C | 0.1 °C | ±0.5 °C | U10-003 | Onset HOBO |
| Relative humidity | 25–95% | 1% | ±3.5–5% | |||
| Miniature wind pressure gauge | Wind pressure | −3735–+3735 Pa | 0.1 Pa | ±1.5% | DP-CALC5815 | TSI |
| CO2 detection recorder | CO2 concentration | 0–5000 ppm | 1 ppm | ±50 ppm | MH-Z14A | WINSEN |
| Infrared thermometer | Wall temperature | −40–800 °C | 0.1 °C | ±1% or ±1.0 °C | FLUKE568 | FLUKE |
| Ventilation Mode | Condition Number | Door Status | Number of Open Sheets of the Window | Window Opening |
|---|---|---|---|---|
| CV | 1–1 | Open | 1 | 30° |
| 1–2 | 2 | 30° | ||
| 1–3 | 1 | 45° | ||
| 1–4 | 2 | 45° | ||
| SV | 2–1 | Closed | 1 | 30° |
| 2–2 | 2 | 30° | ||
| 2–3 | 1 | 45° | ||
| 2–4 | 2 | 45° |
| Serial Number | Mean Wind Speed (m/s) | Dominant Wind Direction | Mean Value | Pearson Correlation Coefficient | |
|---|---|---|---|---|---|
| Simulated Value (Pa) | Measured Value (Pa) | ||||
| 1 | 4.0 | 67.5° | 2.53 | 2.19 | 0.868 |
| 2 | 2.2 | 315° | 1.20 | 1.55 | 0.746 |
| 3 | 2.5 | 112.5° | 0.51 | 0.40 | 0.774 |
| 4 | 2.1 | 112.5° | 0.38 | 0.33 | 0.769 |
| 5 | 3.3 | 67.5° | 0.58 | 0.46 | 0.832 |
| 6 | 1.2 | 45° | 1.12 | 1.40 | 0.809 |
| 7 | 1.7 | 247.5° | 0.47 | 0.31 | 0.798 |
| 8 | 2.4 | 270° | 0.32 | 0.41 | 0.755 |
| 9 | 3.8 | 225° | 1.91 | 2.26 | 0.817 |
| 10 | 2.1 | 112.5° | 0.38 | 0.33 | 0.769 |
| Condition Number | Outdoor Mean Wind Speed (m/s) | Dominant Wind Direction | Average Temperature Difference between Indoor and Outdoor (°C) | |||
|---|---|---|---|---|---|---|
| Simulated Value | Experimental Value | Relative Error | ||||
| 1–1 | 0.2 | 112.5° | 3.9 | 0.319 | 0.335 | 4.8% |
| 1–2 | 3.0 | 22.5° | 3.3 | 0.457 | 0.474 | 3.6% |
| 1–3 | 3.0 | 202.5° | 1.1 | 0.413 | 0.404 | −2.2% |
| 1–4 | 2.6 | 337.5° | 1.4 | 0.270 | 0.261 | −3.4% |
| Condition Number | Outdoor Mean Wind Speed (m/s) | Indoor and Outdoor Average Temperature Difference | |||||
|---|---|---|---|---|---|---|---|
| Simulated Value | Experimental Value | Relative Error | Simulated Value | Experimental Value | Relative Error | ||
| 2–1 | 2.0 | 15.5 | 16.6 | 6.6% | 0.360 | 0.371 | 3.0% |
| 2–2 | 1.2 | 17.5 | 18.7 | 6.4% | 0.363 | 0.356 | −2.0% |
| 2–3 | 1.0 | 18.3 | 19.8 | 7.6% | 0.408 | 0.395 | −3.3% |
| 2–4 | 1.2 | 8.3 | 9.0 | 7.8% | 0.426 | 0.430 | 0.9% |
| Window Types | CV | SV | ||||
|---|---|---|---|---|---|---|
| Ventilation Rate (m3/h) | Thermal Sensation (°C) | Ratio | Ventilation Rate (m3/h) | Thermal Sensation (°C) | Ratio | |
| SW-1/3 | 858.12 | 1.85 | 464.40 | 71.52 | −1.64 | 43.69 |
| CWI-15° | 952.16 | 1.90 | 501.14 | 86.31 | −2.03 | 42.52 |
| CWO-15° | 814.04 | 2.01 | 405.00 | 98.56 | −2.45 | 40.23 |
| THWI-15° | 1428.25 | 1.93 | 740.03 | 133.86 | −2.78 | 48.15 |
| THWO-15° | 1451.76 | 1.70 | 853.98 | 127.24 | −2.77 | 45.94 |
| BHWI-15° | 1572.25 | 2.00 | 786.13 | 119.14 | −3.00 | 39.71 |
| BHWO-15° | 1069.71 | 1.79 | 597.60 | 135.54 | −3.09 | 43.86 |
| SW-2/3 | 1472.33 | 1.71 | 861.87 | 138.90 | −3.31 | 41.98 |
| CWI-30° | 1384.16 | 1.77 | 782.01 | 138.12 | −2.88 | 47.96 |
| CWO-30° | 1378.29 | 1.79 | 769.99 | 143.16 | −3.28 | 43.65 |
| THWI-30° | 1789.71 | 1.72 | 1040.53 | 172.01 | −3.56 | 48.32 |
| THWO-30° | 1751.51 | 1.73 | 1012.43 | 162.48 | −3.32 | 48.94 |
| BHWI-30° | 1901.39 | 1.84 | 1033.36 | 158.60 | −3.72 | 42.63 |
| BHWO-30° | 1316.57 | 1.80 | 731.43 | 155.81 | −3.60 | 43.28 |
| SW-1 | 2004.25 | 1.55 | 1293.26 | 203.94 | −4.17 | 48.93 |
| CWI-45° | 1613.39 | 1.80 | 896.33 | 167.76 | −3.47 | 48.35 |
| CWO-45° | 1625.14 | 1.76 | 923.38 | 168.51 | −3.80 | 44.34 |
| THWI-45° | 1822.04 | 1.76 | 1035.25 | 188.14 | −3.62 | 51.97 |
| THWO-45° | 1895.51 | 1.63 | 1162.89 | 170.79 | −3.32 | 51.44 |
| BHWI-45° | 1892.57 | 1.66 | 1140.10 | 179.72 | −4.14 | 43.41 |
| BHWO-45° | 1498.78 | 1.76 | 851.58 | 173.79 | −3.76 | 46.22 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Yu, Y.; Ye, T.; Bo, Q. Ventilation Characteristics and Performance Evaluation of Different Window-Opening Forms in a Typical Office Room. Appl. Sci. 2021, 11, 8966. https://doi.org/10.3390/app11198966
Wang Y, Yu Y, Ye T, Bo Q. Ventilation Characteristics and Performance Evaluation of Different Window-Opening Forms in a Typical Office Room. Applied Sciences. 2021; 11(19):8966. https://doi.org/10.3390/app11198966
Chicago/Turabian StyleWang, Yuanyuan, Yanzhe Yu, Tianzhen Ye, and Quan Bo. 2021. "Ventilation Characteristics and Performance Evaluation of Different Window-Opening Forms in a Typical Office Room" Applied Sciences 11, no. 19: 8966. https://doi.org/10.3390/app11198966
APA StyleWang, Y., Yu, Y., Ye, T., & Bo, Q. (2021). Ventilation Characteristics and Performance Evaluation of Different Window-Opening Forms in a Typical Office Room. Applied Sciences, 11(19), 8966. https://doi.org/10.3390/app11198966







