Influence of Groove Structure Parameters Based on Optimal Mass Transfer Coefficient on Vaporization Characteristics and Sealing Performance of Liquid Film Mechanical Seals
Abstract
:1. Introduction
2. Establishing the Model
- (1)
- The fluid medium is a Newtonian fluid.
- (2)
- The fluid flow between the sealing interfaces is continuous medium laminar, and the fluid temperature and viscosity do not change with time.
- (3)
- The sealing surface is smooth, i.e., the effect of its roughness on the fluid flow is assumed to be negligible.
- (4)
- The film thickness is very thin, and the pressure and density remain unchanged in the thickness direction.
- (5)
- The temperature of the sealing ring and the mechanical properties of the material do not change with time.
- (6)
- There is no relative slip between the fluid medium and the seal face.
- (7)
- Disturbance and vibration of the system during operation are not accounted for.
3. Solution Settings
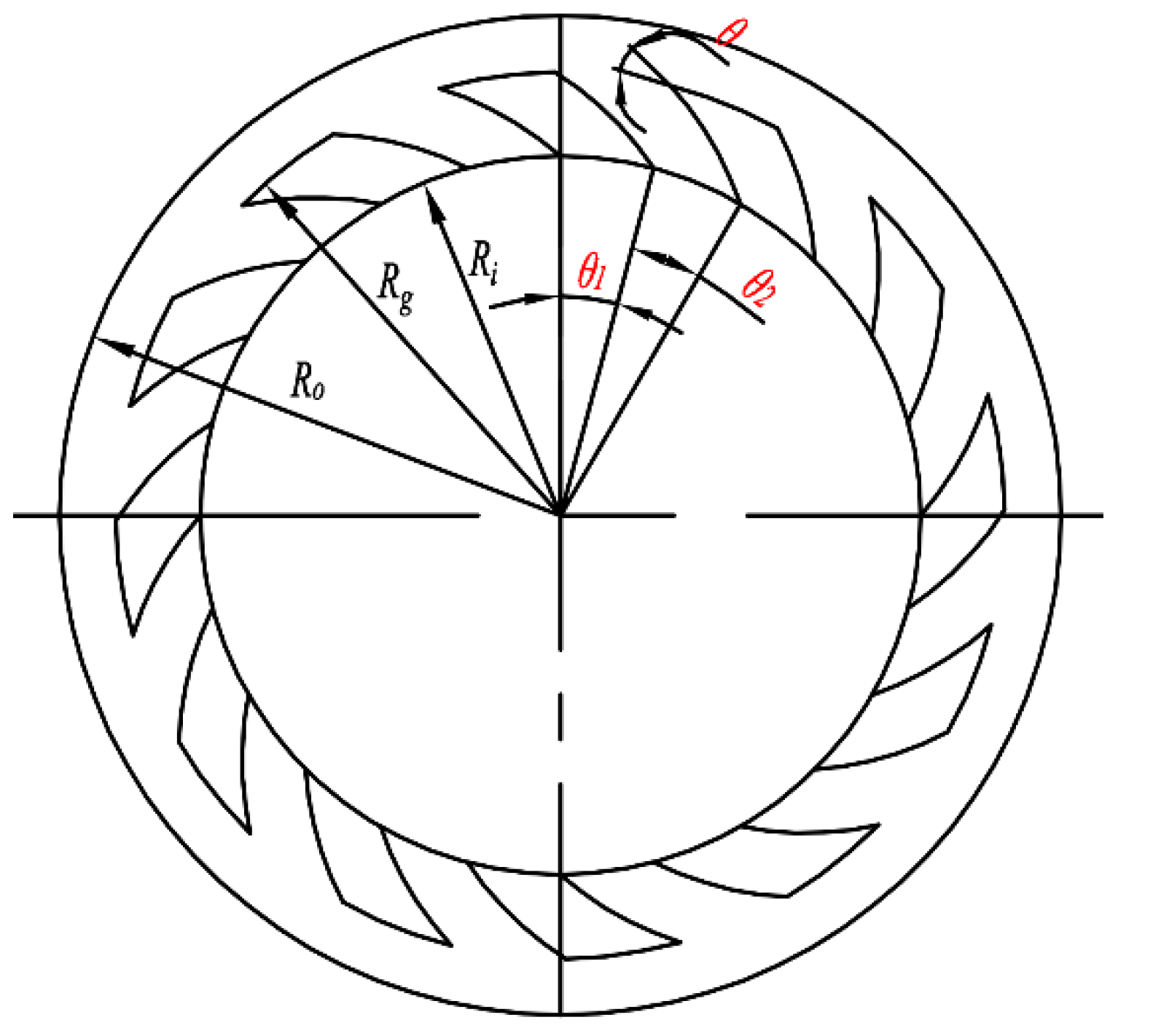
3.1. Computational Domain Geometry Model
3.2. Meshing
3.3. Boundary Conditions and Solver Settings
4. Model Validation
5. Result Analysis
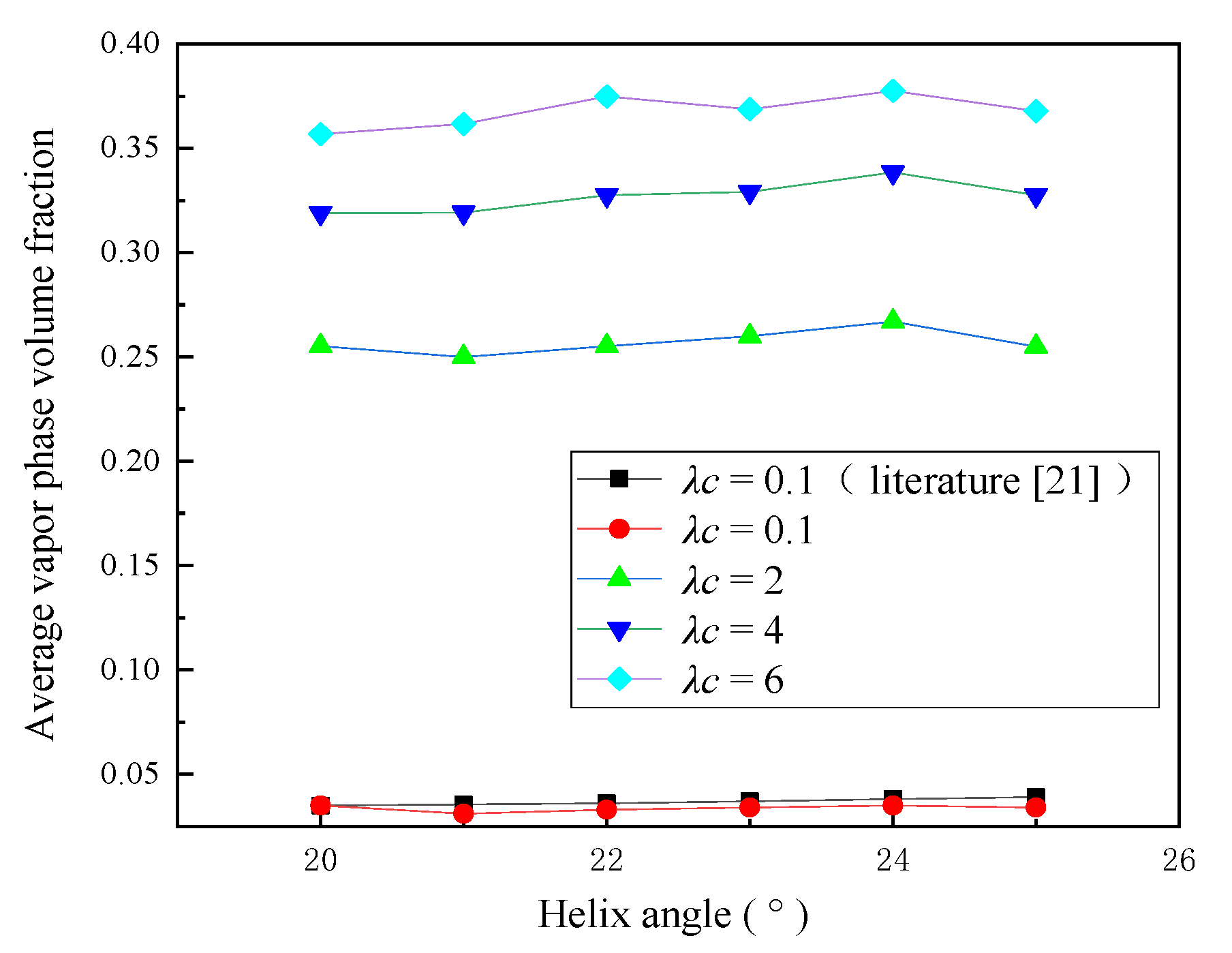
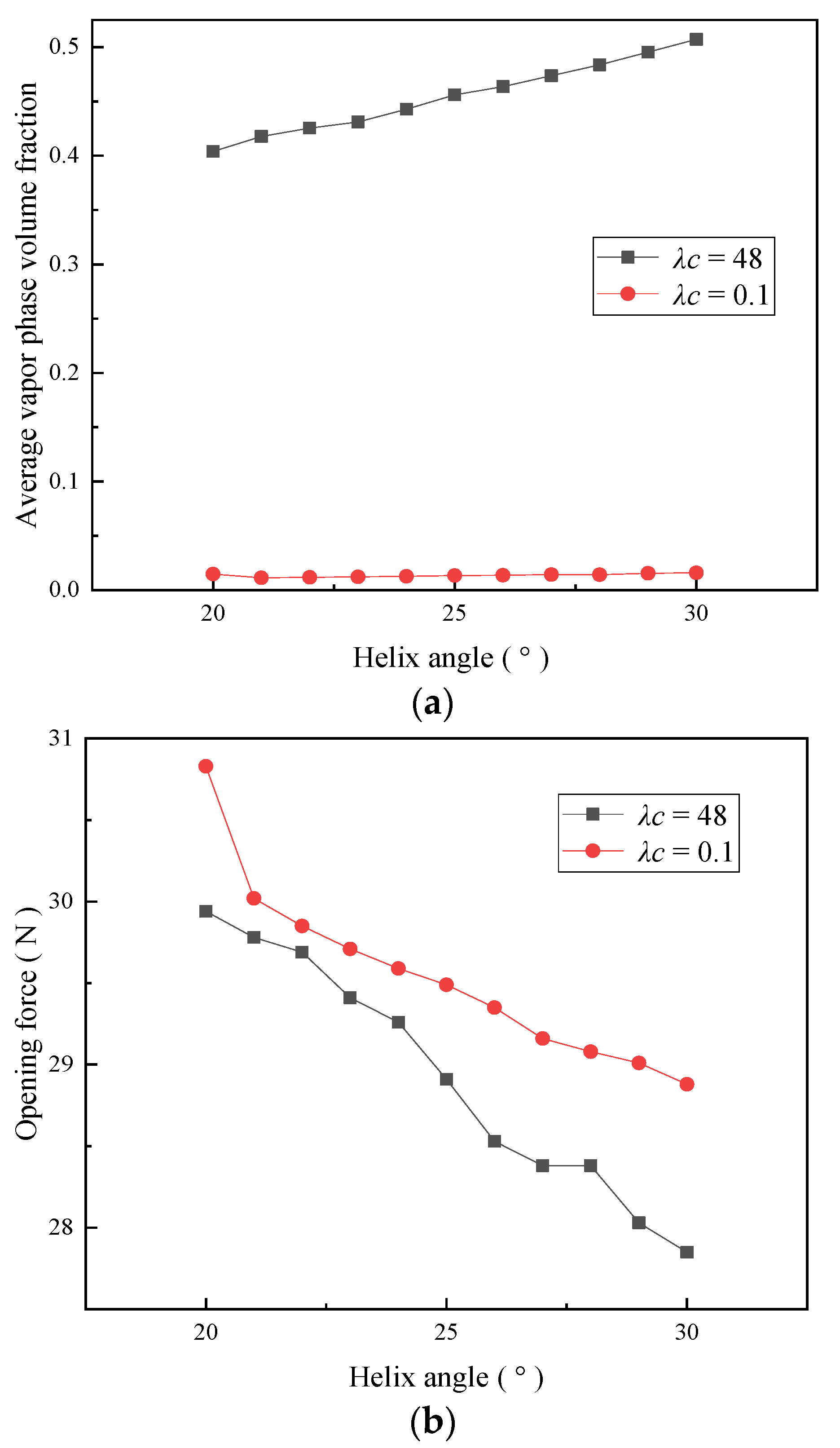
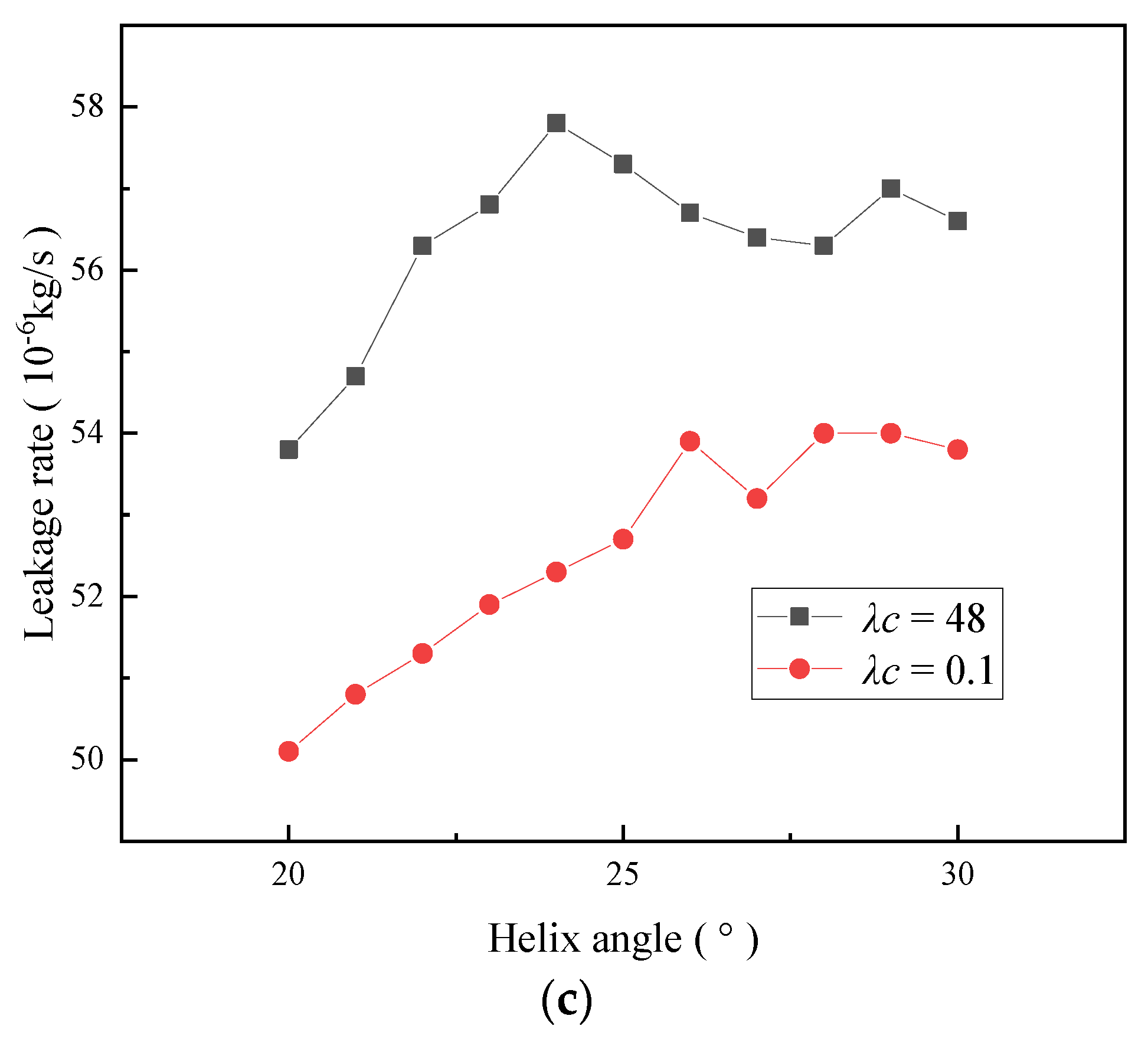
5.1. Effect of Helix Angle on Sealing Performance
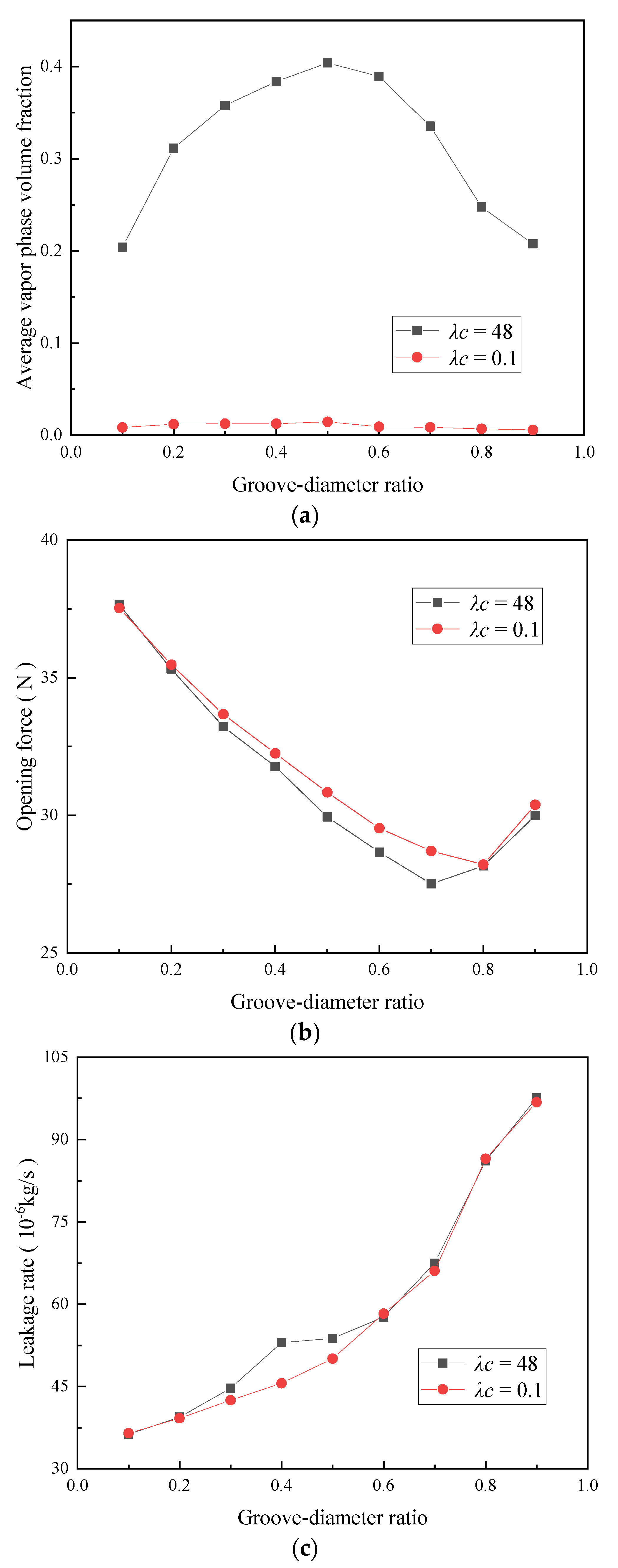
5.2. Effect of the Groove-Diameter Ratio on Sealing Performance
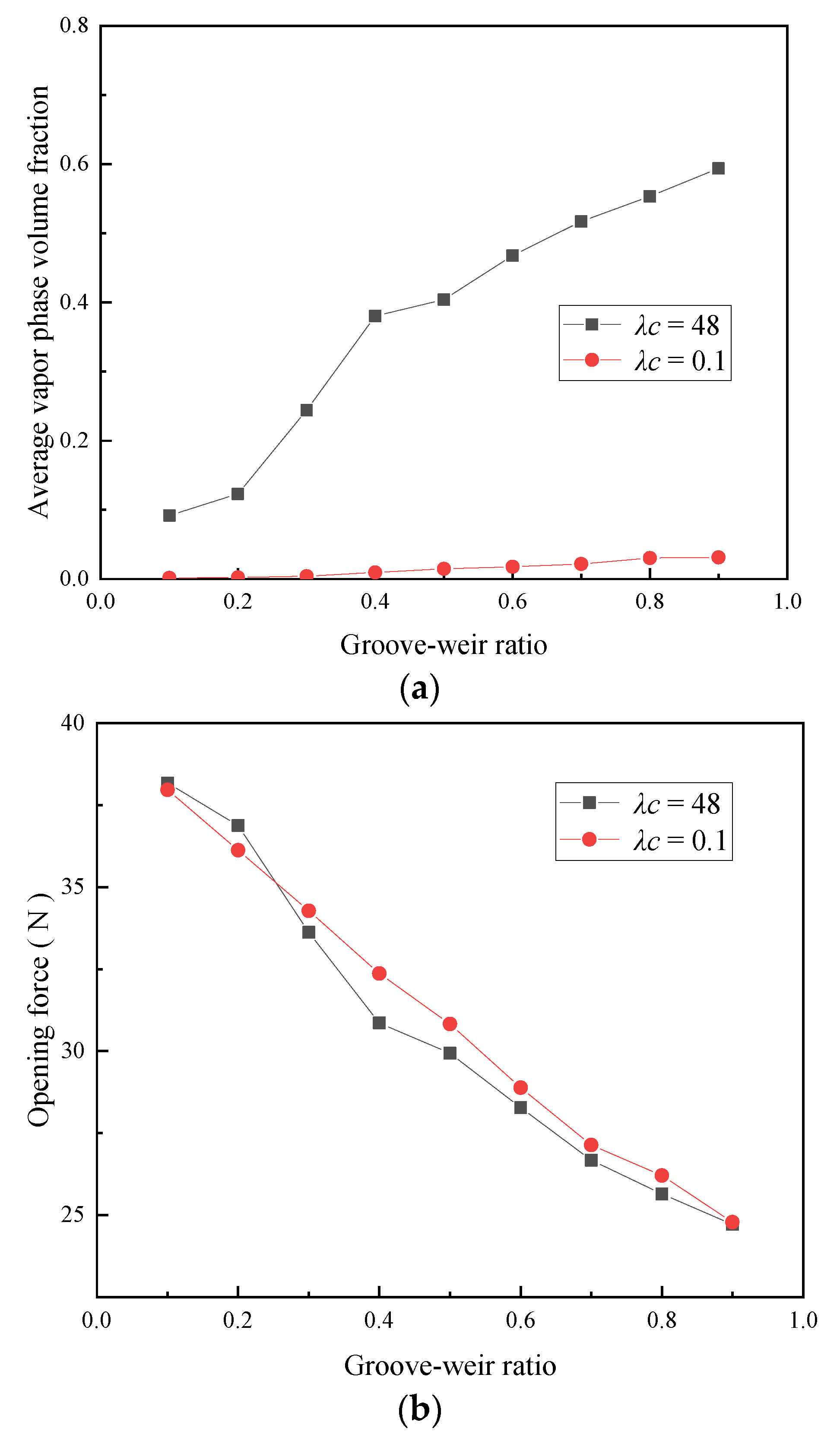
5.3. Effect of the Groove-Weir Ratio on Sealing Performance
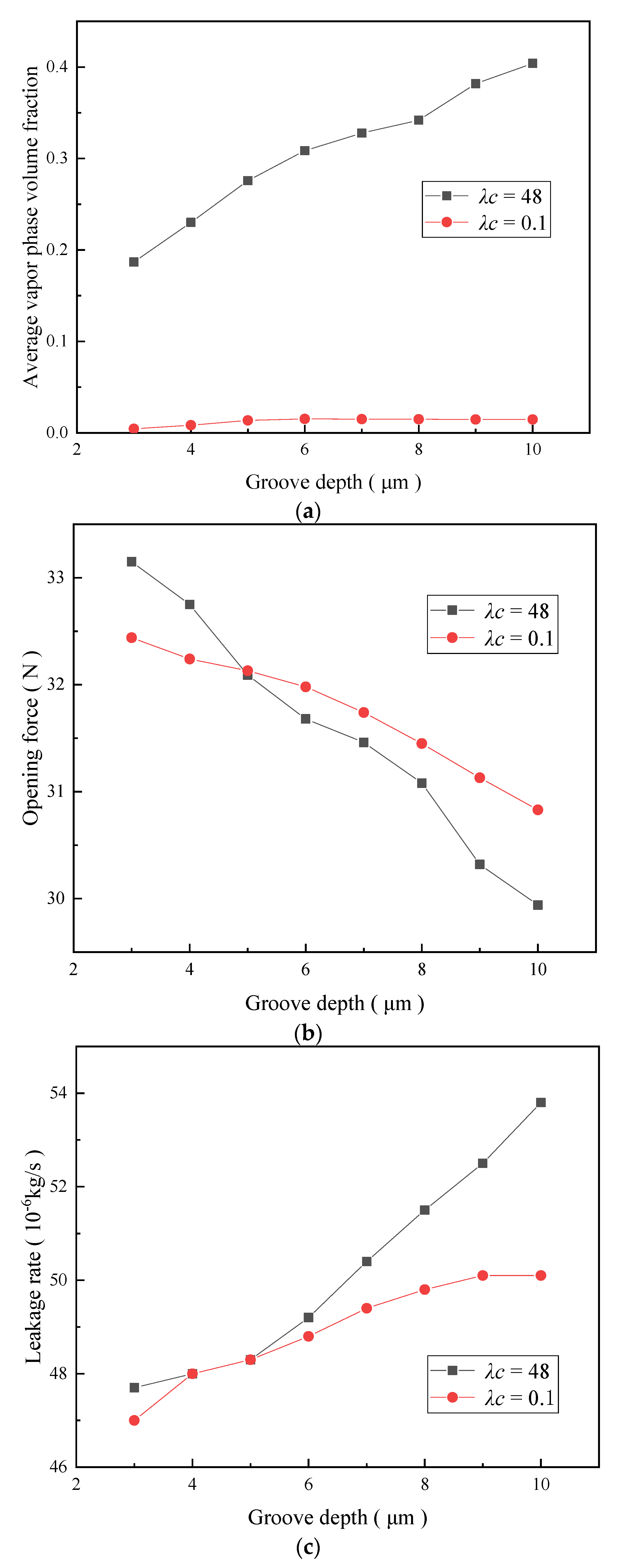
5.4. Effect of Groove Depth on Sealing Performance
6. Conclusions
- (1)
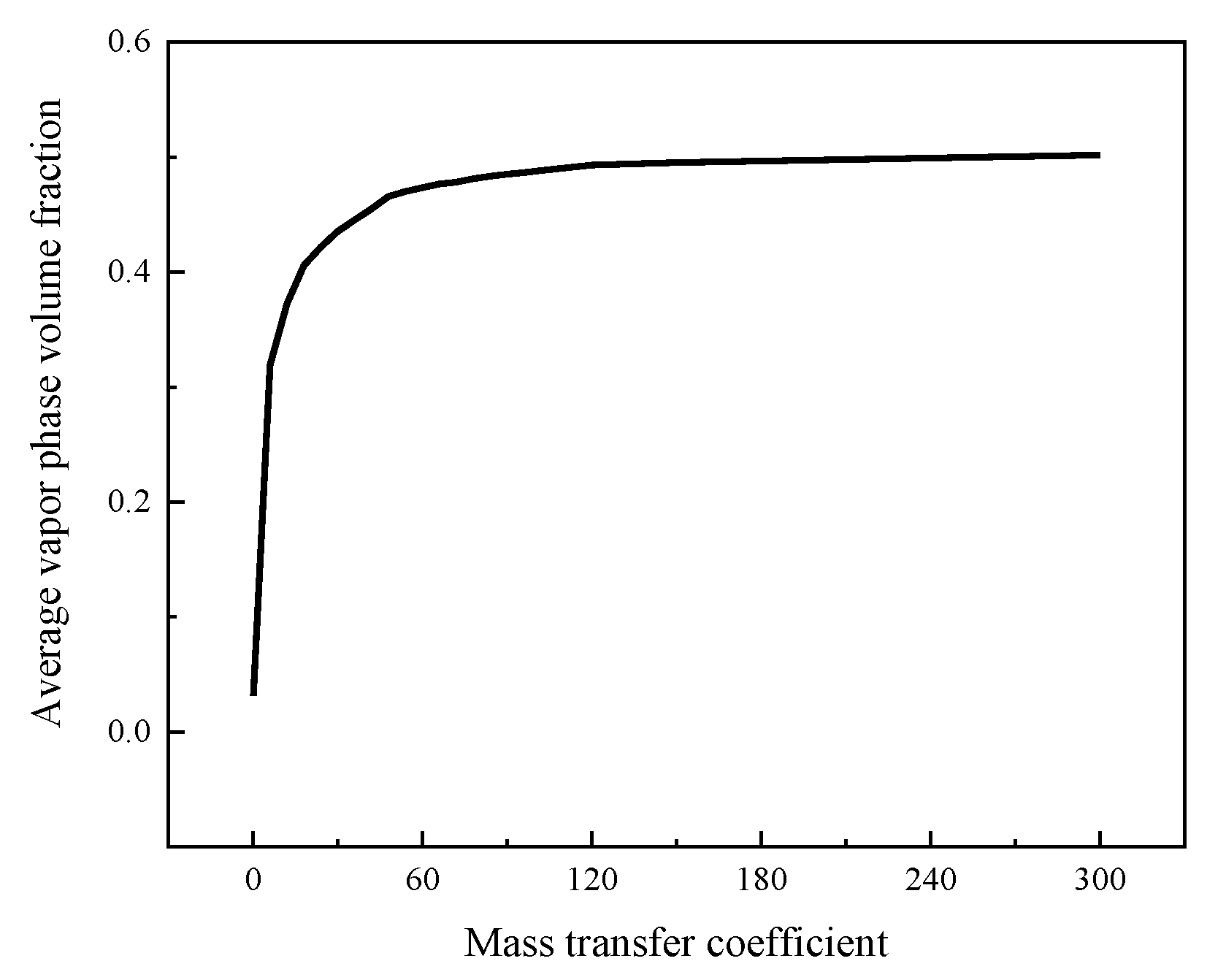
- The phase transition phenomenon of the spiral groove liquid film seal was simulated and calculated. Based on the calculation results, as the mass transfer coefficient increases, the average vapor phase volume fraction first increases and then stabilizes. The average vapor phase volume fraction changes in the same manner under different mass transfer coefficients. However, the difference between the calculated values is obvious, and the influence of the mass transfer coefficient cannot be ignored. However, the effect of the change in the mass transfer coefficient on the opening force and the leakage rate can be assumed to be negligible. Therefore, when performing the numerical analysis of the average vapor phase volume fraction simulation, it is necessary to determine the mass transfer coefficient before performing the subsequent calculation and analysis.
- (2)
- The average vapor phase volume fraction increases with an increase in the helix angle, groove-weir ratio, and groove depth. Moreover, the average vapor phase volume fraction first increases and then decreases with an increase in the groove-diameter ratio. The opening force decreases with an increase in the helix angle, groove-weir ratio, and groove depth. By comparison, the opening force first decreases and then increases with an increase in the groove-diameter ratio. The leakage rate first increases and then stabilizes with an increase in the helix angle. Moreover, the leakage rate increases continuously with an increase in the groove-diameter ratio, groove-weir ratio, and groove depth. The effect of the helix angle and the groove depth on the leakage rate is less obvious than the effect of the groove-diameter ratio and groove-weir ratio. As such, it can be assumed to be negligible.
- (3)
- This paper represents an analysis of the influence of single-factor structural parameters based on the optimal mass transfer coefficient on the phase transition of the spiral groove mechanical seal liquid film. In future works, the influence of structural parameters on the phase transition of the liquid film under the interaction of multiple factors will be discussed. Moreover, the effect of changes in operating conditions on the phase transition and sealing performance parameters will also be investigated.
- (4)
- The current study of the influence of the change in the mass transfer coefficient on the vaporization of liquid film fills an existing research gap. It has important theoretical and engineering significance for the design and application of mechanical seals with different structural parameters, controlling the degree of phase change, improving the sealing stability, and improving the sealing performance.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Du, P. Research and progress of mechanical seals operating with vaporization transition. Eng. Technol. Mag. 2016, 12, 224. [Google Scholar]
- Yang, X.; Meng, X.K.; Peng, X.D. A TEHD lubrication analysis of surface textured mechanical seals. Tribology 2018, 38, 204–212. [Google Scholar]
- Li, F.C.; Wang, Y.L.; Liu, J.; Ding, S.Y.; Xiang, L.I. Analysis and study on failure mechanism of mechanical seals in running. Hydraul. Pneum. Seals 2019, 39, 46–49. [Google Scholar]
- Zhang, X.; Shi, J.; Wang, S.; Zhang, C.; Tomovic, M. Leakage model and failure factors analysis of mechanical seals. In Proceedings of the 2016 IEEE 11th Conference on Industrial Electronics and Applications (ICIEA), Hefei, China, 5–7 June 2016. [Google Scholar]
- Chen, H.L.; Wu, Q.B.; Zuo, M.Z.; Cheng, X.; Ji, H.; Li, S. Overview on liquid film cavitation in mechanical seal faces. J. Drain. Irrig. Mach. Eng. 2015, 33, 138–144. [Google Scholar]
- Song, W.; Wang, C.; Wei, Y.; Xu, H.; Lu, J. Experimental research on drag reduction characteristics of underwater vehicle during pitching. Acta Armamentarii 2019, 40, 1902–1910. [Google Scholar]
- Peng, X.D.; Jin, J.; Meng, X.K.; Jiang, J.B.; Zhao, W.J.; Li, J.Y. Research progress on the liquid face seal of vapor-liquid Two-Phase flow. Tribology 2019, 39, 643–655. [Google Scholar]
- Zwart, P.J.; Gerber, A.G.; Belamri, T. A two-phase flow model for predicting cavitation dynamics. In Proceedings of the 5th International Conference on Multiphase Flow, Yokohama, Japan, 30 May–4 June 2004. [Google Scholar]
- Habil, S.I. Physical and numerical modeling of unsteady cavitation dynamics. In Proceedings of the 4th International Conference on Multiphase Flow, New Orleans, LA, USA, 27 May–1 June 2001. [Google Scholar]
- Singhal, A.K.; Athavale, M.M.; Li, H.Y. Mathematical basis and validation of the full cavitation model. J. Fluids Eng. 2002, 124, 617–624. [Google Scholar] [CrossRef]
- Xu, A.; Shyy, W.; Zhao, T. Lattice Boltzmann modeling of transport phenomena in fuel cells and flow batteries. Acta Mech. Sin. 2017, 33, 555–574. [Google Scholar] [CrossRef]
- Safari, H.; Rahimian, M.H.; Krafczyk, M. Consistent simulation of droplet evaporation based on the phase-field multiphase lattice Boltzmann method. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2014, 90, 033305. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Kang, Q.; Francois, M.; He, Y.; Luo, K. Lattice Boltzmann modeling of boiling heat transfer: The boiling curve and the effects of wettability. Int. J. Heat Mass Transf. 2015, 85, 787–796. [Google Scholar] [CrossRef] [Green Version]
- Lee, W.H. Pressure iteration scheme for Two-Phase flow modeling. In Multiphase Transport Fundamentals, Reactor Safety, Applications; Hemisphere Publishing: Washington, DC, USA, 1980. [Google Scholar]
- Chen, H.; Wang, B.; Ren, K.; Li, T.; Zhao, B. Influence of cavitation thermal effect on lubrication properties of upstream pumping mechanical seal. CIESC J. 2016, 67, 4334–4343. [Google Scholar]
- Chen, H.L.; Han, T.; Li, X.W.; Lu, J.C.; Xie, X.F. Analysis of internal friction and viscosity-temperature effect on vaporization and properties of sealing liquid film. J. Jiangsu Univ. (Nat. Sci. Ed.) 2020, 41, 661–669. [Google Scholar]
- Chen, H.; Gui, K.; Li, X.; Han, T.; Xie, X.; Lu, J. Influence of operating parameters on vaporization characteristics and properties of liquid film of mechanical seal. China Mech. Eng. 2021, 32, 2–11. [Google Scholar] [CrossRef] [Green Version]
- Shi, J.X. Analysis of Mechanical Seal Phase Transition Radisu and Temperature; Beijing University of Chemical Technology: Beijing, China, 2013. [Google Scholar]
- Liu, H.H. Study on Performance of End Face Seals Used in the Condition of Low Temperature and Easily Vaporized Liquid Medium; Beijing University of Chemical Technology: Beijing, China, 2014. [Google Scholar]
- Cao, H.; Hao, M.; Li, Z.; Yang, W.; Sun, Z.; Wang, Y.; Ren, F. Effect of phase change on performance of spiral groove liquid film seals. CIESC J. 2017, 68, 3190–3201. [Google Scholar]
- Cao, H.; Hao, M.; Li, Z.; Yang, W.; Wang, Y.; Yuan, J. Performance analysis of internal pressure type spiral groove liquid film seals based on phase change. CIESC J. 2017, 68, 3532–3540. [Google Scholar]
- Cao, H.; Hao, M.; Yang, W.; Wang, Y.; Li, Y.; Xu, L. Phase change phenomenon and properties of double spiral groove liquid film seals. CIESC J. 2018, 69, 2110–2119. [Google Scholar]
- Wang, X.; Shi, L.; Huang, W.; Wang, X. A Multi-Objective optimization approach on spiral grooves for gas mechanical seals. J. Tribol. 2018, 140, 041701. [Google Scholar] [CrossRef]
- Wang, X.; Shi, L.; Huang, W.; Wang, X. Closure to Discussion of “A Multi-Objective optimization approach on spiral grooves for gas mechanical seals” (X. Wang, L. Shi, W. Huang, and X. Wang, 2018, ASME J. Tribol., 140(4), p. 041701). J. Tribol. 2019, 141, 026001. [Google Scholar] [CrossRef]
- Ma, R.M.; Feng, R.P.; Li, S.X.; Wang, J.X.; Liu, Z.W.; Song, R.L. Optimum analysis of vaporization and phase change performance of spiral groove hydrodynamic seal liquid film. J. Mech. Electr. Eng. 2020, 37, 999–1005. [Google Scholar]
- Gao, W.; Huang, W.; Wang, T.; Liu, Y.; Wang, Z.; Wang, Y. Numerical model of two-phase mechanical face seal with shallow grooves based on finite volume method. Ind. Lubr. Tribol. 2020, 72, 1303–1309. [Google Scholar] [CrossRef]
- Da, E.R.; Del, D.C. Numerical simulation of laminar liquid film condensation in a horizontal circular minichannel. J. Heat Transf. -Trans. of the ASME 2012, 134, 1–8. [Google Scholar]
- Yang, Z.; Peng, X.F.; Ye, P. Numerical and experimental investigation of two phase flow during boiling in a coiled tube. Int. J. Heat Mass Transf. 2008, 51, 1003–1016. [Google Scholar] [CrossRef]
- Zhu, Z.; Li, J.; Peng, H.; Liu, D. Nature-Inspired Structures Applied in Heat Transfer Enhancement and Drag Reduction. Micromachines 2021, 12, 656. [Google Scholar] [CrossRef] [PubMed]
- Qiu, G.D.; Cai, W.H.; Wu, Z.Y.; Jiang, Y.; Yao, Y. Analysis on the value of coefficient of mass transfer with phase change in Lee’s equation. J. Harbin Inst. Technol. 2014, 46, 15–19. [Google Scholar]
- Li, Y.; Song, P.Y.; Xu, H.J. Performance analyses of the spiral groove dry gas seal with inner annular groove. Appl. Mech. Mater. 2013, 420, 51–55. [Google Scholar] [CrossRef]
- ANSYS Inc. ANSYS14. 0 FLUENT Theory Guid; ANSYS Inc.: Canonsburg, PA, USA, 2011. [Google Scholar]
- Wallis, G.B. One-Dimensional Two-Phase Flow; McGraw-Hill Companies: New York, NY, USA, 1969. [Google Scholar]
- Li, X.W. Research on Vaporization Characteristics of Fluid Film and Performance in Hydrodynamic Mechanical Seals; Jiangsu University: Zhenjiang, China, 2019. [Google Scholar]
- Hu, K.; Li, Z.B. ANSYS ICEM CFD Engineering Examples in Detail; POSTS & TELECOM PRESS: Beijing, China, 2014. [Google Scholar]
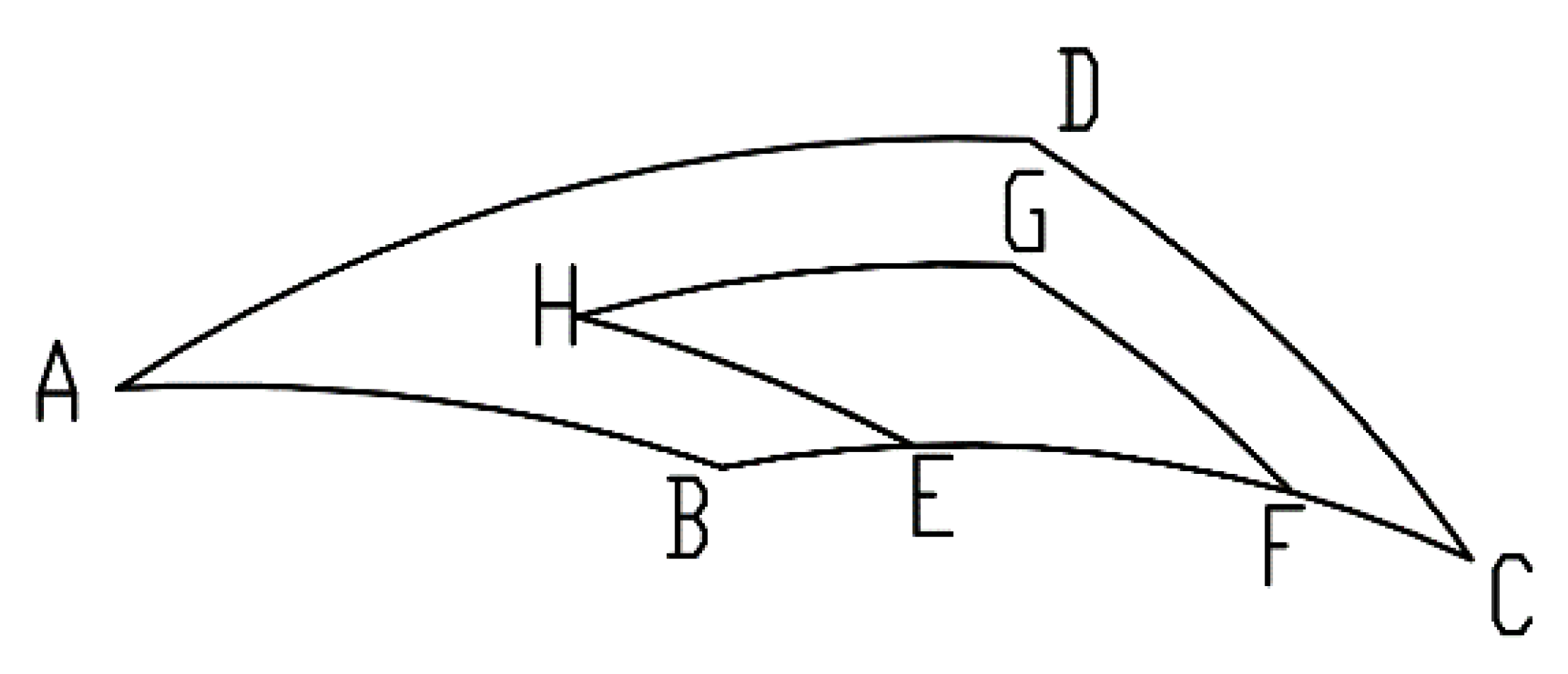

| Boundary | Boundary Type |
|---|---|
| liquid film AD | pressure-inlet |
| liquid film BC | pressure-outlet |
| spiral groove EF | pressure-outlet |
| liquid film AB, CD | periodic boundary |
| the upper surface of the liquid film and the lower surface of the spiral groove | interface |
| spiral groove EH, GH, FG | moving wall |
| the upper surface of the spiral groove | moving wall |
| other walls | stationary wall |
| Parameter | Ranges |
|---|---|
| helix angle | 20–30° |
| groove-diameter ratio | 0.1–0.9 |
| groove-weir ratio | 0.1–0.9 |
| groove depth | 3–10 μm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Ma, C.; Zhang, Y.; Sun, J.; Yu, Q. Influence of Groove Structure Parameters Based on Optimal Mass Transfer Coefficient on Vaporization Characteristics and Sealing Performance of Liquid Film Mechanical Seals. Appl. Sci. 2021, 11, 8941. https://doi.org/10.3390/app11198941
Xu X, Ma C, Zhang Y, Sun J, Yu Q. Influence of Groove Structure Parameters Based on Optimal Mass Transfer Coefficient on Vaporization Characteristics and Sealing Performance of Liquid Film Mechanical Seals. Applied Sciences. 2021; 11(19):8941. https://doi.org/10.3390/app11198941
Chicago/Turabian StyleXu, Xiaodong, Chenbo Ma, Yuyan Zhang, Jianjun Sun, and Qiuping Yu. 2021. "Influence of Groove Structure Parameters Based on Optimal Mass Transfer Coefficient on Vaporization Characteristics and Sealing Performance of Liquid Film Mechanical Seals" Applied Sciences 11, no. 19: 8941. https://doi.org/10.3390/app11198941
APA StyleXu, X., Ma, C., Zhang, Y., Sun, J., & Yu, Q. (2021). Influence of Groove Structure Parameters Based on Optimal Mass Transfer Coefficient on Vaporization Characteristics and Sealing Performance of Liquid Film Mechanical Seals. Applied Sciences, 11(19), 8941. https://doi.org/10.3390/app11198941






