Tuning the Cell and Biological Tissue Environment through Magneto-Active Materials
Abstract
:1. Introduction
2. Mechanically Mediated Biological Processes
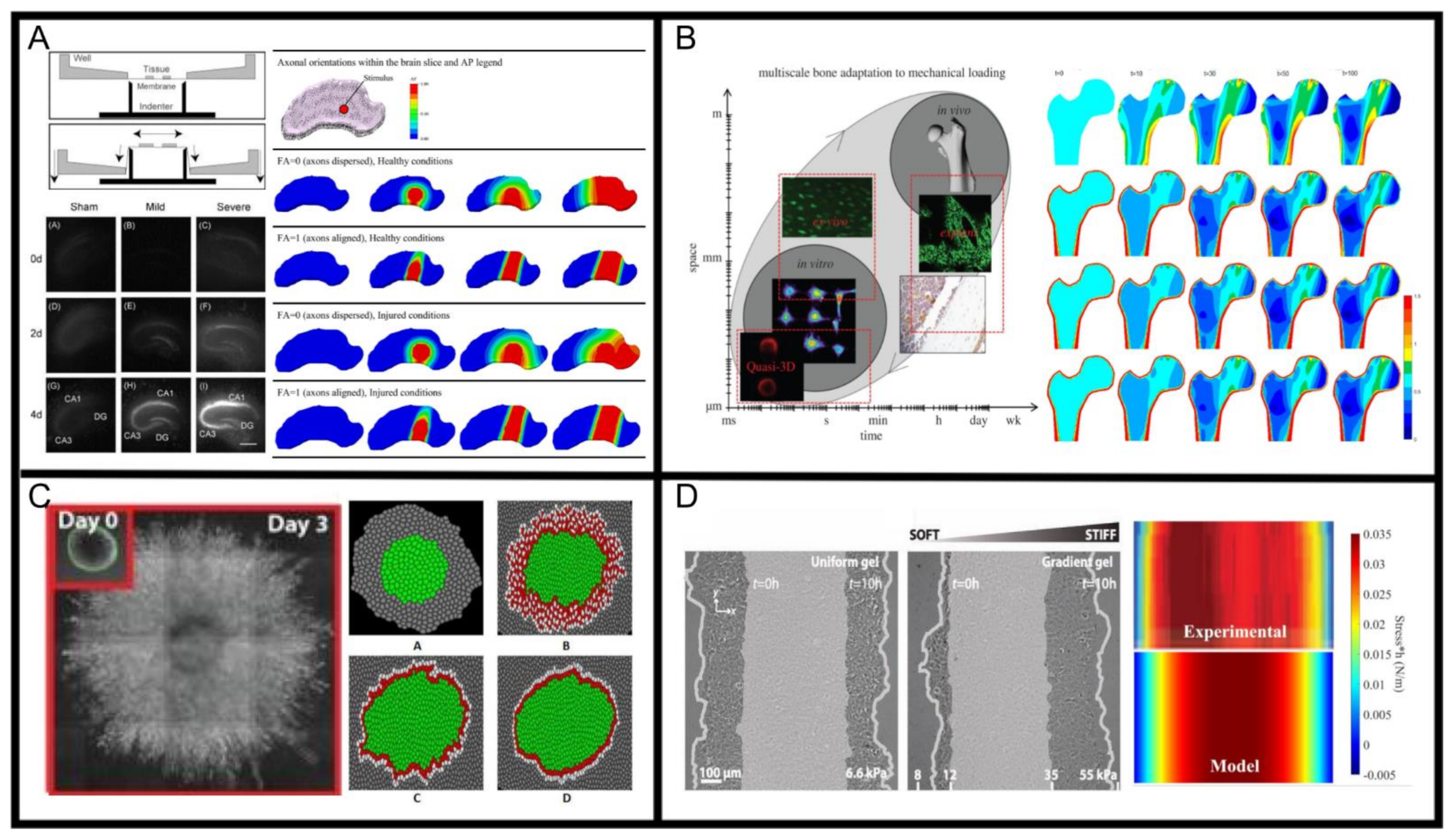
2.1. Mechanical Effects on Nervous System Behaviour
2.2. Mechanical Effects on Bone Development and Healing
2.3. Mechanical Effects on Collective Cell Migration Underlying Morphogenesis Tissue Regeneration and Cancer Progression
3. Theoretical and Computational Frameworks for Mechanically Mediated Biological Processes
3.1. Modelling Mechanical Effects on Nervous System Behaviour
3.2. Modelling Mechanical Effects on Bone Development and Healing
3.3. Modelling Mechanical Effects on Collective Cell Migration Underlying Morphogenesis Tissue Regeneration and Cancer Progression
4. Fundamentals of Smart Polymeric Materials: Focus on Magneto-Active Elastomers and Hydrogels
4.1. Introduction to Smart Polymeric Materials
4.2. Magnetorheological Elastomers (MREs)
4.2.1. Fabrication of Magnetorheological Elastomers
4.2.2. Magnetorheological Elastomers in Soft Robotics
4.2.3. Magnetorheological Elastomers as Dynamic Cell Culture Substrata
4.3. Magneto-Active Hydrogels
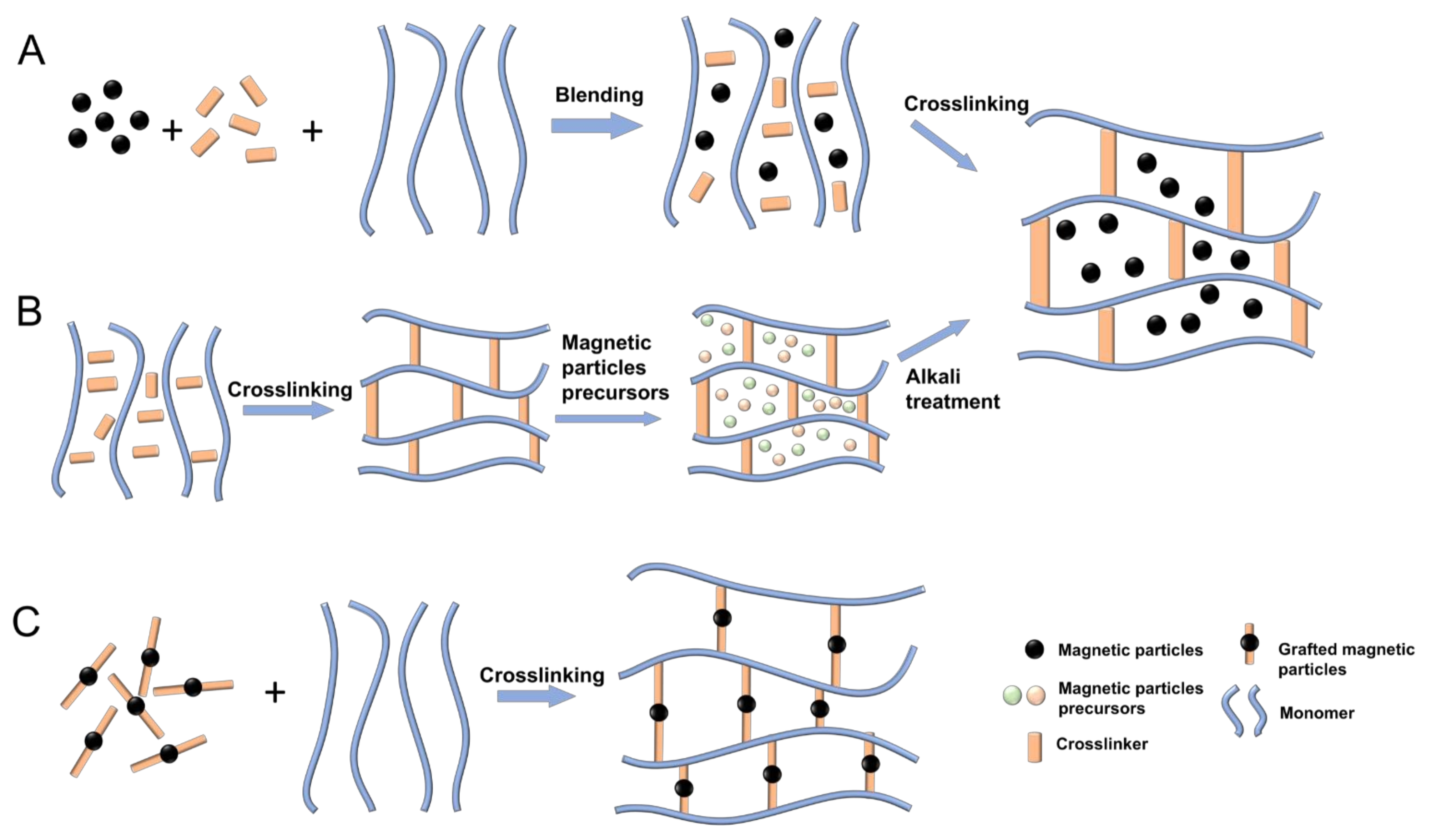
Fabrication Techniques
- (i)
- Blending Method (Figure 2A)MNPs and hydrogels are prepared separately in a sequential order. The prepared MNP sediment is then dispersed in an aqueous or oil phase (i.e., a ferrofluid) to avoid oxidisation and aggregation. Finally, the mixture of the ferrofluid and the hydrogel precursor solution are crosslinked, resulting in the encapsulation of the MNPs in the hydrogel. The main advantage offered by the blending method is the simplicity of the process. Furthermore, both components necessary for the fabrication are commercially available. Another advantage is the fact that both components are prepared separately, which offers the possibility to achieve a uniform particle size in hydrogels over a wide range from nanometres to micrometres, whether by adjusting the concentration of the reactants, the stirring speed, and the preparation cycle, or by purchasing the desired MNPs. However, it is challenging to achieve a uniform MNP distribution within the hydrogels, and MNPs may diffuse out of the magnetic hydrogels when immersed in a liquid solution [134].
- (ii)
- In Situ Precipitation Method (Figure 2B)In the in situ precipitation method, the hydrogel networks act as a chemical reactor. An inorganic salt with iron ions reacts with precipitating agents to generate MNPs inside the hydrogel polymeric network. Firstly, hydrogels are fabricated via temperature change, radical polymerisation, or a photo-crosslinking reaction. Secondly, the hydrogels are placed into a concentrated aqueous solution containing Fe 2+ and Fe 3+, and the ferrous ions are taken at a molar ratio of 1:2 until swelling equilibrium is reached. Finally, the swollen hydrogels with absorbed Fe 2+ and Fe 3+ are immersed into an alkali solution for MNP precipitation. The in situ precipitation method has several advantages in the fabrication of magnetic hydrogels. Firstly, many inorganic particles can be introduced into the hydrogel network, ensuring that colloidal-sized particles can be well dispersed in the matrix. Secondly, the preparation process is simple and low-cost. However, the in situ precipitation method is only suitable for specific hydrogels with a stable network, otherwise the hydrogel network may be destroyed by alkali solution during the preparation process [134].
- (iii)
- Grafting-Onto Method (Figure 2C)In the grafting-onto method, covalent bonds are formed between the hydrogel network and the MNPs. These covalent bonds are achieved by grafting several functional groups onto the surface of the MNPs, which work as nano-crosslinkers to form a covalent coupling with the monomers when polymerised. The main advantage offered by the grafting-onto method deals with the problem of particle diffusion into the media. Both previous methods consisted of a physical encapsulation of the particles. With this method, the direct covalent coupling between the hydrogel matrix and the magnetic particles leads to a more permanent particle encapsulation. However, the grafting of the functional groups onto the magnetic particles is a difficult task with a long preparation cycle and high cost, which makes this method a complex fabrication process [134].
4.4. Three-Dimensional Printing of Magneto-Active Polymers
4.5. Metabolism of MAPs
5. Theoretical and Computational Mechanical Frameworks for Magneto-Active Polymers
5.1. Constitutive Modelling of Polymeric Matrix
5.2. Constitutive Modelling of Magnetorheological Elastomers
5.2.1. Continuum-Based Models
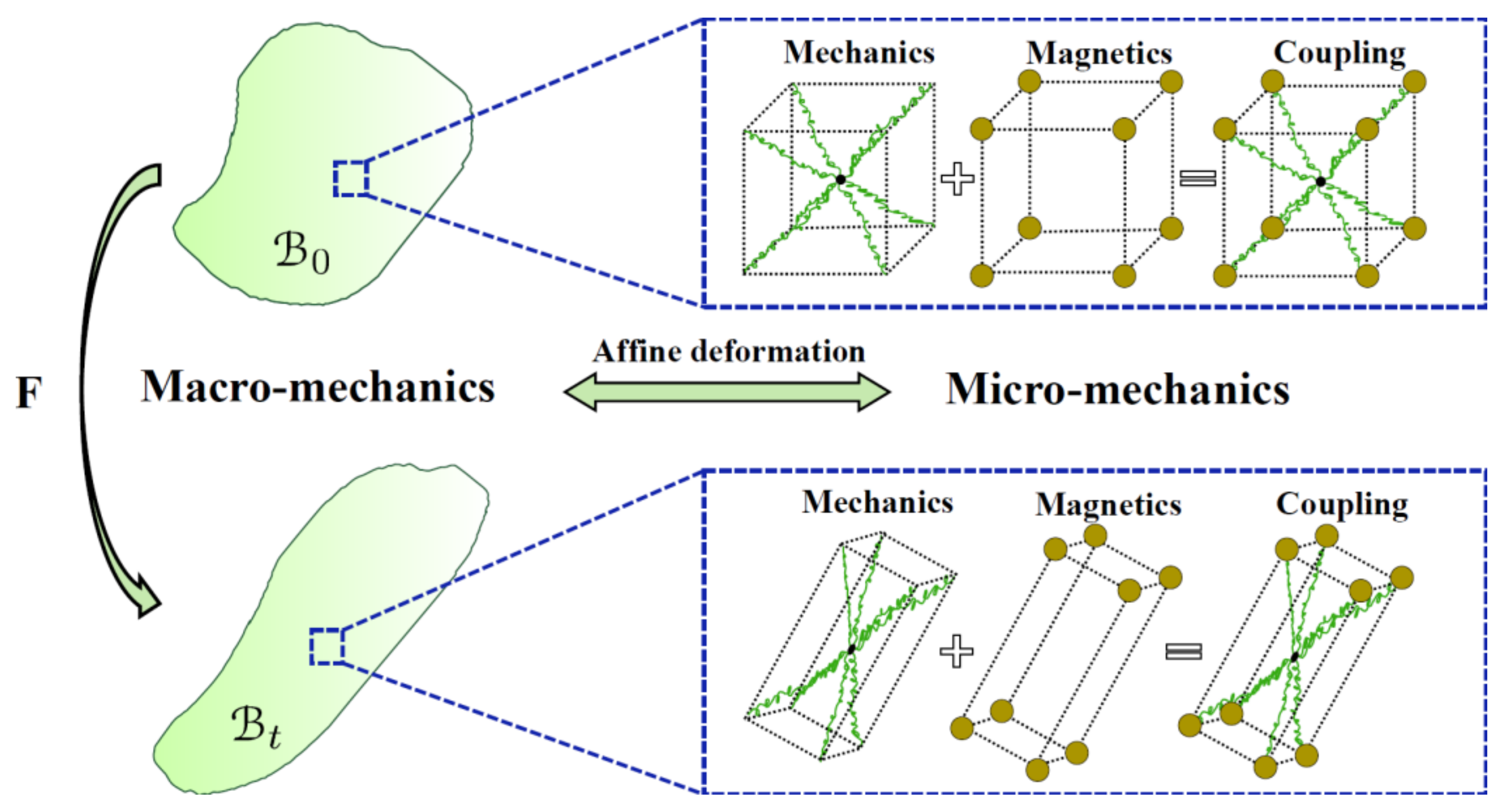
5.2.2. Micro-Mechanical-Based Models
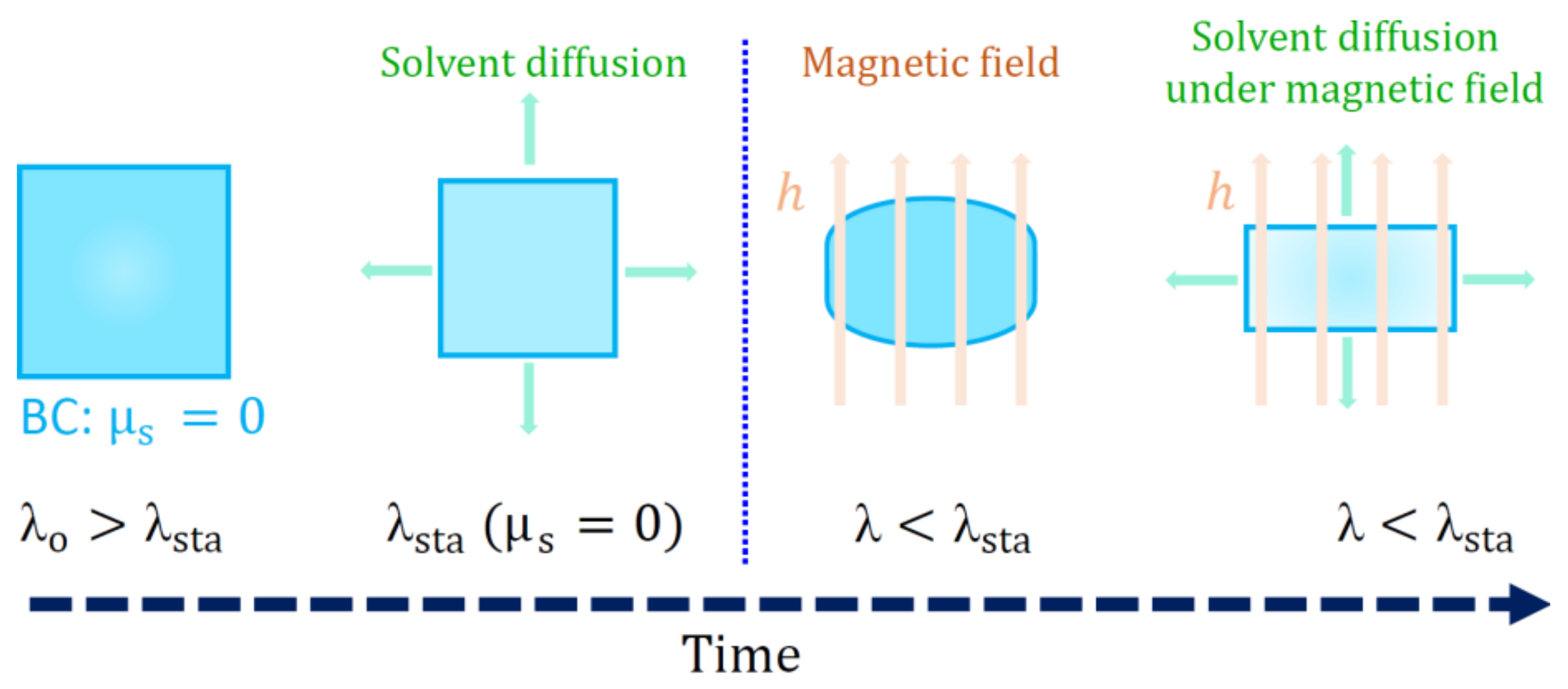
5.3. Constitutive Modelling of Magneto-Active Hydrogels
6. Magneto-Active Polymers in Biomedical Applications
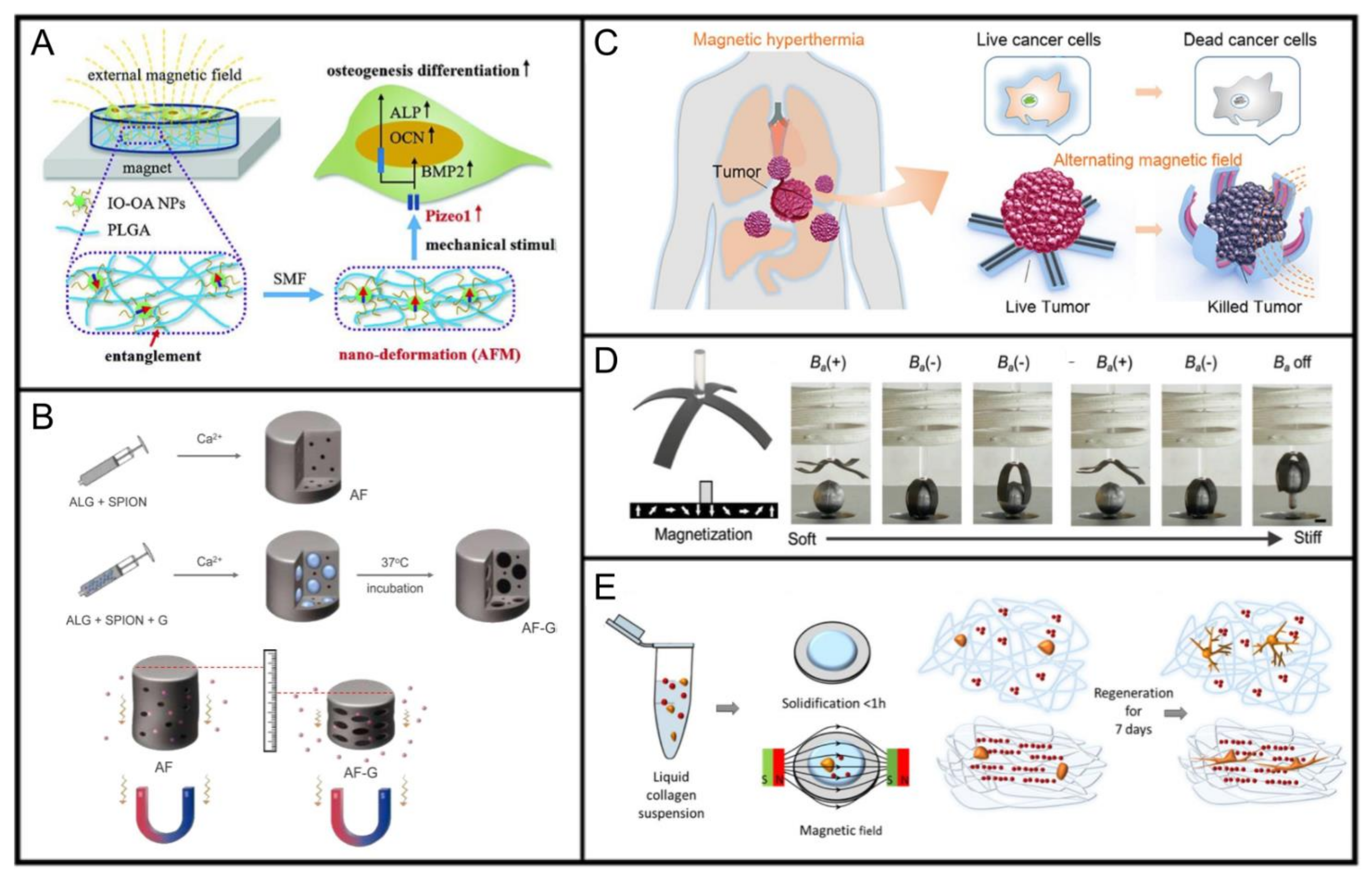
6.1. MAPs for Bone and Tendon Tissue Engineering
6.2. MAPs for Drug Delivery
6.3. MAPs for Tissue Hyperthermia
6.4. MAPs for Artificial Muscles
6.5. MAPs for Neuronal Regeneration
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Morrison, B.; Cater, H.L.; Benham, C.D.; Sundstrom, L.E. An in vitro model of traumatic brain injury utilising two-dimensional stretch of organotypic hippocampal slice cultures. J. Neurosci. Methods 2006, 150, 192–201. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Gonzalez, D.; Jerusalem, A. Energy based mechano-electrophysiological model of CNS damage at the tissue scale. J. Mech. Phys. Solids 2019, 125, 22–37. [Google Scholar] [CrossRef]
- Brown, G.N.; Sattler, R.L.; Guo, X.E. Experimental studies of bone mechanoadaptation: Bridging in vitro and in vivo studies with multiscale systems. Interface Focus 2016, 6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schmidt, I.; Papastavrou, A.; Steinmann, P. Concurrent consideration of cortical and cancellous bone within continuum bone remodelling. Comput. Methods Biomech. Biomed. Eng. 2021, 24, 1–12. [Google Scholar] [CrossRef]
- Valencia, A.M.J.; Wu, P.-H.; Yogurtcu, O.; Rao, P.; Digiacomo, J.; Godet, I.; He, L.; Lee, M.-H.; Gilkes, D.; Sun, S.X.; et al. Collective cancer cell invasion induced by coordinated contractile stresses. Oncotarget 2015, 6, 43438–43451. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Naveed, H.; Xu, L.X.; Li, Y.; Liang, J. Effects of mechanical properties on tumor invasion: Insights from a cellular model. In Proceedings of the 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Chicago, IL, USA, 26–30 August 2014; IEEE: New York, NY, USA; pp. 6818–6821. [Google Scholar]
- Sunyer, R.; Conte, V.; Escribano, J.; Elosegui-Artola, A.; Labernadie, A.; Valon, L.; Navajas, D.; García-Aznar, J.M.; Muñoz, J.J.; Roca-Cusachs, P.; et al. Collective cell durotaxis emerges from long-range intercellular force transmission. Science 2016, 353, 1157–1161. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Garcia-Gonzalez, D.; Muñoz-Barrutia, A. Computational insights into the influence of substrate stiffness on collective cell migration. Extrem. Mech. Lett. 2020, 40, 100928. [Google Scholar] [CrossRef]
- Budday, S.; Ovaert, T.C.; Holzapfel, G.A.; Steinmann, P.; Kuhl, E. Fifty Shades of Brain: A Review on the Mechanical Testing and Modeling of Brain Tissue. Arch. Comput. Methods Eng. 2019, 27, 1187–1230. [Google Scholar] [CrossRef] [Green Version]
- Tyler, W.J. The mechanobiology of brain function. Nat. Rev. Neurosci. 2012, 13, 867–878. [Google Scholar] [CrossRef] [PubMed]
- Calhoun, M.A.; Bentil, S.A.; Elliott, E.; Otero, J.J.; Winter, J.O.; Dupaix, R.B. Beyond Linear Elastic Modulus: Viscoelastic Models for Brain and Brain Mimetic Hydrogels. ACS Biomater. Sci. Eng. 2019, 5, 3964–3973. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.-B.; Franze, K.; Seifert, G.; Steinhauser, C.; Kirchhoff, F.; Wolburg, H.; Guck, J.; Janmey, P.; Wei, E.-Q.; Kas, J.; et al. Viscoelastic properties of individual glial cells and neurons in the CNS. Proc. Natl. Acad. Sci. USA 2006, 103, 17759–17764. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anderson, D.K.; Hall, E.D. Pathophysiology of spinal cord trauma. Ann. Emerg. Med. 1993, 22, 987–992. [Google Scholar] [CrossRef]
- Maikos, J.T.; Qian, Z.; Metaxas, D.; Shreiber, D. Finite Element Analysis of Spinal Cord Injury in the Rat. J. Neurotrauma 2008, 25, 795–816. [Google Scholar] [CrossRef] [PubMed]
- Warden, D. Military TBI during the Iraq and Afghanistan Wars. J. Head Trauma Rehabil. 2006, 21, 398–402. [Google Scholar] [CrossRef] [Green Version]
- Jannesar, S.; Allen, M.; Mills, S.; Gibbons, A.; Bresnahan, J.C.; Salegio, E.A.; Sparrey, C.J. Compressive mechanical characterization of non-human primate spinal cord white matter. Acta Biomater. 2018, 74, 260–269. [Google Scholar] [CrossRef] [PubMed]
- Wolter, A.; Rapp, A.E.; Durst, M.S.; Hildebrand, L.; Löhning, M.; Buttgereit, F.; Schmidt-Bleek, K.; Jirkof, P.; Lang, A. Systematic review on the reporting accuracy of experimental details in publications using mouse femoral fracture models. Bone 2021, 152, 116088. [Google Scholar] [CrossRef] [PubMed]
- Jha, R.M.; Kochanek, P.M.; Simard, J.M. Pathophysiology and treatment of cerebral edema in traumatic brain injury. Neuropharmacology 2019, 145, 230–246. [Google Scholar] [CrossRef]
- Simpson, D.M.; Payne, S.J.; Panerai, R.B. The INfoMATAS project: Methods for assessing cerebral autoregulation in stroke. Br. J. Pharmacol. 2021. [Google Scholar] [CrossRef]
- Bing, Y.; Garcia-Gonzalez, D.; Voets, N.; Jérusalem, A. Medical imaging based in silico head model for ischaemic stroke simulation. J. Mech. Behav. Biomed. Mater. 2019, 101, 103442. [Google Scholar] [CrossRef]
- McDermott, A.M.; Herberg, S.; Mason, D.E.; Collins, J.M.; Pearson, H.B.; Dawahare, J.H.; Tang, R.; Patwa, A.N.; Grinstaff, M.W.; Kelly, D.J.; et al. Recapitulating bone development through engineered mesenchymal condensations and mechanical cues for tissue regeneration. Sci. Transl. Med. 2019, 11, eaav7756. [Google Scholar] [CrossRef] [PubMed]
- Rosa, N.; Simoes, R.; Magalhães, F.D.; Marques, A.T. From mechanical stimulus to bone formation: A review. Med. Eng. Phys. 2015, 37, 719–728. [Google Scholar] [CrossRef] [Green Version]
- Stock, J.T. Wolff’s law (bone functional adaptation). In The International Encyclopedia of Biological Anthropology; Wiley: Hoboken, NJ, USA, 2018; pp. 1–2. [Google Scholar] [CrossRef]
- Papastavrou, A.; Schmidt, I.; Steinmann, P. On biological availability dependent bone remodeling. Comput. Methods Biomech. Biomed. Eng. 2020, 23, 432–444. [Google Scholar] [CrossRef] [PubMed]
- Kummer, B. Basics of Pauwels’ theory of the functional adaptation of bones. Der Orthopäde 1995, 24, 387–393. [Google Scholar] [PubMed]
- Claes, L.; Heigele, C. Magnitudes of local stress and strain along bony surfaces predict the course and type of fracture healing. J. Biomech. 1999, 32, 255–266. [Google Scholar] [CrossRef]
- Handorf, A.M.; Zhou, Y.; Halanski, M.A.; Li, W.-J. Tissue Stiffness Dictates Development, Homeostasis, and Disease Progression. Organogenesis 2015, 11, 1–15. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schell, H.; Duda, G.N.; Peters, A.; Tsitsilonis, S.; Johnson, K.A.; Schmidt-Bleek, K. The haematoma and its role in bone healing. J. Exp. Orthop. 2017, 4, 1–11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Einhorn, T.A.; Gerstenfeld, L.C. Fracture healing: Mechanisms and interventions. Nat. Rev. Rheumatol. 2015, 11, 45–54. [Google Scholar] [CrossRef] [Green Version]
- Nyary, T.; Scammell, B.E. Principles of bone and joint injuries and their healing. Surgery 2018, 36, 7–14. [Google Scholar] [CrossRef] [Green Version]
- Strube, P.; Sentuerk, U.; Riha, T.; Kaspar, K.; Mueller, M.; Kasper, G.; Matziolis, G.; Duda, G.N.; Perka, C. Influence of age and mechanical stability on bone defect healing: Age reverses mechanical effects. Bone 2008, 42, 758–764. [Google Scholar] [CrossRef] [PubMed]
- Frohlich, M.; Grayson, W.; Wan, L.; Marolt, D.; Drobnic, M.; Novakovic, G.V. Tissue Engineered Bone Grafts: Biological Requirements, Tissue Culture and Clinical Relevance. Curr. Stem Cell Res. Ther. 2008, 3, 254–264. [Google Scholar] [CrossRef] [Green Version]
- Carroll, S.F.; Buckley, C.; Kelly, D.J. Cyclic Tensile Strain Can Play a Role in Directing both Intramembranous and Endochondral Ossification of Mesenchymal Stem Cells. Front. Bioeng. Biotechnol. 2017, 5, 73. [Google Scholar] [CrossRef]
- Hadjidakis, D.J.; Androulakis, I.I. Bone Remodeling. Ann. Acad. Sci. 2006, 1092, 385–396. [Google Scholar] [CrossRef] [PubMed]
- Thomas, J.D.; Kehoe, J.L. Bone Nonunion; StatPearls Publishing: Treasure Island, FL, USA, 2021. [Google Scholar]
- Ghiasi, M.S.; Chen, J.; Vaziri, A.; Rodriguez, E.K.; Nazarian, A. Bone fracture healing in mechanobiological modeling: A review of principles and methods. Bone Rep. 2017, 6, 87–100. [Google Scholar] [CrossRef]
- García-Aznar, J.M.; Nasello, G.; Hervas-Raluy, S.; Pérez, M.Á.; Gómez-Benito, M.J. Multiscale modeling of bone tissue mechanobiology. Bone 2021, 151, 116032. [Google Scholar] [CrossRef] [PubMed]
- Ghiasi, M.S.; Chen, J.E.; Rodriguez, E.K.; Vaziri, A.; Nazarian, A. Computational modeling of human bone fracture healing affected by different conditions of initial healing stage. BMC Musculoskelet. Disord. 2019, 20, 562–614. [Google Scholar] [CrossRef] [PubMed]
- Borgiani, E.; Duda, G.N.; Checa, S. Multiscale Modeling of Bone Healing: Toward a Systems Biology Approach. Front. Physiol. 2017, 8, 287. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Friedl, P.; Gilmour, D. Collective cell migration in morphogenesis, regeneration and cancer. Nat. Rev. Mol. Cell Biol. 2009, 10, 445–457. [Google Scholar] [CrossRef]
- Schwarz, U.S.; Ziebert, F. When tissues collide. Nat. Mater. 2017, 16, 972–973. [Google Scholar] [CrossRef]
- Barriga, E.H.; Franze, K.; Charras, G.; Mayor, R. Tissue stiffening coordinates morphogenesis by triggering collective cell migration in vivo. Nat. Cell Biol. 2018, 554, 523–527. [Google Scholar] [CrossRef]
- Anon, E.; Serra-Picamal, X.; Hersen, P.; Gauthier, N.C.; Sheetz, M.P.; Trepat, X.; Ladoux, B. Cell crawling mediates collective cell migration to close undamaged epithelial gaps. Proc. Natl. Acad. Sci. USA 2012, 109, 10891–10896. [Google Scholar] [CrossRef] [Green Version]
- Barnes, L.A.; Marshall, C.D.; Leavitt, T.; Hu, M.S.; Moore, A.L.; Gonzalez, J.G.; Longaker, M.T.; Gurtner, G.C. Mechanical Forces in Cutaneous Wound Healing: Emerging Therapies to Minimize Scar Formation. Adv. Wound Care 2018, 7, 47–56. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Malandrino, A.; Mak, M.; Kamm, R.D.; Moeendarbary, E. Complex mechanics of the heterogeneous extracellular matrix in cancer. Extreme Mech. Lett. 2018, 21, 25–34. [Google Scholar] [CrossRef]
- Lo, C.-M.; Wang, H.-B.; Dembo, M.; Wang, Y.-L. Cell Movement Is Guided by the Rigidity of the Substrate. Biophys. J. 2000, 79, 144–152. [Google Scholar] [CrossRef] [Green Version]
- Küsters, B.; Kats, G.; Roodink, I.; Verrijp, K.; Wesseling, P.; Ruiter, D.J.; De Waal, R.M.W.; Leenders, W. Micronodular transformation as a novel mechanism of VEGF-A-induced metastasis. Oncogene 2007, 26, 5808–5815. [Google Scholar] [CrossRef] [Green Version]
- Soler-Cardona, A.; Forsthuber, A.; Lipp, K.; Ebersberger, S.; Heinz, M.; Schossleitner, K.; Buchberger, E.; Gröger, M.; Petzelbauer, P.; Hoeller, C.; et al. CXCL5 Facilitates Melanoma Cell–Neutrophil Interaction and Lymph Node Metastasis. J. Investig. Dermatol. 2018, 138, 1627–1635. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Paul, C.D.; Mistriotis, P.; Konstantopoulos, K. Cancer cell motility: Lessons from migration in confined spaces. Nat. Rev. Cancer 2017, 17, 131–140. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.-J.; Le Berre, M.; Lautenschläger, F.; Maiuri, P.; Callan-Jones, A.; Heuze, M.; Takaki, T.; Voituriez, R.; Piel, M. Confinement and Low Adhesion Induce Fast Amoeboid Migration of Slow Mesenchymal Cells. Cell 2015, 160, 659–672. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wisniewski, E.O.; Mistriotis, P.; Bera, K.; Law, R.A.; Zhang, J.; Nikolic, M.; Weiger, M.; Parlani, M.; Tuntithavornwat, S.; Afthinos, A.; et al. Dorsoventral polarity directs cell responses to migration track geometries. Sci. Adv. 2020, 6, eaba6505. [Google Scholar] [CrossRef] [PubMed]
- Karimi, A.; Shojaei, A.; Tehrani, P. Mechanical properties of the human spinal cord under the compressive loading. J. Chem. Neuroanat. 2017, 86, 15–18. [Google Scholar] [CrossRef]
- Kleiven, S.; Hardy, W.N. Correlation of an FE Model of the Human Head with Local Brain Motion--Consequences for Injury Prediction. Stapp Car Crash J. 2002, 46, 123–144. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alvarez, V.S.; Kleiven, S. Effect of pediatric growth on cervical spine kinematics and deformations in automotive crashes. J. Biomech. 2018, 71, 76–83. [Google Scholar] [CrossRef]
- Giordano, C.; Zappalà, S.; Kleiven, S. Anisotropic finite element models for brain injury prediction: The sensitivity of axonal strain to white matter tract inter-subject variability. Biomech. Model. Mechanobiol. 2017, 16, 1269–1293. [Google Scholar] [CrossRef] [PubMed]
- Wright, R.M.; Post, A.; Hoshizaki, B.; Ramesh, K.T. A Multiscale Computational Approach to Estimating Axonal Damage under Inertial Loading of the Head. J. Neurotrauma 2013, 30, 102–118. [Google Scholar] [CrossRef]
- Garcia-Gonzalez, D.; Race, N.; Voets, N.L.; Jenkins, D.R.; Sotiropoulos, S.; Acosta, G.; Cruz-Haces, M.; Tang, J.; Shi, R.; Jérusalem, A. Cognition based bTBI mechanistic criteria; a tool for preventive and therapeutic innovations. Sci. Rep. 2018, 8, 1–14. [Google Scholar] [CrossRef]
- Boucher, P.-A.; Joós, B.; Morris, C.E. Coupled left-shift of Nav channels: Modeling the Na+-loading and dysfunctional excitability of damaged axons. J. Comput. Neurosci. 2012, 33, 301–319. [Google Scholar] [CrossRef] [PubMed]
- Babbs, C.F.; Shi, R. Subtle Paranodal Injury Slows Impulse Conduction in a Mathematical Model of Myelinated Axons. PLoS ONE 2013, 8, e67767. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jérusalem, A.; García-Grajales, J.A.; Merchan-Perez, A.; Peña, J.M. A computational model coupling mechanics and electrophysiology in spinal cord injury. Biomech. Model. Mechanobiol. 2014, 13, 883–896. [Google Scholar] [CrossRef] [Green Version]
- García-Grajales, J.A.; Rucabado, G.; García-Dopico, A.; Peña, J.-M.; Jerusalem, A. Neurite, a Finite Difference Large Scale Parallel Program for the Simulation of Electrical Signal Propagation in Neurites under Mechanical Loading. PLoS ONE 2015, 10, e0116532. [Google Scholar] [CrossRef] [PubMed]
- Kwong, M.T.; Bianchi, F.; Malboubi, M.; García-Grajales, J.A.; Homsi, L.; Thompson, M.; Ye, H.; Noels, L.; Jérusalem, A. 3D finite element formulation for mechanical–electrophysiological coupling in axonopathy. Comput. Methods Appl. Mech. Eng. 2018, 346, 1025–1050. [Google Scholar] [CrossRef] [Green Version]
- Cinelli, I.; Destrade, M.; McHugh, P.; Duffy, M. Effects of nerve bundle geometry on neurotrauma evaluation. Int. J. Numer. Methods Biomed. Eng. 2018, 34, e3118. [Google Scholar] [CrossRef] [PubMed]
- Cinelli, I.; Destrade, M.; Duffy, M.; McHugh, P. Electrothermal Equivalent Three-Dimensional Finite-Element Model of a Single Neuron. IEEE Trans. Biomed. Eng. 2017, 65, 1373–1381. [Google Scholar] [CrossRef]
- Cinelli, I.; Destrade, M.; Duffy, M.; McHugh, P. Electro-mechanical response of a 3D nerve bundle model to mechanical loads leading to axonal injury. Int. J. Numer. Methods Biomed. Eng. 2018, 34, e2942. [Google Scholar] [CrossRef] [PubMed]
- El Hady, A.; Machta, B.B. Mechanical surface waves accompany action potential propagation. Nat. Commun. 2015, 6, 6697. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Engelbrecht, J.; Tamm, K.; Peets, T. Internal variables used for describing the signal propagation in axons. Contin. Mech. Thermodyn. 2020, 32, 1619–1627. [Google Scholar] [CrossRef]
- Peets, T.; Tamm, K.; Engelbrecht, J. On the Physical Background of Nerve Pulse Propagation: Heat and Energy. J. Non-Equilib. Thermodyn. 2021, 46. [Google Scholar] [CrossRef]
- Engelbrecht, J.; Tamm, K.; Peets, T. Modelling of processes in nerve fibres at the interface of physiology and mathematics. Biomech. Model. Mechanobiol. 2020, 19, 2491–2498. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Garcia-Gonzalez, D.; Jérusalem, A. Computational model of the mechanoelectrophysiological coupling in axons with application to neuromodulation. Phys. Rev. E 2019, 99, 032406. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jerusalem, A.; Al-Rekabi, Z.; Chen, H.; Ercole, A.; Malboubi, M.; Tamayo-Elizalde, M.; Verhagen, L.; Contera, S. Electrophysiological-mechanical coupling in the neuronal membrane and its role in ultrasound neuromodulation and general anaesthesia. Acta Biomater. 2019, 97, 116–140. [Google Scholar] [CrossRef] [PubMed]
- Chan, B.P.; Leong, K.W. Scaffolding in tissue engineering: General approaches and tissue-specific considerations. Eur. Spine, J. 2008, 17, 467–479. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Basson, M.A. Signaling in Cell Differentiation and Morphogenesis. Cold Spring Harb. Perspect. Biol. 2012, 4, a008151. [Google Scholar] [CrossRef] [Green Version]
- Geris, L.; Gerisch, A.; Sloten, J.V.; Weiner, R.; Van Oosterwyck, H. Angiogenesis in bone fracture healing: A bioregulatory model. J. Theor. Biol. 2008, 251, 137–158. [Google Scholar] [CrossRef]
- Bailón-Plaza, A.; van der Meulen, M.C.H. A Mathematical Framework to Study the Effects of Growth Factor Influences on Fracture Healing. J. Theor. Biol. 2001, 212, 191–209. [Google Scholar] [CrossRef]
- Buenzli, P.R.; Pivonka, P.; Gardiner, B.; Smith, D.W. Modelling the anabolic response of bone using a cell population model. J. Theor. Biol. 2012, 307, 42–52. [Google Scholar] [CrossRef] [Green Version]
- Carlier, A.; van Gastel, N.; Geris, L.; Carmeliet, G.; Van Oosterwyck, H. Size Does Matter: An Integrative In Vivo-In Silico Approach for the Treatment of Critical Size Bone Defects. PLoS Comput. Biol. 2014, 10, e1003888. [Google Scholar] [CrossRef] [Green Version]
- Carlier, A.; Geris, L.; Bentley, K.; Carmeliet, G.; Carmeliet, P.; Van Oosterwyck, H. MOSAIC: A Multiscale Model of Osteogenesis and Sprouting Angiogenesis with Lateral Inhibition of Endothelial Cells. PLoS Comput. Biol. 2012, 8, e1002724. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lacroix, D.; Prendergast, P. A mechano-regulation model for tissue differentiation during fracture healing: Analysis of gap size and loading. J. Biomech. 2002, 35, 1163–1171. [Google Scholar] [CrossRef]
- Lacroix, D.; Prendergast, P.J.; Li, G.; Marsh, D. Biomechanical model to simulate tissue differentiation and bone regeneration: Application to fracture healing. Med. Biol. Eng. Comput. 2002, 40, 14–21. [Google Scholar] [CrossRef]
- Checa, S.; Prendergast, P.J. A Mechanobiological Model for Tissue Differentiation that Includes Angiogenesis: A Lattice-Based Modeling Approach. Ann. Biomed. Eng. 2009, 37, 129–145. [Google Scholar] [CrossRef] [PubMed]
- Wilson, C.J.; Schuetz, M.A.; Epari, D.R. Effects of strain artefacts arising from a pre-defined callus domain in models of bone healing mechanobiology. Biomech. Model. Mechanobiol. 2015, 14, 1129–1141. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Prendergast, P.; Huiskes, R.; Søballe, K. Biophysical stimuli on cells during tissue differentiation at implant interfaces. J. Biomech. 1997, 30, 539–548. [Google Scholar] [CrossRef] [Green Version]
- Ribeiro, F.O.; Gómez-Benito, M.J.; Folgado, J.; Fernandes, P.R.; García-Aznar, J.M. In silico Mechano-Chemical Model of Bone Healing for the Regeneration of Critical Defects: The Effect of BMP. PLoS ONE 2015, 10, e0127722. [Google Scholar] [CrossRef] [Green Version]
- Isaksson, H.; Wilson, W.; van Donkelaar, C.C.; Huiskes, R.; Ito, K. Comparison of biophysical stimuli for mechano-regulation of tissue differentiation during fracture healing. J. Biomech. 2006, 39, 1507–1516. [Google Scholar] [CrossRef] [PubMed]
- Alierta, J.A.; Pérez, M.A.; García-Aznar, J.M. An interface finite element model can be used to predict healing outcome of bone fractures. J. Mech. Behav. Biomed. Mater. 2014, 29, 328–338. [Google Scholar] [CrossRef]
- Comellas, E.; Gasser, T.C.; Bellomo, F.J.; Oller, S. A homeostatic-driven turnover remodelling constitutive model for healing in soft tissues. J. R. Soc. Interface 2016, 13, 20151081. [Google Scholar] [CrossRef]
- Alert, R.; Trepat, X. Physical Models of Collective Cell Migration. Annu. Rev. Condens. Matter Phys. 2020, 11, 77–101. [Google Scholar] [CrossRef] [Green Version]
- Köpf, M.H.; Pismen, L.M. A continuum model of epithelial spreading. Soft Matter 2013, 9, 3727–3734. [Google Scholar] [CrossRef]
- Alert, R.; Blanch-Mercader, C.; Casademunt, J. Active Fingering Instability in Tissue Spreading. Phys. Rev. Lett. 2019, 122, 088104. [Google Scholar] [CrossRef] [Green Version]
- Notbohm, J.; Banerjee, S.; Utuje, K.J.; Gweon, B.; Jang, H.; Park, Y.; Shin, J.; Butler, J.P.; Fredberg, J.J.; Marchetti, M.C. Cellular Contraction and Polarization Drive Collective Cellular Motion. Biophys. J. 2016, 110, 2729–2738. [Google Scholar] [CrossRef] [Green Version]
- Metzcar, J.; Wang, Y.; Heiland, R.; Macklin, P. A Review of Cell-Based Computational Modeling in Cancer Biology. JCO Clin. Cancer Inform. 2019, 3, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Weerasinghe, H.N.; Burrage, P.M.; Burrage, K.; Nicolau, D.V. Mathematical Models of Cancer Cell Plasticity. J. Oncol. 2019, 2019, 2403483. [Google Scholar] [CrossRef] [PubMed]
- Aguilar, M.R.; Román, J.S. Introduction to smart polymers and their applications. In Smart Polymers and their Applications, 2nd edition; Woodhead Publishing: Cambridge, UK, 2014; pp. 1–11. [Google Scholar] [CrossRef]
- Khan, F.; Tanaka, M. Designing Smart Biomaterials for Tissue Engineering. Int. J. Mol. Sci. 2017, 19, 17. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kowalski, P.S.; Bhattacharya, C.; Afewerki, S.; Langer, R.S. Smart Biomaterials: Recent Advances and Future Directions. ACS Biomater. Sci. Eng. 2018, 4, 3809–3817. [Google Scholar] [CrossRef]
- Fenton, O.S.; Olafson, K.N.; Pillai, P.S.; Mitchell, M.; Langer, R. Advances in Biomaterials for Drug Delivery. Adv. Mater. 2018, 30, e1705328. [Google Scholar] [CrossRef] [PubMed]
- Holzapfel, B.M.; Reichert, J.C.; Schantz, J.-T.; Gbureck, U.; Rackwitz, L.; Nöth, U.; Jakob, F.; Rudert, M.; Groll, J.; Hutmacher, D.W. How smart do biomaterials need to be? A translational science and clinical point of view. Adv. Drug Deliv. Rev. 2013, 65, 581–603. [Google Scholar] [CrossRef] [PubMed]
- Vihola, H.; Laukkanen, A.; Valtola, L.; Tenhu, H.; Hirvonen, J.T. Cytotoxicity of thermosensitive polymers poly(N-isopropylacrylamide), poly(N-vinylcaprolactam) and amphiphilically modified poly(N-vinylcaprolactam). Biomaterials 2005, 26, 3055–3064. [Google Scholar] [CrossRef]
- Vihola, H.; Marttila, A.; Pakkanen, J.; Andersson, M.; Laukkanen, A.; Kaukonen, A.; Tenhu, H.; Hirvonen, J. Cell–polymer interactions of fluorescent polystyrene latex particles coated with thermosensitive poly(N-isopropylacrylamide) and poly(N-vinylcaprolactam) or grafted with poly(ethylene oxide)-macromonomer. Int. J. Pharm. 2007, 343, 238–246. [Google Scholar] [CrossRef]
- Kim, M.S.; Hyun, H.; Seo, K.S.; Cho, Y.H.; Lee, J.W.; Lee, C.R.; Khang, G.; Lee, H.B. Preparation and characterization of MPEG–PCL diblock copolymers with thermo-responsive sol–gel–sol phase transition. J. Polym. Sci. Part. A Polym. Chem. 2006, 44, 5413–5423. [Google Scholar] [CrossRef]
- Yoon, J.A.; Gayathri, C.; Gil, R.R.; Kowalewski, T.; Matyjaszewski, K. Comparison of the Thermoresponsive Deswelling Kinetics of Poly(2-(2-methoxyethoxy)ethyl methacrylate) Hydrogels Prepared by ATRP and FRP. Macromolecules 2010, 43, 4791–4797. [Google Scholar] [CrossRef]
- Hu, Z.; Cai, T.; Chi, C. Thermoresponsive oligo(ethylene glycol)-methacrylate- based polymers and microgels. Soft Matter 2010, 6, 2115–2123. [Google Scholar] [CrossRef]
- Becer, R.; Hahn, S.; Fijten, M.W.M.; Thijs, H.M.L.; Hoogenboom, R.; Schubert, U. Libraries of methacrylic acid and oligo(ethylene glycol) methacrylate copolymers with LCST behavior. J. Polym. Sci. Part. A Polym. Chem. 2008, 46, 7138–7147. [Google Scholar] [CrossRef]
- Shimizu, K.; Fujita, H.; Nagamori, E. Oxygen plasma-treated thermoresponsive polymer surfaces for cell sheet engineering. Biotechnol. Bioeng. 2010, 106, 303–310. [Google Scholar] [CrossRef] [PubMed]
- Stile, R.A.; Healy, K.E. Thermo-Responsive Peptide-Modified Hydrogels for Tissue Regeneration. Biomacromolecules 2001, 2, 185–194. [Google Scholar] [CrossRef]
- Bertrand, O.; Gohy, J.-F. Photo-responsive polymers: Synthesis and applications. Polym. Chem. 2016, 8, 52–73. [Google Scholar] [CrossRef]
- Manouras, T.; Vamvakaki, M. Field responsive materials: Photo-, electro-, magnetic- and ultrasound-sensitive polymers. Polym. Chem. 2017, 8, 74–96. [Google Scholar] [CrossRef]
- Chang, L.; Liu, Y.; Yang, Q.; Yu, L.; Liu, J.; Zhu, Z.; Lu, P.; Wu, Y.; Hu, Y. Ionic Electroactive Polymers Used in Bionic Robots: A Review. J. Bionic Eng. 2018, 15, 765–782. [Google Scholar] [CrossRef]
- Liu, T.-Y.; Hu, S.-H.; Liu, K.-H.; Liu, D.-M.; Chen, S.-Y. Preparation and characterization of smart magnetic hydrogels and its use for drug release. J. Magn. Magn. Mater. 2006, 304, e397–e399. [Google Scholar] [CrossRef]
- Zrínyi, M.; Barsi, L.; Büki, A. Ferrogel: A new magneto-controlled elastic medium. Polym. Gels Netw. 1997, 5, 415–427. [Google Scholar] [CrossRef]
- Barbucci, R.; Pasqui, D.; Giani, G.; De Cagna, M.; Fini, M.; Giardino, R.; Atrei, A. A novel strategy for engineering hydrogels with ferromagnetic nanoparticles as crosslinkers of the polymer chains. Potential applications as a targeted drug delivery system. Soft Matter 2011, 7, 5558–5565. [Google Scholar] [CrossRef]
- Zhang, N.; Lock, J.; Sallee, A.; Liu, H. Magnetic Nanocomposite Hydrogel for Potential Cartilage Tissue Engineering: Synthesis, Characterization, and Cytocompatibility with Bone Marrow Derived Mesenchymal Stem Cells. ACS Appl. Mater. Interfaces 2015, 7, 20987–20998. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.J.; Kwon, S.H.; Choi, H.J.; Chung, K.H.; Jung, J.H. Enhanced magnetorheological performance of carbonyl iron/natural rubber composite elastomer with gamma-ferrite additive. Colloid Polym. Sci. 2018, 296, 1609–1613. [Google Scholar] [CrossRef]
- Bidan, C.; Fratzl, M.; Coullomb, A.; Moreau, P.; Lombard, A.H.; Wang, I.; Balland, M.; Boudou, T.; Dempsey, N.M.; Devillers, T.; et al. Magneto-active substrates for local mechanical stimulation of living cells. Sci. Rep. 2018, 8, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Reyes-Ortega, F. 3—pH-responsive polymers: Properties, synthesis and applications. In Smart Polymers and their Applications; Aguilar, M.R., Román, J.S., Eds.; Woodhead Publishing: Cambridge, UK, 2014; pp. 45–92. [Google Scholar] [CrossRef]
- Zhang, J.; Jiang, X.; Wen, X.; Xu, Q.; Zeng, H.; Zhao, Y.; Liu, M.; Wang, Z.; Hu, X.; Wang, Y. Bio-responsive smart polymers and biomedical applications. J. Phys. Mater. 2019, 2, 032004. [Google Scholar] [CrossRef]
- Zrinyi, M. 5 -Magnetically responsive polymer gels and elastomers: Properties, synthesis and applications. In Smart Polymers and their Applications; Woodhead Publishing: Cambridge, UK, 2014; pp. 134–165. [Google Scholar] [CrossRef]
- Moreno, M.; Gonzalez-Rico, J.; Lopez-Donaire, M.; Arias, A.; Garcia-Gonzalez, D. New experimental insights into magneto-mechanical rate dependences of magnetorheological elastomers. Compos. Part. B Eng. 2021, 224, 109148. [Google Scholar] [CrossRef]
- Han, Y.; Mohla, A.; Huang, X.; Hong, W.; Faidley, L.E. Magnetostriction and Field Stiffening of Magneto-Active Elastomers. Int. J. Appl. Mech. 2015, 7, 1550001. [Google Scholar] [CrossRef] [Green Version]
- Bastola, A.K.; Hossain, M. A review on magneto-mechanical characterizations of magnetorheological elastomers. Compos. Part. B: Eng. 2020, 200, 108348. [Google Scholar] [CrossRef]
- Bastola, A.K.; Paudel, M.; Li, L.; Li, W. Recent progress of magnetorheological elastomers: A review. Smart Mater. Struct. 2020, 29, 123002. [Google Scholar] [CrossRef]
- Winger, J.; Schümann, M.; Kupka, A.; Odenbach, S. Influence of the particle size on the magnetorheological effect of magnetorheological elastomers. J. Magn. Magn. Mater. 2019, 481, 176–182. [Google Scholar] [CrossRef]
- Zhao, R.; Kim, Y.; Chester, S.A.; Sharma, P.; Zhao, X. Mechanics of hard-magnetic soft materials. J. Mech. Phys. Solids 2019, 124, 244–263. [Google Scholar] [CrossRef]
- Kim, Y.; Yuk, H.; Zhao, R.; Chester, S.A.; Zhao, X. Printing ferromagnetic domains for untethered fast-transforming soft materials. Nat. Cell Biol. 2018, 558, 274–279. [Google Scholar] [CrossRef]
- Liu, X.; Liu, J.; Lin, S.; Zhao, X. Hydrogel machines. Mater. Today 2020, 36, 102–124. [Google Scholar] [CrossRef]
- Goffin, J.M.; Pittet, P.; Csucs, G.; Lussi, J.W.; Meister, J.-J.; Hinz, B. Focal adhesion size controls tension-dependent recruitment of α-smooth muscle actin to stress fibers. J. Cell Biol. 2006, 172, 259–268. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sunyer, R.; Jin, A.; Nossal, R.; Sackett, D.L. Fabrication of Hydrogels with Steep Stiffness Gradients for Studying Cell Mechanical Response. PLoS ONE 2012, 7, e46107. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yamada, N.; Okano, T.; Sakai, H.; Karikusa, F.; Sawasaki, Y.; Sakurai, Y. Thermo-responsive polymeric surfaces; control of attachment and detachment of cultured cells. Die Makromol. Chemie Rapid Commun. 1990, 11, 571–576. [Google Scholar] [CrossRef]
- Chan, E.W.L.; Park, S.; Yousaf, M.N. An Electroactive Catalytic Dynamic Substrate that Immobilizes and Releases Patterned Ligands, Proteins, and Cells. Angew. Chem. Int. Ed. 2008, 47, 6267–6271. [Google Scholar] [CrossRef]
- Mayer, M.; Rabindranath, R.; Börner, J.; Hörner, E.; Bentz, A.; Salgado, J.; Han, H.; Böse, H.; Probst, J.; Shamonin, M.; et al. Ultra-Soft PDMS-Based Magnetoactive Elastomers as Dynamic Cell Culture Substrata. PLoS ONE 2013, 8, e76196. [Google Scholar] [CrossRef] [Green Version]
- Garcia-Gonzalez, D.; Moreno, M.; Valencia, L.; Arias, A.; Velasco, D. Influence of elastomeric matrix and particle volume fraction on the mechanical response of magneto-active polymers. Compos. Part. B Eng. 2021, 215, 108796. [Google Scholar] [CrossRef]
- Tang, J.; Qiao, Y.; Chu, Y.; Tong, Z.; Zhou, Y.; Zhang, W.; Xie, S.; Hu, J.; Wang, T. Magnetic double-network hydrogels for tissue hyperthermia and drug release. J. Mater. Chem. B 2019, 7, 1311–1321. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Huang, G.; Zhang, X.; Li, B.; Chen, Y.; Lu, T.; Lu, T.J.; Xu, F. Magnetic Hydrogels and Their Potential Biomedical Applications. Adv. Funct. Mater. 2013, 23, 660–672. [Google Scholar] [CrossRef]
- Champeau, M.; Heinze, A.H.; Viana, T.N.; de Souza, E.R.; Chinellato, A.C.; Titotto, S. 4D Printing of Hydrogels: A Review. Adv. Funct. Mater. 2020, 30. [Google Scholar] [CrossRef]
- Chu, H.; Yang, W.; Sun, L.; Cai, S.; Yang, R.; Liang, W.; Yu, H.; Liu, L. 4D Printing: A Review on Recent Progresses. Micromachines 2020, 11, 796. [Google Scholar] [CrossRef]
- Kumar, S.B.; Jeevamalar, J.; Ramu, P.; Suresh, G.; Senthilnathan, K. Evaluation in 4D printing—A review. Mater. Today Proc. 2021, 45, 1433–1437. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Q.; Yi, S.; Lin, Z.; Wang, C.; Chen, Z.; Jiang, L. 4D Printing of Magnetoactive Soft Materials for On-Demand Magnetic Actuation Transformation. ACS Appl. Mater. Interfaces 2021, 13, 4174–4184. [Google Scholar] [CrossRef] [PubMed]
- Hamidi, A.; Tadesse, Y. 3D printing of very soft elastomer and sacrificial carbohydrate glass/elastomer structures for robotic applications. Mater. Des. 2020, 187, 108324. [Google Scholar] [CrossRef]
- Lantean, S.; Barrera, G.; Pirri, C.F.; Tiberto, P.; Sangermano, M.; Roppolo, I.; Rizza, G. 3D Printing of Magnetoresponsive Polymeric Materials with Tunable Mechanical and Magnetic Properties by Digital Light Processing. Adv. Mater. Technol. 2019, 4. [Google Scholar] [CrossRef]
- Wang, S.; Lee, J.M.; Yeong, W.Y. Smart hydrogels for 3D bioprinting. Int. J. Bioprinting 2015, 1, 3–14. [Google Scholar] [CrossRef] [Green Version]
- Sindersberger, D.; Diermeier, A.; Prem, N.; Monkman, G.J. Printing of hybrid magneto active polymers with 6 degrees of freedom. Mater. Today Commun. 2018, 15, 269–274. [Google Scholar] [CrossRef]
- Ji, Z.; Yan, C.; Yu, B.; Wang, X.; Zhou, F. Multimaterials 3D Printing for Free Assembly Manufacturing of Magnetic Driving Soft Actuator. Adv. Mater. Interfaces 2017, 4, 1700629. [Google Scholar] [CrossRef]
- Tang, J.; Yin, Q.; Shi, M.; Yang, M.; Yang, H.; Sun, B.; Guo, B.; Wang, T. Programmable shape transformation of 3D printed magnetic hydrogel composite for hyperthermia cancer therapy. Extrem. Mech. Lett. 2021, 46, 101305. [Google Scholar] [CrossRef]
- Zhu, W.; Li, J.; Leong, Y.J.; Rozen, I.; Qu, X.; Dong, R.; Wu, Z.; Gao, W.; Chung, P.H.; Wang, J.; et al. 3D-Printed Artificial Microfish. Adv. Mater. 2015, 27, 4411–4417. [Google Scholar] [CrossRef] [Green Version]
- Saroia, J.; Wang, Y.; Wei, Q.; Zhang, K.; Lu, T.; Zhang, B. A review on biocompatibility nature of hydrogels with 3D printing techniques, tissue engineering application and its future prospective. Bio-Des. Manuf. 2018, 1, 265–279. [Google Scholar] [CrossRef]
- Markides, H.; Rotherham, M.; EI Haj, A.J. Biocompatibility and Toxicity of Magnetic Nanoparticles in Regenerative Medicine. J. Nanomater. 2012, 2012. [Google Scholar] [CrossRef] [Green Version]
- Mahmoudi, M.; Simchi, A.; Imani, M.; Shokrgozar, M.A.; Milani, A.S.; Häfeli, U.O.; Stroeve, P. A new approach for the in vitro identification of the cytotoxicity of superparamagnetic iron oxide nanoparticles. Colloids Surf. B 2010, 75, 300–309. [Google Scholar] [CrossRef] [PubMed]
- Huang, D.; Chuang, T.; Hung, Y.; Lu, F.; Wu, S.; Mou, C.; Yao, M.; Chen, Y. Internalization of mesoporous silica nanoparticles induces transient but not sufficient osteogenic signals in human mesenchymal stem cells. Toxicol. Appl. Pharmacol. 2008, 231, 208–215. [Google Scholar] [CrossRef]
- Sun, C.; Lee, J.S.H.; Zhang, M. Magnetic nanoparticles in MR imaging and drug delivery. Adv. Drug Delivery Rev. 2008, 60, 1252–1265. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.-T.; Weiss, L. The Role of the Sinus Wall in the Passage of Erythrocytes Through the Spleen. Blood 1973, 41, 529–537. [Google Scholar] [CrossRef] [PubMed]
- Arruebo, M.; Fernández-Pacheco, R.; Ricardo Ibarra, M.; Santamaría, J. Magnetic nanoparticles for drug delivery. Nano Today 2007, 2, 22–32. [Google Scholar] [CrossRef]
- Garcia-Gonzalez, D.; Hossain, M. Microstructural modelling of hard-magnetic soft materials: Dipole–dipole interactions versus Zeeman effect. Extreme Mech. Lett. 2021, 48, 101382. [Google Scholar] [CrossRef]
- Garcia-Gonzalez, D.; Hossain, M. A microstructural-based approach to model magneto-viscoelastic materials at finite strains. Int. J. Solids Struct. 2021, 208-209, 119–132. [Google Scholar] [CrossRef]
- Matin, G.Z.; Zand, M.M.; Tehrani, M.S.; Wendland, B.R.; Dargazany, R. A visco-hyperelastic constitutive model of short- and long-term viscous effects on isotropic soft tissues. Proc. Inst. Mech. Eng. Part. C J. Mech. Eng. Sci. 2019, 234, 3–17. [Google Scholar] [CrossRef]
- Dorfmann, A.; Ogden, R. A constitutive model for the Mullins effect with permanent set in particle-reinforced rubber. Int. J. Solids Struct. 2004, 41, 1855–1878. [Google Scholar] [CrossRef]
- Garcia-Gonzalez, D.; Landis, C.M. Magneto-diffusion-viscohyperelasticity for magneto-active hydrogels: Rate dependences across time scales. J. Mech. Phys. Solids 2020, 139, 103934. [Google Scholar] [CrossRef]
- Hong, W.; Zhao, X.; Zhou, J.; Suo, Z. A theory of coupled diffusion and large deformation in polymeric gels. J. Mech. Phys. Solids 2008, 56, 1779–1793. [Google Scholar] [CrossRef]
- Dortdivanlioglu, B.; Linder, C. Diffusion-driven swelling-induced instabilities of hydrogels. J. Mech. Phys. Solids 2019, 125, 38–52. [Google Scholar] [CrossRef]
- Pao, Y.-H. Electromagnetic Forces in Deformable Continua. Mech. Today 1978, 4, 209–305. [Google Scholar] [CrossRef]
- Eringen, A.C.; Maugin, G.A. Electrodynamics of Continua I; Springer: New York, NY, USA, 1990. [Google Scholar]
- Gérard, A.M. Essential Properties of Electromagnetic Solids. In Continuum Mechanics of Electromagnetic Solids; Elsevier Science Ltd: New York, NY, USA, 1988; Volume 33, pp. 1–61. [Google Scholar]
- Dorfmann, A. Nonlinear magnetoelastic deformations. Q. J. Mech. Appl. Math. 2004, 57, 599–622. [Google Scholar] [CrossRef]
- Bustamante, R. Transversely isotropic nonlinear magneto-active elastomers. Acta Mech. 2009, 210, 183–214. [Google Scholar] [CrossRef]
- Saxena, P.; Hossain, M.; Steinmann, P. A theory of finite deformation magneto-viscoelasticity. Int. J. Solids Struct. 2013, 50, 3886–3897. [Google Scholar] [CrossRef] [Green Version]
- Nedjar, B. A modelling framework for finite strain magnetoviscoelasticity. Math. Mech. Solids 2020, 25, 288–304. [Google Scholar] [CrossRef]
- Garcia-Gonzalez, D. Magneto-visco-hyperelasticity for hard-magnetic soft materials: Theory and numerical applications. Smart Mater. Struct. 2019, 28, 085020. [Google Scholar] [CrossRef]
- Danas, K.; Kankanala, S.; Triantafyllidis, N. Experiments and modeling of iron-particle-filled magnetorheological elastomers. J. Mech. Phys. Solids 2012, 60, 120–138. [Google Scholar] [CrossRef]
- Carlson, J.D.; Jolly, M.R. MR fluid, foam and elastomer devices. Mechatronics 2000, 10, 555–569. [Google Scholar] [CrossRef]
- Ivaneyko, D.; Toshchevikov, V.; Saphiannikova, M.; Heinrich, G. Mechanical properties of magneto-sensitive elastomers: Unification of the continuum-mechanics and microscopic theoretical approaches. Soft Matter 2014, 10, 2213–2225. [Google Scholar] [CrossRef] [Green Version]
- Mukherjee, D.; Bodelot, L.; Danas, K. Microstructurally-guided explicit continuum models for isotropic magnetorheological elastomers with iron particles. Int. J. Non-Linear Mech. 2020, 120, 103380. [Google Scholar] [CrossRef] [Green Version]
- Mukherjee, D.; Rambausek, M.; Danas, K. An explicit dissipative model for isotropic hard magnetorheological elastomers. J. Mech. Phys. Solids 2021, 151, 104361. [Google Scholar] [CrossRef]
- Zabihyan, R.; Mergheim, J.; Pelteret, J.; Brands, B.; Steinmann, P. FE2 simulations of magnetorheological elastomers: Influence of microscopic boundary conditions, microstructures and free space on the macroscopic responses of MREs. Int. J. Solids Struct. 2020, 193-194, 338–356. [Google Scholar] [CrossRef]
- Nam, S.; Stowers, R.; Lou, J.; Xia, Y.; Chaudhuri, O. Varying PEG density to control stress relaxation in alginate-PEG hydrogels for 3D cell culture studies. Biomatererials 2019, 200, 15–24. [Google Scholar] [CrossRef]
- Yang, J.; Shao, C.; Meng, L. Strain Rate-Dependent Viscoelasticity and Fracture Mechanics of Cellulose Nanofibril Composite Hydrogels. Langmuir 2019, 35, 10542–10550. [Google Scholar] [CrossRef]
- Hu, X.; Zhou, J.; Daniel, W.F.M.; Vatankhah-Varnoosfaderani, M.; Dobrynin, A.V.; Sheiko, S.S. Dynamics of Dual Networks: Strain Rate and Temperature Effects in Hydrogels with Reversible H-Bonds. Macromolecules 2017, 50, 652–659. [Google Scholar] [CrossRef]
- Wang, C.; Wiener, C.G.; Fukuto, M.; Li, R.; Yager, K.G.; Weiss, R.A.; Vogt, B.D. Strain rate dependent nanostructure of hydrogels with reversible hydrophobic associations during uniaxial extension. Soft Matter 2019, 15, 227–236. [Google Scholar] [CrossRef]
- Delavoipière, J.; Tran, Y.; Verneuil, E.; Chateauminois, A. Poroelastic indentation of mechanically confined hydrogel layers. Soft Matter 2016, 12, 8049–8058. [Google Scholar] [CrossRef] [Green Version]
- Esteki, M.H.; Alemrajabi, A.A.; Hall, C.M.; Sheridan, G.K.; Azadi, M.; Moeendarbary, E. A new framework for characterization of poroelastic materials using indentation. Acta Biomater. 2020, 102, 138–148. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zhao, X.; Suo, Z.; Jiang, H. A finite element method for transient analysis of concurrent large deformation and mass transport in gels. J. Appl. Phys. 2009, 105, 093522. [Google Scholar] [CrossRef]
- Lucantonio, A.; Nardinocchi, P.; Teresi, L. Transient analysis of swelling-induced large deformations in polymer gels. J. Mech. Phys. Solids 2013, 61, 205–218. [Google Scholar] [CrossRef]
- Bouklas, N.; Landis, C.M.; Huang, R. A nonlinear, transient finite element method for coupled solvent diffusion and large deformation of hydrogels. J. Mech. Phys. Solids 2015, 79, 21–43. [Google Scholar] [CrossRef]
- Bacca, M.; Mcmeeking, R.M. A viscoelastic constitutive law for hydrogels. Meccanica 2017, 52, 3345–3355. [Google Scholar] [CrossRef]
- Liu, Q.; Li, H.; Lam, K.Y. Development of a Multiphysics Model to Characterize the Responsive Behavior of Magnetic-Sensitive Hydrogels with Finite Deformation. J. Phys. Chem. B 2017, 121, 5633–5646. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Li, H.; Lam, K.Y. Optimization of Deformable Magnetic-Sensitive Hydrogel-Based Targeting System in Suspension Fluid for Site-Specific Drug Delivery. Mol. Pharm. 2018, 15, 4632–4642. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Liu, M.; Li, H.; Lam, K. Multiphysics modeling of responsive deformation of dual magnetic-pH-sensitive hydrogel. Int. J. Solids Struct. 2020, 190, 76–92. [Google Scholar] [CrossRef]
- Gebhart, P.; Wallmersperger, T. A general framework for the modeling of porous ferrogels at finite strains. J. Mech. Phys. Solids 2019, 122, 69–83. [Google Scholar] [CrossRef]
- Ganguly, S.; Margel, S. Review: Remotely controlled magneto-regulation of therapeutics from magnetoelastic gel matrices. Biotechnol. Adv. 2020, 44, 107611. [Google Scholar] [CrossRef] [PubMed]
- Adedoyin, A.A.; Ekenseair, A.K. Biomedical applications of magneto-responsive scaffolds. Nano Res. 2018, 11, 5049–5064. [Google Scholar] [CrossRef]
- Ze, Q.; Kuang, X.; Wu, S.; Wong, J.; Montgomery, S.M.; Zhang, R.; Kovitz, J.M.; Yang, F.; Qi, H.J.; Zhao, R. Magnetic Shape Memory Polymers with Integrated Multifunctional Shape Manipulation. Adv. Mater. 2019, 32. [Google Scholar] [CrossRef] [PubMed]
- Kim, C.; Kim, H.; Park, H.; Lee, K.Y. Controlling the porous structure of alginate ferrogel for anticancer drug delivery under magnetic stimulation. Carbohydr. Polym. 2019, 223, 115045. [Google Scholar] [CrossRef]
- Thévenot, J.; Oliveira, H.; Sandre, O.; Lecommandoux, S. Magnetic responsive polymer composite materials. Chem. Soc. Rev. 2013, 42, 7099–7116. [Google Scholar] [CrossRef] [Green Version]
- Fan, D.; Wang, Q.; Zhu, T.; Wang, H.; Liu, B.; Wang, Y.; Liu, Z.; Liu, X.; Fan, D.; Wang, X. Recent Advances of Magnetic Nanomaterials in Bone Tissue Repair. Front. Chem. 2020, 8. [Google Scholar] [CrossRef] [PubMed]
- Hu, R.; Zheng, H.; Cao, J.; Davoudi, Z.; Wang, Q. Self-Assembled Hyaluronic Acid Nanoparticles for pH-Sensitive Release of Doxorubicin: Synthesis and In Vitro Characterization. J. Biomed. Nanotechnol. 2017, 13, 1058–1068. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Kim, J.; Cezar, C.A.; Huebsch, N.; Lee, K.; Bouhadir, K.; Mooney, D.J. Active scaffolds for on-demand drug and cell delivery. Proc. Natl. Acad. Sci. USA 2010, 108, 67–72. [Google Scholar] [CrossRef] [Green Version]
- Al-Attar, T.; Madihally, S.V. Recent advances in the combination delivery of drug for leukemia and other cancers. Expert Opin. Drug Deliv. 2020, 17, 213–223. [Google Scholar] [CrossRef]
- Zheng, H.; Yin, L.; Zhang, X.; Zhang, H.; Hu, R.; Yin, Y.; Qiu, T.; Xiong, X.; Wang, Q. Redox Sensitive Shell and Core Crosslinked Hyaluronic Acid Nanocarriers for Tumor-Targeted Drug Delivery. J. Biomed. Nanotechnol. 2016, 12, 1641–1653. [Google Scholar] [CrossRef]
- Antman-Passig, M.; Shefi, O. Remote Magnetic Orientation of 3D Collagen Hydrogels for Directed Neuronal Regeneration. Nano Lett. 2016, 16, 2567–2573. [Google Scholar] [CrossRef]
- Socoliuc, V.; Peddis, D.; Petrenko, V.I.; Avdeev, M.V.; Susan-Resiga, D.; Szabó, T.; Turcu, R.; Tombácz, E.; Vékás, L. Magnetic Nanoparticle Systems for Nanomedicine—A Materials Science Perspective. Magnetochemistry. 2020, 6, 2. [Google Scholar] [CrossRef] [Green Version]
- Hajinasab, A.; Saber-Samandari, S.; Ahmadi, S.; Alamara, K. Preparation and characterization of a biocompatible magnetic scaffold for biomedical engineering. Mater. Chem. Phys. 2018, 204, 378–387. [Google Scholar] [CrossRef]
- Wei, C.; Lv, Y. Preparation and Application of Magnetic Responsive Materials in Bone Tissue Engineering. Curr. Stem Cell Res. Ther. 2020, 15, 428–440. [Google Scholar] [CrossRef]
- Fuhrer, R.; Hofmann, S.; Hild, N.; Vetsch, J.R.; Herrmann, I.K.; Grass, R.N.; Stark, W.J. Pressureless Mechanical Induction of Stem Cell Differentiation Is Dose and Frequency Dependent. PLoS ONE 2013, 8, e81362. [Google Scholar] [CrossRef] [PubMed]
- Meng, J.; Xiao, B.; Zhang, Y.; Liu, J.; Xue, H.; Lei, J.; Kong, H.; Huang, Y.; Jin, Z.; Gu, N.; et al. Super-paramagnetic responsive nanofibrous scaffolds under static magnetic field enhance osteogenesis for bone repair in vivo. Sci. Rep. 2013, 3, 2655. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guo, C.; Kaufman, L.J. Flow and magnetic field induced collagen alignment. Biomatererials 2007, 28, 1105–1114. [Google Scholar] [CrossRef] [PubMed]
- Tampieri, A.; Landi, E.; Valentini, F.; Sandri, M.; D’Alessandro, T.; Dediu, V.; Marcacci, M. A conceptually new type of bio-hybrid scaffold for bone regeneration. Nanotechnology 2010, 22, 015104. [Google Scholar] [CrossRef] [PubMed]
- Bock, N.; Riminucci, A.; Dionigi, C.; Russo, A.; Tampieri, A.; Landi, E.; Goranov, V.; Marcacci, M.; Dediu, V. A novel route in bone tissue engineering: Magnetic biomimetic scaffolds. Acta Biomater. 2010, 6, 786–796. [Google Scholar] [CrossRef]
- Silva, E.D.; Babo, P.; Costa-Almeida, R.; Domingues, R.; Mendes, B.B.; Paz, E.; Freitas, P.; Rodrigues, M.; Granja, P.; Gomes, M.E. Multifunctional magnetic-responsive hydrogels to engineer tendon-to-bone interface. Nanomed. Nanotechnol. Biol. Med. 2018, 14, 2375–2385. [Google Scholar] [CrossRef] [Green Version]
- Karagiorgis, S.; Tsamis, A.; Voutouri, C.; Turcu, R.; Porav, S.A.; Socoliuc, V.; Vekas, L.; Louca, M.; Stylianopoulos, T.; Vavourakis, V.; et al. Engineered magnetoactive collagen hydrogels with tunable and predictable mechanical response. Mater. Sci. Eng. C 2020, 114, 111089. [Google Scholar] [CrossRef] [PubMed]
- Fernandes, M.M.; Correia, D.M.; Ribeiro, C.; Castro, N.; Correia, V.M.G.; Lanceros-Mendez, S. Bioinspired Three-Dimensional Magnetoactive Scaffolds for Bone Tissue Engineering. ACS Appl. Mater. Interfaces 2019, 11, 45265–45275. [Google Scholar] [CrossRef] [PubMed]
- Henstock, J.R.; Rotherham, M.; Rashidi, H.; Shakesheff, K.; El Haj, A.J. Remotely Activated Mechanotransduction via Magnetic Nanoparticles Promotes Mineralization Synergistically with Bone Morphogenetic Protein 2: Applications for Injectable Cell Therapy. STEM CELLS Transl. Med. 2014, 3, 1363–1374. [Google Scholar] [CrossRef]
- Yang, W.; Zhu, P.; Huang, H.; Zheng, Y.; Liu, J.; Feng, L.; Guo, H.; Tang, S.; Guo, R. Functionalization of Novel Theranostic Hydrogels with Kartogenin-Grafted USPIO Nanoparticles to Enhance Cartilage Regeneration. ACS Appl. Mater. Interfaces 2019, 11, 34744–34754. [Google Scholar] [CrossRef]
- Abaci, H.E.; Guo, Z.; Coffman, A.; Gillette, B.; Lee, W.-H.; Sia, S.K.; Christiano, A.M. Human Skin Constructs with Spatially Controlled Vasculature Using Primary and iPSC-Derived Endothelial Cells. Adv. Heal. Mater. 2016, 5, 1800–1807. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pankhurst, A.Q.; Thanh, N.T.K.; Jones, S.K.; Dobson, J. Progress in applications of magnetic nanoparticles in biomedicine. J. Phys. D Appl. Phys. 2009, 42, 224001. [Google Scholar] [CrossRef] [Green Version]
- Wu, S.; Hu, W.; Ze, Q.; Sitti, M.; Zhao, R. Multifunctional magnetic soft composites: A review. Multifunct. Mater. 2020, 3, 042003. [Google Scholar] [CrossRef]
- Jalili, N.A.; Jaiswal, M.K.; Peak, C.W.; Cross, L.M.; Gaharwar, A.K. Injectable nanoengineered stimuli-responsive hydrogels for on-demand and localized therapeutic delivery. Nanoscale 2017, 9, 15379–15389. [Google Scholar] [CrossRef] [PubMed]
- Di, J.; Yu, J.; Wang, Q.; Yao, S.; Suo, D.; Ye, Y.; Pless, M.; Zhu, Y.; Jing, Y.; Gu, Z. Ultrasound-triggered noninvasive regulation of blood glucose levels using microgels integrated with insulin nanocapsules. Nano Res. 2017, 10, 1393–1402. [Google Scholar] [CrossRef]
- Turcheniuk, K.; Khanal, M.; Motorina, A.; Subramanian, P.; Barras, A.; Zaitsev, V.; Kuncser, V.; Leca, A.; Martoriati, A.; Cailliau, K.; et al. Insulin loaded iron magnetic nanoparticle–graphene oxide composites: Synthesis, characterization and application for in vivo delivery of insulin. RSC Adv. 2014, 4, 865–875. [Google Scholar] [CrossRef]
- Cheng, J.; Teply, B.A.; Jeong, S.Y.; Yim, C.H.; Ho, D.; Sherifi, I.; Jon, S.; Farokhzad, O.C.; Khademhosseini, A.; Langer, R.S. Magnetically Responsive Polymeric Microparticles for Oral Delivery of Protein Drugs. Pharm. Res. 2006, 23, 557–564. [Google Scholar] [CrossRef]
- Casolaro, M.; Casolaro, I. Pulsed release of antidepressants from nanocomposite hydrogels. Biol. Eng. Med. 2017, 3, 1–8. [Google Scholar] [CrossRef] [Green Version]
- SNazarizadeh, A.; Asri-Rezaie, S. Comparative study of antidiabetic activity and oxidative stress induced by zinc oxide nanoparticles and zinc sulfate in diabetic rats. AAPS PharmSciTech 2016, 17, 834–843. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dobson, J. Magnetic nanoparticles for gene and drug delivery. Int. J. Nanomed. 2008, 3, 169–180. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, D.T.; Nguyen, N.-M.; Vu, D.-M.; Tran, M.-D.; Ta, V.-T. On-Demand Release of Drug from Magnetic Nanoparticle-Loaded Alginate Beads. J. Anal. Methods Chem. 2021, 2021, 1–7. [Google Scholar] [CrossRef]
- Giani, G.; Fedi, S.; Barbucci, R. Hybrid Magnetic Hydrogel: A Potential System for Controlled Drug Delivery by Means of Alternating Magnetic Fields. Polymers 2012, 4, 1157–1169. [Google Scholar] [CrossRef] [Green Version]
- Lin, F.; Zheng, J.; Guo, W.; Zhu, Z.; Wang, Z.; Dong, B.; Lin, C.; Huang, B.; Lu, B. Smart cellulose-derived magnetic hydrogel with rapid swelling and deswelling properties for remotely controlled drug release. Cellulose 2019, 26, 6861–6877. [Google Scholar] [CrossRef]
- Jalili, N.A.; Muscarello, M.; Gaharwar, A.K. Nanoengineered thermoresponsive magnetic hydrogels for biomedical applications. Bioeng. Transl. Med. 2016, 1, 297–305. [Google Scholar] [CrossRef] [PubMed]
- Van der Zee, J. Heating the patient: A promising approach? Ann. Oncol. 2002, 13, 1173–1184. [Google Scholar] [CrossRef]
- Ang, K.; Venkatraman, S.; Ramanujan, R. Magnetic PNIPA hydrogels for hyperthermia applications in cancer therapy. Mater. Sci. Eng. C 2007, 27, 347–351. [Google Scholar] [CrossRef]
- Meenach, S.A.; Hilt, J.Z.; Anderson, K.W. Poly(ethylene glycol)-based magnetic hydrogel nanocomposites for hyperthermia cancer therapy. Acta Biomater. 2010, 6, 1039–1046. [Google Scholar] [CrossRef]
- Park, N.; Kim, J. Hydrogel-Based Artificial Muscles: Overview and Recent Progress. Adv. Intell. Syst. 2020, 2. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.-E.; Van Tieu, M.; Hwang, S.Y.; Lee, M.-H. Magnetic Particles: Their Applications from Sample Preparations to Biosensing Platforms. Micromachines 2020, 11, 302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, Y.-T.; Kolhatkar, A.G.; Zenasni, O.; Xu, S.; Lee, T.R. Biosensing Using Magnetic Particle Detection Techniques. Sensors 2017, 17, 2300. [Google Scholar] [CrossRef]
- Sun, T.F.T.; Shi, Q.; Huang, Q.; Wang, H.; Xiong, X.; Hu, C. Magnetic alginate microfibers as scaffolding elements for the fabrication of microvascular-like structures. Acta Biomater. 2018, 66, 272–281. [Google Scholar] [CrossRef]
- Fass, J.N.; Odde, D.J. Tensile Force-Dependent Neurite Elicitation via Anti-β1 Integrin Antibody-Coated Magnetic Beads. Biophys. J. 2003, 85, 623–636. [Google Scholar] [CrossRef] [Green Version]
- Kratz, S.R.A.; Eilenberger, C.; Schuller, P.; Bachmann, B.; Spitz, S.; Ertl, P.; Rothbauer, M. Characterization of four functional biocompatible pressure-sensitive adhesives for rapid prototyping of cell-based lab-on-a-chip and organ-on-a-chip systems. Sci. Rep. 2019, 9, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Calvo-Correas, T.; Shirole, A.; Crippa, F.; Fink, A.; Weder, C.; Corcuera, M.A.; Eceiza, A. Biocompatible thermo- and magneto-responsive shape-memory polyurethane bionanocomposites. Mater. Sci. Eng. C 2019, 97, 658–668. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Z.; Li, X.; Zhang, Y.; Yin, M.; Li, J.; Song, H.; Shi, J.; Ling, D.; Wang, L.; et al. Deciphering active biocompatibility of iron oxide nanoparticles from their intrinsic antagonism. Nano Res. 2018, 11, 2746–2755. [Google Scholar] [CrossRef]
- Janko, C.; Zaloga, J.; Pöttler, M.; Dürr, S.; Eberbeck, D.; Tietze, R.; Lyer, S.; Alexiou, C. Strategies to optimize the biocompatibility of iron oxide nanoparticles—SPIONs safe by design. J. Magn. Magn. Mater. 2017, 431, 281–284. [Google Scholar] [CrossRef]
- Singh, N.; Jenkins, G.; Asadi, R.; Doak, S. Potential toxicity of superparamagnetic iron oxide nanoparticles (SPION). Nano Rev. 2010, 1, 1–15. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gholami, A.; Rasoul-Amini, S.; Ebrahiminezhad, A.; Abootalebi, N.; Niroumand, U.; Ebrahimi, N.; Ghasemi, Y. Magnetic properties and antimicrobial effect of amino and lipoamino acid coated iron oxide nanoparticles. Minerva Biotecnol. 2016, 28, 177–186. [Google Scholar]
- Bao, Y.; Wen, T.; Samia, A.C.S.; Khandhar, A.P.; Krishnan, K.M. Magnetic nanoparticles: Material engineering and emerging applications in lithography and biomedicine. J. Mater. Sci. 2016, 51, 513–553. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Issa, B.; Obaidat, I.M.; Albiss, B.A.; Haik, Y. Magnetic Nanoparticles: Surface Effects and Properties Related to Biomedicine Applications. Int. J. Mol. Sci. 2013, 14, 21266–21305. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schlachter, E.K.; Widmer, H.R.; Bregy, A.; Lönnfors-Weitzel, T.; Vajtai, I.; Corazza, N.; Bernau, V.J.; Weitzel, T.; Mordasini, P.; Slotboom, J.; et al. Metabolic pathway and distribution of superparamagnetic iron oxide nanoparticles: In vivo study. Int. J. Nanomed. 2011, 6, 1793–1800. [Google Scholar] [CrossRef] [Green Version]
| Stimulus | Materials | Applications |
|---|---|---|
| Temperature | PNIPAAm, PDEAAm, PVCL, PDMAEMA, PEG [99,100,101,102,103,104,105,106]. | Drug and gene delivery, tissue engineering (substrates and injectable gels). |
| Light | PEG and PMA hydrogels modified with light responsive pyrenylmethyl esters, o-nitrobenzyl esters or coumarinyl esters [107]. | Drug delivery (light can penetrate the skin); smart surfaces; nanostructures. |
| Electrical field | Ionic polymer-metal composites: perfluorinated polymers and styrenic copolymers [108]. | Drug delivery, actuators in soft robotics, artificial muscles [109]. |
| Magnetic field | Polymeric matrix laden with magnetic particles (nano or micro, hard or soft) [110,111,112,113,114,115]. | Frug delivery, remote actuation, soft robotics, tissue engineering. |
| pH | Polyelectrolyte polymers with weak acidic or basic groups that accept or release protons in response to a change in the environmental pH [116]. | Drug delivery, gene carriers, biosensors. |
| Biomolecules | Polymers modified to respond to the presence of certain biological cues (signals, enzymes, ATP, etc.) [117]. | Drug delivery, biosensors, tissue engineering and regenerative medicine. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonzalez-Rico, J.; Nunez-Sardinha, E.; Valencia, L.; Arias, A.; Muñoz-Barrutia, A.; Velasco, D.; Garcia-Gonzalez, D. Tuning the Cell and Biological Tissue Environment through Magneto-Active Materials. Appl. Sci. 2021, 11, 8746. https://doi.org/10.3390/app11188746
Gonzalez-Rico J, Nunez-Sardinha E, Valencia L, Arias A, Muñoz-Barrutia A, Velasco D, Garcia-Gonzalez D. Tuning the Cell and Biological Tissue Environment through Magneto-Active Materials. Applied Sciences. 2021; 11(18):8746. https://doi.org/10.3390/app11188746
Chicago/Turabian StyleGonzalez-Rico, Jorge, Emanuel Nunez-Sardinha, Leticia Valencia, Angel Arias, Arrate Muñoz-Barrutia, Diego Velasco, and Daniel Garcia-Gonzalez. 2021. "Tuning the Cell and Biological Tissue Environment through Magneto-Active Materials" Applied Sciences 11, no. 18: 8746. https://doi.org/10.3390/app11188746
APA StyleGonzalez-Rico, J., Nunez-Sardinha, E., Valencia, L., Arias, A., Muñoz-Barrutia, A., Velasco, D., & Garcia-Gonzalez, D. (2021). Tuning the Cell and Biological Tissue Environment through Magneto-Active Materials. Applied Sciences, 11(18), 8746. https://doi.org/10.3390/app11188746








