Evaluating the Seismic Capacity of Dry-Joint Masonry Arch Structures via the Combined Finite-Discrete Element Method
Abstract
:1. Introduction
2. FDEM Modelling
2.1. Voussoir Discretisation
2.2. Element Motions
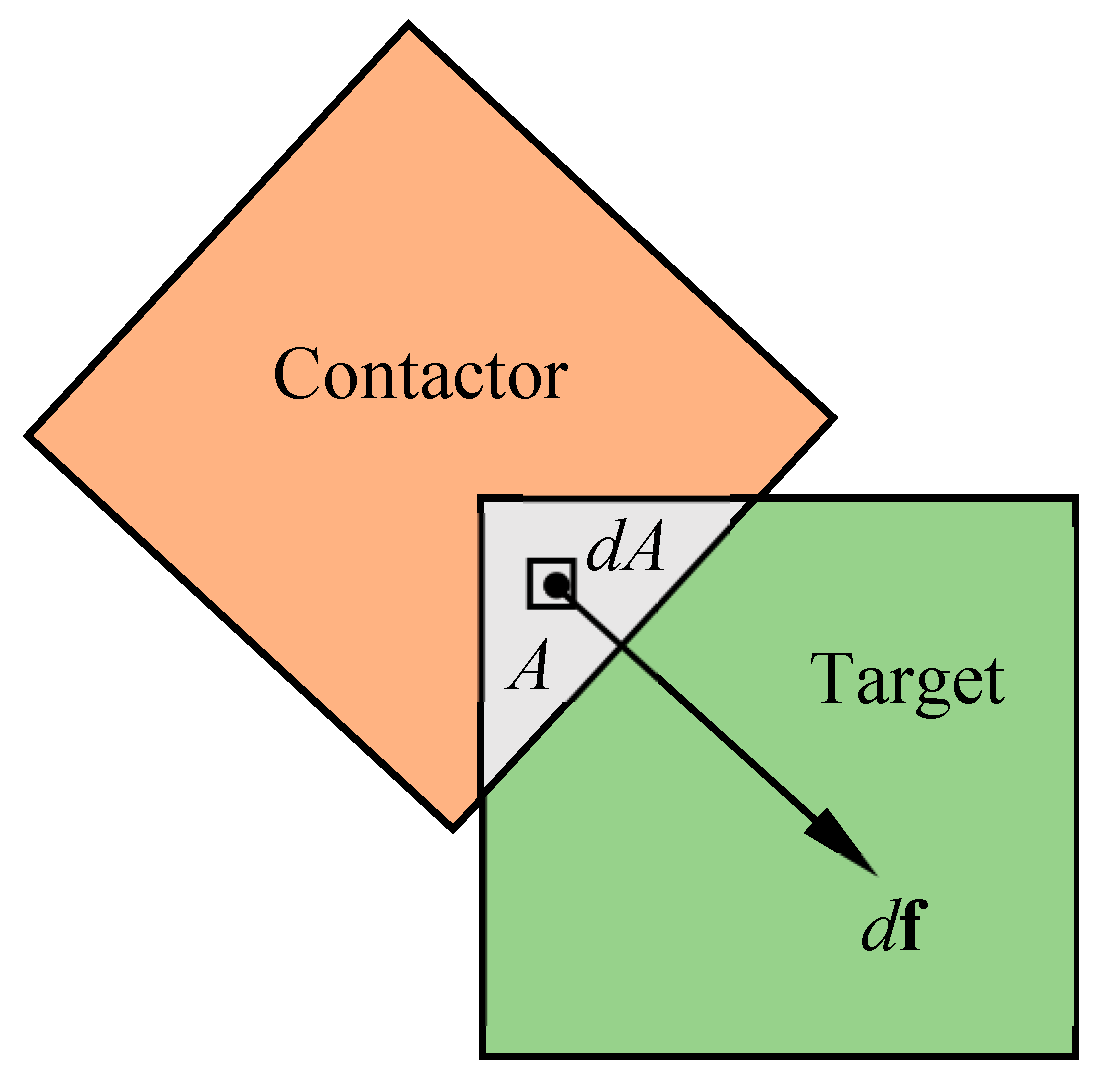
2.3. Contact Forces
3. Numerical Examples
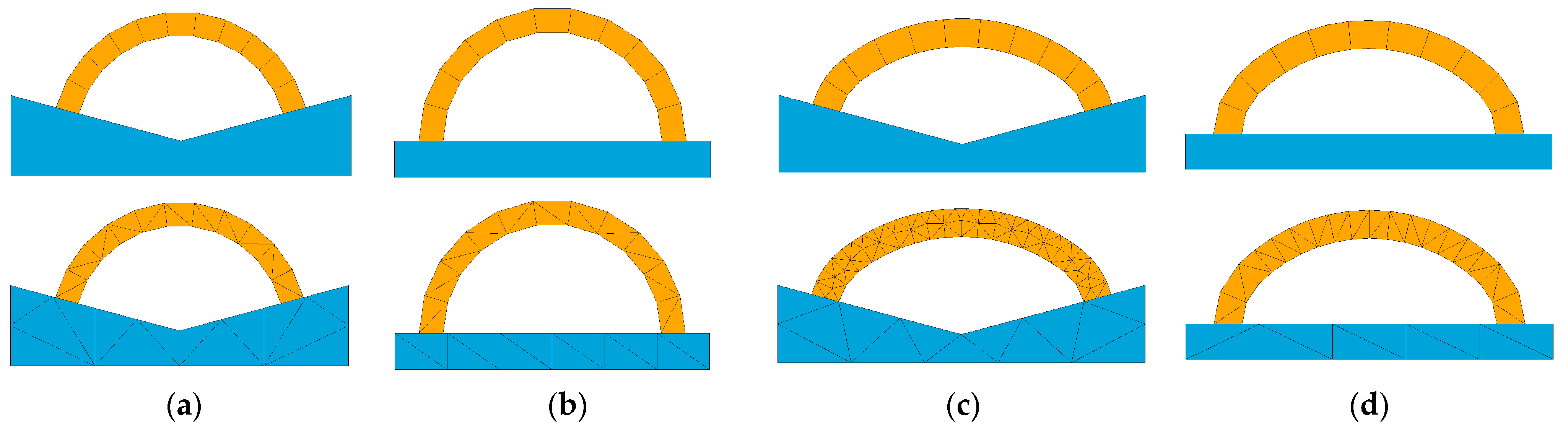
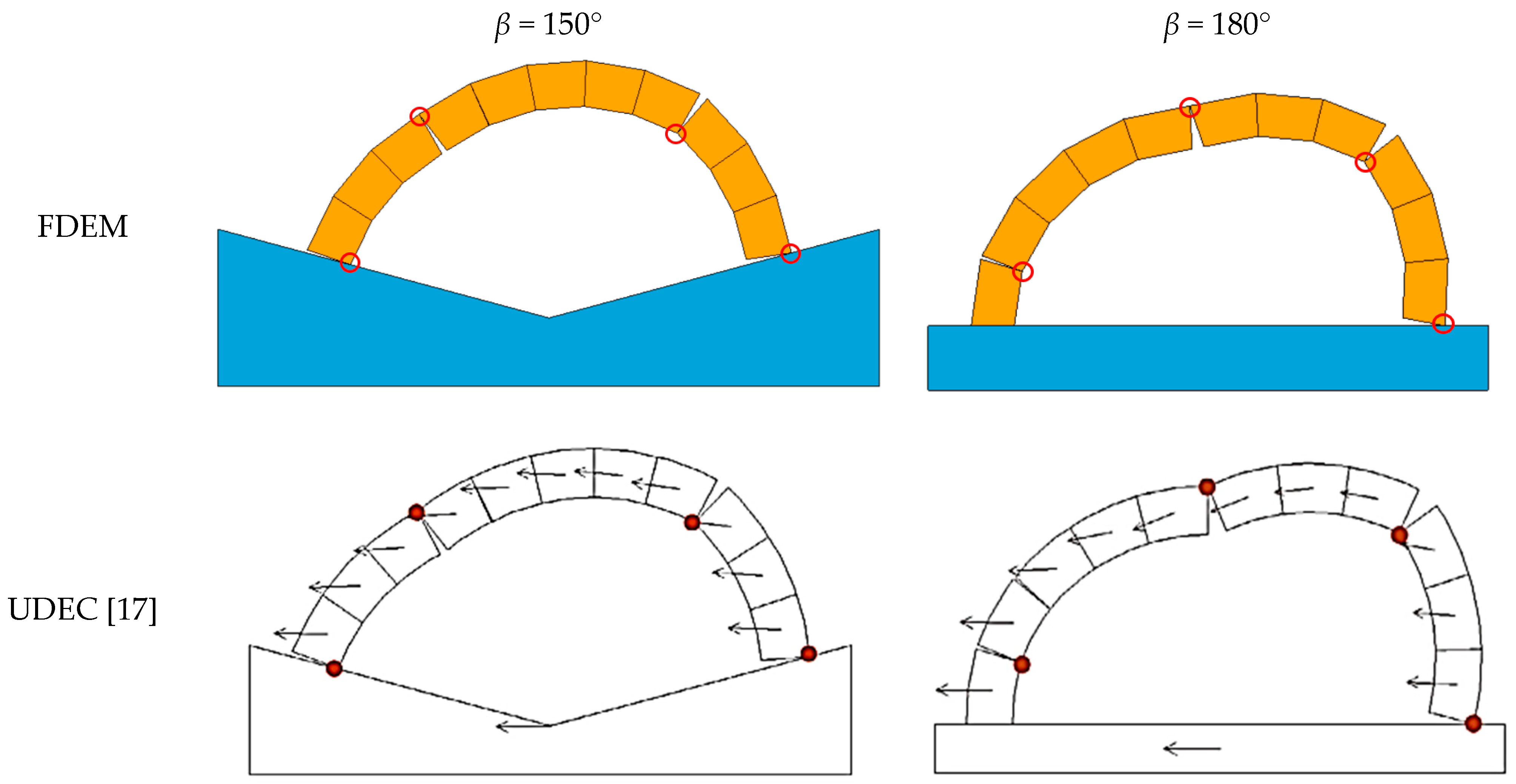
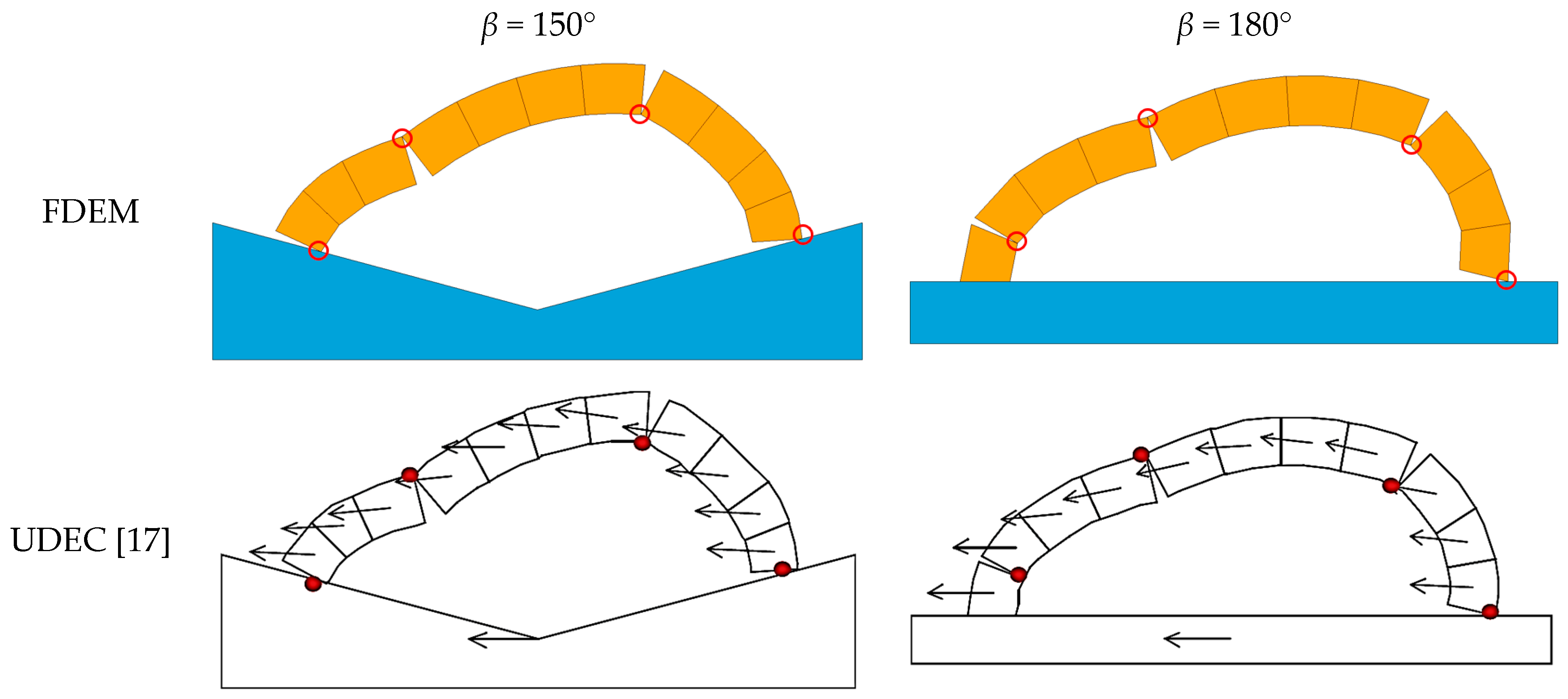
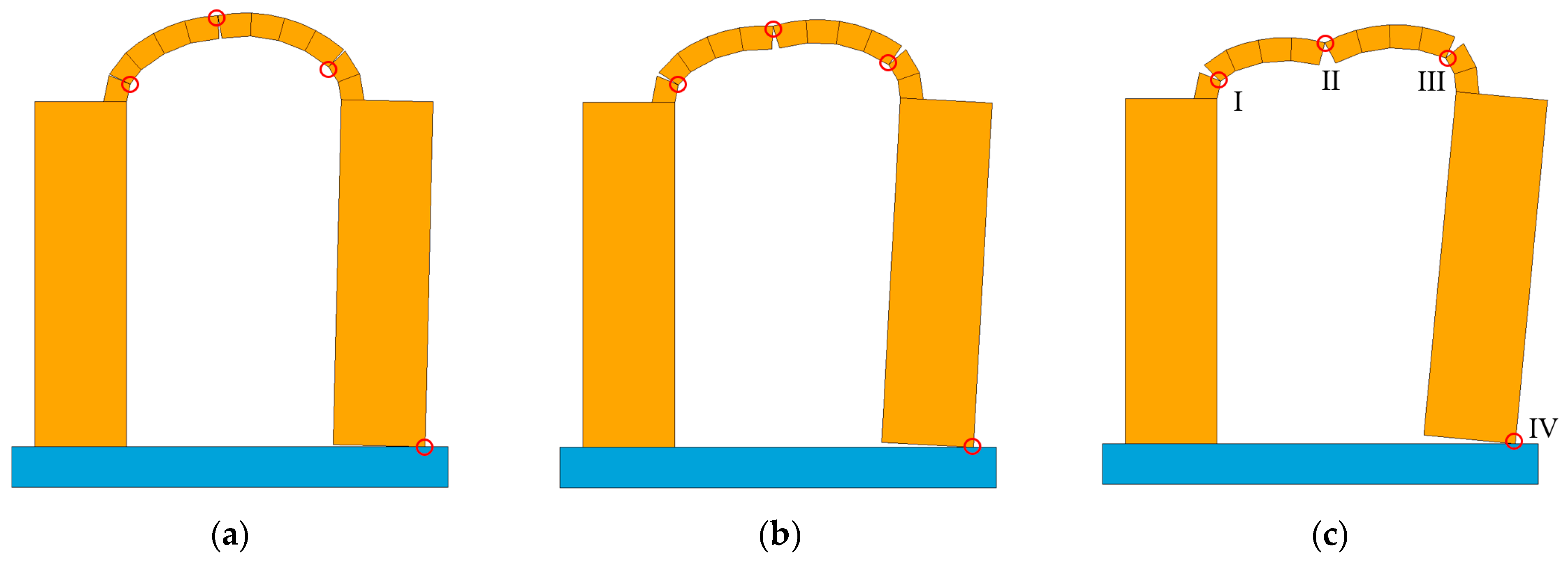
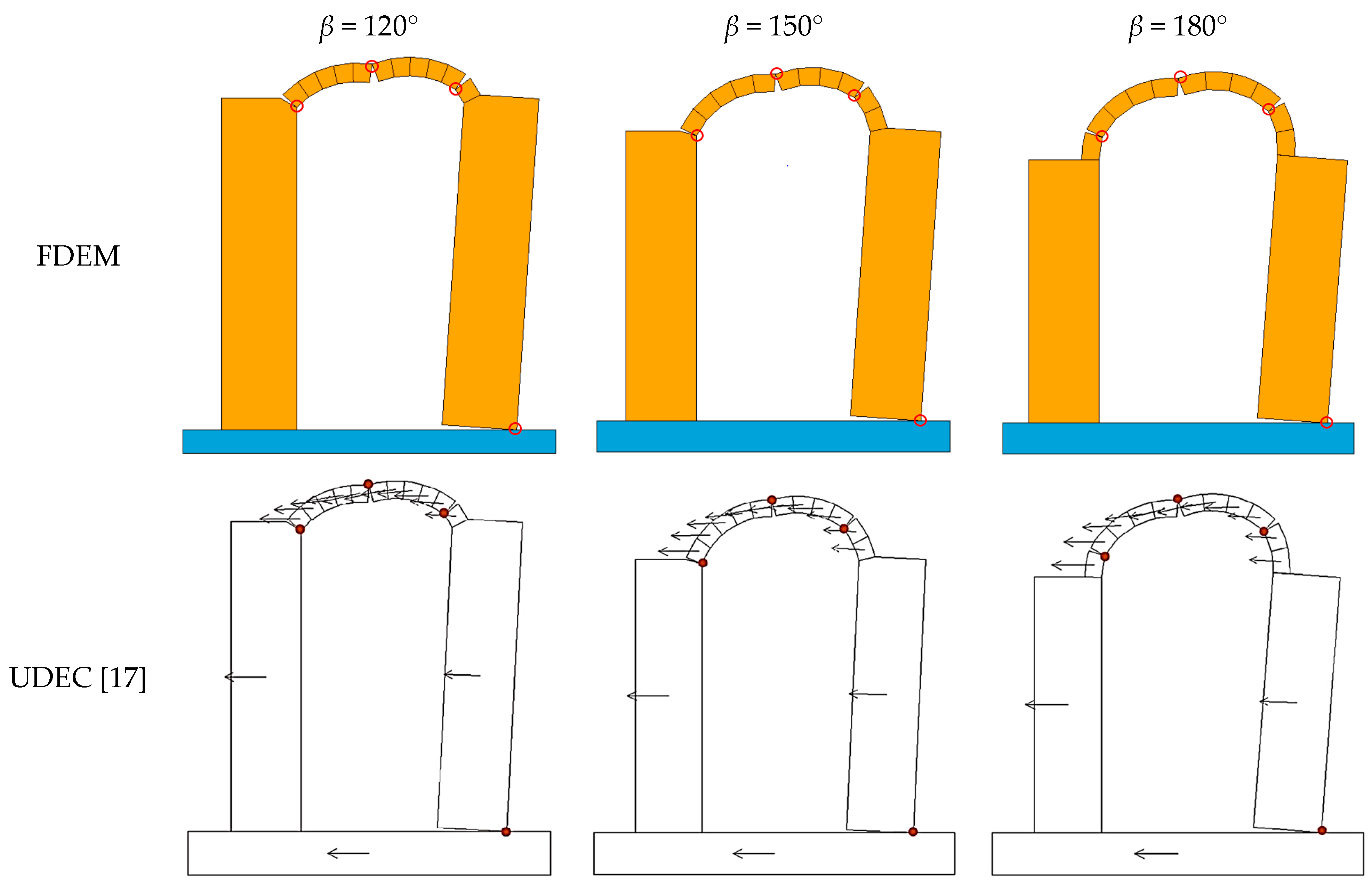
3.1. Arches without Buttresses
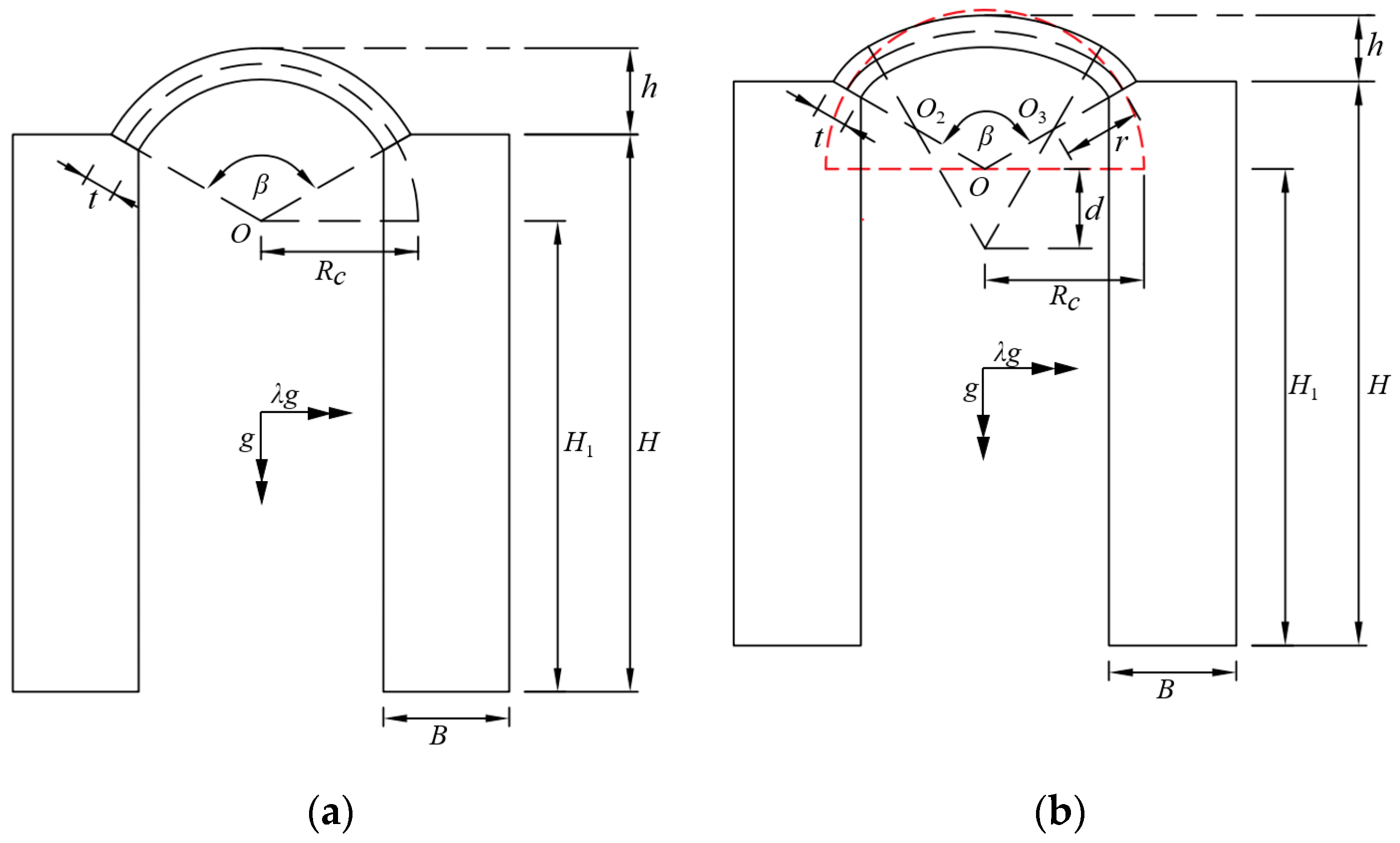
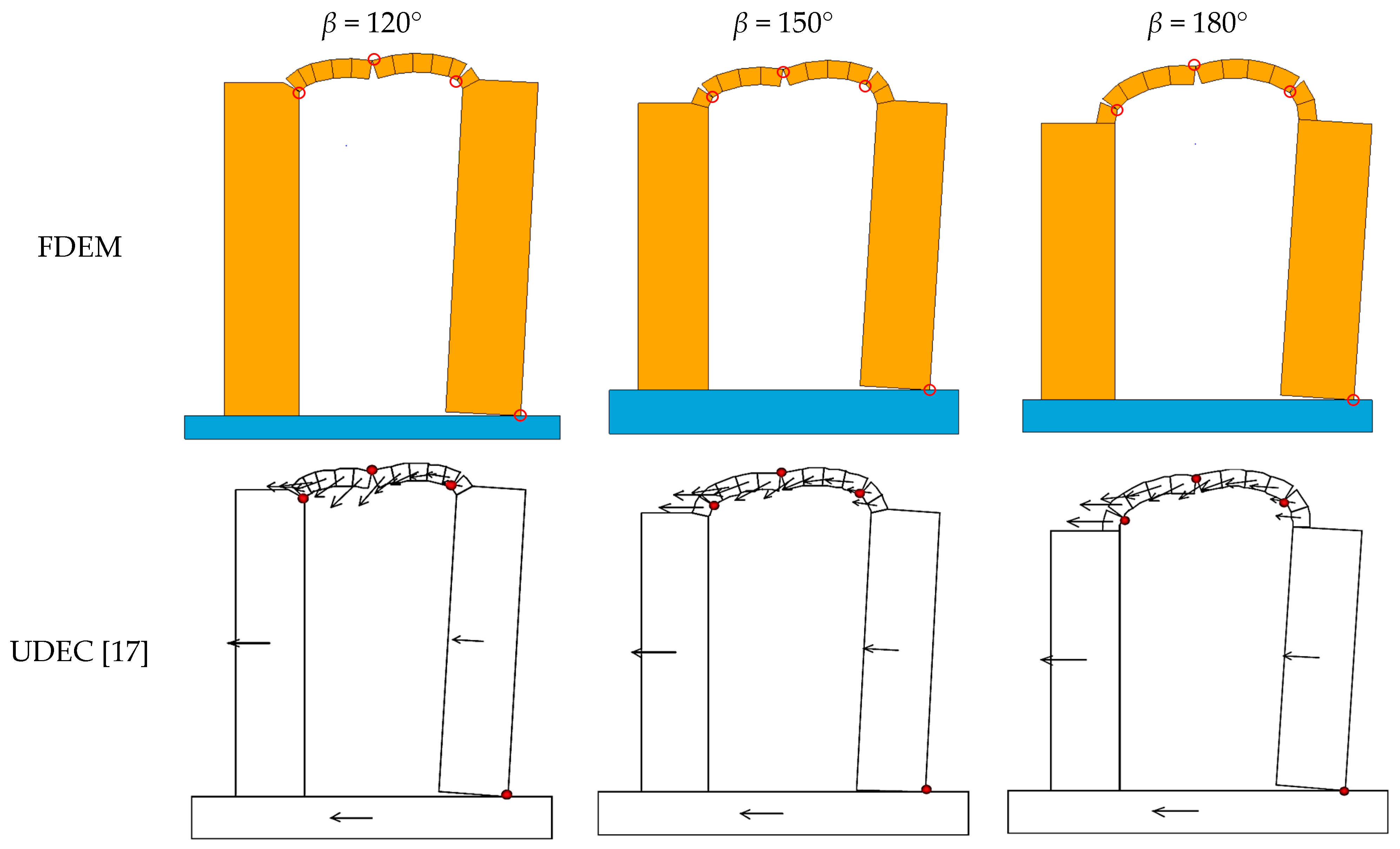
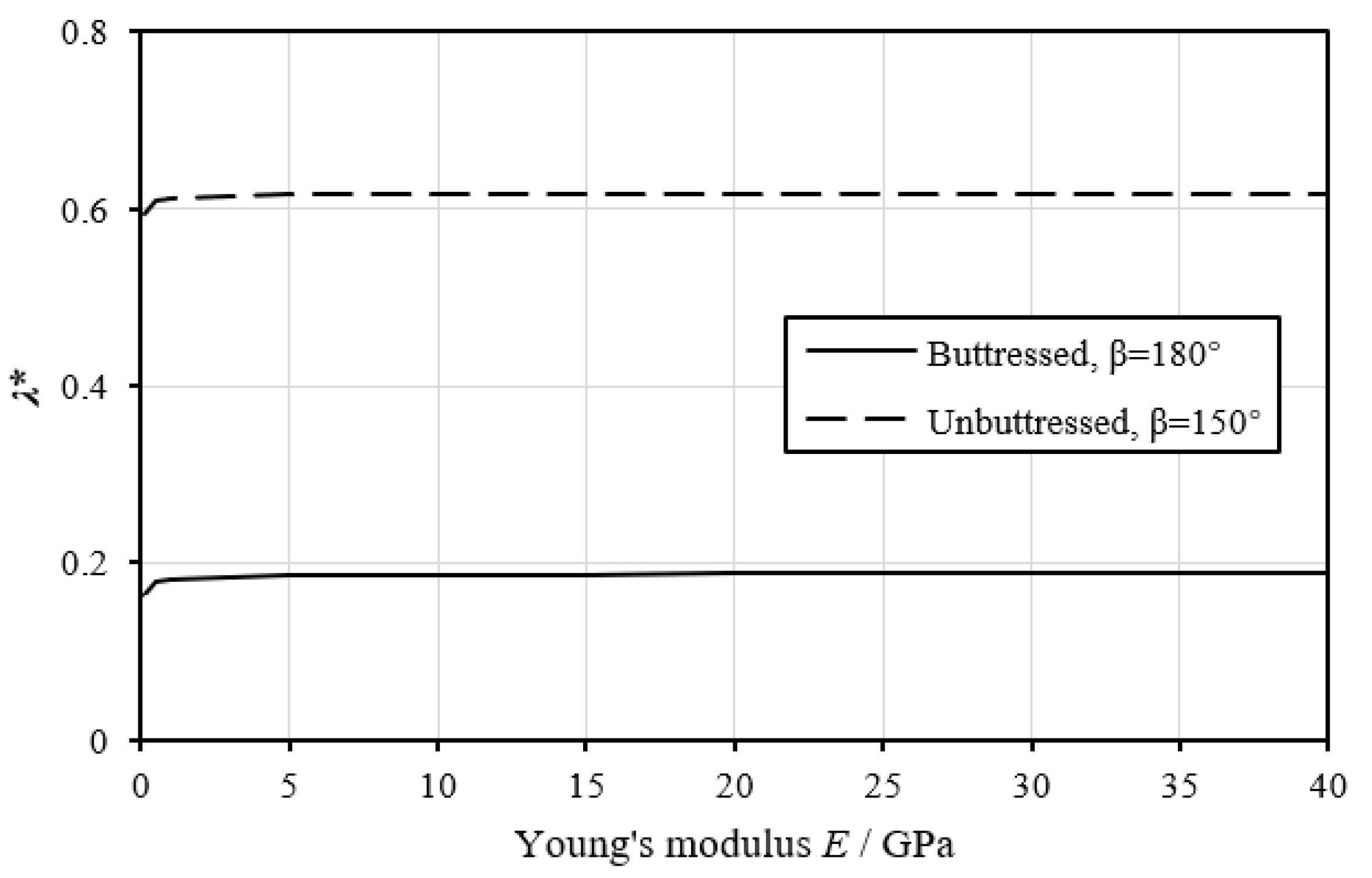
3.2. Buttressed Arches
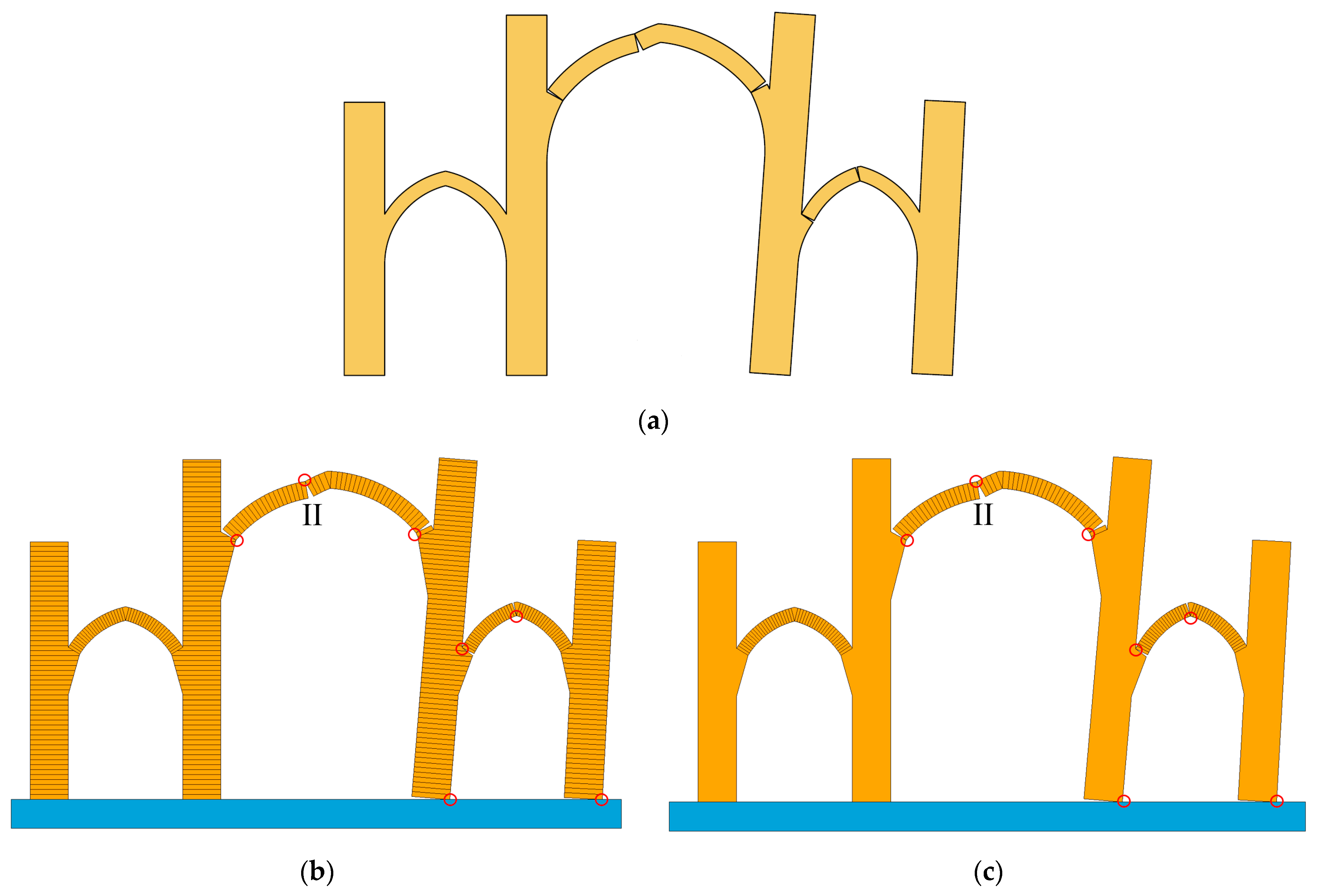
3.3. A Multi-Span Pointed Arch Church
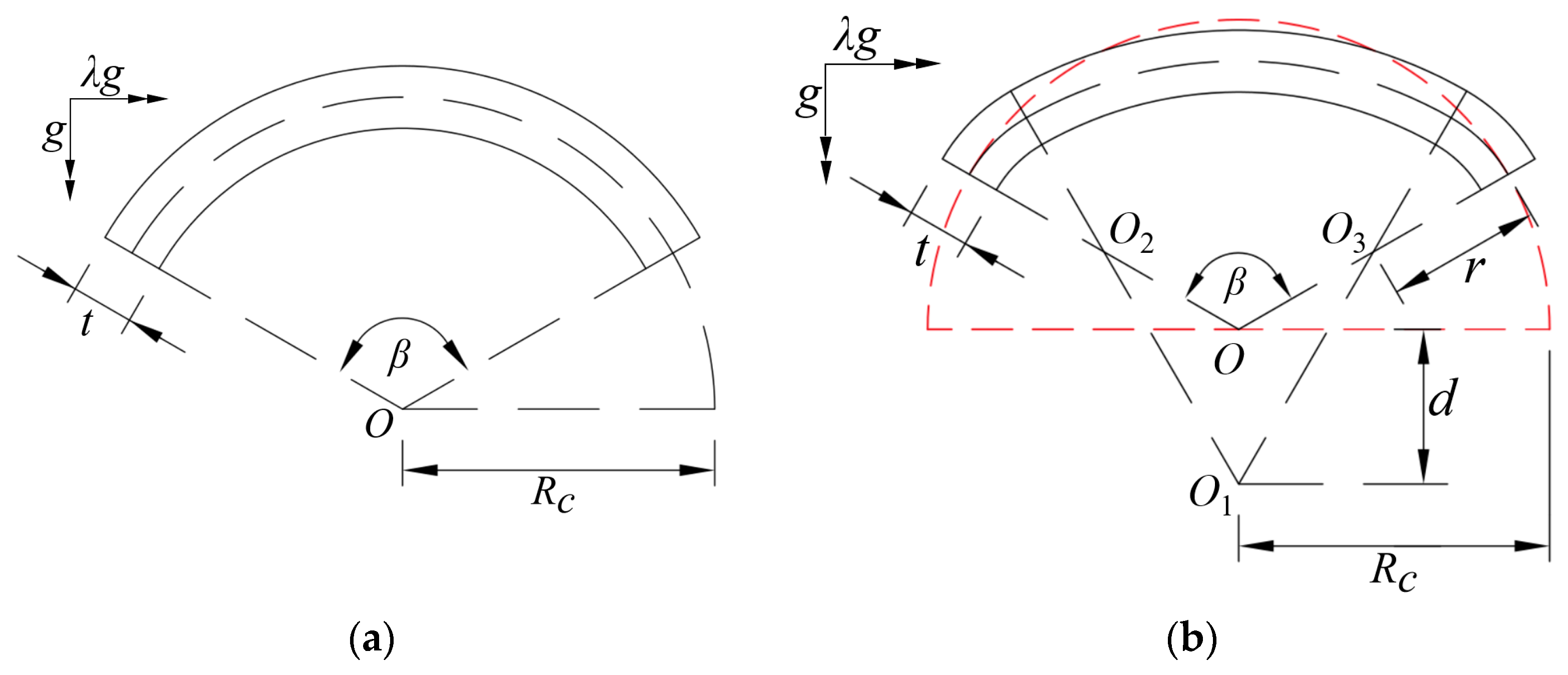
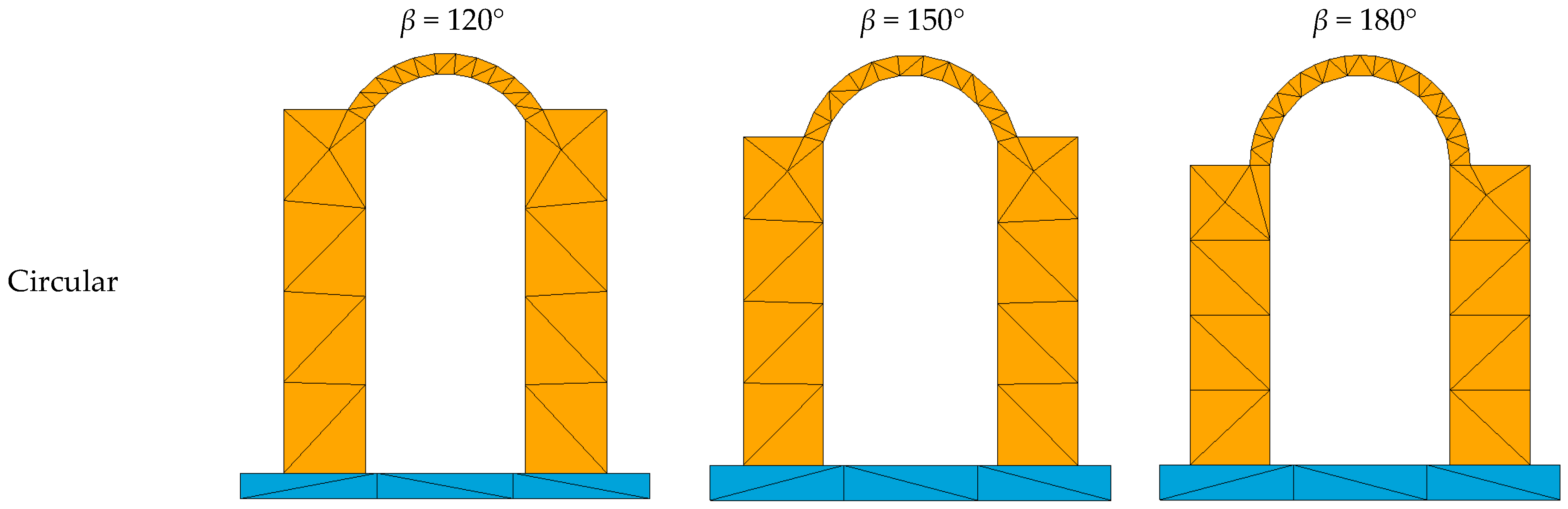
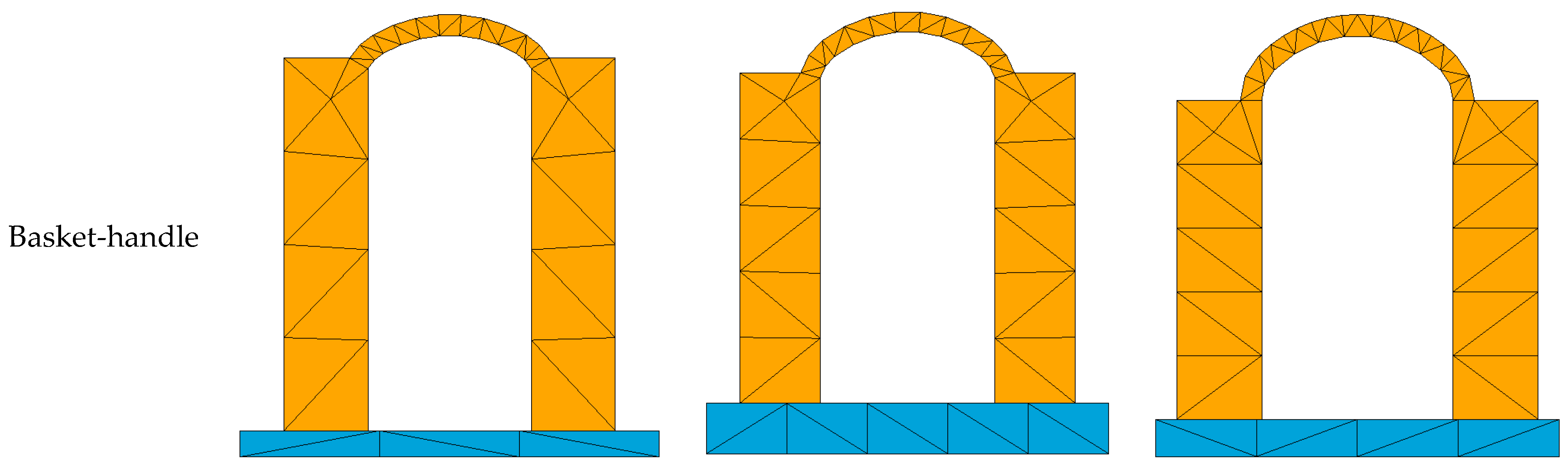
4. Parametric Investigation
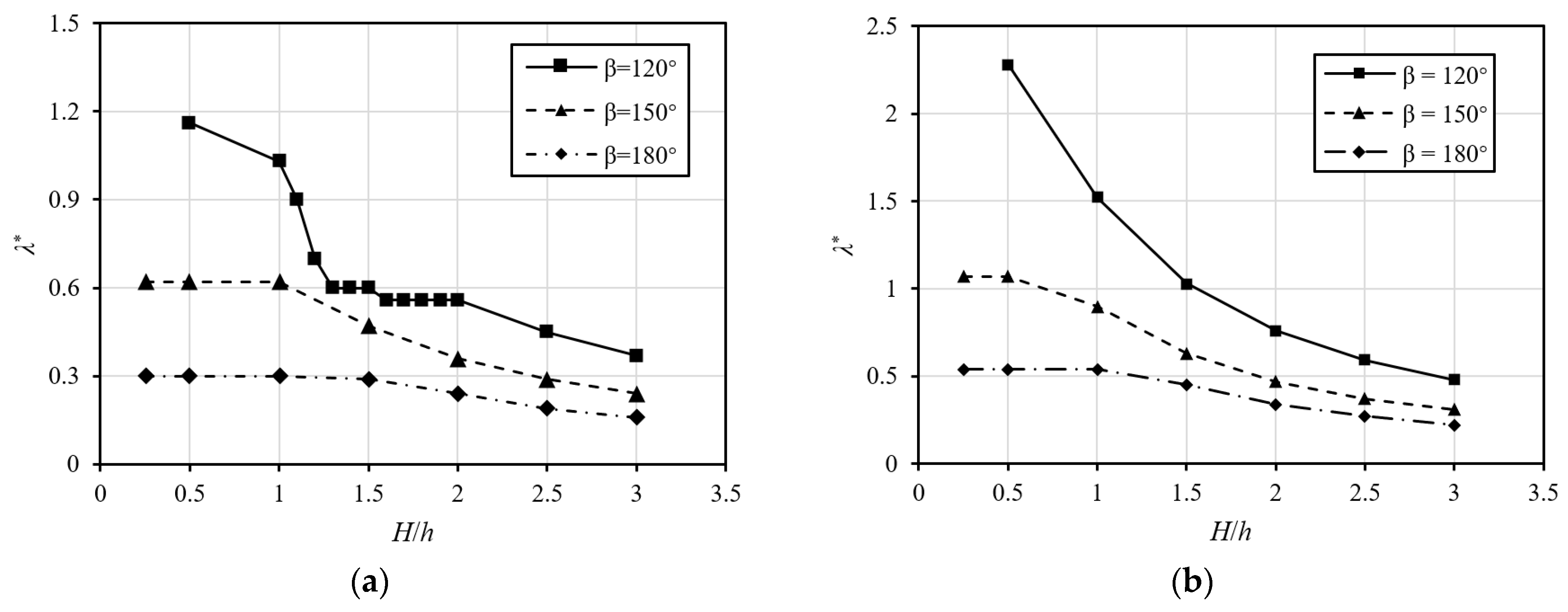
4.1. H/h
4.2. B/Rc
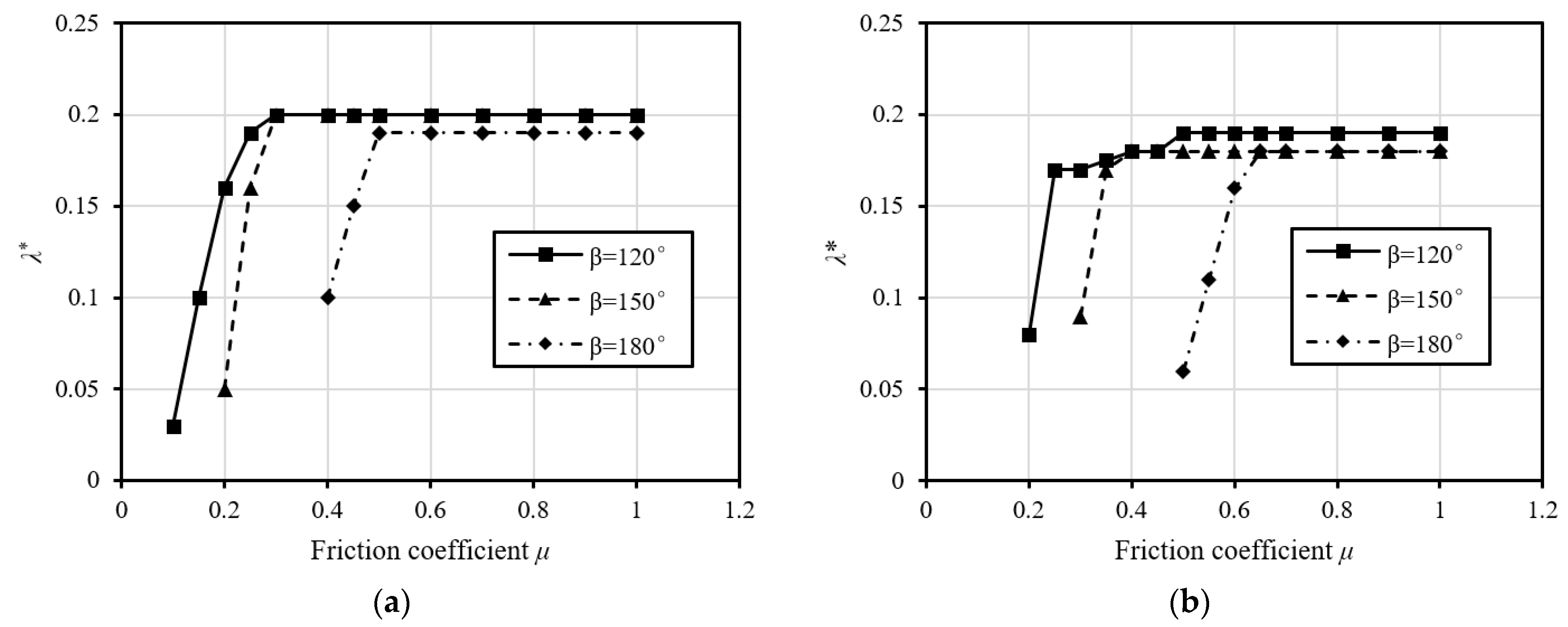
4.3. Friction Coefficient
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Heyman, J. The stone skeleton. Int. J. Solids Struct. 1966, 2, 249–279. [Google Scholar] [CrossRef]
- Oppenheim, I.J. The masonry arch as a four-link mechanism under base motion. Earthq. Eng. Struct. Dyn. 1992, 21, 1005–1017. [Google Scholar] [CrossRef]
- Clemente, P. Introduction to dynamics of stone arches. Earthq. Eng. Struct. Dyn. 1998, 27, 513–522. [Google Scholar] [CrossRef]
- Clemente, P.; Raithel, A. The mechanism model in the seismic check of stone arches. In Arch Bridges; CRC Press: Boca Raton, FL, USA, 2020; pp. 123–129. [Google Scholar] [CrossRef]
- Baratta, A.; Zuccaro, G.; Binetti, A. Strength capacity of a No-Tension portal arch-frame under combined seismic and ash loads. J. Volcanol. Geotherm. Res. 2004, 133, 369–376. [Google Scholar] [CrossRef]
- De Lorenzis, L.; DeJong, M.; Ochsendorf, J. Failure of masonry arches under impulse base motion. Earthq. Eng. Struct. Dyn. 2007, 36, 2119–2136. [Google Scholar] [CrossRef]
- Silva, B.; Benetta, M.D.; da Porto, F.; Modena, C. Experimental assessment of in-plane behaviour of three-leaf stone masonry walls. Constr. Build. Mater. 2014, 53, 149–161. [Google Scholar] [CrossRef]
- Gaetani, A.; Lourenco, P.; Monti, G.; Moroni, M. Shaking table tests and numerical analyses on a scaled dry-joint arch undergoing windowed sine pulses. Bull. Earthq. Eng. 2017, 15, 4939–4961. [Google Scholar] [CrossRef] [Green Version]
- Restrepo-Vélez, L.F.; Magenes, G.; Griffith, M.C. Dry Stone Masonry Walls in Bending—Part I: Static Tests. Int. J. Archit. Herit. 2014, 8, 1–28. [Google Scholar] [CrossRef]
- De Luca, A.; Giordano, A.; Mele, E. A simplified procedure for assessing the seismic capacity of masonry arches. Eng. Struct. 2004, 26, 1915–1929. [Google Scholar] [CrossRef]
- De Santis, S.; de Felice, G. A fibre beam-based approach for the evaluation of the seismic capacity of masonry arches. Earthq. Eng. Struct. Dyn. 2014, 43, 1661–1681. [Google Scholar] [CrossRef]
- Bencardino, F.; Nisticò, M.; Verre, S. Experimental Investigation and Numerical Analysis of Bond Behavior in SRG-Strengthened Masonry Prisms Using UHTSS and Stainless-Steel Fibers. Fibers 2020, 8, 8. [Google Scholar] [CrossRef] [Green Version]
- Giordano, A.; Mele, E.; De Luca, A. Modelling of historical masonry structures: Comparison of different approaches through a case study. Eng. Struct. 2002, 24, 1057–1069. [Google Scholar] [CrossRef]
- Bićanić, N.; Stirling, C.; Pearce, C.J. Discontinuous modelling of masonry bridges. Comput. Mech. 2003, 31, 60–68. [Google Scholar] [CrossRef]
- Tóth, A.R.; Orbán, Z.; Bagi, K. Discrete element analysis of a stone masonry arch. Mech. Res. Commun. 2009, 36, 469–480. [Google Scholar] [CrossRef]
- Dimitri, R.; De Lorenzis, L.; Zavarise, G. Numerical study on the dynamic behavior of masonry columns and arches on buttresses with the discrete element method. Eng. Struct. 2011, 33, 3172–3188. [Google Scholar] [CrossRef]
- Dimitri, R.; Tornabene, F. A parametric investigation of the seismic capacity for masonry arches and portals of different shapes. Eng. Fail. Anal. 2015, 52, 1–34. [Google Scholar] [CrossRef]
- Foti, D.; Vacca, V.; Facchini, I. DEM modeling and experimental analysis of the static behavior of a dry-joints masonry cross vaults. Constr. Build. Mater. 2018, 170, 111–120. [Google Scholar] [CrossRef]
- Drei, A.; Milani, G.; Sincraian, G. DEM numerical approach for masonry aqueducts in seismic zone: Two valuable Portuguese examples. Int. J. Mason. Res. Innov. 2017, 2, 1–29. [Google Scholar] [CrossRef]
- Forgács, T.; Sarhosis, V.; Bagi, K. Minimum thickness of semi-circular skewed masonry arches. Eng. Struct. 2017, 140, 317–336. [Google Scholar] [CrossRef] [Green Version]
- Pulatsu, B.; Erdogmus, E.; Lourenço, P.B. Comparison of in-plane and out-of-plane failure modes of masonry arch bridges using discontinuum analysis. Eng. Struct. 2018, 178, 24–36. [Google Scholar] [CrossRef]
- Gonen, S.; Pulatsu, B.; Erdogmus, E.; Karaesmen, E.; Karaesmen, E. Quasi-Static Nonlinear Seismic Assessment of a Fourth Century, A.D. Roman Aqueduct in Istanbul, Turkey. Heritage 2021, 4, 25. [Google Scholar] [CrossRef]
- Funari, M.F.; Mehrotra, A.; Lourenço, P.B. A Tool for the Rapid Seismic Assessment of Historic Masonry Structures Based on Limit Analysis Optimisation and Rocking Dynamics. Appl. Sci. 2021, 11, 942. [Google Scholar] [CrossRef]
- Munjiza, A. Discrete Elements in Transient Dynamics of Fractured Media. Ph.D. Thesis, University of Wales, Swansea, UK, 1992. [Google Scholar]
- Munjiza, A.; Andrews, K.R.F. NBS contact detection algorithm for bodies of similar size. Int. J. Numer. Methods Eng. 1998, 43, 131–149. [Google Scholar] [CrossRef]
- Munjiza, A.; Andrews, K.R.F.; White, J.K. Combined single and smeared crack model in combined finite-discrete element analysis. Int. J. Numer. Methods Eng. 1999, 44, 41–57. [Google Scholar] [CrossRef]
- Munjiza, A.; John, N.W.M. Mesh size sensitivity of the combined FEM/DEM fracture and fragmentation algorithms. Eng. Fract. Mech. 2002, 69, 281–295. [Google Scholar] [CrossRef]
- Munjiza, A. The Combined Finite-Discrete Element Method; John Wiley and Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Munjiza, A.A.; Knight, E.E.; Rougier, E. Computational Mechanics of Discontinua; John Wiley and Sons: Hoboken, NJ, USA, 2011. [Google Scholar] [CrossRef]
- Munjiza, A.; Rougier, E.; Knight, E.E. Large Strain Finite Element Method: A Practical Course; John Wiley and Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Chen, X.; Chan, A.H. Modelling impact fracture and fragmentation of laminated glass using the combined finite-discrete element method. Int. J. Impact Eng. 2018, 112, 15–29. [Google Scholar] [CrossRef]
- Chen, X.; Chan, A. Soft impact responses of laminated glass simulated with the combined finite-discrete element method. Eng. Comput. 2018, 35, 1460–1480. [Google Scholar] [CrossRef]
- Munjiza, A.; Lei, Z.; Divic, V.; Peros, B. Fracture and fragmentation of thin shells using the combined finite-discrete element method. Int. J. Numer. Methods Eng. 2013, 95, 478–498. [Google Scholar] [CrossRef]
- Chen, X.; Wang, H. Slope Failure of Noncohesive Media Modelled with the Combined Finite–Discrete Element Method. Appl. Sci. 2019, 9, 579. [Google Scholar] [CrossRef] [Green Version]
- Deng, P.; Liu, Q.; Huang, X.; Bo, Y.; Liu, Q.; Li, W. Sensitivity analysis of fracture energies for the combined finite-discrete element method (FDEM). Eng. Fract. Mech. 2021, 251, 107793. [Google Scholar] [CrossRef]
- Munjiza, A.; Smoljanović, H.; Živaljić, N.; Mihanovic, A.; Divić, V.; Uzelac, I.; Nikolić, Ž.; Balić, I.; Trogrlić, B. Structural applications of the combined finite–discrete element method. Comput. Part. Mech. 2020, 7, 1029–1046. [Google Scholar] [CrossRef]
- Smoljanović, H.; Živaljić, N.; Nikolic, Z. A combined finite-discrete element analysis of dry stone masonry structures. Eng. Struct. 2013, 52, 89–100. [Google Scholar] [CrossRef]
- Smoljanović, H.; Nikolić, Ž.; Živaljić, N. A finite-discrete element model for dry stone masonry structures strengthened with steel clamps and bolts. Eng. Struct. 2015, 90, 117–129. [Google Scholar] [CrossRef]
- Smoljanović, H.; Nikolic, Z.; Živaljić, N. A combined finite–discrete numerical model for analysis of masonry structures. Eng. Fract. Mech. 2015, 136, 1–14. [Google Scholar] [CrossRef]
- Smoljanović, H.; Živaljić, N.; Nikolić, Ž.; Munjiza, A. Numerical analysis of 3D dry-stone masonry structures by combined finite-discrete element method. Int. J. Solids Struct. 2018, 136–137, 150–167. [Google Scholar] [CrossRef]
- Balić, I.; Zivaljic, N.; Smoljanović, H.; Trogrlic, B. Seismic resistance of dry stone arches under in-plane seismic loading. Struct. Eng. Mech. 2016, 58, 243–257. [Google Scholar] [CrossRef]
- Chen, X.; Wang, H.; Chan, A.H.; Agrawal, A.K. Dynamic failure of dry-joint masonry arch structures modelled with the combined finite–discrete element method. Comput. Part. Mech. 2020, 7, 1017–1028. [Google Scholar] [CrossRef]
- Chen, X.; Wang, H.; Chan, A.H.C.; Agrawal, A.K.; Cheng, Y. Collapse simulation of masonry arches induced by spreading supports with the combined finite–discrete element method. Comput. Part. Mech. 2020, 8, 721–735. [Google Scholar] [CrossRef]
- Chen, X.; Wang, X.; Wang, H.; Agrawal, A.K.; Chan, A.H.; Cheng, Y. Simulating the failure of masonry walls subjected to support settlement with the combined finite-discrete element method. J. Build. Eng. 2021, 43, 102558. [Google Scholar] [CrossRef]
- Munjiza, A. Manual for the “y” fem/dem Computer Program. 2000. Available online: https://www.geogroup.utoronto.ca/wp-content/uploads/YManual.pdf (accessed on 10 September 2021).
- Lemos, J.V. Discrete element modeling of masonry structures. Int. J. Archit. Herit. 2007, 1, 190–213. [Google Scholar] [CrossRef]
- Nodargi, N.A.; Bisegna, P. A unifying computational approach for the lower-bound limit analysis of systems of masonry arches and buttresses. Eng. Struct. 2020, 221, 110999. [Google Scholar] [CrossRef]
- Alexakis, H.; Makris, N. Hinging Mechanisms of Masonry Single-Nave Barrel Vaults Subjected to Lateral and Gravity Loads. J. Struct. Eng. 2017, 143, 04017026. [Google Scholar] [CrossRef]
- Pulatsu, B.; Erdogmus, E.; Bretas, E.M.; Lourenço, P.B. In-Plane Static Response of Dry-Joint Masonry Arch-Pier Structures. In Proceedings of the AEI 2019: Integrated Building Solutions—The National Agenda AEI 2019 Conference, Tysons, VA, USA, 3–6 April 2019; pp. 240–248. [Google Scholar]


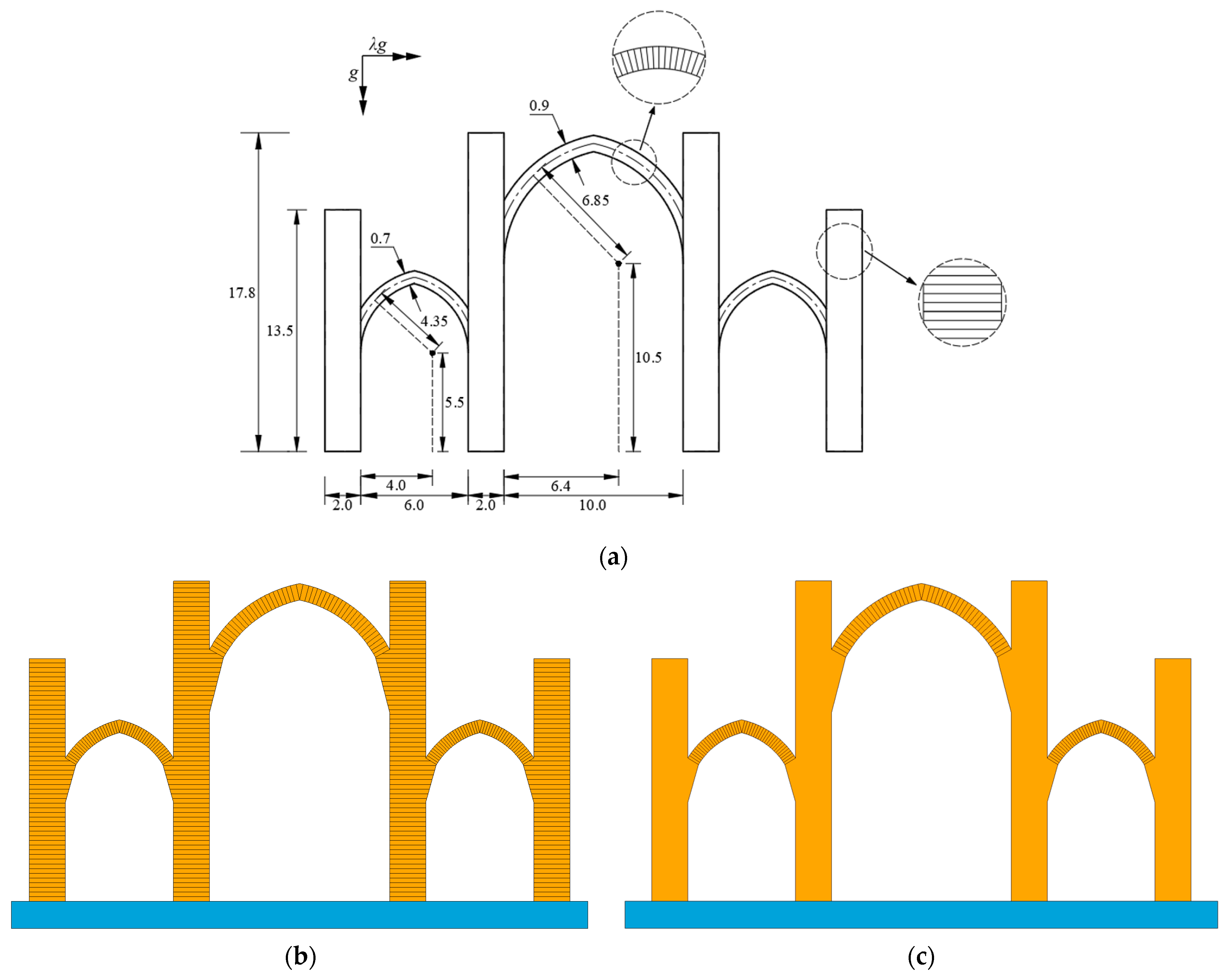


| Young’s Modulus (GPa) | Poisson’s Ratio | Density (kg/m3) |
|---|---|---|
| 40.0 | 0.2 | 2000.0 |
| Embrace Angle β (°) | λ * | |||
|---|---|---|---|---|
| FDEM/e (%) | Limit Analysis [17] | UDEC [17]/e (%) | ||
| Circular | 120 | 1.14/10.2 | 1.27 | 1.28/0.79 |
| 150 | 0.618/0.32 | 0.62 | 0.64/3.23 | |
| 180 | 0.294/1.38 | 0.29 | 0.31/6.90 | |
| Basket-handle | 120 | 2.10/10.6 | 2.35 | 2.38/1.28 |
| 150 | 1.067/0.66 | 1.06 | 1.10/3.77 | |
| 180 | 0.539/0.19 | 0.54 | 0.56/3.70 | |
| Embrace Angle β (°) | λ * | |||
|---|---|---|---|---|
| FDEM/e (%) | Limit Analysis [17] | UDEC [17]/e (%) | ||
| Circular | 120 | 0.166/3.75 | 0.16 | 0.17/6.25 |
| 150 | 0.178/1.11 | 0.18 | 0.18/0.00 | |
| 180 | 0.188/1.05 | 0.19 | 0.21/10.53 | |
| Basket-handle | 120 | 0.150/7.14 | 0.14 | 0.15/7.14 |
| 150 | 0.160/6.67 | 0.15 | 0.16/6.67 | |
| 180 | 0.174/8.75 | 0.16 | 0.17/6.25 | |
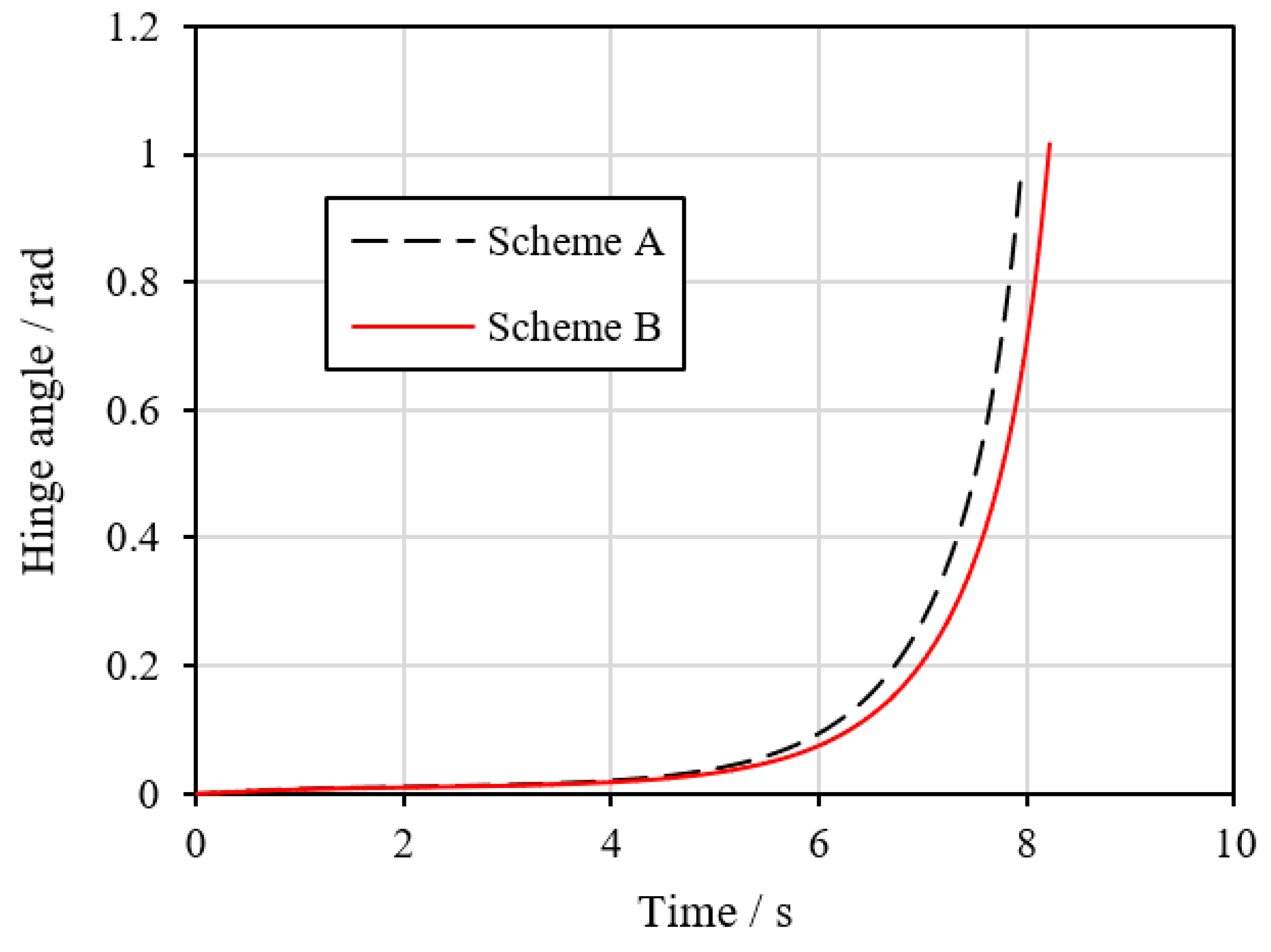
| FDEM | Limit Analysis [47] | ||
|---|---|---|---|
| Scheme A | Scheme B | ||
| λ*/e (%) | 0.0883/0.1 | 0.0883/0.1 | 0.0882 |
| Embrace Angle β | B/Rc | |
|---|---|---|
| Circular | 120° | 0.38 |
| 150° | 0.37 | |
| 180° | 0.37 | |
| Basket-handle | 120° | 0.43 |
| 150° | 0.43 | |
| 180° | 0.43 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Chen, X.; Wang, H.; Chan, A.H.C.; Cheng, Y. Evaluating the Seismic Capacity of Dry-Joint Masonry Arch Structures via the Combined Finite-Discrete Element Method. Appl. Sci. 2021, 11, 8725. https://doi.org/10.3390/app11188725
Li W, Chen X, Wang H, Chan AHC, Cheng Y. Evaluating the Seismic Capacity of Dry-Joint Masonry Arch Structures via the Combined Finite-Discrete Element Method. Applied Sciences. 2021; 11(18):8725. https://doi.org/10.3390/app11188725
Chicago/Turabian StyleLi, Wangpeng, Xudong Chen, Hongfan Wang, Andrew H. C. Chan, and Yingyao Cheng. 2021. "Evaluating the Seismic Capacity of Dry-Joint Masonry Arch Structures via the Combined Finite-Discrete Element Method" Applied Sciences 11, no. 18: 8725. https://doi.org/10.3390/app11188725
APA StyleLi, W., Chen, X., Wang, H., Chan, A. H. C., & Cheng, Y. (2021). Evaluating the Seismic Capacity of Dry-Joint Masonry Arch Structures via the Combined Finite-Discrete Element Method. Applied Sciences, 11(18), 8725. https://doi.org/10.3390/app11188725






