1. Introduction
Cycloid-pin drives have the advantages of high transmission ratios, transmission accuracy, torsional stiffness, transmission efficiency, and compact structures. Cycloid-pin drives have been widely used in high-precision equipment, such as industrial robots, machine tools, and assembly and conveying equipment. This type of equipment usually requires frequent forward and reverse rotation during work and has high position accuracy requirements, which mainly depend on the transmission error (TE) and backlash of cycloid-pin drives. Establishing a calculation method for the TE and backlash, while comprehensively considering the effects of profile modifications (PMs), manufacturing errors (MEs), and assembly errors (AEs), is of great significance for optimizing the tooth profile design of a cycloid gear and the tolerance allocation during the installation of a gear pair. It can also provide the error excitation data for the accurate dynamic analysis of cycloid drives.
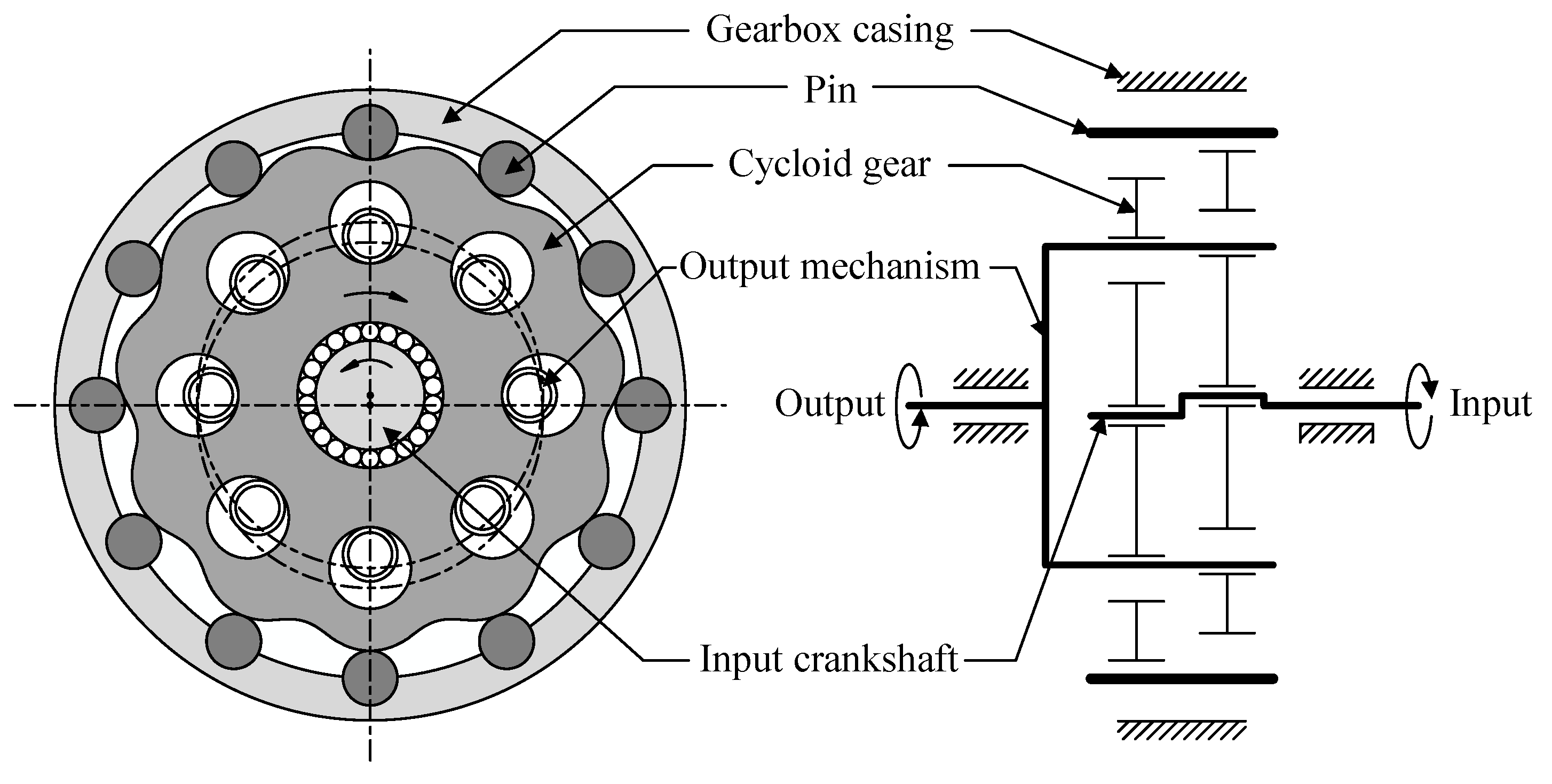
The cycloid-pin gear reducer was initially introduced by Botsiber and Kingston [
1] and Pollitt [
2]. Then a series of novel cycloidal reducers was presented to obtain higher rigidity [
3,
4,
5] or more compact structure [
6,
7,
8]. A typical structure of cycloid-pin gear reducer is shown in
Figure 1, which includes a gearbox casing, an input crankshaft, an output mechanism, two cycloid gears, and pins. During the transmission process, the cycloid gear not only rotates counterclockwise with the input crankshaft around the center of the pin center circle, but it also rotates clockwise around its own center to drive the output mechanism to rotate. For each cycloid gear, ideally, all the pins are in contact with it during the transmission process, and half of the pins transmit the load. Due to the multi-tooth meshing characteristics of cycloid-pin drives, these drives are more sensitive to MEs and AEs, and the tooth interference can easily occur in the transmission process. However, MEs and AEs are inevitable in practice, and these errors will change the number of contact teeth, the load distribution between teeth, the torsional stiffness, and other meshing characteristics, thereby adversely affecting the TE and backlash of cycloid-pin drives. In the published works, Blanche and Yang [
9,
10] first studied the influence of manufacturing tolerances on torque ripples and backlash, but only the profile tolerance was considered in their analysis model. Lin et al. [
11] investigated the influence of the manufacturing tolerance on the TE of a cycloidal gear reducer, and more types of manufacturing tolerance were considered in their analysis model, such as the pin radius error, pin position error, tooth profile error, and pitch error in the tooth profile. Li et al. [
12] also studied the effects of tooth profile and pitch errors on the TE and backlash of a cycloidal-pin gear, achieving the effective pre-control of the tooth profile and the meshing contact performance. Li et al. [
13] investigated the influence of the clearance and eccentricity errors on the gear ratio, transmission error, bearing load, and contact stress of a cycloid reducer. Han and Guo [
14] analyzed the global sensitivity of the transmission accuracy for cycloid-pin drives with the Sobol method in comprehensive consideration of the nonlinear and uncertainty factors, such as the MEs, AEs, and bearing clearances. Ivanović et al. [
15] studied the effects of the profile geometrical parameters of a trochoidal gear on the gearing process, clearance height change, and pulsation of a drive moment. Hidaka et al. [
16,
17] analyzed the TE of K-H-V-type planetary gears with cycloid gears based on a two-dimensional model with twenty degrees of freedom. Meng et al. [
18] analyzed the effects of the kinematics parameters on the transmission performance of a 2K-H pin-cycloid planetary mechanism based on a static analysis of the actual meshing transmission process between the gear pairs considering friction. In the above studies, the analysis models of the TE and backlash were mostly established in a two-dimensional plane, and the MEs that were considered were mostly along the tooth profile direction, while the MEs along the tooth-width direction were rarely involved. Additionally, the studies of the effects of the AEs on the TE and backlash were incomplete. Only the influence of the eccentricity errors was analyzed, while the effects of misalignment deviations were not considered.
To avoid the tooth interference caused by MEs and AEs and obtain better lubrication conditions, profile modifications (PMs) are necessary for cycloid-pin drives. This also has a non-negligible effect on the TE and backlash of cycloid-pin drives. Sun et al. [
5] proposed a compound modification method combining negative isometric and negative offset modification to reduce the influence of PMs on backlash. Li et al. [
19] proposed a novel method for PMs to improve the motion accuracy and modification quality that comprehensively considered the effects of the backlash, pressure angle distribution, and tooth tip and root clearance. In addition, many scholars have studied the torsional stiffness, transmission efficiency, load analysis, and optimization design methods of cycloid-pin drives. In terms of torsional stiffness, Kumar et al. [
20] proposed a new method for estimating the elastic torsional compliance of single-stage cycloidal drives based on static experimental results. Li et al. [
21] proposed a new method to calculate the mesh stiffness of a cycloid-pin gear pair considering the effects of PMs and the eccentricity error based on the unloaded tooth contact analysis and the nonlinear Hertzian contact theory. Liu et al. [
22] calculated the torsional stiffness of a cycloid gear using the Majumdar–Bhushan contact model and the finite element method. In terms of transmission efficiency, Garlo et al. [
23] proposed a simplified procedure to calculate the force distribution on cycloid drive elements, the power losses, and the theoretical mechanical efficiency. Mackic et al. [
24] analyzed the effects of design parameters on the efficiency of a cycloidal gear drive, such as the pitch radius and number of housing rollers. Sensinger [
25] derived the efficiency equations for cycloid drives using Del Castillo’s framework. In terms of load analysis, Malhotra and Parameswaran [
26] investigated the influence of the design parameters of a cycloid speed reducer on forces and contact stress. Xu et al. [
27] proposed a method for analyzing the contact dynamics of the multi-tooth meshing in a cycloid-pin drive considering the effect of the turning-arm cylindrical roller bearing. In terms of the optimization design methods of cycloid-pin drives, Wang et al. [
28] proposed an optimization design method for cycloid drives with the goal of maximizing efficiency and minimizing volume based on a genetic algorithm. Wang et al. [
29] proposed a multi-objective optimal model for cycloid-pin drives in which the objective functions were used for the bending stress of the pins, the force of the crank bearing, and the reducer volume. With the development of computing technology in recent years, the finite element method has been widely used in the research of cycloid-pin drives. For example, Li [
30] carried out loaded gear contact analysis and strength calculations for trochoidal gear reducers based on a mechanics model and a finite element method. Tran et al. [
31] studied the lost motion of a cycloid reducer using a combined finite element and kinematic analysis and concluded that the backlash of a cycloid reducer was not only related to the torsional stiffness but also to the tolerance. However, the multi-tooth meshing characteristics of cycloid-pin drives often lead to a huge finite element model, low computational efficiency, and expensive computational costs.
Cycloid-pin gear pairs are the key components of the cycloid-pin drives. To accurately calculate the TE and backlash of a cycloid-pin gear pair, a novel calculation method based on error tooth surfaces is presented that has the ability to consider the influence of some abnormal meshing phenomena caused by PMs, MEs, and AEs on the TE and backlash, such as the instantaneous mesh-apart of tooth pairs and the eccentric load on the tooth surface. In this paper, the first section reviews the research on the TE, backlash, and other meshing characteristics of cycloid-pin drives. An error tooth surface model of a cycloid gear and pin considering the PMs, MEs, and AEs is established in
Section 2.
Section 3 describes in detail the principle of the novel calculation method of TE and backlash. The presented method is verified by comparing the results with the theoretical analysis results and the literature, as delineated in
Section 4.
Section 5 describes the investigation of the effects of the PMs, MEs, and AEs on the TE and backlash of the cycloid-pin gear pair through a series of simulation cases, and the analysis of the abnormal meshing phenomena caused by these errors in the transmission process.
Section 6 presents the conclusions of this study, and the significance of the proposed method is summarized.
2. Error Tooth Surface Model of Cycloid Gear and Pin
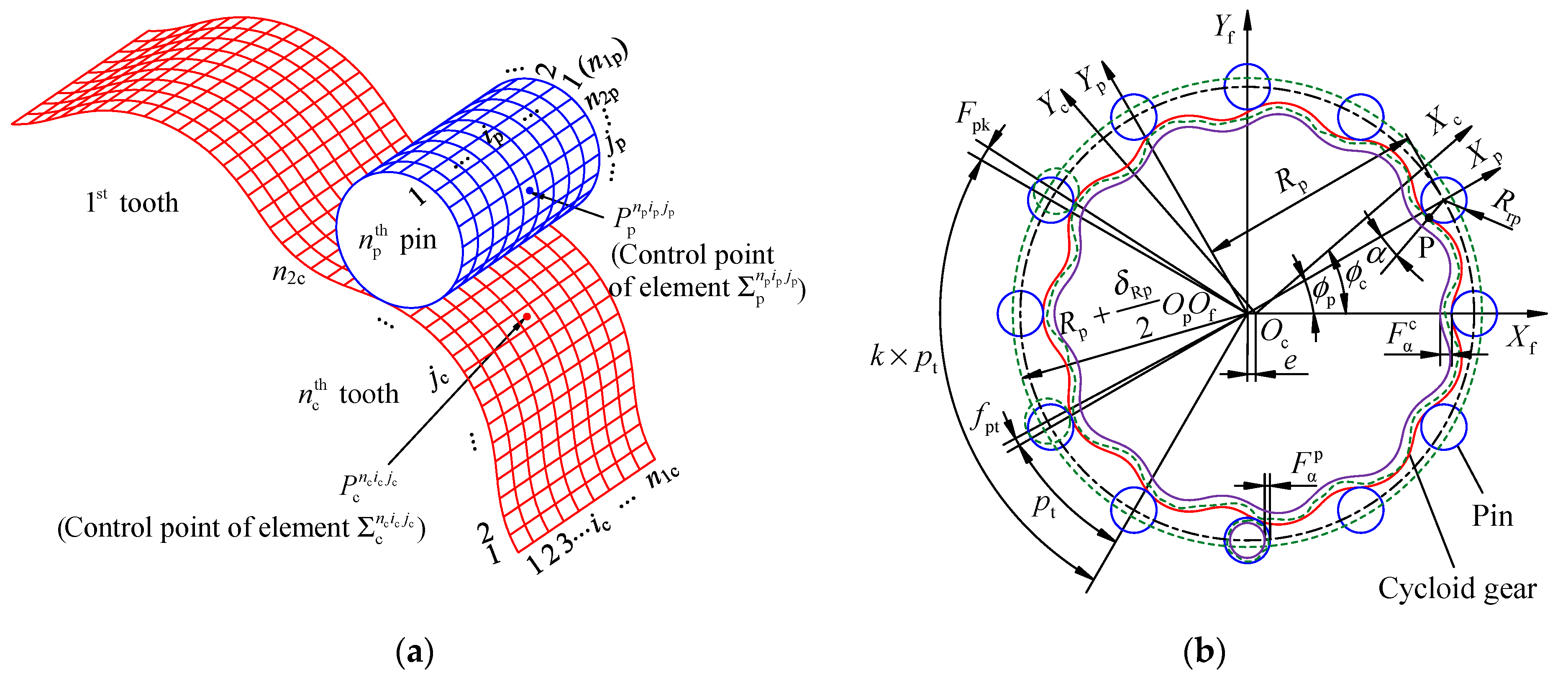
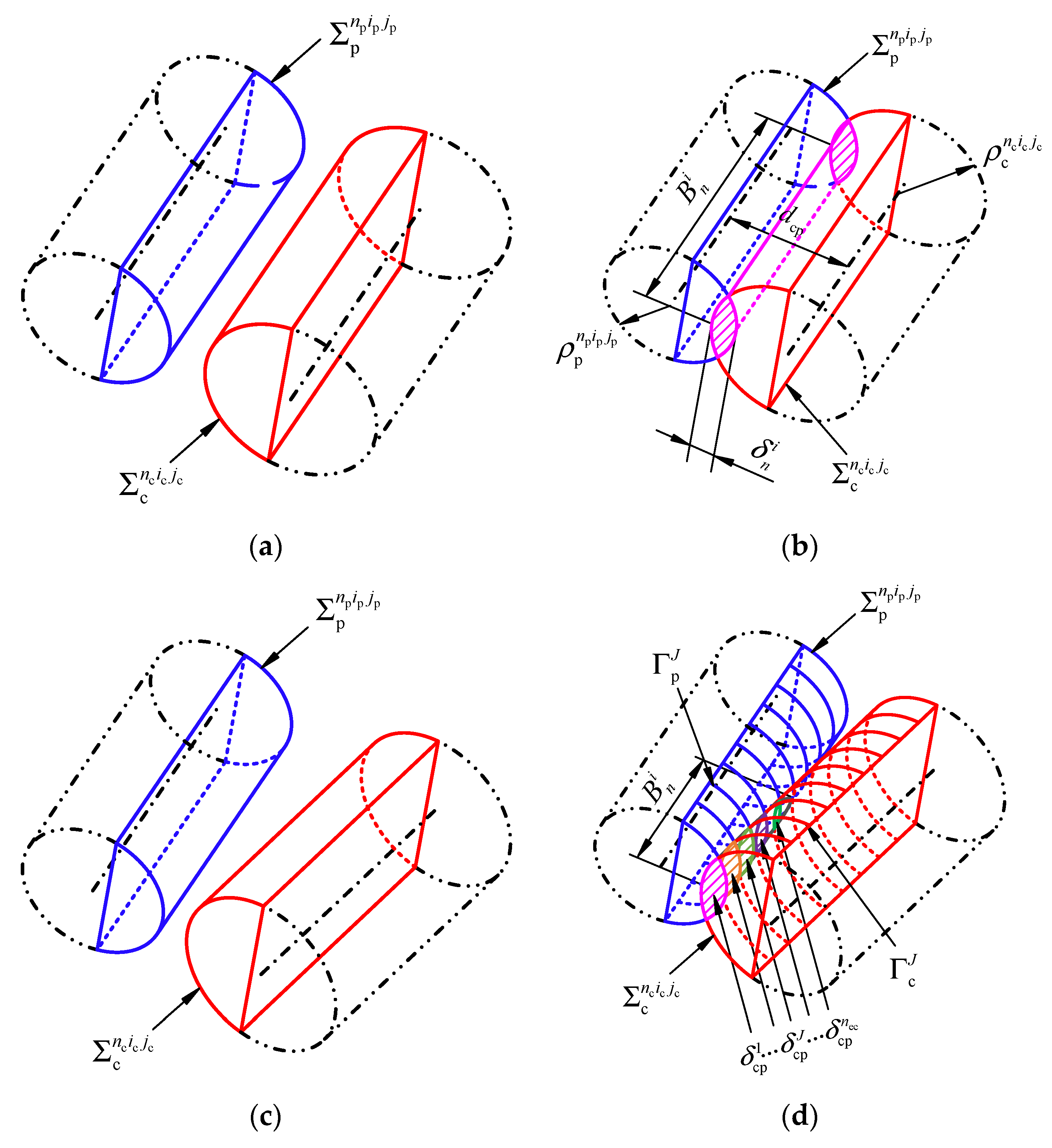
A reasonable tooth surface model comprehensively considering PMs, MEs, and AEs is the key to accurately calculating the TE and backlash of a cycloid-pin gear pair. In this study, the tooth surfaces of a cycloid gear and pin are discretized into multiple elements with the same size, as shown in
Figure 2a. The surfaces of the
cycloid tooth and the
pin are discretized into
n1c and
n1p elements along the tooth width, and into
n2c and
n2p elements along the tooth profile.
ic and
ip are the indices of the discrete elements along the tooth width, and
jc and
jp are the indices of the discrete elements along the tooth profile. Each discrete element on the tooth surface is approximately represented as a cylindrical surface within a certain coordinate range and each discrete element has a corresponding control point defined at the center of the element. The radius of the equivalent cylindrical surface is equal to the radius of curvature at the element control point, and its axis is parallel to the axis of the cycloid gear and pin. Once the coordinates, radius of curvature, and normal vector at the element control point and the axis direction vector of the approximate cylinder corresponding to the discrete element are determined, the equivalent cylindrical surface is unique.
The coordinate systems for generating the tooth surfaces of a cycloid gear and pin with PMs and MEs are shown in
Figure 2b. The coordinate systems
XfOfYf,
XcOcYc, and
XpOpYp are rigidly connected to the frame, cycloid gear, and pin, respectively.
Rrp and
Rp are the radii of the pin and the pin center circle, respectively.
e is the eccentric distance between
Oc and
Of. The rotation angles of
XcOcYc and
XpOpYp are defined as
ϕc and
ϕp, respectively, and they have the relationship
ϕc/
ϕp =
zp/
zc, where
zp and
zc represent the number of pins and the teeth of cycloid gear, respectively.
α is the angle parameter at the contact point P. The red and blue solid lines are the theoretical tooth profile of the cycloid gear and pin, respectively. Based on the previous publication [
5], the PMs of a cycloid gear can be divided into four types, namely, isometric modification, offset modification, angle rotation modification, and compound modification. Since the angle rotation modification cannot produce a gap between the tooth tip and root of a cycloid gear and the pins, it cannot be used alone, and is not considered in this study. The tooth surface of a cycloid gear with the isometric modification and the offset modification can be obtained by changing
Rrp and
Rp, and the tooth surface with the compound modification can be obtained by changing them at the same time. Thus, the coordinates of the element control point of a cycloid gear considering PMs are given as follows:
where the superscripts
nc,
ic, and
jc indicate the
ic ×
jc element on the
tooth of cycloid gear, and the subscript c1 represents the tooth surface of a cycloid gear with PMs, and
Bc is the tooth width of a cycloid gear, and Δ
Rrp and Δ
Rp are the modification amounts of the isometric modification and the offset modification, respectively.
α can be calculated with:
It is worth noting that the arc length of the cycloid tooth profile is a nonlinear function of
ϕp. If the tooth surface of the cycloid gear is discrete with the same
ϕp in the tooth profile direction, the arc lengths between the adjacent element control points along the tooth profile are not equal, and the element control points are concentrated on the convex tooth surface. To improve the calculation accuracy of the TE and backlash, the tooth surface of the cycloid gear along the tooth profile direction is discrete with the same arc length. The arc length corresponding to different
ϕp can be obtained with numerical integration. Then
ϕp is fitted as a polynomial function of the arc length. It is assumed that
N is the order of the polynomial function, and
AN,
AN−1, ⋯,
A1,
A0 are the coefficients of the polynomial function. The
in Equation (1) can be calculated with:
where
Sc is the total arc length of a single tooth profile of the cycloid gear.
In
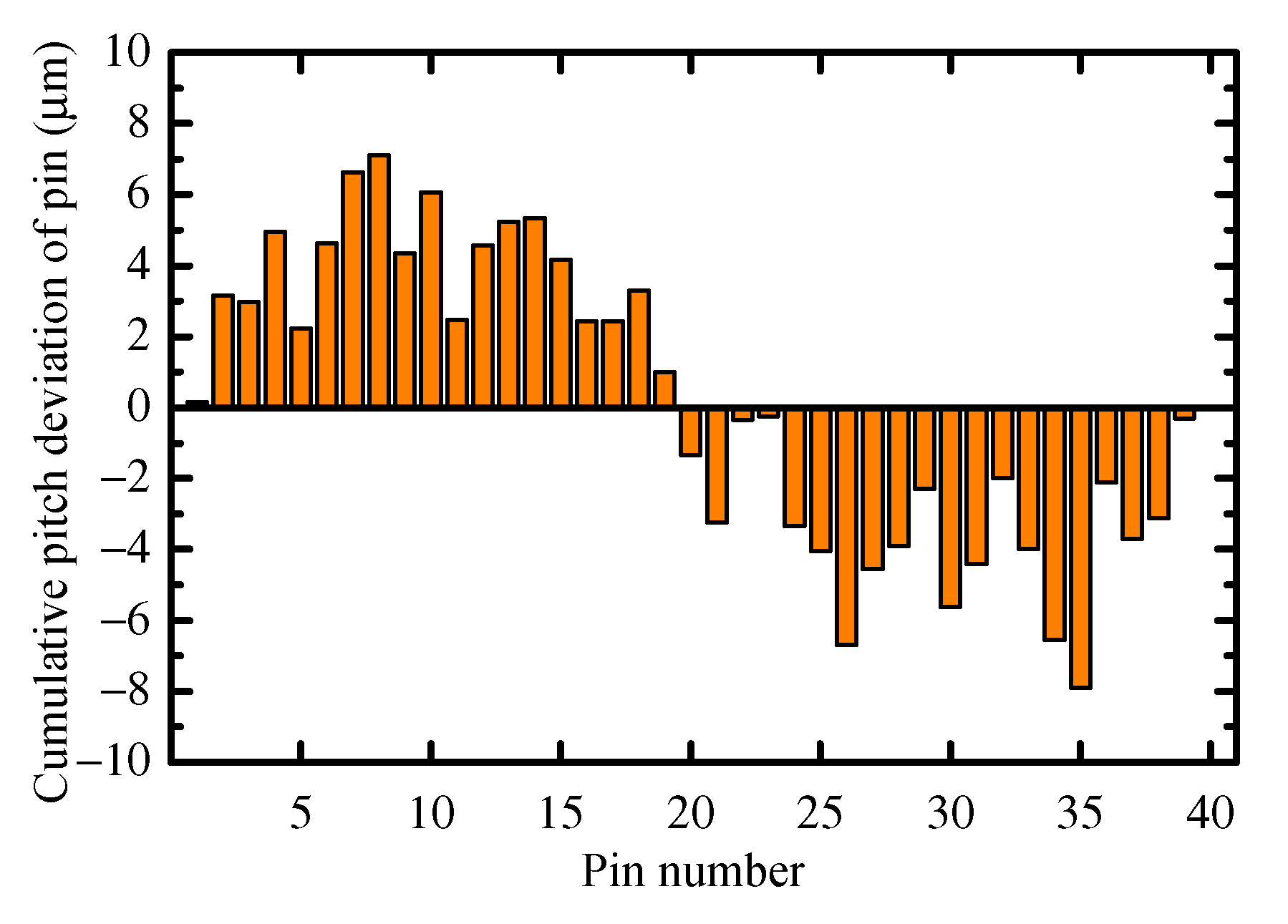
Figure 2b, the green dashed line indicates the error tooth profiles of a cycloid gear and pin with MEs. The MEs of the pin considered in this study include the total profile deviation (
), single pitch deviation (
fpt), total cumulative pitch deviation (
Fp), and pin center circle diameter deviation (
δRp).
pt is the single pitch of a pin. Since the pitch deviations of the cycloid gear and pin have similar effects on the TE and backlash, the pitch deviation of the cycloid gear can be equivalently converted to the pins, and only the total profile deviation of the cycloid gear (
) is considered in this study. The error profile of the cycloid gear is located between the theoretical tooth profile and the virtual tooth profile (see the solid purple line in
Figure 2b) defined by the total profile deviation (
). According to gear conjugate theory and coordinate transformation principle, the coordinates of the element control points of the cycloid gear and pin considering PMs and MEs are given as:
where the subscript c2 in Equation (4) represents the tooth surfaces of a cycloid gear with PMs and MEs, and the superscripts
np,
ip, and
jp indicate the
ip ×
jp element on the
pin, and
and
are the profile deviation of each element of the cycloid gear and pin, respectively.
Bp is the tooth width of a pin, and
is the single pitch deviation of the
zth pin. It is known that the MEs of a gear are distributed according to a probability in their tolerance ranges. Thus,
,
,
, and
δRp can be obtained through different probability distribution functions according to their tolerance ranges. Additionally, the pitch deviation of the pin (
) must also meet the tolerance range of the total cumulative pitch deviation (
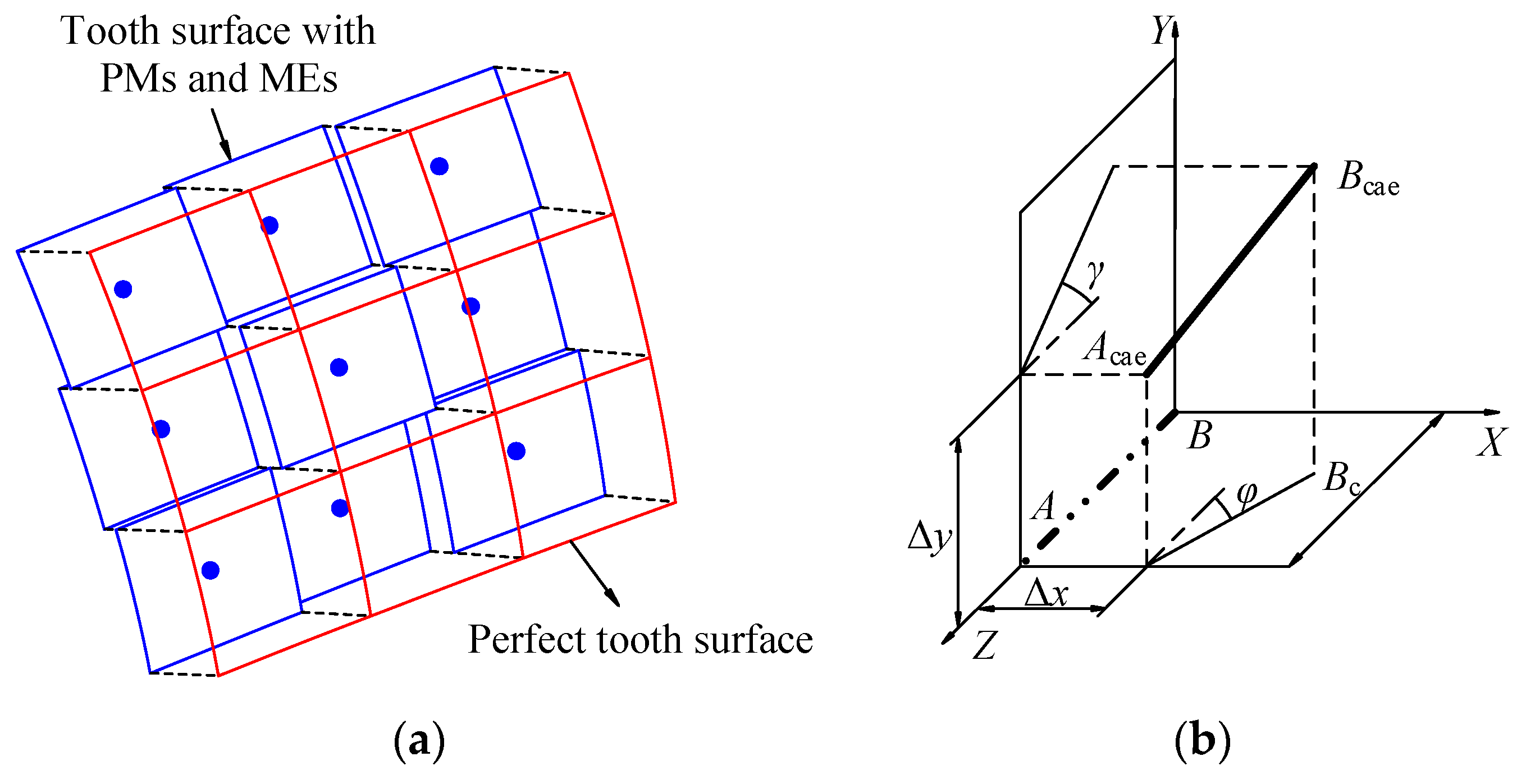
Fp). The part of the tooth surface of cycloid gear considering PMs and MEs is shown in
Figure 3a, and it is composed of multiple discrete elements with different distances from the perfect tooth surface. Similarly, the tooth surface of the pin considering MEs has the same characteristics.
Figure 3b shows the definition of the AEs in this study. The AEs of cycloid gear and pin are equivalently transferred to the axis position of the cycloid gear to simplify the error tooth surface model.
AB is the theoretical axis position of the cycloid gear without AEs, and
AcaeBcae is the new axis position of the cycloid gear when the AEs are considered. The AEs are indicated by four parameters, where Δ
x and Δ
y are called the center distance deviations, and
φ and
γ are the misalignment deviations on the
XBZ-plane and the
YBZ-plane, respectively. The different AEs can be obtained using different combinations of the above four parameters. The coordinates of the element control point
ic ×
jc on the
tooth surface of the cycloid gear considering AEs are given as follows:
where
Mae is the coordinate transformation matrix considering AEs, which is given as follows:
To summarize, the coordinates of each element control point of the cycloid gear and pin considering PMs, MEs, and AEs have been obtained. Additionally, the radius of curvature and the normal vector at each control point, as well as the axis direction vector of the approximate cylinder corresponding to each element are also necessary to uniquely determine the position and size of the equivalent cylindrical surface corresponding to each element. The radii of curvature at each element control point of the cycloid gear and pin are given as follows:
where
can be negative (−) for a concave surface and positive (+) for a convex surface.
The normal vectors at each element control point of the cycloid gear and pin are respectively given as follows:
The axis direction vectors of the approximate cylinder of each element of the cycloid gear and pin are given as follows:
3. Calculation Principle of Transmission Error and Backlash
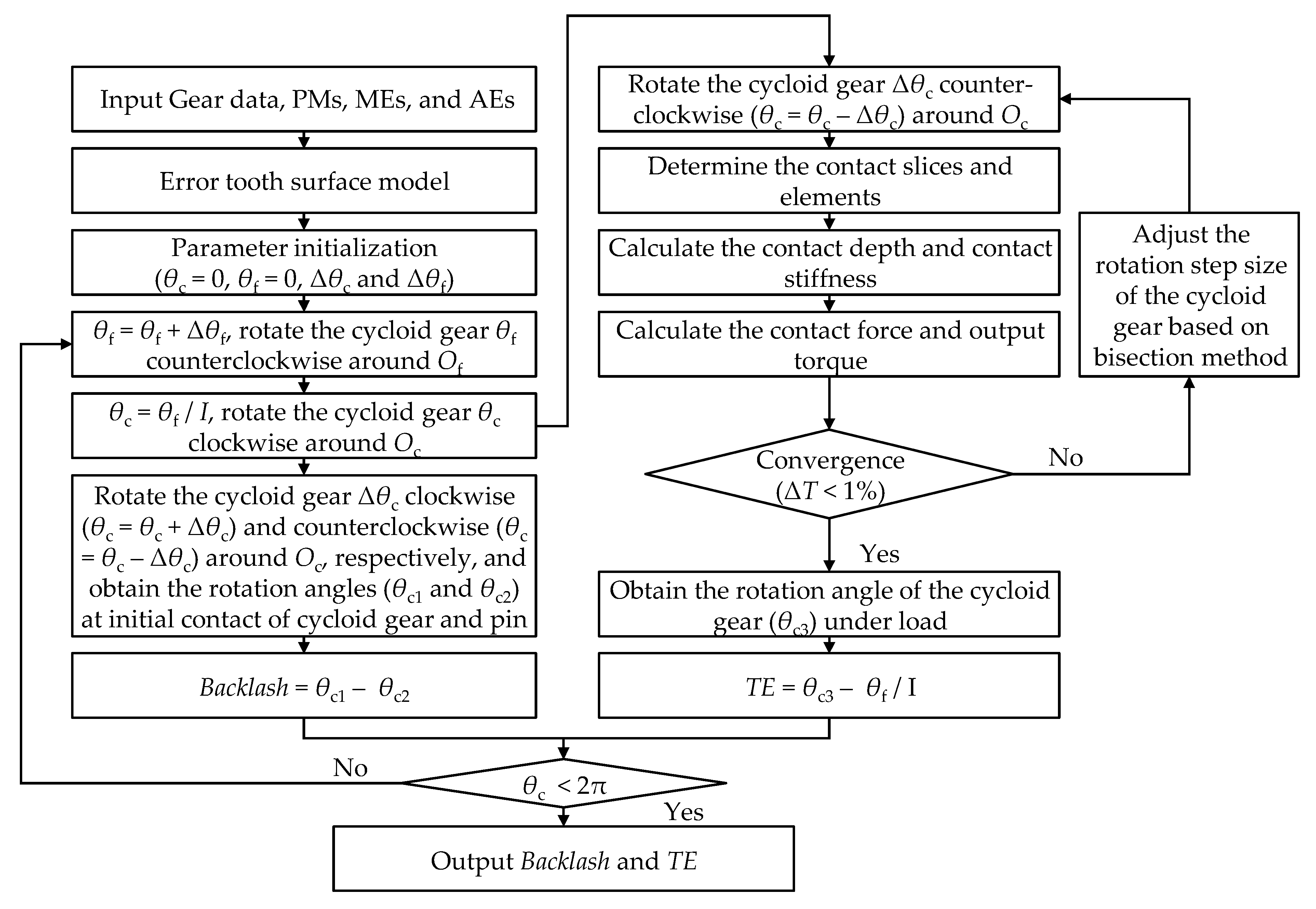
As shown in
Figure 4, the TE and backlash of the cycloid-pin pair are calculated with an iterative process. Firstly, the error tooth surface model proposed in
Section 2 is generated based on the input gear data, PMs, MEs, and AEs.
Figure 5a shows the tooth contact model of the cycloid gear and pin.
XfOfYf is the fixed coordinate system established at the center of the pin center circle (
Of), and the center of the cycloid gear is defined as
Oc. The eccentric distance between
Of and
Oc is
e. It is well known that a cycloid gear not only rotates counterclockwise with the input crankshaft around
Of, but also rotates clockwise around
Oc to drive the output mechanism to rotate. The rotation angles of the cycloid gear around
Of and
Oc are defined as
θf and
θc, respectively, and the rotation step sizes of the cycloid gear around
Of and
Oc are defined as Δ
θf and Δ
θc, respectively. At the first position of the cycloid gear,
θf and
θc are initialized to zero.
To calculate the TE and backlash corresponding to each input angle of the gear pair, the cycloid gear is first rotated
θf (
θf =
θf + Δ
θf) counterclockwise around
Of and
θc (
θc =
θf/
I) clockwise around
Oc with coordinated transformation, when the cycloid gear and the pins are in the theoretical meshing position.
I is the transmission ratio of the cycloid-pin gear pair. The coordinate transformation matrices of the cycloid gear rotating around
Of and
Oc (
Mof and
Moc) are given as follows:
As shown in
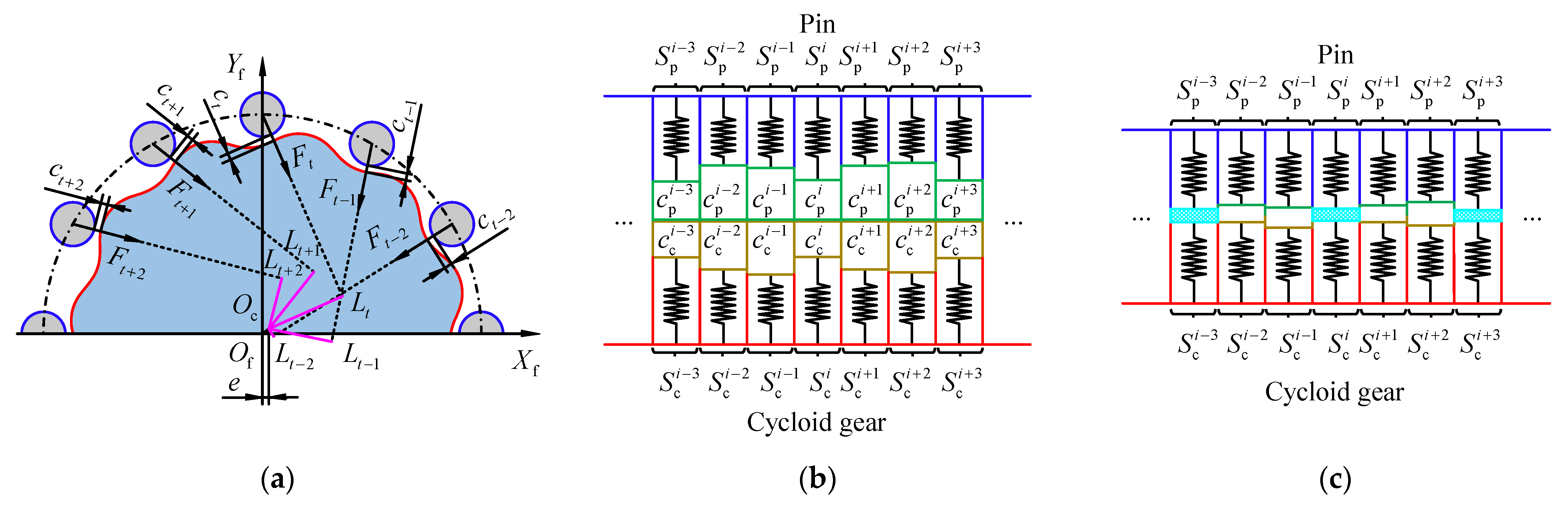
Figure 5a, when the cycloid gear is in the theoretical meshing position, there is a different initial clearance (⋯,
ct−2,
ct−1,
ct,
ct+1,
ct+2, ⋯) between the cycloid gear and each pin due to the influences of the PMs, MEs, and AEs. In published works, the slicing method has been widely used to calculate the mesh stiffness of a helical gear pair [
32,
33,
34,
35,
36]. According to the error tooth surface model proposed in
Section 2, the cycloid gear and pin can also be regarded as composed of
n1c and
n1p slices, respectively, and each slice is composed of
n2c and
n2p elements (see
Figure 2a). Thus, as shown in
Figure 5b, the clearance
ct is the minimum clearance in all slices (⋯,
,
,
, ⋯, and, ⋯,
,
,
, ⋯) along the tooth width direction. Since each group of slices (
and
) is also composed of multiple discrete elements, the clearance (
) between each group of slices is the minimum clearance of all elements on the two slices. Then the cycloid gear is rotated counterclockwise by Δ
θc around
Oc to approach the pin. As the cycloid gear continues to rotate around
Oc, the clearances
are continuously reduced and contact deflection even occurs (see
Figure 5c). In the initial stage of contact between the cycloid gear and pin, the total output torque generated by the gear pair is not enough to balance the external load, and the iterative process is continued until the difference between the total output torque and the external load converge within 1%. To improve the calculation efficiency, the rotation step size (Δ
θc) is adjusted according to the bisection method.
When the total output torque of the gear pair is balanced with the external load, the rotation angle of the cycloid gear around
Oc is defined as
θc3. The TE is given as follows:
In contrast to the TE, the calculation of the backlash does not consider the influence of the tooth deflection under a load. When the cycloid gear is rotated to the theoretical meshing position, the cycloid gear is rotated clockwise and counterclockwise around
Oc, and the rotation angles (
θc1 and
θc2) of the cycloid gear around
Oc at the initial contact in the two directions are obtained. The backlash is given as follows:
According to the above detailed description of the calculation process of the TE and backlash, the determination of the contact between the cycloid gear and pin and the calculation of the output torque generated by the cycloid-pin gear pair in the iteration process are the keys to calculating the TE and backlash. According to the principle of the slicing method, it is assumed that each slice along the tooth width is independent and that the load on one slice cannot convey deflections to the neighboring slices [
37]. Additionally, due to the geometry of a cycloid-pin gear pair, the contact deflection is much larger than the tooth bending and shear deflections, and it is regarded as local deflection [
13]. Thus, only the contact deflection between the tooth surfaces is considered in this study, and it is feasible to ignore the influence of the load deflection between the adjacent slices along the tooth width.
As mentioned above, each slice in
Figure 5b is composed of multiple discrete elements, and each discrete element is approximately represented as a cylindrical surface. The position and the size of these cylindrical surfaces have been determined according to the description in
Section 2. Thus, the contact of each group of slices can be converted into the contact of the corresponding equivalent cylindrical surfaces. There are four possible contact status for any two elements on each group of slices. As shown in
Figure 6a,b, when the misalignment deviations (
φ and
γ) are not considered, the axes of the two elements (
and
) are parallel to each other. The contact width is equal to the element width, and the contact depth is equal to the difference between the sum of the radii of curvature and the distance between the centers of curvature corresponding to the two control points. The contact width and depth are given as follows:
where
dcp is the distance between the centers of curvature corresponding to the two control points, which can be obtained based on the coordinates, radius of curvature, and normal vector at the element control point, as well as the axis direction vector of the approximate cylinder described in
Section 2. When the contact depth
is greater than zero, the two elements are in contact. Otherwise, they are not involved in contact.
As shown in
Figure 6c,d, when the misalignment deviations (
φ and
γ) are considered, the axis of cycloid gear is not parallel to the axis of the pin. To calculate the contact depth in these two cases, the two cylindrical surfaces are discretized into
ne arcs. It is assumed that there are
nec pairs of arcs that meet the above contact condition, and the mean of their contact depth is approximated to the contact depth of the two discrete elements. The contact width and depth are given as follows:
where
is the contact depth of the arcs
and
.
The Hertzian contact stiffness of any two elements is given as follows [
13]:
where
Ec and
Ep are the modulus of elasticity, and
υc and
υp are the Poisson’s ratios, where the subscripts c and p represent cycloid gear and pin, respectively.
is the contact width and
is the semi-Hertzian contact width, which can be calculated with:
where
E* and
ρ* are the equivalent elasticity modulus and the equivalent radius of curvature, respectively.
The total output torque generated by the cycloid-pin gear pair is given as follows:
where
zpc is the number of contacted pins and
is the arm of force of the slice
(see
Figure 5a), which is given as follows:
where in the vector
PQ, P is the control point of the contact element
on the slice
. The coordinates of P can be obtained using Equation (6), and Q is the corresponding point of P on the axis of the cycloid gear. The coordinates of Q are given as follows:
Thus, the vector
PQ is given as follows:
4. Validation of Proposed Method
To verify the effectiveness of the proposed calculation method of the TE and backlash, a cycloid-pin gear pair (see
Table 1) is applied to the presented method, and the calculation results are discussed in this section. The number of discrete elements of the cycloid gear (
n1c) and pin (
n1p) along the tooth profile is 800, and the number of discrete elements along the tooth width (
n2c and
n2p) is 100. The rotation step sizes Δ
θf and Δ
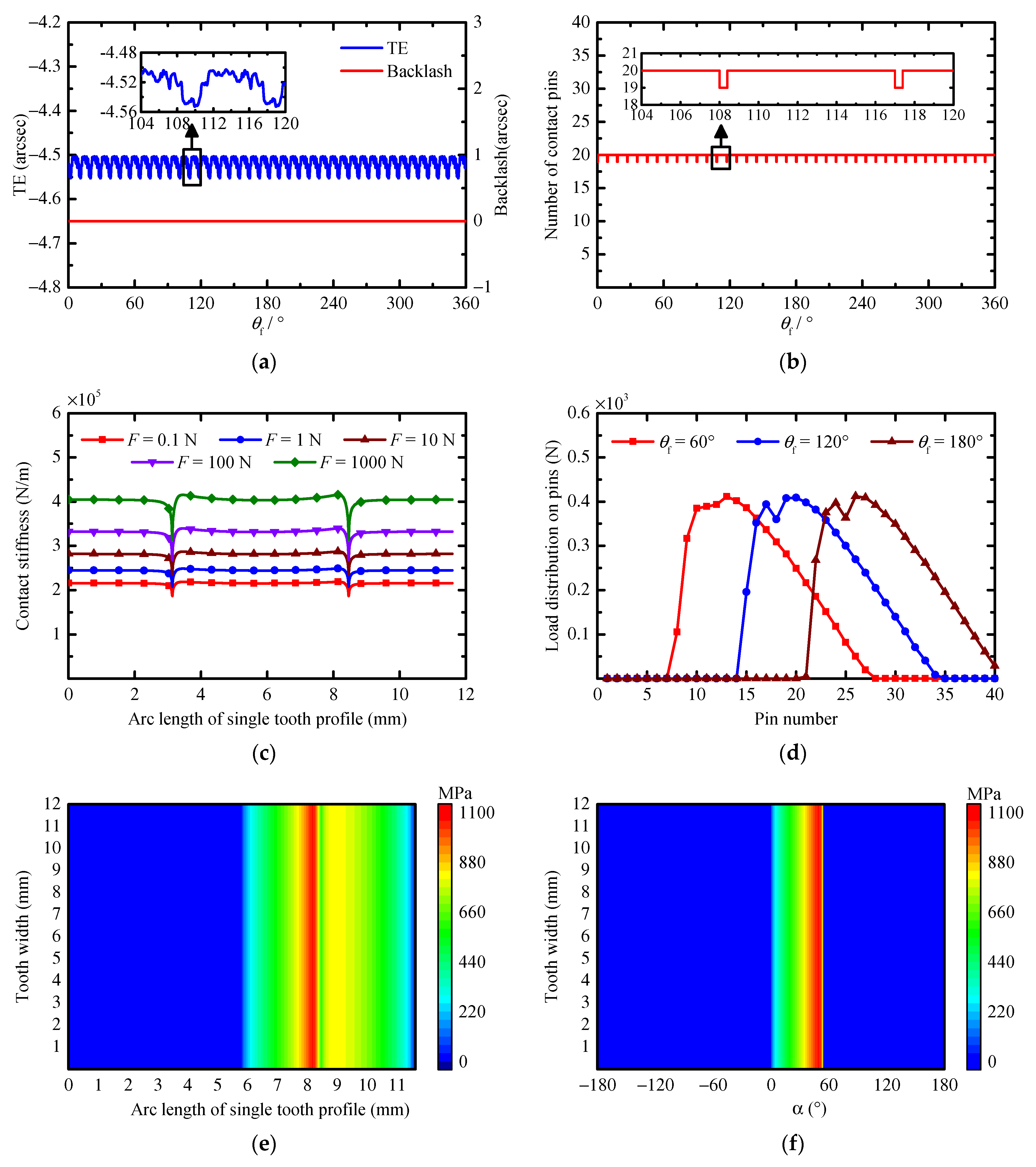
θc are 0.1° and 1/60 arcsec, respectively. When the tooth surfaces of the cycloid gear and pin are perfect surfaces without errors, the calculation results are as shown in
Figure 7. In the rest of paper, the terms “MTE” and “MB” refer to the mean values of the TE and backlash, respectively, the terms “PPTE” and “PPB” refer to the peak-to-peak values of the TE and backlash, respectively, and the term “MCS” refers to the maximum contact stress on the tooth surface.
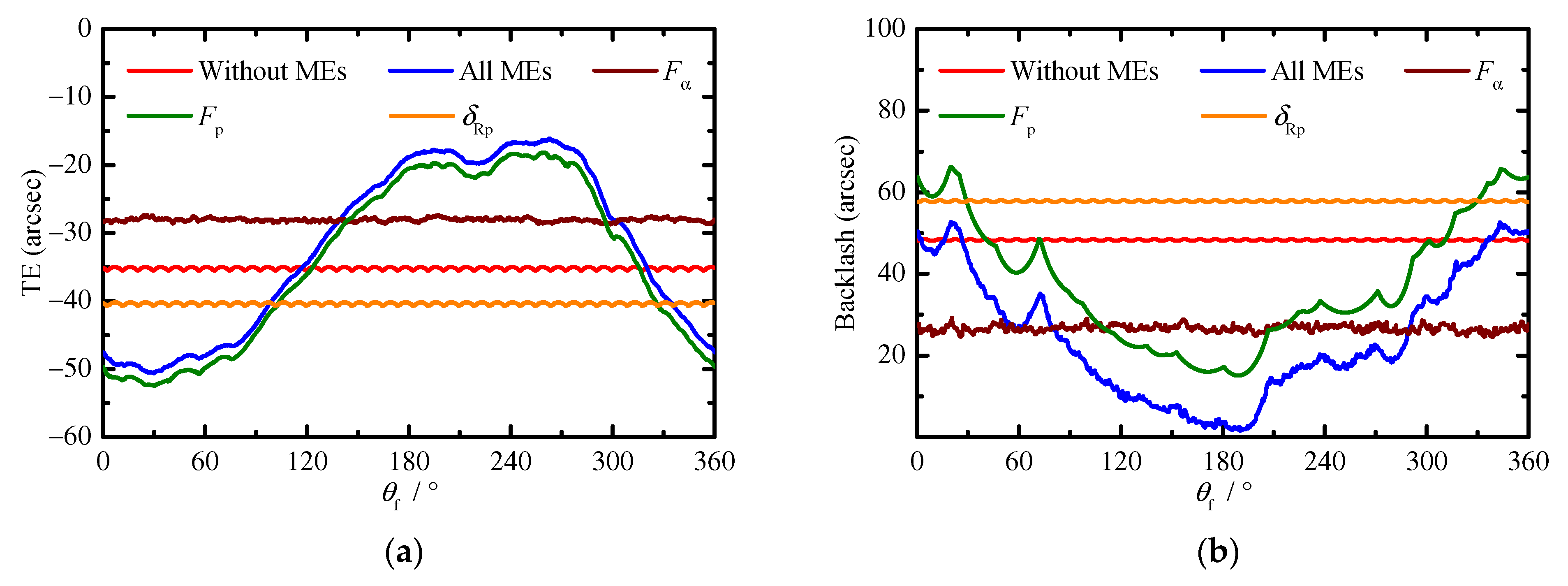
As shown in
Figure 7a, the backlash is always equal to zero during the entire meshing cycle, which is because the influence of the PMs, MEs, AEs, and the tooth deflection under a load are not considered when calculating the backlash. Additionally, according to
Figure 7a,b, it is not difficult to find that both the TE and the number of contact pins change periodically with
θf, and the maximum number and the minimum number of contact pins are 20 and 19, respectively. Theoretically, when the tooth surfaces are perfect, half of the pins are always in contact with the cycloid gear during the entire meshing cycle. However, due to the influence of the tooth deflection under a load, the tooth pair in the critical contact state loses contact.
The MTE and PPTE are −4.5206 arcsec and 0.0531 arcsec, respectively. According to Equation (16), due to the tooth deflection under a load, the actual rotation angle of the cycloid gear around
Oc is greater than its theoretical value, resulting in a negative mean value. Additionally, both the contact stiffness and the load shared on each pin are different at the different positions of
θf, which leads to the different tooth deflection under a load. This is the reason why the TE has small fluctuations between its peaks and troughs. During the transmission of the cycloid-pin gear pair, the position of the contact point on the cycloid tooth surface changes with the rotation of the cycloid gear. However, according to Equations (22) and (23), the contact stiffness has a nonlinear relationship with the radius of curvature of the cycloid gear and the contact force. As shown in
Figure 2a, the tooth surface of the cycloid gear is discrete with the same arc length along the tooth profile, and
Figure 7c shows the relationship between the contact stiffness and the contact force at different arc lengths of the single cycloid tooth profile. This shows that the contact stiffness is different at the same arc length position under different loads. This is because the semi-Hertzian contact width increases with the increase in the load, which increases the contact stiffness. Additionally, the contact stiffness is different at different arc length positions under the same load, especially in the transition region of the concave and convex tooth profiles. This is because the radius of curvature of the cycloid gear varies greatly in the transition region, because the radius of curvature at the transition point is theoretically infinite.
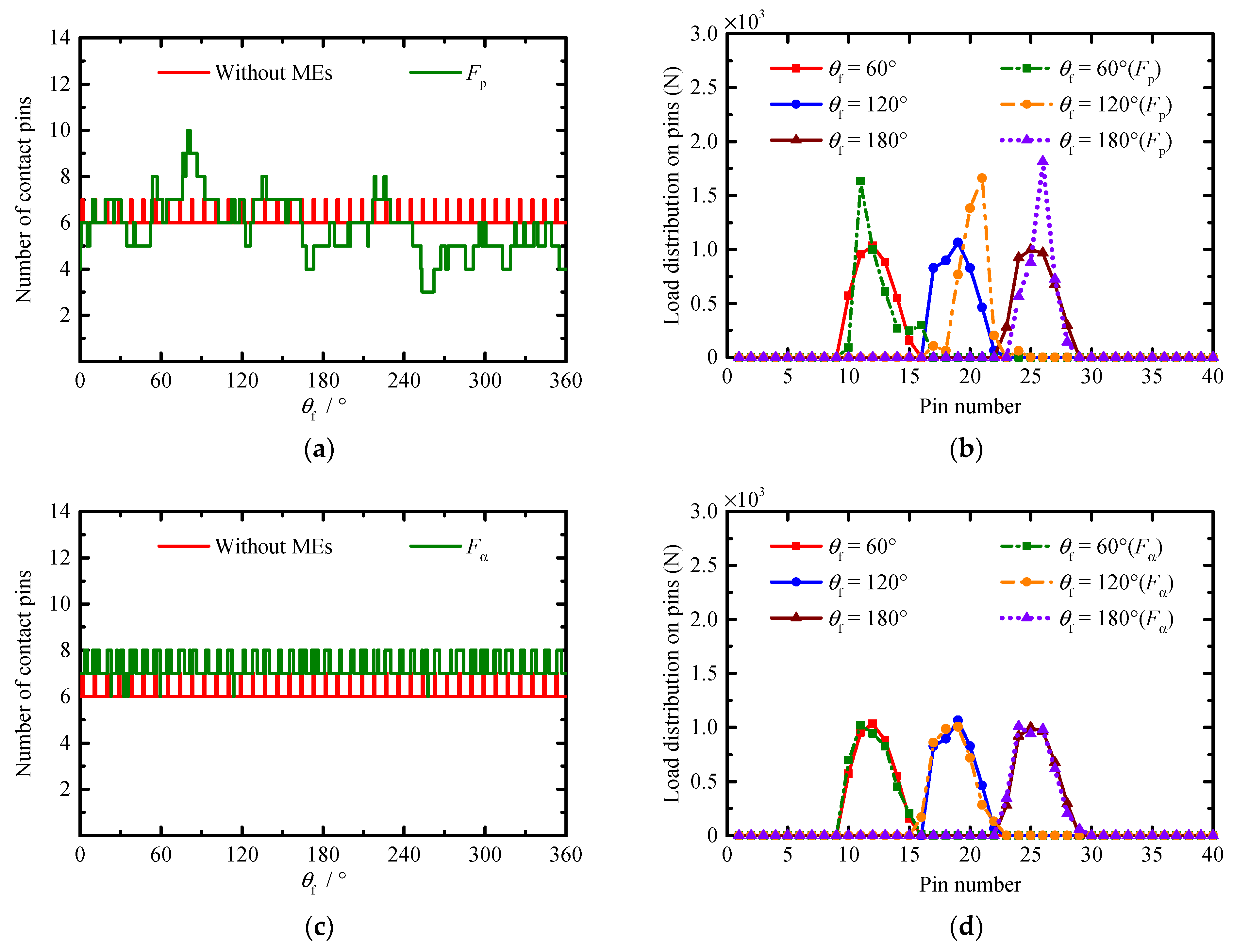
Figure 7d shows the load distribution on the pins when
θf = 60°, 120°, and 180°. The load distribution on the pins shows a trend of first increasing and then decreasing. In addition, there is a significant decrease in the load on one of the pins near the maximum load region, such as the 25th pin, when
θf = 180°. This is because the corresponding contact point of this pin is located near the transition region between the convex and concave tooth surfaces of cycloid gear, and the radius of curvature at the contact point is too large, resulting in a significant reduction in the contact stiffness.
Finally, the contact stress distributions on the tooth surface of the cycloid gear and pin are obtained based on Hertzian contact theory (see
Figure 7e,f). This shows that the MCS is 1067.50 MPa. During the entire meshing cycle, half of the tooth surface of the single cycloid tooth is engaged in meshing, and the contact range of the tooth surface of pin ranges from zero to 54.45°, which is very close to the maximum value of
α (54.3692°) calculated with Equation (2). The error of the maximum value of
α is related to the number of discrete elements of the pin along the tooth profile. The MCS of the cycloid gear is located in the transition region of the concave and convex tooth surfaces and is close to the convex tooth surface. The MCS of the pin is at the position of the maximum value of
α. The above results are consistent with the theoretical analysis results and the results in the literature [
13,
26,
27], which verifies the feasibility and effectiveness of the presented calculation method.
6. Conclusions
In this study, a novel approach for calculating the transmission accuracy of a cycloid-pin gear pair based on a three-dimensional error tooth surface model has been proposed. Compared with the traditional analysis method for a cycloid-pin gear pair, this method has the capability to consider the influence of some abnormal meshing phenomena caused by PMs, MEs, and AEs on the tooth contact state, TE, and backlash, such as the instantaneous mesh-apart of tooth pairs and the eccentric load on a tooth surface. The feasibility and effectiveness of this method is validated by comparison with the theoretical analysis results and the results in the literature.
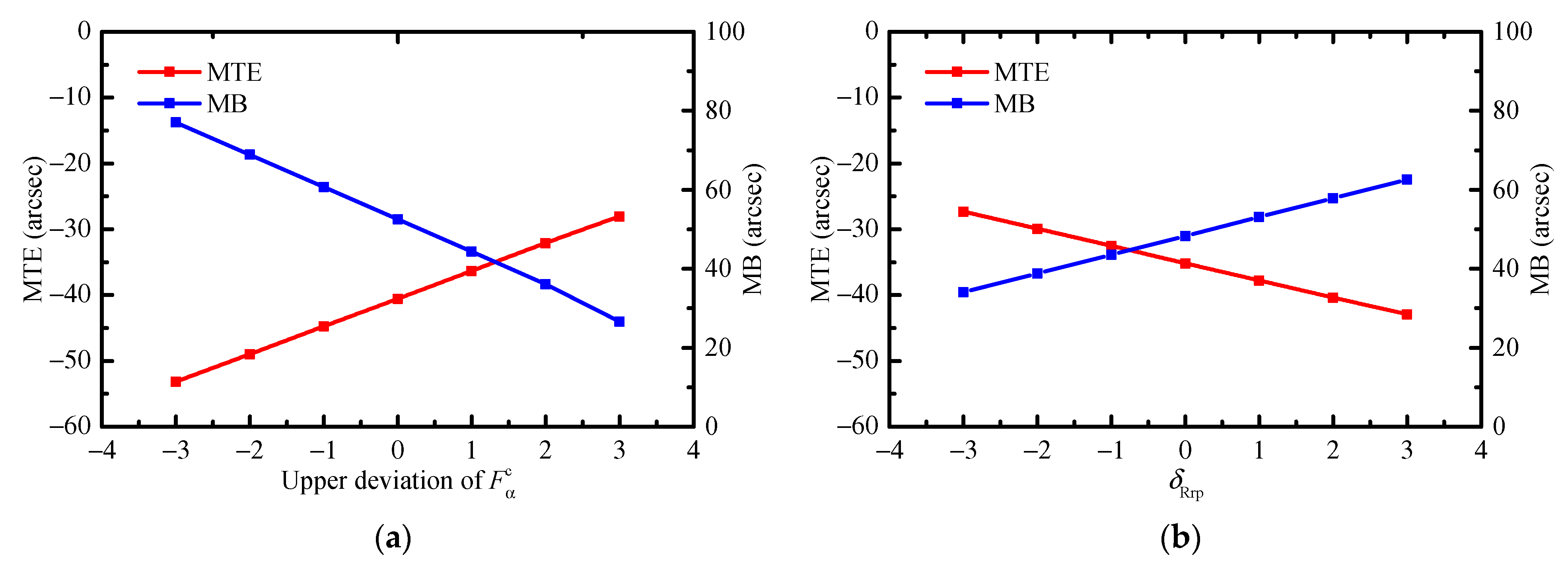
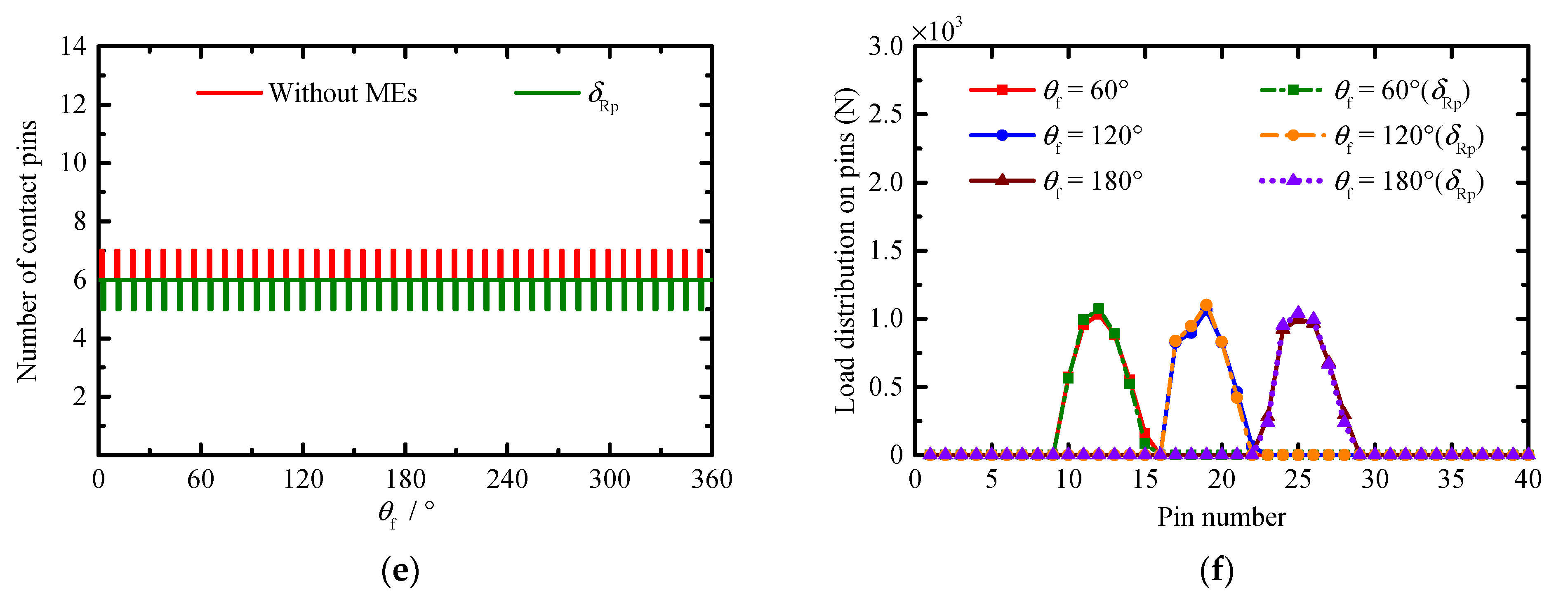
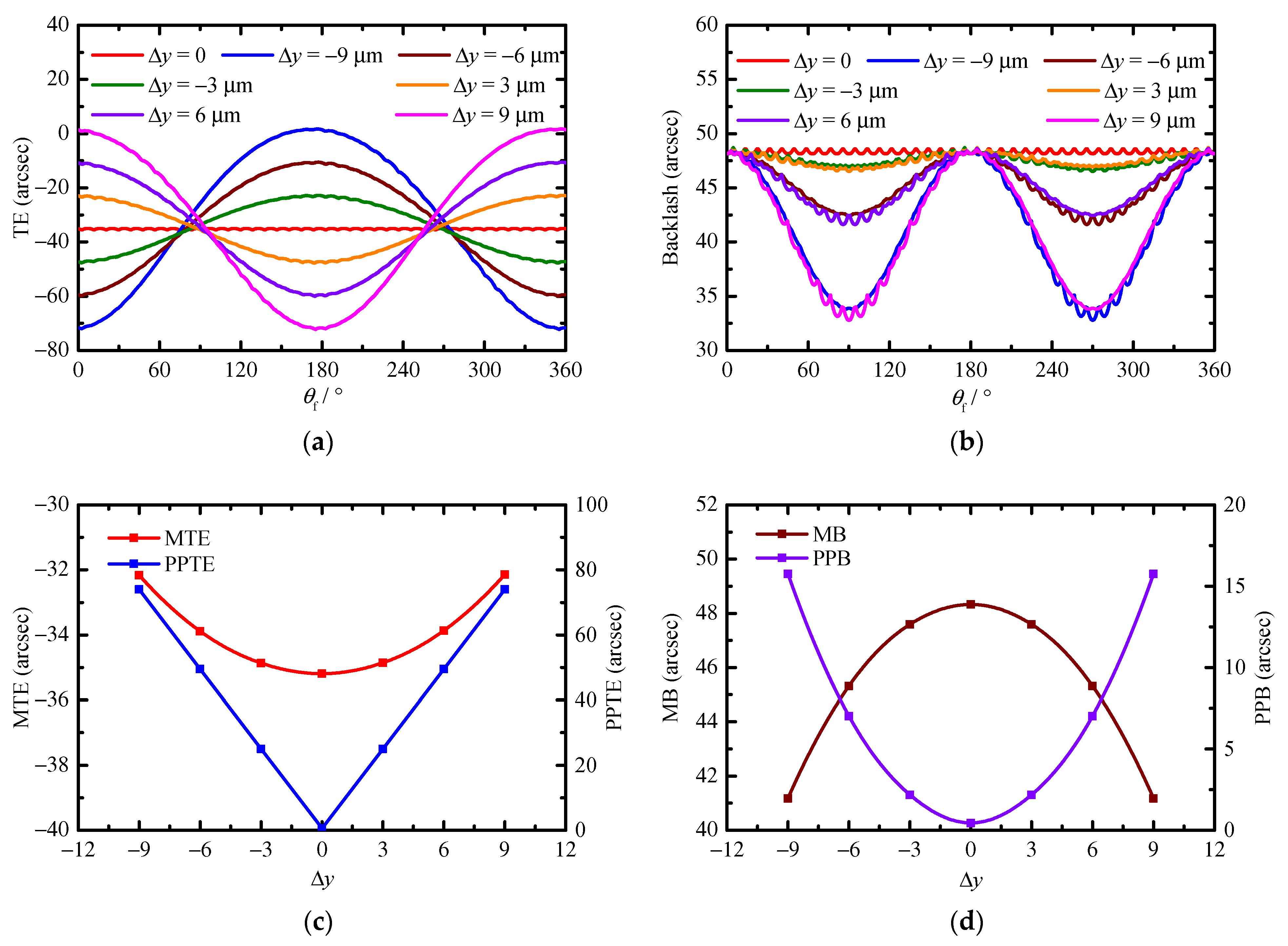
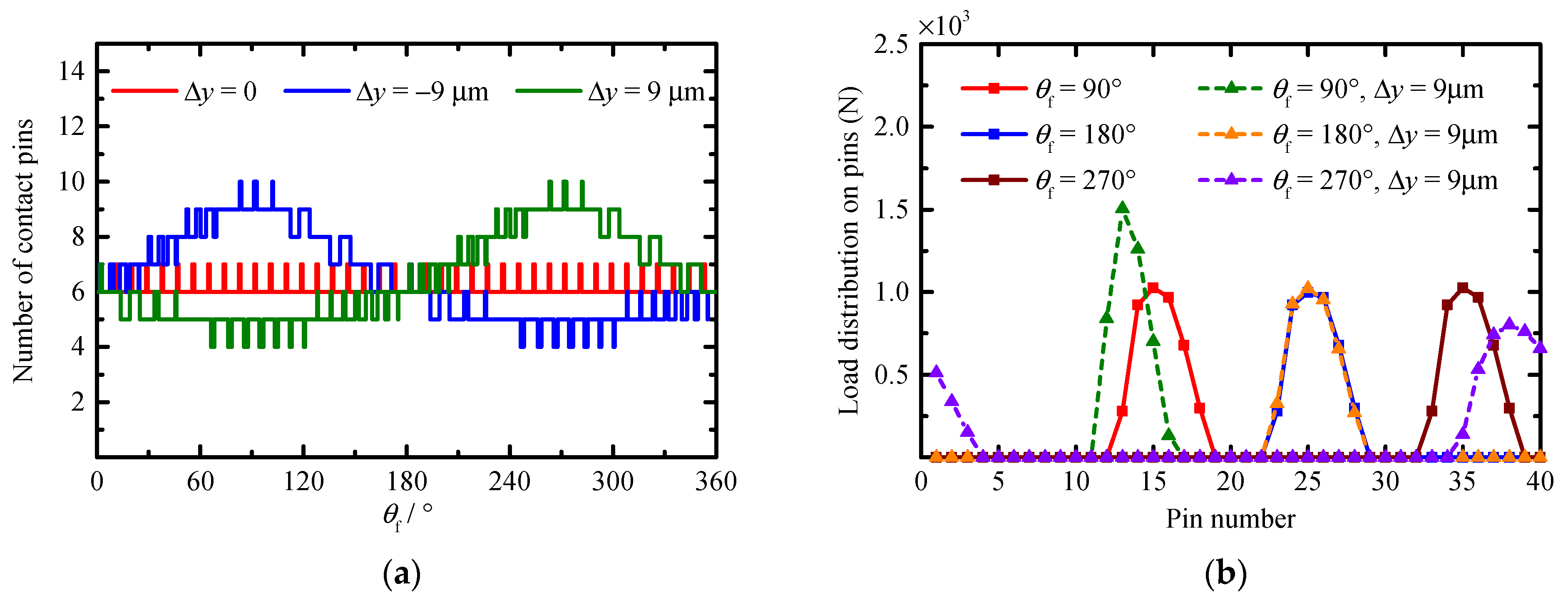
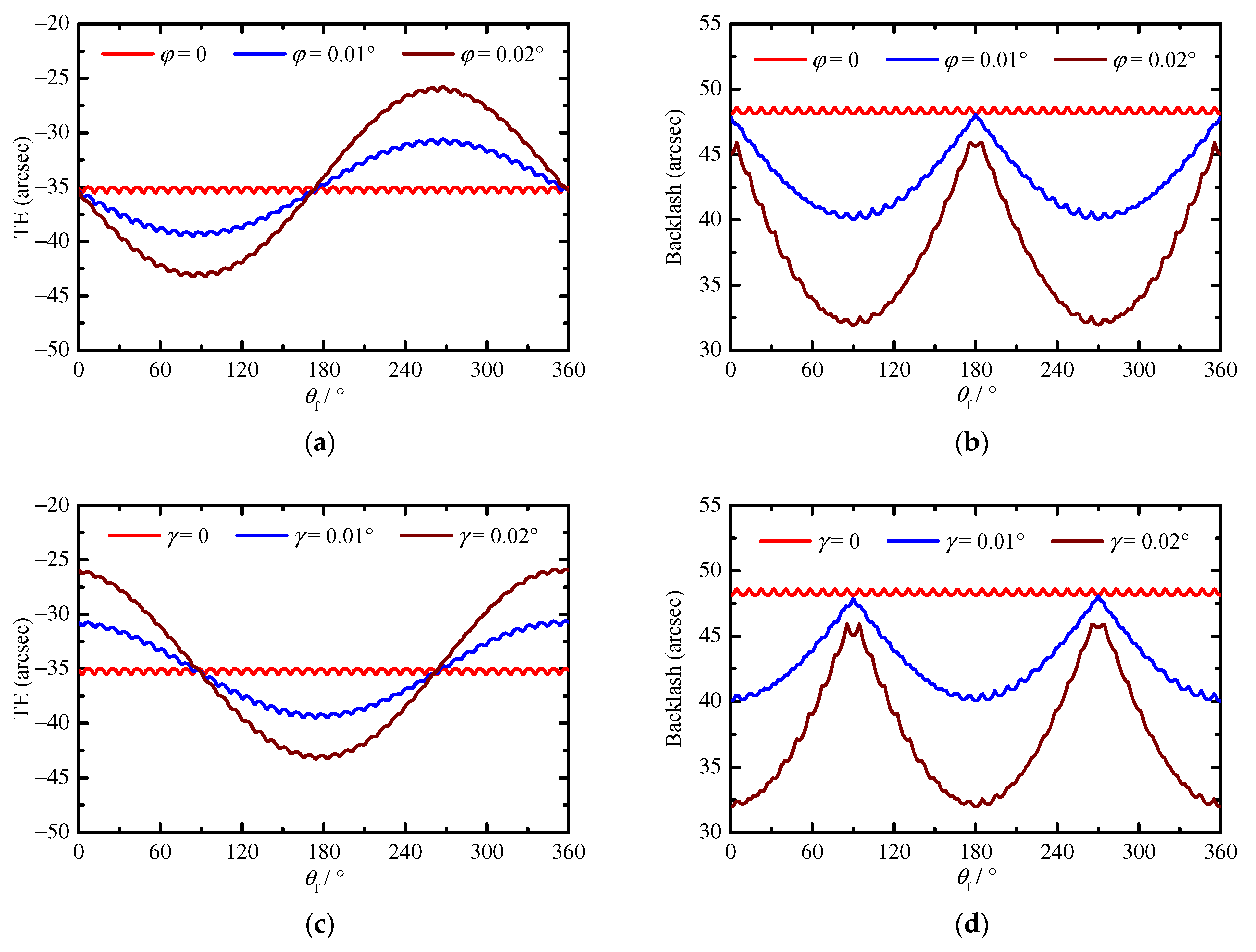
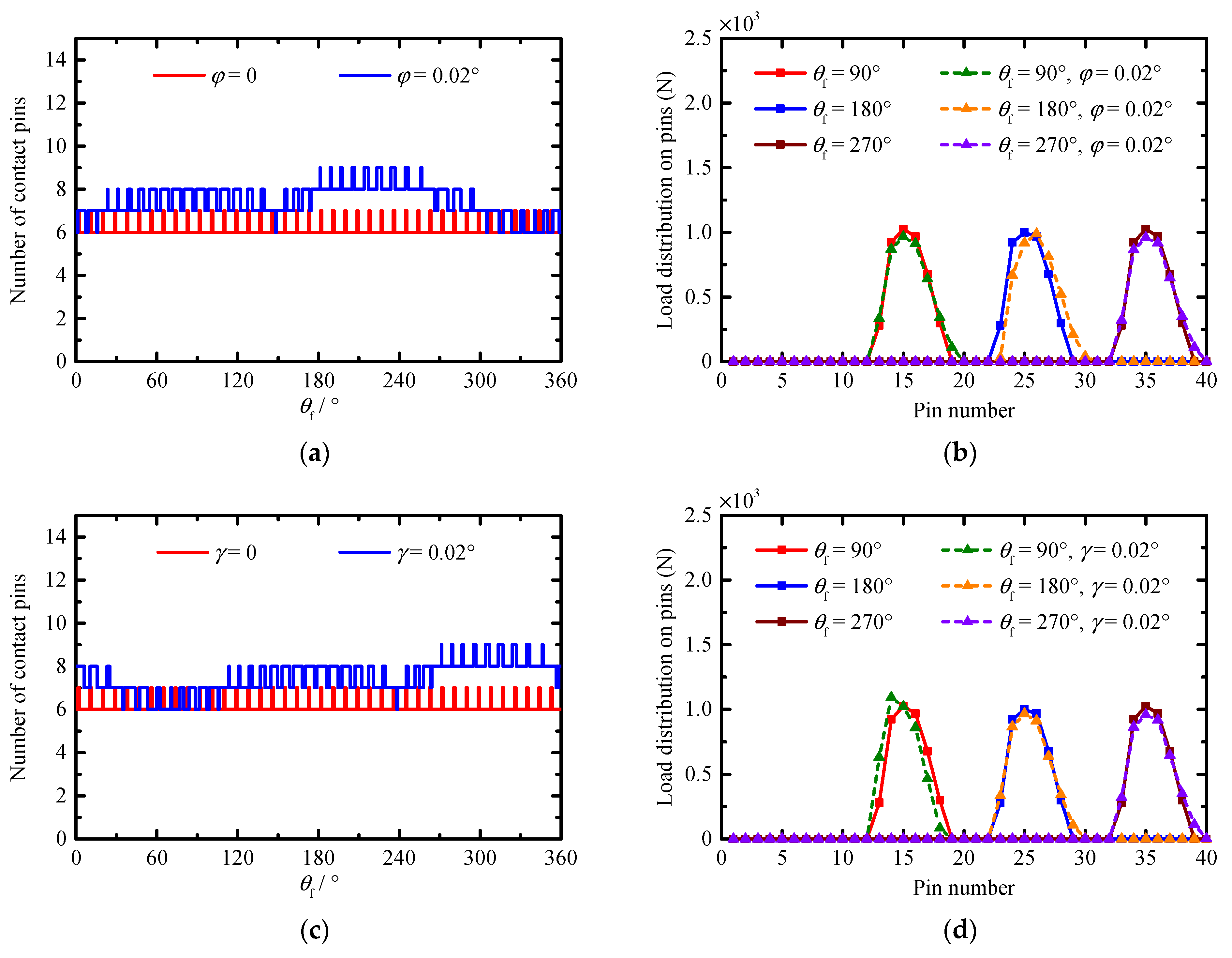
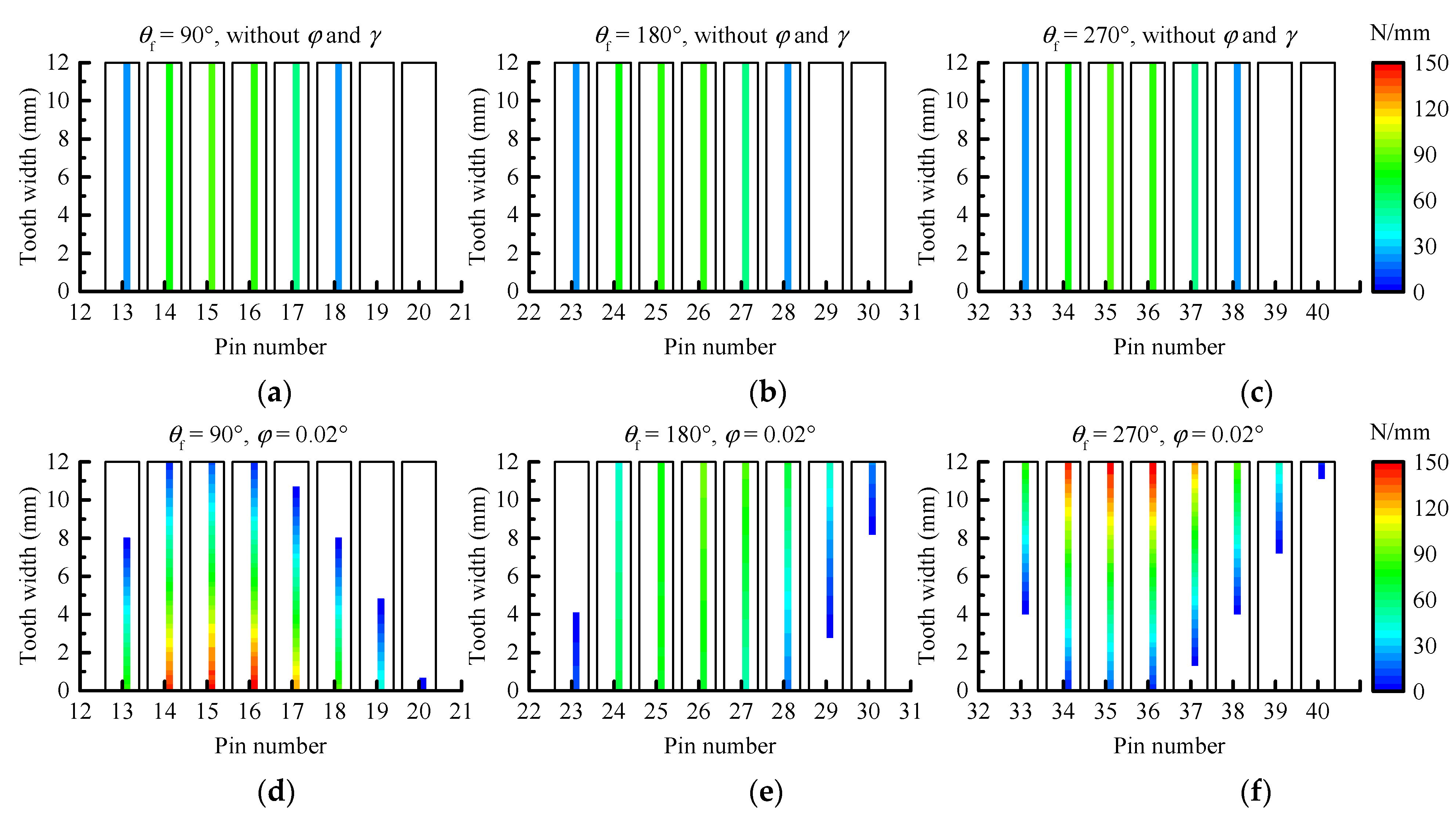
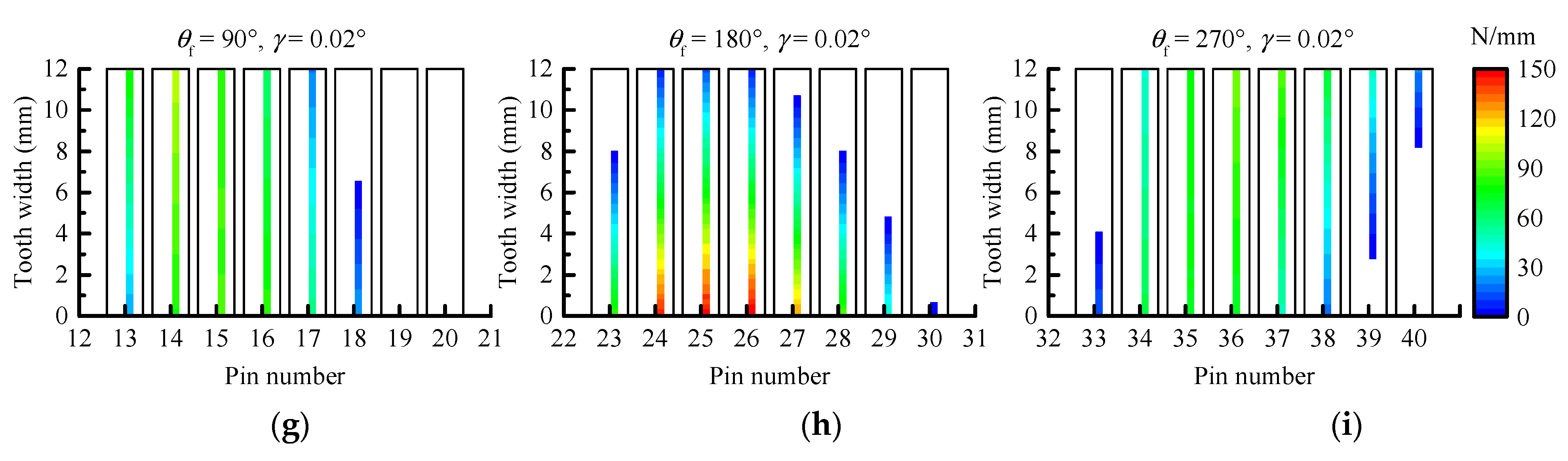
Based on this method, a series of cases is simulated to quantitatively study the influence of PMs, MEs, and AEs on the TE, backlash, the number of contact pins, load distribution on pins, contact stress, and instantaneous contact lines on the tooth surface of a pin. The obtained results show that the compound modification of the negative isometric and negative offset should be preferred in order to avoid the tooth interference and to obtain higher transmission accuracy. With this compound modification method, although the increase in the modification amount improves the transmission accuracy; this increase also leads to a decrease in the mean of the number of contact pins and an increase in the MCS. Among the MEs and AEs, the pitch deviation, the center distance deviation, and the misalignment deviations are the main influencing factors of the TE and backlash. They not only change the waveform of the TE and backlash curves, but also the main source of the peak-to-peak values of the TE and backlash, while the profile deviation and the pin center circle diameter deviation mainly affect the mean values of the TE and backlash. In addition, the pitch deviation and the center distance deviation will cause the number of contact pins to fluctuate in a large range, and they will cause the load on some pins to increase significantly. Under the influence of the misalignment deviations, although the mean of the number of contact pins increases and the load distribution on the pins does not change significantly, a serious eccentric load occurs on the tooth surface of some contact pins. The increase in the load on the pins and the occurrence of the eccentric load not only increase the MCS and shorten the contact fatigue lifetime of the tooth surface, but they also accelerate the tooth surface wear and reduce the transmission accuracy lifetime of the cycloid-pin gear pair.
The proposed method and the above conclusions are of great significance for the optimal design of the tooth profile of a cycloid gear, the tolerance allocation during the installation of a gear pair, and the accurate prediction of the TE and backlash of a cycloid-pin gear pair. The error tooth surface in this study is obtained through different probability distribution functions based on the tolerance range of various errors, and this method is expected to be used for the prediction of the transmission accuracy range of the gear pair in engineering practice. The error tooth surface can also be generated using the measurement coordinates of the element control point on the tooth surface, and this method can provide more accurate internal excitation data for the dynamic analysis of a cycloid-pin gear pair, which will be implemented in future research.