Scheduling Period Selection Based on Stability Analysis for Engagement Control Task of Automatic Clutches
Abstract
:1. Introduction
2. System Modeling
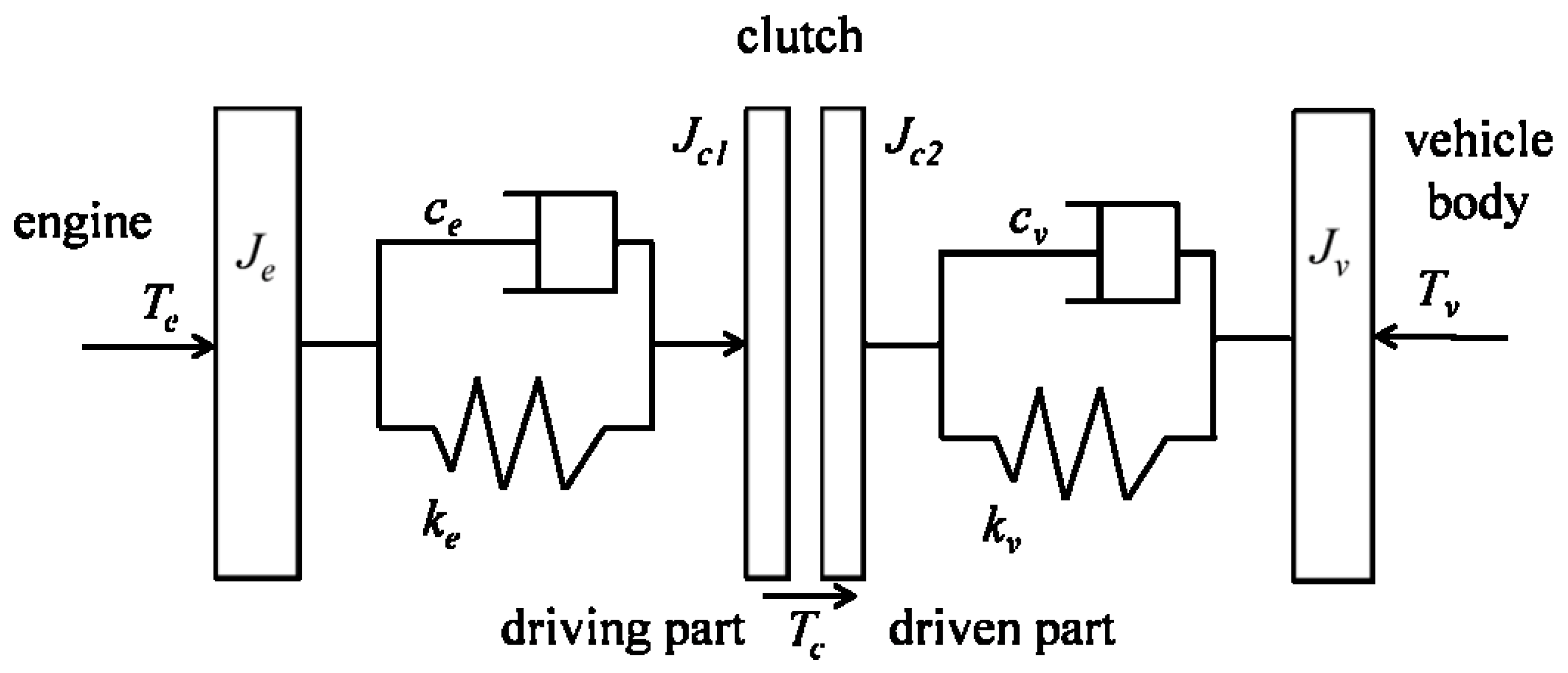
2.1. Powertrain Model
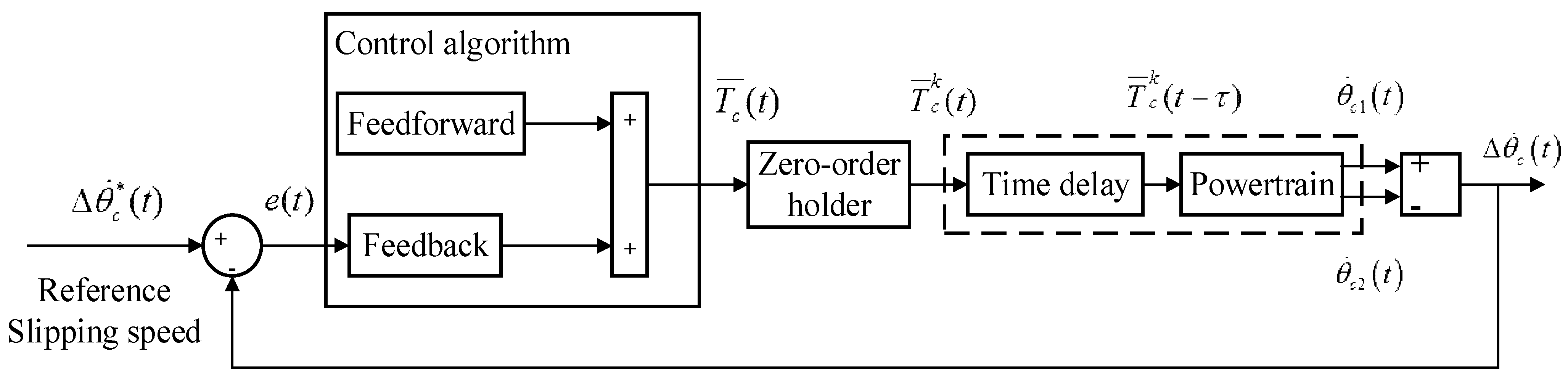
2.2. Control Algorithm
2.3. Zero-Order Holder
3. Stability Analysis for the Slipping Phase
3.1. Transfer Function in the S-Plane
3.2. Discretization by Z-Transform
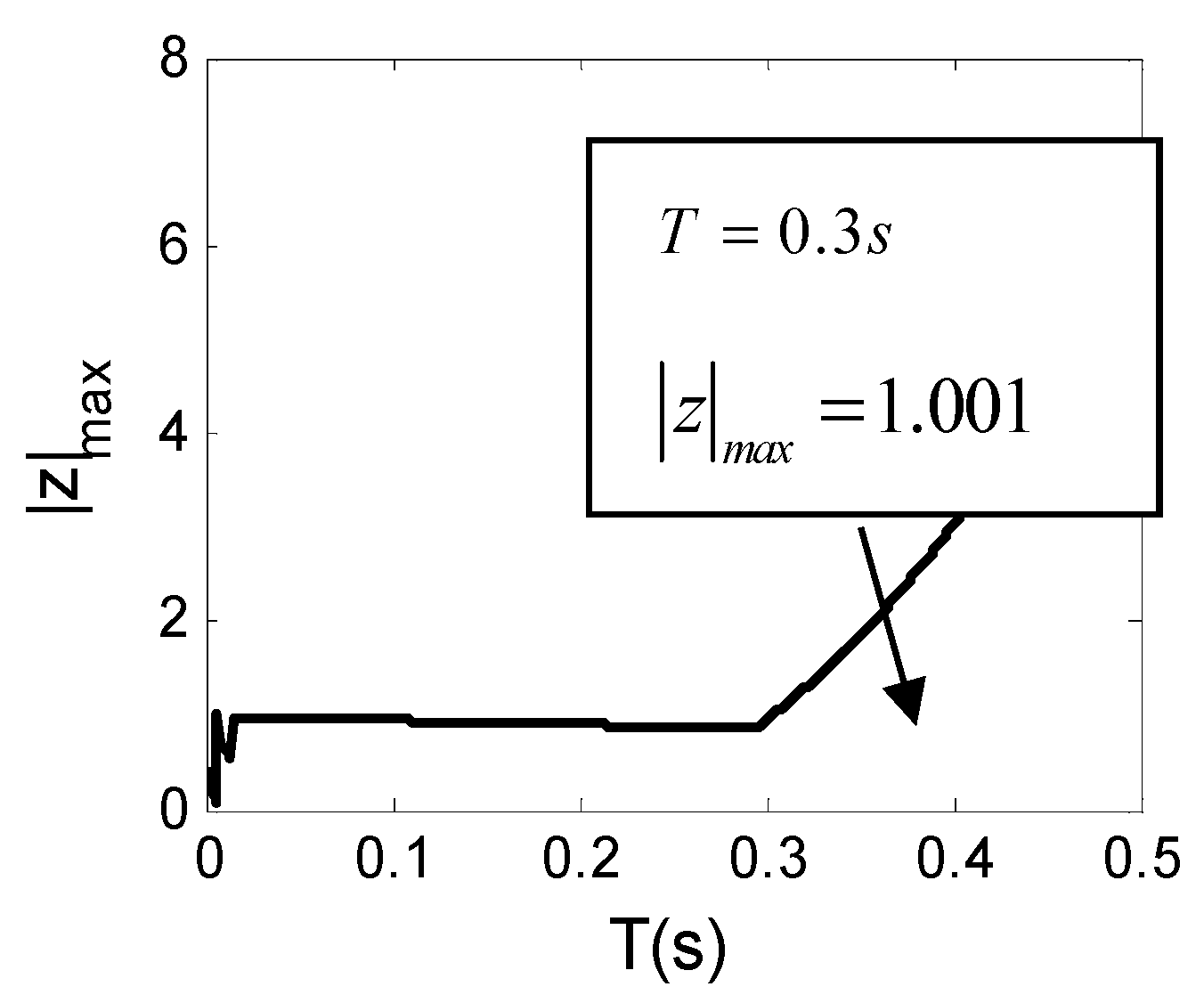
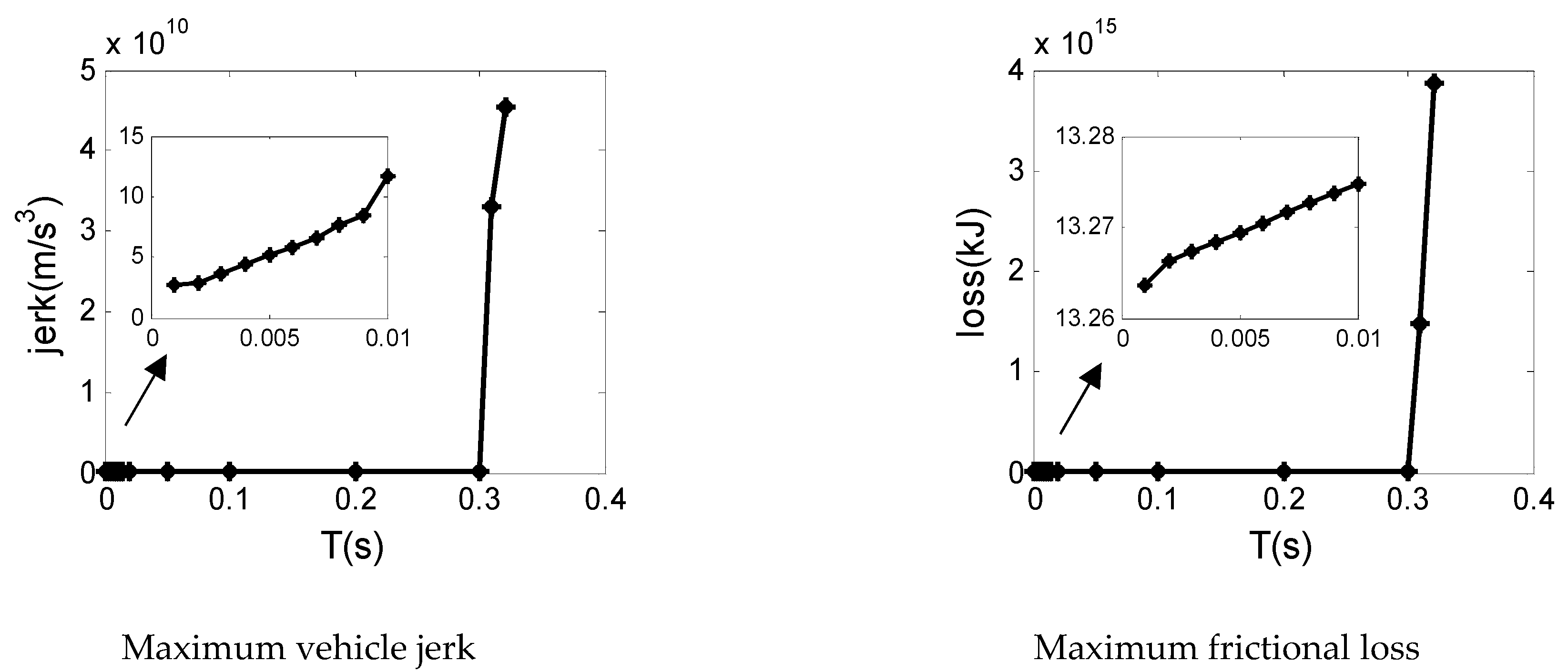
3.3. Critical Period Regarding Stability
3.4. Sensitivity Analysis
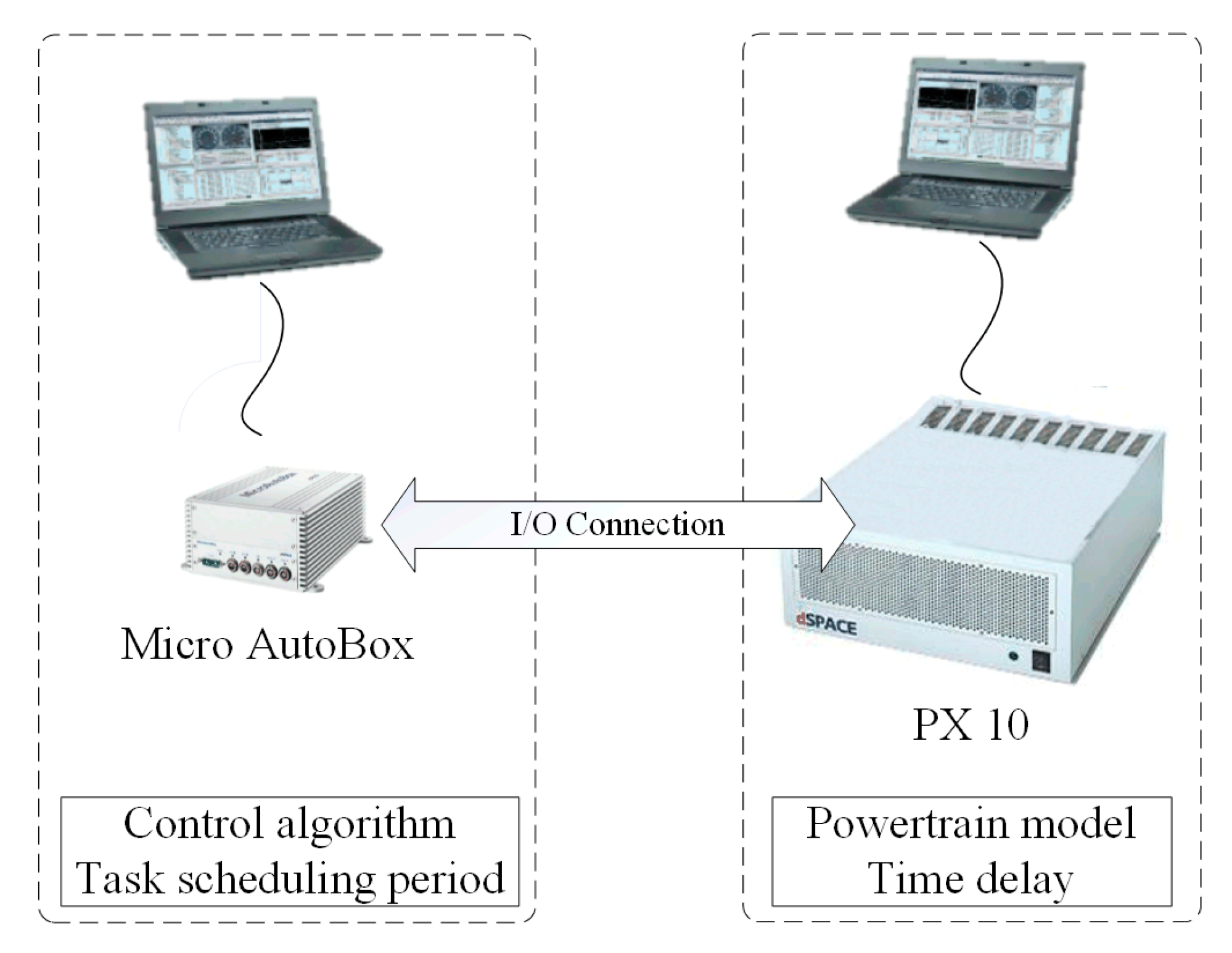
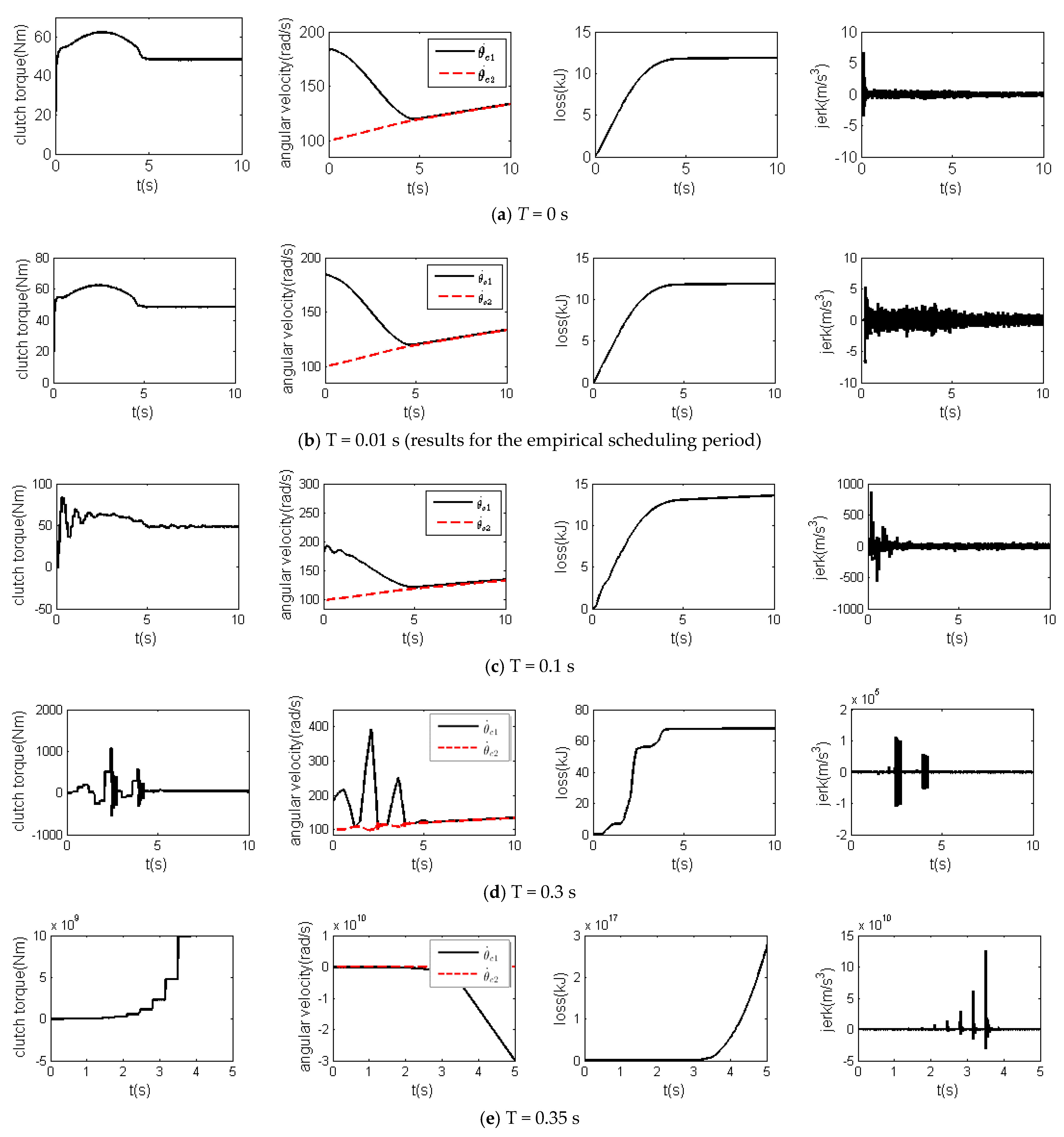
4. Real-Time Test from Slipping to Being Locked Phase
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xiong, W.; Zhang, Y.; Yin, C. Optimal energy management for a series–parallel hybrid electric bus. Energy Convers. Manag. 2009, 50, 1730–1738. [Google Scholar] [CrossRef]
- Chao, Y.; Jian, S.; Liang, L.; Li, S.; Cao, D. Economical launching and accelerating control strategy for a single-shaft parallel hybrid electric bus. Mech. Syst. Signal Process. 2016, 76, 649–664. [Google Scholar]
- Vasca, F.; Iannelli, L.; Senatore, A.; Reale, G. Torque Transmissibility Assessment for Automotive Dry-Clutch Engagement. IEEE/ASME Trans. Mechatron. 2010, 16, 564–573. [Google Scholar] [CrossRef]
- Chen, L.; Xi, G. Stability and response of a self-amplified braking system under velocity-dependent actuation force. Nonlinear Dyn. 2014, 78, 2459–2477. [Google Scholar] [CrossRef]
- Chen, L.; Liu, F.; Yao, J.; Ding, Z.; Lee, C.; Kao, C.-K.; Samie, F.; Huang, Y.; Yin, C. Design and validation of clutch-to-clutch shift actuator using dual-wedge mechanism. Mechatronics 2017, 42, 81–95. [Google Scholar] [CrossRef]
- Liu, F.; Chen, L.; Li, D.; Yin, C. Improved clutch slip control for automated transmissions. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 232, 3181–3199. [Google Scholar] [CrossRef]
- Yao, J.; Chen, L.; Liu, F.; Yin, C. Experimental study on improvement in the shift quality for an automatic transmission using a motor-driven wedge clutch. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2014, 228, 663–673. [Google Scholar] [CrossRef]
- Li, D.; Liu, L.; Liu, Y.-J.; Tong, S.; Chen, C.L.P. Fuzzy Approximation-Based Adaptive Control of Nonlinear Uncertain State Constrained Systems with Time-Varying Delays. IEEE Trans. Fuzzy Syst. 2019, 28, 1620–1630. [Google Scholar] [CrossRef]
- Tafti, H.D.; Sangwongwanich, A.; Yang, Y.; Pou, J.; Konstantinou, G.; Blaabjerg, F. An Adaptive Control Scheme for Flexible Power Point Tracking in Photovoltaic Systems. IEEE Trans. Power Electron. 2019, 34, 5451–5463. [Google Scholar] [CrossRef] [Green Version]
- Huang, T.; Yang, K.; Zhu, Y.; Tang, Q.; Cheng, M.; Wang, Y. LFT-Structured Uncertainty State-Space Modeling for State Feedback Robust Control of the Ultra-Precision Wafer Stage. IEEE Trans. Ind. Electron. 2019, 66, 8567–8577. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, Y.; Chen, Z.; Zhu, S. Parameter Identification and Model-Based Nonlinear Robust Control of Fluidic Soft Bending Actuators. IEEE/ASME Trans. Mechatron. 2019, 24, 1346–1355. [Google Scholar] [CrossRef]
- Gu, K. A further refinement of discretized Lyapunov functional method for the stability of time-delay systems. Int. J. Control 2001, 74, 967–976. [Google Scholar] [CrossRef]
- Wang, B.; Yu, X.; Li, X. ZOH Discretization Effect on Higher-Order Sliding-Mode Control Systems. IEEE Trans. Ind. Electron. 2008, 55, 4055–4064. [Google Scholar] [CrossRef]
- Liu, J.; Peng, B.; Zhang, T. Effect of discretization on dynamical behavior of SEIR and SIR models with nonlinear incidence. Appl. Math. Lett. 2015, 39, 60–66. [Google Scholar] [CrossRef]
- Wu, Y.; Buttazzo, G.; Bini, E.; Cervin, A. Parameter Selection for Real-Time Controllers in Resource-Constrained Systems. IEEE Trans. Ind. Inform. 2010, 6, 610–620. [Google Scholar] [CrossRef]
- Aydin, H.; Melhem, R.; Mosse, D.; Mejfa-Alvarez, P. Optimal reward-based scheduling of periodic real-time tasks. IEEE Trans. Comput. 2003, 1, 50. [Google Scholar] [CrossRef] [Green Version]
- Mayank, J.; Mondal, A.; Sarkar, A. Control-schedule co-design for fast stabilization in real time systems facing repeated reconfigurations. Des. Autom. Embed. Syst. 2019, 23, 79–101. [Google Scholar] [CrossRef]
- Wang, T.; Zhou, C.; Hui, L.; He, J.; Jian, G. Hybrid Scheduling and Quantized Output Feedback Control for Networked Control Systems. Int. J. Control. Autom. Syst. 2018, 16, 197–206. [Google Scholar] [CrossRef]
- Dai, S.-L.; Lin, H.; Ge, S.S. Scheduling-and-Control Codesign for a Collection of Networked Control Systems with Uncertain Delays. IEEE Trans. Control Syst. Technol. 2009, 18, 66–78. [Google Scholar] [CrossRef]
- Cervin, A.; Velasco, M.; Marti, P.; Camacho, A. Optimal Online Sampling Period Assignment: Theory and Experiments. IEEE Trans. Control Syst. Technol. 2011, 19, 902–910. [Google Scholar] [CrossRef]
- Min, Z.; Jin, W.; Ma, A. Co-design of optimal feedback scheduling strategy and fault detection for networked control systems. In Proceedings of the 2016 IEEE Chinese Guidance, Navigation and Control Conference (CGNCC), Nanjing, China, 12–14 August 2016; pp. 216–221. [Google Scholar]
- Yun, N.; Liang, Y.; Yang, H. Event-triggered robust control and dynamic scheduling co-design for networked control system. In Proceedings of the 2017 14th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 10–14 January 2017; pp. 237–243. [Google Scholar]
- Wen, S.; Guo, G.; Wong, W.S. Hybrid event-time-triggered networked control systems: Scheduling-event-control co-design. Inf. Sci. 2015, 305, 269–284. [Google Scholar] [CrossRef]
- ArnellP, R.D.; Davies, B.; Halling, J.; Whomes, T.L. Tribology: Principles and Design Applications, 1st ed.; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Chen, L.; Xi, G.; Sun, J. Torque Coordination Control During Mode Transition for a Series–Parallel Hybrid Electric Vehicle. IEEE Trans. Veh. Technol. 2012, 61, 2936–2949. [Google Scholar] [CrossRef]
- Wang, X.; Li, L.; Yang, C. Hierarchical Control of Dry Clutch for Engine-Start Process in a Parallel Hybrid Electric Vehicle. IEEE Trans. Transp. Electrif. 2016, 2, 231–243. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, L.; Xi, G. System dynamic modelling and adaptive optimal control for automatic clutch engagement of vehicles. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2002, 216, 983–991. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, X.; He, K.; Yang, C. Model reference self-learning fuzzy control method for automated mechanical clutch. Int. J. Adv. Manuf. Technol. 2016, 94, 3163–3172. [Google Scholar] [CrossRef]
- Dorf, C.R.; Bishop, R. Modern Control Systems, 7th ed.; Pearson Prentice Hall: Hoboken, NJ, USA, 1994. [Google Scholar]
- Seto, D.; Lehoczky, J.P.; Sha, L.; Shin, K.G. On task schedulability in real-time control systems. In Proceedings of the 17th IEEE Real-Time Systems Symposium, Washington, WA, USA, 4–6 December 1996; pp. 13–21. [Google Scholar] [CrossRef]
- Bini, E.; Natale, M.D. Optimal Task Rate Selection in Fixed Priority Systems. In Proceedings of the IEEE International Real-Time Systems Symposium, Miami, FL, USA, 5–8 December 2005; pp. 399–409. [Google Scholar]
- Balbastre, P.; Ripoll, I.; Crespo, A. Optimal deadline assignment for periodic real-time tasks in dynamic priority systems. In Proceedings of the Euromicro Conference on Real-Time Systems, Dresden, Germany, 5–7 July 2006. [Google Scholar] [CrossRef]
- Hoang, H.; Buttazzo, G.; Jonsson, M.; Karlsson, S. Computing the Minimum EDF Feasible Deadline in Periodic Systems. In Proceedings of the IEEE International Conference on Embedded and Real-Time Computing Systems and Applications, Sydney, Australia, 16–18 August 2006; pp. 125–134. [Google Scholar]
- Reimann, S.; Wu, W.; Liu, S. Real-Time Scheduling of PI Control Tasks. IEEE Trans. Control. Syst. Technol. 2015, 24, 1118–1125. [Google Scholar] [CrossRef]


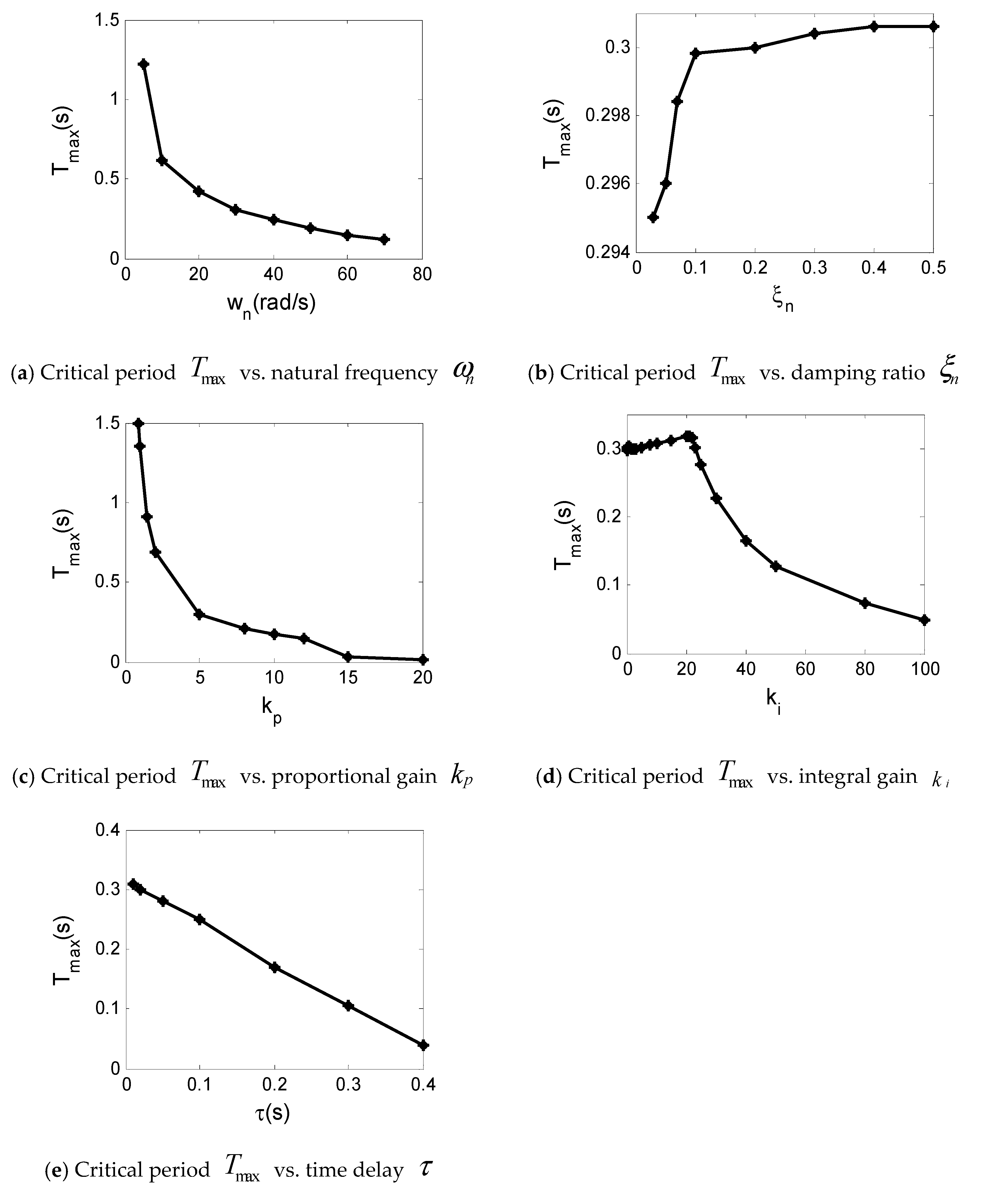
| Symbol | Value | Symbol | Value | Symbol | Value |
|---|---|---|---|---|---|
| 0.1 kg·m2 | 0.5 kg·m2 | 0.5 kg·m2 | |||
| 10 kg·m2 | 1000 Nm/rad | 10,000 Nm/rad | |||
| 10 kg·m2 | 20 kg·m2 | 5 | |||
| 1 | 10 ms |
| Symbol | Value | Symbol | Value | Symbol | Value |
|---|---|---|---|---|---|
| 1600 kg | 0.15 m | 0.44 | |||
| 0.4 | 0.32 | 1.8 m2 | |||
| 1.205 kg/m3 | 0.0015 | 0.32 m | |||
| 2 | 3.5 |
| T < 0.01 s | 0.01 s ≤ T ≤ 0.30 s | T > 0.30 s | |
|---|---|---|---|
| Average increasing rate of vehicle jerk (m/s4) | 7.1 × 102 | 1.6 × 105 | 2.3 × 1012 |
| Average increasing rate of frictional loss (J/s) | 1.2 × 103 | 2.7 × 105 | 1.9 × 1020 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, Z.; Chen, L.; Chen, J.; Cheng, X.; Yin, C. Scheduling Period Selection Based on Stability Analysis for Engagement Control Task of Automatic Clutches. Appl. Sci. 2021, 11, 8636. https://doi.org/10.3390/app11188636
Ding Z, Chen L, Chen J, Cheng X, Yin C. Scheduling Period Selection Based on Stability Analysis for Engagement Control Task of Automatic Clutches. Applied Sciences. 2021; 11(18):8636. https://doi.org/10.3390/app11188636
Chicago/Turabian StyleDing, Zhao, Li Chen, Jun Chen, Xiaoxuan Cheng, and Chengliang Yin. 2021. "Scheduling Period Selection Based on Stability Analysis for Engagement Control Task of Automatic Clutches" Applied Sciences 11, no. 18: 8636. https://doi.org/10.3390/app11188636
APA StyleDing, Z., Chen, L., Chen, J., Cheng, X., & Yin, C. (2021). Scheduling Period Selection Based on Stability Analysis for Engagement Control Task of Automatic Clutches. Applied Sciences, 11(18), 8636. https://doi.org/10.3390/app11188636





