Cross-Correlation Wavelet-Domain-Based Particle Swarm Optimization for Lightning Mapping
Abstract
:1. Introduction
2. Materials and Methods
2.1. Database
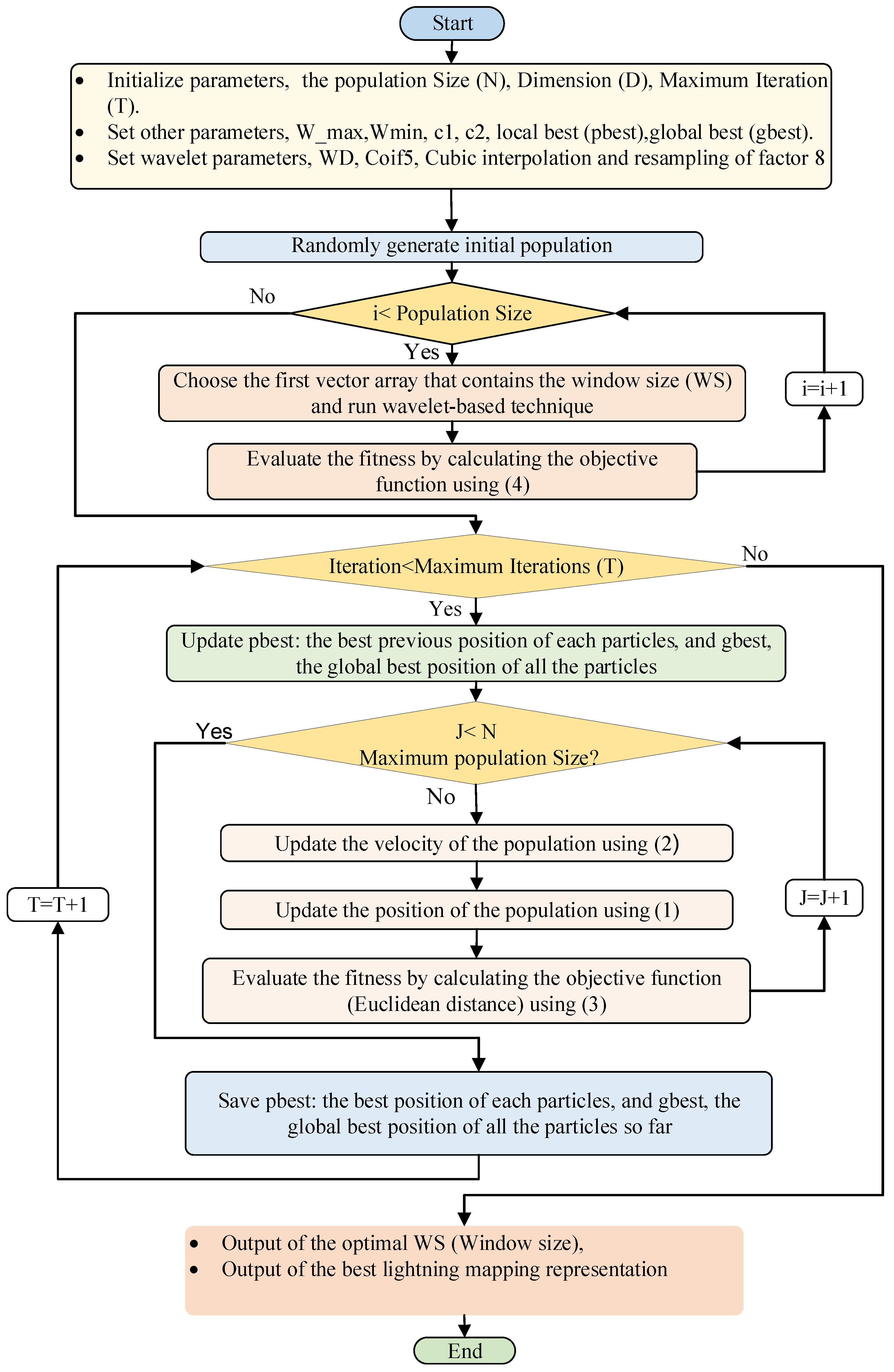
2.2. Lightning Mapping Optimization
2.3. Objective Function
2.4. Optimization Constraints and PSO Parameters
3. Results and Discussions
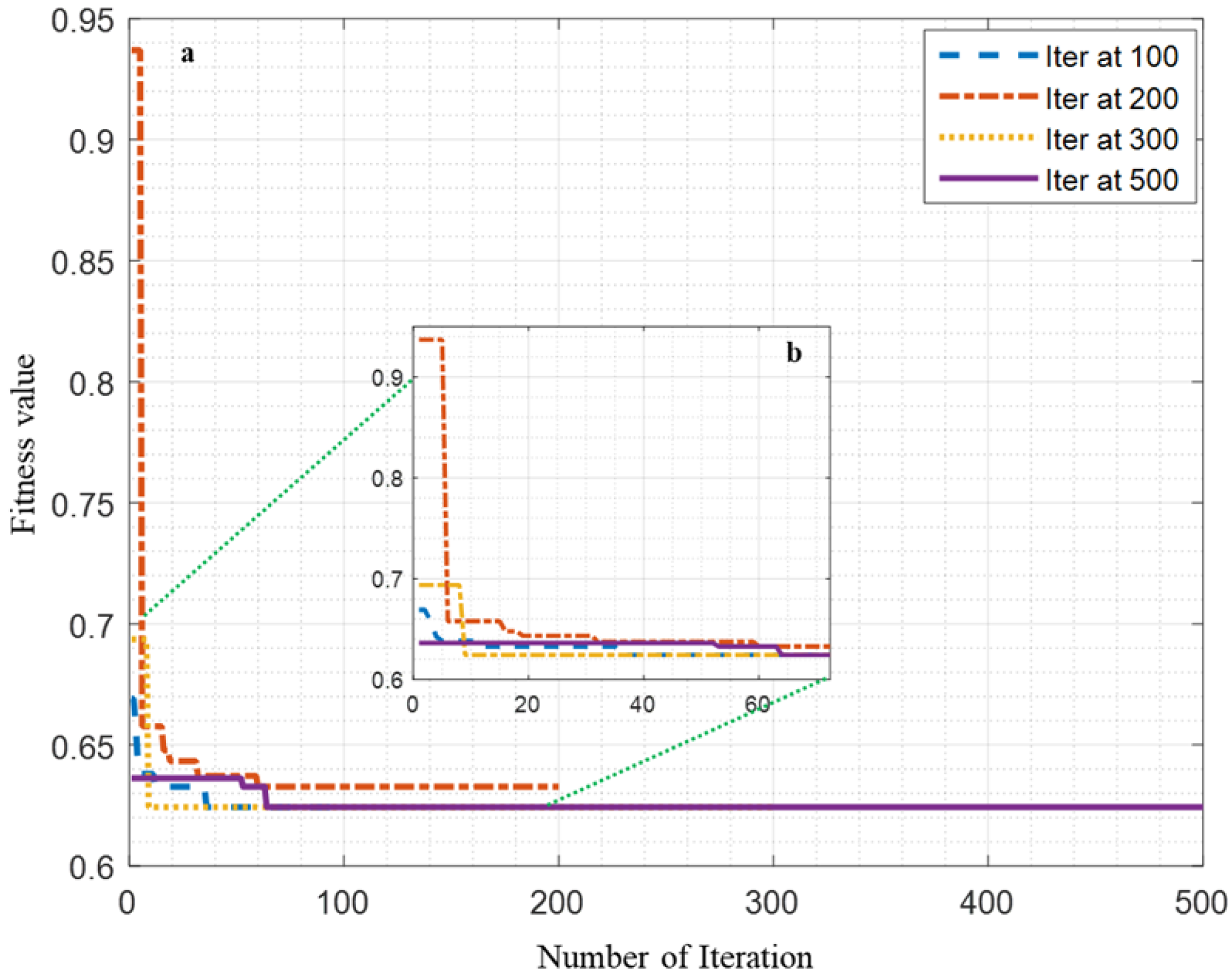
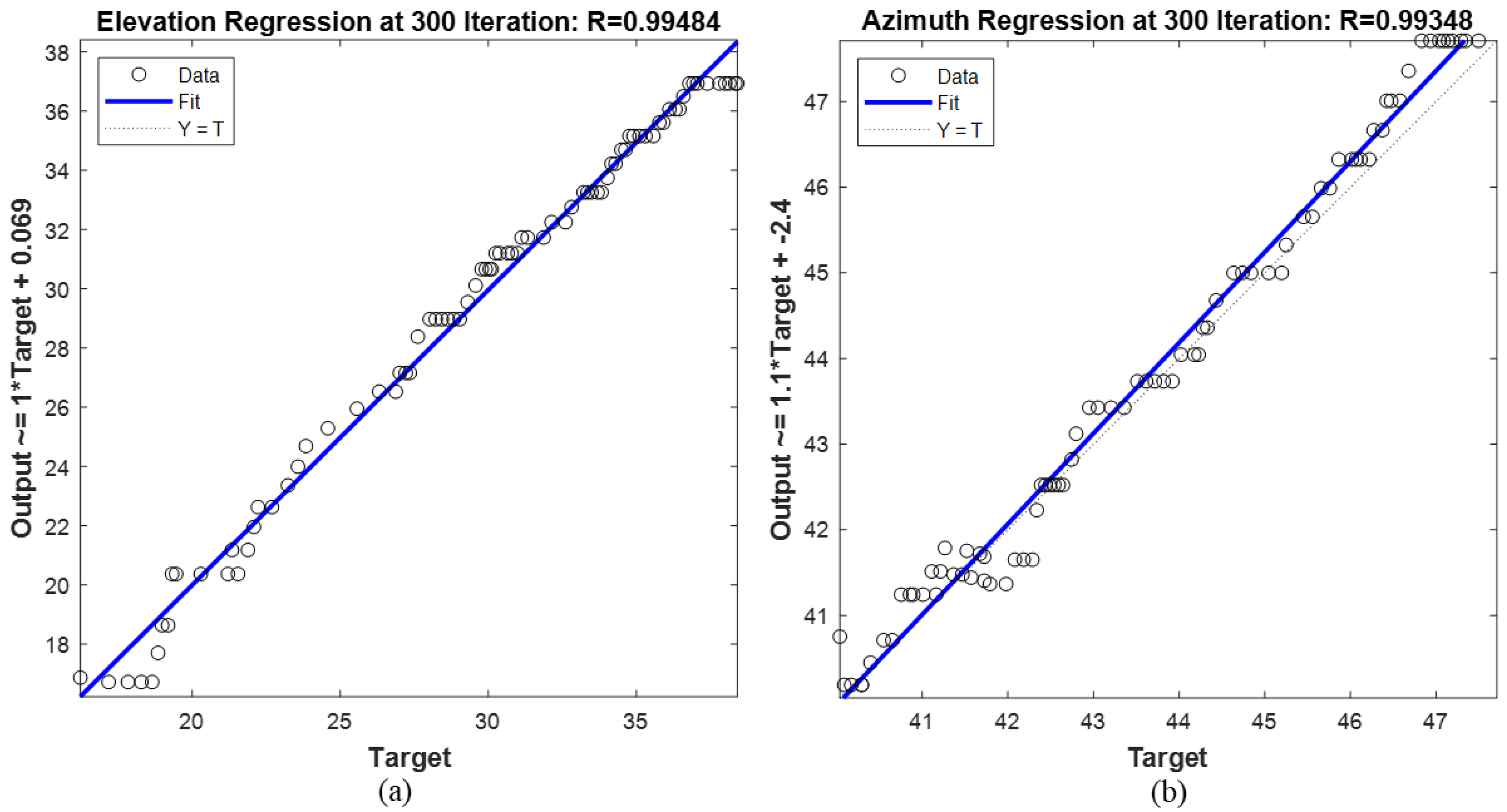
3.1. Optimal Selection of PSO Parameters Using Simulated Data
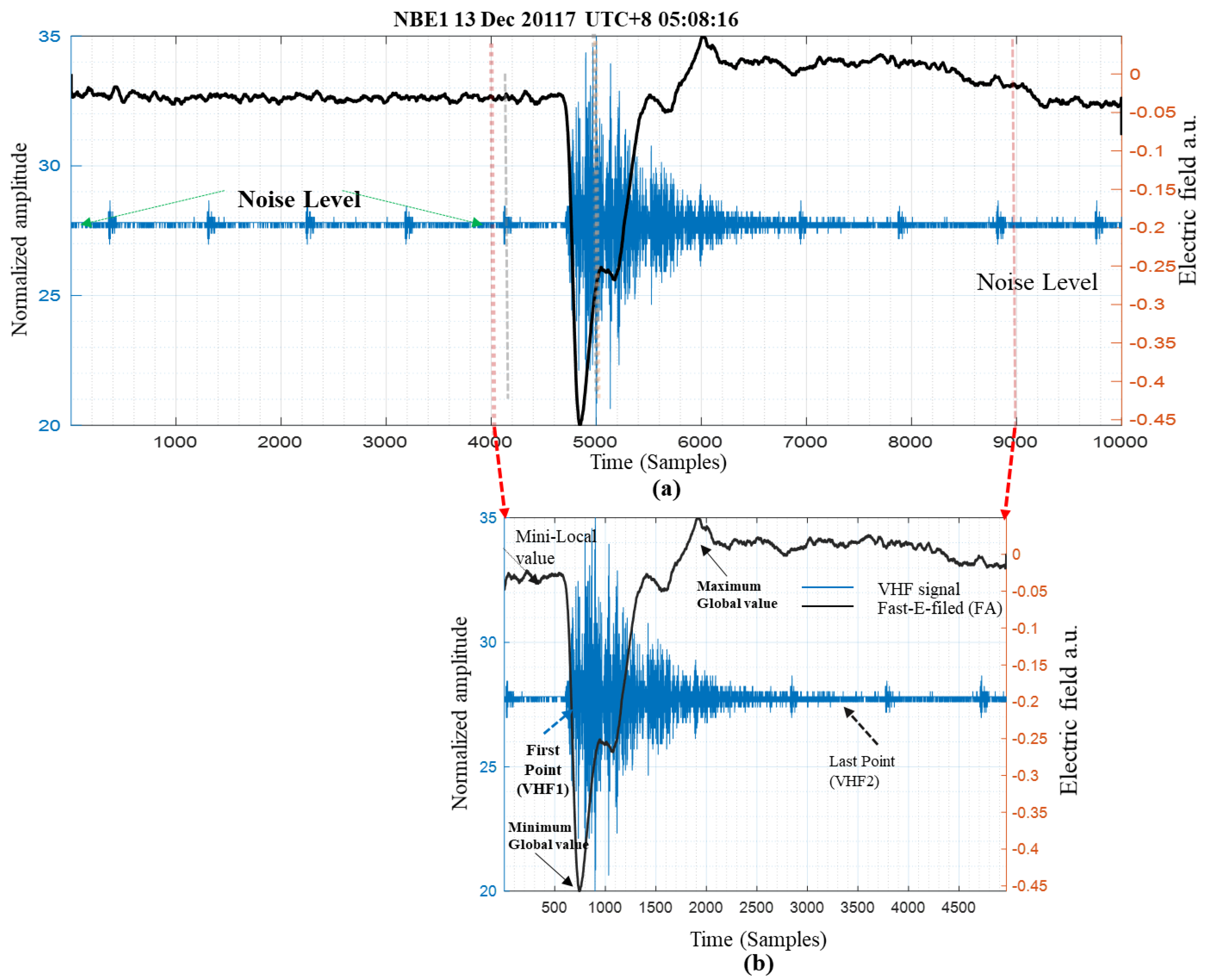
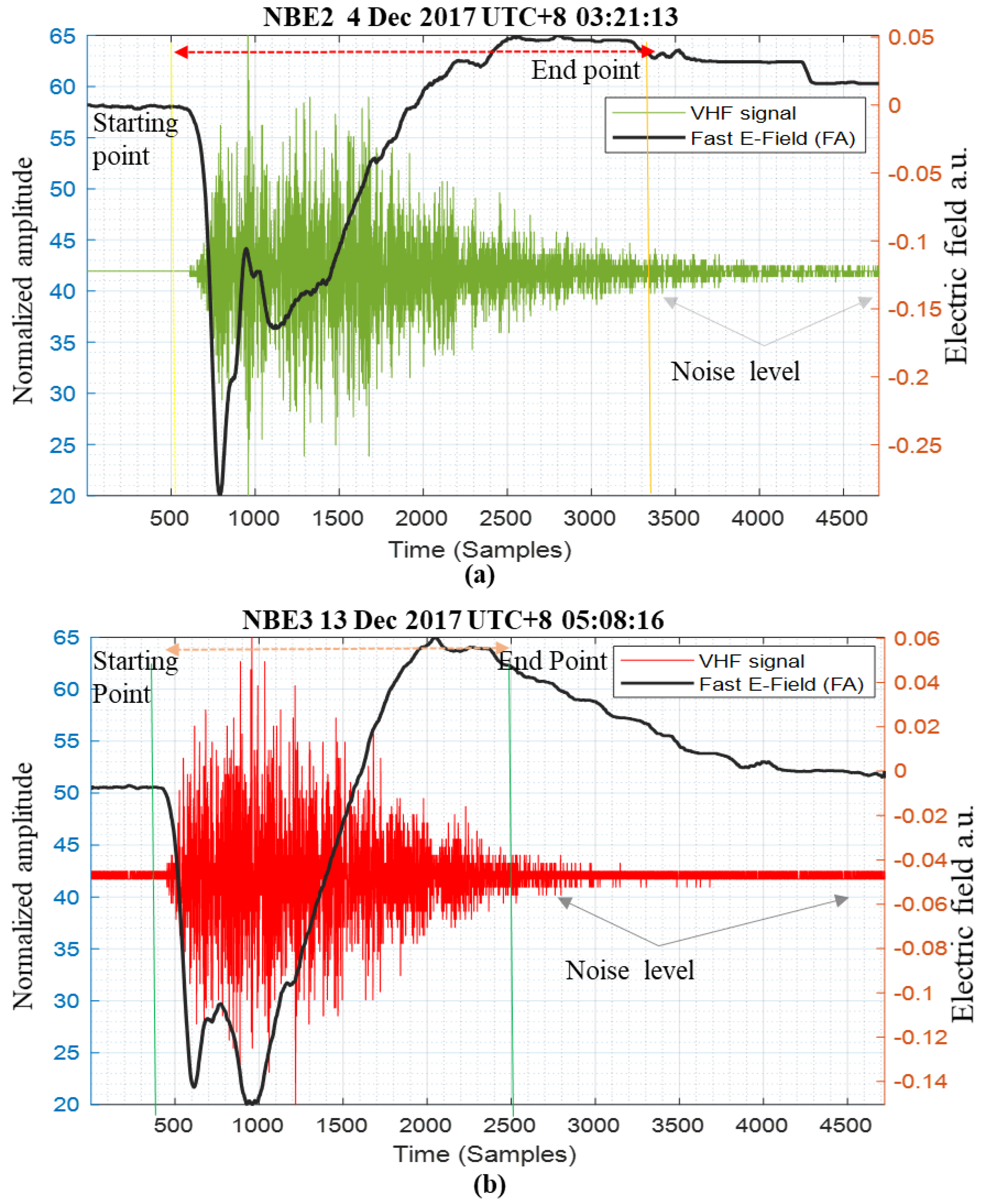
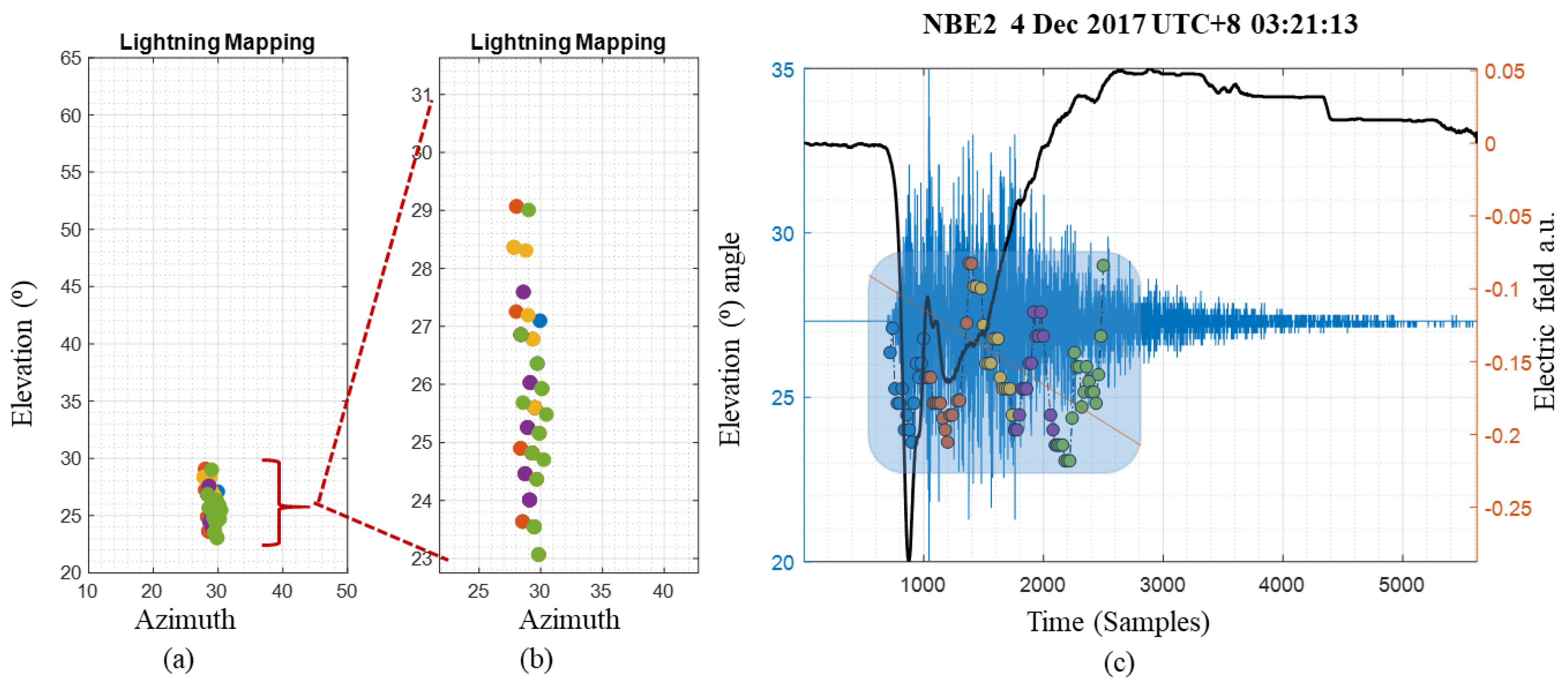
3.2. Evaluations on Real Lightning Data
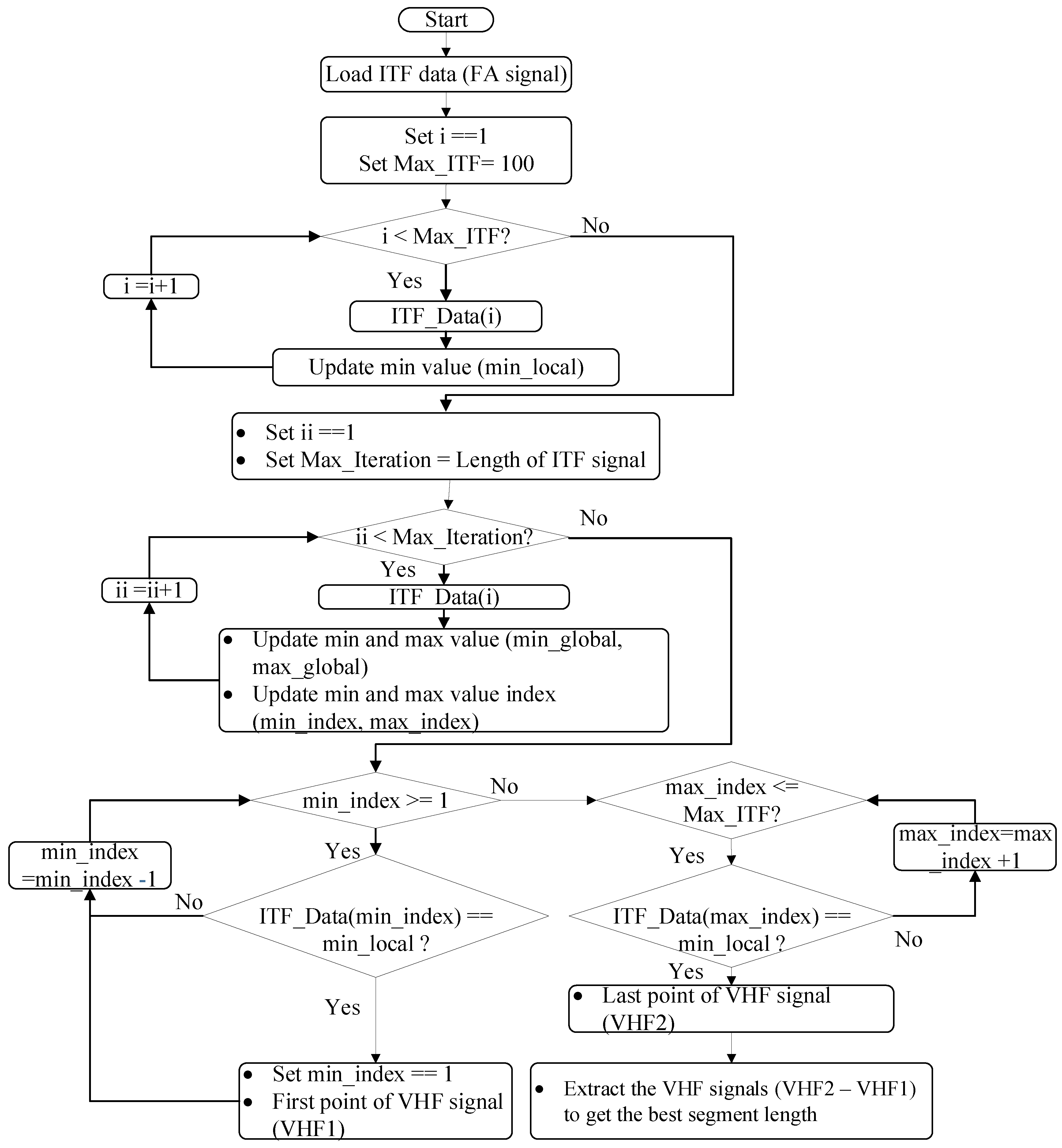
Evaluation of the Lightning Event Extraction Method
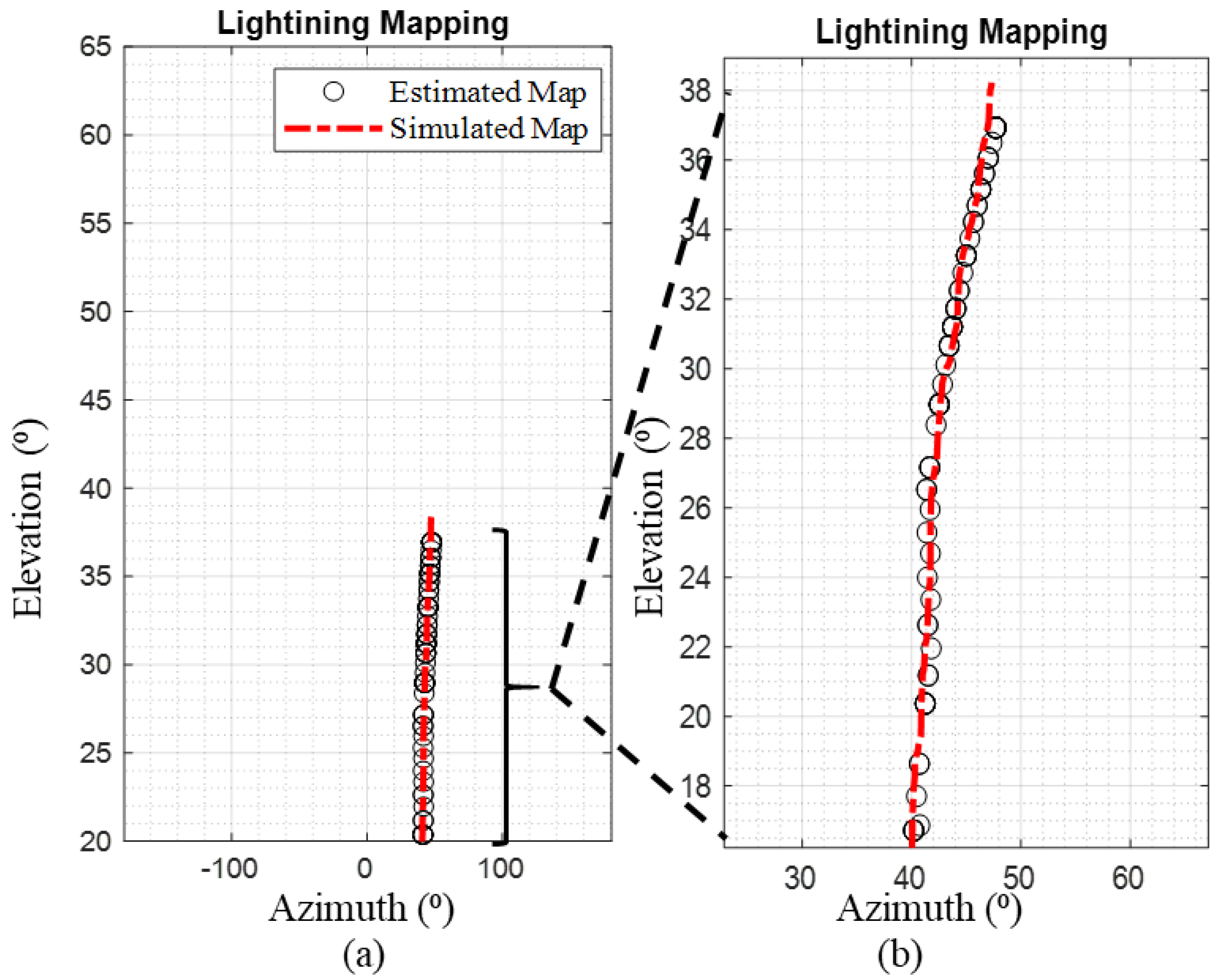
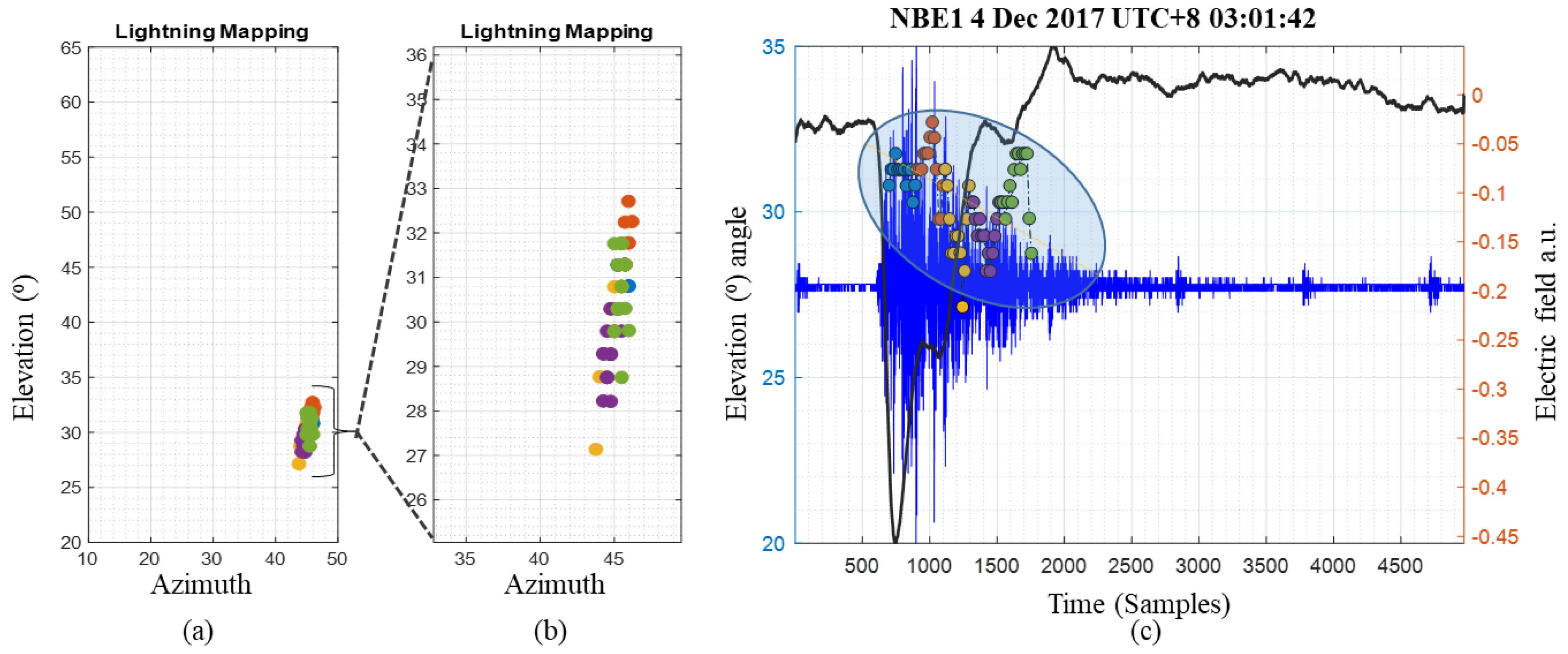
3.3. Lightning Mapping Optimization
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alammari, A.; Alkahtani, A.A.; Ahmad, M.R.; Noman, F.M.; Esa, M.R.M.; Kawasaki, Z.; Tiong, S.K. Lightning Mapping: Techniques, Challenges, and Opportunities. IEEE Access 2020, 8, 190064–190082. [Google Scholar] [CrossRef]
- Rison, W.; Thomas, R.J.; Krehbiel, P.R.; Hamlin, T.; Harlin, J. A GPS-based Three-Dimensional Lightning Mapping System: Initial Observations in Central New Mexico W. Geophys. Res. Lett. 1999, 26, 3573–3576. [Google Scholar] [CrossRef] [Green Version]
- Alammari, A.; Alkahtani, A.A.; Ahmad, M.R.; Noman, F.; Esa, M.R.M.; Sabri, M.H.M.; Mohammad, S.A.; Al-Khaleefa, A.S.; Kawasaki, Z.; Agelidis, V. Kalman Filter and Wavelet Cross-Correlation for VHF Broadband Interferometer Lightning Mapping. Appl. Sci. 2020, 10, 4238. [Google Scholar] [CrossRef]
- Stock, M.G.; Akita, M.; Krehbiel, P.R.; Rison, W.; Edens, H.E.; Kawasaki, Z.; A Stanley, M. Continuous broadband digital interferometry of lightning using a generalized cross-correlation algorithm. J. Geophys. Res. Atmos. 2014, 119, 3134–3165. [Google Scholar] [CrossRef]
- Akita, M.; Stock, M.; Kawasaki, Z.; Krehbiel, P.; Rison, W.; Stanley, M. Data processing procedure using distribution of slopes of phase differences for broadband VHF interferometer. J. Geophys. Res. Atmos. 2014, 119, 6085–6104. [Google Scholar] [CrossRef]
- Sun, Z.; Qie, X.; Liu, M.; Cao, D.; Wang, D. Lightning VHF radiation location system based on short-baseline TDOA—Validation in rocket-triggered lightning. Atmospheric Res. 2013, 129-130, 58–66. [Google Scholar] [CrossRef]
- Kawasaki, Z. Review of the Location of VHF Pulses Associated with Lightning Discharge. AerospaceLab 2012, 1, 1–7. [Google Scholar]
- Stock, M.; Krehbiel, P. Multiple baseline lightning interferometry—Improving the detection of low amplitude VHF sources. In Proceedings of the 2014 International Conference on Lightning Protection (ICLP), Shanghai, China, 11–18 October 2014; pp. 293–300. [Google Scholar]
- Cuturi, M.; Fukumizu, K. Kernels on structured objects through nested histograms. Adv. Neural Inf. Process. Syst. 2007, 336, 329–336. [Google Scholar]
- Shaw, R.; Srivastava, S. Particle swarm optimization: A new tool to invert geophysical data. Geophysics 2007, 72, F75–F83. [Google Scholar] [CrossRef]
- Liang, R.-H.; Tsai, S.-R.; Chen, Y.-T.; Tseng, W.-T. Optimal power flow by a fuzzy based hybrid particle swarm optimization approach. Electr. Power Syst. Res. 2011, 81, 1466–1474. [Google Scholar] [CrossRef]
- Zheng, D.; Zhang, Y.; Lu, W.; Zhang, Y.; Dong, W.; Chen, S.; Dan, J. Optical and electrical observations of an abnormal triggered lightning event with two upward propagations. Acta Meteorol. Sin. 2012, 26, 529–540. [Google Scholar] [CrossRef]
- Song, X.; Tang, L.; Lv, X.; Fang, H.; Gu, H. Application of particle swarm optimization to interpret Rayleigh wave dispersion curves. J. Appl. Geophys. 2012, 84, 1–13. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, S.; Lu, W.; Zheng, D.; Dong, W.; Li, B.; Chen, S.; Zhang, Y.; Chen, L. Experiments of artificially triggered lightning and its application in Conghua, Guangdong, China. Atmos. Res. 2014, 135–136, 330–343. [Google Scholar] [CrossRef]
- Abido, M. Optimal power flow using particle swarm optimization. Int. J. Electr. Power Energy Syst. 2002, 24, 563–571. [Google Scholar] [CrossRef]
- Zheng, D.; Zhang, Y.; Zhang, Y.; Lu, W.; Yan, X.; Chen, S.; Xu, L.; Huang, Z.; You, J.; Zhang, R.; et al. Characteristics of the initial stage and return stroke currents of rocket-triggered lightning flashes in southern China. J. Geophys. Res. Atmos. 2017, 122, 6431–6452. [Google Scholar] [CrossRef]
- Aydilek, I.B. A hybrid firefly and particle swarm optimization algorithm for computationally expensive numerical problems. Appl. Soft Comput. J. 2018, 66, 232–249. [Google Scholar] [CrossRef]
- Ramarao, G.; Chandrasekaran, K. Use of PSO to determine lightning channelbase-current function parameters for standard severe negative first and subsequent return stroke approximation. IET Sci. Meas. Technol. 2019, 13, 42–52. [Google Scholar] [CrossRef]
- Alyasseri, Z.A.A.; Khader, A.T.; Al-Betar, M.A.; Abasi, A.K.; Makhadmeh, S.N. EEG Signals Denoising Using Optimal Wavelet Transform Hybridized with Efficient Metaheuristic Methods. IEEE Access 2020, 8, 10584–10605. [Google Scholar] [CrossRef]
- Freitas, D.; Lopes, L.G.; Morgado-Dias, F. Particle Swarm Optimisation: A Historical Review Up to the Current Developments. Entropy 2020, 22, 362. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, Z.; Wen, Y.; Zhao, W.; Zhu, H. Particle swarm optimization-based algorithm for lightning location estimation. In Proceedings of the 2010 Sixth International Conference on Natural Computation, Yantai, China, 10–12 August 2010; Volume 5, pp. 2668–2672. [Google Scholar] [CrossRef]
- Guo, X.; Zhu, Y.; Chen, H.; Zhao, L.; Chen, X.; Gao, Y. Research and Validation of Lightning Location Based on Particle Swarm Optimization Algorithm. In Proceedings of the 2015 International Conference on Intelligent Systems Research and Mechatronics Engineering, Zhengzhou, China, 11–13 April 2015; Volume 121, pp. 815–818. [Google Scholar] [CrossRef] [Green Version]
- Fan, X.; Yao, W.; Zhang, Y.; Xu, L.; Zhang, Y.; Krehbiel, P.R.; Zheng, D.; Liu, H.; Lyu, W.; Chen, S.; et al. Parametric Reconstruction Method for the Long Time-Series Return-Stroke Current of Triggered Lightning Based on the Particle Swarm Optimization Algorithm. IEEE Access 2020, 8, 115133–115147. [Google Scholar] [CrossRef]
- Mohammad, S.A.; Ahmad, M.R.; Alkahtani, A.A.; Esa, M.R.; Sidik, M.A.; Nawawi, Z.; Jambak, M.I.; Baharin, S.A.; Sabri, M.H.; Yusop, N.; et al. The evaluation of parallel plate antenna with variation of air gaps separation and copper plate area. Test Eng. Manag. 2019, 81, 5663–5670. [Google Scholar]
- Abeywardhana, R.; Sonnadara, U.; Abegunawardana, S.; Fernando, M.; Cooray, V. Lightning Localization Based on VHF Broadband Interferometer Developed in Sri Lanka. In Proceedings of the 2018 34th International Conference on Lightning Protection (ICLP), Rzeszow, Poland, 2–7 September 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Zhang, H.; Gu, S.; Chen, J.; Zhao, C.; Wu, M.; Yan, B.; Wang, Y. Single-Station-Based Lightning Mapping System With Electromagnetic and Thunder Signals. IEEE Trans. Plasma Sci. 2019, 47, 1421–1428. [Google Scholar] [CrossRef]
- Ghazvinian, H.; Mousavi, S.-F.; Karami, H.; Farzin, S.; Ehteram, M.; Hossain, S.; Fai, C.M.; Bin Hashim, H.; Singh, V.P.; Ros, F.C.; et al. Integrated support vector regression and an improved particle swarm optimization-based model for solar radiation prediction. PLoS ONE 2019, 14, e0217634. [Google Scholar] [CrossRef] [PubMed]



| Parameters | Description |
|---|---|
| 0.9 | |
| 0.4 | |
| Acceleration coefficients and | 2 |
| Initial window size (Ws) | = 512, = 100, initial 256 |
| No of population | 2 |
| Number of iterations | 100, 200, 300, and 500 |
| Cross-correlation wavelet domain | CCWD |
| Parameters | Sampling Ratio | Iteration Sets | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 100 Iteration | 200 Iteration | 300 Iteration | 500 Iteration | ||||||
| Linear | Cubic | Linear | Cubic | Linear | Cubic | Linear | Cubic | ||
| Window size (Ws) | 4 | 282.71 | 446.33 | 290.41 | 446 | 282.55 | 425.56 | 282.46 | 419.72 |
| 8 | 457.50 | 446.82 | 544.86 | 451.55 | 466.08 | 452.43 | 466.63 | 451.24 | |
| Objective function | 4 | 0.6243 | 0.7702 | 0.6328 | 0.7944 | 0.6243 | 0.7913 | 0.6243 | 0.7923 |
| 8 | 0.7829 | 0.7271 | 0.7940 | 0.7273 | 0.7836 | 0.7325 | 0.7836 | 0.7273 | |
| NBE | Higher Altitude | Elevation | Captured time | OV | Ws | Length | Time Window | Lightning Event Extraction Method | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Event Start | Event End | Segment Length | ||||||||
| +NBE1 | (15°~66°) | (25°~32°) | 4 December 2017, UTC+8 03:01:42 | 32 | 282 | 4500 | 18 µs | 4596 | 7164 | 2568 |
| +NBE2 | (15°~80°) | (22°~29°) | 4 December 2017, UTC+8 03:21:13 | 32 | 282 | 5000 | 20 µs | 4695 | 7877 | 3218 |
| +NBE3 | (15°~80°) | (23°~30.5°) | 13 December 2017, UTC+8 5:08:16 | 32 | 282 | 4500 | 19 µs | 4520 | 6840 | 2320 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alammari, A.; Alkahtani, A.A.; Ahmad, M.R.; Aljanad, A.; Noman, F.; Kawasaki, Z. Cross-Correlation Wavelet-Domain-Based Particle Swarm Optimization for Lightning Mapping. Appl. Sci. 2021, 11, 8634. https://doi.org/10.3390/app11188634
Alammari A, Alkahtani AA, Ahmad MR, Aljanad A, Noman F, Kawasaki Z. Cross-Correlation Wavelet-Domain-Based Particle Swarm Optimization for Lightning Mapping. Applied Sciences. 2021; 11(18):8634. https://doi.org/10.3390/app11188634
Chicago/Turabian StyleAlammari, Ammar, Ammar Ahmed Alkahtani, Mohd Riduan Ahmad, Ahmed Aljanad, Fuad Noman, and Zen Kawasaki. 2021. "Cross-Correlation Wavelet-Domain-Based Particle Swarm Optimization for Lightning Mapping" Applied Sciences 11, no. 18: 8634. https://doi.org/10.3390/app11188634
APA StyleAlammari, A., Alkahtani, A. A., Ahmad, M. R., Aljanad, A., Noman, F., & Kawasaki, Z. (2021). Cross-Correlation Wavelet-Domain-Based Particle Swarm Optimization for Lightning Mapping. Applied Sciences, 11(18), 8634. https://doi.org/10.3390/app11188634






